| Issue |
A&A
Volume 496, Number 1, March II 2009
|
|
|---|---|---|
| Page(s) | 207 - 216 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:200811229 | |
| Published online | 20 January 2009 | |
Magneto-thermal evolution of neutron stars
J. A. Pons1 - J. A. Miralles1 - U. Geppert2
1 - Departament de Física Aplicada, Universitat d'Alacant,
Ap. Correus 99, 03080 Alacant, Spain
2 -
German Aerospace Center, Institute for Space Systems, Rutherfordstr. 2, 12489 Berlin, Germany
Received 27 October 2008 / Accepted 14 December 2008
Abstract
Context. The presence of magnetic fields in the crust of neutron stars (NSs) causes a non-spherically symmetric temperature distribution. The strong temperature dependence of the magnetic diffusivity and thermal conductivity, together with the heat generated by magnetic dissipation, couple the magnetic and thermal evolution of NSs, which can no longer be formulated as separated one-dimensional problems.
Aims. We study the mutual influence of thermal and magnetic evolution in a neutron star's crust in axial symmetry. Taking realistic microphysical inputs into account, we find the heat released by Joule effect consistent with the circulation of currents in the crust, and we incorporate its effects in 2D cooling calculations.
Methods. We solve the induction equation numerically using a hybrid method (spectral in angles, but a finite-differences scheme in the radial direction), coupled to the thermal diffusion equation. To improve the boundary conditions, we also revisit the envelope stationary solutions updating the well known
![]() -relations to include the effect of 2D heat transfer calculations and new microphysical inputs.
-relations to include the effect of 2D heat transfer calculations and new microphysical inputs.
Results. We present the first longterm 2D simulations of the coupled magneto-thermal evolution of neutron stars. This substantially improves previous works in which a very crude approximation in at least one of the parts (thermal or magnetic diffusion) has been adopted. Our results show that the feedback between Joule heating and magnetic diffusion is strong, resulting in a faster dissipation of the stronger fields during the first
105-106 years of an NS's life. As a consequence, all neutron stars born with fields over a critical value (>
![]() G) reach similar field strengths (
G) reach similar field strengths (![]()
![]() G) at late times. Irrespective of the initial magnetic field strength, the temperature becomes so low after 106 years that the magnetic diffusion timescale becomes longer than the typical ages of radiopulsars, thus apparently resulting in no dissipation of the field in old NS. We also confirm the strong correlation between the magnetic field and the surface temperature of relatively young NSs discussed in preliminary works. The effective temperature of models with strong internal toroidal components are systematically higher than those of models with purely poloidal fields, due to the additional energy reservoir stored in the toroidal field that is gradually released as the field dissipates.
G) at late times. Irrespective of the initial magnetic field strength, the temperature becomes so low after 106 years that the magnetic diffusion timescale becomes longer than the typical ages of radiopulsars, thus apparently resulting in no dissipation of the field in old NS. We also confirm the strong correlation between the magnetic field and the surface temperature of relatively young NSs discussed in preliminary works. The effective temperature of models with strong internal toroidal components are systematically higher than those of models with purely poloidal fields, due to the additional energy reservoir stored in the toroidal field that is gradually released as the field dissipates.
Key words: stars: neutron - stars: evolution - stars: magnetic fields
1 Introduction
The neutron star (NS) magnetic field (MF) maintained by electric currents circulating in the crust modifies the crustal temperature distribution by means of two mechanisms. The first one stems from the anisotropy of thermal conductivity in presence of a strong MF and causes important changes in how heat flux flows from the core through the crust and envelope up to the surface. The second mechanism is the generation of heat caused by MF dissipation that results in a non-spherically symmetric allocation of heating sources. Therefore, besides its tensorial character due to the presence of the MF (which eventually results in the Hall drift of the field), the magnetic diffusivity becomes a non-spherically symmetric quantity. Under these conditions, an initially purely dipolar field evolves very quickly in a magnetized NS to generate a complex structure including toroidal fields and/or higher order multipoles. Different studies of magneto-hydrostatic equilibrium configurations indicate that stable configurations require both toroidal and poloidal components (see e.g. Reisenegger 2008, and references therein).
The complexity of the problem has limited previous works
to partial studies of the complete problem.
The anisotropic heat flux and its consequences for the - in principle observable -
surface temperature (![]() )
distribution has been considered by
Geppert et al. (2006,2004) and Pérez-Azorín et al. (2006b,a), but for
fixed, prescribed MF.
The longterm effect of Joule heating has also been recently discussed by
Pons et al. (2007); Aguilera et al. (2008c) or Urpin & Konenkov (2008)
(see also references therein), although in a very crude approach.
In Aguilera et al. (2008b) a full 2D cooling code
is used to describe the temperature evolution, but the Joule heating rate is estimated
by an analytical approximation and considered to be uniform. In Urpin & Konenkov (2008)
the former results of Miralles et al. (1998) are revisited in the context
of high field radio-pulsars, but with the simplified approach of considering the
diffusion of a one-mode (dipolar) poloidal field, without actually performing consistent
simulations, including the temperature evolution.
On the other hand, the evolution of the MF including
the influence of the Hall term at early times has been studied
in Pons & Geppert (2007). The Hall drift causes a somewhat faster dissipation for
strong initial fields due to the reorganization of the field on smaller scales.
In this work the temporal evolution of the temperature
has been prescribed according to a generally accepted cooling law
and assumed to be the same in the whole crust. The effect of ambipolar
diffusion in the liquid core can also be relevant, as recently studied
for example in Hoyos et al. (2008).
)
distribution has been considered by
Geppert et al. (2006,2004) and Pérez-Azorín et al. (2006b,a), but for
fixed, prescribed MF.
The longterm effect of Joule heating has also been recently discussed by
Pons et al. (2007); Aguilera et al. (2008c) or Urpin & Konenkov (2008)
(see also references therein), although in a very crude approach.
In Aguilera et al. (2008b) a full 2D cooling code
is used to describe the temperature evolution, but the Joule heating rate is estimated
by an analytical approximation and considered to be uniform. In Urpin & Konenkov (2008)
the former results of Miralles et al. (1998) are revisited in the context
of high field radio-pulsars, but with the simplified approach of considering the
diffusion of a one-mode (dipolar) poloidal field, without actually performing consistent
simulations, including the temperature evolution.
On the other hand, the evolution of the MF including
the influence of the Hall term at early times has been studied
in Pons & Geppert (2007). The Hall drift causes a somewhat faster dissipation for
strong initial fields due to the reorganization of the field on smaller scales.
In this work the temporal evolution of the temperature
has been prescribed according to a generally accepted cooling law
and assumed to be the same in the whole crust. The effect of ambipolar
diffusion in the liquid core can also be relevant, as recently studied
for example in Hoyos et al. (2008).
One of the causes of complex MF geometries in the crust is the non-spherically symmetric
magnetic diffusivity. It is effective even if the Hall drift is negligible.
Since the temperature within the crust is no longer uniform,
the magnetic diffusivity in this approach
becomes a function of both the radial and the polar coordinates, thus
rendering the one-mode approximation inappropriate.
Up to now, the effect of the dependence of the magnetic diffusivity on the polar
angle ![]() (if axial symmetry is assumed) has not been considered.
In some studies about cooling of NSs, the source term in the thermal diffusion equation
includes an angular-averaged Joule heating rate,
where the heat production is uniform in spherical shells at a given radius r
(Aguilera et al. 2008c; Page et al. 2000; Urpin & Konenkov 2008). These are not fully consistent calculations,
because the currents can be very intense locally and release heat in a highly non-spherically
symmetric
way. Therefore, it is important to attack the problem of the full magneto-thermal
evolution of NSs by solving simultaneously the induction equation and the heat transfer
equation, taking into account the anisotropy of the thermal conductivity and the electrical
resistivity tensors in a consistent way. This is the main goal of this paper, in which we
solve this problem (in axial symmetry) for the first time.
The aim is to provide a self-consistent model for the coupled
evolution of the MF and temperature in axially symmetric NSs, in general relativity,
and including the effect of angular variations of temperature in the magnetic
diffusivity and the thermal conductivity.
We also revisit the envelope stationary solutions, while updating
the well known
(if axial symmetry is assumed) has not been considered.
In some studies about cooling of NSs, the source term in the thermal diffusion equation
includes an angular-averaged Joule heating rate,
where the heat production is uniform in spherical shells at a given radius r
(Aguilera et al. 2008c; Page et al. 2000; Urpin & Konenkov 2008). These are not fully consistent calculations,
because the currents can be very intense locally and release heat in a highly non-spherically
symmetric
way. Therefore, it is important to attack the problem of the full magneto-thermal
evolution of NSs by solving simultaneously the induction equation and the heat transfer
equation, taking into account the anisotropy of the thermal conductivity and the electrical
resistivity tensors in a consistent way. This is the main goal of this paper, in which we
solve this problem (in axial symmetry) for the first time.
The aim is to provide a self-consistent model for the coupled
evolution of the MF and temperature in axially symmetric NSs, in general relativity,
and including the effect of angular variations of temperature in the magnetic
diffusivity and the thermal conductivity.
We also revisit the envelope stationary solutions, while updating
the well known
![]() -relations to include the effect of 2D heat transfer
calculations and new advances in microphysical ingredients (phonons, ion-ion interactions).
We provide new fits to solutions of the equilibrium magnetic envelope that can be used
as boundary conditions in multidimensional cooling simulations.
-relations to include the effect of 2D heat transfer
calculations and new advances in microphysical ingredients (phonons, ion-ion interactions).
We provide new fits to solutions of the equilibrium magnetic envelope that can be used
as boundary conditions in multidimensional cooling simulations.
The paper is organized as follows. In the next section we derive and present the basic equations together with the boundary conditions. Next we describe the input microphysics and discuss the effect of superfluid neutrons on the heat flux anisotropy. The next section is devoted to presenting the magneto-thermal evolution. Finally we discuss the results by comparing them with observable consequences.
2 Basic equations
The thermal evolution of the NS is calculated using the code described in Aguilera et al. (2008b). For the evolution of the MF we basically follow the formalism already used in Pons & Geppert (2007). We address the interested reader to these references for more details about the cooling code and the MF evolution code that we have merged and coupled to perform the simulations presented later in this paper. In the next sections we just summarize the basic equations that are solved with the purpose of introducing notation and for the sake of completeness.
2.1 Heat transfer equation
Assuming that deformations with respect to the spherically symmetric case due
to rotation, MF, and temperature distribution do not affect
the metric in the interior of an NS, we use the standard static metric
where
where
where
2.2 The induction equation
The Maxwell equations (in the Gaussian system) relative to an observer at rest (Eulerian observer)
for the static metric given by Eq. (1) are
where again the differential operators are defined according to the spatial coordinate system,
In the comoving frame, which corresponds to the Eulerian frame, since matter is at rest,
electric field and density current are related through Ohm's law. This
law establishes a proportionality between the current and the electric field, which can be written
as
![]() ,
,
![]() being the electric conductivity. In the presence of strong
MFs,
being the electric conductivity. In the presence of strong
MFs, ![]() becomes a tensor and Ohm's law must be
written as
becomes a tensor and Ohm's law must be
written as
![]() or equivalently
or equivalently
![]() ,
where
,
where
![]() is the resistivity tensor.
This tensor can be decomposed in symmetric and antisymmetric parts (Landau & Lifshitz 1960).
The symmetric part, for nonquantizing fields is isotropic and determined by the scalar
is the resistivity tensor.
This tensor can be decomposed in symmetric and antisymmetric parts (Landau & Lifshitz 1960).
The symmetric part, for nonquantizing fields is isotropic and determined by the scalar
![]() ,
where
,
where
![]() is the electric conductivity
in the direction of the MF. The antisymmetric part of the resistivity tensor can
be represented by a vector proportional to
is the electric conductivity
in the direction of the MF. The antisymmetric part of the resistivity tensor can
be represented by a vector proportional to ![]() .
The electric field
.
The electric field ![]() is then written in the form (Ziman 1979)
is then written in the form (Ziman 1979)
where
If we neglect the displacement current term in the Ampère-Maxwell equation
(second equation in 4), and make use of Eq. (5), the Faraday induction
equation (fourth equation in 4) can be written as
where we have introduced the magnetic diffusivity
There are two main differences from the induction equation employed in Pons & Geppert (2007): the relativistic factors are included and the magnetic diffusivity is not assumed to be spherically symmetric.
Since both ![]() and the metric factor
and the metric factor
![]() only depend on the radial coordinate
(it is justified to neglect the structural deformations induced by MFs), the nonlinear Hall term
can be treated in the same way as done by Pons & Geppert (2007).
However, the magnetic diffusivity through its temperature dependence
also depends on the polar angle,
only depend on the radial coordinate
(it is justified to neglect the structural deformations induced by MFs), the nonlinear Hall term
can be treated in the same way as done by Pons & Geppert (2007).
However, the magnetic diffusivity through its temperature dependence
also depends on the polar angle,
![]() ,
thus requiring an extension of
the previous formalism.
The influence of the Hall term at early times has been studied
in Pons & Geppert (2007), resulting in a somewhat faster dissipation for
strong initial fields due to the reorganization of the field on smaller scales.
The numerical treatment of the non-linear term is complex and very
computationally-limited.
In this paper our goal is to perform coupled (magneto-thermal) longterm simulations,
thus from now on we focus on the linear part of the induction equation.
,
thus requiring an extension of
the previous formalism.
The influence of the Hall term at early times has been studied
in Pons & Geppert (2007), resulting in a somewhat faster dissipation for
strong initial fields due to the reorganization of the field on smaller scales.
The numerical treatment of the non-linear term is complex and very
computationally-limited.
In this paper our goal is to perform coupled (magneto-thermal) longterm simulations,
thus from now on we focus on the linear part of the induction equation.
The linear part of the induction Eq. (6) reads
We decompose the MF into its poloidal and toroidal part (Rädler et al. 2001)
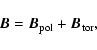 |
(8) |
and use their representation in terms of two scalar functions
We now expand the functions
where Yn is the spherical harmonic Ynm for m=0.
The poloidal and toroidal parts of the MF can be written as
where
and
If
2.3 Microphysics
The microphysical ingredients that enter into the heat transport and induction equation are the specific heat, the thermal conductivity, the neutrino emissivity, and the magnetic diffusivity. In the solid crust, the dominant contribution to the specific heat is that from electrons and ions, while electrons, lattice phonons, and collective modes of superfluid neutrons contribute to the thermal conductivity. We refer the reader to a detailed description of the employed equations of state, the thermal conductivity, the specific heat, and the neutrino emissivities, given in Sect. 4 of Aguilera et al. (2008b). In this paper we assume the minimal cooling scenario (Page et al. 2004) which includes neutrino emission from the Cooper pair breaking and formation process, but we do not take any direct Urca process into account, due either to nucleons or to exotic matter (hyperons, Bose condensates, or deconfined quarks).
In addition, it has been shown by Chugunov & Haensel (2007) that the ionic contribution
to the total thermal conductivity
is negligible in the crust, but it may play a role for low temperatures in the envelope.
Very recently (Aguilera et al. 2008a) have studied the possible effects of
collective modes of superfluid neutrons.
They found that this process may dominate the thermal conductivity in the inner
crust when its temperature is ![]() 107 K. For such relatively old NSs, heat
transport by superfluid neutrons counteracts the anisotropy in the electron
conductivity caused by a strong crustal field and, eventually,
turns the inner crust isothermal.
In this work we have updated our microphysics and also
included these two new contributions to the thermal conductivity.
107 K. For such relatively old NSs, heat
transport by superfluid neutrons counteracts the anisotropy in the electron
conductivity caused by a strong crustal field and, eventually,
turns the inner crust isothermal.
In this work we have updated our microphysics and also
included these two new contributions to the thermal conductivity.
The only relevant contributions to the electrical resistivity are electron-phonon
and electron-impurity collisions (Flowers & Itoh 1976).
While the efficiency of electron-phonon collisions strongly depends
on the crustal temperature, the electron-impurity scattering is much less sensitive to it.
However, both processes may be strongly affected by the presence of a strong
MF that suppresses the conductivity components perpendicular to the field lines
(Canuto & Chiuderi 1970; Itoh 1975). As in Pons & Geppert (2007), we calculated the
electrical resistivity by using the electron relaxation time provided by Potekhin's
public code![]() .
We used an impurity concentration parameter of 0.1.
The definition of this parameter and a discussion about how it affects electronic
transport can be found in 5.1.1 of Pérez-Azorín et al. (2006a).
Jones (1999) has shown that disorder in the inner crust
could result in an impurity parameter
.
We used an impurity concentration parameter of 0.1.
The definition of this parameter and a discussion about how it affects electronic
transport can be found in 5.1.1 of Pérez-Azorín et al. (2006a).
Jones (1999) has shown that disorder in the inner crust
could result in an impurity parameter ![]() 10, which leads to higher electrical
resistivity and enhanced ohmic decay. However, this effect only becomes important
for sufficiently cool NSs.
10, which leads to higher electrical
resistivity and enhanced ohmic decay. However, this effect only becomes important
for sufficiently cool NSs.
2.4 Joule heating
Joule heating couples the thermal and magnetic evolution by contributing
to the source term ![]() in Eq. (2), which for large fields can result
in a higher temperature and therefore a greater magnetic diffusivity. This feedback
may lead to a faster dissipation of the MF if it is strong enough to really
alter the temperature of the crust.
In this paper, Joule heating is consistently taken into account
in a cooling simulation for the first time.
As the MF evolves in time, we compute the local values of the electrical current density
at each point of the computational grid, which is simply
in Eq. (2), which for large fields can result
in a higher temperature and therefore a greater magnetic diffusivity. This feedback
may lead to a faster dissipation of the MF if it is strong enough to really
alter the temperature of the crust.
In this paper, Joule heating is consistently taken into account
in a cooling simulation for the first time.
As the MF evolves in time, we compute the local values of the electrical current density
at each point of the computational grid, which is simply
| (14) |
The corresponding components of the current density are
We evaluate the heating source term by
where
which is easily interpreted. If we integrate over the whole volume, the magnetic energy losses are caused by Joule heating and Poynting flux through the boundaries. This latter term vanishes since we do not consider the possibility of having electromagnetic waves (i.e. we neglect displacement currents).
2.5 Magnetic boundary conditions
Since we restrict ourselves to MF configurations confined to the crust,
the inner boundary conditions are determined by the requirement that
the normal component of the MF and the tangential components of the electric field
has to vanish at
![]() .
This is a consequence of the assumption
that the core is in a superconducting state and the Meissner-Ochsenfeld effect
prevents the MF from penetrating. Therefore we apply the following boundary conditions
at
.
This is a consequence of the assumption
that the core is in a superconducting state and the Meissner-Ochsenfeld effect
prevents the MF from penetrating. Therefore we apply the following boundary conditions
at
![]() :
:
A detailed derivation is given in Pons & Geppert (2007). In the limit of vanishing Hall-drift this reduces to
For the outer BC we require all components of the MF to be
continuous across
![]() to match the relativistic vacuum solution. Hence,
let us first consider the stationary solution for outer space. In the absence
of external currents, the toroidal component of the MF must vanish, and each
multipole of the poloidal field must satisfy (in the stationary case)
to match the relativistic vacuum solution. Hence,
let us first consider the stationary solution for outer space. In the absence
of external currents, the toroidal component of the MF must vanish, and each
multipole of the poloidal field must satisfy (in the stationary case)
where z=2 G M/c2 r, which corresponds to the compactness parameter at
This second-order differential equation has analytical solutions for each
value of n, although they cannot be written in a closed analytic
form valid for any n. For example, for n=1 and n=2 we have
![\begin{displaymath}\Phi_1 = C_1 r^2 \left[ \ln(1-z)
+ z + \frac{z^2}{2}\right] + C_2 r^2
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img90.gif) |
(21) |
![\begin{displaymath}\Phi_2 = C_1 r^3 \left[ (4-3z) \ln(1-z)
+ 4z - {z^2} - \frac{z^3}{6}\right] + C_2 r^3 (4-3z)
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img91.gif) |
(22) |
where C1 and C2 are arbitrary integration constants that must be fixed according to the value of the magnetic multipole moments. Regularity of the external solution at
Note that regularity at
For practical reasons, we write the outer boundary conditions
at
![]() as
as
where fn is a relativistic factor that only depends on the compactness ratio
3 Thermal boundary conditions: blanketing envelopes revisited
The very different thermal relaxation timescales of the envelope and the crust
of NSs makes any attempt to perform cooling simulations
in a numerical grid that includes both regions simultaneously computationally expensive.
Since radiative equilibrium is established in the low-density region much faster
than the crust evolves, the usual approach is to use
results of stationary, plane-parallel, envelope models to obtain a phenomenological fit
that relates the temperature at the bottom of the envelope ![]() ,
with the surface
temperature
,
with the surface
temperature ![]() .
This
.
This
![]() phenomenological function
is used to implement boundary
conditions, because it allows the calculation of the surface flux for a given temperature at
the base of the envelope. The location of
phenomenological function
is used to implement boundary
conditions, because it allows the calculation of the surface flux for a given temperature at
the base of the envelope. The location of
![]() is generally chosen to correspond to some density between the neutron drip point
is generally chosen to correspond to some density between the neutron drip point
![]() g cm-3 and
g cm-3 and
![]() g cm-3.
Examples of such models of magnetized envelopes have been constructed by Potekhin & Yakovlev (2001)
and later upgraded in Potekhin et al. (2007) to include the effect of the neutrino
emissivity in the outer crust.
They derived an analytic form of the
g cm-3.
Examples of such models of magnetized envelopes have been constructed by Potekhin & Yakovlev (2001)
and later upgraded in Potekhin et al. (2007) to include the effect of the neutrino
emissivity in the outer crust.
They derived an analytic form of the
![]() relation that reads
relation that reads
where
![\begin{displaymath}T_{\rm s}^{(0)} \approx 10^6 ~
g_{14}^{1/4}\left[(7\zeta)^{2.25}+(\zeta/3)^{1.25}\right]^{1/4}~~{\rm K},
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img101.gif) |
(27) |
and
The function
![]() has been fitted by
decomposing into transversal and longitudinal parts as
has been fitted by
decomposing into transversal and longitudinal parts as
where
where B12=B in units of 1012 G. These fits are valid for B < 1016 G and
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1229fig1.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg113.gif) |
Figure 1:
Surface temperature as a function of temperature at the neutron drip
point for two models of NS envelopes with different MF strengths.
The thin dashed lines are the analytical fits from (Potekhin & Yakovlev 2001) for
MF parallel ( |
| Open with DEXTER | |
To avoid solving the hydrostatic equilibrium equations in two dimensions, we have
built a spherically symmetric iron envelope model with a zero temperature equation
of state. With this fixed background, we calculated stationary solutions of
the heat transport equation in 2D, with a given MF geometry (dipole solution).
At first glance, this may seem inaccurate, since finite temperature
effects may be relevant at low density but, as explained in Gudmundsson et al. (1983),
the main regulator of the
![]() -relation is the sensitivity strip where the
opacity is maximum. This strip marks the transition from electronic heat transfer
to the radiation-dominated one. It lies at relatively high densities except for very
low temperatures. Hence, structural changes at low density do not affect the
solution, even for extreme cases such as a condensed surface (Potekhin et al. 2007).
To test the validity of this assumption and to compare with previous works,
we have taken the crustal MF to be either purely
radial (labelled
-relation is the sensitivity strip where the
opacity is maximum. This strip marks the transition from electronic heat transfer
to the radiation-dominated one. It lies at relatively high densities except for very
low temperatures. Hence, structural changes at low density do not affect the
solution, even for extreme cases such as a condensed surface (Potekhin et al. 2007).
To test the validity of this assumption and to compare with previous works,
we have taken the crustal MF to be either purely
radial (labelled ![]() ,
parallel to the normal to the surface)
or purely tangential to the surface (labelled
,
parallel to the normal to the surface)
or purely tangential to the surface (labelled ![]() ).
In these two limiting cases, the heat flux is purely radial, and we have reproduced
within a 5% the
).
In these two limiting cases, the heat flux is purely radial, and we have reproduced
within a 5% the
![]() relation given by Potekhin & Yakovlev (2001) if
neutrino emissivities are not considered. The minor
differences are probably due to the different EOS or NS model; i.e., our neutron
drip point is at
relation given by Potekhin & Yakovlev (2001) if
neutrino emissivities are not considered. The minor
differences are probably due to the different EOS or NS model; i.e., our neutron
drip point is at
![]() g/cm3, while theirs is at
g/cm3, while theirs is at
![]() .
Our results for purely parallel or purely tangential
fields including the neutrino emissivity in the outer crust are compared to
the analytical fit from Potekhin & Yakovlev (2001) (without the effect of neutrino emissivity)
in Fig. 1. The agreement is very good in those cases where neutrino emission is not
important (low temperature).
Moreover, our results for radial and tangential MF can be directly compared
to Figs. 4 and 5 of Potekhin et al. (2007), in which neutrino emissivity effects are
considered. The very good agreement with this work indicates that the use of a
zero-temperature EOS for solving the hydrostatic equilibrium equation is a valid
approximation.
The same comment applies to the effects
of strong MF in the low-density EOS, as long as they are only noticeable at densities
where radiation dominates the heat transport.
Finally, to check the effect of using an EOS in which the
thermal contribution to the pressure is neglected to obtain the mechanical
structure of the envelope, we also recalculated some of the
models using new envelope structures obtained by solving the hydrostatic equilibrium
equations for a finite temperature
EOS and assuming the temperature profile of the previous models. We find the same
surface temperatures in both models (within a 1%), further confirming the validity of
our approach.
.
Our results for purely parallel or purely tangential
fields including the neutrino emissivity in the outer crust are compared to
the analytical fit from Potekhin & Yakovlev (2001) (without the effect of neutrino emissivity)
in Fig. 1. The agreement is very good in those cases where neutrino emission is not
important (low temperature).
Moreover, our results for radial and tangential MF can be directly compared
to Figs. 4 and 5 of Potekhin et al. (2007), in which neutrino emissivity effects are
considered. The very good agreement with this work indicates that the use of a
zero-temperature EOS for solving the hydrostatic equilibrium equation is a valid
approximation.
The same comment applies to the effects
of strong MF in the low-density EOS, as long as they are only noticeable at densities
where radiation dominates the heat transport.
Finally, to check the effect of using an EOS in which the
thermal contribution to the pressure is neglected to obtain the mechanical
structure of the envelope, we also recalculated some of the
models using new envelope structures obtained by solving the hydrostatic equilibrium
equations for a finite temperature
EOS and assuming the temperature profile of the previous models. We find the same
surface temperatures in both models (within a 1%), further confirming the validity of
our approach.
For 2D models, Fig. 1 shows our 2D transport results with a dipolar field.
The quoted value of the MF corresponds to the strength at the magnetic pole.
Our results confirm that the effect of ion/phonon transport in the envelope
is to reduce the large anisotropy obtained in previous magnetized models.
In addition,
by performing 2D heat transport calculations through the magnetized envelope,
we take into account the meridional heat fluxes driven by the meridional temperature
gradients between pole and equator, and we find that the anisotropy is further
reduced. This effect is more relevant for high fields, resulting in an equatorial
temperature about a factor 3 lower than the polar temperature, in contrast to
the 2-3 orders of magnitude obtained in previous models.
For practical purposes, we made fits of our results keeping a similar
functional form to Eq. (30), but only changing the form of
![]() and
and
![]() as follows:
as follows:
We find that this formula reproduces the correct numerical results for the
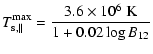 |
|||
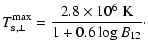 |
(32) |
It must be stressed that these upper limits are obtained by including the outer crust (
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1229fig2.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg126.gif) |
Figure 2:
Stationary 2D solutions of magnetized envelopes:
surface temperature profiles as a function of the polar angle for
|
| Open with DEXTER | |
4 Results
We present the results now of our numerical simulations of the magneto-thermal
evolution of NSs and its dependence on the initial MF structure and strength.
We restrict this presentation to a selection of the initial models described
in Aguilera et al. (2008b). Our model A at t=0 consists of a dipolar
(n=1) poloidal field according to Eq. (13) of Aguilera et al. (2008b), parameterized
by the value of the radial component at the magnetic pole, ![]() .
In model B
we add a quadrupolar (n=2) toroidal
component obeying Eq. (11) of Aguilera et al. (2008b) to the initial dipolar field, with a
maximum value of
.
In model B
we add a quadrupolar (n=2) toroidal
component obeying Eq. (11) of Aguilera et al. (2008b) to the initial dipolar field, with a
maximum value of ![]()
![]() .
This model represents the case
of a strong toroidal component confined in the crust.
We recall that we focus on the purely diffusive case in this paper, i.e., the Hall term
in the induction equation is neglected. This term needs a separate specific numerical
treatment that is out of the current capabilities of our code and will be discussed
in later work. Its influence can be important either at very early times or,
as we point out at the end of the section, at late times during the photon cooling era.
For most of the first
105-106 years of a NS life we do not expect qualitative
changes from our present results.
.
This model represents the case
of a strong toroidal component confined in the crust.
We recall that we focus on the purely diffusive case in this paper, i.e., the Hall term
in the induction equation is neglected. This term needs a separate specific numerical
treatment that is out of the current capabilities of our code and will be discussed
in later work. Its influence can be important either at very early times or,
as we point out at the end of the section, at late times during the photon cooling era.
For most of the first
105-106 years of a NS life we do not expect qualitative
changes from our present results.
To begin our discussion, we present in Fig. 3 the power spectra
for model A with three initial fields of
![]() ,
1014, and 1015 G at the age of
,
1014, and 1015 G at the age of
![]() years.
We see how the coupling between different modes due to the angular
dependence of
years.
We see how the coupling between different modes due to the angular
dependence of ![]() fills the shorter wavelength modes (initially only
the dipolar poloidal component n=1 is present). Only odd multipoles
are present because the initial model is symmetric with respect to the
equatorial plane.
At this age, the cascade has filled out all large wavenumber modes and is
saturated following an n-4 power law approximately for the cases with
large initial fields.
This result shows that, even if the influence of the nonlinear Hall
term is negligible, the thermo-magnetic coupled evolution results in a complex field geometry
that cannot be described by a single mode.
Although the dominant mode is still the dipole, the distribution of part of the energy
in higher order modes leads to a slightly faster dissipation.
fills the shorter wavelength modes (initially only
the dipolar poloidal component n=1 is present). Only odd multipoles
are present because the initial model is symmetric with respect to the
equatorial plane.
At this age, the cascade has filled out all large wavenumber modes and is
saturated following an n-4 power law approximately for the cases with
large initial fields.
This result shows that, even if the influence of the nonlinear Hall
term is negligible, the thermo-magnetic coupled evolution results in a complex field geometry
that cannot be described by a single mode.
Although the dominant mode is still the dipole, the distribution of part of the energy
in higher order modes leads to a slightly faster dissipation.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1229fig3.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg128.gif) |
Figure 3:
Power spectrum at
|
| Open with DEXTER | |
In Fig. 4 we show the crustal temperature distribution of a NS at different ages (t=10, 100 and 500 kyr), together with the poloidal field lines. The tendency of the surfaces of constant temperature to be aligned with the magnetic field lines discussed in Pérez-Azorín et al. (2006a) and Geppert et al. (2004) is clearly visible, but there is an important difference with respect to previous works. The consistent inclusion of the Joule heating source results in a larger energy deposition in the region where currents are more intense. In this particular model this happens at low latitudes, since the currents that maintain a poloidal field are toroidal. Thus more heat is released close to the equator. While the polar regions are always in thermal equilibrium with the core, the equator is insulated because of the reduced thermal conductivity across magnetic field lines. As a consequence, the heat released at early times in the equatorial region cannot flow across field lines into the core, where it would be rapidly lost by neutrino emission. It is only allowed to flow towards the surface along field lines. This modifies the traditionally accepted temperature distribution consisting of hot poles and a cooler equator (insulated from the warmer core). Instead we find that the equatorial region of the outer crust is actually warmer than the poles. In models with weak MFs, when the effect of Joule heating becomes less effective, the situation is inverted and the thermal distribution with hot polar caps is recovered. Notice the large difference between polar and equatorial temperatures, up to a factor of 2 at early times (the numbers next to the color scale indicate the maximum and minimum temperature at each evolutionary time), in contrast with the nearly isothermal crusts at late times.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{1229fig4.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg129.gif) |
Figure 4:
Temperature distribution in the crust of a NS (i.e. up to the bottom of
the envelope) at different
ages. The initial MF is purely poloidal with
(
|
| Open with DEXTER | |
We must recall that the anisotropy in ![]() (at the bottom of the envelope)
is not necessarily the same as that of
(at the bottom of the envelope)
is not necessarily the same as that of ![]() .
The blanketing effect of the
envelope, and/or atmospheric effects should be taken into account before a
comparison with observations. In Fig. 5 we plot the evolution of both
the temperature at the bottom of the envelope (top panel) and the surface
temperature (bottom panel) as a function of the polar angle.
.
The blanketing effect of the
envelope, and/or atmospheric effects should be taken into account before a
comparison with observations. In Fig. 5 we plot the evolution of both
the temperature at the bottom of the envelope (top panel) and the surface
temperature (bottom panel) as a function of the polar angle.
In Fig. 6, we show a sample of cooling curves (effective temperature versus
true age) for models A and B but varying the initial strength
of the field. For high fields the effect of Joule heating
is visible from the very beginning of the evolution. The effective temperature of a young,
t=103 yr magnetar with
![]() G is higher by a factor of 2 than that of a
NS with a standard
G is higher by a factor of 2 than that of a
NS with a standard
![]() G, and it is kept nearly
constant for a much longer time. The effect is further enhanced
in model B thanks to the extra energy stored in the toroidal field.
In spite of some quantitative differences, our improved simulations confirm the
qualitative results described in Aguilera et al. (2008c), where a phenomenological
MF decay law has been adopted. The most important difference is the somewhat higher
temperature reached in these models, when compared to Aguilera et al. (2008c).
The difference stems from the particular location of the heat dissipated
by the Joule effect in the regions where currents are intense, as opposed to
the homogeneous distribution of energy in the formerly adopted phenomenological
model.
G, and it is kept nearly
constant for a much longer time. The effect is further enhanced
in model B thanks to the extra energy stored in the toroidal field.
In spite of some quantitative differences, our improved simulations confirm the
qualitative results described in Aguilera et al. (2008c), where a phenomenological
MF decay law has been adopted. The most important difference is the somewhat higher
temperature reached in these models, when compared to Aguilera et al. (2008c).
The difference stems from the particular location of the heat dissipated
by the Joule effect in the regions where currents are intense, as opposed to
the homogeneous distribution of energy in the formerly adopted phenomenological
model.
In Fig. 7 we show the value of the MF at the pole as a function of time
for models A and B with different initial field strengths.
Naively, we can divide the models in two groups: strong initial
field
![]() G and weak initial field
G and weak initial field
![]() G.
The plot shows that models with strong initial fields are subject to a faster decay
than those with weaker fields.
Models with weak initial fields are subject to decay in a more or less similar manner. The
field typically decays in about a factor of two on a timescale of few 106 years and then
remains nearly constant, due to the increase in the magnetic diffusion timescale as the
star cools down.
G.
The plot shows that models with strong initial fields are subject to a faster decay
than those with weaker fields.
Models with weak initial fields are subject to decay in a more or less similar manner. The
field typically decays in about a factor of two on a timescale of few 106 years and then
remains nearly constant, due to the increase in the magnetic diffusion timescale as the
star cools down.
Models with initially large fields behave in a different way. Since the magnetic energy
stored in the crust is now large enough to significantly affect the thermal evolution
when it is steadily released by Joule heating, it results in a higher average temperature
of the crust. But this process
has a back-reaction: the higher temperatures imply higher resistivity and therefore faster
decay. Interestingly, at t>106 yr, all models with large poloidal initial fields seem
to converge to an asymptotic fiducial value of
![]() G, while
all models with strong toroidal fields converge to a lower value of
G, while
all models with strong toroidal fields converge to a lower value of
![]() G, because of the higher temperatures
reached on average during the evolution.
G, because of the higher temperatures
reached on average during the evolution.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1229fig5.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg134.gif) |
Figure 5:
Temperature profiles at the base of the envelope
( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1229fig6.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg138.gif) |
Figure 6:
Cooling curves. Effective temperature as a function of age
for different initial field strengths ( from bottom to top
|
| Open with DEXTER | |
![\begin{displaymath}\frac{\partial \vec{B}}{\partial t}= - \frac{c^2}{4\pi} \vec{...
...e}^{\nu}\vec{B})\right] \times \vec{e_{B}}~
\right\} \right) ,
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img141.gif) |
(33) |
where
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1229fig7.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg143.gif) |
Figure 7:
Evolution of the MF strength at the pole |
| Open with DEXTER | |
In this form, the interpretation of
![]() is straightforward: when the
magnetization parameter exceeds unity, the Hall drift term dominates.
The effect of the Hall drift term at early times has been discussed in detail in
(Pons & Geppert 2007). As a rule of thumb, when
is straightforward: when the
magnetization parameter exceeds unity, the Hall drift term dominates.
The effect of the Hall drift term at early times has been discussed in detail in
(Pons & Geppert 2007). As a rule of thumb, when
![]() ,
the effect
of the Hall drift significantly changes the evolution, while more moderate values
lead to a somewhat faster dissipation due to reorganization of the field in smaller
scales. Because of numerical limitations, in this work we have restricted ourselves
to the purely diffusive case, but it is worth looking at the evolution
of this parameter as shown in Fig. 8. Here we
show radial profiles of the magnetization parameter in the crust
for model A and three different initial values of
,
the effect
of the Hall drift significantly changes the evolution, while more moderate values
lead to a somewhat faster dissipation due to reorganization of the field in smaller
scales. Because of numerical limitations, in this work we have restricted ourselves
to the purely diffusive case, but it is worth looking at the evolution
of this parameter as shown in Fig. 8. Here we
show radial profiles of the magnetization parameter in the crust
for model A and three different initial values of ![]() .
The upper panel corresponds to t=104 yr and the lower panel to t=106 years.
At early times, the scaling of
.
The upper panel corresponds to t=104 yr and the lower panel to t=106 years.
At early times, the scaling of
![]() with
with ![]() is visible
and only in magnetars must one expect high values in the inner crust.
However, the back-reaction of the field evolution on the temperature has some
interesting implications. At late times, the temperature of low-field NSs is lower
than that of highly magnetized NS, so that the temperature dependence of the
electron relaxation time overcomes the effect of the MF, and it turns out
that the former magnetars are less magnetized than NSs born with moderate
fields. In addition, at ages of
is visible
and only in magnetars must one expect high values in the inner crust.
However, the back-reaction of the field evolution on the temperature has some
interesting implications. At late times, the temperature of low-field NSs is lower
than that of highly magnetized NS, so that the temperature dependence of the
electron relaxation time overcomes the effect of the MF, and it turns out
that the former magnetars are less magnetized than NSs born with moderate
fields. In addition, at ages of ![]() 106 yrs, the temperature is low enough
to ensure that the magnetization parameter is very large for all models studied,
especially in the inner crust (where the conductivity is higher). This opens up
more questions about the late evolution of NSs that is likely to be dominated
by the nonlinear Hall term in most NSs. In particular, the possibility of the
Hall instability (Rheinhardt & Geppert 2002) or implications on the evolution of the braking index
are worth exploring.
106 yrs, the temperature is low enough
to ensure that the magnetization parameter is very large for all models studied,
especially in the inner crust (where the conductivity is higher). This opens up
more questions about the late evolution of NSs that is likely to be dominated
by the nonlinear Hall term in most NSs. In particular, the possibility of the
Hall instability (Rheinhardt & Geppert 2002) or implications on the evolution of the braking index
are worth exploring.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1229fig8.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg145.gif) |
Figure 8:
Radial equatorial profiles of the magnetization parameter
|
| Open with DEXTER | |
5 Conclusions
We performed consistent 2D simulations of the coupled magneto-thermal
evolution of NSs for the first time, including realistic microphysical input and
general relativistic corrections. By properly taking the interplay of
the MF and temperature evolution into account in cooling simulations, we have
found that their mutual influence is important
and affects the outcome when the initial field strength is close to
or larger than a critical value of
![]() G.
It has effects on both the temperature and the field strength.
G.
It has effects on both the temperature and the field strength.
The average effective temperature of a NS born with
![]() is barely affected, while those born as magnetars are subject to significant
heating by the dissipation of currents in the crust. In addition, since
heating is locally important in the regions where currents are more intense,
the surface temperature distribution can be very different depending on
the field geometry. While the pole (or other regions in which the field
lines are nearly radial through the crust) is in thermal equilibrium with the
core and has its same temperature, regions in which the field lines are tangential
remain essentially thermally isolated. This can produce cooler areas if no
heating process is considered or, conversely, hotter regions if heating is
important. This is the case of poloidal fields, in which currents are located
near the equatorial region which remains warmer than the rest of
the crust during a long time. The effective temperature of
models with strong internal toroidal components are systematically higher than that
of models with purely poloidal fields, due to the additional energy reservoir stored
in the toroidal field that is gradually released as the field dissipates.
is barely affected, while those born as magnetars are subject to significant
heating by the dissipation of currents in the crust. In addition, since
heating is locally important in the regions where currents are more intense,
the surface temperature distribution can be very different depending on
the field geometry. While the pole (or other regions in which the field
lines are nearly radial through the crust) is in thermal equilibrium with the
core and has its same temperature, regions in which the field lines are tangential
remain essentially thermally isolated. This can produce cooler areas if no
heating process is considered or, conversely, hotter regions if heating is
important. This is the case of poloidal fields, in which currents are located
near the equatorial region which remains warmer than the rest of
the crust during a long time. The effective temperature of
models with strong internal toroidal components are systematically higher than that
of models with purely poloidal fields, due to the additional energy reservoir stored
in the toroidal field that is gradually released as the field dissipates.
In the models with stronger fields, and
as a result of the average higher temperatures,
the crustal electrical resistivity is enhanced and magnetic diffusion proceeds faster
during the first
105-106 years of a NS's life. As a consequence,
all NSs born with fields larger than a critical value (>
![]() G)
reach similar field strengths (
G)
reach similar field strengths (![]()
![]() G) at late times,
irrespective of the initial strength.
After 106 years the temperature is so low that the magnetic
diffusion timescale becomes longer than the typical ages of radiopulsars,
resulting in apparently no dissipation of the field in old NSs. We
confirm the strong correlation between the MF and the surface temperature
of relatively young NSs discussed in preliminary works.
If the MF of magnetars is caused by superconducting currents in the core
(as opposed to crustal currents), the longer diffusion timescale in the core
would allow magnetars to live much longer with their original large fields.
Thus, observations of magnetars can help to discern between models with currents
located in the crust or in the core.
G) at late times,
irrespective of the initial strength.
After 106 years the temperature is so low that the magnetic
diffusion timescale becomes longer than the typical ages of radiopulsars,
resulting in apparently no dissipation of the field in old NSs. We
confirm the strong correlation between the MF and the surface temperature
of relatively young NSs discussed in preliminary works.
If the MF of magnetars is caused by superconducting currents in the core
(as opposed to crustal currents), the longer diffusion timescale in the core
would allow magnetars to live much longer with their original large fields.
Thus, observations of magnetars can help to discern between models with currents
located in the crust or in the core.
It should be mentioned that magnetic field evolution by ambipolar diffusion in the core may produce qualitatively similar effects to those obtained in this work, keeping the temperature high while the field is strong and stopping field decay when the temperature drops (see e.g. Reisenegger 2008). In this work we have not considered the MF evolution in the core because ambipolar diffusion is usually considered under the assumption that the core is in a nonsuperfluid state and therefore is important during the very early stages of evolution. We are more interested in the longterm evolution, after the temperature rapidly drops below the critical temperature for nucleon superfluidity. To quantify the relative importance of both effects one would need to consider ambipolar diffusion in a superconducting fluid coupled to the dissipation of crustal currents studied here.
The detection of magnetars with true ages (the spin-down age can
be seriously overestimated)
![]() yr, or the detection of a young highly magnetized
NS with T<106 K would be a serious challenge for crustal field
models. At present our results agree with the known population of high field
NSs and magnetars and support the idea of the existence of a strong crustal MF
component in magnetars.
yr, or the detection of a young highly magnetized
NS with T<106 K would be a serious challenge for crustal field
models. At present our results agree with the known population of high field
NSs and magnetars and support the idea of the existence of a strong crustal MF
component in magnetars.
Given the complexity of the feedback between temperature and MF, it seems necessary to extend this work in two main lines that can shed new light on our knowledge of the cooling theory of NS: engaging 3D simulations and including the Hall term in the induction equation. The complex geometry that may arise in a realistic case with hot spots and irregular fields is certainly not treatable with our present code and needs further investigation. Similarly, the influence of the Hall term at late times when the temperature is so low that the magnetic diffusivity is negligible or a consistent treatment of ambipolar diffusion in a superconducting fluid coupled to the dissipation of crustal currents can produce new interesting effects so both are issues worth exploring in future work.
Acknowledgements
We thank D.N. Aguilera for valuable comments and providing updated conductivity routines used in the simulations, and Andreas Reisenegger for a critical reading and his constructive and helpful comments. This research has been supported by the Spanish MEC grant AYA 2007-67626-C03-02 and the Research Network Program Compstar funded by the ESF. U. Geppert thanks the University of Alicante for support under its visitors program.
References
- Aguilera, D. N., Cirigliano, V., Pons, J. A., Reddy, S., & Sharma, R. 2008a, ArXiv e-prints, 807 (In the text)
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008b, A&A, 486, 255 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008c, ApJ, 673, L167 [NASA ADS] [CrossRef]
- Canuto, V., & Chiuderi, C. 1970, Phys. Rev. D, 1, 2219 [NASA ADS] [CrossRef]
- Chugunov, A. I., & Haensel, P. 2007, MNRAS, 381, 1143 [NASA ADS] [CrossRef] (In the text)
- Flowers, E., & Itoh, N. 1976, ApJ, 206, 218 [NASA ADS] [CrossRef] (In the text)
- Geppert, U., Küker, M., & Page, D. 2004, A&A, 426, 267 [NASA ADS] [CrossRef] [EDP Sciences]
- Geppert, U., Küker, M., & Page, D. 2006, A&A, 457, 937 [NASA ADS] [CrossRef] [EDP Sciences]
- Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] (In the text)
- Hoyos, J., Reisenegger, A., & Valdivia, J. A. 2008, A&A, 487, 789 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Itoh, N. 1975, MNRAS, 173, 1P [NASA ADS]
- Jones, P. B. 1999, Phys. Rev. Lett., 83, 3589 [NASA ADS] [CrossRef] (In the text)
- Landau, L., & Lifshitz, E. 1960, Electrodynamics of Continuous Media (Addison Wesley) (In the text)
- Miralles, J. A., Urpin, V., & Konenkov, D. 1998, ApJ, 503, 368 [NASA ADS] [CrossRef] (In the text)
- Page, D., Geppert, U., & Zannias, T. 2000, A&A, 360, 1052 [NASA ADS]
- Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] (In the text)
- Pérez-Azorín, J. F., Miralles, J. A., & Pons, J. A. 2006a, A&A, 451, 1009 [NASA ADS] [CrossRef] [EDP Sciences]
- Pérez-Azorín, J. F., Pons, J. A., Miralles, J. A., & Miniutti, G. 2006b, A&A, 459, 175 [NASA ADS] [CrossRef] [EDP Sciences]
- Pons, J. A., & Geppert, U. 2007, A&A, 470, 303 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pons, J. A., Link, B., Miralles, J. A., & Geppert, U. 2007, Phys. Rev. Lett., 98, 071101 [NASA ADS] [CrossRef]
- Potekhin, A. Y., & Yakovlev, D. G. 2001, A&A, 374, 213 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 2007, Ap&SS, 308, 353 [NASA ADS] [CrossRef] (In the text)
- Rädler, K.-H., Fuchs, H., Geppert, U., Rheinhardt, M., & Zannias, T. 2001, Phys. Rev. D, 64, 083008 [NASA ADS] [CrossRef] (In the text)
- Reisenegger, A. 2008, ArXiv e-prints, 809 (In the text)
- Rheinhardt, M., & Geppert, U. 2002, Phys. Rev. Lett., 88, 101103 [NASA ADS] [CrossRef] (In the text)
- Urpin, V., & Konenkov, D. 2008, A&A, 483, 223 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ziman, J. 1979, Principles of the Theory of Solids (Cambridge University Press) (In the text)
Footnotes
All Figures
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1229fig1.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg113.gif) |
Figure 1:
Surface temperature as a function of temperature at the neutron drip
point for two models of NS envelopes with different MF strengths.
The thin dashed lines are the analytical fits from (Potekhin & Yakovlev 2001) for
MF parallel ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{1229fig2.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg126.gif) |
Figure 2:
Stationary 2D solutions of magnetized envelopes:
surface temperature profiles as a function of the polar angle for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1229fig3.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg128.gif) |
Figure 3:
Power spectrum at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{1229fig4.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg129.gif) |
Figure 4:
Temperature distribution in the crust of a NS (i.e. up to the bottom of
the envelope) at different
ages. The initial MF is purely poloidal with
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1229fig5.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg134.gif) |
Figure 5:
Temperature profiles at the base of the envelope
( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1229fig6.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg138.gif) |
Figure 6:
Cooling curves. Effective temperature as a function of age
for different initial field strengths ( from bottom to top
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1229fig7.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg143.gif) |
Figure 7:
Evolution of the MF strength at the pole |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1229fig8.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11229-08/Timg145.gif) |
Figure 8:
Radial equatorial profiles of the magnetization parameter
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



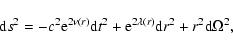
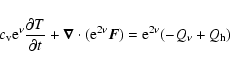
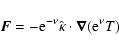
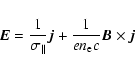
![\begin{displaymath}
\frac{\partial \vec{B}}{\partial t}= -\vec{\nabla}\times\lef...
...abla}\times({\rm e}^{\nu}\vec{B})\right]\times
\vec{B}\right\}
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img51.gif)
![\begin{displaymath}\frac{\partial\vec B}{\partial t}= - \nabla \times\left[\eta
~\nabla \times ({\rm e}^{\nu} \vec{B}) \right].
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img55.gif)
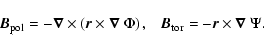
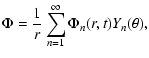
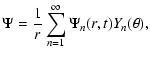
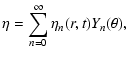
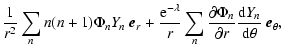
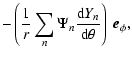
![$\displaystyle \frac{\partial \Phi_n}{\partial t} = {\rm e}^{\nu}
\sum_{k,k'} \e...
...r} \right)
\frac{\partial \Phi_k}{\partial r}
-\frac{k(k+1)}{r^2} \Phi_k\right]$](/articles/aa/full_html/2009/10/aa11229-08/img71.gif)
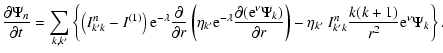
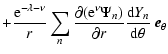
![$\displaystyle + \frac{1}{r} \sum_{n} \left[ {\rm e}^{-2\lambda}
\frac{\partial^...
...+1)}{r^2}\Phi_{n}
\right] \frac{{\rm d} Y_{n}}{{\rm d} \theta} ~\vec{e}_{\phi}.$](/articles/aa/full_html/2009/10/aa11229-08/img80.gif)
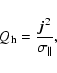
![\begin{displaymath}\frac{\partial}{\partial t} \left({\rm e}^{\nu}\frac{B^2}{8 \...
... {\rm e}^{2\nu}\frac{1}{4 \pi} \vec{E} \times \vec{B} \right],
\end{displaymath}](/articles/aa/full_html/2009/10/aa11229-08/img82.gif)
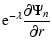
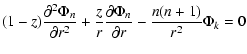
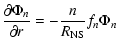
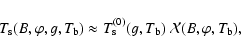
![$\displaystyle \mathcal{X}_\perp(B,T_{\rm b}) = \frac{\sqrt{1 + 0.1076 B_{12} (0...
...m b,9})^{-0.559}}}
{\left[1 + 0.819 B_{12}/ (0.03+T_{\rm b,9})\right]^{0.6463}}$](/articles/aa/full_html/2009/10/aa11229-08/img111.gif)
![$\displaystyle \mathcal{X}_\perp(B,T_{\rm b}) = \frac{\sqrt{1 + 0.07 B_{12} (0.0...
...m b,9})^{-0.559}}}
{\left[1 + 0.9 B_{12}/ (0.03+T_{\rm b,9})\right]^{0.4}}\cdot$](/articles/aa/full_html/2009/10/aa11229-08/img118.gif)