| Issue |
A&A
Volume 496, Number 1, March II 2009
|
|
|---|---|---|
| Page(s) | 223 - 227 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811174 | |
| Published online | 30 January 2009 | |
Updated pre-main sequence tracks at low metallicities for
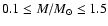
![[*]](/icons/foot_motif.gif)
M. Di Criscienzo - P. Ventura - F. D'Antona
Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monte Porzio Catone, Rome, Italy
Received 17 October 2008 / Accepted 21 December 2008
Abstract
Context. Young populations at
![]() are being examined to understand the role of metallicity in the first phases of stellar evolution. For the analysis it is necessary to assign mass and age to Pre-Main Sequence (PMS) stars. While it is well known that the mass and age determination of PMS stars is strongly affected by the convection treatment, extending any calibration to metallicities different from solar is very artificial, in the absence of any calibrators for the convective parameters. For solar abundance, Mixing Length Theory models have been calibrated by using the results of 2D radiative-hydrodynamical models (MLT-
are being examined to understand the role of metallicity in the first phases of stellar evolution. For the analysis it is necessary to assign mass and age to Pre-Main Sequence (PMS) stars. While it is well known that the mass and age determination of PMS stars is strongly affected by the convection treatment, extending any calibration to metallicities different from solar is very artificial, in the absence of any calibrators for the convective parameters. For solar abundance, Mixing Length Theory models have been calibrated by using the results of 2D radiative-hydrodynamical models (MLT-
![]() ), that are very similar to those computed with non-grey ATLAS9 atmosphere boundary conditions and a full spectrum of turbulence (FST) convection model both in the atmosphere and in the interior (NEMO-FST models).
), that are very similar to those computed with non-grey ATLAS9 atmosphere boundary conditions and a full spectrum of turbulence (FST) convection model both in the atmosphere and in the interior (NEMO-FST models).
Aims. While MLT-
![]() models are not available for lower metallicities, we extend to lower Z the NEMO-FST models, under the hypothesis that in such a way we are simulating the results of MLT-
models are not available for lower metallicities, we extend to lower Z the NEMO-FST models, under the hypothesis that in such a way we are simulating the results of MLT-
![]() models also at smaller Z.
models also at smaller Z.
Methods. We use standard stellar computation techniques in which the atmospheric boundary conditions are derived making use of model atmosphere grids. This allows us to take into account the non greyness of the atmosphere, but adds a new parameter to the stellar structure uncertainty, namely the efficiency of convection in the atmospheric structure, if convection is computed in the atmospheric grid by a model different to the model adopted for the interior integration.
Results. We present PMS models for low mass stars from 0.1 to 1.5 ![]() for metallicities [Fe/H] = -0.5, -1.0 and -2.0. The calculations include the most recent interior physics and the latest generation of non-grey atmosphere models. At fixed luminosity more metal poor isochrones are hotter than solar ones by
for metallicities [Fe/H] = -0.5, -1.0 and -2.0. The calculations include the most recent interior physics and the latest generation of non-grey atmosphere models. At fixed luminosity more metal poor isochrones are hotter than solar ones by ![]()
![]()
![]() /
/![]()
![]()
![]() 0.03-0.05 in the range in Z from 0.02 to 0.0002 and for ages from 105 to 107 yr.
0.03-0.05 in the range in Z from 0.02 to 0.0002 and for ages from 105 to 107 yr.
Key words: stars: evolution - stars: pre-main sequence
1 Introduction
The study of Pre-Main Sequence (PMS) stars is important to trace the modalities of star formation in space and time, to date young stellar systems by means of age tracers which do not suffer the uncertainty in the physics of the upper main sequence stars, to derive the initial mass function of very low mass stars and brown dwarfs, and to understand the modalities of stellar rotational evolution and depletion of light elements. Theoretical tracks and isochrones provide an essential tool to understand and interpret the experimental data currently available for young objects. Since most of these sources are located in nearby Galactic star forming regions, this research has been generally limited so far to solar chemistry or close to it (e.g. Siess et al. 2000).
Now that young populations at
![]() are being examined (e.g. Romaniello et al. 2006), it
becomes essential to understand the role of metallicity in the first phases of stellar evolution, thus demanding further investigations at lower metallicities.
are being examined (e.g. Romaniello et al. 2006), it
becomes essential to understand the role of metallicity in the first phases of stellar evolution, thus demanding further investigations at lower metallicities.
On the other hand, the description of the PMS evolution of stars is one of the most delicate tasks in the context of stellar astrophysics: the location of the theoretical tracks on the Hertzprung-Russell (HR) plane depends critically on the ingredients used to calculate the models, the equation of state and opacities (e.g. D'Antona 1993), the boundary conditions used to match the integration of the interior with the atmospheric structure (Baraffe et al. 2002), and the treatment of convection (D'Antona & Mazzitelli 1994). Detailed investigations by Montalban et al. (2004)
showed that, at
![]() s where atmospheric convection is present, its modelling plays an important role in determining the radius of these structures, and thus the exact excursion of
the theoretical track on the HR diagram; this is the most critical parameter in the computation down to
s where atmospheric convection is present, its modelling plays an important role in determining the radius of these structures, and thus the exact excursion of
the theoretical track on the HR diagram; this is the most critical parameter in the computation down to
![]()
![]() 4000 K. Below this temperature, both molecular opacities and convection treatment are the dominant uncertainties. Unfortunately, convection is a rather complex phenomenon, that is poorly known from first principles, so that it is commonly treated by means of purely local approaches, the most popular of which is the Mixing Length Theory (Böhm-Vitense 1958, MLT), where all the physical uncertainties are hidden below the unique parameter
4000 K. Below this temperature, both molecular opacities and convection treatment are the dominant uncertainties. Unfortunately, convection is a rather complex phenomenon, that is poorly known from first principles, so that it is commonly treated by means of purely local approaches, the most popular of which is the Mixing Length Theory (Böhm-Vitense 1958, MLT), where all the physical uncertainties are hidden below the unique parameter
![]() ,
l being the mixing scale and
,
l being the mixing scale and ![]() the pressure scale height; among other attempts to model convection locally, the Full Spectrum of Turbulence (FST) model by Canuto & Mazzitelli (1991, CM) and Canuto et al. (1996, CGM) has been widely used in recent years.
the pressure scale height; among other attempts to model convection locally, the Full Spectrum of Turbulence (FST) model by Canuto & Mazzitelli (1991, CM) and Canuto et al. (1996, CGM) has been widely used in recent years.
A potentially powerful tool to ``calibrate'' the convective model for the description of these evolutionary stages is the comparison between the theoretical loci in the HR plane and the position of PMS binaries, for which a rather precise estimation of the masses of the two components is possible (e.g. Stassun et al. 2004; Boden et al. 2005). The results obtained so far are rather
ambiguous, and reveal the difficulty in finding a unique description of convection, holding in all cases. Baraffe et al. (2002) found that several masses in PMS binaries demand an MLT parameter
![]() ,
but some others, lying in the same region of the HR diagram, require a much lower efficiency, e.g.
,
but some others, lying in the same region of the HR diagram, require a much lower efficiency, e.g. ![]() .
Stassun et al. (2004) also found that models with inefficient convection in the interior should be preferred. In the case of the binary components of V1174Ori they found a very good agreement with the models by Montalban et al. (2004), employing the FST convection both in the interior and in the atmospheres computed by Heiter et al. (2002). 2D and 3D radiative hydrodynamical simulations should provide more realistic results (Ludwig et al. 2002; Trampedach et al. 1999). Based on their 2D computations, Ludwig et al. (1999) provided a calibration of the MLT parameter
.
Stassun et al. (2004) also found that models with inefficient convection in the interior should be preferred. In the case of the binary components of V1174Ori they found a very good agreement with the models by Montalban et al. (2004), employing the FST convection both in the interior and in the atmospheres computed by Heiter et al. (2002). 2D and 3D radiative hydrodynamical simulations should provide more realistic results (Ludwig et al. 2002; Trampedach et al. 1999). Based on their 2D computations, Ludwig et al. (1999) provided a calibration of the MLT parameter ![]() for various effective temperatures and gravities: the meaning of this calibration is that the parameter describes the average efficiency of convection within the whole superadiabatic zone, in the
region of
for various effective temperatures and gravities: the meaning of this calibration is that the parameter describes the average efficiency of convection within the whole superadiabatic zone, in the
region of
![]() and gravity explored by the 2D models. This efficiency is not constant, but varies with the position of the star in the HR diagram. Montalban & D'Antona (2006) adopted such a calibration and computed the corresponding tracks (MLT-
and gravity explored by the 2D models. This efficiency is not constant, but varies with the position of the star in the HR diagram. Montalban & D'Antona (2006) adopted such a calibration and computed the corresponding tracks (MLT-
![]() tracks) for solar metallicity. Examination of binary location with respect to the MLT-
tracks) for solar metallicity. Examination of binary location with respect to the MLT-
![]() tracks shows the same difficulties as previous track sets, although they result in an excellent agreement with the components of the binary V773 Tau (Boden et al. 2007). The MLT-
tracks shows the same difficulties as previous track sets, although they result in an excellent agreement with the components of the binary V773 Tau (Boden et al. 2007). The MLT-
![]() tracks are not in agreement with the lithium depletion patterns in young clusters with solar system abundance, but this additional feature can be attributed to the high metal abundance generally adopted for the solar model (Montalban & D'Antona 2006). The same work shows that the FST non-grey tracks of solar composition, with boundary conditions based on model atmospheres in which convection adopts the same FST model (Heiter et al. 2002), present a striking similarity to the results of MLT-
tracks are not in agreement with the lithium depletion patterns in young clusters with solar system abundance, but this additional feature can be attributed to the high metal abundance generally adopted for the solar model (Montalban & D'Antona 2006). The same work shows that the FST non-grey tracks of solar composition, with boundary conditions based on model atmospheres in which convection adopts the same FST model (Heiter et al. 2002), present a striking similarity to the results of MLT-
![]() models.
models.
The scope of this paper is to extend the computations by Montalban & D'Antona (2006) to lower
metallicities, by naively assuming that FST models can approximate the results of MLT-
![]() simulations also at lower metallicity. As we wish to provide a more extended set of results, while the FST model atmospheres are available only at
simulations also at lower metallicity. As we wish to provide a more extended set of results, while the FST model atmospheres are available only at
![]()
![]() 4000 K, we adopt a way to extend the computation to lower
4000 K, we adopt a way to extend the computation to lower
![]() .
We then use MLT non grey models based on
the atmospheric structures by Allard & Hauschildt (1997, AH97) and choose the combination of atmospheric and interior convection efficiency that provides results similar to the FST tracks at
.
We then use MLT non grey models based on
the atmospheric structures by Allard & Hauschildt (1997, AH97) and choose the combination of atmospheric and interior convection efficiency that provides results similar to the FST tracks at
![]()
![]() 4000 K.
4000 K.
2 The ATON code
The evolutionary sequences presented in the following sections were calculated by means of the ATON code for stellar evolution; a detailed description of the numerical structure of ATON can be found in Ventura et al. (2007).
The micro-physics adopted concerning the radiative and conductive opacities, and the equation of state (EOS) was recently updated.
At low temperatures, we use the latest release of the opacity tables by Ferguson et al. (2005),
completed for
![]() K by the OPAL opacities, in the version documented
by Iglesias & Rogers (1996).
K by the OPAL opacities, in the version documented
by Iglesias & Rogers (1996).
The EOS adopted in most of the T-P plane is the latest release of the OPAL EOS![]() , overwritten in the pressure ionization regime by the EOS from Saumon et al. (1995), and extended to the high-density, high temperature domain according to the treatment by Stolzmann & Blöcker (2000).
, overwritten in the pressure ionization regime by the EOS from Saumon et al. (1995), and extended to the high-density, high temperature domain according to the treatment by Stolzmann & Blöcker (2000).
The formal borders of the convective regions were found by means of the classic Schwartzschild criterium. The FST scheme (CM or CGM) was used to determine the temperature gradient in zones unstable to convection. Nuclear burning within convective regions was treated according to the instantaneous mixing approximation.
We computed models for three metallicities [Fe/H] = -0.5, -1.0 and 2.0 with an adopted helium mass fraction Y=0.25. The solar metallicity is assumed to be Z=0.02 and the solar mixture for opacities and EOS is taken from Grevesse & Sauval (1999). In this work we adopted solar-scaled mixtures in all cases, though ![]() -enhanced mixtures are also available.
-enhanced mixtures are also available.
2.1 Atmospheric structure and boundary conditions
In the atmosphere, the opacities have a strong dependence on the frequency, so that an atmospheric integration based on a Rosseland-type average or on an approximate T(![]() ) relation, like in a grey atmosphere, is not adequate for the description of the structure. Often this problem is attacked by assuming the stratification temperature vs. pressure by integrating appropriate
model atmospheres, as for example by means of the Kurucz code (Kurucz 1998). Below
) relation, like in a grey atmosphere, is not adequate for the description of the structure. Often this problem is attacked by assuming the stratification temperature vs. pressure by integrating appropriate
model atmospheres, as for example by means of the Kurucz code (Kurucz 1998). Below ![]() 4000 K, the role of triatomic molecules becomes important, and the most adequate model atmospheres so far are the models by Allard & Hauschildt (1997). Generally, the boundary conditions for the interior structure computation are then the physical quantities deriving from such integration down to a fixed value of the optical depth
4000 K, the role of triatomic molecules becomes important, and the most adequate model atmospheres so far are the models by Allard & Hauschildt (1997). Generally, the boundary conditions for the interior structure computation are then the physical quantities deriving from such integration down to a fixed value of the optical depth ![]() ,
namely
,
namely
![]() .
Tables of boundary conditions at the chosen
.
Tables of boundary conditions at the chosen
![]() are used to derive the stellar gravity and
are used to derive the stellar gravity and
![]() by interpolation. This procedure hides a problem: the stellar convection in the atmosphere is computed
by assuming an efficiency of convection. In the MLT model, for example, the grids of model atmospheres are computed by fixing the
by interpolation. This procedure hides a problem: the stellar convection in the atmosphere is computed
by assuming an efficiency of convection. In the MLT model, for example, the grids of model atmospheres are computed by fixing the ![]() parameter to a value
parameter to a value
![]() .
For the interior computation, it may be necessary to adopt a different
.
For the interior computation, it may be necessary to adopt a different ![]() .
For example, in order to fit the solar model (that is, to obtain the solar radius at the solar age), a value
.
For example, in order to fit the solar model (that is, to obtain the solar radius at the solar age), a value
![]() = 1.9 is used by Baraffe et al. (2002), while the AH97 grid adopted for the atmospheric integration has
= 1.9 is used by Baraffe et al. (2002), while the AH97 grid adopted for the atmospheric integration has
![]() = 1. As the MLT must be generally understood as a way of obtaining an ``average'' efficiency of convection, more than a model that allows usto derive the correct temperature atmospheric structure, this problem is not highly relevant, but we should remember that in this way we are introducing a dependence of the structure on another parameter, namely
= 1. As the MLT must be generally understood as a way of obtaining an ``average'' efficiency of convection, more than a model that allows usto derive the correct temperature atmospheric structure, this problem is not highly relevant, but we should remember that in this way we are introducing a dependence of the structure on another parameter, namely
![]() .
This problem is fully discussed by Montalban et al. (2004).
.
This problem is fully discussed by Montalban et al. (2004).
Heiter et al. (2002) made available grids computed by means of an improved version of Kurucz code (NEMO; Castelli 1997; Kurucz 1998). They considered both MLT models with
![]() = 0.5, FST models following CM and FST models according to CGM. If FST convection is adopted both in the atmospheric grid and in the interior, the model computation does not show temperature gradient discontinuities (Montalban et al. 2004).
= 0.5, FST models following CM and FST models according to CGM. If FST convection is adopted both in the atmospheric grid and in the interior, the model computation does not show temperature gradient discontinuities (Montalban et al. 2004).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1174fig1.ps}
\par\end{figure}](/articles/aa/full_html/2009/10/aa11174-08/Timg26.gif) |
Figure 1:
Evolutionary tracks for the labelled metallicities and for masses 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5 |
| Open with DEXTER | |
Different sets of boundary conditions were considered in this work: FST-NEMO grids (with CGM convection) and the AH97 grids. The boundary conditions (BCs) at fixed values of photospheric
optical depth
![]() contain, for each
contain, for each
![]() ,
gravity and metallicity, the temperature, pressure and geometrical depth at the chosen
,
gravity and metallicity, the temperature, pressure and geometrical depth at the chosen
![]() .
The last quantity is the difference between the radius where convection begins and
.
The last quantity is the difference between the radius where convection begins and
![]() becomes larger than
becomes larger than
![]() and the radius at
and the radius at
![]() ,
a quantity necessary for the
computation of the FST fluxes. As suggested by Heiter et al. (2002), we choose
,
a quantity necessary for the
computation of the FST fluxes. As suggested by Heiter et al. (2002), we choose
![]() = 10, to avoid discrepancies in the physical quantities due to the turbulent pressure (not included in the atmosphere modeling but present in the integration of the interior) and to reduce the differences due to different opacity tables used at both sides of
= 10, to avoid discrepancies in the physical quantities due to the turbulent pressure (not included in the atmosphere modeling but present in the integration of the interior) and to reduce the differences due to different opacity tables used at both sides of
![]() .
The boundary conditions for the internal structure are determined by spline interpolation of these tables. From initial
.
The boundary conditions for the internal structure are determined by spline interpolation of these tables. From initial
![]() and
and ![]()
![]() we determine P and T at the last point of the internal structure (
we determine P and T at the last point of the internal structure (
![]() ). An iterative procedure is performed until the P(
). An iterative procedure is performed until the P(
![]() )
and
T(
)
and
T(
![]() ) values derived from the interior and from the atmosphere models converge. The
) values derived from the interior and from the atmosphere models converge. The
![]() range of these grids is between 4000-10 000 K, at lower
range of these grids is between 4000-10 000 K, at lower
![]() we used
AH97 models, which include the contribution of many more molecular lines dominating the opacities than ATLAS9. In the AH97 models, convection is treated with MLT and
we used
AH97 models, which include the contribution of many more molecular lines dominating the opacities than ATLAS9. In the AH97 models, convection is treated with MLT and
![]() .
For metallicities lower than solar the available models have 3000
.
For metallicities lower than solar the available models have 3000 ![]()
![]()
![]() 10 000 K and surface gravity from
10 000 K and surface gravity from
![]() to 6.0.
to 6.0.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1174fig2.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11174-08/Timg32.gif) |
Figure 2:
Non-grey evolutionary tracks for 0.6 |
| Open with DEXTER | |
3 The evolutionary tracks
In Fig. 1 we present evolutionary tracks computed with non grey atmospheres for masses in the range
![]() ,
and for metallicities [Fe/H] = 0.0, -0.5, -1.0, -2.0.
,
and for metallicities [Fe/H] = 0.0, -0.5, -1.0, -2.0.
In the top-left panel the solar tracks at
![]() are directly taken from previous computations by Montalban et al. (2004), which were performed using the NEMO-FST grids by Heiter et al. (2002) available only for
are directly taken from previous computations by Montalban et al. (2004), which were performed using the NEMO-FST grids by Heiter et al. (2002) available only for
![]()
![]() 4000 K. The comparison of these solar metallicity tracks with other models present in the literature, in particular with those of Siess et al. (2000), was made by Montalban et al. (2004).
4000 K. The comparison of these solar metallicity tracks with other models present in the literature, in particular with those of Siess et al. (2000), was made by Montalban et al. (2004).
However Montalban & D'Antona (2006) have shown that these models are very similar to the MLT-
![]() models; here we extend the computation to lower metallicities.
models; here we extend the computation to lower metallicities.
Since measurements suggest a primordial abundance of deuterium ![]() 3.0-5.0
3.0-5.0 ![]() 10-5 (e.g. Tosi 1996), we fix the initial deuterium abundance at
10-5 (e.g. Tosi 1996), we fix the initial deuterium abundance at ![]() = 4
= 4 ![]() 10-5 by mass, fairly representative of the D-abundance of the Population II stars. A value
10-5 by mass, fairly representative of the D-abundance of the Population II stars. A value ![]() = 2
= 2 ![]() 10-5 is often adopted for models with solar abundances (Siess et al. 2000).
10-5 is often adopted for models with solar abundances (Siess et al. 2000).
NEMO models are available only for
![]()
![]() 4000 K. Within the context of non grey modelling, the only atmospheres available at lower
4000 K. Within the context of non grey modelling, the only atmospheres available at lower
![]() are those by Allard & Hauschildt (1997), that
use the MLT treatment of convection. We therefore decided to extend our models to lower masses by using these atmosphere models. The same convection model is adopted in the interior computation, and the match with atmospheres is performed at
are those by Allard & Hauschildt (1997), that
use the MLT treatment of convection. We therefore decided to extend our models to lower masses by using these atmosphere models. The same convection model is adopted in the interior computation, and the match with atmospheres is performed at
![]() = 10 in the first case and
= 10 in the first case and
![]() in the second one. The free parameter
in the second one. The free parameter
![]() was set in order to provide a reasonable continuity between the FST tracks and the MLT ones at temperatures just exceeding 4000 K. Figure 2 shows that
was set in order to provide a reasonable continuity between the FST tracks and the MLT ones at temperatures just exceeding 4000 K. Figure 2 shows that
![]() is a reasonable choice especially at lower metallicity (see also the evolutionary tracks for
is a reasonable choice especially at lower metallicity (see also the evolutionary tracks for
![]() in
Fig. 1). For these MLT models we choose
in
Fig. 1). For these MLT models we choose
![]() which is a good compromise since we avoid having a large influence from
which is a good compromise since we avoid having a large influence from
![]() (Montalban et al. 2004). The evolutionary tracks computed with the MLT treatment of convection are indicated with dashed lines in Fig. 1; since the AH97 atmospheres are available only in the range of gravities
(Montalban et al. 2004). The evolutionary tracks computed with the MLT treatment of convection are indicated with dashed lines in Fig. 1; since the AH97 atmospheres are available only in the range of gravities ![]() g
g ![]() 3.5, we had to skip the deuterium burning phase from our computations.
3.5, we had to skip the deuterium burning phase from our computations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1174fig3.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11174-08/Timg38.gif) |
Figure 3: Comparison between the isochrones calculated for 105, 106, 107 yr for different metallicities ( from left to right: [Fe/H] = -2.0, -1.0, -0.5, 0). |
| Open with DEXTER | |
As outlined in the introduction, PMS stars can be very useful age tracers. Comparing the theoretical results with the observed loci of stellar sources in associations requires the computation of the isochrones. In Fig. 3 we report three different groups of isochrones (corresponding to 105, 106, 107 yr) for each of the metallicities investigated.
The youngest isochrones do not include the low mass stars, because, as already stressed, we started the evolution after the deuterium burning phase. For very low mass models (those with AH97 atmospheres) we skip the D burning phase, thus the ages of these PMS stars must be taken with
caution. At 107 yr, for example, including D burning would have increased the age by about only 3![]() at 0.5
at 0.5 ![]() ,
but by about 30
,
but by about 30![]() at 0.1
at 0.1 ![]() (D'Antona & Mazzitelli 1997). Young ages as low as 105 yr are also uncertain, because of the unclear role played by the protostellar accretion phase (Palla 2001). It is evident from the figure that at fixed age and luminosity more metal poor isochrones are hotter by an amount almost independent of luminosity and that these amounts became lower at lower metallicity. The effect is mostly due to the opacity reduction, as is well known in the study of main sequence models.
(D'Antona & Mazzitelli 1997). Young ages as low as 105 yr are also uncertain, because of the unclear role played by the protostellar accretion phase (Palla 2001). It is evident from the figure that at fixed age and luminosity more metal poor isochrones are hotter by an amount almost independent of luminosity and that these amounts became lower at lower metallicity. The effect is mostly due to the opacity reduction, as is well known in the study of main sequence models.
4 Conclusions
A grid of stellar evolutionary tracks for low metallicity Pre-Main Sequence stars with masses between 0.1 and 1.5 ![]() was presented. These models are based on up-to-date physics and updated non grey atmosphere models were used. A coherent treatment of convection in the interior and exterior region of the star was employed at
was presented. These models are based on up-to-date physics and updated non grey atmosphere models were used. A coherent treatment of convection in the interior and exterior region of the star was employed at
![]()
![]() 4000 K. We extended our computations to models of smaller masses by using the AH97 grid of model atmospheres. The
parameters
4000 K. We extended our computations to models of smaller masses by using the AH97 grid of model atmospheres. The
parameters
![]() and
and
![]() were chosen to provide a smooth transition between the two model sets. This, of course, is only an estimate of the problem of Pre-Main Sequence models at low metallicity.
were chosen to provide a smooth transition between the two model sets. This, of course, is only an estimate of the problem of Pre-Main Sequence models at low metallicity.
The models (available in electronic form at http://www.mporzio.astro.it/%7Etsa/) can now be compared with to the complex realm of very young objects, providing important information on ages and star formation processes, as well as providing some new constraints for PMS models.
Acknowledgements
It is a pleasure to thank J. Montalban for having provided the tables of boundary conditions for low metallicities and for invaluable comments on the manuscript. Financial support for this study was provided by MIUR under the PRIN project ``Asteroseismology: a necessary tool for the advancement in the study of stellar structure, dynamics and evolution'', P. I. L. Paternó.
References
- Allard, f., & Hauschildt, P. 1997, The NEXTGEN model grids, Web location: http://hobbes.hs.uni-hamburg.de/yeti/mdwarfs.html (In the text)
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 2002, A&A, 382, 563 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boden, A., Sargent, A., Akeson, R., et al. 2005, ApJ, 635, 442 [NASA ADS] [CrossRef]
- Boden, A. F., Torres, G., Sargent, A. I., et al. 2007, ApJ, 670, 1214 [NASA ADS] [CrossRef] (In the text)
- Böhm-Vitense, E. 1958, Z. Astroph., 46, 1 (In the text)
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] (In the text)
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] (In the text)
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS]
- D'Antona, F. 1993, ASPC, 40, 395 [NASA ADS] (In the text)
- D'Antona, F., & Mazzitelli, I. 1994, ApJS, 90, 467 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F., & Mazzitelli, I. 1997, MmSAI, 68, 807 [NASA ADS] (In the text)
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] (In the text)
- Grevesse, N., & Sauval, A. J. 1999, A&A, 347, 348G [NASA ADS] (In the text)
- Heiter, U., Kupka, F., van't Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] (In the text)
- Kurucz, R. L. 1998, http://cfaku5.harvard.edu/ (In the text)
- Ludwig, H., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] (In the text)
- Ludwig, H.-G., Allard, F., & Hauschildt, P. H. 2002, A&A, 395, 9 [CrossRef]
- Montalban, J., & D'Antona, F. 2006, MNRAS, 370, 1823 [NASA ADS] (In the text)
- Montalban, J., D'Antona, F., Kupka, F., & Heiter, U. 2004, A&A, 416, 1081 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Palla, F. 2001, ASPC, 243, 525 [NASA ADS] (In the text)
- Romaniello, M., Scuderi, S., Panagia, N., Salerno, R. M., & Blanco, C. 2006, A&A, 955, 969 (In the text)
- Saumon, D., Chabrier, G., & Van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] (In the text)
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] (In the text)
- Stassun, K., Mathieu, R., Vaz, L., Stroud, N., & Vrba, F. 2004, ApJS, 151, 357 [NASA ADS] [CrossRef]
- Stolzmann, W., & Blöcker, T. 2000, A&A, 361, 1152 [NASA ADS] (In the text)
- Tosi, M. 1996, in From Stars to Galaxies: the Impact of Stellar Physics on Galaxy Evolution, ASP Conf. Ser., San Francisco, 98, 299 (In the text)
- Trampedach, R., Stein, R. F., Christensen-Dalsgaard, J., & Nordlund, A. 1999, in Stellar Structure: Theory and Test of Connective Energy Transport, ASP Conf. Ser., San Francisco, 173, 233
- Ventura, P., D'Antona, F., & Mazzitelli, I. 2007, Ap&SS, 420 (In the text)
Footnotes
- ...
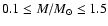
![[*]](/icons/foot_motif.gif)
- These evolutionary tracks and isochrones are available in electronic form at a WEB site http://www.mporzio.astro.it/%7Etsa/
- ... EOS
![[*]](/icons/foot_motif.gif)
- http://physci.llnl.gov/Research/OPAL/EOS_2005/
All Figures
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1174fig1.ps}
\par\end{figure}](/articles/aa/full_html/2009/10/aa11174-08/Timg26.gif) |
Figure 1:
Evolutionary tracks for the labelled metallicities and for masses 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1174fig2.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11174-08/Timg32.gif) |
Figure 2:
Non-grey evolutionary tracks for 0.6 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1174fig3.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa11174-08/Timg38.gif) |
Figure 3: Comparison between the isochrones calculated for 105, 106, 107 yr for different metallicities ( from left to right: [Fe/H] = -2.0, -1.0, -0.5, 0). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


