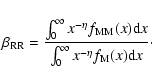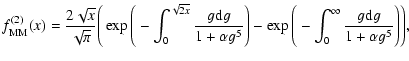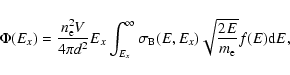EDP Sciences
Home All issues Volume 496 / No 1 (March II 2009) A&A, 496 1 (2009) 25-30 Full HTML
Free Access
Issue
A&A
Volume 496, Number 1, March II 2009
Page(s) 25 - 30
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200811095
Published online 30 January 2009

An analysis of electron distributions in galaxy clusters by means of the flux ratio of iron lines FeXXV and XXVI

D. A. Prokhorov1,2 - F. Durret1 - V. Dogiel 3 - S. Colafrancesco4,5,6


1 - Institut d'Astrophysique de Paris, CNRS, UMR 7095, Université Pierre et Marie Curie, 98bis Bd Arago, 75014 Paris, France
2 - Moscow Institute of Physics and Technology, Institutskii lane, 141700 Moscow Region, Dolgoprudnii, Russia
3 - Lebedev Physical Institute, 117924 Moscow, Russia
4 - ASI Science Data Center, ASDC c/o ESRIN, via G. Galilei 00044 Frascati, Italy
5 - ASI, Viale Liegi 26, Roma, Italy
6 - INAF - Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio, Italy

Received 6 October 2008 / Accepted 5 December 2008

Abstract
Aims. The interpretation of hard X-ray emission from galaxy clusters is still ambiguous and different proposed models can be probed using various observational methods. Here we explore a new method based on Fe-line observations.
Methods. Spectral-line emissivities have usually been calculated by assuming a Maxwellian electron distribution. In this paper, a generalized approach to calculating the iron-line flux for a modified Maxwellian distribution is considered.
Results. We calculated the flux ratio of iron lines for various possible populations of electrons proposed to account for measurements of hard X-ray excess-emission from the clusters A2199 and Coma. We found that the influence of the suprathermal electron population on the flux ratio is more significant in low temperature clusters (as Abell 2199) than in high temperature clusters (as Coma).

Key words: radiation mechanisms: non-thermal - galaxies: clusters: general - X-rays: galaxies: clusters

1 Introduction

Observations with BeppoSAX have detected hard X-ray tails in the X-ray spectra of some galaxy clusters such as the Coma cluster (Fusco-Femiano et al. 1999) and Abell 2199 (Kaastra et al. 1998, 1999). These tails, which have been reproduced by power-law spectra, are in excess of the thermal bremsstrahlung X-ray emission from the hot intracluster medium (ICM). The evidence and the nature of hard tails in these and other clusters was discussed by Rephaeli et al. (2008). The hard X-ray fluxes from galaxy clusters are usually interpreted as being due to either inverse Compton scattering (ICS) of relativistic electrons on relic photons (Sarazin & Lieu 1998) or as bremsstrahlung emission from nonthermal, subrelativistic electrons (see e.g. Sarazin & Kempner 2000), or from thermal electrons with a Maxwellian spectrum distorted by the particle acceleration mechanism (Dogiel 2000; Dogiel et al. 2007).

The more traditional interpretation based on the ICS emission from a relativistic, electron population faces a serious problem. The combination of hard X-ray and radio observations of the Coma cluster within the ICS model is a strong indication of a low magnetic-field strength, $B \sim0.1~\mu$G, much lower than the values derived from Faraday rotation measurements (see e.g. Clarke et al. 2001). The situation in Abell 2199 is more extreme because no extended, diffuse, radio emission is detected from this cluster. The discovery of the hard X-ray emission of the cluster A2199 implies a weak ICM magnetic field of $\la$$0.07~\mu$G, if the hard X-ray emission is ICS (Kempner & Sarazin 2000).

Bremsstrahlung radiation from suprathermal electrons with energies higher than 10 keV (nonthermal electrons or thermal electrons with a distorted Maxwellian spectrum) may explain the hard X-ray excess emission observed in the Coma cluster and Abell 2199 (e.g. Sarazin & Kempner 2000; Dogiel 2000). This is an alternative to the traditional but problematic inverse Compton scattering interpretation. These subrelativistic electrons would form a particle population in excess of that of the thermal gas. A possible explanation for this population would be that they are particles being accelerated to higher energies, either by intracluster shocks or by turbulence in the ICM (e.g. Dogiel 2000).

The most reliable way resolving whether the observed hard X-rays are due to ICS or are evidence of a modified thermal distribution in clusters is to probe such a distribution directly.

The Sunyaev-Zel'dovich (SZ) effect signal, the spectrum of which depends on the electron distribution function in clusters of galaxies, can be used to discriminate among different interpretations of the X-ray excess (Colafrancesco 2007; Dogiel et al. 2007). A study of the influence of suprathermal electrons on the SZ effect was completed for the Coma and Abell 2199 clusters by Blasi et al. (2000) and Shimon & Rephaeli (2002). However, realistical models of suprathermal electrons in Coma and Abell 2199 predict a spectral distortion of the cosmic microwave background radiation due to these electrons that is only a small fraction of the corresponding SZ effect produced by the hot intracluster gas (see e.g. Shimon & Rephaeli 2002; Dogiel et al. 2007). Therefore, the observation of the impact of suprathermal electrons on the cosmic microwave background will be challenging from the experimental side (see Dogiel et al. 2007).

In this paper, we consider a new way of discriminating between the different interpretations of the X-ray excess, namely the flux ratio of the emission lines due to FeK$\alpha$ transitions: FeXXV (helium-like) and FeXXVI (hydrogen-like). This flux ratio is extremely sensitive to the population of electrons with energies higher than the ionization potential of a FeXXV ion (which is $\approx$8.8 keV) and is a promising tool for revealing the presence of suprathermal electrons in galaxy clusters.

A generalized approach to calculating iron line fluxes is considered in Sect. 2. The flux ratio of the emission lines due to the FeK$\alpha$ transitions is calculated for the modified thermal distributions in the clusters Abell 2199 and Coma in Sect. 3. The possibility of separating the thermal and non-thermal components by using the shape of the bremsstrahlung continuum spectrum is discussed in Sect. 4. We draw our conclusions in Sect. 5.

2 The flux ratio of the FeXXV and XXVI iron lines

Since the fluxes of the FeXXV and FeXXVI lines have the same dependence on the metal abundance, as well as on the emission measure, their ratio is independent of these parameters. This iron line ratio can therefore be used to determine the temperature of the intracluster gas (e.g. Nevalainen et al. 2003). In this section, we propose a generalized approach to calculate the iron-line flux ratio for modified Maxwellian electron distributions.

2.1 Ionization and recombination rates

The ionization rates, recombination rates, and emissivity in a spectral line have usually been calculated for a Maxwellian electron distribution (e.g. Arnaud & Raymond 1992). However, in many low-density astrophysical plasmas, the electron distribution may differ from a Maxwellian distribution. The influence of the shape of the electron distribution on the ionization and recombination rates in various physical conditions was examined by Porquet et al. (2001).

A Maxwellian distribution is generally assumed to describe the electron distribution in galaxy clusters. The modified Maxwellian electron distributions that are expected in galaxy clusters with a hard X-ray excess seem to be described reasonably by a Maxwellian distribution at low energy and by a power-law distribution at higher energy (e.g. Sarazin & Kempner 2000).

It is convenient to express the electron distribution in terms of the reduced energy x=E/kT:

$\displaystyle {\rm d}n_{{\rm e}}(x)=n_{{\rm e}} f(x) {\rm d}x ,$     (1)

where $n_{{\rm e}}$ is the electron density and k is the Boltzmann constant.

We consider a collisional process with cross section $\sigma(E)$, varying with the energy E of the incident electron. The corresponding rate coefficient $\Gamma$ (cm3 s-1), either for a Maxwellian distribution or a modified thermal distribution, f(x), is obtained by averaging the product of the cross section by the electron velocity over the electron distribution function:

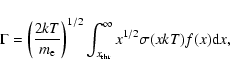\begin{displaymath}\Gamma=\left(\frac{2kT}{m_{{\rm e}}}\right)^{1/2} \int^{\infty}_{x_{{\rm thr}}} x^{1/2} \sigma(xkT) f(x) {\rm d}x, \end{displaymath} (2)

where $m_{{\rm e}}$ is the electron mass, $x_{{\rm thr}}=E_{{\rm thr}}/(kT)$, and $E_{{\rm thr}}$corresponds to the threshold energy of the considered process.

For recombination processes, no threshold energy is involved and $x_{{\rm thr}}=0$. The rates are denoted by $C_{{\rm I}}$, $\alpha_{{\rm RR}}$ and $\alpha_{{\rm DR}}$ for the ionization, radiative and dielectronic recombination-processes, respectively, for a Maxwellian electron distribution.

In equilibrium, the ionic fractions do not depend on the electron density, and the ionic fraction ratio $\xi_{{\rm FeXXV}}/\xi_{{\rm FeXXVI}}$ of two adjacent stages FeXXV and FeXXVI for a Maxwellian distribution can be expressed by:

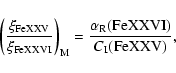\begin{displaymath}\left(\frac{\xi_{{\rm FeXXV}}}{\xi_{{\rm FeXXVI}}}\right)_{{\... ...rac{\alpha_{{\rm R}}({\rm FeXXVI})}{C_{{\rm I}}({\rm FeXXV})}, \end{displaymath} (3)

where $C_{{\rm I}}({\rm FeXXV})$ and $\alpha_{{\rm R}}({\rm FeXXVI})$ are the ionization and the total recombination rates of the ions FeXXV and FeXXVI, respectively.

For the direct ionization cross-section of FeXXV, we use the parametric formula in Arnaud & Rothenflug (1985):

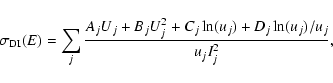\begin{displaymath}\sigma_{{\rm DI}}(E)=\sum_{{j}} \frac{A_{{j}}U_{{j}}+B_{{j}}U... ...}\ln(u_{{j}})+D_{{j}}\ln(u_{{j}})/u_{{j}}} {u_{{j}}I^2_{{j}}}, \end{displaymath} (4)

where u=E/Ij, Uj=1-1/uj, E is the incident electron energy, and Ij is the collisional ionization potential for the level j considered.

The sum is performed over the subshells j of the ionized ion, and for the ion FeXXV, the 1s subshell is considered (Arnaud & Raymond 1992). The parameters A, B, C, and D (in units of 10-14 cm2 eV2) and I (in eV) are taken from Arnaud & Raymond (1992). The autoionization process of the FeXXV ion can be neglected (Arnaud & Raymond 1992).

The ratio of the ionization rate in a modified Maxwellian distribution to that for a Maxwellian distribution is:

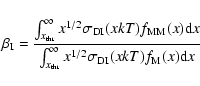\begin{displaymath}\beta_{{\rm I}}=\frac{\int^{\infty}_{x_{{\rm thr}}} x^{1/2}\s... ... thr}}} x^{1/2}\sigma_{{\rm DI}}(xkT) f_{{\rm M}}(x) {\rm d}x} \end{displaymath} (5)

where $f_{{\rm MM}}(x)$ is the modified Maxwellian distribution, $f_{{\rm M}}(x)$ is the Maxwellian distribution, and $\sigma_{{\rm DI}}$ is the direct ionization cross-section of the ion FeXXV. The ionization rate is very sensitive to the fraction of electrons above the threshold energy.

The recombination of a free electron can proceed either by means of a radiative free-bound transition $({\rm FeXXVI}+{\rm e}^{-}\rightarrow {\rm FeXXV}+h\nu)$ or by a radiationless dielectronic recombination.

The radiative recombination rates are less affected by a modified thermal distribution than the ionization rates, since the cross section for recombination decreases with energy and there is no threshold. To estimate the radiative recombination-rate ratio, we follow the methods used by Owocki & Scudder (1983) and Porquet et al. (2001). The ratio of the radiative recombination rate in a modified Maxwellian distribution to that for a Maxwellian distribution is:

\begin{displaymath}\beta_{{\rm RR}}=\frac{\int^{\infty}_{0} x^{-\eta} f_{{\rm MM... ...d}x}{\int^{\infty}_{0} x^{-\eta} f_{{\rm M}}(x) {\rm d}x}\cdot \end{displaymath} (6)

Following the method of Porquet et al. (2001), we used the value $\eta=0.8$ for an iron ion corresponding to the mean value $\langle \eta\rangle$ reported in Arnaud & Rothenflug (1985).

The dielectronic recombination is a resonant process involving bound states at discrete energies Ei and can be computed by summing the contribution of many such bound states. Following the method used by Owocki & Scudder (1983), we assume that the corresponding dielectronic recombination cross section can be approximated by:

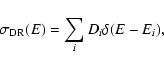\begin{displaymath}\sigma_{\rm DR}(E)=\sum_{{i}} D_{{i}} \delta(E-E_{{i}}), \end{displaymath} (7)

where $D_{{\rm }i}$ are the dielectronic recombination coefficients.

The ratio of the dielectronic recombination rate in a modified Maxwellian distribution to that in a Maxwellian distribution is:

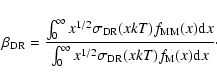\begin{displaymath}\beta_{{\rm DR}}=\frac{\int^{\infty}_{0} x^{1/2}\sigma_{{\rm ... ...0} x^{1/2}\sigma_{{\rm DR}}(xkT) f_{{\rm M}}(x) {\rm d}x}\cdot \end{displaymath} (8)

For the ion FeXXVI, there is one bound state of energy E1=5.3 keV. If the break energy up to which the electron distribution is Maxwellian is higher than this bound state energy, then the dielectronic recombination rate is not influenced by the suprathermal electrons.

Thus, the ionic fraction ratio $\xi_{{\rm FeXXV}}/\xi_{{\rm FeXXVI}}$ of two adjacent stages FeXXV and FeXXVI for a modified Maxwellian distribution can be written as:

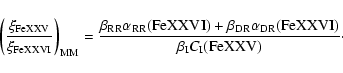\begin{displaymath}\left(\frac{\xi_{{\rm FeXXV}}}{\xi_{{\rm FeXXVI}}}\right)_{{\... ...({\rm FeXXVI})}{\beta_{{\rm I} }C_{{\rm I}}({\rm FeXXV})}\cdot \end{displaymath} (9)

2.2 Excitation rates and iron line flux ratio

In the coronal model (see e.g. Mewe 1999), the line spectrum is dominated by radiative decay following electron impact excitation, plus a smaller contribution of recombination lines. We assume here that all iron ions that are to be excited are in the ground state (see e.g. Mewe & Gronenschild 1981). Considering only the dominant process of collisional excitation (Tatischeff 2003), the volume emissivity $P^{ab}_{{\rm Fe}^{+i}}$ (in units of photons cm-3 s-1) of a particular line transition $a\rightarrow b$ in an ion Fe+i can be written as

\begin{displaymath}P^{ab}({\rm Fe}^{+i})=n_{{\rm e}} n_{{\rm H}} a_{{\rm Fe}} \xi_{{\rm Fe}^{+i}} S^{ga}_{{\rm Fe}^{+i}} B_{ab} , \end{displaymath} (10)

where $n_{\rm H}$ is the H ionic number density (cm-3), $a_{{\rm Fe}}$ is the abundance of iron relative to hydrogen, $\xi_{{\rm Fe}^{+i}}$ is the ionic fraction of ion Fe+i, $S^{ga}_{{\rm Fe}^{+i}}$ is the rate for electron-impact excitation of an ion Fe+i from its ground state to its excited state a, and Bab is the radiative branching ratio of the transition $a\rightarrow b$ among all possible transitions from the level a.

The excitation rates $S^{ga}_{{\rm Fe}^{+i}}[f(x)]$ are functionals that are calculated by averaging the product of the corresponding cross section and electron velocity over the electron distribution functions f(x):

\begin{displaymath}S^{ga}_{{\rm Fe}^{+i}}[f(x)] = \left(\frac{2kT}{m_{{\rm e}}}\... ...x^{1/2}\sigma^{{\rm Fe}^{+i}}_{{\rm ex}}(x k T) f(x) {\rm d}x, \end{displaymath} (11)

where $\sigma^{{\rm Fe}^{+i}}_{{\rm ex}}$ is the excitation section of the ion Fe+i, $x_{{\rm thr},~ {\rm ex}} =E_{{\rm thr},~ {\rm ex}}/(kT)$, and $E_{{\rm thr},~ {\rm ex}}$ corresponds to the threshold energy of the excitation process.

The emission lines due to FeK$\alpha$ transitions of ions FeXXV and FeXXVI are at 6.7 keV and 6.9 keV, respectively. Ions with closed-shell configurations are more stable than those with partially filled shells; thus, He-like FeXXV, whose ground state is 1s2, is dominant over a large temperature range, because its ionization rate is relatively low compared to those of adjacent ions (e.g. Arnaud & Raymond 1992). The strongest line emission is then the He-like FeK$\alpha$ line complex at 6.7 keV, which corresponds to the transitions $\rm 1s^2{-}1s2p ^{1}P$, $\rm 1s^2{-}1s2p^{3}P$, $\rm 1s^2{-}1s2s^{3}S$. At high temperatures (e.g., kT=8 keV), the hydrogen-like iron line ( $\rm 2p \rightarrow 1s$transition) at 6.9 keV also becomes intense.

The electron-impact-excitation-scaled cross-sections of the helium-like ion FeXXV (including impact excitation from $\rm 1^{1}S$to $\rm 2^{1}P$, $\rm 2^{3}P$, $ \rm 2^{3}S$ levels) are taken from the article of Bazylev & Chibisov (1981):

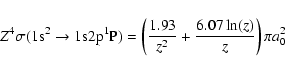\begin{displaymath}Z^4 \sigma( {\rm 1s^2\rightarrow 1s2p^1P})=\left(\frac{1.93}{z^2}+\frac{6.07 \ln(z)}{z}\right) \pi a^2_{0} \end{displaymath} (12)


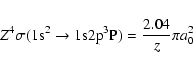\begin{displaymath}Z^4 \sigma({\rm 1s^2\rightarrow 1s2p^3P})=\frac{2.04}{z} \pi a^2_{0} \end{displaymath} (13)


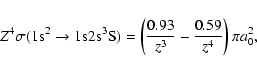\begin{displaymath}Z^4 \sigma({\rm 1s^2\rightarrow 1s2s^3S})= \left(\frac{0.93}{z^3}-\frac{0.59}{z^4}\right) \pi a^2_{0}, \end{displaymath} (14)

where a0 is the Bohr radius, z is the incident electron energy in threshold units, and Z is the ion nuclear charge.

The electron-impact-excitation-scaled cross-section for the hydrogen-like ion FeXXVI is taken from the paper of Fisher et al. (1997):

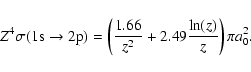\begin{displaymath}Z^4 \sigma({\rm 1s\rightarrow 2p})= \left(\frac{1.66}{z^2}+2.49\frac{\ln(z)}{z}\right) \pi a^2_{0}. \end{displaymath} (15)

There are also contributions from excitations to higher levels, which may radiatively decay to the upper levels of the He-like triplet and H-like doublet. These so-called cascade effects cannot generally be ignored. The electron-impact-excitation-scaled cross-sections of an iron ion from its ground state to the higher levels are taken from the article of Bazylev & Chibisov (1981).

Taking into account electron-impact-excitation, the flux ratio of the iron lines FeXXV and FeXXVI is then

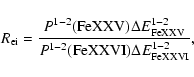\begin{displaymath}R_{{\rm ei}}=\frac{P^{1-2}({\rm FeXXV}) \Delta E^{1-2}_{{\rm FeXXV}}}{P^{1-2}({\rm FeXXVI}) \Delta E^{1-2}_{{\rm FeXXVI}}} , \end{displaymath} (16)

where the volume emissivities $P^{1-2}({\rm FeXXV})$ and $P^{1-2}({\rm FeXXVI})$ are for the He-like triplet and the H-like doublet, and the energies $\Delta E^{1-2}_{{\rm FeXXV}}$and $\Delta E^{1-2}_{{\rm FeXXVI}}$ equal 6.7 keV and 6.9 keV, respectively.

According to Eq. (10), the expression for the flux ratio in terms of ionic fractions and excitation rates is given by

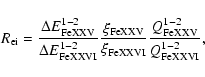\begin{displaymath}R_{{{\rm ei}}}=\frac{\Delta E^{1-2}_{{\rm FeXXV}}}{\Delta E^{... ...XVI}} }\frac{Q^{1-2}_{{\rm FeXXV}}}{Q^{1-2}_{{\rm FeXXVI}} } , \end{displaymath} (17)

where the rate coefficients are $Q^{1-2}_{{\rm FeXXV}}=\sum\limits_{a}\sum\limits_{b (<a)} S^{1s^2-a}_{{\rm FeXXV}} B_{ab}$, $Q^{1-2}_{{\rm FeXXVI}}=\sum\limits_{a}\sum\limits_{b (<a)} S^{1s-a}_{{\rm FeXXVI}} B_{ab}$. The excited states bcorrespond to the upper levels of the He-like triplet and the H-like doublet, and the radiative, branching ratios are given by,

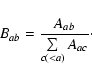\begin{displaymath}B_{ab}=\frac{A_{ab}}{\sum\limits_{c (<a)} A_{ac}} \cdot \end{displaymath} (18)

All necessary transition probabilities Aac are taken from Ralchenko et al. (2008).

However, in plasmas in collisional ionization equilibrium, radiative recombination contributes about 10% of the total line flux. We calculated the rate coefficients for the contribution of radiative recombination to spectral-line formation with Eq. (A.9) in Mewe et al. (1985). The influence of the suprathermal, electron population on the radiative recombination rates was described by Owocki & Scudder (1983) (see Eq. (6)). Although, as noted below, the ratio of the radiative recombination rates $\beta_{\rm RR}$ depends slightly on the presence of suprathermal electrons in the spectrum, the ionic fractions of FeXXVI and of FeXXVII, and, therefore, the line emissivities vary with the presence of suprathermal electrons.

Taking into account both electron-impact-excitation and radiative recombination the line flux ratio is given by

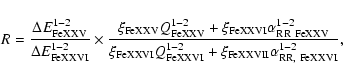\begin{displaymath}R=\frac{\Delta E^{1-2}_{{\rm FeXXV}}}{\Delta E^{1-2}_{{\rm Fe... ...+ \xi_{{\rm FeXXVII}}\alpha^{1-2}_{{\rm RR},\ {\rm FeXXVI}} }, \end{displaymath} (19)

where $\alpha^{1-2}_{{\rm RR},\ {\rm FeXXV}}$ and $\alpha^{1-2}_{{\rm RR},\ {\rm FeXXVI}}$ are the rate coefficients for the contribution from radiative recombination to the spectral lines FeXXV (He-like triplet) and FeXXVI (H-like doublet), respectively. The ionic fractions of $\xi_{{\rm FeXXVII}}$ and $\xi_{{\rm FeXXVI}}$ were calculated following the same method as in Sect. 2.1.

Figure 1 shows the iron-line flux ratios for the pure Maxwellian distribution calculated in this section (dot-dashed line) and those obtained from the MEKAL model (points) by Nevalainen et al. (2003).

3 An analysis of electron spectra in clusters

Bremsstrahlung from suprathermal electrons has been invoked as a possible explanation for hard X-ray tails in the X-ray spectra of some galaxy clusters. In this section, we calculate the impact of suprathermal electrons on the FeXXV and FeXXVI emission-line flux ratio in the clusters A2199 and Coma.

 \begin{figure} \par\includegraphics[width=7.5cm,clip]{1095fig1.eps} \end{figure} Figure 1:

Iron-line flux ratios R for a Maxwellian electron distribution (dot-dashed line), a modified Maxwellian distribution $f^{(1)}_{{\rm MM}}$ (dashed line), and a modified Maxwellian distribution $f^{(2)}_{{\rm MM}}$ (solid line) in the temperature range 4.5 keV < kT < 8.5 keV.
Open with DEXTER

3.1 The galaxy cluster Abell 2199

A2199 is a bright cluster at redshift z=0.03. Its average gas temperature is kT=4.7 keV (Kaastra et al. 1999). Spatially resolved spectroscopy indicates a hard tail in the X-ray spectrum of this galaxy cluster (Kaastra et al. 1998). To understand the nature of this hard tail, Sarazin & Kempner (2000) applied a non-thermal bremsstrahlung model with an electron distribution function $f^{(1)}_{\rm MM}(x)$ given by:

                    $\displaystyle f^{(1)}_{{\rm MM}}(x)$ = $\displaystyle f_{{\rm M}}(x), \ \ \ \ \ \ x<3$  
$\displaystyle f^{(1)}_{{\rm MM}}(x)$ = $\displaystyle f_{{\rm M}}(x) + \lambda x^{-(\mu+1)/2}, \ \ \ \ x\geqslant3,$ (20)

where $\mu=3.33$, $\lambda=0.34$ is found from the condition that the non-thermal electron population is 8.1% of the thermal population (Sarazin & Kempner 2000).

The ratio of the radiative recombination rates $\beta_{\rm RR}$ (see Eq. (6)) is 1.013 for the electron distribution function $f^{(1)}_{\rm MM}(x)$. Since the break energy of 3kT is higher than the bound-state energy 5.3 keV for the cluster temperature, the ratio of the dielectronic recombination rates is 1. Therefore, the recombination rates are not affected by suprathermal electrons.

In Fig. 1, we compare the flux ratios R for a Maxwellian electron distribution (dot-dashed line) and for a modified Maxwellian distribution $f^{(1)}_{{\rm MM}}$ (dashed line) in the temperature range 4.5 keV < kT < 8.5 keV.

For the galaxy cluster A2199 (kT=4.7 keV), the flux ratio R for a modified Maxwellian distribution $f^{(1)}_{{\rm MM}}$ decreases by $\approx$$27\%$ with respect to the case of a Maxwellian distribution. This value of the flux ratio would correspond to a thermal, electron spectrum (i.e. without suprathermal electrons) with an effective temperature of kT = 5.4 keV.

3.2 The Coma cluster

The Coma cluster is a rich, hot, nearby (z=0.02) galaxy cluster. Its average temperature is kT=8.2 keV as derived from XMM-Newton observations (Arnaud et al. 2001).

Hard X-ray radiation was detected in excess of thermal emission in the Coma cluster by its first Beppo-SAX observation (Fusco-Femiano et al. 1999), and confirmed by a second independent observation after a time interval of about 3 yr (Fusco-Femiano et al. 2004). The reliability of the Fusco-Femiano et al. (1999, 2004) analyses was discussed further by Rossetti & Molendi (2004, 2007) and by Fusco-Femiano et al. (2007).

The presence of a second component in the X-ray spectrum of the Coma cluster was also derived from two RXTE observations (Rephaeli & Gruber 2002).

The spectrum of background and accelerated electrons was found by Gurevich (1960) from a kinetic equation describing stochastic particle acceleration:

$\displaystyle f^{(2)}_{{\rm MM}}(x)= \frac{2\sqrt{x}}{\sqrt{\pi}} \Bigg(\exp\Bi... ...Bigg) -\exp\Bigg(-\int^{\infty}_{0}\frac{g {\rm d}g}{1+\alpha g^5}\Bigg)\Bigg),$     (21)

where the parameter $\alpha=9\times 10^{-4}$ was derived by Dogiel (2000) from the bremsstrahlung model for the origin of the hard X-ray emission from the Coma cluster. Here x=E/(kT) is the reduced energy and the integration was completed for the quantity $g=p/\sqrt{m_{{\rm e}}kT}$, which is the dimensionless momentum.

The ratio of the radiative recombination rates $\beta_{\rm RR}$ (see Eq. (6)) is 1.01 for the electron distribution function $f^{(2)}_{{\rm MM}}(x)$. For values kT in the range 4.5-8.5 keV, the values of $\beta_{{\rm DR}}$ are found in the range 1.0005-1.0025. Therefore, the recombination rates are unaffected by suprathermal electrons.

In Fig. 1, we compare the flux ratios R for the Maxwellian electron distribution (dot-dashed line) and the modified Maxwellian distribution $f^{(2)}_{{\rm MM}}$ (solid line) in the temperature range 4.5 keV <kT< 8.5 keV.

For the Coma cluster (kT=8.2 keV), the flux ratio R for a modified Maxwellian distribution $f^{(2)}_{{\rm MM}}$ decreases by $\approx$$9\%$ with respect to the case of a Maxwellian distribution. This value of the flux ratio would correspond to a thermal, electron spectrum (i.e. without suprathermal electrons) with the effective temperature of kT = 8.6 keV.

3.3 A synthetic low temperature cluster

In Sects. 3.1 and 3.2, iron-line flux ratios were calculated for low-temperature and high-temperature galaxy clusters (Abell 2199 and Coma respectively). As shown in Fig. 1, the impact of a suprathermal, electron population on the iron-line flux ratio is stronger in low-temperature clusters. For a specific example we demonstrate how the effective temperature inferred from the flux ratio of the iron lines can yield important constraints on the fraction of suprathermal electrons. For this purpose, a synthetic cluster with temperature kT=4.7 keV and an electron distribution function $f^{(1)}_{{\rm MM}}$ is considered. The dependence of the effective temperature on the fraction of suprathermal electrons is shown in Fig. 2.

 \begin{figure} \par\includegraphics[width=7.5cm,clip]{1095fig2.eps} \end{figure} Figure 2:

Dependence of the effective temperature kT (given in units of keV) on the fraction of suprathermal electrons in a cluster of temperature 4.7 keV.
Open with DEXTER

Since the effective temperature varies significantly with the suprathermal, electron fraction, the iron flux ratio can be used to reveal a suprathermal, electron population in low temperature clusters and in cluster cool cores.

4 The continuum spectrum

Non-thermal electrons change the flux ratio R and lead to an apparently higher temperature derived from the iron line ratio (i.e. the effective temperature, see Sect. 3 and Fig. 2). Alternatively, the temperature can be measured from the bremsstrahlung-spectrum curvature. However, in the presence of non-thermal electrons, these same electrons will also generate non-thermal bremsstrahlung, which alters the shape of the continuum spectrum. We present a method for determining the temperature of the thermal part of a more complex electron distribution from the bremsstrahlung spectrum. A disagreement between both temperatures will depend on the strength of the non-thermal electron component.

To separate the contributions of thermal (low-energy) and non-thermal (high-energy) electron components to the bremsstrahlung spectrum, we study the features of the energy flux spectrum.

The bremsstrahlung energy flux can be given by

\begin{displaymath}\Phi(E_{{x}})= \frac{n^2_{{\rm e}} V}{4\pi d^2} E_{{x}}\int^{... ...m B}}(E, E_{{x}}) \sqrt{\frac{2E}{m_{{\rm e}}}} f(E) {\rm d}E, \end{displaymath} (22)

where V is the cluster volume, d is the distance to the galaxy cluster, and $\sigma_{{\rm B}}(E, E_{{x}})$ is the bremsstrahlung cross-section. For the sake of illustration, we consider the bremsstrahlung cross-section in the form of $\sigma_{{\rm B}}(E, E_{{x}})={\rm const.}/E_{{x}}E$ (following the approximation from the paper of Ginzburg 1979). Then, for a Maxwellian electron distribution, the dependence of the energy flux on the photon energy is given by $\Phi(E_{{x}})\propto \exp(-E_{{x}}/kT)$. For modified Maxwellian electron distributions, the energy flux at low photon energies has two components: thermal $\Phi_{1}(E_{{x}})=C_{1} \exp(-E_{{x}}/kT)$ and non-thermal $\Phi_{2}(E_{{x}})=C_{2}$. The non-thermal component of the bremsstrahlung energy flux is constant if the low limit of the integral in Eq. (22) is smaller than the energy $E_{{\rm M}}$ at which the electron distribution deviates from a Maxwellian distribution ( $E_{{\rm M}}=14$ keV for the cluster A2199 (Kempner et al. 2000); and $E_{{\rm M}}=30$ keV for the Coma cluster (Dogiel 2000)). Considering the energy band with $E_{{x}}<E_{{\rm M}}$, it is possible to fit the energy flux spectrum with a function $\Phi(E_{{x}})=C_{1} \exp(-E_{{x}}/kT)+C_{2}$ and calculate the normalization constants C1 and C2, and also the temperature T of the thermal part of the electron distribution from the bremsstrahlung spectrum.

An analysis of RXTE measurements of the Coma cluster (Rephaeli & Gruber 2002) provided evidence of the presence of a second spectral component at energies up to $\sim$20 keV, since the fit for a single isothermal model was of poor quality. When a second thermal component was added, the best-fit temperatures of the primary and secondary components were then kT1=7.5 keV and the very high value $kT_{2}\simeq37.1$ keV. The contribution of the second component $\Phi_{2}(E_{{x}})\propto \exp(-E_{{x}}/kT_{2})$ to the low-energy continuum spectrum is flat as noted above. Therefore, the thermal and non-thermal components can, in principle, be separated by studying the shape of the continuum spectrum.

From Eq. (22), we calculated the energy fluxes $\Phi (E_{{x}})$ of the Coma cluster in the range 4-20 keV for a Maxwellian electron distribution and for a modified Maxwellian distribution  $f^{(2)}_{{\rm MM}}$, as shown in Fig. 3. The values of the cluster parameters (e.g. temperature, and density) were taken from Dogiel (2000). The difference between the total 4-20 keV fluxes (i.e. the total 4-20 keV flux of the second spectral component) was $\approx$7%. The spectral components must be separated to obtain the temperature from the bremsstrahlung, continuum spectrum.

 \begin{figure} \par\includegraphics[width=7.5cm,clip]{1095fig3.eps} \end{figure} Figure 3:

The energy flux $\Phi (E_{{x}})$ of the Coma cluster in the range 4-20 keV for a Maxwellian electron distribution (dashed line) and for a modified Maxwellian distribution $f^{(2)}_{{\rm MM}}$ (solid line).
Open with DEXTER

5 Conclusions

We have shown in this paper that the iron-line flux ratio depends on the presence of suprathermal electrons proposed to account for measurements of hard X-ray excess emission from galaxy clusters. The influence of the energetic, suprathermal, electron population on the iron-line flux ratio is more significant in low temperature clusters (such as Abell 2199) than in high temperature clusters (as Coma) because the fraction of thermal electrons with energies higher than the helium-like iron ionization-potential in low temperature clusters is smaller than that in high temperature clusters.

Since the decrease in the flux ratio of He-like $K_{\alpha}$ to H-like $K_{\alpha}$ lines is expected for modified Maxwellian distributions in A2199 and Coma with respect to the case of a Maxwellian distribution, the observation of the flux ratio is a tool for testing the nonthermal, electron, bremsstrahlung model, and discriminating between different interpretations of the X-ray excess. To demonstrate the presence and measure the strength of the non-thermal electron component, we propose comparing the temperatures obtained from the iron-line flux ratio and the low-energy continuum spectrum.

The spectral resolution of XMM-Newton is sufficient for measuring the flux ratio of the iron lines in hot temperature clusters. The constraint of the flux ratio for Coma within a radius 5$^{\prime}$is 1.6+0.9-0.6 (Nevalainen et al. 2003). However, the XMM-Newton sensitivity in this high-temperature regime is insufficient to reveal the contribution from suprathermal electrons in the Coma cluster (see Fig. 1).

At low temperatures (e.g. kT<5 keV), the FeXXVI line is weak and is below the noise level of the available XMM-Newton data (Nevalainen et al. 2003). Therefore, the iron-line flux ratio cannot be measured by XMM-Newton in cooler clusters. On the other hand, the flux ratio of the iron lines in low temperature clusters is measurable with data from XMM-Newton, if the fraction of suprathermal electrons is sufficiently high (see Fig. 2).

Suzaku is also able to measure these two Fe lines in hot clusters due to its good spectral resolution (e.g. Fujita et al. 2008).

We have considered the He-like triplet and the H-like doublet iron lines in this paper. Although XMM-Newton and Suzaku can distinguish the He-like from the H-like complex, their spectral resolution of $\sim$100 eV causes that the observed line features do not only consist of the pure He-like triplet and H-like doublet, but each of these is blended with a multitude of satellite lines (e.g. Gabriel 1972; Dubau et al. 1981). For instance, for a temperature of 4.5 keV, about $\sim$30% of the flux from both line complexes is due to these satellite lines. To analyse the influence of satellite lines on the measurement precision of the iron-line flux ratio, we calculated the flux ratio $R_{\rm B}$ of the two (6.6-6.7 keV) and (6.9-7.0 keV) blends using a line list[*], and found that in the temperature range [4.5-8.5 keV] the values of R and $R_{\rm B}$ differ by less than 5%. Therefore, the blend flux ratio $R_{\rm B}$ as well as the ratio R can be used to measure the temperature in this temperature range.

The autoionizing levels responsible for the satellites are excited by electrons at precisely the energies $E_{{\rm s}}$ (see Eq. (40) from Mewe & Gronenschild 1981) corresponding to those levels. Since the energies $E_{{\rm s}}$ are lower than the energy $E_{{\rm M}}$ at which the electron distributions in the Abell 2199 and Coma clusters deviate from a Maxwellian distribution, the exciting electrons belong to the thermal part of the electron distribution. Taking into account this fact and the dependence of the ionicfractions on the distribution function (see Sect. 2.1), we estimate that the decreases in the flux ratios $R_{\rm B}$ for modified Maxwellian distributions in A2199 and Coma with respect to a Maxwellian distribution are 30% and 10%, respectively.

New high-spectral-resolution instruments with higher sensitivity, such as XEUS, are needed to resolve the lines and measure the flux ratio of the iron $K_{\alpha}$ lines with the purpose of testing these hard X-ray tail interpretations.

Acknowledgements

We are grateful to Jelle Kaastra and Jean-Luc Sauvageot for valuable discussions and to the referee for constructive comments.

D.P. and V.D. are partly supported by the RFBR grant 08-02-00170-a, the NSC-RFBR Joint Research Project 95WFA0700088 and by the grant of the President of the Russian Federation ``Scientific School of Academician V. L. Ginzburg''.

References

Footnotes

... list[*]
http://www.sron.nl/divisions/hea/spex/version1.10/line/index.html

All Figures

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1095fig1.eps} \end{figure} Figure 1:

Iron-line flux ratios R for a Maxwellian electron distribution (dot-dashed line), a modified Maxwellian distribution $f^{(1)}_{{\rm MM}}$ (dashed line), and a modified Maxwellian distribution $f^{(2)}_{{\rm MM}}$ (solid line) in the temperature range 4.5 keV < kT < 8.5 keV.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1095fig2.eps} \end{figure} Figure 2:

Dependence of the effective temperature kT (given in units of keV) on the fraction of suprathermal electrons in a cluster of temperature 4.7 keV.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1095fig3.eps} \end{figure} Figure 3:

The energy flux $\Phi (E_{{x}})$ of the Coma cluster in the range 4-20 keV for a Maxwellian electron distribution (dashed line) and for a modified Maxwellian distribution $f^{(2)}_{{\rm MM}}$ (solid line).
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.