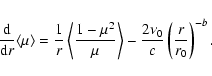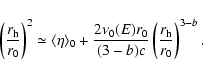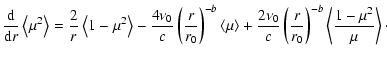EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 496 / No 1 (March II 2009) A&A, 496 1 (2009) 129-131 Full HTML
Open Access
Issue
A&A
Volume 496, Number 1, March II 2009
Page(s) 129 - 131
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361:200810857
Published online 20 January 2009

Estimating the size of the cosmic-ray halo using particle distribution moments
(Research Note)

Y. E. Litvinenko

Department of Mathematics, University of Waikato, PB 3105, Hamilton, New Zealand

Received 26 August 2008 / Accepted 6 January 2009

Abstract
Context. Particle transport in many astrophysical problems can be described either by the Fokker-Planck equation or by an equivalent system of stochastic differential equations.
Aims. It is shown that the latter method can be applied to the problem of defining the size of the cosmic-ray galactic halo.
Methods. Analytical expressions for the leading moments of the pitch-angle distribution of relativistic particles are determined. Particle scattering and escape are analyzed in terms of the moments.
Results. In the case of an anisotropic distribution, the first moment leads to an expression for the halo size, identified with the particle escape from the region of strong scattering. Previous studies are generalized by analyzing the case of a strictly isotropic initial distribution. A new expression for the variance of the distribution is derived, which illustrates the anisotropization of the distribution.
Conclusions. Stochastic calculus tools allow one to analyze physically motivated forms for the scattering rate, so that a detailed realistic model can be developed.

Key words: cosmic rays - galaxies: halos - scattering

1 Introduction

Knowledge of evolving nonthermal particle distributions, resulting from particle interaction with a background plasma, is important in a variety of astrophysical applications. A well-known example is provided by modeling accelerated electrons in the flaring solar corona, which undergo Coulomb collisions and generate hard X-ray emission in flares (e.g., Leach & Petrosian 1981; MacKinnon 1991). Particle interaction with turbulent magnetic fields has been repeatedly studied in the context of cosmic-ray transport (e.g., Earl 1974; Toptygin 1985; Hein & Spanier 2008). Of particular interest is the relationship between the angular distribution of relativistic galactic cosmic rays and the formation of a galactic cosmic-ray halo. This halo is typically defined as a region surrounding the galactic disk, in which the cosmic-ray density significantly exceeds that in the intergalactic medium (e.g., Ginzburg & Ptuskin 1976; Dogiel et al. 1993). In all these cases, scattering strongly influences the evolving particle distributions, yet accurate description of scattering represents a significant mathematical difficulty because scattering leads to stochastic effects in particle orbits.

Mean-scattering approximation neglects dispersion in the particle distribution and leads to a relationship between the average pitch angle and kinetic energy of a particle (e.g., Craig et al. 1985). Defining the mean rates of change of these quantities, however, is not always straightforward (e.g., MacKinnon 1988; Conway et al. 1998). In any case, to go beyond the mean-scattering approximation and explore the spread around the mean values, the distribution function must be determined by solving the Fokker-Planck equation. This is typically done using numerical methods. Although analytical solutions can help in developing a better understanding of the problem, usually they can be found only in two limiting cases. A series expansion in terms of Legendre polynomials for the cosine of the pitch angle (or expressions obtained by perturbation techniques) can provide a reasonable level of accuracy if the distribution function is quasi-isotropic (e.g., Earl 1974; MacKinnon 1991). Approximate analytical expressions can also be derived in the opposite limit of strongly anisotropic (runaway) particle distributions (e.g., Leach & Petrosian 1981).

A new approach to the problem of nonthermal particle transport, described by the linearized Fokker-Planck equation, had been suggested by Conway et al. (1998). The idea is to avoid solving the equation for the distribution function explicitly. Instead, analytical expressions for the moments of the distribution function are determined from an equivalent system of stochastic differential equations. Features of the particle transport are then analyzed in terms of the moments. The approach has been used to provide analytical description of collisionally evolving energetic electrons in solar flares, including systematical derivation of the mean-scattering approximation and application of the second-order moments to interpret radiation from flare loop-top hard X-ray sources (Conway et al. 1998; Conway 2000).

The purpose of this note is to point out that Conway et al.'s approach can help in developing some insight into how the size of the galactic cosmic-ray halo is related to properties of evolving anisotropic particle distributions in a scattering medium.

2 Fokker-Planck and Ito equations

The galactic cosmic-ray halo (e.g., Bulanov et al. 1976; Stecker & Jones 1977) can be defined as a region where the cosmic-ray particles remain effectively confined because of their scattering in turbulent magnetic fields (Dogiel et al. 1993, 1994). The size of the region follows from the solution of the corresponding kinetic equation, which shows the transition from a diffusive regime to a runaway behavior. The transition identifies the halo size. Other models typically introduce the halo phenomenologically and focus instead on describing the diffusive propagation of cosmic-ray particles in galaxies (e.g., Lerche & Schlickeiser 1982).

Following Dogiel et al. (1993), consider the propagation of energetic particles in a galaxy. Assuming typical length scales to be greater than those of the particle sources, the axisymmetric particle distribution function $f (r, \mu, v, t)$ is described by the following kinetic equation:

\begin{displaymath}\frac{\partial f}{\partial t} + \mu v \frac{\partial f}{\part... ...eft[ (1 - \mu^2) \frac{\partial f}{\partial \mu} \right] + q. \end{displaymath} (1)

Here t is time, r is the length of the radius vector, v is the particle speed, and $\mu = \cos \theta$ is the cosine of the pitch angle. Here and in what follows, the relativistic case is considered, v = c, so that the solution to the kinetic equation depends on the total particle energy E as a parameter. The cosmic-ray interaction with magnetic field fluctuations is described by the scattering term on the righthand side of the equation. The spatial dependence of the scattering frequency $\nu (E, r)$ is motivated by the decrease of the magnetic energy density with distance from the galactic center:

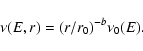\begin{displaymath}\nu (E, r) = (r/r_0)^{-b} \nu_0 (E). \end{displaymath} (2)

where $\nu_0 (E) \sim E^{-a}$. For the case of a localized point-like cosmic-ray source, the particle source function is given by $q = q (E) \delta (r)$.

Instead of solving the kinetic equation by determining approximate solutions in the diffusion and runaway regions and matching them in a transition region (Dogiel et al. 1993), note that the equation can be recast in the following form:

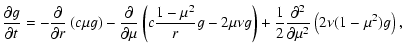$\displaystyle \frac{\partial g}{\partial t} = - \frac{\partial}{\partial r} \le... ...ac{1}{2} \frac{\partial^2}{\partial \mu^2} \left( 2 \nu (1 - \mu^2) g \right) ,$     (3)

where r > 0 and g = r2 f. Using the Ito stochastic calculus, the equation in this form can be shown to be equivalent to a system of stochastic ordinary differential equations. Application of the standard theory (e.g., Gardiner 1985; MacKinnon & Craig 1991) leads to the following system:

\begin{displaymath}{\rm d}r = c \mu {\rm d}t, \end{displaymath} (4)


$\displaystyle {\rm d} \mu = \left[ c \frac{1 - \mu^2}{r} - 2 \left( \frac{r}{r_... ... \left( \frac{r}{r_0} \right)^{-b} \nu_0 (1 - \mu^2) \right]^{1/2} {\rm d}W(t),$     (5)

where dW represents the Wiener process with the zero mean and the variance equal to t. While this is a standard definition (Gardiner 1985), note for clarity that MacKinnon & Craig (1991) and Conway et al. (1998) adopted a different definition of W, in which the variance is given by 2t.

Because only one of the two equations above contains a noise term, they can be easily combined into the following equation:

$\displaystyle {\rm d} \mu = \left[ \frac{1 - \mu^2}{r \mu} - \frac{2\nu_0}{c} \left( \frac{r}{r_0} \right)^{-b} \right] {\rm d}r$$\displaystyle + \left[ \frac{2\nu_0}{c} \left( \frac{r}{r_0} \right)^{-b} \frac{1 - \mu^2}{\mu} \right]^{1/2} {\rm d}W(r).$     (6)

This stochastic differential equation leads to ordinary differential equations for the moments of the particle distribution and thus provides the basis for the analysis that follows.

3 Moments of the particle distribution

Consider first the limiting case of a strongly anisotropic distribution, so that $\mu \simeq 1$ is the main region of interest. Averaging the exact Eq. (6) gives the following equation for the first moment of the angular distribution:

\begin{displaymath}\frac{\rm d}{{\rm d}r} \langle \mu \rangle = \frac{1}{r} ... ...angle - \frac{2 \nu_0}{c} \left( \frac{r}{r_0} \right)^{-b}. \end{displaymath} (7)

In the limit $\eta = 1 - \mu \to 0$, the equation takes a simpler form:

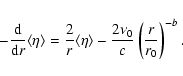\begin{displaymath}- \frac{\rm d}{{\rm d}r} \langle \eta \rangle = \frac{2}{r}... ...rangle - \frac{2 \nu_0}{c} \left( \frac{r}{r_0} \right)^{-b}. \end{displaymath} (8)

The solution is given by

\begin{displaymath}\langle \eta \rangle = \left( \frac{r_0}{r} \right)^{2} \lef... ...u_0 r_0}{(3-b) c} \left( \frac{r}{r_0} \right)^{3-b} \right]. \end{displaymath} (9)

Clearly b>1 provides a sufficient condition for an anisotropic distribution formation. Now the condition $\langle \eta (r_{\rm h}) \rangle \simeq 1$ gives the cosmic-ray halo size $r_{\rm h}$, identified with the particle escape region:

\begin{displaymath}\left( \frac{r_{\rm h}}{r_0} \right)^{2} \simeq \langle \eta ... ... (E) r_0}{(3-b) c} \left( \frac{r_{\rm h}}{r_0} \right)^{3-b}. \end{displaymath} (10)

This estimate generalizes Eq. (12) in Dogiel et al. (1993). In particular, their Eq. (12) does not contain the first term on the righthand side, which can describe the effect of adiabatic focusing in the presence of a large-scale regular magnetic field. Notably, Dogiel et al.'s analysis implies a different numerical factor in the expression for $ \langle \eta \rangle$ because a factor of 2 is missing and the term $-2 \nu \eta \partial f / \partial \eta$ is neglected on the righthand side of their Eq. (14). Thus the present analysis appears to be not only somewhat simpler but also more accurate.

The stochastic differential Eq. (6) retains the full information about the evolution of the particle distribution function. The key point is that equations describing distribution moments of any order can be easily written down using the Ito formula (e.g., Mikosch 1998). This allows one to analyze the problem in both diffusion and runaway regions in a straightforward manner. For example, the equation for the second moment is obtained by using Eq. (6) in the Ito formula for ${\rm d} \mu^2 = 2 \mu {\rm d} \mu + ({\rm d} \mu)^2 $ and averaging:

$\displaystyle \frac{\rm d}{{\rm d}r} \left\langle \mu^2 \right\rangle = \frac{2... ...rac{r}{r_0} \right)^{-b} \left\langle \frac{1 - \mu^2}{\mu} \right\rangle \cdot$     (11)

Combining the exact Eqs. (7) and (11) gives
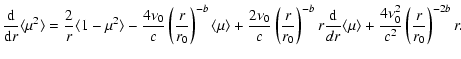$\displaystyle \frac{\rm d}{{\rm d}r} \langle \mu^2 \rangle = \frac{2}{r} \langl... ...angle \mu \rangle + \frac{4 \nu_0^2}{c^2} \left( \frac{r}{r_0} \right)^{-2b} r.$     (12)

Now suppose that the initial distribution is isotropic, $\langle \mu \rangle_0 = 0$ at r=r0. Since $ {\rm d} \langle \mu^2 \rangle / {\rm d}r > 0 $, the dispersion of the distribution will inevitably increase. Assuming that $\langle \mu \rangle \simeq 0$ for r sufficiently close to r0, the equation above can be solved to give a completely new result for the dispersion:
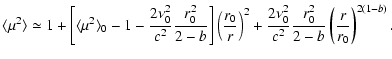$\displaystyle \langle \mu^2 \rangle \simeq 1 + \left[ \langle \mu^2 \rangle_0 -... ... \frac{2 \nu_0^2}{c^2} \frac{r_0^2}{2-b} \left( \frac{r}{r_0} \right)^{2(1-b)}.$     (13)

The approximate expression for $ \langle \mu^2 \rangle $ breaks down for sufficiently large r where $ \langle \mu \rangle $ is no longer negligible. The expression for $ \langle \mu^2 \rangle $ shows that even a strictly isotropic distribution at r=r0 eventually becomes localized at $\mu \simeq 1$. The localization corresponds to the cosmic-ray escape from the strong-scattering region and thus justifies the previous treatment in the limit $\mu \to 1$.

4 Discussion

The Fokker-Planck equation that emerges in many astrophysical problems is well known to be formally equivalent to a system of stochastic differential equations. The stochastic system can be used to derive analytical expressions for the moments of the particle distribution, which yield significant information on the evolution of the distribution. The usefulness of this approach had been illustrated by its application to the transport of accelerated electrons in flaring loops in the solar corona (Conway et al. 1998).

The main aim of this note was to demonstrate that the significant potential of Conway et al.'s approach is by no means limited to description of fast electrons in solar flares. It is shown here how the method can be used to calculate the size of the galactic cosmic-ray halo, defined by the efficiency of the escape of relativistic particles in a scattering medium. As a practical matter, once the stochastic equations are written down, the technique involves averaging and solving ordinary differential equations. This should be contrasted with the traditional approach (Dogiel et al. 1993) that generally involves solving partial differential equations. A simpler technique reduces both the need for lengthy calculations and the potential for error.

As shown above, angular distribution moments can be systematically determined from the averaged stochastic differential equations in both the diffusion and runaway regions of the particle distribution. In principle the stochastic equations contain all the information about the distribution function and the moments can be used to construct the complete solution. The key advantage of the present method is that the first few moments of the distribution, which are relatively simple in form, directly lead to an expression for the halo size as a function of the particle energy and the scattering rate. Thus the low-order moments provide a simpler direct way of addressing the particular question of the halo size definition.

Note for clarity that the solution based on the first few moments cannot be useful for certain types of distribution. As pointed out by the referee, an obvious example would be a power-law distribution ${\sim}(\mu - \mu_0)^{-\alpha}$. It is unlikely, however, that this would significantly limit the usefulness of the approach in general, because such singular angular distributions of accelerated particles are unlikely to be generated by any of the standard particle acceleration mechanisms in astrophysics (e.g., Schlickeiser 2002, and references therein).

It is straighforward to generalize the method to incorporate additional effects, so that a detailed physical model can be eventually developed. For instance, no additional difficulty arises when regular energy losses are taken into consideration in the kinetic equation for the cosmic-ray particles. Other physically motivated forms for the scattering rate dependencies on the particle energy and position can also be analyzed.

Acknowledgements
This work was supported by NASA (grants NNX07AI04G and NNX08AG44G), NSF (grant ATM-0734032), and by a research fellowship from the Alexander von Humboldt Foundation. Comments by the anonymous referee are gratefully acknowledged.

References

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.