A giant bar induced by a merger event at z = 0.4?

S. Peirani; F. Hammer; H. Flores; Y. Yang; E. Athanassoula

doi:10.1051/0004-6361/200810760

Press Release

Free Access

Issue		A&A Volume 496, Number 1, March II 2009


Page(s)		51 - 56
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/200810760
Published online		30 January 2009

A giant bar induced by a merger event at z = 0.4?

S. Peirani¹ - F. Hammer² - H. Flores² - Y. Yang² - E. Athanassoula³

1 - Institut d'Astrophysique de Paris, 98 bis Bd Arago, 75014 Paris, France
2 - GEPI, Observatoire de Paris, CNRS, University Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
3 - LAM, UMR6110, CNRS/Université de Provence, Technopôle de Marseille-Etoile, 38 rue Frédéric Joliot Curie, 13388 Marseille Cedex 20, France

Received 6 August 2008 / Accepted 3 December 2008

Abstract
Context. Disk galaxies are the most common galaxy population in the local universe. However, the formation of their disks and structures - in particular their bars - is still a matter of debate.
Aims. We present a physical model of the formation of J033239.72-275154.7, a galaxy observed at z=0.41 that contains a large, young bar of size 6 kpc. The study of this system is particularly interesting to the understanding of the connection between mergers and bars, as well as the properties and fate of this system in relation to disk galaxy formation.
Methods. We compare the morphological and kinematic properties of J033239.72-275154.7, the latter obtained by the GIRAFFE spectrograph, to those derived from the merger of two spiral galaxies described by idealized N-body simulations, including a star formation prescription.
Results. We found that the general morphological shape and most of the dynamical properties of the object can be well reproduced by a model in which the satellite is initially placed in a retrograde orbit and the mass ratio of the system is 1:3. In this scenario, a bar forms in the host galaxy after the first passage of the satellite, where a significant fraction of the available gas is consumed in an induced burst. In its later evolution, however, we find that J033239.72-275154.7, whose major progenitor was an Sab galaxy, will probably become a S0 galaxy. This is mainly due to the violent relaxation and the angular momentum loss experienced by the host galaxy during the merger process, which is caused by the adopted orbital parameters. This result suggests that the building of the Hubble sequence is influenced significantly by the last major collision. In the present case, the merger leads to a severe damage of the disk of the progenitor, leading to an evolution towards a more bulge-dominated galaxy.

Key words: galaxies: evolution - galaxies: kinematics and dynamics - galaxies: interactions - methods: N-body simulations

1 Introduction

The formation of disk galaxies remains an outstanding puzzle in contemporary astrophysics (see Mayer et al. 2008, for a review). According to hierarchical models of structure formation, mergers and interaction of galaxies are an essential ingredient of galaxy formation and evolution. Earlier works and numerical simulations demonstrated that the remnants of mergers of entirely stellar progenitors are more likely to be elliptical galaxies (Toomre 1977; Barnes 1988; Barnes & Hernquist 1992; Hernquist 1992; Lima-Neto & Combes 1995; Balcells & González 1998; Naab et al. 1999) and later studies extended this result to gas-rich progenitors (Springel & Hernquist 2005; Robertson et al. 2006; Hopkins et al. 2008). Whether this is consistent, or inconsistent with the fraction of disk galaxies present in the local universe depends on the typical number of expected mergers per galaxy (see for instance Kazantzidis et al. 2007). These predictions appear to be inconsistent with observations that suggest that disk galaxies represent the majority (70%) of the galaxy population observed in the local universe (see Hammer et al. 2005; Nakamura et al. 2004, and references therein). To help resolve these issues, Hammer et al. (2005) suggested that disks could be rebuilt during encounters of gas-rich spirals. This proposition was inspired by the simultaneous increase, up to z=1, in the merger rate, in the fraction of actively star-forming galaxies (including luminous IR galaxies, LIRGs) and in the fraction of peculiar galaxies (including those with compact morphologies). These studies were followed by simulations of gas-rich mergers (Springel & Hernquist 2005; Robertson et al. 2006; Governato et al. 2007; Hopkins et al. 2008), which demonstrating that under certain conditions a disk may be rebuilt after a merger. This conclusion had been already reached by Barnes (2002), although these simulations have been less convincing because they do not include a prescription for star formation. Lotz et al. (2006) also analysed a large suite of simulated equal-mass, gas-rich mergers and found that most merger remnants appear disc-like and dusty. This scenario is also consistent with the results of other simulations and semi-analytical models which claim that, without merger processes, most of galaxies and their host dark matter halos cannot acquire the required angular momentum to form disks (see Peirani et al. 2004; Puech et al. 2007, and references therein). The formation of bars is also a fundamental issue in the evolution of disk galaxies, particularly since it has been shown that only about one third of them were in place at z = 0.8 (Sheth et al. 2008).

Our aim is to reproduce by numerical modelling the general morphology (e.g. the presence of a bar and substructures), the dynamical properties of the gas component (velocity fields), the photometric properties of the stars (e.g. colors, star formation rate) of J033239.72-275154.7, a galaxy located at z=0.41 for which we have high quality imaging and kinematical data. This work will also provide useful input to disk formation models, since it provides information about the potential progenitors of the present-day galaxy disks, as well as constraints on their formation (e.g. initial orbital configuration and mass ratio of the system) and possible fate. This work is a subsidiary project of a VLT large program entitled IMAGES (``Intermediate-MAss Galaxy Evolution Sequence'', Yang et al. 2008), which is gathering high quality kinematics for a representative sample of $\sim$ 100 massive galaxies at z=0.4-0.75 and with $M_J(AB)\leq-20.3$ . Using the GIRAFFE spectrograph at the VLT, the kinematic properties of 65 of these galaxies, for instance J033239.72-275154.7, have been derived. This galaxy lies at z=0.41, is classified as a merger from an analysis lead by Neichel et al. (2008), and exhibits a large, young bar. This bar has a size of 6 kpc, i.e. quite large, since 72% of barred galaxies in a sample of 2000 galaxies from the SDSS have a size smaller than this (Barazza et al. 2008). This bar also has an extremely blue color, that is consistent with a starburst, i.e. with ages well below a few 100s of Myr. This is contrasting to many bars in the local universe known to contain relatively old and red stars (Sheth et al. 2003). This paper is organized as follows: in Sect. 2, we present the general morphological and kinetic properties of J033239.72-275154.7, and in Sect. 3, a short description of the numerical modelling and the results obtained. We present our conclusions in Sect. 4.

2 General properties of J033239.72-275154.7

Table 1: Properties of J033239.72-275154.7.

J033239.72-275154.7 was first presented by Yang et al. (2008). Table 1 summarizes its overall properties, including photometry, morphological parameters, and kinematical measurements (provided by the IMAGES data base that can be retrieved from Yang et al. 2008; Neichel et al. 2008; Puech et al. 2008). This object has a stellar mass of $2.0\times 10^{10}~M_\odot$ , a K-band magnitude of M_K=-20.94, and displays a peculiar morphology and kinematics. Its center is dominated by an elongated structure, most likely a giant, thin bar of semi-major axis 0.85 arcsec or about 6 kpc. Neichel et al. (2008) found that its color is approximately b-z=0.8, i.e. typical of a starburst (see their Figs. 8 and 12). This bar is embedded within a diffuse region, which is probably a disk, due e.g. to features that resemble tidal arms (one blue at the upper right on the sky and another on the left), although very irregular, with several blue clumps. Closed to its center, there is a significant concentration of light that we sometimes refer to as the core, which is probably a small bulge Its color is roughly b-z=1.8, as found for galaxies of late type to Sbc (Neichel et al. 2008). The bar is asymmetric, extending spatially far more towards the upper-right side of the core. On the other side of the core, the bar is redder and part of it disappears at UV wavelengths. The discrepancy in color between the two sides is roughly 0.3 mag, as shown by the CDFS-GOODS observations (b-band observations, thus UV rest-frame at z=0.4). At the bottom of the galaxy, there are two bright adjacent knots, which dominate the rest-frame UV light. These knots have the color of a pure starburst and could be hardly resolved. Due to the irregularity of the disk and the existence of bright, tidal arms, it is difficult to measure its position and inclination angle accurately. From the shape of the outer isophotes, we find that the photometric major axis is roughly in the upper-right to lower-left direction and the inclination should be between $28^\circ$ and $35^\circ$ . The star formation rate (SFR) is moderate ( ${\it SFR}_{\rm IR}=6.6$ , ${\it SFR}_{2800}=4.2$ ) and the dust does not affect its overall color significantly. Note that SFRs were estimated using the 2800A and 15 micron luminosities, respectively. Those were converted to SFR using the method described in Kennicutt (1998). Luminosities have been estimated using interpolated relations between observed photometric points provided by HST/ACS, EIS and Spitzer/MIPS, using the method described in Hammer et al. (2001, 2005). The ratio of the ${\it SFR}_{\rm IR}$ to the ${\it SFR}_{2800}$ is consistent with Av=0.22 (standard extinction curve), which is low. Finally, the electron density is modest, including at the blue knots.

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=3.6cm]{760fig1.ps}}\rota... ...fig3.eps}}\rotatebox{0}{\includegraphics[width=4.4cm]{760fig4.eps}} \end{figure}$	Figure 1: B-V-z color map of J033239.72-275154.7 from HST/ACS ( upper left panel) and distribution of the galaxy within the GIRAFFE grid ( upper right panel). The lower panels show the velocity field map ( lower left panel) and the associated $\sigma$ -map ( lower right panel).
Open with DEXTER

The velocity field (VF) is obviously complex (see Fig. 1). The kinematical major axis is almost parallel to the bar and offset by more than one GIRAFFE pixel from the bulge, towards the prominent blue knots (in the bottom). The pixel scale is 0.52 arcsec and the full width half maximum spectral resolution is 23 km s^-1. Details of the GIRAFFE instruments can be found in Flores et al. (2006) and Yang et al. (2008). The small VF amplitude is dominated by the two star-bursting clumps and by the blue arm/giant tidal tail. Even so, the velocity amplitude is relatively small, of the order of 30 km s^-1. The velocity dispersion map is almost featureless at a value of 30-40 km s^-1 over most of the galaxy. Nevertheless, it has a clear, localised $\sigma$ peak (50 km s^-1), which is offset by 2 GIRAFFE pixels from the bulge and could coincide (to within half a GIRAFFE pixel) with a small and relatively blue clump at the upper-right located roughly where the blue, tidal arm joins the disk. The signal-to-noise ratio in this pixel is quite high ( $\sim$ 50).

All evidence supports the conclusion that strong interaction and/or merging is at work in this system. For example, the dynamical axis is off-center and passes through the region where the two bright knots lie. There are strong tidal arms, and the value of $V_{\rm rot}$ / $\sigma$ is small (about 1-2 depending on the exact value of the inclination). The velocity dispersion is about 30-40 km s^-1 over most of the galaxy. Given the VF values and the measured inclination, the rotational velocity is far below the value expected from the tully-fisher (TF) relation, which is $V_{\rm rot}=125$ km s^-1. This value was taken from Hammer et al. (2007), who carefully estimated the various samples used to derive this relationship. Given the spatial resolution, it is not easy to derive a rotation curve. Nevertheless, thorough modelling of the velocity fields was completed by Puech et al. (2008), who investigated the redshift evolution of the Tully-Fisher relation. Given its kinematical and morphological properties, it is thus unlikely that J033239.72-275154.7 can be a rotating disk hosting two giant HII regions because: (1) the two knots have a z-band luminosity corresponding to one third of the total z luminosity (the relative photometry was completed using apertures of diameter equal to the full width half maximum of the knot luminosity, using the IRAF/DAOPHOT/ package); (2) the dynamical axis is strongly off-center; (3) the value of $\sigma$ is high and that of $V_{\rm rot}$ is low.

Could merging of the two bright knots with J033239.72-275154.7 be responsible for producing a giant bar with a relatively blue color? N-body simulations have shown that a small companion merging with a disk galaxy could, depending on its density and its orbit, either destroy a pre-existing bar (Athanassoula 1999; Berentzen et al. 2003), or trigger its formation (Walker et al. 1996; Berentzen et al. 2004).

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=18cm]{760fig5.eps}} \end{figure}$	Figure 2: Time evolution of the projected star number density. The light blue arrows indicate the specific rotation of each galaxy, while the yellow dashed lines show the motion of the satellite. In panel 6, we superposed the GIRAFFE grid. Each frame is 40 kpc $\times$ 40 kpc in size.
Open with DEXTER

3 Simulations

We briefly describe the numerical methodology used to model J033239.72-275154.7. We use idealized N-body simulations of the merger of two spiral galaxies. One of the most difficult part of this work results from the huge number of free parameters in the initial conditions, for instance related to the mass ratio and the orbital configuration of the system, or the star formation prescription. We performed more than 100 simulations and present our fiducial modelling. First, as mentioned in Sect. 2, the dynamical axis of the system is off-center and the velocity field strongly indicates that the satellite is moving toward the main object. By trying different orbital configurations, we found that retrograde orbits for the satellite are more consistent with the orientation of the tidal arms of the main galaxy (in the left and upper right parts) and the specific position of the accreted satellite. Second, different mass ratios of the system, different inclinations between the two orbit planes, and different pericentric distances were tested at the same time in attempting to reproduce the amplitudes of the observed VF and $\sigma$ map. For instance, since the VF amplitudes are small, the inclination between the two orbital planes should also be small. It is also worth mentioning that we restricted our study to parabolic orbits (Khochfar & Burkert 2006) to reduce the number of free parameters. Finally, different parameters related to the star formation recipes (see below) have also been tested in order to obtain results consistent with the observations.

3.1 Initial conditions and numerical method

Our galaxies consist of a spherical dark matter halo (with a Hernquist profile, Hernquist 1990), a disk, containing both stars and gas, and a bulge. In both objects, the disk and the bulge represent respectively 15% and 5% of the total mass. The baryon fraction used here is slightly higher than the cosmic baryon fraction ( $\sim$ 16.7%) derived by Komatsu et al. (2008) in order to compare to and match the results of Barnes (2002). We note that the gas fraction of the disk is 25% in the host galaxy, whereas it is 50% in the accreted satellite. These gas fractions are consistent with the estimations of Liang et al. (2006), Gavazzi et al. (2008), and Rodrigues et al. (2008). However, the Gavazzi et al. (2008) measurements were completed for the local universe, while using the M-Z relationship, Liang et al. (2006) were able to estimate the mass evolution in the gas phase of z=0.6 galaxies, and found that, on average, galaxies at z=0.6 have a factor of two more gas than at the present day. The host galaxy has a stellar mass of $1.3 \times 10^{10}~M_{\odot}$ and is most likely to be a Sab galaxy. Galaxies are created following Springel et al. (2005). Dark matter haloes have a concentration parameter of $C_{\rm host}=14$ and $C_{\rm sat}=15$ for the host and the satellite, respectively, in good agreement with Dolag et al. (2004). Their spin parameter is defined to be $\lambda ={J\mid E \mid ^{1/2}}/{GM^{5/2}}$ , where J is the angular momentum, E is the total energy of the halo, and M is its mass, and equals $\lambda_{\rm host}=\lambda_{\rm sat}=0.05$ to ensure that the rotation curves of the galaxies are closed to the baryonic TF relation (McGaugh 2005). Indeed, their maximum circular velocity is 140 km s^-1 and 98 km s^-1, respectively. In our fiducial model, the satellite is placed on a retrograde, parabolic orbit (Khochfar & Burkert 2006) with a pericentric distance $R_{\rm p}=2.1$ kpc and initial separation of 20 kpc. The inclination between the two orbital planes is $15^\circ$ and the galaxy spins are opposed each other. We note that the initial separation between the two galaxies is quite small in order to reduce the high computational cost of all experiments. A larger distance would decrease the halos overlap at the beginning of the simulation, but this should not change the main results and conclusions of this paper.

The simulation is performed using GADGET2 (Springel 2005) with added prescriptions for cooling, star formation, and feedback from type Ia and II supernovae (SN). Approximately 275 000 particles are used for the experiment, and the masses (M), gravitational softening lengths ( $\epsilon$ ), and number of particles (N) of each component involved are summarized in Table 2.

Table 2: Masses (M), gravitational softening lengths ( $\epsilon$ ) and number of particles (N) of each component used in the simulations.

The cooling and star formation (SF) recipes follow the prescriptions of Thomas & Couchman (1992) and Katz et al. (1996), respectively. Gas particles with T>10⁴ K cool at constant density for the duration of a timestep. Gas particles with $T< 2\times 10^4$ K, number density n > 0.1 cm^-3, overdensity $\Delta \rho_{\rm gas} > 100$ , and ${\bf\nabla . \upsilon} <0$ form stars according to the standard SFR prescription: ${\rm d}\rho_*/{\rm d}t = c_* \rho_{\rm gas}/t_{\rm dyn}$ , where $\rho_*$ refers to the stellar density, $t_{\rm dyn}$ is the dynamical timescale of the gas, and c_* is the SF efficiency. Assuming a constant, dynamical time scale across the timestep, the fractional change in stellar density is $\Delta \rho_*/\rho_* = 1-\exp(-c_* \Delta t/t_{\rm dyn})$ . For each gas particle, we select a random number (r) between 0 and 1 and convert it into a star if $r<\Delta \rho_*/\rho_*$ .

Instead of assuming ``instantaneous'' energy injection, we include the effective lifetime of SN progenitors using the rate of energy injection $H_{\rm SN}$ . For this, we consider stellar lifetimes in the mass ranges of $0.8~M_\odot~<m<8.0~M_\odot$ and $8.0~M_\odot<m<80.0~M_\odot$ for type Ia and type II progenitors, respectively. Using a Salpeter initial mass function for type II SN, we find that:

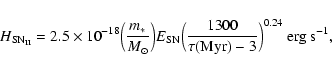$\begin{displaymath}H_{{\rm SN}_{\rm II}}=2.5\times10^{-18}\Big(\frac{m_*}{M_\odo... ...{1300}{\tau(\textnormal{Myr})-3}\Big)^{0.24}~{\rm erg~s^{-1}}, \end{displaymath}$

(1)

where $E_{\rm SN}=10^{51}$ erg, m_* is the mass of the stellar population, and $3.53 < \tau <29$ Myr. For type Ia SN, the heating is delayed, since they appear t₀=0.8-1.0 Gyr after the onset of star formation. Following de Freitas Pacheco (1998), the probability of one event on a timescale $\tau$ after the onset of star formation is given by:

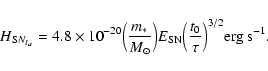$\begin{displaymath}H_{{\rm S}N_{I_a}}=4.8\times10^{-20}\Big(\frac{m_*}{M_\odot}\Big)E_{\rm SN}\Big(\frac{t_0}{\tau}\Big)^{3/2} {\rm erg~s^{-1}}. \end{displaymath}$

(2)

Equations (1) and (2) are used to compute the energy released by SN derived from a star particle i (E_i). A fraction $\gamma$ of this energy is deposited in the jth neighbour gas particle by applying a radial kick to its velocity with a magnitude $\Delta v_j = \sqrt{(2w_j\gamma E_i/m_j)}$ , where w_j is the weighting based on the smoothing kernel and m_j is the mass of gas particle j. We note that all gas neighbours are located in a sphere of radius $R_{\rm SN}$ , centered on the SN progenitor, to avoid spurious injection of energy outside the SN's region of influence. In the following, we use the following standard values: $\gamma=0.1$ , $R_{\rm SN}=0.4$ kpc, and c_* = 0.01.

3.2 Results

Figure 2 illustrates the time evolution of the projected stellar number density of the system. After 0.36 Gyr from the beginning of the simulation, the system has a stellar mass of $\sim$ $1.92 \times 10^{10}~M_{\odot}$ and exhibits, from a morphological point of view, a general shape and pattern similar to the observed galaxy system. The disc of the more massive galaxy has not yet been destroyed, reflecting the early stage of the dynamical process, and is viewed in Figs. 2 and 3 at an inclination of $\sim$ $26^\circ$ , as inferred from its outer isophote. The bar of the host galaxy has roughly the correct orientation and length ( $\sim$ 5 kpc), and the projected position of the satellite remnant is in approximate agreement with these values. However, many difficulties remain e.g. in reproducing the blue arm or tidal tail on the upper right and the fact that the companion should be split into two distinct, bright knots.

In the present scenario, the bar forms after the first encounter with the satellite, since at that time there is a strong triggering. In good agreement with the observations, it is particularly clear in the newly formed stars, since those, being on near-circular orbits, are more prone to the bar instability. Also in good agreement is the fact that the newly formed stars are also located in the satellite remnant (Fig. 3). Moreover, according to our model, J033239.72-275154.7 is observed when the satellite is about to experience a the second encounter with the host. At this specific time, the SFR is $\sim$ $9~M_\odot\;{\rm yr}^{-1}$ (Fig. 3) in good agreement with the observational estimation.

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=4.4cm]{760fig6.eps}}\rotatebox{0}{\includegraphics[width=4.4cm]{760fig7.ps}} \end{figure}$	Figure 3: The star formation rate obtained from our model ( left panel) and projected distribution of newly formed stars at t=0.36 Gyr ( right panel). The arrows in the left panel correspond to the SFR at the first encounter (1), at t=0.36 Gyr (2) and at the final plunge (3).
Open with DEXTER

The VF and $\sigma$ map of the gas component derived from our numerical model are represented in the GIRAFFE format in Fig. 4. The determination of the radial velocities is presented at the orientation of Figs. 2 and 3. The observed VF and its amplitude are faithfully reproduced and show that the initial inclination between the two orbital planes is consistent. The $\sigma$ map is relatively flat around a mean value of 35-40 km s^-1, in good agreement with the observations. It exhibits two maxima of roughly the correct value, but located at positions other than those observed. However, these two maxima are located in regions that are not well resolved in gas particles and thus the resulting pixel values are insignificant.

After 4.26 Gyr, corresponding to the present time z=0, the final object is characterized by a bulge-to-disk ratio close to 1.04, as derived from the mass-profile decomposition along the major axis of the final product (see Fig. 5). For this decomposition, we used standard models for the disk and bulge, namely an exponential disk (Sérsic profile with index n=1) and a bulge following de Vaucouleurs law (Sérsic profile with index n=4), in which the free parameters are the bulge and disk radius and the bulge and disk flux. The rotational support parameter $V_{\rm maj}/\sigma_{\rm c}=1.62$ , where $V_{\rm maj}$ is the maximum of the major axis rotation speed and $\sigma_{\rm c}$ the central velocity dispersion. This last parameter is estimated by considering all star particles within a sphere of radius 0.5 kpc. These previous derived values are strongly indicative of the formation of a S0 galaxy being observed.

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=4.4cm]{760fig8.eps}}\rotatebox{0}{\includegraphics[width=4.4cm]{760fig9.eps}} \end{figure}$	Figure 4: Maps of the velocity field ( on the left) and $\sigma$ field ( on the right) of the gas component obtained from our simulation.
Open with DEXTER

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=8.8cm, height=6cm]{760fig10.eps}} \end{figure}$	Figure 5: Mass profile decomposition along the major axis of the final product. The mass profile of the final product is show by the black line. The green dotted-dashed line, the blue dashed line and the red dotted line indicate the disk component, the bulge component and the sum of them, respectively.
Open with DEXTER

4 Discussion and conclusions

In this paper, we have presented photometric and kinematic data of J033239.72-275154.7 and completed a detailed comparison with an N-body simulation. A first interesting and important result is that among all the simulations that we have realized with specific orbital parameters and progenitor mass ratios, the combination of parameters such as the star formation history, VF, and $\sigma$ map place strong constraints on the models and can remove the degeneracy in the good candidates based on morphological criteria only.

We found that our fiducial model can approximately reproduce the general morphological shape and the total stellar mass of the object, as well as observed SF rate, VF, and intensity of the $\sigma$ map. This specifically includes the reproduction of the giant, young bar, its location and shape, the relative projected location of the companion, the overall morphological shape of the galaxy, its low rotation, and its off-center dynamical axis. The model predicts a deceleration in the velocity of the host galaxy due to exchanges of angular momentum with the companion (see Fig. 2). However, using these idealized simulations, we have been unable to reproduce many features, such as the blue arm or tidal tail in the upper right part of the observed galaxy system, the morphological patterns of the two bright knots of the satellite remnant, and the location of the $\sigma$ peaks. These discrepancies with observations can be easily understood as being due to the huge parameter space covered by the simulations. These include the properties of the progenitors (halo: disk: bulge: gas mass ratios and relative extents, shape of their density profiles, and kinematics), the geometry of the encounter and of its viewing angle, the gas properties, and the SF, cooling, and feedback modeling. On the other hand, the discrepancies with observations may also have an astrophysical origin and/or be due to a more complex formation scenario. Several possibilities - such as multiple encounters or progenitors with specific properties - come to mind, but would increase substantially the already vast free-parameter space.

In spite of these difficulties, it is encouraging that our simple numerical modelling is able to build a consistent picture of the formation of J033239.72-275154.7. This system is consistent with having been formed from a merger of two objects with a mass ratio 1:3. The simulation indicates that a bar is forming in the host galaxy after the first passage of the satellite where an important fraction of available gas is consumed in the induced burst, giving a plausible explanation of the observed blue colors of the bar and the satellite remnant. Moreover, both the VF and $\sigma$ map derived from the simulations are able to reproduce the observational values and thus support this scenario. In its future evolution, we inferred that J033239.72-275154.7 may become a S0 galaxy, as suggested by the results of our simulations. This is mainly explained by the fact that the host galaxy experiences a violent relaxation and loses angular momentum during the merger process due to the retrograde orbit of the satellite. Moreover, by losing angular momentum, some of the gas may also sink toward the center of the galaxy where it may be converted into new stars and then accelerate the growth of the bulge.

To finish, we note that recent numerical studies have demonstrated that gas-rich mergers can produce remnant disks, provided that strong feedback processes are considered and if both the stellar and gas components do not experience a significant angular momentum loss (Springel & Hernquist 2005; Robertson et al. 2006; Governato et al. 2007; Hopkins et al. 2008). In this work, we propose an extreme scenario in which: i) the initial orbital configuration of the merger event does not permit the latter criteria to be satisfied; and ii) the progenitors of the system (in our numerical model) may not be sufficiently gas rich to reform a significant disk according those past theoretical studies. However, the present results are consistent with previous studies in highlighting the fundamental role played by the last major event in building the Hubble sequence (see e.g. Hammer et al. 2005 and 2007). It would thus be interesting to determine the frequency of various orbital configurations during merger events, and to compare our theoretical predictions for simulated galaxies at redshift z=0 with the galaxy population in the local universe to confirm this galaxy formation scenario.

Acknowledgements

S. P. acknowledges the financial support through a ANR grant. E. A. from ANR-06-BLAN-0172. We warmly thank the referee Brant Robertson for an insightful review that considerably improved the quality of the original manuscript. S. P. also warmly thank Y. Kakazu for interesting conversations and for her moral support.

References

Athanassoula, E. 1999, in Galactic discs, J. Sellwood, & J. Goodman, PASP Conf. Ser. 160, 351 (In the text)
Balcells, M., & González, A. C. 1998, ApJ, 505, L109 [NASA ADS] [CrossRef] (In the text)
Barazza, F. D., Jogee, S., & Marinova, I. 2008, ApJ, 675, 1194 [NASA ADS] [CrossRef] (In the text)
Barnes, J. E. 1988, ApJ, 331, 699 [NASA ADS] [CrossRef] (In the text)
Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef] (In the text)
Barnes, J. E., & Hernquist, L. 1992, ARA&A, 30, 705 [NASA ADS] [CrossRef] (In the text)
Berentzen, I., Athanassoula, E., Heller, C., & Fricke, K. J. 2003, MNRAS, 341, 343 [NASA ADS] [CrossRef] (In the text)
Berentzen, I., Athanassoula, E., Heller, C., & Fricke, K. J. 2004, MNRAS, 347, 220 [NASA ADS] [CrossRef] (In the text)
de Freitas Pacheco, J. A. 1998, AJ, 116, 1701 [NASA ADS] [CrossRef] (In the text)
Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gavazzi, G., Giovanelli, R., & Haynes, M. P. et al. 2008, A&A, 482, 43 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Governato, F., Willman, B., Mayer, L., et al. 2007, MNRAS, 374, 1479 [NASA ADS] [CrossRef] (In the text)
Hammer, F., Gruel, N., Thuan, T. X., Flores, H., & Infante, L. 2001, ApJ, 550, 570 [NASA ADS] [CrossRef] (In the text)
Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Hammer, F., Puech, M., Chemin, L., et al. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] (In the text)
Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] (In the text)
Hernquist, L. 1992, ApJ, 400, 460 [NASA ADS] [CrossRef] (In the text)
Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2008 [arXiv:0806.1739] (In the text)
Katz, N., Weinberg, D. H., & Hernquist, L. 1996, ApJS, 105, 19 [NASA ADS] [CrossRef] (In the text)
Kazantzidis, S., Bullock, J. S., Zentner, A. R., Kravtsov, A. V., & Moustakas, L. A. 2007 [arXiv:0708.1949] (In the text)
Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] (In the text)
Khochfar, S., & Burkert, A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Komatsu, E., Dunkley, J., & Nolta, M. R. 2008 [arXiv:0803.0547] (In the text)
Liang, Y. C., Hammer, F., & Flores, H. 2006, A&A, 447, 113 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lima-Neto, G. B., & Combes, F. 1995, A&A, 294, 657 [NASA ADS] (In the text)
Lotz, J. M., Madau, P., Giavalisco, M., Primack, J., & Ferguson, H. C. 2006, ApJ, 636, 592 [NASA ADS] [CrossRef] (In the text)
McGaugh, S. S. 2005, ApJ, 632, 859 [NASA ADS] [CrossRef] (In the text)
Mayer, L., Governato, F., & Kaufmann, T. 2008 [arXiv:0801.3845] (In the text)
Naab, T., Burkert, A., & Hernquist, L. 1999, ApJ, 523, L133 [NASA ADS] [CrossRef] (In the text)
Nakamura, O., Fukugita, M., Brinkmann, J., & Schneider, D. P. 2004, AJ, 127, 2511 [NASA ADS] [CrossRef] (In the text)
Neichel, B., Hammer, F., Puech, M., et al. 2008, A&A, 484, 159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Peirani, S., Mohayaee, R., & de Freitas Pacheco, J. A. 2004, MNRAS, 348, 921 [NASA ADS] [CrossRef] (In the text)
Puech, M., Hammer, F., Lehnert, M. D., & Flores, H. 2007, A&A, 466, 83 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Puech, M., Flores, H., Hammer, F., et al. 2008, A&A, 484, 173 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Rodrigues, M., et al. 2008 [arXiv:0810.0272] (In the text)
Robertson, B., Bullock, J. S., Cox, T. J., et al. 2006, ApJ, 645, 986 [NASA ADS] [CrossRef] (In the text)
Sheth, K., Regan, M. W., Scoville, N. Z., & Strubbe, L. E. 2003, ApJ, 592, L13 [NASA ADS] [CrossRef] (In the text)
Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [NASA ADS] [CrossRef] (In the text)
Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef]
Springel, V., & Hernquist, L. 2005, ApJ, 622, L9 [NASA ADS] [CrossRef] (In the text)
Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [NASA ADS] [CrossRef]
Thomas, P. A., & Couchman, H. M. P. 1992, MNRAS, 257, 11 [NASA ADS] (In the text)
Toomre, A. 1977, Evolution of Galaxies and Stellar Populations, 401 [NASA ADS] (In the text)
Walker, I. R., Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121 [NASA ADS] [CrossRef] (In the text)
Yang, Y., Flores, H., Hammer, F., et al. 2008, A&A, 477, 789 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

All Tables

Table 1: Properties of J033239.72-275154.7.

Table 2: Masses (M), gravitational softening lengths ( $\epsilon$ ) and number of particles (N) of each component used in the simulations.

All Figures

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=3.6cm]{760fig1.ps}}\rota... ...fig3.eps}}\rotatebox{0}{\includegraphics[width=4.4cm]{760fig4.eps}} \end{figure}$	Figure 1: B-V-z color map of J033239.72-275154.7 from HST/ACS ( upper left panel) and distribution of the galaxy within the GIRAFFE grid ( upper right panel). The lower panels show the velocity field map ( lower left panel) and the associated $\sigma$ -map ( lower right panel).
Open with DEXTER
In the text

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=18cm]{760fig5.eps}} \end{figure}$	Figure 2: Time evolution of the projected star number density. The light blue arrows indicate the specific rotation of each galaxy, while the yellow dashed lines show the motion of the satellite. In panel 6, we superposed the GIRAFFE grid. Each frame is 40 kpc $\times$ 40 kpc in size.
Open with DEXTER
In the text

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=4.4cm]{760fig6.eps}}\rotatebox{0}{\includegraphics[width=4.4cm]{760fig7.ps}} \end{figure}$	Figure 3: The star formation rate obtained from our model ( left panel) and projected distribution of newly formed stars at t=0.36 Gyr ( right panel). The arrows in the left panel correspond to the SFR at the first encounter (1), at t=0.36 Gyr (2) and at the final plunge (3).
Open with DEXTER
In the text

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=4.4cm]{760fig8.eps}}\rotatebox{0}{\includegraphics[width=4.4cm]{760fig9.eps}} \end{figure}$	Figure 4: Maps of the velocity field ( on the left) and $\sigma$ field ( on the right) of the gas component obtained from our simulation.
Open with DEXTER
In the text

$\begin{figure} \par\rotatebox{0}{\includegraphics[width=8.8cm, height=6cm]{760fig10.eps}} \end{figure}$	Figure 5: Mass profile decomposition along the major axis of the final product. The mass profile of the final product is show by the black line. The green dotted-dashed line, the blue dashed line and the red dotted line indicate the disk component, the bulge component and the sum of them, respectively.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.