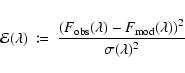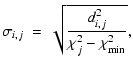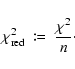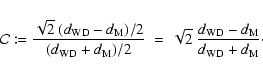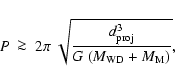| Issue |
A&A
Volume 496, Number 1, March II 2009
|
|
|---|---|---|
| Page(s) | 191 - 205 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:200810632 | |
| Published online | 20 November 2008 | |
Spectral analysis of 636 white dwarf-M star binaries from the sloan digital sky survey![[*]](/icons/foot_motif.gif)
R. Heller1 - D. Homeier2 - S. Dreizler3 - R. Østensen4
1 - Hamburger Sternwarte (Universität Hamburg), Gojenbergsweg 112, 21029 Hamburg, Germany
2 - Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1. 37077 Göttingen, Germany
3 - Institut für Astrophysik, Georg-August-Universität Göttingen, Friedrich-Hund-Platz 1. 37077 Göttingen, Germany
4 - Institute of Astronomy, Katholieke Universiteit Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received 17 July 2008 / Accepted 3 October 2008
Abstract
Context. We present a catalog of 857 white dwarf (WD)-M binaries from the sixth data release (DR6) of the Sloan Digital Sky Survey (SDSS), most of which were previously identified. For 636 of them, we complete a spectral analysis and derive the basic parameters of their stellar constituents and their distances from Earth.
Aims. We attempt to measure fundamental parameters of these systems by completing spectral analyses. We propose to test models typically applied in fitting procedures and constrain likely and appropriate evolutionary scenarios for the systems.
Methods. We use a ![]() minimization technique to decompose each combined spectrum and derive independent parameter estimates for its components. The possibility of alignment by chance is demoted to statistical insignificance, hence, we use physical interaction of the binary constituents as input parameter. Additionally, we check the corresponding photometric data from the SDSS to find optically resolved systems.
minimization technique to decompose each combined spectrum and derive independent parameter estimates for its components. The possibility of alignment by chance is demoted to statistical insignificance, hence, we use physical interaction of the binary constituents as input parameter. Additionally, we check the corresponding photometric data from the SDSS to find optically resolved systems.
Results. Forty-one of the stellar duets in our spectroscopic sample are optically resolved in their respective SDSS images. For these systems, we also derive a minimum true spatial separation and a lower limit to their orbital periods, typically which are some 104 yr. Spectra of 167 stellar duets show significant hydrogen emission and in most cases no additional He I or He II features. We also find that 20 of the 636 WDs are fitted to be DOs, with 16 measured to have
![]() around 40 000 K. Furthermore, we identify 70 very low-mass objects (VLMOs), which are secondaries of masses smaller than about 0.1
around 40 000 K. Furthermore, we identify 70 very low-mass objects (VLMOs), which are secondaries of masses smaller than about 0.1 ![]() ,
to be candidate substellar companions.
,
to be candidate substellar companions.
Conclusions. Although various selection effects may play a role, the fraction 6.4% of WD-M star binaries with orbital separations of around 500 AU is a criterion for evolutionary models of stellar binary systems. Of the 167 spectra with hydrogen emission, 8 had already been found to be post-common envelope binaries (PCEBs) and 4 are systems with strong irradiation processes on the M dwarf. The remaining 155 Balmer-emitting binaries probably harbor an active M dwarf (dM), corresponding to a fraction of 24.4%. The excess of cool DOs is most likely due to additional WDs in the DB-DO
![]() range, for which no detailed fitting was completed. The trend of the M stars being closer to Earth than the WD component is probably due to an underestimation of the theoretical M star radii.
range, for which no detailed fitting was completed. The trend of the M stars being closer to Earth than the WD component is probably due to an underestimation of the theoretical M star radii.
Key words: binaries: spectroscopic - white dwarfs - stars: late-type - stars: fundamental parameters - methods: data analysis - binaries: visual
1 Introduction
The study of white dwarf (WD)-M star systems is an important research area because they constitute a common final stage object of stellar evolution, a WD, and the most frequent type of star: the M component. Close WD-M binaries are also progenitor candidates for cataclysmic variables (CVs) and type Ia supernovae. WD-M binaries consist of two stars of radically different structure and evolutionary stage that originate in interstellar matter (ISM) of identical composition at the same time, on cosmological scales, and in the same region of space. Many of the constituents of the systems do not only interact gravitationally, which may lead to mutual mass exchange and substantial gravitational radiation, but they also affect each other due to their magnetic fields. With this paper, we attempt to improve the knowledge of the basic parameters of WD-M systems.
The Sloan Digital Sky Survey (SDSS) provides an invaluable observational data set with which to complete such a study. Raymond et al. (2003) first attempted to study WD-M dwarf (dM)
pairs in the SDSS and identified 109 of these objects. In our master sample, there are 99 of them but we discarded 32 for our purposes because of reasons given at the end of Sect. 2. Silvestri et al. (2007) presented a study of 1253 detached close binary systems from the SDSS data release 5 (DR5) (Adelman-McCarthy et al. 2007), most of them which consisted of WD primaries and M dwarf companions. Our master sample comprises 857 WD-M star systems, 690 of which have been published by Silvestri et al. (2007). Rebassa-Mansergas et al. (2007) presented investigations of 101 white dwarf main-sequence binaries (WDMSs) with multiple spectra from the SDSS, using model atmosphere fitting for the WD primaries and spectral typing based on the M-dwarf template spectra of Beuermann et al. (1998) and Bochanski et al. (2007) for the secondaries. Significant radial velocity variations were found for 18 systems, indicative of sufficiently close orbits to be post-common envelope binaries (PCEBs), and Sect. 5.2 is devoted to this subject. Another study of WD-M binaries was completed by Wachter et al. (2003), who focused on the observational identification methods with data from the Two Micron All-Sky Survey (2MASS) incremental data release. Catalogs of WDs in the
SDSS were given by Kleinman et al. (2004, DR1) and Eisenstein et al. (2006, DR4) and many are included in our sample. Four binaries from our master sample are in Luyten's WD catalogs for the years from 1970 to 1977 (Luyten 1999), which contains 6546 objects, and no binary is in his sample of 6210 objects from 1940 to 1987 (Luyten 1997). The original accuracy of the position in J1950 coordinates was 0.1 min in Right Ascension (1.5
![]() or 0.025
or 0.025![]() )
and 1
)
and 1
![]() in Declination (0.017
in Declination (0.017![]() ), as stated in the respective VizieR reference. We used the J2000 coordinates calculated by VizieR to relate stars with each other. Another earlier study of WDs in wide binaries was completed by Greenstein (1986), and we found three of his 56 systems to be in our master sample, one of a quality too low for a reliable analysis. We also show fits for the three binary systems mentioned in Hügelmeyer et al. (2006). From our sample, 153 systems were not included in any of the mentioned studies.
), as stated in the respective VizieR reference. We used the J2000 coordinates calculated by VizieR to relate stars with each other. Another earlier study of WDs in wide binaries was completed by Greenstein (1986), and we found three of his 56 systems to be in our master sample, one of a quality too low for a reliable analysis. We also show fits for the three binary systems mentioned in Hügelmeyer et al. (2006). From our sample, 153 systems were not included in any of the mentioned studies.
The present work introduces a novel method of analyzing WD-dM binaries by fitting simultaneously model spectra for both the white dwarf and the main-sequence star to the composite spectrum to derive the atmospheric parameters of both stars. Unlike the aforementioned studies, we thus obviate the need to calibrate empirical relations between physical parameters and spectral types. Although current cool-star atmosphere models may still have some shortcomings in fitting M-dwarf spectra, this approach avoids possible biases due to systematic differences between single M-dwarfs and those in close binaries.
In Sect. 2, we provide an overview of the observational principles and our target selection criteria. We also state the premises for our procedure, e.g. we calculate the
probability of WD-M alignment by chance (Sect. 2.1). The calculation of the theoretical spectra used in the fitting process is described in Sect. 3. In Sect. 4, we then provide a detailed description of the mathematical methods we used: this represents the major part of this paper, since the ![]() method that we use differs from
those typically applied to decompose combined spectra. With our relatively large sample of 636 systems, we present a statistical refinement of the SDSS WD and the M dwarf temperature functions in Sect. 5. We also find 41 optically resolved binaries with accordingly wide-separated constituents of long orbital periods (Sect. 5.3).
method that we use differs from
those typically applied to decompose combined spectra. With our relatively large sample of 636 systems, we present a statistical refinement of the SDSS WD and the M dwarf temperature functions in Sect. 5. We also find 41 optically resolved binaries with accordingly wide-separated constituents of long orbital periods (Sect. 5.3).
2 Observations
The observational data were taken from the SDSS DR6, which was performed using the 2.5-m telescope at the Apache Point Observatory in southern New Mexico through June 2006 (Adelman-McCarthy et al. 2008). WD-M star binaries are a byproduct of this survey which was focused on quasi-stellar objects. The most significant part of the analysis for this paper was completed using the SDSS spectra, covering the spectral range from 3800 to 9200 ![]() at an inverse resolution of
at an inverse resolution of
![]() .
Targets for SDSS spectroscopic follow-up observations were selected on the basis of photometric results.
.
Targets for SDSS spectroscopic follow-up observations were selected on the basis of photometric results.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{0632fig01_left.eps}\hspace*{...
...space*{1.2cm}
\includegraphics[width=7cm,clip]{0632fig01_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg32.gif) |
Figure 1: Left: the localizations of our master sample in the (u-r)-space; middle: the localizations of our master sample in the (i-z)-space; right: comparison of the color-color localizations of our master sample with the WD-M sample of Silvestri et al. (2006). Those objects from our study with g-r > 0.2 come from the EDR, on which we did not impose the (g-r)-cutoff. |
| Open with DEXTER | |
The spectroscopic dataset used in this study consisted of 857 objects that were labeled as WD-M dwarf binaries during a search for hot subdwarf stars in the SDSS dataset. Finding hot subdwarfs is relatively easy, because they can be clearly distinguished from normal stars by their UV-excess, a property that they have in common only with WDs. While the hot subdwarfs dominated the population of UV-bright stars in earlier studies such as the PG survey (Green et al. 1986), the depth of the SDSS ensures that the numbers of hot subdwarfs taper out as the volume surveyed extends beyond the Galactic disk. White dwarf stars, on the other hand, are some five magnitudes fainter, and their spatial proximity allows their numbers to increase steadily with increasing magnitude until they outnumber the hot subdwarfs by 100 to 1 for g > 19. Kleinman et al. (2004) presented a catalog of spectroscopically identified WDs in the DR1. In our latest detection survey of UV-bright stars in the SDSS, we detected a total of 639 hot subdwarfs and 11 752 white dwarf stars.
The SDSS spectroscopic survey targets a range of objects based on its properties measured in the photometric ugriz survey, i.e. depending on whether a source is extended or point-like and its position in color-color space. The survey was optimized for detecting quasars and faint galaxies, but since these are scattered over significant parts of color-color space, the main strategy of the SDSS selection procedure is to avoid the main stellar loci. It is also worth noting that this procedure became more effective after the early data release (EDR) of the survey, so the selection biases are not constant even within the original SDSS dataset.
Our selection procedure resembles that of the SDSS' own in that we investigated a large fraction of color-color space in the EDR release, and refined our search area for the data sets of subsequent releases. Of particular importance for the WD-M sample was the cutoff in g-r. For the EDR, we imposed no cutoff, but in later releases we imposed g-r < 0.2 in addition to the u-g < 0.8 criterion used to select stars with a UV excess. While g-r < 0.2 includes effectively all hot subdwarf stars, including systems with F- to G-class companions, this limit cuts straight through the locus of WD-dM stars as illustrated in Fig. 1. The truncated region of color-color space is also where the data for the most significant part of the quasars is found, and the SDSS survey therefore imposes a positive bias on WD binaries located in this region, while giving lower priority to objects with negative g-r, where single WD stars are found. However, due to our selection procedure, only a fraction of the WD binaries with g-r < 0.2 is included in this study. Also, the cool end of the WD population is found to be located redward of the corner of our selection region at u-g = 0.8 and g-r = 0.2. At this point, the WD sequence reaches into the population of normal halo stars, which the SDSS selection procedure - as well as our color-color cuts - avoids. A more detailed explanation of the color-color loci of WD-M star systems within the SDSS is given in Smolcic et al. (2004).
Our sample is made up of 857 objects, which represents our master sample (see Fig. 1). We then discard noisy spectra and those in which either the WD or the red companion have rather weak features. Only spectra showing either a WD with a hydrogen-dominated atmosphere (DA white dwarfs) or a WD with clear helium features (DO or DB white dwarfs) are retained. Furthermore, we reject spectra with pollution from nearby light sources, which we verified with the aid of the photometric data. WD-M pairs with cool WDs and dominant red components are discarded preferentially from our sample by the selection method, in addition to systems with significant light contribution due to mass overflow. The identification of our subsample of 636 systems is therefore subject to severe selection effects.
2.1 Premises
As a basis for our investigations, we rely on three premises:
- 1.
- Due to our model grid resolution of 0.5 dex for the surface gravity of the M star (
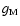 )
and the low resolution of the SDSS spectra, the uncertainties in our fits for
)
and the low resolution of the SDSS spectra, the uncertainties in our fits for
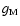 are too large to provide useful constraints on the secondary masses. We assume instead a mass-radius relation for unevolved main sequence stars by using the evolutionary models of Chabrier & Baraffe (1997) for a fixed M star age of 1010 yr to deduce the radius (
are too large to provide useful constraints on the secondary masses. We assume instead a mass-radius relation for unevolved main sequence stars by using the evolutionary models of Chabrier & Baraffe (1997) for a fixed M star age of 1010 yr to deduce the radius (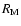 )
and mass (
)
and mass (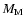 )
of the M star from its fitted effective temperature (
)
of the M star from its fitted effective temperature (
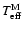 )
and metallicity [Fe/H]
)
and metallicity [Fe/H]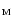 .
For the mass range considered here, evolution effects on the main sequence are negligible within a Hubble time, thus only pre-main sequence stars with ages
.
For the mass range considered here, evolution effects on the main sequence are negligible within a Hubble time, thus only pre-main sequence stars with ages 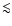 5
5 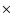 108 yr might introduce larger errors in the radius estimate. Such young ages, however, can be excluded due to the cooling ages of the white dwarfs in almost all cases.
108 yr might introduce larger errors in the radius estimate. Such young ages, however, can be excluded due to the cooling ages of the white dwarfs in almost all cases.
- 2.
- Similarly, the errors in the surface gravity of the WD (
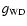 )
from our fits are in most cases inadequately high for a meaningful deduction of the WD radii. However, as shown
by Hu et al. (2007), most of the SDSS DAs have masses that cluster closely around the peak of the field white dwarf mass distribution at 0.58
)
from our fits are in most cases inadequately high for a meaningful deduction of the WD radii. However, as shown
by Hu et al. (2007), most of the SDSS DAs have masses that cluster closely around the peak of the field white dwarf mass distribution at 0.58 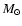 .
There are observational
indications of higher WD masses in magnetic CVs (mCVs) compared with the masses of field WDs (Cropper et al. 1998; Ramsay 2000; Ritter & Kolb 1998, and references therein). The maximum of the WD mass function in those binaries, although not as distinctive as the peak in field-WD masses, appears to be located between 0.7
.
There are observational
indications of higher WD masses in magnetic CVs (mCVs) compared with the masses of field WDs (Cropper et al. 1998; Ramsay 2000; Ritter & Kolb 1998, and references therein). The maximum of the WD mass function in those binaries, although not as distinctive as the peak in field-WD masses, appears to be located between 0.7 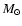 and
0.8
and
0.8 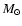 .
Although we cannot assess the orbital separations of the duets in our sample, except for some known close binaries (PCEBs) and optically resolved duets, we find no indications, such as accretion disk features, for a single mCV in our sample (see Sect. 6). We therefore use a fixed WD mass (
.
Although we cannot assess the orbital separations of the duets in our sample, except for some known close binaries (PCEBs) and optically resolved duets, we find no indications, such as accretion disk features, for a single mCV in our sample (see Sect. 6). We therefore use a fixed WD mass (
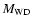 )
of 0.6
)
of 0.6 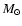 and the WD temperature (
and the WD temperature (
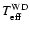 )
derived from the fit to estimate the radius of the WD (
)
derived from the fit to estimate the radius of the WD (
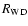 )
from the evolutionary tracks calculated by Wood (1994). These models are available for 0.4, 0.5, 0.6, 0.7, 0.8, and 1.0
)
from the evolutionary tracks calculated by Wood (1994). These models are available for 0.4, 0.5, 0.6, 0.7, 0.8, and 1.0 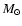 .
.
- 3.
- The probability of an alignment of a WD and an M star by chance is found to be negligible. Our reasoning is based on the fact that our binaries found their way into the sample due to the
high flux contribution of the WD to the blue part of the spectrum. Hence, WDs are a preferred byproduct of the SDSS and some have M star companions. We compute the probability
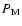 of
finding at least one M star within a circle of diameter equal to that of an SDSS fiber on the celestial plane, which is
of
finding at least one M star within a circle of diameter equal to that of an SDSS fiber on the celestial plane, which is
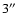 (Adelman-McCarthy et al. 2008), by chance. It is given
by the Poisson probability of finding
(Adelman-McCarthy et al. 2008), by chance. It is given
by the Poisson probability of finding 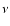 objects
objects
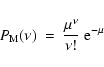
(1)
and, in our case,
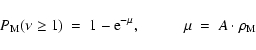
(2)
where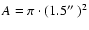 is the probed area and
is the probed area and
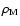 is the area density of M stars on the celestial plane. To estimate
is the area density of M stars on the celestial plane. To estimate
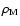 ,
we refer to private communication with Bochanski, who measured the field luminosity function of stars in the DR6. From there, we derived star counts in the SDSS u-, g-, r-, i- and z- filters for the magnitude range of our sample: 15 < u, g, r, i, z < 20.5. These counts yield
,
we refer to private communication with Bochanski, who measured the field luminosity function of stars in the DR6. From there, we derived star counts in the SDSS u-, g-, r-, i- and z- filters for the magnitude range of our sample: 15 < u, g, r, i, z < 20.5. These counts yield
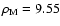
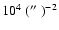 ,
and we get
,
and we get
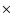 10-3 and an expectation value of
10-3 and an expectation value of
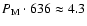 to be the number of WD-M binaries aligned by chance within our sample. This is why we may use physical interaction of the binary constituents as a basic principle.
to be the number of WD-M binaries aligned by chance within our sample. This is why we may use physical interaction of the binary constituents as a basic principle.
3 Models
The central element of our analysis is the synthesis of binary spectra from of theoretical spectra based on model atmosphere calculations for white dwarfs and main sequence stars, respectively. Models for the full parameter range of interest were pre-computed, providing two grids for the spaces of white dwarf parameters
![]() and
and
![]() and M dwarf parameters
and M dwarf parameters
![]() ,
,
![]() and [Fe/H]
and [Fe/H]![]() ,
respectively. White dwarf spectra were calculated for pure hydrogen atmospheres covering surface gravities of
,
respectively. White dwarf spectra were calculated for pure hydrogen atmospheres covering surface gravities of
![]() with a step size of 0.5 dex in a temperature range from 6 to 90 kK. We adopted steps of 1 kK between 6 and 30 kK, steps of 2 kK between 30 and 50 kK, and steps of 5 kK for temperatures above 50 kK. This core model grid was supplemented with existing models for extremely hot (
with a step size of 0.5 dex in a temperature range from 6 to 90 kK. We adopted steps of 1 kK between 6 and 30 kK, steps of 2 kK between 30 and 50 kK, and steps of 5 kK for temperatures above 50 kK. This core model grid was supplemented with existing models for extremely hot (
![]() )
or lower-gravity (
)
or lower-gravity (
![]() )
atmospheres and for hot helium-rich atmospheres. The latter were available for
)
atmospheres and for hot helium-rich atmospheres. The latter were available for
![]() in the range of
in the range of
![]() every 5 kK. The grid of the MS spectra was almost complete for
every 5 kK. The grid of the MS spectra was almost complete for
![]() every 200 K, [Fe/H]
every 200 K, [Fe/H]
![]() and
and
![]() .
.
The white dwarf models were computed by Koester using his codes developed for static, plane-parallel, stellar atmospheres in radiative, hydrostatic, and local thermodynamic equilibrium (LTE), as described in detail in Finley et al. (1997). The main body of this grid covers fully-blanketed pure hydrogen (DA) atmospheres. These models consider convective flux according to the mixing length approximation (MLT), by using a variation of the standard formulation of Mihalas (1978) designated as ML2 in the notation of Finley et al. (1997, and references therein), and adopting a mixing length of
![]() (in units of pressure scale height). This setup was demonstrated to be one of the most effective available configurations for reproducing DA spectra at high resolution and S/N (Koester et al. 2001; Homeier et al. 1998). This grid was extended by an existing set of hydrogen atmosphere models based on the same input physics to cover the more extreme parts of the white dwarf parameter space in high
(in units of pressure scale height). This setup was demonstrated to be one of the most effective available configurations for reproducing DA spectra at high resolution and S/N (Koester et al. 2001; Homeier et al. 1998). This grid was extended by an existing set of hydrogen atmosphere models based on the same input physics to cover the more extreme parts of the white dwarf parameter space in high
![]() and lower gravity (sdB-like atmospheres). In addition, for those hot white dwarfs that could not be reproduced accurately by DA spectra the sequence of helium-rich (DO) models was used. These models assume a helium-to-hydrogen mixing ratio of 100:1 and the ML1 MLT version with
and lower gravity (sdB-like atmospheres). In addition, for those hot white dwarfs that could not be reproduced accurately by DA spectra the sequence of helium-rich (DO) models was used. These models assume a helium-to-hydrogen mixing ratio of 100:1 and the ML1 MLT version with
![]() as described in Jordan et al. (1997). These latter models only cover the spectrum up to
as described in Jordan et al. (1997). These latter models only cover the spectrum up to
![]() ,
and thus an important part of the dM flux had to be masked out in the analysis. However, none of the primaries were identified to be in the low-gravity or ultra-hot domain of the DAs/sdBs, and a more quantitative analysis of the helium-rich white dwarfs was beyond the scope of this work, as detailed below.
,
and thus an important part of the dM flux had to be masked out in the analysis. However, none of the primaries were identified to be in the low-gravity or ultra-hot domain of the DAs/sdBs, and a more quantitative analysis of the helium-rich white dwarfs was beyond the scope of this work, as detailed below.
The secondary spectra were calculated with version 14.2 of the multi-purpose stellar atmosphere code PHOENIX (Hauschildt & Baron 1999) for 1D spherically symmetric, static atmospheres in LTE, which consider convective instability in the framework of MLT according to Mihalas (1978) with a mixing length parameter
![]() .
Our models follow the general setup used for the first GAIA grid (Brott & Hauschildt 2005), which included a number of updates from the NextGen grid (Hauschildt et al. 1999) and the microphysics described by Allard et al. (2001), but ignores the effects of condensate formation. We therefore restricted the range of validity of these models to
.
Our models follow the general setup used for the first GAIA grid (Brott & Hauschildt 2005), which included a number of updates from the NextGen grid (Hauschildt et al. 1999) and the microphysics described by Allard et al. (2001), but ignores the effects of condensate formation. We therefore restricted the range of validity of these models to
![]() K. Major modifications relative to the models of Brott & Hauschildt (2005) included updating of the (scaled) elemental
abundances to the revised solar composition of Asplund et al. (2005) and considering microturbulent line broadening with a statistical velocity
K. Major modifications relative to the models of Brott & Hauschildt (2005) included updating of the (scaled) elemental
abundances to the revised solar composition of Asplund et al. (2005) and considering microturbulent line broadening with a statistical velocity
![]() ,
which provided a more reliable description of the observed line profiles in cooler stars (Bean et al. 2006; Sousa et al. 2008).
,
which provided a more reliable description of the observed line profiles in cooler stars (Bean et al. 2006; Sousa et al. 2008).
4 Mathematical treatment
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{0632fig02.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg66.gif) |
Figure 2:
Example for our fitting procedure; Top: observed SDSS spectrum of J1009+0244 and the DA-dM combination in our fitting routine. As mentioned in Silvestri et al. (2006), the feature close to 5600 |
| Open with DEXTER | |
To decompose a composite spectrum, one usually fits a WD model to its hot region, i.e. the relatively blue wavelength range of the spectrum, where contamination of the companion star's light is rather weak. In the next step, this best-fit model for the WD is subtracted from the combined spectrum to obtain a spectrum most closely resembling the light of the secondary. Depending on the
density of the model grid and the success of the preceding fit, one improves the quality of the replicated spectrum with each of those iteration steps, while ![]() is reduced, approaching the
local
is reduced, approaching the
local ![]() minimum in the respective parameter space. Although this proceeds rapidly, there is the danger of being trapped inside a local minimum instead of the global minimum. This procedure also implies a mutual dependence of the computed flux scaling factors. We therefore propose an alternative technique.
minimum in the respective parameter space. Although this proceeds rapidly, there is the danger of being trapped inside a local minimum instead of the global minimum. This procedure also implies a mutual dependence of the computed flux scaling factors. We therefore propose an alternative technique.
With our ![]() fitting method, we operate in a five-dimensional parameter space, spanned by
fitting method, we operate in a five-dimensional parameter space, spanned by
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and [Fe/H]
,
and [Fe/H]![]() .
Each observed flux data point
.
Each observed flux data point
![]() in a binary spectrum with a total number of m observed data points is reproduced by a combination of two single-star models xi and yi. These are weighted with scaling factors a and b, respectively, depending on the distances of the stars. With the definition of
in a binary spectrum with a total number of m observed data points is reproduced by a combination of two single-star models xi and yi. These are weighted with scaling factors a and b, respectively, depending on the distances of the stars. With the definition of ![]() from Press et al. (1992, Eq. (15.1.5)), we have
from Press et al. (1992, Eq. (15.1.5)), we have
with
![\begin{displaymath}%
\chi^2 \ \coloneqq \ [(F_{i}^{{\rm obs}} - a~x_{i} -
b~y_{i})^2]. %
\end{displaymath}](/articles/aa/full_html/2009/10/aa10632-08/img71.gif) |
(4) |
Since we attempt to identify that model combination of models x and y that corresponds to the global
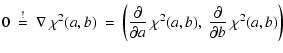 |
|||
| (5) |
With
![\begin{displaymath}%
\nabla \ \chi^2(a,b) \!=\! -2~\left([x_{i}~(F_{i}^{{\rm obs...
...y_{i}~(F_{i}^{{\rm obs}} \!-\!
a~x_{i} \!-\! b~y_{i})] \right)
\end{displaymath}](/articles/aa/full_html/2009/10/aa10632-08/img74.gif) |
(6) |
we obtain
![$\displaystyle %
\left( \begin{array}{c}
~\!\! [ F_{i}^{{\rm obs}}~x_{i} ]\\
~\...
...{i}^2]
\end{array}\Bigl)}_{Z}
\left(\begin{array}{c}
a\\
b
\end{array}\right),$](/articles/aa/full_html/2009/10/aa10632-08/img75.gif) |
(7) |
which is equivalent to
This finally leads us to
Equation (9) provides the scaling factors for both the WD and the M star model, which we then use to compute
Additionally, we introduce
![]() as an estimate of the fit, which is defined to be
as an estimate of the fit, which is defined to be
and resembles the definition of
given in Zhang et al. (1986) to calculate the 1
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0632fig03.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg86.gif) |
Figure 3:
Projection of the |
| Open with DEXTER | |
We define
![]() to be the number of parameters, such that we have
to be the number of parameters, such that we have
![]() ,
and m as the number of data points in an SDSS spectrum. We have mainly
,
and m as the number of data points in an SDSS spectrum. We have mainly
![]() ,
but, in some
cases, parts of a spectrum must be discarded, then m becomes smaller. We denote the number of statistically independent data points in the spectrum for an inverse resolution R, by
,
but, in some
cases, parts of a spectrum must be discarded, then m becomes smaller. We denote the number of statistically independent data points in the spectrum for an inverse resolution R, by
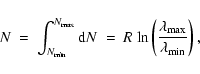 |
(12) |
where
We use the concept of the quantile that provides an estimation of how probable a computed
which provides the probability of
4.1 Distances
When
![]() is inferred from the fixed value of
is inferred from the fixed value of
![]() ,
the fitted
,
the fitted
![]() ,
and by using models from Wood (1994), we derive the distance
,
and by using models from Wood (1994), we derive the distance
![]() of the WD from Earth by obtaining the scaling factor a from our fitting method, which scales the model flux to the observed flux. Since
of the WD from Earth by obtaining the scaling factor a from our fitting method, which scales the model flux to the observed flux. Since
![]() ,
we have
,
we have
![\begin{displaymath}%
d_{{\rm WD}}~[{\rm pc}] \ = \ \frac{R_{{\rm WD}}~[R_{\odot}]}{1~{\rm pc} ~ \sqrt{a} / R_{\odot}}\cdot
\end{displaymath}](/articles/aa/full_html/2009/10/aa10632-08/img97.gif) |
(15) |
A similar procedure is applied to deduce the distance
Thus, a discrepancy between
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0632fig04.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg103.gif) |
Figure 4:
Geometrical explanation of the distance evaluation coefficient
|
| Open with DEXTER | |
4.2 Optically resolved binaries
In addition to the spectroscopic data, we also studied the photometric data. Since we hardly detect the smeared Airy disks of the objects, we are unable to derive any morphological information, but a possible separation of the spot centers allows us to estimate their projected mutual distance
![]() .
For this purpose, we use the averaged distance
.
For this purpose, we use the averaged distance
![]() of the system from Earth, the displacement D of the stars on the SDSS images in units of pixels, and the
given resolution
of the system from Earth, the displacement D of the stars on the SDSS images in units of pixels, and the
given resolution ![]() of the images in
of the images in
![]() pixel. We calculate the angular separation
pixel. We calculate the angular separation ![]() in units of radians by means of
in units of radians by means of
![]() and by using geometry,
and by using geometry,
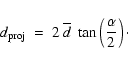 |
(17) |
The projected distance, however, is shorter than the true spatial separation r (see Fig. 5). If we knew r of a system and were able to measure
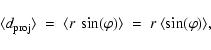 |
(18) |
where the mean of the sine of the projection angular
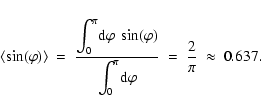 |
(19) |
This implies, that the true spatial separation is, on average, about
Using the optical separation of the stars, we can use the visible separation and estimate the period of the system by means of
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0632fig05.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg115.gif) |
Figure 5:
|
| Open with DEXTER | |
where we assume that
![]() on the basis of arguments given above and for the sake of consistency with the fitting procedure. We derive
on the basis of arguments given above and for the sake of consistency with the fitting procedure. We derive
![]() from evolutionary tables calculated by Baraffe et al. (1998) (see Sect. 2.1). Equation (20) may only provide an approximate approach, due not only to the uncertainties in the masses but also because of the approximation of the projection of the mutual distance is smaller and almost equal to the sum of the major axes
from evolutionary tables calculated by Baraffe et al. (1998) (see Sect. 2.1). Equation (20) may only provide an approximate approach, due not only to the uncertainties in the masses but also because of the approximation of the projection of the mutual distance is smaller and almost equal to the sum of the major axes
![]() and
and ![]() of the ellipses on which the stars move:
of the ellipses on which the stars move:
![]() .
If we take into account the averaged correction of the projection, then the corrected period
.
If we take into account the averaged correction of the projection, then the corrected period
![]() is longer than P. We note that deviations
is longer than P. We note that deviations
![]() from
from
![]() have a significant effect, since the mass was already used for the derivation of
have a significant effect, since the mass was already used for the derivation of
![]() .
Since
.
Since
![]() ,
we derive
,
we derive
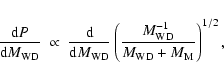 |
(21) |
which leads to
| |
|||
| (22) |
Thus, deviations in the period are more significant when the mass of the white dwarf is lower and, for
5 Results
The temperature function for our WDs can be seen in Fig. 7. As mentioned above, it is subject to considerable selection effects. While the strong peak at 17 000 K belongs to the DAs, the second and smaller peak at 40 000 K, which is the lowest temperature in our DO model grid, stems from the cool helium-rich WDs. We convolved the original data distribution with a Gaussian probability function about each data point, to account for the uncertainty in the derived parameters. As a measurement of standard deviation, we used 2000 K and normalized the distribution to 1. Since most of the WDs in our sample have a surface gravity of between 7 and 8 dex (see Fig. 11), the shape of the WD-distance function in Fig. 9 is similar to that of the temperature function.
In Fig. 8, we show the temperature function for the M stars. Although the standard
deviation is merely a tenth of that for
![]() ,
the function is not so smooth because of the relatively low number of model grid points. The tail towards temperatures higher than those of M stars is due to 4 objects at
,
the function is not so smooth because of the relatively low number of model grid points. The tail towards temperatures higher than those of M stars is due to 4 objects at
![]() K with insecure fits, i.e. because of He emission in the spectrum or large distances to Earth and therefore weak spectral features. Our results for the other free parameters,
K with insecure fits, i.e. because of He emission in the spectrum or large distances to Earth and therefore weak spectral features. Our results for the other free parameters,
![]() and [Fe/H]
and [Fe/H]
![]() ,
can be seen in Figs. 12 and 13, while the distance distribution for the M stars is given in Fig. 10.
,
can be seen in Figs. 12 and 13, while the distance distribution for the M stars is given in Fig. 10.
As shown in Hu et al. (2007), the standard deviation from the maximum of the WD mass function at
![]() is
is ![]()
![]() .
This corresponds to an error in our WD distances of
.
This corresponds to an error in our WD distances of ![]()
![]() ,
and this uncertainty creates dispersion in the data from the diagonal in the
,
and this uncertainty creates dispersion in the data from the diagonal in the
![]() plot, namely
plot, namely
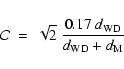 |
(23) |
and for physical systems with
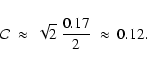 |
(24) |
Taking into account all the other error sources mentioned before, we would expect the systems to be mainly distributed within the fan of
For all of the analyzed spectra, pn = 1 (see Eq. (14)), which implies that a ![]() equal to or smaller than the calculated
equal to or smaller than the calculated
![]() is probable for the respective number of degrees of freedom. In other words, the quality of our fits is poor in mathematical context. The standard deviations of the measured parameters are quite weak in
terms of physical significance. As an example, we consider J1009+0244 (see Fig. 3). We compute
is probable for the respective number of degrees of freedom. In other words, the quality of our fits is poor in mathematical context. The standard deviations of the measured parameters are quite weak in
terms of physical significance. As an example, we consider J1009+0244 (see Fig. 3). We compute
![]() ,
and
,
and
![]() ,
which demonstrates that the systematic errors are larger than the mathematical ones. For a conservative estimate of the errors due to the incomplete molecular data in the M star
models, SDSS flux calibration errors and interstellar reddening, we refer to Hügelmeyer et al. (2006), and assume an uncertainty of 2000 K for the WDs with temperatures smaller than 50 000 K and a 1-
,
which demonstrates that the systematic errors are larger than the mathematical ones. For a conservative estimate of the errors due to the incomplete molecular data in the M star
models, SDSS flux calibration errors and interstellar reddening, we refer to Hügelmeyer et al. (2006), and assume an uncertainty of 2000 K for the WDs with temperatures smaller than 50 000 K and a 1-![]() interval of 100 K for the MS stars. For
interval of 100 K for the MS stars. For
![]() K, the absolute value of our accuracy is given by half of the model step width of
5000 K. Our accuracy in the surface gravities is limited by the low resolution of the SDSS spectra and the step size of our model grid, and we therefore have
K, the absolute value of our accuracy is given by half of the model step width of
5000 K. Our accuracy in the surface gravities is limited by the low resolution of the SDSS spectra and the step size of our model grid, and we therefore have
![]() dex
dex ![]()
![]()
![]() . The metallicity determination is only accurate to about 0.3 dex.
. The metallicity determination is only accurate to about 0.3 dex.
![\begin{figure}
\par\includegraphics[width=8.25cm,clip]{0632fig06_left.eps}\includegraphics[width=8.5cm,clip]{0632fig06_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg144.gif) |
Figure 6:
Distribution of the derived distances of the stellar components of our systems; the diagonal is the ideal for physical binaries. The dotted curves span a tolerance fan for
|
| Open with DEXTER | |
5.1 White dwarfs showing He lines
From our original input sample, 616 spectra can be fitted well using a DA primary. However, among the remaining systems, He features are evident in a small number in the primary spectrum. These are most readily apparent at relatively high
![]() ,
since spectra with distinctive DB features were efficiently removed in the initial selection. We found that 20 of the remaining spectra, which were dominated mainly by the He II Bracket-equivalent series, were fitted more accurately by spectra from our DO model library. These stars cluster predominantly at the cool end of the DO sequence: 16 of 20 are fitted with the lowest effective temperature in the DO grid of 40 000 K. Many of the them show stronger He I lines in addition to He II, and would probably be classified more accurately as DBO, according to the nomenclature of Wesemael et al. (1993). We suspect that this distribution does not reflect the true luminosity function of Helium-rich white dwarfs, but is rather biased by a contribution of WDs below the
,
since spectra with distinctive DB features were efficiently removed in the initial selection. We found that 20 of the remaining spectra, which were dominated mainly by the He II Bracket-equivalent series, were fitted more accurately by spectra from our DO model library. These stars cluster predominantly at the cool end of the DO sequence: 16 of 20 are fitted with the lowest effective temperature in the DO grid of 40 000 K. Many of the them show stronger He I lines in addition to He II, and would probably be classified more accurately as DBO, according to the nomenclature of Wesemael et al. (1993). We suspect that this distribution does not reflect the true luminosity function of Helium-rich white dwarfs, but is rather biased by a contribution of WDs below the
![]() limit of our DO models. Since the number of these systems, and an additional number of potential DB systems that could neither be fitted by DA nor DO models and were omitted from our catalog, is too small for a meaningful statistical analysis, we have not attempted to obtain more reliable fits with additional DB models.
limit of our DO models. Since the number of these systems, and an additional number of potential DB systems that could neither be fitted by DA nor DO models and were omitted from our catalog, is too small for a meaningful statistical analysis, we have not attempted to obtain more reliable fits with additional DB models.
Three DOs in our sample (J0756+4216, J0916+0521, and J1336-0131) were already studied by Hügelmeyer et al. (2006). For the first one, the parameter values derived in our study are in good agreement with those of the cited publication. While they found the white dwarf to show an effective temperature of 52.5 ![]() 0.8 kK at
0.8 kK at
![]()
![]() 0.05 dex, we find
0.05 dex, we find
![]()
![]() 5 kK and
5 kK and
![]()
![]() 0.5 dex. For the MS companion, they derived
0.5 dex. For the MS companion, they derived
![]()
![]() 0.2 kK,
0.2 kK,
![]()
![]() 0.5 dex, and
0.5 dex, and
![]() ,
whereas we measure
,
whereas we measure
![]()
![]() 0.1 kK,
0.1 kK,
![]()
![]() 0.5 dex, and
0.5 dex, and
![]() .
.
The second binary, J0916+0521, was proposed by Hügelmeyer et al. (2006) to be one of the few optical pairs aligned by chance. With
![]() for that system, we tend to confirm their findings although the data points for many systems are located in the same region of the
for that system, we tend to confirm their findings although the data points for many systems are located in the same region of the
![]() diagram around J0916+0521. The other parameter values do not differ
significantly from each other, except for the M star masses, for which they derived
diagram around J0916+0521. The other parameter values do not differ
significantly from each other, except for the M star masses, for which they derived
![]() ,
while we find
,
while we find
![]() due to
due to ![]() 10% lower
10% lower
![]() and subsolar metallicity found in our fit. Our results for the third system, J1336-0131, agree with the values given by Hügelmeyer et al. (2006).
and subsolar metallicity found in our fit. Our results for the third system, J1336-0131, agree with the values given by Hügelmeyer et al. (2006).
5.2 Spectra with emission
In the spectra of 167 objects in our sample we find at least H![]() emission, and some of them also exhibit other types of Balmer emission. Most of these systems probably harbor an active M dwarf with chromospheric emission, or the respective M star might be irradiated by the primary, and experience photoionization and recombination. These systems are non-accreting since they do not show He I or He II features. A more detailed treatment of emission in WD-M star binaries is given in Silvestri et al. (2006). For an assessment of the magnetic activity, we scanned our fits for pronounced peaks in
emission, and some of them also exhibit other types of Balmer emission. Most of these systems probably harbor an active M dwarf with chromospheric emission, or the respective M star might be irradiated by the primary, and experience photoionization and recombination. These systems are non-accreting since they do not show He I or He II features. A more detailed treatment of emission in WD-M star binaries is given in Silvestri et al. (2006). For an assessment of the magnetic activity, we scanned our fits for pronounced peaks in
![]() ,
as defined by Eq. (10). An example is shown in the lower panel of Fig. 2. Our M dwarf models did not consider H
,
as defined by Eq. (10). An example is shown in the lower panel of Fig. 2. Our M dwarf models did not consider H![]() emission, and therefore the spike in the fitting error at the H
emission, and therefore the spike in the fitting error at the H![]() wavelength was - if present at all - always related to an emission feature in that line. We decided to attribute the peak in
wavelength was - if present at all - always related to an emission feature in that line. We decided to attribute the peak in
![]() close to 6563
close to 6563 ![]() to H
to H![]() emission, if it exceeded the ambient noise level by at least a fraction of three.
emission, if it exceeded the ambient noise level by at least a fraction of three.
In their study of 101 WDMSs, Rebassa-Mansergas et al. (2007) identified 18 PCEBs and PCEB candidates of which 12 are included in our master sample (see Table 3). Eleven of them are in our spectroscopic sample and 8 of them are marked as H emitters therein. Due to the strong H![]() contamination of the PCEB (candidate) spectra our fits are often inconsistent in terms of
contamination of the PCEB (candidate) spectra our fits are often inconsistent in terms of
![]() and
and ![]() ,
whereas they should ideally be equal. If the parameter values of our best-fit solution differed significantly from those provided by Rebassa-Mansergas et al. (2007),
we chose to adopt instead the parameters corresponding to their solutions.
,
whereas they should ideally be equal. If the parameter values of our best-fit solution differed significantly from those provided by Rebassa-Mansergas et al. (2007),
we chose to adopt instead the parameters corresponding to their solutions.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig07.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg155.gif) |
Figure 7: Temperature function for the WDs; while the major peak at 17 000 K belongs to the DAs, the bump at 40 000 K is due to the preferential selection of cool DOs for our sample. This plot looks very similar to that shown in Silvestri et al. (2006), except for the DO feature and that it is smoothed. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig08.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg156.gif) |
Figure 8:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig09.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg157.gif) |
Figure 9: The distribution of the WD distances in our sample is a consequence of the restricted magnitude range of the SDSS. It has its maximum at 354 pc. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig10.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg158.gif) |
Figure 10: The distribution of the M star distances in our sample is a consequence of the restricted magnitude range of the SDSS. Its maximum is at 334 pc. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig11.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg159.gif) |
Figure 11: Distribution of the WD surface gravities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig12.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg160.gif) |
Figure 12:
Distribution of the M star surface gravities; the few objects with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig13.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg161.gif) |
Figure 13:
Metallicities of the M stars in our sample, normalized to 1; the plot shows a distinct peak at [Fe/H] |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{0632fig14.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg162.gif) |
Figure 14:
As an example for one of the 41 optically resolved binaries with further treatment, we show the SDSS image of J1127-0028. The image resolution is 0.025
|
| Open with DEXTER | |
As an example, we refer to J0052-0053, which shows an ambiguous
![]() distribution. This is probably due to the weak WD and M star features in the spectrum and due to the large distance of the system. The results of our fitting routine for J0052-0053 are
distribution. This is probably due to the weak WD and M star features in the spectrum and due to the large distance of the system. The results of our fitting routine for J0052-0053 are
![]() K, log
K, log
![]() ,
and a distance to Earth of 1612 pc for the WD. The corresponding parameters for its companion are computed to be
,
and a distance to Earth of 1612 pc for the WD. The corresponding parameters for its companion are computed to be
![]() K, log
K, log
![]() ,
[Fe/H]
,
[Fe/H]![]() = 0.0, and
= 0.0, and
![]() pc. The respective distance evaluation coefficient of
pc. The respective distance evaluation coefficient of
![]() emphasizes the grave dissonance in the objects' distances from Earth. It should be close to zero for consistent fits as defined in Eq. (16). Hence, we fix the parameters for the WD to be
emphasizes the grave dissonance in the objects' distances from Earth. It should be close to zero for consistent fits as defined in Eq. (16). Hence, we fix the parameters for the WD to be
![]() ,
,
![]() K and log
K and log
![]() - following Rebassa-Mansergas et al. (2007) - and set
- following Rebassa-Mansergas et al. (2007) - and set
![]() K to enforce
K to enforce
![]() .
Using this procedure, we deduce
.
Using this procedure, we deduce
![]() pc and
pc and
![]() pc, in good agreement with the value of 505 pc for the distance of the WD derived by Rebassa-Mansergas et al. (2007) (see Table 2 for the whole result).
pc, in good agreement with the value of 505 pc for the distance of the WD derived by Rebassa-Mansergas et al. (2007) (see Table 2 for the whole result).
We also find 4 systems showing He I and He II emission, in addition to H![]() features, that harbor a hot primary (
features, that harbor a hot primary (
![]() K). Since He I is not typically observed in active M dwarfs, these objects might either be CVs, i.e. binaries that undergo mass transfer, or their mutual separation might just be large enough as to avoid mass overflow on the one hand but close enough to produce the emission lines by irradiation effects on the other hand. J1249+0357 was actually classified as CV by Downes et al. (2001) and Szkody et al. (2004). However, its CV status can be doubted since the spectrum shows no features of an accretion disk and the He emission lines are not dynamically broadened by a potentially rotating disk. The emission features in J1317+6731 and J1439-0106 are most likely due to irradiation of the M component. Their spectra show strong H
K). Since He I is not typically observed in active M dwarfs, these objects might either be CVs, i.e. binaries that undergo mass transfer, or their mutual separation might just be large enough as to avoid mass overflow on the one hand but close enough to produce the emission lines by irradiation effects on the other hand. J1249+0357 was actually classified as CV by Downes et al. (2001) and Szkody et al. (2004). However, its CV status can be doubted since the spectrum shows no features of an accretion disk and the He emission lines are not dynamically broadened by a potentially rotating disk. The emission features in J1317+6731 and J1439-0106 are most likely due to irradiation of the M component. Their spectra show strong H![]() as well as He I and He II emission. Both objects were already mentioned in Silvestri et al. (2006) and the detection of the latter one was originally published in Raymond et al. (2003). The system J2125-0107 that we fitted with a DO primary from our model grid is actually known to be a close system with a PG1159 primary (Schuh et al. 2009; Nagel et al. 2006; Schuh et al. 2008). We misclassified that object since we did not include PG 1159 models in our repertoire. Our value for
as well as He I and He II emission. Both objects were already mentioned in Silvestri et al. (2006) and the detection of the latter one was originally published in Raymond et al. (2003). The system J2125-0107 that we fitted with a DO primary from our model grid is actually known to be a close system with a PG1159 primary (Schuh et al. 2009; Nagel et al. 2006; Schuh et al. 2008). We misclassified that object since we did not include PG 1159 models in our repertoire. Our value for
![]() of 4000 K should be taken with reservation due to the known strong irradiation processes from the hot primary on the MS companion.
of 4000 K should be taken with reservation due to the known strong irradiation processes from the hot primary on the MS companion.
Table 1: Optically resolved binaries (41 objects).
From the 167 spectra with H emission features, we subtract 8 known PCEB candidates and the 4 systems from the previous paragraph, which yields 155 WD-M star binaries, corresponding to a fraction of 24.4%, that probably harbor an active M dwarf. Although this value matches the number found by West et al. (2004) for active field M dwarfs in the SDSS, our sample of MS stars mainly consists of stars with spectral types earlier than M5 (see Fig. 15). For this range, and in particular for dM stars earlier than M4, the activity fraction from West et al. (2004) is much smaller than 10%. Silvestri et al. (2006) detected a significantly higher fraction of active M dwarfs in WD-M binaries (between 20% and 50% from M0 to M5), which they attributed to a rotational spin-up of the secondary due to gravitational interaction with the WD. They also reported a lack of active dM stars with ages > 0.8 Gyr. Since they imposed a less stringent (g-r) cutoff (<0.7) for most of their sample than we had (<0.2), hotter, and thus younger, WDs passed their selection process, which would increase their fraction of active M dwarfs to a higher value than ours. Nevertheless, our results for the fraction of active M dwarfs is in better agreement with the results found by Silvestri et al. (2006) than it fits to the low fraction found by West et al. (2004). Even if we consider only unresolved
binaries, as Silvestri et al. (2006) did, our fraction of binary systems with
H![]() emission that probably originates in the M component does not decrease below 23.2%.
emission that probably originates in the M component does not decrease below 23.2%.
Table 2: Example table of results for 636 WD-M star binaries.
Table 3: Excerpt of our catalog, the master sample, of 857 WD-M binary stars.
5.3 Optically resolved binaries
Of our 636 binaries, 41 were chosen for follow-up studies because, firstly, the red star was found to be located within an area around the WD that was covered by the SDSS fiber and, secondly,
these stars had a sufficiently wide separation to enable us to distinguish between the two components. Figure 14 provides a typical illustration of these systems. For photometric binaries with a separation clearly larger than the SDSS fiber radius of
![]() ,
we assume that the M star on the SDSS image is not the one represented in the spectrum. The respective fitting results are indicated in Table 2 and should be interpreted with caution
since we may be unable to determine if a significant fraction of the light contribution from the red star was collected by the fiber, despite the separation being larger than
,
we assume that the M star on the SDSS image is not the one represented in the spectrum. The respective fitting results are indicated in Table 2 and should be interpreted with caution
since we may be unable to determine if a significant fraction of the light contribution from the red star was collected by the fiber, despite the separation being larger than
![]() .
The results for the 41 clearly separated objects can be seen in Table 1. The typical projected distances are large and of the order of some hundred AU with a mean value of roughly 650 AU. The widest separation that we find is 1700 AU for J1006+5633, where the true spatial separation should be even wider. The orbital periods that we derive are typically of the order of 104 yr with J1006+5633 indicating a period of
.
The results for the 41 clearly separated objects can be seen in Table 1. The typical projected distances are large and of the order of some hundred AU with a mean value of roughly 650 AU. The widest separation that we find is 1700 AU for J1006+5633, where the true spatial separation should be even wider. The orbital periods that we derive are typically of the order of 104 yr with J1006+5633 indicating a period of ![]() 70 000 yr.
70 000 yr.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0632fig15_left.eps}\hspace*{1cm}
\includegraphics[width=7.7cm,clip]{0632fig15_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg192.gif) |
Figure 15:
Left: comparison of the spectral types given in Rebassa-Mansergas et al. (2007) with the effective temperatures we deduced for 41 M stars, that match both their sample and ours; 11 of them are marked as PCEBs, as confirmed in their study via RV measurements. The labels indicate the counts per grid point. Right: comparison of the spectral types given in Silvestri et al. (2006) with the effective temperatures we derived for 446 M stars, that match both their sample and ours; The number of M dwarf stars per grid point is projected onto the plane spanned by
|
| Open with DEXTER | |
5.4 Very low-mass objects
We flagged the secondaries in our sample to be very low-mass objects (VLMOs), provided that they had a mass ![]()
![]() and
and
![]() ,
or
,
or
![]() and
and
![]() ,
to identify potential candidates for substellar companions. Seventy M stars in our reservoir are VLMO according to this definition (see the electronic version of this paper for the table of results). The M masses were calculated from the fitted
,
to identify potential candidates for substellar companions. Seventy M stars in our reservoir are VLMO according to this definition (see the electronic version of this paper for the table of results). The M masses were calculated from the fitted
![]() and [Fe/H]
and [Fe/H]![]() using evolutionary tables calculated by Baraffe et al. (1998). Their models are available for
using evolutionary tables calculated by Baraffe et al. (1998). Their models are available for
![]() ,
-1.5, -1.3, -1, -0.5, and 0, while no specific tracks exist for those M stars, which are fitted to have
,
-1.5, -1.3, -1, -0.5, and 0, while no specific tracks exist for those M stars, which are fitted to have
![]() .
Since radius and mass at constant
.
Since radius and mass at constant
![]() decrease monotonously with metallicity in the other tracks, we can only quote the [Fe/H]
decrease monotonously with metallicity in the other tracks, we can only quote the [Fe/H]![]() = 0 values as a lower limit for
= 0 values as a lower limit for
![]() and
and
![]() ,
and consequently also for
,
and consequently also for
![]() .
However, there is only one VLMO candidate in our sample that has a metallicity of +0.3: J1323+3018. The other 69 VLMO candidates are most accurately fitted with
.
However, there is only one VLMO candidate in our sample that has a metallicity of +0.3: J1323+3018. The other 69 VLMO candidates are most accurately fitted with
![]() .
.
If any of the VLMOs were found to be substellar, they would of course by definition be in the cooling phase of their evolution, and more significant deviations from the old main-sequence models would be expected for these objects, biasing the radius estimate and thus also the assessment of the distance.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0632fig16_left.eps}\includegraphics[width=8.5cm,clip]{0632fig16_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg202.gif) |
Figure 16:
Left: distribution of the derived distances of the stellar components from Rebassa-Mansergas et al. (2007); in contrast to our results, their binaries tend to have a larger value for |
| Open with DEXTER | |
6 Discussion
The M star temperatures that we fitted are in good agreement with the spectral types derived by Rebassa-Mansergas et al. (2007). In Fig. 15, we compare our fits for
![]() with their spectral types for 41 objects (left panel) and with the spectral classification from Silvestri et al. (2006) (right panel) for 446 objects, which were both in our own and their sample. The authors of the latter publication derived their dM types on the basis of template spectra and color indices as described in Hawley et al. (2002). Since we project the number of M dwarfs per
with their spectral types for 41 objects (left panel) and with the spectral classification from Silvestri et al. (2006) (right panel) for 446 objects, which were both in our own and their sample. The authors of the latter publication derived their dM types on the basis of template spectra and color indices as described in Hawley et al. (2002). Since we project the number of M dwarfs per
![]() and per spectral type onto the plane spanned by these two parameters, this plot is related to Fig. 8. In both of the figures, the maximum is reached at (3200 K, M4), and the plot shows a monotone decrease of the spectral type with increasing temperature. These counts probably do not relate directly to the true
and per spectral type onto the plane spanned by these two parameters, this plot is related to Fig. 8. In both of the figures, the maximum is reached at (3200 K, M4), and the plot shows a monotone decrease of the spectral type with increasing temperature. These counts probably do not relate directly to the true
![]() or spectral type function due to selection effects such as the increasing number of M dwarfs towards later types on the one hand, and decreasing visibility of the secondary component on the other hand.
or spectral type function due to selection effects such as the increasing number of M dwarfs towards later types on the one hand, and decreasing visibility of the secondary component on the other hand.
In the Rebassa-Mansergas et al. (2007) study, the MS stars showed a tendency to be at larger distances from Earth than the WD primary (see Fig. 16). The authors ascribed this trend to spots on the secondaries' surfaces, which would cause the spectral types to appear too early. The radii derived from the spectral type-radius relation would then have been too large, in addition to the computed distances of the MS stars. In our study, we observe the opposite trend, namely
![]() being smaller than
being smaller than
![]() ,
and we consider three possible effects contributing to that trend:
,
and we consider three possible effects contributing to that trend:
- 1.
- Reiners (2005) showed that the absorption in the TiO
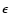 -band is systematically underestimated by PHOENIX M star spectra. Since as a primary temperature indicator, this band system deepens with decreasing
-band is systematically underestimated by PHOENIX M star spectra. Since as a primary temperature indicator, this band system deepens with decreasing
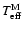 ,
model spectra fits to this feature may also underestimate systematically
,
model spectra fits to this feature may also underestimate systematically
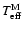 .
This effect, if present in our models as well, would cause
.
This effect, if present in our models as well, would cause 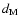 to be systematically underestimated. Figure 2 shows indeed that the model predicts a relatively strong TiO
to be systematically underestimated. Figure 2 shows indeed that the model predicts a relatively strong TiO 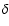 -band at 8870 Å compared with the
-band at 8870 Å compared with the 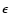 -band at 8450 Å. However, the mismatch is not severe, and the
-band at 8450 Å. However, the mismatch is not severe, and the 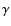 -band at 7055 Å is reproduced well. We therefore do not expect uncertainties in the molecular opacities to introduce a strong bias in our results.
-band at 7055 Å is reproduced well. We therefore do not expect uncertainties in the molecular opacities to introduce a strong bias in our results.
- 2.
- As mentioned in Sect. 2.1, there is observational evidence that the masses of WDs in magnetic, accreting binaries are mainly between 0.7
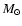 and 0.8
and 0.8 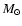 ,
instead of around 0.6
,
instead of around 0.6 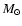 as for field WDs. There is no evidence for accretion in any of the spectra in our sample. Only 11 out of the 636 objects presented here are known to be close systems, i.e. PCEBs, while 41 are quite widely separated as inferred from the SDSS images. We cannot assess of the remaining orbits on the basis of our data, and we cannot state if the WD masses are close to 0.7 or even 0.8
as for field WDs. There is no evidence for accretion in any of the spectra in our sample. Only 11 out of the 636 objects presented here are known to be close systems, i.e. PCEBs, while 41 are quite widely separated as inferred from the SDSS images. We cannot assess of the remaining orbits on the basis of our data, and we cannot state if the WD masses are close to 0.7 or even 0.8 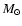 .
However, a trend towards higher WD masses would be compatible with a bias towards
.
However, a trend towards higher WD masses would be compatible with a bias towards
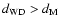 .
An increase in mass leads to a decrease in radius for a WD, and consequently a smaller distance to Earth is required to reproduce the observed flux. Our possible underestimation of
.
An increase in mass leads to a decrease in radius for a WD, and consequently a smaller distance to Earth is required to reproduce the observed flux. Our possible underestimation of
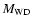 could thus contribute to a systematic overestimation of
could thus contribute to a systematic overestimation of
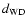 .
.
- 3.
- Based on the effective temperature and the metallicity from our spectral fits, the M star radii that we deduced from the Chabrier & Baraffe (1997) model tracks are systematically underestimated for low-mass objects (
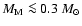 ,
see Fig. 16). This discrepancy between theory and observations is well known in the research field of low-mass stars and emerged in observations of eclipsing binary systems with a low-mass component (Ribas et al. 2007). With our - in statistical terms - large sample, we support this claim. We encourage the reader to look at Fig. 16 to see that the trend vanishes for MS stars with masses
,
see Fig. 16). This discrepancy between theory and observations is well known in the research field of low-mass stars and emerged in observations of eclipsing binary systems with a low-mass component (Ribas et al. 2007). With our - in statistical terms - large sample, we support this claim. We encourage the reader to look at Fig. 16 to see that the trend vanishes for MS stars with masses
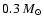 !
!
There is a relatively large number of widely-separated binaries with orbital distances ![]() 250 AU and up to 1700 AU: 41/636 = 6.4%. This is, however, not a stable assessment; we suggest five effects that may smear the optical-binary fraction to either higher or lower values.
250 AU and up to 1700 AU: 41/636 = 6.4%. This is, however, not a stable assessment; we suggest five effects that may smear the optical-binary fraction to either higher or lower values.
- 1.
- If two objects are so close together that they appear as one elongated object, the SDSS classification procedure may preselect it as a possible galaxy. This would imply that we have underestimated the true optical-binary fraction.
- 2.
- A small number of physical pairs aligned along the line of sight could also drive the true optical-binary fraction to a higher value. We would have failed them to detect because of their unfavorable geometrical constellation.
- 3.
- Some of the stellar duets on the SDSS images with angular distances >
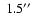 could also be physical pairs (but the secondary on the image would not be the one represented in the respective SDSS spectrum).
could also be physical pairs (but the secondary on the image would not be the one represented in the respective SDSS spectrum).
- 4.
- A significant contingent of binaries with mass overflow from the MS companion to the WD are supposed to be located out of the color-color region that we studied in compiling our sample. These stellar duets are close systems with no optical separation on the SDSS images, which pushes the optical-binary fraction to lower values.
- 5.
- The statistical considerations presented in Sect. 2.1 demonstrated that about 4 of the binaries in our sample should be aligned by chance - without a common evolutionary background. Probably none, or at most one, of the optical binaries is one of these outliers.
Acknowledgements
R. Heller is supported by a Ph.D. scholarship of the DFG Graduiertenkolleg 1351 ``Extrasolar Planets and their Host Stars''. We thank D. Koester for his computations of the WD spectra grid and we also acknowledge the anonymous referee for his useful contributions. We also appreciate the remarks by B. Gänsicke and S. Schuh referring to Sect. 5.2. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] (In the text)
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] (In the text)
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] (In the text)
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ASP Conf. Ser., 336, 25 (In the text)
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] (In the text)
- Bean, J. L., Sneden, C., Hauschildt, P. H., Johns-Krull, C. M., & Benedict, G. F. 2006, ApJ, 652, 1604 [NASA ADS] [CrossRef]
- Beuermann, K., Baraffe, I., Kolb, U., & Weichhold, M. 1998, A&A, 339, 518 [NASA ADS] (In the text)
- Bochanski, J. J., West, A. A., Hawley, S. L., & Covey, K. R. 2007, AJ, 133, 531 [NASA ADS] [CrossRef] (In the text)
- Brott, I., & Hauschildt, P. H. 2005, in The Three-Dimensional Universe with Gaia, ESA SP-576, 565 (In the text)
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] (In the text)
- Cropper, M., Ramsay, G., & Wu, K. 1998, MNRAS, 293, 222 [NASA ADS] [CrossRef]
- Downes, R. A., Webbink, R. F., Shara, M. M., et al. 2001, PASP, 113, 764 [NASA ADS] [CrossRef] (In the text)
- Eisenstein, D. J., Liebert, J., Harris, H. C., et al. 2006, ApJS, 167, 40 [NASA ADS] [CrossRef] (In the text)
- Finley, D. S., Koester, D., & Basri, G. 1997, ApJ, 488, 375 [NASA ADS] [CrossRef] (In the text)
- Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 [NASA ADS] [CrossRef] (In the text)
- Greenstein, J. L. 1986, AJ, 92, 867 [NASA ADS] [CrossRef] (In the text)
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 102, 41 [CrossRef] (In the text)
- Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999, ApJ, 525, 871 [NASA ADS] [CrossRef] (In the text)
- Hawley, S. L., Covey, K. R., Knapp, G. R., et al. 2002, AJ, 123, 3409 [NASA ADS] [CrossRef] (In the text)
- Homeier, D., Koester, D., Hagen, H.-J., et al. 1998, A&A, 338, 563 [NASA ADS]
- Hu, Q., Wu, C., & Wu, X.-B. 2007, A&A, 466, 627 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hügelmeyer, S. D., Dreizler, S., Homeier, D., et al. 2006, A&A, 454, 617 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jordan, S., Napiwotzki, R., Koester, D., & Rauch, T. 1997, A&A, 318, 461 [NASA ADS] (In the text)
- Kleinman, S. J., Harris, H. C., Eisenstein, D. J., et al. 2004, ApJ, 607, 426 [NASA ADS] [CrossRef] (In the text)
- Koester, D., Napiwotzki, R., Christlieb, N., et al. 2001, A&A, 378, 556 [NASA ADS] [CrossRef] [EDP Sciences]
- Luyten, W. J. 1997, VizieR Online Data Catalog, 1130, 0 (In the text)
- Luyten, W. J. 1999, VizieR Online Data Catalog, 3070, 0 (In the text)
- Mihalas, D. 1978, Stellar atmospheres/2nd edn./ (San Francisco: W. H. Freeman and Co.), 650 [NASA ADS] (In the text)
- Nagel, T., Schuh, S., Kusterer, D.-J., et al. 2006, A&A, 448, L25 [NASA ADS] [CrossRef] [EDP Sciences]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, The Art of Scientific Computing, Numerical recipes in C++, 2nd edn. (Cambridge: Cambridge University Press) (In the text)
- Ramsay, G. 2000, MNRAS, 314, 403 [NASA ADS] [CrossRef]
- Raymond, S. N., Szkody, P., Hawley, S. L., et al. 2003, AJ, 125, 2621 [NASA ADS] [CrossRef] (In the text)
- Rebassa-Mansergas, A., Gänsicke, B. T., Rodríguez-Gil, P., Schreiber, M. R., & Koester, D. 2007, MNRAS, 382, 1377 [NASA ADS] (In the text)
- Reiners, A. 2005, Astron. Nachr., 326, 930 [NASA ADS] [CrossRef] (In the text)
- Ribas, I., Morales, J., Jordi, C., et al. 2007, ArXiv e-prints, 711 (In the text)
- Ritter, H., & Kolb, U. 1998, A&AS, 129, 83 [NASA ADS] [CrossRef] [EDP Sciences]
- Schuh, S., Beek, B., & Nagel, T. 2009, Proceedings of the 16th European White Dwarf Workshop; to be published in J. Phys.: Conf. Ser.
- Schuh, S., Traulsen, I., Nagel, T., et al. 2008, Astron. Nachr., 329, 376 [NASA ADS]
- Silvestri, N. M., Hawley, S. L., West, A. A., et al. 2006, AJ, 131, 1674 [NASA ADS] [CrossRef] (In the text)
- Silvestri, N. M., Lemagie, M. P., Hawley, S. L., et al. 2007, AJ, 134, 741 [NASA ADS] [CrossRef] (In the text)
- Smolcic, V., Ivezic, Z., Knapp, G. R., et al. 2004, ApJ, 615, L141 [NASA ADS] [CrossRef] (In the text)
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, accepted
- Szkody, P., Henden, A., Fraser, O., et al. 2004, AJ, 128, 1882 [NASA ADS] [CrossRef] (In the text)
- Wachter, S., Hoard, D. W., Hansen, K. H., et al. 2003, ApJ, 586, 1356 [NASA ADS] [CrossRef] (In the text)
- Weinberg, M. D., Shapiro, S. L., & Wasserman, I. 1987, ApJ, 312, 367 [NASA ADS] [CrossRef] (In the text)
- Wesemael, F., Greenstein, J. L., Liebert, J., et al. 1993, PASP, 105, 761 [NASA ADS] [CrossRef] (In the text)
- West, A. A., Hawley, S. L., Walkowicz, L. M., et al. 2004, AJ, 128, 426 [NASA ADS] [CrossRef] (In the text)
- Wood, M. 1994, in The Equation of State in Astrophysics, IAU Colloq., 147, 612 (In the text)
- Zhang, E.-H., Robinson, E. L., & Nather, R. E. 1986, ApJ, 305, 740 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... survey
![[*]](/icons/foot_motif.gif)
- Table 1 is also available in electronic form at the CDS and Full Tables 2 and 3 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/496/191
- ...
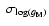
![[*]](/icons/foot_motif.gif)
- Reiners (2005) provided an even more conservative error estimate of 1 dex, due to the low resolution of the spectra.
All Tables
Table 1: Optically resolved binaries (41 objects).
Table 2: Example table of results for 636 WD-M star binaries.
Table 3: Excerpt of our catalog, the master sample, of 857 WD-M binary stars.
All Figures
![\begin{figure}
\par\includegraphics[width=4cm,clip]{0632fig01_left.eps}\hspace*{...
...space*{1.2cm}
\includegraphics[width=7cm,clip]{0632fig01_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg32.gif) |
Figure 1: Left: the localizations of our master sample in the (u-r)-space; middle: the localizations of our master sample in the (i-z)-space; right: comparison of the color-color localizations of our master sample with the WD-M sample of Silvestri et al. (2006). Those objects from our study with g-r > 0.2 come from the EDR, on which we did not impose the (g-r)-cutoff. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{0632fig02.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg66.gif) |
Figure 2:
Example for our fitting procedure; Top: observed SDSS spectrum of J1009+0244 and the DA-dM combination in our fitting routine. As mentioned in Silvestri et al. (2006), the feature close to 5600 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0632fig03.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg86.gif) |
Figure 3:
Projection of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0632fig04.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg103.gif) |
Figure 4:
Geometrical explanation of the distance evaluation coefficient
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0632fig05.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg115.gif) |
Figure 5:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.25cm,clip]{0632fig06_left.eps}\includegraphics[width=8.5cm,clip]{0632fig06_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg144.gif) |
Figure 6:
Distribution of the derived distances of the stellar components of our systems; the diagonal is the ideal for physical binaries. The dotted curves span a tolerance fan for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig07.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg155.gif) |
Figure 7: Temperature function for the WDs; while the major peak at 17 000 K belongs to the DAs, the bump at 40 000 K is due to the preferential selection of cool DOs for our sample. This plot looks very similar to that shown in Silvestri et al. (2006), except for the DO feature and that it is smoothed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig08.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg156.gif) |
Figure 8:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig09.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg157.gif) |
Figure 9: The distribution of the WD distances in our sample is a consequence of the restricted magnitude range of the SDSS. It has its maximum at 354 pc. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig10.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg158.gif) |
Figure 10: The distribution of the M star distances in our sample is a consequence of the restricted magnitude range of the SDSS. Its maximum is at 334 pc. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig11.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg159.gif) |
Figure 11: Distribution of the WD surface gravities. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig12.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg160.gif) |
Figure 12:
Distribution of the M star surface gravities; the few objects with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0632fig13.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg161.gif) |
Figure 13:
Metallicities of the M stars in our sample, normalized to 1; the plot shows a distinct peak at [Fe/H] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{0632fig14.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg162.gif) |
Figure 14:
As an example for one of the 41 optically resolved binaries with further treatment, we show the SDSS image of J1127-0028. The image resolution is 0.025
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0632fig15_left.eps}\hspace*{1cm}
\includegraphics[width=7.7cm,clip]{0632fig15_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg192.gif) |
Figure 15:
Left: comparison of the spectral types given in Rebassa-Mansergas et al. (2007) with the effective temperatures we deduced for 41 M stars, that match both their sample and ours; 11 of them are marked as PCEBs, as confirmed in their study via RV measurements. The labels indicate the counts per grid point. Right: comparison of the spectral types given in Silvestri et al. (2006) with the effective temperatures we derived for 446 M stars, that match both their sample and ours; The number of M dwarf stars per grid point is projected onto the plane spanned by
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0632fig16_left.eps}\includegraphics[width=8.5cm,clip]{0632fig16_right.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa10632-08/Timg202.gif) |
Figure 16:
Left: distribution of the derived distances of the stellar components from Rebassa-Mansergas et al. (2007); in contrast to our results, their binaries tend to have a larger value for |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



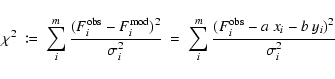
![\begin{displaymath}%
\left( \begin{array}{c}
a\\
b\\
\end{array}\right) \
=...
...
~\!\! [F_{i}^{{\rm obs}}~y_{i}]\\
\end{array}\right)\cdot
\end{displaymath}](/articles/aa/full_html/2009/10/aa10632-08/img76.gif)
![\begin{displaymath}%
\left( \begin{array}{c}
a\\
b\\
\end{array}\right) \
=...
...ight)
\frac{1}{[x_{i}^2]~[y_{i}^2] \!-\! [x_{i}~y_{i}]^2}\cdot
\end{displaymath}](/articles/aa/full_html/2009/10/aa10632-08/img77.gif)