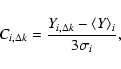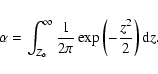Regularity in dynamic spectra of Jovian radio decameter S-bursts

O. V. Arkhypov; H. O. Rucker

doi:10.1051/0004-6361/200810583

Home

All issues

Volume 496 / No 1 (March II 2009)

A&A, 496 1 (2009) 269-274

Full HTML

Free Access

Issue		A&A Volume 496, Number 1, March II 2009


Page(s)		269 - 274
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200810583
Published online		30 January 2009

Regularity in dynamic spectra of Jovian radio decameter S-bursts

O. V. Arkhypov^1,2 - H. O. Rucker³

1 - Institute of Radio Astronomy, National Academy of Sciences of Ukraine, Chervonopraporna 4, 61002 Kharkiv, Ukraine
2 - Department of Space Radio Physics, Kharkiv V. N. Karazin National University, Svoboda Square 4, 61077 Kharkiv , Ukraine
3 - Space Research Institute, Austrian Academy of Sciences, Schmiedlstrasse 6, 8042 Graz, Austria

Received 12 July 2008 / Accepted 8 January 2009

Abstract
Short (S-) bursts of Jovian decametric emission show random behavior with very complicated forms in the dynamic spectrum. We first draw attention to the correlation properties of S-bursts as an indicator of their hidden regularity. Thus we calculate the linear correlation coefficient $r(f-f_{o}, \Delta t)$ between the spectral intensity in the current (f) and the reference (f_o) frequency channels with $\Delta t$ time shift. The result is displayed in the form of 2D-correlation image, where the pixel brightness reflects the r estimate, and the pixel's co-ordinates are f and $\Delta t$ . The non-trivial and stabile correlation patterns are found, described, and discussed here. Apparently, there is the hidden wave-like modulation of the whole S-burst storm in the form of a correlation or anti-correlation between emissions at different radio frequencies with short time scales from 0.02 s to 0.8 s.

Key words: planets and satellites: individual: Jupiter - magnetohydrodynamics (MHD) - waves - plasmas - radiation mechanisms: non-thermal

1 Introduction

Short (S-) bursts of Jovian decametric emission (DAM), with a typical duration of $\sim$ 1 ms at fixed radio frequency, usually appear as lines in the dynamic spectrum, i.e. on the time-frequency plane. It is generally accepted that such a form of the S-burst reflects the motion of a radio source along a magnetic line with a decrease in the emission frequency in accordance with the local gyrofrequency of electrons (Zarka 1998). Often, quasi-linear S-bursts are associated with narrow band (NB) emission, which shows very complicated oscillations in f around some frequency (e.g., Boudjada et al. 2000). Figure 1 demonstrates such features in the dynamical spectrum, which is recorded with the world's largest decameter radio telescope UTR-2, located close to Kharkov (Ukraine).

From Fig. 1 it follows that S/NB-emission shows a random behavior with some regular components in the dynamic spectrum. Up the present, S-burst statistics have rarely been investigated. Calvert et al. (1988) studied the statistics of inter-burst spacing at fixed radio frequency. It has been found that S-bursts are associated in randomly-spaced groups within which their spacing is approximately periodic. Such a group predominantly consists of only a few S-bursts. Another approach is to study the form of individual S-bursts in dynamic spectra for an average estimate of their frequency drift rate (e.g., Hess et al. 2007, and references therein). There have been studies that use the amplitude information of S-bursts; but with shortest time scales of $\leq$ 0.1 ms, only random noise statistics are detected (e.g. Ryabov et al. 2007, and the review therein). However, just the amplitude can give valuable information on S-burst statistics. A possible correlation between S-bursts at different frequencies and times has not been studied yet. Arkhypov & Rucker (2008a) searched for the correlation between S-bursts in 2 to 3 selected frequency channels. At that time, a specific correlation pattern was found. However, the majority of frequency channels were excluded from this particular analysis.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{0583fig1.eps} \end{figure}$	Figure 1: An example of DAM dynamic spectra with random S/NB-events in two bands is recorded 2002 August 9, 11:30 UT, using the Kharkov UTR-2 radio telescope. Interferences exhibit as numerous horizontal solid and dashed stripes.
Open with DEXTER

To fill this analysis gap, we calculated the correlation coefficient between S-burst emission in all available frequency channels with different time shifts and the resolutions of 2 ms to 6 ms. The advantage of the correlation approach is simple and effective extraction of regularity from chaos. Section 2 describes the experimental material and method of correlation analysis. The phenomenology of the correlation patterns found is described in Sect. 3. We analyze our findings in Sect. 4, and our conclusions are summarized in Sect. 5.

2 Material and method

We used the archive records of DAM from the collection of the Space Research Institute of the Austrian Academy of Sciences (Graz, Austria). The dynamic spectra of highest resolution (2 to 6 ms and 12.5 kHz) are recorded during an observation campaign within the framework of the INTAS project 03-51-5727 with the largest decametric radio telescope UTR-2 (Institute of Radio Astronomy, Kharkiv, Ukraine). The Digital Signal Processors (DSP) and other technical details are described in Konovalenko et al. (2001). The parameters of the spectra used are summarized in Table 1. The selected spectra show only Io-B S-burst emission with some admixture of NB-events.

Table 1: Studied spectra of Jovian decametric emission.

For each spectrum we select the reference channel with the radio frequency f_o, which usually is centered on the well-defined S-burst band. Then the linear correlation coefficient r is calculated between the reference channel number i_o and each other channel with various time shifts:

$\begin{displaymath}% r_{i,\Delta k}=\frac{1}{n} \sum_{k=1}^{m} \frac{[F_{i0,k}-\... ..._{i,k+\Delta k}-\langle F\rangle_{i}]}{\sigma_{io}\sigma_{i}}, \end{displaymath}$

(1)

where i and k are the pixel numbers in the frequency and time scales, m is the width of analyzed dynamic spectrum in pixels, n is the number of terms in the sum, $\Delta k$ is a pixel (time) shift, F_i,kand $\langle F\rangle_{i}$ are the spectral intensity and its average value at constant i or radio frequency, and $\sigma_{i}$ is the dispersion of the spectral intensity on the line. As a result, calculated matrix $r(i,\Delta k)$ is linearly coded on 256 levels of grey shading as a 2D-correlation image (Fig. 2b).

Unfortunately, interferences appear as numerous artifacts in the form of horizontal stripes in Fig. 2b. Moreover, the correlation pattern is frequently hidden in darkness except for the central peak. To visualize the whole correlation pattern, we used the normalized parameter $C_{i,\Delta k}$ :

$\begin{displaymath}% C_{i,\Delta k} =\frac{Y_{i,\Delta k} - \langle Y \rangle_{i}}{3 \sigma_{i}}, \end{displaymath}$

(2)

where $Y_{i,\Delta k}=\lg (r_{i,\Delta k} +1)$ , and $\langle Y\rangle_{i}$ and $\sigma_{i}$ are the average $Y_{i,\Delta k}$ value and its dispersion for each frequency channel ( $i={\rm const.}$ ). The $C_{i,\Delta k}$ obtained is coded into the pixel's brightness in 256 grey-shading levels for the mapping. The resulting image (Fig. 2c) shows the clear correlation pattern with bright details of positive r and dark pixels of anti-correlation.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig2.eps} \end{figure}$

Figure 2:

An example of DAM 2D-correlation analysis: a) the fragment of the analyzed record of the S-burst emission (2002 August 9, 11:30 UT; UTR-2 radio telescope); b) the raw pattern of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference ( f_o= 23.75 MHz) frequency channels with $\Delta t$ time shift; c) the plotting of $C_{i,\Delta k}$ parameter (see Eq. (2)); d) only significance features ( $\alpha =0.005$ ) of the c) image; e) the threshold scheme of c).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{0583fig3.eps} \end{figure}$	Figure 3: Demonstration of the Gaussian-like nature of w histograms. The Gaussian solid curve satisfactorily approximates the histogram (grey) calculated for the spectrum of 2002 August 2 (9:30 UT) with intensive S-burst emission. The vertical scale is number (n) of w estimates per one bin of the histogram.
Open with DEXTER

To cut out any obviously insignificant correlation pattern, we verified the null hypothesis (no correlation) with the standard transformation of correlation coefficient r into the value $w=\frac{1}{2} \ln \frac{1+r}{1-r}$ , which has the normal distribution (Fig. 3; Bendat & Piersol 1986). If there is no correlation between spectral intensity in two frequency channels, the average of w distribution is zero, and its dispersion is $\sigma_{w}=1/\sqrt{N-3}$ , where N is the number of measurements in one channel (in the present case N = 9983). The probability ( $\alpha$ ) of deviation $w/\sigma_{w}>Z_{\alpha}$ is well known for the normal distribution of normalized random variable $z=w/\sigma_{w}$ :

$\begin{displaymath}% \alpha=\int_{Z_{\alpha}}^{\infty}\frac{1}{2\pi}\exp \left(-\frac{z^{2}}{2}\right){\rm d}z. \end{displaymath}$

(3)

Hence, the confidence interval with $2\alpha$ -significance is $\frac{\eta_{2}-1}{1+\eta_{2}}<w<\frac{\eta_{1}-1}{1+\eta_{1}}$ , where $\eta_{1,2}=\exp({\pm}\frac{2Z_{\alpha}}{\sqrt{N-3}})$ . In our case ( $N \gg 1$ and $r \ll 1$ ), we have $w \simeq r$ and $\eta_{1,2}=1$ $\pm$ $\frac{2Z_{\alpha}}{\sqrt{N}}\simeq 1$ . Hence, the confidence interval of the null hypothesis can be approximated as $-\frac{Z_{\alpha}}{\sqrt{N}}<r<\frac{Z_{\alpha}}{\sqrt{N}}$ . Its borders ( $\pm$ 0.0258) are calculated with $\alpha =0.005$ and $Z_{\alpha}=2.575$ . Correspondingly, the null hypothesis predicts that -0.0258<r<0.0258 with the probability of $1 - 2 \alpha$ = 0.99. Such formally non-significant features are replaced by the uniform grey color with the average gradation in Fig. 2d. In contrast, the correlation features with |r|>0.0258 are mapped in Fig. 2d as the potentially significant details.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig4.eps} \end{figure}$

Figure 4:

The 2D-correlation analysis of an NB-event: a) the fragment of analyzed dynamic spectrum (2002 August 2, 09:00 UT; UTR-2 radio telescope); b) the raw map of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference ( f_o=19.6 MHz) frequency channels with $\Delta t$ time shift; c) the plotting of $C_{i,\Delta k}$ parameter (see Eq. (2)); d) only significance features ( $\alpha =0.005$ ) of the c) image; e) the threshold scheme of c).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig5.eps} \end{figure}$

Figure 5:

The 2D-correlation analysis of the broadband chaotic S-storm: a) the fragment of analyzed dynamic spectrum (2002 August 2, 9:30 UT; UTR-2 radio telescope); b) the raw pattern of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference (f_o=20 MHz) frequency channels with $\Delta t$ time shift; c) only significance features ( $\alpha =0.005$ ) of the b) image; d) the mapping of $C_{i,\Delta k}$ parameter (see Eq. (2)); e) the threshold scheme of c).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig6.eps} \end{figure}$

Figure 6:

The 2D-correlation analysis of a periodic S-train: a) the fragment of analyzed dynamic spectrum (2002 August 2, 10:15 UT; UTR-2 radio telescope); b) the raw map of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference (f_o= 25 MHz) frequency channels with $\Delta t$ time shift; c) the mapping of $C_{i,\Delta k}$ parameter (see Eq. (2)); d) only significance features ( $\alpha =0.005$ ) of the c) image; e) the threshold scheme of c).

Open with DEXTER

To select the most significant correlation features in Fig. 2c, we map the pixels only above the adopted brightness threshold (b_o). Such pixels are shown with a white color in Fig. 2e. The mirror threshold (255-b_o) is used for anti-correlation pixels, which are mapped with a black color in Fig. 2e. Such schematics are useful for qualitative analysis.

3 Phenomenology of 2D-correlation

Figure 2 is a typical example of the 2D-correlation pattern of S-bursts. The white strip in the center is the main feature with the autocorrelation peak r=1 at the reference frequency f_o and the time shift $\Delta t=0$ . Its declination reflects the average frequency drift rate of S-bursts. The absence of clear periodicity in the correlation pattern argues for the chaotic emission.

Moreover, there are the surprising dark stripes of anti-correlation in Figs. 2b,c. These dark details are present among the significant 2D-correlation features (Fig. 2d). Apparently, the white and dark stripes form the double pattern or DP (Fig. 2e). In all studied spectra, without exceptions, we found such interlacing DP stripes. It is interesting that even an NB-event (Fig. 4a) also shows such anti-correlation regions in the form of dark stripe segments in the 2D-correlation pattern (Figs. 4b-e). Hence, the correlation DP is a real and stable property of S/NB-emission, hitherto unknown.

Apparently, the described DP-features are part of a more general pattern as illustrated in Fig. 5. In Fig. 5a we see the broadband chaotic S-storm, which consists of three S-burst bands around 20, 23, and 25 MHz. After processing, it is clear that the emission in the reference 20 MHz-band anti-correlates with S-bursts at 21.5 to 23.5 MHz, but correlates with 25 MHz-band (Figs. 5b-e). The spectral intensity variations with a long time scale (up to 0.8 s) of S-burst groups form the horizontal bands in Fig. 5c. These bands show significant correlation between emissions at 20 MHz and 24.5 MHz, but clear anti-correlation with intermediate radiation at 23 MHz. The short bursts ( $\sim$ 0.01 s) form the drifting narrow band of interlacing DPs with same correlation/anti-correlation order (Fig. 5e).

Even quasi-periodic S-train (Fig. 6a) has the traces of a 2D-correlation pattern (Fig. 6e), which consists of the DP-elements, although the dark stripe is masked by multiple white lines (compare Figs. 2e, 5e). As a result, the described DP correlation seems to be the invariant with a common cause for different forms of S/NB-emission.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig7.eps} \end{figure}$

Figure 7:

The test for the equipment response on drifting impulses (rare S-bursts): a) the fragment of analyzed dynamic spectrum (2002 August 9, 10:30 UT; UTR-2 radio telescope); b) the raw pattern of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference ( f_o=19.25 MHz) frequency channels with $\Delta t$ time shift; d) the visualization of the pattern like to Figs. 2c, 4c, 5d, 6c. In contrast to the listed figures, the dark anti-correlation stripe is absent. Hence, the DP-effect is not an apparatus/processing artifact from individual signals, but one appears as the collective effect of numerous S-bursts from Jupiter.

Open with DEXTER

Moreover, we additionally studied the equipment response on drifting impulses (rare S-bursts). Figure 7 demonstrates the absence any hint of dark anti-correlation stripe. Hence, the DP-effect is not an apparatus/processing artifact from individual signals, but one appears as the collective effect of numerous S-bursts from Jupiter. This is the strong argument for the Jovian nature of DP-correlation. Recently the DP-correlation effect was confirmed with the different equipment and data set of the Nançay Radio Observatory (Zarka P., personal communication).

4 Analysis

Obviously, the double pattern of correlation describes some typical associations of S-bursts. To clarify the physical origin of negative correlations in DP-patterns, we study the original spectra in detail. It appears that certain groups of S-bursts dominate in the dynamic spectrum where a subsequent S-burst (in the same frequency channel) is located at mainly higher frequencies than the previous one. The result of this time-frequency shift is the zones with the emission deficit and hence anti-correlation at $\Delta t (f-f_{o})<0$ . Figure 8 shows a sample of such structures with the highest resolution (2 ms) from our data set.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig8.eps} \end{figure}$	Figure 8: Example of S-burst structures with statistically stable zones of the emission deficit in the spectrum of highest resolution (2 ms) 2000 March 30, 12:15 UT a), which are responsible for the anti-correlation (dark) strips in the 2D-correlation pattern b). Here the $C_{i,\Delta k}$ parameter is shown after processing of the whole 9.486-s recording with f_o=26.5 MHz.
Open with DEXTER

The simplest group consists of only two shifted bursts. To verify the connection of these burst pairs with a 2D-correlation effect, we generated the artificial dynamic spectrum Fig. 9a. After its processing with our algorithm used for original spectra, we found the same 2D-correlation pattern (Fig. 9b). It is important that anti-correlation strips are absent if the simple superposition of randomized pairs of shifted S-bursts is generated. Anti-correlation appears only when the superposition of such a pair with an other is infrequent; hence, the stable presence of dark (anti-correlation) strips in Figs. 2, 4, 5 contradicts the model with multiple and independent radio sources.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig9.eps} \end{figure}$	Figure 9: Simplest shifted structures in the form of shifted S-pairs as an explanation of the DP-effect: a) the modeling of these forms in the synthetic spectrum (only its fragment is shown); b) the DP-pattern ( $C_{i,\Delta k}$ parameter) after processing of the synthetic spectrum a) with f_o=24 MHz.
Open with DEXTER

Apparently, in the different S-burst bands we compare the different groups of bursts to obtain the positive or negative correlation. The low level of anti-correlation (r < 0.1) is a result of the high off-duty factor of S-bursts. If f_o is selected at low frequency below the train of S-bursts, where unrelated S-bursts are present, the background noise is slightly under the average spectral intensity in the reference frequency channel because of the high off-duty factor of S-bursts, making $F_{i0,k}-\langle F\rangle_{io}$ in Eq. (1) slightly negative. Its product with $F_{i,k+\Delta k}-\langle F\rangle_{i}$ of an S-burst at high f makes a negative contribution to the sum in Eq. (1). As a result, the S-train forms the region of a slightly negative correlation in the 2D-correlation pattern.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fi10.eps} \end{figure}$	Figure 10: The effect of f_o selection in 2D-correlation ( $C_{i,\Delta k}$ parameter) of broadband S-storm 2002 August 2, 9:30 UT. This figure is a supplement to Fig. 5. It shows that, independent of the f_o selection, the zones of correlation (bright) adjoin the regions of anti-correlation (dark) along the central band inclined in accordance with the typical S-burst drift.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fi11.eps} \end{figure}$	Figure 11: The zebra structure in a 2D-correlation pattern from Fig. 5e correlates with the horizontal bands of S-bursts (clusters of vertical black fibers) about the arrowed frequencies. Both figures are based on the whole dynamic spectrum of 2002 August 2 (9:30 UT; UTR-2 radio telescope).
Open with DEXTER

The effect of f_o selection is shown in Fig. 10. It is important that, with any f_o, the zones of correlation (bright) adjoin the regions of anti-correlation (dark) along the central lane inclined in accordance with the typical S-burst drift. Naturally, the low amplitude and rarity of S-burst emission in the reference channel (e.g., f_o=17.9 MHz or f_o=26.6 MHz) decrease the clearness of a 2D-correlation pattern. The best result is obtained with the reference at f_o=20 MHz, where the maximal S-burst activity occurs (Fig. 5). One can see there that the central lane from S-bursts is a zebra consisting of alternating bright and dark parts from correlated/anti-correlated signals. In fact, such a zebra structure remains independently from f_o selection (e.g., f_o=25.1 MHz in Fig. 10). Although this zebra correlates with the bands of S-bursts (Fig. 11), this structure exists even with the selection of the reference frequency between S-bands at f_o=21.3 MHz or 24 MHz (Fig. 10). The re-appearance of the correlation at frequencies behind the anti-correlation bands argue for the global trans-storm regular modulation of individual S-bursts.

We consider the described zebra structure in a 2D-correlation pattern as an important result earlier unknown. From the zebra-effect it follows that there is a global process introducing some regularity in the chaotic S-burst medley. Apparently, the DP-patterns (Figs. 2, 4, 6) are fragments of such a global modulation. The S-bursts show the stable relation between their appearance (i.e. correlation coefficient r) and frequency (Fig. 11). According to the standard model (e.g., Zarka 1998), S-bursts are generated on the active magnetic lines, which are activated by the Io satellite. The frequency f of each component of the emitted band is approximately equal to the local electron cyclotron frequency f_ce at the point of the active line from which it was emitted; hence, the r-f relation describes the r variations in space or rather in the altitude of S-burst source along the active magnetic line. The recurrence or cyclicity of the zebra pattern with f or in space argues for some wave process related to the source altitude. However, the attempt to interpret this effect is a matter of an other study (Arkhypov & Rucker 2008b).

5 Conclusions

It is shown that the 2D-correlation analysis is an effective method for studying the highly complex structure of Jovian S-burst storms in dynamic spectra. As a result, the new information on S-burst emission has been obtained.

1.: The hidden regularity, hitherto unknown, is found in random S-bursts as the double correlation pattern in the form of correlated and anti-correlated stripes.
2.: The double pattern of correlation describes the typical associations of S-bursts where the following S-burst (in the same frequency channel) is located at mainly higher frequencies than the previous one.
3.: Typical 2D correlation pattern can be modeled with the simplest S-groups consisting of only two shifted bursts in a pair. The results of this modeling exclude the model with elementary S-burst superposition.
4.: The S-bursts in separate S-bands are not independent. There is a global and regular modulation of the whole S-storm. Thus, S-burst emission in the adjacent S-bands is anti-correlated as predicted (Arkhypov & Rucker 2008a). This effect appears as the periodical zebra structure in a 2D-correlation pattern at the time shift up to 0.8 s.

Acknowledgements

We used the dynamic spectra of S-storms, which have been recorded by an observation compaign within the frame of the INTAS project 03-51-5727 (A. Lecacheux, H. O. Rucker, A. A. Konovalenko, and Yu. Tokarev) with the UTR-2 radio telescope. We thank Dr. Philippe Zarka for his amazing efforts to verify the DP-correlation effect with the data of the Nançay Radio Observatory.

References

Arkhypov, O. V., & Rucker, H. O. 2006, A&A, 452, 347 [NASA ADS] [CrossRef] [EDP Sciences]
Arkhypov, O. V., & Rucker, H. O. 2008a, A&A, 482, 1009 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Arkhypov, O. V., & Rucker, H. O. 2008b, in EPSC Abstracts, 3, European Planetary Science Congress 2008, EPSC2008-A-00286 (CD) (In the text)
Bendat, J. S., & Piersol, A. G. 1986, Random data, Analysis and measurement procedures (N.Y.: Wiley & Sons), Chap. 4.8.1 (In the text)
Boudjada, M. Y., Galopeau, P. H. M., Rucker, H. O., & Lecacheux, A. 2000, A&A, 363, 316 [NASA ADS] (In the text)
Calvert, W., Leblanc, Y., & Ellis, G. R. A. 1988, ApJ, 335, 976 [NASA ADS] [CrossRef] (In the text)
Hess, S., Zarka, P., & Mottez, F. 2007, Planet. Space Sci., 55, 89 [NASA ADS] [CrossRef] (In the text)
Konovalenko, A. A., Lecacheux, A., Rosolen, C., & Rucker, H. O. 2001, in Planetary Radio Emissions V, ed. H. O. Rucker, M. L. Kaiser, & Y. Leblanc (Vienna: Austrian Acad. Sc. Press), 63 (In the text)
Ryabov, V. B., Ryabov, B. P., Vavriv, D. M., et al. 2007, J. Geoph. Res., 112, A9 [CrossRef], A09206 (In the text)
Zarka, P. 1998, J. Geophys. Res., 103, E9 [CrossRef], 20159 (In the text)

All Tables

Table 1: Studied spectra of Jovian decametric emission.

All Figures

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{0583fig1.eps} \end{figure}$	Figure 1: An example of DAM dynamic spectra with random S/NB-events in two bands is recorded 2002 August 9, 11:30 UT, using the Kharkov UTR-2 radio telescope. Interferences exhibit as numerous horizontal solid and dashed stripes.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig2.eps} \end{figure}$	Figure 2: An example of DAM 2D-correlation analysis: a) the fragment of the analyzed record of the S-burst emission (2002 August 9, 11:30 UT; UTR-2 radio telescope); b) the raw pattern of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference ( f_o= 23.75 MHz) frequency channels with $\Delta t$ time shift; c) the plotting of $C_{i,\Delta k}$ parameter (see Eq. (2)); d) only significance features ( $\alpha =0.005$ ) of the c) image; e) the threshold scheme of c).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6.5cm,clip]{0583fig3.eps} \end{figure}$	Figure 3: Demonstration of the Gaussian-like nature of w histograms. The Gaussian solid curve satisfactorily approximates the histogram (grey) calculated for the spectrum of 2002 August 2 (9:30 UT) with intensive S-burst emission. The vertical scale is number (n) of w estimates per one bin of the histogram.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig4.eps} \end{figure}$	Figure 4: The 2D-correlation analysis of an NB-event: a) the fragment of analyzed dynamic spectrum (2002 August 2, 09:00 UT; UTR-2 radio telescope); b) the raw map of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference ( f_o=19.6 MHz) frequency channels with $\Delta t$ time shift; c) the plotting of $C_{i,\Delta k}$ parameter (see Eq. (2)); d) only significance features ( $\alpha =0.005$ ) of the c) image; e) the threshold scheme of c).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig5.eps} \end{figure}$	Figure 5: The 2D-correlation analysis of the broadband chaotic S-storm: a) the fragment of analyzed dynamic spectrum (2002 August 2, 9:30 UT; UTR-2 radio telescope); b) the raw pattern of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference (f_o=20 MHz) frequency channels with $\Delta t$ time shift; c) only significance features ( $\alpha =0.005$ ) of the b) image; d) the mapping of $C_{i,\Delta k}$ parameter (see Eq. (2)); e) the threshold scheme of c).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig6.eps} \end{figure}$	Figure 6: The 2D-correlation analysis of a periodic S-train: a) the fragment of analyzed dynamic spectrum (2002 August 2, 10:15 UT; UTR-2 radio telescope); b) the raw map of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference (f_o= 25 MHz) frequency channels with $\Delta t$ time shift; c) the mapping of $C_{i,\Delta k}$ parameter (see Eq. (2)); d) only significance features ( $\alpha =0.005$ ) of the c) image; e) the threshold scheme of c).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig7.eps} \end{figure}$	Figure 7: The test for the equipment response on drifting impulses (rare S-bursts): a) the fragment of analyzed dynamic spectrum (2002 August 9, 10:30 UT; UTR-2 radio telescope); b) the raw pattern of linear correlation coefficient $r(f, \Delta t)$ between spectral intensity in the current (f) and the reference ( f_o=19.25 MHz) frequency channels with $\Delta t$ time shift; d) the visualization of the pattern like to Figs. 2c, 4c, 5d, 6c. In contrast to the listed figures, the dark anti-correlation stripe is absent. Hence, the DP-effect is not an apparatus/processing artifact from individual signals, but one appears as the collective effect of numerous S-bursts from Jupiter.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig8.eps} \end{figure}$	Figure 8: Example of S-burst structures with statistically stable zones of the emission deficit in the spectrum of highest resolution (2 ms) 2000 March 30, 12:15 UT a), which are responsible for the anti-correlation (dark) strips in the 2D-correlation pattern b). Here the $C_{i,\Delta k}$ parameter is shown after processing of the whole 9.486-s recording with f_o=26.5 MHz.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fig9.eps} \end{figure}$	Figure 9: Simplest shifted structures in the form of shifted S-pairs as an explanation of the DP-effect: a) the modeling of these forms in the synthetic spectrum (only its fragment is shown); b) the DP-pattern ( $C_{i,\Delta k}$ parameter) after processing of the synthetic spectrum a) with f_o=24 MHz.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fi10.eps} \end{figure}$	Figure 10: The effect of f_o selection in 2D-correlation ( $C_{i,\Delta k}$ parameter) of broadband S-storm 2002 August 2, 9:30 UT. This figure is a supplement to Fig. 5. It shows that, independent of the f_o selection, the zones of correlation (bright) adjoin the regions of anti-correlation (dark) along the central band inclined in accordance with the typical S-burst drift.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0583fi11.eps} \end{figure}$	Figure 11: The zebra structure in a 2D-correlation pattern from Fig. 5e correlates with the horizontal bands of S-bursts (clusters of vertical black fibers) about the arrowed frequencies. Both figures are based on the whole dynamic spectrum of 2002 August 2 (9:30 UT; UTR-2 radio telescope).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.