| Issue |
A&A
Volume 496, Number 1, March II 2009
|
|
|---|---|---|
| Page(s) | 107 - 119 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810416 | |
| Published online | 30 January 2009 | |
High-resolution X-ray spectroscopy of the low and high states of the Seyfert 1 galaxy NGC 4051 with Chandra LETGS
K. C. Steenbrugge1 - M. Fenovcík2 - J. S. Kaastra2,3 - E. Costantini2 - F. Verbunt3
1 - St John's College Research Centre, University of Oxford, Oxford, OX1 3JP, UK
2 - SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
3 - Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
Received 18 June 2008 / Accepted 15 January 2009
Abstract
Context. With the new generation of high-resolution X-ray spectrometers the understanding of warm absorbers in active galactic nuclei has improved considerably. However, the important questions regarding the distance and structure of the photoionised wind remain unsolved.
Aims. To constrain the distance of the photoionised wind, we study the variability of the continuum, absorption, and, emission in one of the brightest and most variable low-luminosity AGN: the narrow-line Seyfert galaxy NGC 4051.
Methods. We analyse two observations taken with the Low Energy Transmission Grating Spectrometer of Chandra. We investigated the spectral response to a sudden flux decrease by a factor of 5, which occurred during the second observation.
Results. We detect a highly ionised absorption component with an outflow velocity of -4670 km s-1, one of the highest outflow velocity components observed in a Seyfert 1 galaxy. Furthermore, this is one of the only observations whereby the X-ray observed absorption component is unaccompanied by a corresponding UV absorption component with the same outflow velocity. The spectra contain a relativistic O VIII Ly![]() line with properties similar to those determined for this source with XMM-Newton, and four absorption components spanning a range in ionisation parameter
line with properties similar to those determined for this source with XMM-Newton, and four absorption components spanning a range in ionisation parameter ![]() between 0.07 and 3.19 (log values, and units of 10-9 W m). An emission component producing radiative recombination continua of C VI and C V appears during the low state. The black body temperature decreases with the drop in flux observed in the second observation.
between 0.07 and 3.19 (log values, and units of 10-9 W m). An emission component producing radiative recombination continua of C VI and C V appears during the low state. The black body temperature decreases with the drop in flux observed in the second observation.
Conclusions. For all absorber components we exclude that the ionisation parameter linearly responded to the decrease in flux by a factor of 5. The variability of the absorber suggest that at least three out of four detected components are located in the range 0.02-1 pc. For one component we only have a lower limit of 0.3 pc. These distances are different from earlier suggestions.
Key words: galaxies: Seyfert - quasars: individual: NGC 4051 - galaxies: active - X-rays: galaxies
1 Introduction
The stupendous amount of energy emitted by an active galactic nucleus (AGN) is released by gas that flows towards a super-massive black hole in the centre of a galaxy, presumably via an accretion disc. The average energy of the emitted radiation increases with decreasing distance to the super-massive black hole, thus X-rays provide the best probe of the gas flow in the immediate surroundings of the black hole. From the presence of jets, as well as from blue-shifted ultraviolet absorption lines, we learn that there is gas flowing away from the black hole, in addition to the flow towards it. With the availability of X-ray spectrographs onboard Chandra and XMM-Newton, we can study the lines emitted in the X-ray band from these outflows close to the black hole. The presence of multiple absorption line systems that differ in their level of ionisation or in their outflow velocity constrains the geometry of the outflow (for example NGC 3783, Netzer et al. 2003; NGC 5548, Steenbrugge et al. 2005).
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0416fig1.ps}\hspace*{0.6cm}
\includegraphics[angle=270,width=8.5cm,clip]{0416fig2.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg5.gif) |
Figure 1: The light curve in the zeroth spectral order ( top panels) and hardness ratio ( bottom panels) for the observations of Jan. 2002 and July 2003. The hardness ratio is defined as the ratio of the 2-8 and 8-32 Å counts. The top panel has a bin size of 350 s and the bottom panel has a bin size of 2000 s. Dotted lines denote the different flux states and define the intervals used in creating the four spectra. |
| Open with DEXTER | |
In this paper we describe the X-ray spectra of the narrow-line Seyfert 1 galaxy NGC 4051, obtained with the Low-Energy Transmission Grating (LETG) on board of the Chandra satellite. Emission from the nucleus of NGC 4051 was detected by Hubble (1926), and the galaxy is one of the 12 discussed in the seminal paper by Seyfert (1943). As a member of the Ursa Major cluster (Tully et al. 1996), it has a distance of 18.6 Mpc (Tully & Pierce 2000) and a heliocentric velocity of
700 km s-1 (Verheijen & Sancisi 2001). NGC 4051 is a relatively bright optical object, with
![]() .
The soft excess observed with the Reflection Grating spectrometers (RGS) onboard XMM-Newton is not described well by a multi-temperature disc: Ogle et al. (2004) concludes that the soft excess is due to emission from relativistically broadened O VIII emission lines and its related radiative recombination continuum (RRC). However, Pounds et al. (2004) fitted the EPIC data of the same observation satisfactorily with a power law plus two black body components.
.
The soft excess observed with the Reflection Grating spectrometers (RGS) onboard XMM-Newton is not described well by a multi-temperature disc: Ogle et al. (2004) concludes that the soft excess is due to emission from relativistically broadened O VIII emission lines and its related radiative recombination continuum (RRC). However, Pounds et al. (2004) fitted the EPIC data of the same observation satisfactorily with a power law plus two black body components.
Two absorption line systems, at -2340 ![]() 130 and -600
130 and -600 ![]() 130 km s-1, were detected in the X-ray spectrum with the High Energy Transmission Grating of Chandra
(Collinge et al. 2001). Nine absorption systems with a small range in outflow velocity are detected in the ultraviolet with the Space Telescope Imaging Spectrograph (STIS) and the Far Ultraviolet
Spectroscopic Explorer (FUSE). One of the absorbers observed in the UV may coincide with the -600
130 km s-1, were detected in the X-ray spectrum with the High Energy Transmission Grating of Chandra
(Collinge et al. 2001). Nine absorption systems with a small range in outflow velocity are detected in the ultraviolet with the Space Telescope Imaging Spectrograph (STIS) and the Far Ultraviolet
Spectroscopic Explorer (FUSE). One of the absorbers observed in the UV may coincide with the -600 ![]()
![]() X-ray absorption system, all the others have smaller outflow velocities (Collinge et al. 2001; Kaspi et al. 2004).
X-ray absorption system, all the others have smaller outflow velocities (Collinge et al. 2001; Kaspi et al. 2004).
In a preliminary analysis of our first LETGS spectrum, van der Meer et al. (2003) did not detect the -2340 km s-1 velocity component, but found indications for the presence of an outflow component at an even higher velocity of -4500 km s-1. The second observation, taken when NGC 4051 was in a much higher flux state, allows us to investigate the ionised outflow both in terms of outflow velocity and ionisation structure. In this paper we report the analysis of both observations with the LETGS.
2 Observations and data reduction
In this paper we describe the two observations of NGC 4051 taken with the LETGS (Brinkman et al. 2000) onboard of Chandra. The detector used was the High-Resolution Camera (HRC-S). The observations span the time periods December 31, 2001 17:40:41 to January 1, 2002 19:51:46 and July 23, 2003 00:34:15 to July 24 03:24:43, and have a net exposure time of 94.2 and 96.6 ks, respectively. Henceforth we will we refer to these observations as the Jan. 2002 and Jul. 2003 observations. The data reduction method is described in detail by Kaastra et al. (2002). After event selection we produced background subtracted spectra and light curves. As the HRC-S detector has limited energy resolution, higher spectral orders cannot be separated in the data but are taken into account during spectral fitting. We only use spectra between 2 Å and 80 Å, as the Galactic absorption attenuates the spectrum strongly above ![]() 80 Å.
80 Å.
3 Variability
Figure 1 shows the light curves for each observation. For the Jan. 2002 observation, the average brightness of the source increased noticeably in the second half of the exposure. The source was brighter still during the first ![]() 65 ks of the Jul. 2003 observation and then dropped in about 3 ks to a lower flux level, which is similar to the flux level of the
second half of the first observation. The flux recovered gradually to the high level of the first half of the observation during the final 20 ks. On top of these long-term variations we also detect variability with smaller, but significant, amplitude on timescales of a few thousand seconds. These rapid variations have smaller amplitudes after the rapid flux decrease of the Jul. 2003 observation. In the analysis below we will discuss the spectra at different flux levels, defined by the
lightcurve of Fig. 1: A and B are the first and second half of the Jan. 2002 observation; C and D are the first and second part of the Jul. 2003 observation.
65 ks of the Jul. 2003 observation and then dropped in about 3 ks to a lower flux level, which is similar to the flux level of the
second half of the first observation. The flux recovered gradually to the high level of the first half of the observation during the final 20 ks. On top of these long-term variations we also detect variability with smaller, but significant, amplitude on timescales of a few thousand seconds. These rapid variations have smaller amplitudes after the rapid flux decrease of the Jul. 2003 observation. In the analysis below we will discuss the spectra at different flux levels, defined by the
lightcurve of Fig. 1: A and B are the first and second half of the Jan. 2002 observation; C and D are the first and second part of the Jul. 2003 observation.
In Fig. 1 we also show the hardness ratio, defined as the ratio between the count rates in the 2-8 Å and 8-32 Å band passes. The hardness variation between different flux levels is small, with HR = 0.239 ![]() 0.14, 0.203
0.14, 0.203 ![]() 0.008, 0.161
0.008, 0.161 ![]() 0.003, 0.134
0.003, 0.134 ![]() 0.021 for intervals A-D, respectively with their 1
0.021 for intervals A-D, respectively with their 1![]() error.
error.
4 Spectral data analysis and results
Table 1: The best fit parameters for the different spectral components for the four spectra. All wavelengths and velocities refer to the rest frame of NGC 4051. Numbers in square brackets are calculated from the fit parameters; numbers in round brackets were kept fixed during the fit.
From the above (Fig. 1) it is clear that NGC 4051 shows significant luminosity variability during our observations. As the level of the variations is quite strong (e.g., a factor of five in flux between parts C and D of the July 2003 observation), it is not useful to analyse the integrated spectra as a whole, but we will rather analyse spectra A-D separately, with a focus on the spectral differences between these parts. Statistics prohibit us to do spectral analysis down to the shortest variability timescales of less than 1000 s.
For all spectral fitting we used the SPEX code developed and regularly updated with new models and atomic data at SRON (Kaastra et al. 1996)![]() . As the flux is low in some of the spectra, we cannot use
. As the flux is low in some of the spectra, we cannot use ![]() minimisation, instead we minimise the C-statistic. Note that that the uncertainty in absolute calibration for the Chandra LETGS is 13 mÅ. Therefore a velocity difference smaller than
minimisation, instead we minimise the C-statistic. Note that that the uncertainty in absolute calibration for the Chandra LETGS is 13 mÅ. Therefore a velocity difference smaller than ![]() 200 km s-1 between spectra A/B and C/D is unlikely due to an intrinsic velocity shift.
200 km s-1 between spectra A/B and C/D is unlikely due to an intrinsic velocity shift.
For our spectral model we included different components: a broad-band continuum, narrow and broad emission features, and photoionised absorption. The need for these components and the resulting parameters will be discussed separately.
Noting that spectrum C has the highest signal-to-noise of the four spectra, we decided to fit this spectrum first and then use the best fit model as a template for fitting spectrum B. The signal-to-noise ratios for spectra A and D are poor, therefore we only left a limited number of parameters free when fitting these spectra.
Table 2: Significances of the different spectral components. We list the increase in the C-statistic when the component is omitted from the model and the spectrum is refitted.
The best fit parameters for our spectral model are listed in Table 1. All models
were corrected for Galactic absorption with a column density of 1.31 ![]() 1024 m-2 (Elvis et al. 1989) and for the cosmological redshift (including peculiar motion) of 700 km s-1. All errors correspond to
1024 m-2 (Elvis et al. 1989) and for the cosmological redshift (including peculiar motion) of 700 km s-1. All errors correspond to
![]() (68% confidence). The best fit values for the C-statistics are 2700 (2476), 2658 (2466), 2738 (2599), and 2870 (2610) for components A-D; the numbers in brackets are the degrees of freedom. In Table 2 we show the increase
(68% confidence). The best fit values for the C-statistics are 2700 (2476), 2658 (2466), 2738 (2599), and 2870 (2610) for components A-D; the numbers in brackets are the degrees of freedom. In Table 2 we show the increase ![]() of the C-statistic when a given spectral component is omitted from the model (and re-fitting the spectrum; the omission of a given component can sometimes be partly compensated by adjusting the parameters of the other components). We did this for spectra B and C, the best quality spectra.
of the C-statistic when a given spectral component is omitted from the model (and re-fitting the spectrum; the omission of a given component can sometimes be partly compensated by adjusting the parameters of the other components). We did this for spectra B and C, the best quality spectra.
Finally, in spectrum D we afterwards added a spectral component fitting the radiative recombination continua (RRCs). Only the C V and C VI RRCs are present, and can be identified by
eye in Fig. 2. The temperature and emission measures
![]() with V the emitting volume,
with V the emitting volume, ![]() the electron density,
the electron density, ![]() the density of the recombining ion X giving rise to the observed transitions are given in Table 3.
the density of the recombining ion X giving rise to the observed transitions are given in Table 3.
4.1 Continuum
In spectrum C the continuum cannot be fitted with only a power law. The soft excess can be modelled by adding a black body modified by coherent Compton scattering (Kaastra & Barr 1989). Examining all spectra, we find that the power-law photon index becomes softer as time progresses, and is thus not a simple function of luminosity. The modified black body temperature seems to track the luminosity variations; the temperature is highest for the high state and drops back to a lower value after the drop in flux just before the start of spectrum D.
4.2 The ionised absorber
Thanks to the excellent spectral resolution of the LETG instrument we can study the warm absorber in detail. We fitted the warm absorber with the xabs model in SPEX. In this model, the ionic column densities are not independent quantities, but are linked via the ionisation parameter
![]() ,
where L is the source luminosity, n the hydrogen density and r is the distance from the ionising source. For the spectral energy distribution of the ionising source we used
the standard one included in SPEX (see dot-dash line of Fig. 1 in Steenbrugge et al. 2005). In addition to the ionisation parameter, the fit parameters are the hydrogen column density of the absorber
,
where L is the source luminosity, n the hydrogen density and r is the distance from the ionising source. For the spectral energy distribution of the ionising source we used
the standard one included in SPEX (see dot-dash line of Fig. 1 in Steenbrugge et al. 2005). In addition to the ionisation parameter, the fit parameters are the hydrogen column density of the absorber ![]() ,
the outflow velocity
,
the outflow velocity
![]() ,
and the turbulent velocity
,
and the turbulent velocity
![]() .
The advantage of the xabs model is that all relevant ions are taken into account including also the ones with the weakest absorption features. In the fit the abundances were left frozen to the solar abundances given by Anders & Grevesse (1989).
.
The advantage of the xabs model is that all relevant ions are taken into account including also the ones with the weakest absorption features. In the fit the abundances were left frozen to the solar abundances given by Anders & Grevesse (1989).
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{0416fig3.ps}\vspace*{5mm}
\includegraphics[angle=-90,width=15cm,clip]{0416fig4.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg103.gif) |
Figure 2:
Flux (in units of photons m-2 s-1 Å-1) and our best spectral model. All spectra are binned by a factor of 2 for clarity of display. Note the different continuum levels and shapes between the spectra, especially around the upturn at |
| Open with DEXTER | |
Table 1 lists the best fit values for the four different spectra. To adequately describe the warm absorber in spectrum C we need 4 components. The ionisation parameters range between 0.07 and 3.19 (logarithmic values in 10-9 W m, used throughout this paper). Adding a 5![]() absorption component for spectrum C does not significantly improve the fit, namely
absorption component for spectrum C does not significantly improve the fit, namely ![]() decreases by only 1.91. Figure 3 compares the best fit model with 3 and 4 absorption components and Table 4 gives the best fit parameters for the three-absorber-component fit to spectrum C. The fit with 4 warm absorber components better fits the O V and O IV absorption lines. In the remaining three spectra due to the lower signal to noise ratios, not all four absorption components are detected.
decreases by only 1.91. Figure 3 compares the best fit model with 3 and 4 absorption components and Table 4 gives the best fit parameters for the three-absorber-component fit to spectrum C. The fit with 4 warm absorber components better fits the O V and O IV absorption lines. In the remaining three spectra due to the lower signal to noise ratios, not all four absorption components are detected.
For spectrum B, we need three components. By comparing the parameters of these components to the parameters of the components for spectrum C, we find that component 1, which has the smallest hydrogen column density, is lacking in spectrum B.
The statistical quality of spectra A and D are much poorer; in fitting these spectra, we fixed several parameters to the best-fit values obtained for spectra B and C, respectively. It is quite reasonable to keep the outflow and turbulent velocity constant between observations A/B and also between C/D. When we leave both the column density and the ionisation parameter free in spectrum A, only component 2 is marginally detected. These non-detections do not imply that the warm absorber has disappeared, but merely that the statistical quality of spectra A and D are insufficient to determine its parameters with accuracy. For this reason, we make the additional assumption that the column density of the absorber does not change. Any changes however, are likely to be in the ionization parameter (that is, if it can respond fast enough to the continuum flux variations).
Comparing spectra C and D, only for component 2 a ![]() drop in ionisation parameter is found; the other components are consistent with no change in the warm absorber. Comparing spectra A and B, we find only marginally higher ionisation parameters for components 2-4 in spectrum A.
drop in ionisation parameter is found; the other components are consistent with no change in the warm absorber. Comparing spectra A and B, we find only marginally higher ionisation parameters for components 2-4 in spectrum A.
Figure 4 shows the change in C-statistics for spectra A and D when the ionisation parameter for each component is separately varied. Step size is 0.1 in log ![]() and at each step the goodness of fit is calculated. It is clear from this figure that no significant changes can be detected for components 1, 3 and 4. We discuss the variability of component 2 in more detail later.
and at each step the goodness of fit is calculated. It is clear from this figure that no significant changes can be detected for components 1, 3 and 4. We discuss the variability of component 2 in more detail later.
In Fig. 5 we present the model absorption spectrum for each component, labelling the deepest lines. It thus allows the reader to see which component contributes to which line. The continuum was renormalised to ease identification.
4.3 Broad emission lines
Besides absorption lines, strong emission features are present in the four spectra. We chose two different methods for fitting this excess emission: a model with broadened emission lines and a model in which the absorbers only partially cover the continuum. We first describe the model with broadened emission lines. As was the case for fitting the absorber, we first fitted spectrum C and then used its best fit values as a starting point to fit the other spectra (see Table 1 for best fit parameter values). The presence of a broad O VIII Ly![]() emission feature around 19 Å is illustrated in Fig. 6, which shows a detail of the spectra B and C
including the best fit model with and without relativistically broadened O VIII Ly
emission feature around 19 Å is illustrated in Fig. 6, which shows a detail of the spectra B and C
including the best fit model with and without relativistically broadened O VIII Ly![]() .
Figure 7 shows the model emission spectrum for spectra B and C. Excess emission with at least a 1 Å width, due to the O VII triplet near 22 Å is present in spectra A, C and D. In addition, there is significant excess emission in spectra C and D near 34 Å, the region of the 1s-2p transition in C VI.
.
Figure 7 shows the model emission spectrum for spectra B and C. Excess emission with at least a 1 Å width, due to the O VII triplet near 22 Å is present in spectra A, C and D. In addition, there is significant excess emission in spectra C and D near 34 Å, the region of the 1s-2p transition in C VI.
We modelled the excess emission at 19 Å (see Fig. 7) with a relativistically broadened line, following Ogle et al. (2004) and Branduardi-Raymont et al. (2001). The model used is a narrow emission line convolved with the relativistic disc line profile of Laor (1991). The inner (r1) and outer (r2) disc radii were fixed in our models to the default values (
r1=1.234GM/c2 and
r2=400GM/c2). The rest-frame wavelength of the line was frozen to 18.969 Å, the wavelength of O VIII Ly![]() .
.
We have tried fits with different disc inclinations i, but in all fits the inclination converged to 48![]() ,
within a few degrees. This value is consistent with the one found by
Ogle et al. (2004). The disc inclination is not expected to change significantly over a couple of years. For that reason, and in order to reduce the number of free parameters, we have kept the inclination
frozen to that value in all presented fits. The disc emissivity slope q (with R-q, R the distance to the black hole) was allowed to vary, however.
,
within a few degrees. This value is consistent with the one found by
Ogle et al. (2004). The disc inclination is not expected to change significantly over a couple of years. For that reason, and in order to reduce the number of free parameters, we have kept the inclination
frozen to that value in all presented fits. The disc emissivity slope q (with R-q, R the distance to the black hole) was allowed to vary, however.
In addition to a relativistic O VIII Ly![]() line, we added a Gaussian-shaped broad O VIII line Ly
line, we added a Gaussian-shaped broad O VIII line Ly![]() line (FWHM 0.45 Å) to our model for spectrum C and D. Further broad lines corresponding to the O VII triplet and C VI Ly
line (FWHM 0.45 Å) to our model for spectrum C and D. Further broad lines corresponding to the O VII triplet and C VI Ly![]() line were also needed. For C VI Ly
line were also needed. For C VI Ly![]() ,
we have frozen the wavelength to the rest wavelength of 33.736 Å. For O VII we kept the wavelength as a free parameter: the line is a blend of the
O VII triplet, and the relative contributions of these lines depend on the physical conditions in the source. Such broadened emission lines were first detected in NGC 5548 by Kaastra et al. (2002), and confirmed for that source by Steenbrugge et al. (2005), and were detected in this source by Ogle et al. (2004).
,
we have frozen the wavelength to the rest wavelength of 33.736 Å. For O VII we kept the wavelength as a free parameter: the line is a blend of the
O VII triplet, and the relative contributions of these lines depend on the physical conditions in the source. Such broadened emission lines were first detected in NGC 5548 by Kaastra et al. (2002), and confirmed for that source by Steenbrugge et al. (2005), and were detected in this source by Ogle et al. (2004).
Table 3: The best fit parameters for the RRCs in spectrum D. Thevelocity refers to the rest frame of NGC 4051.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig5.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg114.gif) |
Figure 3: Detail of spectrum C fitted with 3 warm absorber components (thin line) and 4 warm absorber components (thick line). Binning as in Fig. 2. The best fit 3 component model does under-predict the depth of the O V and O IV lines. |
| Open with DEXTER | |
Table 4: The best fit parameters for a three-absorber-component model for spectrum C. Components 1-3 correspond to components 2-4 in Tables 1 and 2.
4.4 Partial covering absorption model
As an alternative to fitting extra emission lines, we fitted the spectra assuming that the absorber does not fully cover the continuum emission. Considering that the excess emission is most significantly detected in spectrum B and C, we first fitted these two spectra (see Table 1 and Fig. 6). In this fit there are no broad emission lines fitted. We fixed the covering factor for the 3 or 4 detected absorption components (spectrum B and C, respectively) to 0.75, and then refitted the continuum parameters (power law and modified black body) and the hydrogen column density and ionization parameter of the detected absorber components. Afterwards we also allowed the covering factor for each absorption component free to vary in the fit.
For spectrum C the best fit covering factors for three of the four absorption components is 1. For warm absorber component 2 the best fit covering factor is 0.7 ![]() 0.13, with an increased hydrogen column density of 0.63
0.13, with an increased hydrogen column density of 0.63 ![]() 1025 m-2 (compared with 0.29
1025 m-2 (compared with 0.29 ![]() 1025 m-2 for a covering factor of 1). Forcing all covering factors to 1 increases
1025 m-2 for a covering factor of 1). Forcing all covering factors to 1 increases ![]() by 17. However, the best fit with partial covering increases
by 17. However, the best fit with partial covering increases ![]() by 70 for a decrease of 7 in degrees of freedom, compared with the best fit model with broad emission lines (4 extra free
parameters in the partial absorption fit compared to 11 in the model with broad emission lines). A comparison between the best fit with broad emission lines and a fit with all absorbers having a covering factor of 0.75 can be seen in the bottom panel of Fig. 8. Note that the continuum long-ward of
by 70 for a decrease of 7 in degrees of freedom, compared with the best fit model with broad emission lines (4 extra free
parameters in the partial absorption fit compared to 11 in the model with broad emission lines). A comparison between the best fit with broad emission lines and a fit with all absorbers having a covering factor of 0.75 can be seen in the bottom panel of Fig. 8. Note that the continuum long-ward of ![]() 24 Å is consistently over-estimated in the fit assuming that the absorber only covers part of the continuum emission.
24 Å is consistently over-estimated in the fit assuming that the absorber only covers part of the continuum emission.
For spectrum B we followed the same procedure, but here the best fit for the covering factors of the three absorption components detected are 1, even if we redid the fitting starting from a covering
factor of only 0.25. The best fit without broad emission lines increases ![]() by 21 and is shown in Fig. 6. Forcing the three absorbers to have a partial covering factor of 0.75 worsens the fit by a further 35 in
by 21 and is shown in Fig. 6. Forcing the three absorbers to have a partial covering factor of 0.75 worsens the fit by a further 35 in ![]() .
This last fit is compared with the best fit with broad emission lines in the upper panel of Fig. 8. Note that again the continuum is over-estimated at long wavelengths, furthermore the model assuming partial covering cannot reproduce the steep rise at 16 Å.
.
This last fit is compared with the best fit with broad emission lines in the upper panel of Fig. 8. Note that again the continuum is over-estimated at long wavelengths, furthermore the model assuming partial covering cannot reproduce the steep rise at 16 Å.
4.5 Narrow emission lines
The O VII forbidden line at 22.10 Å is detected with at least ![]() significance in each individual spectrum. There is no indication for significant flux variability or velocity broadening for this line.
significance in each individual spectrum. There is no indication for significant flux variability or velocity broadening for this line.
In spectrum D a strong, ![]()
![]() significant, RRC from C VI (rest wavelength 25.30 Å) and a
significant, RRC from C VI (rest wavelength 25.30 Å) and a ![]()
![]() significant RRC of C V (rest wavelength 31.62 Å) are present (see Fig. 2 and Table 3). In addition, we have determined limits to the strength of other expected RRCs of oxygen and nitrogen ions (see Table 3). The temperature of the recombining photoionised gas is low but not well
determined (T = 5
significant RRC of C V (rest wavelength 31.62 Å) are present (see Fig. 2 and Table 3). In addition, we have determined limits to the strength of other expected RRCs of oxygen and nitrogen ions (see Table 3). The temperature of the recombining photoionised gas is low but not well
determined (T = 5 ![]() 2 eV). In our final fit we fix the temperature to 5 eV, in order to better assess the significance of this component. There is a strong correlation between the adopted
temperature and the strength of the emission measure. The RRCs show a redshift with respect to the rest frame of the galaxy of
2 eV). In our final fit we fix the temperature to 5 eV, in order to better assess the significance of this component. There is a strong correlation between the adopted
temperature and the strength of the emission measure. The RRCs show a redshift with respect to the rest frame of the galaxy of ![]() 1300 km s-1.
1300 km s-1.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig6.ps}\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig7.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg118.gif) |
Figure 4:
Change ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig8.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg119.gif) |
Figure 5: The model absorption spectra for each of the 4 different absorption components as detected in spectrum C. The continuum was modelled to be flat and was renormalised per component. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{0416fig9.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg120.gif) |
Figure 6:
Detail of spectra B and C with the best fit model (thick line) and the best fit model without the O VIII Ly |
| Open with DEXTER | |
5 Discussion
5.1 Continuum
The uniqueness of the transition between part C and D is that the rather abrupt flux change is preceded and followed by long periods of relative quiescence. This allows us to study the response of the continuum, the broad and narrow emission lines, and the warm absorber to this sudden flux drop. We first describe the difference in the continuum. Figure 9 shows the difference in overall continuum profile for spectrum C and D.
Between spectrum C and D the temperature measured for the modified black body significantly decreases, and the power-law slope becomes softer. The temperature remained constant and the power-law slope softened between spectrum A and B. For Seyfert 1 galaxies, normally, the spectral slope hardens with decreasing luminosity with little or no change in the black body component. Pounds et al. (2004) studying two EPIC spectra taken in a high and a low state of NGC 4051 found that the higher temperature black body component disappeared in the low state. The authors found that the power-law slope did not vary between the high and low state, which is different from our results.
Changes in the warm absorber properties could mimic a temperature change of the modified black body component. To ensure that in the spectra there really is a temperature change we did the following tests. We refitted spectrum D, but freezing the temperature of the modified black body to the best fit value of spectrum C. In the fit the column density and ionisation parameter of the four absorption components were left free to vary. The fit thus obtained was substantially worse (increasing C-statistics by 102), and the fitted ionisation parameters were very similar to those obtained in the original fit of spectrum D. Afterwards, we lowered the ionisation parameter of the only significantly detected warm absorber component in spectrum D by a (linear) factor 5. This decrease matches the decrease in luminosity observed. Leaving the ionisation parameters of the absorber and the temperature of the modified black body free in the fit,we again derive our original fit parameters given in Table 1.
Ogle et al. (2004) studying the XMM-Newton RGS spectrum, find that a multi-temperature disc model is a poor fit to the soft excess, and that instead it is well fitted by the relativistically broadened
O VIII line series. We tested this model on our highest signal-to-noise spectrum, C, by adding to the O VIII Ly![]() line also the Ly
line also the Ly![]() ,
Ly
,
Ly![]() and the RRC emission lines relativistically broadened. As none of these emission features are obvious from a visual inspection, we fixed the relative normalisation of the different lines to the Ly
and the RRC emission lines relativistically broadened. As none of these emission features are obvious from a visual inspection, we fixed the relative normalisation of the different lines to the Ly![]() component: 0.25 for Ly
component: 0.25 for Ly![]() ,
0.1 for Ly
,
0.1 for Ly![]() and 0.21 for the RRC. The parameters q and i were free in the fit, but the same for the four different emission lines. The fit obtained was significantly worse (increasing C-statistics by 195) for the same number of parameters than a fit with
a modified black body.
and 0.21 for the RRC. The parameters q and i were free in the fit, but the same for the four different emission lines. The fit obtained was significantly worse (increasing C-statistics by 195) for the same number of parameters than a fit with
a modified black body.
We conclude that there is emission from a modified black body present in the LETGS spectrum, and that the temperature of this component drops with decreasing luminosity between spectrum C and D.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fi10.ps}\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fi11.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg123.gif) |
Figure 7: Model emission spectra for spectrum B and C, without Galactic absorption and the warm absorber components. Dashed line: power law continuum; dotted line: modified black body continuum; dash-dotted line: sum of power law and modified black body continuum; thin solid lines: relativistic, broad and narrow emission line contributions; thick solid line: total unabsorbed emission spectrum. |
| Open with DEXTER | |
5.2 Relativistically broadened O VIII Ly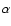 line
line
The relativistically broadened O VIII Ly![]() line which explains part of the RGS soft excess (Ogle et al. 2004) is significantly detected in all spectra (see Table 1). The measured line fluxes do not follow the power law or modified black body continuum flux changes. The emissivity q, assuming R-q, is similar to the value q2 = 5.0 measured by Ogle et al. (2004) for spectrum B, but not for spectrum C. We note that for spectrum A and D the emissivity was
frozen to the value for spectrum B and C respectively. Ogle et al. (2004) in detail discusses the steep emissivity derived as well as the physical parameters in the accretion disc derived from the line
profile and the lack of C VI Ly
line which explains part of the RGS soft excess (Ogle et al. 2004) is significantly detected in all spectra (see Table 1). The measured line fluxes do not follow the power law or modified black body continuum flux changes. The emissivity q, assuming R-q, is similar to the value q2 = 5.0 measured by Ogle et al. (2004) for spectrum B, but not for spectrum C. We note that for spectrum A and D the emissivity was
frozen to the value for spectrum B and C respectively. Ogle et al. (2004) in detail discusses the steep emissivity derived as well as the physical parameters in the accretion disc derived from the line
profile and the lack of C VI Ly![]() relativistic line. The latter places a lower limit on the ionisation parameter. Summarized, the relativistic O VIII Ly
relativistic line. The latter places a lower limit on the ionisation parameter. Summarized, the relativistic O VIII Ly![]() is emitted between 1.6 and 6 gravitational radii,
is emitted between 1.6 and 6 gravitational radii, ![]() > 3.4 and
> 3.4 and ![]() < 1023 m-3.
< 1023 m-3.
The inclination angle for all spectra was consistent with 48![]() ;
very similar to the inclination measured by Ogle et al. (2004). The inclination angle for the narrow line region (NLR) as
derived by Christopoulou et al. (1997) from narrow band [O III] imaging and long-slit spectroscopy using the Manchester Echelle Spectrograph is about 50
;
very similar to the inclination measured by Ogle et al. (2004). The inclination angle for the narrow line region (NLR) as
derived by Christopoulou et al. (1997) from narrow band [O III] imaging and long-slit spectroscopy using the Manchester Echelle Spectrograph is about 50![]() .
This indicates that the narrow
line region, and the gas producing the relativistically broadened emission line lie along the same line of sight. The narrow line region is therefore possibly an extension of the gas producing the
relativistically broadened emission lines. If this is the case, then the gas forming the relativistically broadened emission line is outflowing, similar to the absorption components. From the kinematics, Christopoulou et al. (1997) conclude that the imaged [O III] gas is outflowing. The inclination angle of the host galaxy is at medium angles (Möllenhoff & Heidt 2001), thus gas observed
from the relativistic and narrow emission lines are closely aligned with the host galaxy.
.
This indicates that the narrow
line region, and the gas producing the relativistically broadened emission line lie along the same line of sight. The narrow line region is therefore possibly an extension of the gas producing the
relativistically broadened emission lines. If this is the case, then the gas forming the relativistically broadened emission line is outflowing, similar to the absorption components. From the kinematics, Christopoulou et al. (1997) conclude that the imaged [O III] gas is outflowing. The inclination angle of the host galaxy is at medium angles (Möllenhoff & Heidt 2001), thus gas observed
from the relativistic and narrow emission lines are closely aligned with the host galaxy.
Relativistic line profiles in the soft X-ray band were first reported by Branduardi-Raymont et al. (2001) in the narrow lines Seyfert 1 galaxies MCG -6-30-15 and Mrk 766. Interestingly, the relativistically
broadened O VIII, N VII and C VI Ly![]() lines have only been convincingly detected in narrow line Seyfert 1 galaxies. For MCG -6-30-15 and Mrk 766 the disc line parameters
derived from the soft X-ray band and the Fe-K line are in good agreement. The XMM-Newton observation of NGC 4051 that showed a strong relativistic O VIII line (Ogle et al. 2004) did not show a significant relativistic Fe-K line (Pounds et al. 2004). Unfortunately the LETGS is not sensitive enough in the Fe-K band to directly compare the disc geometry as derived from iron and oxygen
lines. For the physical implications of the relativistic lines in NGC 4051 we refer to the discussion by Ogle et al. (2004).
lines have only been convincingly detected in narrow line Seyfert 1 galaxies. For MCG -6-30-15 and Mrk 766 the disc line parameters
derived from the soft X-ray band and the Fe-K line are in good agreement. The XMM-Newton observation of NGC 4051 that showed a strong relativistic O VIII line (Ogle et al. 2004) did not show a significant relativistic Fe-K line (Pounds et al. 2004). Unfortunately the LETGS is not sensitive enough in the Fe-K band to directly compare the disc geometry as derived from iron and oxygen
lines. For the physical implications of the relativistic lines in NGC 4051 we refer to the discussion by Ogle et al. (2004).
5.3 Broad emission lines
The broad O VII line, centred on the forbidden line, is detected in spectrum C, but the line is weaker or absent in the other spectra. Ogle et al. (2004) detected a broadened O VII emission line with a full width half maximum (FWHM) of 11 000 ![]() 3000 km s-1. This is consistent with the FWHM we derive: 24 000
3000 km s-1. This is consistent with the FWHM we derive: 24 000 ![]() 6000 km s-1. Both values are rather larger than the FWHM determined from the H
6000 km s-1. Both values are rather larger than the FWHM determined from the H![]() and He II broad lines measured in the UV (Peterson et al. 2000). If the broad line region (BLR) has a stratified ionisation structure, then it is expected that the higher ionised O VII line will have a broader width than either the H
and He II broad lines measured in the UV (Peterson et al. 2000). If the broad line region (BLR) has a stratified ionisation structure, then it is expected that the higher ionised O VII line will have a broader width than either the H![]() or lowly ionised He II. At 1.7 Å the width of the broadened O VII line exceeds the separation (0.5 Å) between the forbidden and resonance line. The broadened resonance (and intercombination) lines contribute to the flux and hence the width measured.
or lowly ionised He II. At 1.7 Å the width of the broadened O VII line exceeds the separation (0.5 Å) between the forbidden and resonance line. The broadened resonance (and intercombination) lines contribute to the flux and hence the width measured.
We also detect a broadened C VI line with a width of 3200 ![]() 1000 km s-1, which is smaller by a factor of
1000 km s-1, which is smaller by a factor of ![]() 7 than the O VII line. This value is fairly similar to the FWHM derived for the H
7 than the O VII line. This value is fairly similar to the FWHM derived for the H![]() line (1100
line (1100 ![]() 190, Peterson et al. 2000) and the width measured for this line in the RGS spectrum (1200 km s-1, Ogle et al. 2004). The smaller width is consistent in terms of a stratified BLR model, with the fact that C VI is formed at lower
ionisation parameters.
190, Peterson et al. 2000) and the width measured for this line in the RGS spectrum (1200 km s-1, Ogle et al. 2004). The smaller width is consistent in terms of a stratified BLR model, with the fact that C VI is formed at lower
ionisation parameters.
In spectrum C on top of the relativistically broadened O VIII Ly![]() emission line there is a broadened O VIII Ly
emission line there is a broadened O VIII Ly![]() emission line.
emission line.
Costantini et al. (2007) studying Mrk 279 did detect broadened emission lines with better statistics than is the case for NGC 4051. The authors conclude that the broad X-ray emission lines originate from a stratified BLR. The above findings for NGC 4051 are consistent with this conclusion.
5.4 Narrow emission features
During our observations we detect various narrow emission features in the spectra. The narrow forbidden O VII line was significantly detected in all spectra, and all flux values are
consistent with each other to within 1![]() (see Table 1). This is consistent with the picture that the O VII forbidden line is formed at the narrow line region further out. The width of this line (it is unresolved), precludes it being formed as part of the outflow.
(see Table 1). This is consistent with the picture that the O VII forbidden line is formed at the narrow line region further out. The width of this line (it is unresolved), precludes it being formed as part of the outflow.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{0416fi12.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg124.gif) |
Figure 8: Top: detail of the spectrum for the best fit (thick line) model with broad emission lines and the best fit (thin line) assuming the absorber has a covering factor of .75 for spectrum B. Bottom: same as above but for spectrum C. |
| Open with DEXTER | |
In spectrum D we detect the C VI RRC and the C V RRC. In the other three spectra these features are not detected. The shapes and centroids of individual RRCs are determined by
the temperature of the recombining gas, the emission measure of the relevant ion, and by the motion (velocity broadening) of the recombining gas. We derived the temperature and emission measure for
the RRCs assuming no velocity broadening. We have investigated the effect of broadening by including a velocity broadening component in our RRC spectral model. On the basis of the goodness of fit we exclude that the turbulent velocity in the recombining gas is greater than
![]() .
Both the temperature and emission measure are within the error bars the same for models with and without a velocity broadening of
.
Both the temperature and emission measure are within the error bars the same for models with and without a velocity broadening of
![]() .
.
If we interpret the maximum velocity broadening as due to Keplerian velocity at the location where the RRC is formed and assume a black hole mass of M=3 ![]()
![]() (McHardy et al. 2004) we obtain a minimum distance for the recombining gas of
(McHardy et al. 2004) we obtain a minimum distance for the recombining gas of ![]()
![]() 1012 m, or
1012 m, or ![]() 4500 Schwarzschild radii.
4500 Schwarzschild radii.
From the fitted temperature of the RRC of T = 5 ![]() 2 eV, we derive an ionisation parameter
2 eV, we derive an ionisation parameter
![]() .
With the ionising luminosity of the source (L=2.8
.
With the ionising luminosity of the source (L=2.8 ![]() 1035 W), the minimum distance derived above and the definition of
1035 W), the minimum distance derived above and the definition of ![]() ,
we obtain a maximum density of 4
,
we obtain a maximum density of 4 ![]() 1017 m-3. It is possible to estimate a lower limit to the volume of the RRC emitting source using the observed ionic emission measure of the C VI RRC (3.9
1017 m-3. It is possible to estimate a lower limit to the volume of the RRC emitting source using the observed ionic emission measure of the C VI RRC (3.9 ![]() 1066 m-3), a solar carbon abundance (Anders & Grevesse 1989) and a fraction of 60% in the form of C VII (appropriate for
1066 m-3), a solar carbon abundance (Anders & Grevesse 1989) and a fraction of 60% in the form of C VII (appropriate for
![]() ). We find an emitting volume of V=1035 m3. Note that the volume might be larger than the emitting volume if the filling factor is smaller than unity. We should note that CLOUDY (Ferland et al. 2004) version 95.06 calculates the size of the clouds to be of order 1011 m, thus a filling factor of less than unity is rather unlikely. We equate this volume to
). We find an emitting volume of V=1035 m3. Note that the volume might be larger than the emitting volume if the filling factor is smaller than unity. We should note that CLOUDY (Ferland et al. 2004) version 95.06 calculates the size of the clouds to be of order 1011 m, thus a filling factor of less than unity is rather unlikely. We equate this volume to
![]() where
where ![]() the characteristic thickness of the emitter in the radial direction and
the characteristic thickness of the emitter in the radial direction and ![]() the solid angle sustained by the emitter. Dividing the above formula by R3 and substituting the values for the volume and minimum distance we find
the solid angle sustained by the emitter. Dividing the above formula by R3 and substituting the values for the volume and minimum distance we find
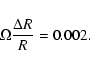 |
(1) |
Taking for the distance a value of 4
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fi13.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg134.gif) |
Figure 9: The spectrum for part C and D, clearly showing the difference in continuum shape. The difference is due to a lower flux in the power-law component and a lower temperature for the modified black body component in spectrum D. |
| Open with DEXTER | |
Another constraint follows from the column density ![]() through the emitting region. This can be written as
through the emitting region. This can be written as
![]() (assuming the filling factor is unity, see Eq. (1)). Taking the minimum radius and maximum density we can get an indication of the
column density:
(assuming the filling factor is unity, see Eq. (1)). Taking the minimum radius and maximum density we can get an indication of the
column density:
![]()
![]()
![]() m-2.
m-2.
A possible origin of the RRCs is that the gas in one (or more) of the warm absorber components is recombining. To test this hypothesis, we compare the properties of the recombining gas with that of the warm absorber components. The large estimated column density for the RRC is only derived for absorption component 4. However for this component the ionisation parameter is substantially higher, making a connection between this absorption component and the gas producing the RRCs unlikely. Component 2 has a similar ionisation parameter to the RRCs but its column density in spectrum B and C is substantially smaller. Thus this connection is also unlikely. Alternatively the RRCs could originate in the thin, ionised skin of the accretion disc. The width of the C VI broad emission line is similar to the maximum broadening of the RRCs. Also the ionization parameters are similar.
For
![]() we expect that most of the oxygen gas will recombine into O VII, thus we expect a strong O VII RRC at 16.77 Å. This RRC is not observed, and we can place an upper limit for the emission measure of 0.6
we expect that most of the oxygen gas will recombine into O VII, thus we expect a strong O VII RRC at 16.77 Å. This RRC is not observed, and we can place an upper limit for the emission measure of 0.6 ![]() 1066 m-3. It is possible that, the many absorption lines due to different iron ions mask the presence of the O VII RRC, or that the temperature is lower than 5 eV.
1066 m-3. It is possible that, the many absorption lines due to different iron ions mask the presence of the O VII RRC, or that the temperature is lower than 5 eV.
Ogle et al. (2004) detected the C VI RRC in the high flux state RGS spectrum; Pounds et al. (2004) detected in a different low state RGS spectrum the C VI and O VII RRCs. Both authors derive a temperature of 3 eV, consistent with our derived temperature of 5 ![]() 2 eV.
2 eV.
5.5 The ionised absorber
In our spectra, we have found evidence for the presence of four warm absorber components (Table 1). The absorption components are discussed in detail below.
5.5.1 Warm absorber component 1
The least ionised component, which has a low outflow velocity and the smallest hydrogen column density, is not detected in spectrum A or B, due to the lower signal to noise in these spectra. The strongest lines are due to O IV, O V and C V.
5.5.2 Warm absorber component 2
This component has a similarly low outflow velocity as component 1, but with a higher ionisation parameter, log ![]() = 0.87. The strongest lines of this component are the deep 1s-2p absorption lines of O VII, O VI and O V. This is the only component for which we measure a decrease by a factor of two in the ionisation parameter between spectrum C and D (see Table 1, Fig. 4). This component, perhaps partly together with
our component 1, corresponds to the low ionisation component found by Krongold et al. (2007). However, they find a column density that is twice as large and a somewhat higher outflow velocity of -500 km s-1.
= 0.87. The strongest lines of this component are the deep 1s-2p absorption lines of O VII, O VI and O V. This is the only component for which we measure a decrease by a factor of two in the ionisation parameter between spectrum C and D (see Table 1, Fig. 4). This component, perhaps partly together with
our component 1, corresponds to the low ionisation component found by Krongold et al. (2007). However, they find a column density that is twice as large and a somewhat higher outflow velocity of -500 km s-1.
5.5.3 Warm absorber component 3
With an outflow velocity of -580 km s-1, component 3 has the largest opacity. The dominant imprints are the Ly![]() transitions of hydrogenic oxygen, nitrogen and carbon. The outflow
velocity and ionisation state are similar to one of the two absorber components reported by Collinge et al. (2001). McKernan et al. (2007) analysing the same spectrum found three components, two of which are consistent with our component 2 and 3. Note that the observed Doppler velocity (sum of the +700 km s-1 heliocentric velocity of NGC 4051, Verheijen & Sancisi (2001), and the intrinsic outflow velocity of
transitions of hydrogenic oxygen, nitrogen and carbon. The outflow
velocity and ionisation state are similar to one of the two absorber components reported by Collinge et al. (2001). McKernan et al. (2007) analysing the same spectrum found three components, two of which are consistent with our component 2 and 3. Note that the observed Doppler velocity (sum of the +700 km s-1 heliocentric velocity of NGC 4051, Verheijen & Sancisi (2001), and the intrinsic outflow velocity of
![]() -600 km s-1) is only +100 km s-1, and less than 2
-600 km s-1) is only +100 km s-1, and less than 2![]() different from 0. Therefore, this absorption could be blended with absorption from our Galaxy or the local group. Pounds et al. (2004) analysed the high state RGS spectrum; and detected an absorber with log
different from 0. Therefore, this absorption could be blended with absorption from our Galaxy or the local group. Pounds et al. (2004) analysed the high state RGS spectrum; and detected an absorber with log ![]() = 2.7 and an outflow velocity of
= 2.7 and an outflow velocity of ![]() -600 km s-1, which can probably be associated with this component. We associate this component with the high ionisation component of Krongold et al. (2007), for which these authors derive a distance of 1-2
-600 km s-1, which can probably be associated with this component. We associate this component with the high ionisation component of Krongold et al. (2007), for which these authors derive a distance of 1-2 ![]() 1013 m based on time
variability; but see Sect. 5.5.6 below.
1013 m based on time
variability; but see Sect. 5.5.6 below.
5.5.4 Warm absorber component 4
The last absorber component has the highest ionisation parameter, hydrogen column density and outflow velocity. The C VI and N VII Ly![]() lines are the deepest detected. The O VIII Ly
lines are the deepest detected. The O VIII Ly![]() blends with and broadens the less blueshifted secondary O VII line. The outflow velocity of -4670 km s-1 was first reported by van der Meer et al. (2003). This is
one of the highest outflow velocities derived from high resolution spectra of Seyfert galaxies, that we are aware of. Collinge et al. (2001) observed for the highest ionised component in a Chandra HETG spectrum of NGC 4051, an outflow velocity component of -2340 km s-1, which is not detected in our spectra. The high velocity component that we detect, and the one reported by Collinge et al. (2001), seem to be the only ionised components detected in the X-rays without a UV absorber at the same outflow velocity. In many AGN the most highly ionised X-ray absorber should not produce any UV absorption lines, however usually a UV absorber with the same outflow velocity as the X-ray absorber is detected. This does not seem to be the case for the -4670 km s-1 component we detect. Both the -2340 km s-1 and the -4670 km s-1 components are highly ionised and therefore detectable with the HETG, the LETG and the RGS. Ogle et al. (2004) do not detect these highly
ionised components in the RGS spectrum. Considering that neither we nor Ogle et al. (2004) detect the -2340 km s-1 component, and that the -4670 km s-1 component is not present in the earlier Chandra HETG and RGS data, these high velocity absorbers either have a variable column
density or are transient.
blends with and broadens the less blueshifted secondary O VII line. The outflow velocity of -4670 km s-1 was first reported by van der Meer et al. (2003). This is
one of the highest outflow velocities derived from high resolution spectra of Seyfert galaxies, that we are aware of. Collinge et al. (2001) observed for the highest ionised component in a Chandra HETG spectrum of NGC 4051, an outflow velocity component of -2340 km s-1, which is not detected in our spectra. The high velocity component that we detect, and the one reported by Collinge et al. (2001), seem to be the only ionised components detected in the X-rays without a UV absorber at the same outflow velocity. In many AGN the most highly ionised X-ray absorber should not produce any UV absorption lines, however usually a UV absorber with the same outflow velocity as the X-ray absorber is detected. This does not seem to be the case for the -4670 km s-1 component we detect. Both the -2340 km s-1 and the -4670 km s-1 components are highly ionised and therefore detectable with the HETG, the LETG and the RGS. Ogle et al. (2004) do not detect these highly
ionised components in the RGS spectrum. Considering that neither we nor Ogle et al. (2004) detect the -2340 km s-1 component, and that the -4670 km s-1 component is not present in the earlier Chandra HETG and RGS data, these high velocity absorbers either have a variable column
density or are transient.
5.5.5 Comparison between the absorber components
The derived hydrogen column density and ionisation parameters for our three absorbers with an ionisation parameter log ![]() < 3 are in agreement with those derived from an RGS observation, in a similar flux state, and given in a figure by Ogle et al. (2004). We confirm, using the parameters measured for spectrum C, that there is an increase in hydrogen column density with increasing ionisation parameter, as observed in this source by Ogle et al. (2004) and in NGC 5548 by
Steenbrugge et al. (2005).
< 3 are in agreement with those derived from an RGS observation, in a similar flux state, and given in a figure by Ogle et al. (2004). We confirm, using the parameters measured for spectrum C, that there is an increase in hydrogen column density with increasing ionisation parameter, as observed in this source by Ogle et al. (2004) and in NGC 5548 by
Steenbrugge et al. (2005).
It is also possible to constrain the opening angle of the outflow. From the ionising luminosity (L=2.8 ![]() 1035 W) and the definition of
1035 W) and the definition of ![]() ,
we get
,
we get
![]() .
As we measure the outflow velocity v, we know that the mass outflow rate per steradian is
.
As we measure the outflow velocity v, we know that the mass outflow rate per steradian is
![]() .
We list this value for each of the absorber components in Table 4, based on our result for spectrum C. Assuming a typical accretion efficiency of 10%, the observed luminosity of NGC 4051 corresponds to an accretion rate of 5
.
We list this value for each of the absorber components in Table 4, based on our result for spectrum C. Assuming a typical accretion efficiency of 10%, the observed luminosity of NGC 4051 corresponds to an accretion rate of 5 ![]()
![]() yr-1. Assuming the mass outflow through the wind is smaller than the accretion onto the black hole, we can put upper limits to the solid angle sustained by the outflow. This assumption seems reasonable as the energy needed to accelerate the outflow must come from the infalling gas. These upper limits are small, typically less than 10-2 to 10-5 sr. Using this same formalism, similar to somewhat larger opening angles were derived for the outflow in NGC 5548 (Steenbrugge et al. 2005).
yr-1. Assuming the mass outflow through the wind is smaller than the accretion onto the black hole, we can put upper limits to the solid angle sustained by the outflow. This assumption seems reasonable as the energy needed to accelerate the outflow must come from the infalling gas. These upper limits are small, typically less than 10-2 to 10-5 sr. Using this same formalism, similar to somewhat larger opening angles were derived for the outflow in NGC 5548 (Steenbrugge et al. 2005).
5.5.6 Time variability of the warm absorber
Our spectral modelling of the warm absorber components is based upon models for photoionisation balance. Whenever the ionising flux of the source changes, the ionisation balance should adjust to the new situation, and the ionisation parameter ![]() should change. The speed at which this happens depends on the density n of the absorbing material. The recombination timescale
should change. The speed at which this happens depends on the density n of the absorbing material. The recombination timescale ![]() for a given ion i is inverse proportional to the gas density. It is given by Bottorff et al. (2000) to be
for a given ion i is inverse proportional to the gas density. It is given by Bottorff et al. (2000) to be
where fi is the relative concentration of ion i of a given element, and
The largest flux change occurs between spectrum C and D. The hard 2-10 keV power-law flux drops suddenly by a factor of 6.1 (
![]() ,
where we define p as the flux ratio of spectrum D to spectrum C). The soft flux (taken here and later as the 0.2-10 keV modified black body flux
from Table 1) decreases by a factor of 5.4 (
,
where we define p as the flux ratio of spectrum D to spectrum C). The soft flux (taken here and later as the 0.2-10 keV modified black body flux
from Table 1) decreases by a factor of 5.4 (
![]() ). Thus, if the density in one of the components is high, we would expect
). Thus, if the density in one of the components is high, we would expect ![]() to decrease by about 0.73, and if the density is low, we expect no change between spectrum C and D. As the low state of spectrum D lasts about 20 ks and our data have insufficient S/N to resolve spectrum D further in time, this gives the limit on the recombination timescale.
to decrease by about 0.73, and if the density is low, we expect no change between spectrum C and D. As the low state of spectrum D lasts about 20 ks and our data have insufficient S/N to resolve spectrum D further in time, this gives the limit on the recombination timescale.
Indeed in components 1, 3 and 4 we see no significant change in ![]() ,
and definitely no change as large as -0.73 (see Table 1), indicating that the recombination timescale is longer than 20 ks. This then gives the lower limits to the distance of these components from the central source as listed in Table 5. In the table the product nr2 is calculated from
,
and definitely no change as large as -0.73 (see Table 1), indicating that the recombination timescale is longer than 20 ks. This then gives the lower limits to the distance of these components from the central source as listed in Table 5. In the table the product nr2 is calculated from ![]() .
The product of recombination timescale and density
.
The product of recombination timescale and density ![]() is calculated from (Eq. (2)), using the total recombination rates of Nahar (1999). Limits on r are calculated from
is calculated from (Eq. (2)), using the total recombination rates of Nahar (1999). Limits on r are calculated from
![]() .
The lower limit for component 3, namely 5
.
The lower limit for component 3, namely 5 ![]() 1014 m (19 light days), disagrees with the distance of 0.5-1 light days derived by Krongold et al. (2007) for this component.
1014 m (19 light days), disagrees with the distance of 0.5-1 light days derived by Krongold et al. (2007) for this component.
Krongold et al. (2007) studied the variability using the relatively low-resolution EPIC data. Some possible reasons for the disagreement are given below. Krongold et al. (2007) do not allow the continuum shape (i.e. photon index and temperature) to vary, while at least in our data the shape of the continuum significantly changes (see Fig. 9). Further, Krongold et al. (2007) do not include a
relativistic O VIII Ly![]() line although in the total and high state spectra their best fit model (see their Figs. 2 and 3) is consistently below the observed continuum between 17 and 19.2 Å. Similarly, the continuum is above their model between 20 and 21.8 Å, where we fit a broadened O VII line. Failure to fit the local continuum correctly will result in too low or too high column densities derived from the line depths.
line although in the total and high state spectra their best fit model (see their Figs. 2 and 3) is consistently below the observed continuum between 17 and 19.2 Å. Similarly, the continuum is above their model between 20 and 21.8 Å, where we fit a broadened O VII line. Failure to fit the local continuum correctly will result in too low or too high column densities derived from the line depths.
Table 5:
Observed and calculated parameters for the four warmabsorber components of spectrum C.
Krongold et al. (2007) included only two absorption components and have problem fitting some of the oxygen
lines. Therefore, their model cannot explain the O V absorption line at 22.4 Å, which is easily observed in their published RGS spectrum. Furthermore, the depth of the O VII line is
overestimated in the high state, and underestimated it in the low state. Oxygen lines are diagnostically important because of their large oscillator strength (i.e. strong lines) and the rather large range in ionisation parameters they span. One can thus determine (over
this ionisation range) the ionisation structure without having to worry about abundance effects. Finally, long term differences between our observations and those of Krongold et al. (2007), could explain the differences found in ionisation variability behaviour.
Krongold et al. (2007) claim to detect variability in the ionisation parameters on timescales of 2-3 ks, leading to a much larger derived density and thus closer location of the absorber.
In our component 2, we see a decrease of a factor of 2 (
Next we investigate the long term variability, by comparing spectrum B to spectrum C in a similar way as we did above for spectra D and C. The soft and hard flux of spectrum B have
Finally, we have an independent short term comparison by comparing spectrum A to spectrum B, although our discriminating power is smaller here, because of the smaller flux jump (
In this study we have investigated the spectral properties of NGC 4051, observed by Chandra-LETGS on two occasions for a total of 180 ks. Due to the flux variations within each observation, we split each observation into 2 spectra, to be fit separately. In the
highest signal-to-noise spectrum, C, we detect four absorption components. Our main results are:
![]()
![]() 0.16), suggesting that the recombination time is indeed 20 ks or smaller. This now gives an upper limit to the distance of 3
0.16), suggesting that the recombination time is indeed 20 ks or smaller. This now gives an upper limit to the distance of 3 ![]() 1015 m or 110 light days (see Table 5). This
is higher than, but consistent with the upper limit of 3.5 light days for the low ionisation component of Krongold et al. (2007). That the change in
1015 m or 110 light days (see Table 5). This
is higher than, but consistent with the upper limit of 3.5 light days for the low ionisation component of Krongold et al. (2007). That the change in ![]() is not the expected value of -0.73 may have two reasons, which we cannot be distinguished in our present data. The recombination
timescale might be close to our upper limit, so that the gas is still recombining at the end of interval D. Alternatively, the flux changes in the invisible EUV band might be smaller, and these may be more important for the low ionisation gas than the X-ray continuum (the dominant
oxygen ions for component 2 are O VI and O V).
is not the expected value of -0.73 may have two reasons, which we cannot be distinguished in our present data. The recombination
timescale might be close to our upper limit, so that the gas is still recombining at the end of interval D. Alternatively, the flux changes in the invisible EUV band might be smaller, and these may be more important for the low ionisation gas than the X-ray continuum (the dominant
oxygen ions for component 2 are O VI and O V).
![]() and
and
![]() ,
respectively. Taking a typical value of -0.4, we see that all visible
components in spectrum B (components 2-4) are in agreement with such a change in
,
respectively. Taking a typical value of -0.4, we see that all visible
components in spectrum B (components 2-4) are in agreement with such a change in ![]() (
(
![]()
![]() 0.22, -0.34
0.22, -0.34 ![]() 0.26 and -0.27
0.26 and -0.27 ![]() 0.19). We conclude that the recombination timescale for these components is likely faster than 570 days, the interval between both observations. This gives interesting upper limits to the distance of components 3 and 4 (see Table 4) of about 1 pc. We should note that components 2-4 could coexist in the same location, but that component 1 and 2 can not coexist in the same location, due to the lack of variability in component 1, even over 570 days.
0.19). We conclude that the recombination timescale for these components is likely faster than 570 days, the interval between both observations. This gives interesting upper limits to the distance of components 3 and 4 (see Table 4) of about 1 pc. We should note that components 2-4 could coexist in the same location, but that component 1 and 2 can not coexist in the same location, due to the lack of variability in component 1, even over 570 days.
![]() and -0.21 for the soft and hard band, respectively). The error bars on the ionisation parameter for components 3 and 4 preclude a definite conclusion here; for component 2, we see an increase in spectrum A of
and -0.21 for the soft and hard band, respectively). The error bars on the ionisation parameter for components 3 and 4 preclude a definite conclusion here; for component 2, we see an increase in spectrum A of
![]()
![]() 0.32, which favours the no change scenario, but does not exclude a small response compatible with
0.32, which favours the no change scenario, but does not exclude a small response compatible with
![]() .
We also note that, of all our four spectra, the flux during spectrum A shows the largest variations within the given interval (Fig. 1), so the establishment of any (quasi)-equilibrium during that interval may be questioned.
.
We also note that, of all our four spectra, the flux during spectrum A shows the largest variations within the given interval (Fig. 1), so the establishment of any (quasi)-equilibrium during that interval may be questioned.
6 Summary
![]() and C VI Ly
and C VI Ly![]() are detected. These lines show a simple Gaussian profile, suggesting an
origin in the BLR.
are detected. These lines show a simple Gaussian profile, suggesting an
origin in the BLR.
![]() line, similar to the findings by Ogle et al. (2004).
line, similar to the findings by Ogle et al. (2004).
K.C.S. thanks St John's College for a fellowship. SRON is supported financially by NWO, the Netherlands Organization for Scientific Research.
References
Footnotes
All Tables
Table 1: The best fit parameters for the different spectral components for the four spectra. All wavelengths and velocities refer to the rest frame of NGC 4051. Numbers in square brackets are calculated from the fit parameters; numbers in round brackets were kept fixed during the fit.
Table 2: Significances of the different spectral components. We list the increase in the C-statistic when the component is omitted from the model and the spectrum is refitted.
Table 3: The best fit parameters for the RRCs in spectrum D. Thevelocity refers to the rest frame of NGC 4051.
Table 4: The best fit parameters for a three-absorber-component model for spectrum C. Components 1-3 correspond to components 2-4 in Tables 1 and 2.
Table 5: Observed and calculated parameters for the four warmabsorber components of spectrum C.
All Figures
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{0416fig1.ps}\hspace*{0.6cm}
\includegraphics[angle=270,width=8.5cm,clip]{0416fig2.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg5.gif) |
Figure 1: The light curve in the zeroth spectral order ( top panels) and hardness ratio ( bottom panels) for the observations of Jan. 2002 and July 2003. The hardness ratio is defined as the ratio of the 2-8 and 8-32 Å counts. The top panel has a bin size of 350 s and the bottom panel has a bin size of 2000 s. Dotted lines denote the different flux states and define the intervals used in creating the four spectra. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{0416fig3.ps}\vspace*{5mm}
\includegraphics[angle=-90,width=15cm,clip]{0416fig4.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg103.gif) |
Figure 2:
Flux (in units of photons m-2 s-1 Å-1) and our best spectral model. All spectra are binned by a factor of 2 for clarity of display. Note the different continuum levels and shapes between the spectra, especially around the upturn at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig5.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg114.gif) |
Figure 3: Detail of spectrum C fitted with 3 warm absorber components (thin line) and 4 warm absorber components (thick line). Binning as in Fig. 2. The best fit 3 component model does under-predict the depth of the O V and O IV lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig6.ps}\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig7.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg118.gif) |
Figure 4:
Change ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fig8.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg119.gif) |
Figure 5: The model absorption spectra for each of the 4 different absorption components as detected in spectrum C. The continuum was modelled to be flat and was renormalised per component. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{0416fig9.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg120.gif) |
Figure 6:
Detail of spectra B and C with the best fit model (thick line) and the best fit model without the O VIII Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fi10.ps}\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fi11.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg123.gif) |
Figure 7: Model emission spectra for spectrum B and C, without Galactic absorption and the warm absorber components. Dashed line: power law continuum; dotted line: modified black body continuum; dash-dotted line: sum of power law and modified black body continuum; thin solid lines: relativistic, broad and narrow emission line contributions; thick solid line: total unabsorbed emission spectrum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{0416fi12.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg124.gif) |
Figure 8: Top: detail of the spectrum for the best fit (thick line) model with broad emission lines and the best fit (thin line) assuming the absorber has a covering factor of .75 for spectrum B. Bottom: same as above but for spectrum C. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{0416fi13.ps}
\end{figure}](/articles/aa/full_html/2009/10/aa10416-08/Timg134.gif) |
Figure 9: The spectrum for part C and D, clearly showing the difference in continuum shape. The difference is due to a lower flux in the power-law component and a lower temperature for the modified black body component in spectrum D. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}%
\tau_i n = \bigl[
\alpha_i ( \frac{f_{i+1}}{f_i} - \frac{\alpha_{i-1}}{\alpha_i} )
\bigr]^{-1}
\end{displaymath}](/articles/aa/full_html/2009/10/aa10416-08/img142.gif)