| Issue |
A&A
Volume 495, Number 3, March I 2009
|
|
|---|---|---|
| Page(s) | 819 - 826 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200811341 | |
| Published online | 30 January 2009 | |
The Milky Way's external disc constrained by 2MASS star counts
C. Reylé1 - D. J. Marshall2 - A. C. Robin1 - M. Schultheis1
1 - Observatoire de Besançon, Institut UTINAM, Université de Franche-Comté, BP 1615, 25010 Besançon Cedex, France
2 -
Département de Physique et Centre de Recherche en Astrophysique de Québec, Université Laval, Québec, G1K 7P4, Canada
Received 13 November 2008 / Accepted 13 December 2008
Abstract
Context. Thanks to recent large-scale surveys in the near infrared, such as 2MASS, the galactic plane that most suffers from extinction is revealed so its overall structure can be studied.
Aims. This work aims at constraining the structure of the Milky Way external disc as seen in 2MASS data, and in particular the warp.
Methods. We use the Two Micron All Sky Survey (hereafter 2MASS) along with the Stellar Population Synthesis Model of the Galaxy, developed in Besançon, to constrain the external disc parameters, such as its scale length, its cutoff radius, and the slope of the warp. To properly interpret the observations, the simulated stars are reddened using a 3D extinction map. The shape of the stellar warp is then compared with previous results and with similar structures in gas and dust.
Results. We find new constraints on the stellar disc, which is shown to be asymmetrical, similar to observations of HI. The positive longitude side is found to be easily modelled with S-shaped warp but with a significantly smaller slope than the one seen in the HI warp. At negative longitudes, the disc presents peculiarities that are not reproduced well by any simple model. Finally, comparing with the warp seen in the dust, it seems to follow an intermediate slope between the gas and the stars.
Key words: Galaxy: disk - galaxie: structure - surveys
1 Introduction
In recent years wide surveys have been obtained thanks to wide-field mosaic of CCD cameras and helped by the availability of dedicated telescopes both from the ground and from space. These large data sets benefit Galactic structure studies; however, interstellar extinction remains a serious obstacle for observing stars in the Milky Way, and for interpreting these observations in terms of Galactic structure. As the extinction suffered in the near infrared is roughly an order of magnitude lower than in the visible, recent infrared surveys provide a suitable tool for probing further into the densest parts of the Galaxy, namely the Galactic plane.Among them, the 2MASS survey (Skrutskie et al. 2006) has provided one of these rich data sets from which substantial results have been obtained. The homogeneity of these data sets is a great help for avoiding systematic bias and bad links from one set to another, which have created trouble in data interpretation in the past, disentangling real cosmic substructure from local zero point errors for example.
Analysis of near infrared data in the whole Galactic plane can bring important clues to stellar populations. In particular, a good knowledge of the disc structure is crucial to characterising the overdensities found close to the Galactic plane, such as the Canis Major overdensity. This structure located at
![]() ,
,
![]() was revealed by Martin et al. (2004a). Its nature is still under debate. While several studies based on kinematics, star counts, and
CMD studies of this
field conclude that it is a dwarf galaxy (Martínez-Delgado et al. 2005; Butler 2007; Martin et al. 2004b,2005; De Jong 2007), other authors have tested several warp models and claime that the warp is still a
possible explanation of the Canis Major overdensity (López-Corredoira 2006; Momany et al. 2006,2004). It shows how important it is to have a good description of the Galactic disc structure.
was revealed by Martin et al. (2004a). Its nature is still under debate. While several studies based on kinematics, star counts, and
CMD studies of this
field conclude that it is a dwarf galaxy (Martínez-Delgado et al. 2005; Butler 2007; Martin et al. 2004b,2005; De Jong 2007), other authors have tested several warp models and claime that the warp is still a
possible explanation of the Canis Major overdensity (López-Corredoira 2006; Momany et al. 2006,2004). It shows how important it is to have a good description of the Galactic disc structure.
Warps are a common feature in external galaxies (Bosma 1991). Radio observations have revealed that the Milky Way itself hosts a warp and a flared disc. The warp and flares have been observed in HI data (Henderson et al. 1982; Burton 1988; Diplas & Savage 1991; Nakanishi & Sofue 2003; Levine et al. 2006; Burton & te Lintel Hekkert 1986), in molecular clouds (Grabelsky et al. 1987; May et al. 1997; Wouterlout et al. 1990), from OB stars (Reed 1996; Miyamoto et al. 1988) and finally in COBE data (Freudenreich 1998; Drimmel & Spergel 2001; Porcel et al. 1997). The warp and flare in the Galaxy have also been detected in the interstellar dust (Freudenreich et al. 1994; Marshall et al. 2006). Derrière & Robin (2001) analysed DENIS (Epchtein et al. 1999) star counts in several fields in the Galactic plane and show evidence of a warp and a flare in the stellar disc. More recently López-Corredoira et al. (2002) have modelled a stellar warp from the analysis of the stellar populations in the 2MASS survey.
Warps may have originated from interactions between the disc and (i) the dark halo (if angular momenta are not aligned); (ii) nearby satellite galaxies, such as the Sagittarius dwarf or the Magellanic clouds; (iii) infalling intergalactic gas. From the analysis of their angular momenta, Bailin (2003) argues that the Milky Way warp and the Sagittarius Dwarf Galaxy may be coupled. Garcia-Ruiz (2002) used N-body simulations to explore the possibility that the warp has been created by tidal forces caused by the Magellanic Clouds. They find that neither orientation nor amplitude of the warp can be reproduced this way. In contrast, Weinberg & Blitz (2006) used perturbation theory to show that a Magellanic Cloud as the origin for the warp of the Milky Way can explain most quantitative features of the outer HI layer. Alternatively, López-Corredoira et al. (2002) propose that the warp is due to intergalactic accretion flows onto the Milky Way disc.
Here we report on our analysis of the external stellar disc of the Galaxy and, particularly the warp, as seen from near-infrared star counts using a Galaxy model. We overview the stellar population synthesis approach and the basic inputs of the model, in particular for the external disc (Sect. 2). In Sect. 3 we briefly describe the determination of a 3D map of interstellar extinction and show a first comparison between the Galaxy model and the 2MASS survey in the Galactic plane. We then describe (Sect. 4) the constraints obtained from comparing model predictions using different disc models with 2MASS data and compare them with results from other studies. In Sect. 5 we provisionally draw conclusions on the comparison between the gaseous warp and the stellar warp and about the origin of this warp.
2 The Galaxy model
2.1 Stellar population synthesis approach
To analyse the large data set provided by 2MASS, we use a stellar-population synthesis approach (the Galaxy model, Robin et al. 2003). This model aims at assembling current scenarii of galaxy formation and evolution, theories of stellar formation and evolution, models of stellar atmospheres, and dynamical constraints, in order to make a consistent picture explaining currently available observations. When scenarii of Galaxy formation and evolution are inferred from suitable constraints, they may be tested using population synthesis models whose predictions can be directly compared with observations. This synthetic approach ensures that biases have been correctly taken into account and that the scenario is compatible with many kinds of constraint.
The validity of any Galactic model is always questionable, as it describes a smooth Galaxy, while inhomogeneities exist, either in the disc or the halo. The issue is not to make a perfect model that reproduces the known Galaxy on any scale. Rather, one aims to produce a useful tool for computing the probable stellar content of large data sets, therefore to test the usefulness of such data to answer a given question relative to Galactic structure and evolution.
The model we use is the Galaxy model developed in Besançon. Its originality, as compared to a few other population-synthesis models presently available for the Galaxy, is the dynamical self-consistency. The Boltzmann equation allows the scale height of an isothermal and relaxed population to be constrained by its velocity dispersion and the Galactic potential (Bienaymé et al. 1987). The use of this dynamical constraint avoids a set of free parameters that is quite difficult to determine: the scale height of the thin disc at different ages.
2.2 Basic scheme
The model assumes that stars belong to four main populations: the thin disc, the thick disc, the stellar halo (or spheroid), and the outer bulge. The modelling of each population is based on a set of evolutionary tracks, assumptions on density distributions, constrained either by dynamical considerations or by empirical data, and guided by a scenario of formation and evolution, that is to say assumptions on the initial mass function (IMF) and the star formation rate (SFR) for each population. More detailed descriptions on these constraints can be found in Haywood et al. (1997) for the thin disc, Reylé & Robin (2001) for the thick disc, Robin et al. (2000) for the spheroid, and Picaud & Robin (2004) for the outer bulge. Recently, the Hipparcos mission and large-scale surveys in the optical and the near-infrared have led to new physical constraints improving our knowledge of the overall structure and evolution of the Galaxy. These new constraints are included in the version of the model described in Robin et al. (2003).
![\begin{figure}
\par\mbox{\includegraphics[width=9cm]{1341fig1a.ps}\includegraphics[width=9cm]{1341fig1b.ps} }\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg10.gif) |
Figure 1: Warp in the dust as seen from the Marshall et al. (2006) 3D extinction map. The plot shows the density of absorbing material at 8 kpc from the sun, as a function of longitude and latitude. The dashed line is the position of the mid-plane expected from a 0.18 slope warp model, and the solid line the position from the fitted slope of 0.14 at positive longitudes and 0.11 at negative longitudes. |
| Open with DEXTER | |
| |
Figure 2:
Comparison between the number of stars from the Galaxy model
|
| Open with DEXTER | |
2.3 The external disc model
The disc is assumed to be axisymmetric and spiral arms are not modelled. The thin disc is divided into 7 age components. The distribution of each disc component is described by an axisymmetric ellipsoid with an axis ratio depending on the age, using an Einasto law. The disc scale length, hR=2530 pc, is derived from the fitting of the old disc parameters on DENIS star counts towards the Galactic bulge direction (Picaud & Robin 2004). Several studies have shown that the edge of the disc is detected at a galactocentric distance of about 14 kpc (Ruphy et al. 1996; Robin et al. 1992). The disc is also warped and flared, and all stellar components in the disc have the same warp and flare.
As in Gyuk et al. (1999), we model the flaring by increasing the scale heights by a factor
![]() ,
beyond a galactocentric radius
,
beyond a galactocentric radius
![]() :
:
The amplitude is taken from Gyuk et al. (1999) (
We first model the warp as S-shaped warp, with a tilted ring model following Porcel et al. (1997).
The height
![]() of the warp over the plane
of the warp over the plane ![]() as a function of galactocentric coordinates is computed using
as a function of galactocentric coordinates is computed using
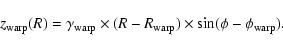
Following Burton (1988), we assume, as a starting point, that the Sun lies on the line of nodes of the warp (
3 Interstellar extinction
The 2MASS survey allows us to study large-scale structures in the Galaxy by comparing with simulations of the Galaxy model, particularly in the Galactic plane where extinction is quite high. The comparison is realistic only if the extinction is known. Without a good estimate of the extinction and of its distance, it is nearly impossible to understand the structure in the thin disc. Hence it is imperative to start by constructing a 3D extinction map of the Galaxy.
Extinction is so clumpy in the Galactic plane that for a large part it determines the number density of stars, more than any other large-scale stellar structure. Thus, it is possible to extract information about the distribution of the extinction from photometry and star counts. Marshall et al. (2006) show that the 3D extinction distribution can be inferred from the colour distributions in the 2MASS survey. Using stellar colours in
![]() as extinction indicators and assuming that all of the model prediction deviations on small scales from observed colours arises from the variation in extinction along the line of sight, they built a
3D extinction map of the Galactic plane. The final resolution in longitude and latitude is 15 arcmin and the resolution in distance varies between 100 pc and
1 kpc, depending on stellar density and on the dust distribution along the line of sight. The resulting 3D extinction map provides an accurate description of the large-scale structure of the disc of dust. These maps clearly show the dust warp in the external disc (Fig. 1). The warp found for the dust differs from the stellar warp model.
as extinction indicators and assuming that all of the model prediction deviations on small scales from observed colours arises from the variation in extinction along the line of sight, they built a
3D extinction map of the Galactic plane. The final resolution in longitude and latitude is 15 arcmin and the resolution in distance varies between 100 pc and
1 kpc, depending on stellar density and on the dust distribution along the line of sight. The resulting 3D extinction map provides an accurate description of the large-scale structure of the disc of dust. These maps clearly show the dust warp in the external disc (Fig. 1). The warp found for the dust differs from the stellar warp model.
After applying the extinction to the simulated stars, it is possible to perform a realistic comparison of the number
![]() of stars from the Galactic model with the number
of stars from the Galactic model with the number
![]() of observed stars in the 2MASS data (Fig. 2). The comparison points to significant discrepancies.
Thus it appears that several galactic components are not properly characterized in the
Galaxy model: (i) the bulge extends too far from the plane; (ii) the disc in the inner part of the Galaxy (
of observed stars in the 2MASS data (Fig. 2). The comparison points to significant discrepancies.
Thus it appears that several galactic components are not properly characterized in the
Galaxy model: (i) the bulge extends too far from the plane; (ii) the disc in the inner part of the Galaxy (
![]() )
has a scale height that is slightly too large; (iii) the warp of the external disc is too strong; and
(iv) the modelled warp is symmetrical, whereas the observations point to an asymmetrical warp.
)
has a scale height that is slightly too large; (iii) the warp of the external disc is too strong; and
(iv) the modelled warp is symmetrical, whereas the observations point to an asymmetrical warp.
In this work we concentrate on the external disc (
![]() )
and propose to derive a better
parametrization in three steps; (i) simulations of the Galaxy are obtained using different parameters; (ii) as the extinction found depends on the parameters in the Galaxy model (the sensitivity of the extinction model to the Galaxy model is discussed in Marshall et al. 2006), the extinction is derived for each set of Galactic parameters using the Marshall et al. (2006) method and applied to the simulated stars; (iii) number counts of simulated and observed stars are statistically compared.
)
and propose to derive a better
parametrization in three steps; (i) simulations of the Galaxy are obtained using different parameters; (ii) as the extinction found depends on the parameters in the Galaxy model (the sensitivity of the extinction model to the Galaxy model is discussed in Marshall et al. 2006), the extinction is derived for each set of Galactic parameters using the Marshall et al. (2006) method and applied to the simulated stars; (iii) number counts of simulated and observed stars are statistically compared.
![\begin{figure}
\par\includegraphics[height=9.5cm,angle=0]{1341fig3a.ps}\includegraphics[height=9.5cm,angle=0]{1341fig3b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg24.gif) |
Figure 3:
2MASS star counts ( top), modelled ones ( middle), and relative difference between the two ( bottom) with
|
| Open with DEXTER | |
4 Results
As seen in Fig. 2, the assumed slope of the warp is not suitable for correctly reproducing the data. The slope value is too high and the simulated warp deviates too far from the ![]() plane.
Too many stars are predicted below the galactic plane at negative longitudes and above the plane at positive longitudes. The overestimate is higher for
plane.
Too many stars are predicted below the galactic plane at negative longitudes and above the plane at positive longitudes. The overestimate is higher for ![]() ,
showing that the stellar warp is asymmetric.
This can be either an apparent asymmetry if the Sun does not lie on the line of nodes or a real asymmetry in the disc; however the effect of the position of the line of nodes does not solve the problem, as explained below. Another possibility is that the asymmetry is due to the distribution of the dust with respect to the stars. In our approach we assumed as a first approximation that a symmetric warp only exists in the stars. The extinction we derive does not suppose any geometry for the large-scale distribution of the dust, but simply finds the extinction needed to correct the simulated stellar colours to fit the observed ones. The dust warp then appears naturally in the extinction distribution, and this dust warp is not symmetrical.
Assuming this dust warp, we then tentatively adjust the star counts on both sides of the galaxy,
to check the values of the northern and the southern warps independently.
As such, it is not possible for us to create a stellar overdensity in the model by a misalignment of the stellar and dusty warps.
,
showing that the stellar warp is asymmetric.
This can be either an apparent asymmetry if the Sun does not lie on the line of nodes or a real asymmetry in the disc; however the effect of the position of the line of nodes does not solve the problem, as explained below. Another possibility is that the asymmetry is due to the distribution of the dust with respect to the stars. In our approach we assumed as a first approximation that a symmetric warp only exists in the stars. The extinction we derive does not suppose any geometry for the large-scale distribution of the dust, but simply finds the extinction needed to correct the simulated stellar colours to fit the observed ones. The dust warp then appears naturally in the extinction distribution, and this dust warp is not symmetrical.
Assuming this dust warp, we then tentatively adjust the star counts on both sides of the galaxy,
to check the values of the northern and the southern warps independently.
As such, it is not possible for us to create a stellar overdensity in the model by a misalignment of the stellar and dusty warps.
Figure 3 (top panel) shows 2MASS star counts in the longitude ranges 120![]() to 60
to 60![]() and
and ![]() to
to
![]() .
They are compared with simulated star counts obtained with the simulations from the
Galaxy model (middle panel). The difference is shown in the bottom panel. In addition to the
overestimate of the warp slope, it appears that the modelled density of stars is too high at
.
They are compared with simulated star counts obtained with the simulations from the
Galaxy model (middle panel). The difference is shown in the bottom panel. In addition to the
overestimate of the warp slope, it appears that the modelled density of stars is too high at
![]() probably due to the value of the scale length hR being too high.
probably due to the value of the scale length hR being too high.
A new simulation with the lower values
![]() and
hR= 2200 pc is shown in Fig. 4.
It substantially improves the agreement between model and data at positive longitudes. The value hR=2200 pc agrees with the one determined by Robin et al. (1992) from star counts towards the anticentre.
However, the comparison is still unsatisfactory at negative longitudes.
A significant discrepancy remains, which cannot be improved by varying the assumed slope, the disc scale length, or the sun-centre distance (assumed to be here
7.9 kpc). Further testing by varying the line of nodes parameter
and
hR= 2200 pc is shown in Fig. 4.
It substantially improves the agreement between model and data at positive longitudes. The value hR=2200 pc agrees with the one determined by Robin et al. (1992) from star counts towards the anticentre.
However, the comparison is still unsatisfactory at negative longitudes.
A significant discrepancy remains, which cannot be improved by varying the assumed slope, the disc scale length, or the sun-centre distance (assumed to be here
7.9 kpc). Further testing by varying the line of nodes parameter
![]() (from
(from ![]() to
to ![]() )
shows that it cannot account for this disc asymmetry either. For the extreme values, the fit is even degraded.
)
shows that it cannot account for this disc asymmetry either. For the extreme values, the fit is even degraded.
![\begin{figure}
\par\includegraphics[height=9cm,angle=0]{1341fig4a.ps}\includegraphics[height=9cm,angle=0]{1341fig4b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg33.gif) |
Figure 4:
Same as Fig. 3 with
|
| Open with DEXTER | |
At negative longitude, this model parametrization (S-shaped warp) is clearly unsatisfactory. In an attempt to improve the fit at negative longitudes, we investigated other warp models, in particular non-axisymmetric ones. It is well known that the HI warp is asymmetric because the gas warp bends back to the Galactic plane in the southern hemisphere at R>15 kpc (Burton 1988). The stellar warp may also follow this feature.
Levine et al. (2006) studied the warp structure from HI surveys in detail and
find that the galactic HI warp is described well by a vertical offset plus two Fourier modes of frequency m=1 and 2, the m=2 mode accounting for the asymmetry.
The height of the mid plane from the ![]() plane takes the following form as a function of the azimuth
plane takes the following form as a function of the azimuth ![]() :
:
where z0, z1, and z2 are the heights of the mid plane, quadratic functions of the galactocentric radius,
With the best-fit parameters from Levine et al. (2006), the m=1 mode dominates up to about R<15 kpc. Closer to the Galactic centre the other modes are unimportant. The m=2 mode is significant at R>20 kpc. This means that the detection of these modes might not be easy with the 2MASS survey if the stellar warp follows the gas warp. Red clump giants at
![]() (the limiting magnitude of 2MASS survey) reach distances of only about 10 kpc from the Sun.
(the limiting magnitude of 2MASS survey) reach distances of only about 10 kpc from the Sun.
To test whether the stellar populations might also follow this gaseous warp, we tentatively modelled the stellar warp with the Levine et al. (2006) model. If we adopt their parameters, the simulated counts do not give an acceptable fit. However, if we adopt a closer value for the starting galactocentric radius of the m=2 mode, 12 kpc instead of 15 kpc, and reduced slopes, the fit at negative longitude is slightly better and still good at a positive longitude, although not as good as the tilted ring model with
![]() (Fig. 4). The result is shown in Fig. 5. The systematic discrepancy remains which is not explained by the two Fourier-mode warp model.
(Fig. 4). The result is shown in Fig. 5. The systematic discrepancy remains which is not explained by the two Fourier-mode warp model.
![\begin{figure}
\par\includegraphics[height=9.2cm,angle=0]{1341fig5a.ps}\includegraphics[height=9.2cm,angle=0]{1341fig5b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg39.gif) |
Figure 5: Same as Fig. 3 with the two Fourier-mode warp model from Levine et al. (2006). This model does not fit the stellar data better than the simple model and the main discrepancy at negative longitudes is not removed. |
| Open with DEXTER | |
We also investigated the possibility of a varying value for the minimum of the flare, such as proposed by Derrière & Robin (2001). However, a lower value
![]() kpc does not improve the comparison.
kpc does not improve the comparison.
A possible explanation is that the truncation in the stellar disc occurs at shorter distances on this side of the disc, since the standard truncation used on the other side of the disc (
![]() kpc)creates an overestimation of the star counts at large distances. Indeed, considering a cutoff radius
kpc)creates an overestimation of the star counts at large distances. Indeed, considering a cutoff radius
![]() kpc
slightly reduces the discrepancies at negative longitudes but still does not satisfy (see Fig. 6). Assuming a lower value for
kpc
slightly reduces the discrepancies at negative longitudes but still does not satisfy (see Fig. 6). Assuming a lower value for ![]() causes a deficit of model stars around longitudes
causes a deficit of model stars around longitudes
![]() .
At positive longitudes, the model with a disc truncation at 12 kpc does not agree as closely as a model with
.
At positive longitudes, the model with a disc truncation at 12 kpc does not agree as closely as a model with
![]() kpc. This could indicate of a varying distance for the edge of the disc as a function of the azimuth. The edge of the disc possibly follows an ellipsoidal shape instead of a circular one.
kpc. This could indicate of a varying distance for the edge of the disc as a function of the azimuth. The edge of the disc possibly follows an ellipsoidal shape instead of a circular one.
![\begin{figure}
\par\includegraphics[height=8.9cm,angle=0,clip=]{1341fig6a.ps}\includegraphics[height=8.9cm,angle=0,clip=]{1341fig6b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg45.gif) |
Figure 6: Same as Fig. 3 with a truncation of the disc at 12 kpc. The main discrepancy at negative longitudes is slightly reduced but not removed. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm,angle=0]{1341fig7a.ps}\includegraphics[width=9cm,angle=0]{1341fig7b.ps} }\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg46.gif) |
Figure 7:
Mid plane of data (thin lines) and model (thick lines) for all stars (solid lines)
and only giants (dotted lines). The simulations are obtained with
|
| Open with DEXTER | |
The mid plane of stars as a function of longitude is given by:
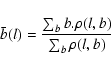
where
5 Discussion
The warp is a structure that appears in all components of the Milky Way disc: stellar, dust, and gas. Hereafter we review recent studies of these different warps and compare them.
5.1 The stellar warp
The maximum height of the mid plane at a galactocentric distance of 12 kpc is 315 pc and smaller than the one found in other studies.
The 3D model for the Milky Way fitted to the far-infrared and near-infrared data from the COBE/DIRBE instrument by Drimmel & Spergel (2001)
assumes that the displacement of the warp follows a quadratic function of the galactocentric radius,
![]() ,
with
,
with
![]() kpc. The maximum height of the plane at 12 kpc from the Galactic centre is 685 pc.
kpc. The maximum height of the plane at 12 kpc from the Galactic centre is 685 pc.
With an elevation of the stellar warp varying as a power law as a function of the galactocentric distance,
![]() ,
López-Corredoira et al. (2002) find a similar value (556 pc), based on the analysis of the old stellar population using data from the 2MASS survey.
,
López-Corredoira et al. (2002) find a similar value (556 pc), based on the analysis of the old stellar population using data from the 2MASS survey.
Momany et al. (2006) derived the structure of the stellar warp using 2MASS red clump and red giant stars selected at heliocentric distances of 3, 7, and 17 kpc. Their results agree with the Drimmel & Spergel (2001) and López-Corredoira et al. (2002) results for the southern warp, whereas the northern warp (at positive longitudes) is less pronounced. Their results agree well with the Yusifov (2004) model based on analysis of the distribution of pulsars.
They invoke two factors that may contribute to the appearance of an asymmetric warp. First, the Sun is not located on the line of nodes Yusifov (2004) find a rather high value
![]() .
Second, the northern warp is located just behind the Norma-Cygnus arm and possible variations in the extinction may produce an apparent asymmetric warp.
.
Second, the northern warp is located just behind the Norma-Cygnus arm and possible variations in the extinction may produce an apparent asymmetric warp.
Figure 8 shows the height of the galactic disc as a function of longitude at an heliocentric distance of 7 kpc (comparable to Fig. 11 in Momany et al. 2006) from these studies of the stellar warp. In contrast, our model of the northern warp agrees with Momany et al. (2006) but our southern warp is smaller than in all other studies.
![\begin{figure}
\par\includegraphics[scale=0.5,clip=]{1341fig8.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg53.gif) |
Figure 8:
Elevation of the disc mid plane as a function of longitude models at a heliocentric distance of 7 kpc from different studies. Solid line: this work
|
| Open with DEXTER | |
5.2 The dust warp
Marshall et al. (2006) detected the dust warp when converting the 3D extinction map into interstellar dust volume density. Figure 1 shows the distribution of dust at 8 kpc from the Sun as a function of longitude. The warp is clearly seen on both sides, but with significant differences. They determine the slope of this dust warp to be 0.14 at positive longitudes and 0.11 at negative ones. They also notice that the warp seems to start earlier at negative longitudes (at 7.8 kpc rather than 8.9 kpc found on the other side).The displacement at a galactocentric distance of 12 kpc is 460 pc, more than the 315 pc value found for the stellar warp in this work.
5.3 The gas warp
Nakanishi & Sofue (2003) find that the HI disc is warped and asymmetric, with more displacement at positive longitudes, in agreement with the dust warp found by Marshall et al. (2006) and the stellar warp in this work. However, the HI warp starts at a galactocentric distance of 12 kpc, which is close to the edge of the stellar disc.
Recently, Levine et al. (2006) has used a superposition of Fourier modes to describe the HI disc. The m=1 mode is dominant at distances shorter than 15 kpc. They find that this mode is nearly linear from 10 to 15 kpc, corresponding to a slope of 0.20, so much higher than what is found in the dust and stellar warps.
5.4 Comparison
These studies reveal a warp present in all components of the disc (stars, dust, gas), all of which are asymmetric and have a similar line of nodes. A comparison of the warp elevation as measured in dust, HI gas, and stars is given in Fig. 9, together with the galactocentric distance at which the warp starts. In our study, the stellar warp slope is significantly less than the HI gas warp, by a factor of about two. There indicates that the HI gas is the strongest, that the dust warp seems a bit smaller and that the stellar warp is significantly smaller; however, if we limit the investigation to short distances (R<12 kpc), the differences between various warp models are less. It is probable that the difference we find with alternate models (López-Corredoira et al. 2002; Drimmel & Spergel 2001; Momany et al. 2006) originates from remote counts at galactocentric distances between 12 and 14 kpc. This comparison tends to show that the different components react differently to the forces at the origin of the warp.
![\begin{figure}
\par\includegraphics[scale=0.5,clip]{1341fig9.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg54.gif) |
Figure 9: Maximum elevation of the disc mid plane from different warp models. Thick solid line: HI Levine et al. (2006) m=1 mode; thin solid line: stellar warp (this paper); dotted line: Marshall et al. (2006) dust model at positive longitudes; dashed line: Marshall et al. (2006) dust warp at negative longitudes. |
| Open with DEXTER | |
In external galaxies, van der Kruit (2008) note that stellar discs look flatter than gas layers. This is understandable in a scheme where the HI warps start close to the truncation radius (truncation seen in the exponential distribution of stars, which may be due to a threshold effect in the star formation efficiency). In this case the stellar warp is only visible in a narrow range of galactocentric radii. Robin et al. (1992) measured the truncation radius in our galaxy to be at about 14 kpc. This is a bit larger than where the HI warp starts, apparently at 10 to 12 kpc, and even larger than where the stellar warp starts (at ![]() 8 kpc galactocentric radius); hence the stellar warp is expected to be detected only between 8 and
14 kpc, at most.
8 kpc galactocentric radius); hence the stellar warp is expected to be detected only between 8 and
14 kpc, at most.
Van der Kruit (2008) suggests a scenario where the inner disc formed initially in a rigid and flat structure, while the HI warp resulted from later infall of gas with different orientations of angular momentum (in the case of a dark matter halo not aligned with the one of the inner Galaxy). This ongoing infall could be identified with the HI flare.
6 Conclusion
From the comparison of 2MASS star counts with a model of population synthesis in the outer regions of the Galaxy, we investigate the external disc structure and, in particular, the warp feature followed by stars. We obtain a good fit on one side of the disc with a scale length hR=2200 pc and a simple warp model following a slope of 0.09 and starting at 8.4 kpc. On the other side, at negative longitudes, the fit remains unsatisfactory either with an S-shaped warp, or a Fourier-mode shape. A shorter truncation of the disc improves the fitting a bit at negative longitudes but degrades it at positive longitudes. This could be an indication of a variation in the distance at which the stellar disc stops as a function of azimuth. Despite the uncertainties, it is clear from our study of the 2MASS star counts that the warp is less obvious in stars than in the gas, and it also shows different shapes of the disc at negative and positive longitudes. There is also a slight tendency for the dust warp to be intermediate between the HI and the stars. More studies are needed to confirm these conclusions, in particular a dynamical approach with kinematical data, which would be helpful in understanding the dynamical evolution of this structure, its origin, and its link to the gaseous warp.
Acknowledgements
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. D.J. Marshall is funded by the National Sciences and Engineering Research Council of Canada through its SRO programme. The CDSClient package was used for the remote querying of the 2MASS dataset.
References
- Bailin, J. 2003, ApJ, 583, L79 [NASA ADS] [CrossRef] (In the text)
- Bienaymé, O., Robin, A. C., & Crézé, M. 1987, A&A, 180, 94 [NASA ADS] (In the text)
- Bosma, A. 1991, in Warped Disks and Inclined Rings around Galaxies, ed. Knudsen, 181 (In the text)
- Burton, W. B., & Te Lintel Hekkert, P. 1986, A&AS, 65, 427 [NASA ADS]
- Burton, W. B. 1988, in Galactic and Extragalactic Radio Astronomy, 2nd version (Springer-Verlag), 295
- Butler, D. J., Martínez-Delgado, D., Rix, H.-W., Peñarrubia, J., & de Jong, J. T. A. 2007, AJ, 133, 2274 [NASA ADS] [CrossRef]
- de Jong, J. T. A., Butler, D. J., Rix, H. W., Dolphin, A. E., & Martínez-Delgado, D. 2007, ApJ, 662, 259 [NASA ADS] [CrossRef]
- Derrière, S., & Robin, A. C. 2001, The New Era of Wide Field Astronomy, ASP Conf. Ser., 232, 229 (In the text)
- Diplas, A., & Savage, B. D. 1991, ApJ, 377, 126 [NASA ADS] [CrossRef]
- Drimmel, R., & Spergel, D. N. 2001, ApJ, 556, 181 [NASA ADS] [CrossRef]
- Epchtein, N., Deul, E., Derriere, S., et al. 1999, A&A, 349, 236 (In the text)
- Freudenreich, H. T. 1998, ApJ, 492, 495 [NASA ADS] [CrossRef]
- Freudenreich, H. T., Berriman, G. B., Dwek, E., et al. 1994, ApJ, 429, L69 [NASA ADS] [CrossRef]
- Garcia-Ruiz, I., Kuijken, K., & Dubinski, J. 2002, MNRAS, 337, 459 [NASA ADS] [CrossRef] (In the text)
- Grabelsky, D. A., Cohen, R. S., Bronfman, L., Thaddeus, P., & May, J. 1987, ApJ, 315, 122 [NASA ADS] [CrossRef]
- Gyuk, G., Flynn, C., & Evans, N. W. 1999, ApJ, 521, 190 [CrossRef] (In the text)
- Haywood, M., Robin, A. C., & Crézé, M. 1997, A&A, 320, 440 (In the text)
- Henderson, A. P., Jackson, P. D., & Kerr, F. J. 1982, ApJ, 263, 116 [NASA ADS] [CrossRef]
- Levine, E. S., Blitz, L., & Heiles, C. 2006, ApJ, 643, 881 [NASA ADS] [CrossRef]
- López-Correidoira 2006, MNRAS, 369, 1911 [NASA ADS] [CrossRef],
- López-Corredoira, M., Cabrera-Lavers, A., Garzón, F., & Hammersley, P. L. 2002, A&A, 394, 883 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences]
- Martin, , N. F., Ibata, R. A., Bellazzini, M., et al. 2004a, MNRAS, 348, 12 [NASA ADS] [CrossRef] (In the text)
- Martin, N. F., Ibata, R. A., Conn, B. C., et al. 2004b, MNRAS, 355, L33 [NASA ADS] [CrossRef]
- Martin, N. F., Ibata, R. A., Conn, B. C., et al. 2005, MNRAS, 362, 906 [NASA ADS] [CrossRef]
- Martínez-Delgado, D., Butler, D. J., Rix, H.-W., et al. 2005, ApJ, 633, 205 [NASA ADS] [CrossRef]
- May, J., Alvarez, H., & Bronfman, L. 1997, A&A, 327, 325
- Miyamoto, M., Yoshizawa, M., & Suzuki, S. 1988, A&A, 194, 107 [NASA ADS]
- Momany, Y., Zaggia, S. R., Bonifacio, P., et al. 2004, A&A, 421, L29 [NASA ADS] [CrossRef] [EDP Sciences]
- Momany, Y., Zaggia, S., Gilmore, G., et al. 2006, A&A, 451, 515 [NASA ADS] [CrossRef] [EDP Sciences]
- Nakanishi, H., & Sofue, Y. 2003, PASJ, 55, 191 [NASA ADS]
- Picaud, S., & Robin, A. C. 2004, A&A, 428, 891 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Porcel, C., Battaner, E., & Jimenez-Vicente, J. 1997, A&A, 322, 103
- Reed, B. C. 1996, AJ, 111, 804 [NASA ADS] [CrossRef]
- Reylé, C., & Robin, A. C. 2001, A&A, 373, 886 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Robin, A. C., Crézé, M., & Mohan, V. 1992, ApJ, 400, L25 [NASA ADS] [CrossRef]
- Robin, A. C., Reylé, C., & Crézé, M. 2000, A&A, 359, 103 [NASA ADS] (In the text)
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences]; Erratum 2004, A&A, 416, 157 [CrossRef] [EDP Sciences] (In the text)
- Rocha-Pinto, H. J., Flynn, C., Scalo, J., et al. 2004, A&A, 423, 517 [NASA ADS] [CrossRef] [EDP Sciences]
- Ruphy, S., Robin, A. C., Epchtein, N., et al. 1996, A&A, 313, L21 [NASA ADS]
- Skrutskie, M. F., Cutri, R. M, Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] (In the text)
- van der Kruit, P. C. 2008, in Formation and Evolution of Galaxy Disks, ed. G. Jose, S. J. Funes, & M. C. Enrico, ASP Conf. Ser. (In the text)
- Weinberg, M. D., & Blitz, L. 2006, ApJ, 641, L33 [NASA ADS] [CrossRef] (In the text)
- Wouterlout, J. G. A., Brand, J., Burton, W. B., & Kwee, K. K. 1990, A&A, 230, 21 [NASA ADS]
- Yusifov, I. 2004, in The Magnetized Interstellar Medium. Copernicus GmbH, Katlenburg-Lindau, ed. B. Uyaniker, W. Reich, & R. Wielebinski, 165 (In the text)
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=9cm]{1341fig1a.ps}\includegraphics[width=9cm]{1341fig1b.ps} }\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg10.gif) |
Figure 1: Warp in the dust as seen from the Marshall et al. (2006) 3D extinction map. The plot shows the density of absorbing material at 8 kpc from the sun, as a function of longitude and latitude. The dashed line is the position of the mid-plane expected from a 0.18 slope warp model, and the solid line the position from the fitted slope of 0.14 at positive longitudes and 0.11 at negative longitudes. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Comparison between the number of stars from the Galaxy model
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=9.5cm,angle=0]{1341fig3a.ps}\includegraphics[height=9.5cm,angle=0]{1341fig3b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg24.gif) |
Figure 3:
2MASS star counts ( top), modelled ones ( middle), and relative difference between the two ( bottom) with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=9cm,angle=0]{1341fig4a.ps}\includegraphics[height=9cm,angle=0]{1341fig4b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg33.gif) |
Figure 4:
Same as Fig. 3 with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=9.2cm,angle=0]{1341fig5a.ps}\includegraphics[height=9.2cm,angle=0]{1341fig5b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg39.gif) |
Figure 5: Same as Fig. 3 with the two Fourier-mode warp model from Levine et al. (2006). This model does not fit the stellar data better than the simple model and the main discrepancy at negative longitudes is not removed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.9cm,angle=0,clip=]{1341fig6a.ps}\includegraphics[height=8.9cm,angle=0,clip=]{1341fig6b.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg45.gif) |
Figure 6: Same as Fig. 3 with a truncation of the disc at 12 kpc. The main discrepancy at negative longitudes is slightly reduced but not removed. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm,angle=0]{1341fig7a.ps}\includegraphics[width=9cm,angle=0]{1341fig7b.ps} }\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg46.gif) |
Figure 7:
Mid plane of data (thin lines) and model (thick lines) for all stars (solid lines)
and only giants (dotted lines). The simulations are obtained with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.5,clip=]{1341fig8.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg53.gif) |
Figure 8:
Elevation of the disc mid plane as a function of longitude models at a heliocentric distance of 7 kpc from different studies. Solid line: this work
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.5,clip]{1341fig9.ps}
\end{figure}](/articles/aa/full_html/2009/09/aa11341-08/Timg54.gif) |
Figure 9: Maximum elevation of the disc mid plane from different warp models. Thick solid line: HI Levine et al. (2006) m=1 mode; thin solid line: stellar warp (this paper); dotted line: Marshall et al. (2006) dust model at positive longitudes; dashed line: Marshall et al. (2006) dust warp at negative longitudes. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


