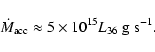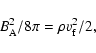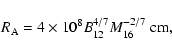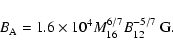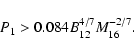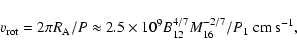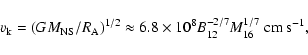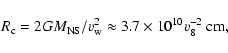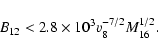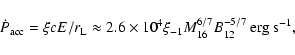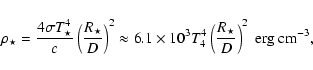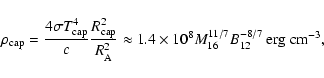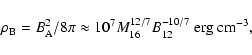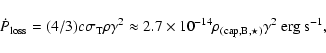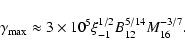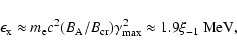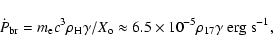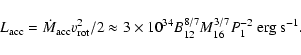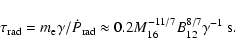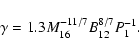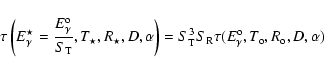| Issue |
A&A
Volume 495, Number 3, March I 2009
|
|
|---|---|---|
| Page(s) | 919 - 929 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:200811063 | |
| Published online | 20 January 2009 | |
Gamma-rays from the vicinity of accreting neutron stars inside compact high-mass X-ray binaries
W. Bednarek
Department of Astrophysics, University of ![]() ódz,
90-236
ódz,
90-236 ![]() ódz, ul. Pomorska 149/153, Poland
ódz, ul. Pomorska 149/153, Poland
Received 1 October 2008 / Accepted 22 November 2008
Abstract
The dense wind of a massive star can be captured partially by a neutron star (NS)
inside a compact binary system. Depending on the parameters of the NS and the wind, the matter can penetrate the inner NS magnetosphere. At some distance from the NS, a turbulent and magnetized transition region is formed due to the balance between the magnetic pressure and the pressure inserted by accreting matter. This region provides good conditions for acceleration of particles to relativistic energies.
The matter at the transition region can farther accrete onto the NS surface (the accretor phase) or be expelled from the NS vicinity (the propeller phase). We consider the consequences of the acceleration of electrons at the transition region, concentrating on the situation in which at least part of the matter falls onto the NS surface. This matter creates a hot spot on the NS surface which emits thermal radiation.
Relativistic electrons lose energy to the synchrotron process and the inverse Compton (IC) scattering of this thermal radiation. We calculate the synchrotron spectra (from X-rays to soft ![]() -rays) and IC spectra (above a few tens of MeV) expected in this scenario. We argue that a population of massive binaries discovered by the INTEGRAL observatory, which contain neutron stars hidden inside dense stellar winds of massive stars, is detectable by the Fermi LAT telescope in the GeV energy
range. As an example, we predict the expected
-rays) and IC spectra (above a few tens of MeV) expected in this scenario. We argue that a population of massive binaries discovered by the INTEGRAL observatory, which contain neutron stars hidden inside dense stellar winds of massive stars, is detectable by the Fermi LAT telescope in the GeV energy
range. As an example, we predict the expected ![]() -ray flux from the source IGR J19140+0951.
-ray flux from the source IGR J19140+0951.
Key words: radiation mechanisms: non-thermal - gamma-rays: theory - X-rays: binaries - stars: binaries: close - stars: neutron
1 Introduction
Massive binary systems, containing a compact object (neutron star or black hole), have long been suspected as being the sites of particle acceleration up to at least TeV energies. Three different type of these objects have now been confirmed as VHE ![]() -ray sources by Cherenkov telescopes. It is clear that at least in one case the
-ray sources by Cherenkov telescopes. It is clear that at least in one case the ![]() -ray emission is due to the acceleration of particles
as a result of the interaction of the energetic pulsar wind with the wind of a massive star.
Other TeV
-ray emission is due to the acceleration of particles
as a result of the interaction of the energetic pulsar wind with the wind of a massive star.
Other TeV ![]() -ray binaries operate either under this same general scenario or the acceleration of particles occurs in the jet launched by the compact object.
In the case of these TeV
-ray binaries operate either under this same general scenario or the acceleration of particles occurs in the jet launched by the compact object.
In the case of these TeV ![]() -ray binaries, the neutron star (pulsar) should rotate sufficiently fast to produce an energetic pulsar wind.
-ray binaries, the neutron star (pulsar) should rotate sufficiently fast to produce an energetic pulsar wind.
In this paper we consider the case of the neutron star is not so energetic that the matter from the stellar wind can penetrate into the inner pulsar magnetosphere. At certain distances from the NS surface, the magnetic pressure balances the
pressure of accreting matter, creating a turbulent transition region. The NS is then enshrouded in a dense cocoon resembling objects called hidden pulsars (see e.g. Tavani 1991; Tavani & Brookshow 1993) or cauldrons (Begelman & Rees 1984; Treves et al. 1993). We note that ![]() -ray emission was predicted from hidden pulsars (Tavani 1993). We study the case in which the electrons are accelerated inside a turbulent, strongly-magnetized, transition region within the inner pulsar magnetosphere. In principle, electrons can reach even
-ray emission was predicted from hidden pulsars (Tavani 1993). We study the case in which the electrons are accelerated inside a turbulent, strongly-magnetized, transition region within the inner pulsar magnetosphere. In principle, electrons can reach even ![]() TeV energies
but, as we show below, due to significant synchrotron energy losses, only
TeV energies
but, as we show below, due to significant synchrotron energy losses, only ![]() -rays in the Fermi LAT telescope energy range may be effectively produced.
-rays in the Fermi LAT telescope energy range may be effectively produced.
The INTEGRAL observatory appears to have discovered a class of compact, high-mass X-ray binaries (see e.g. Chaty et al. 2008; Rodriquez & Bodaghee 2008) that exhibit a mechanism discussed in this paper. These newly discovered massive binaries are compact with orbital periods between a few to several days. Some contain relatively slowly rotating neutron stars that may allow the matter to penetrate the inner NS magnetosphere. According to the classification scheme of X-ray binaries (e.g. Lipunov 1992). These binaries with slowly rotating neutron stars (NS) belong to the propeller and accretor class. In these objects, the matter of the dense stellar wind accretes onto the strongly magnetized NS, interacting with the rigidly rotating inner magnetosphere. In the case of an accretor, most of the matter reaches the NS surface. In the case of a propeller, most of the matter is expelled from the NS vicinity, due to the centrifugal force.
We propose that this general scenario can be applied to a type of obscured compact objects inside massive binaries that has been observed by the INTEGRAL observatory. We perform detailed calculations of the ![]() -rays spectra, including in some cases the inverse Compton (IC) e
-rays spectra, including in some cases the inverse Compton (IC) e![]() pair cascade initiated by relativistic electrons in the radiation field produced on the neutron-star surface. We also account for the synchrotron energy losses of primary electrons and cascade e
pair cascade initiated by relativistic electrons in the radiation field produced on the neutron-star surface. We also account for the synchrotron energy losses of primary electrons and cascade e![]() pairs, to obtain simultaneous synchrotron X-ray spectra. In this scenario, the acceleration of hadrons and the possible production of high energy
pairs, to obtain simultaneous synchrotron X-ray spectra. In this scenario, the acceleration of hadrons and the possible production of high energy ![]() -rays, neutrinos, and neutrons will be discussed in another paper.
-rays, neutrinos, and neutrons will be discussed in another paper.
2 Description of the model
We consider a compact binary system containing a rotating neutron star (NS) and a massive, companion O,B type star. It is assumed that mass from the stellar wind is effectively captured by the strong gravitational potential of the NS. These slowly rotating neutron stars appear at a certain stage of the evolution of the binary system due to the loss of angular momentum either by the pulsar mechanism or as a result of the torque exhibited by the matter accreted from the stellar wind. Depending on the rotational period and surface magnetic field of NS, the accretion process onto the NS can occur in different phases. According to the classification scheme of Lipunov (1992), the accretion process can occur in the phase of accretor (for relatively slower rotators) or in the phase of propeller. For energetic, strongly magnetized and short-period, neutron stars, the accretion process does not occur at all since the matter cannot penetrate below the light cylinder radius. In the case of NS in the accretor and propeller phases, matter from the stellar wind penetrates below the light cylinder radius of the rotating NS magnetosphere. This matter extracts rotational energy from the NS as a result of the interaction of free-falling matter with the rigidly rotating inner NS magnetosphere. In this paper, we consider the direct collision of matter from the stellar wind with the NS magnetosphere (see the general scenario depicted in Fig. 1). As a result of this interaction, a turbulent, magnetized transition region is formed. In the case of the accretor, most of the matter falls onto the NS surface creating a small hot region on the NS surface. In the case of the propeller, most of the matter is expelled from the vicinity of the NS. It is expected that the matter might be also able to accrete in this stage. This would, however, be non-stationary form since, due to the gradual accumulation of matter close to the transition region, the pressure of the matter can overcome the pressure from the rotating magnetosphere. It is supposed that some amount of the matter can accrete but most of it is expelled from the binary system (possibly forming larger scale jets?) for some specific transition parameters describing the accretor/propeller scenario.
We note that in some massive binaries (e.g. Her X-1), the accretion of matter can also occur by the Roche lobe overflow. The accretion disk around the NS is then formed before the matter from the disk interacts directly with the NS magnetosphere. In this paper, we do not discuss this possibility but instead concentrate on a simpler quasi-spherical accretion onto magnetized NS of the matter from the dense wind of the massive star. The accretion from the disk can be easily taken into account in our scenario by introducing a geometrical factor that describes the part of the sphere in which the accretion occurs. Therefore, the accretion from the disk corresponds to one of our discussed cases with an effectively higher accretion rate occurring only inside a limited region determined by the thickness of the accretion disk.
| |
Figure 1:
Schematic representation of the model discussed in this paper.
The wind from a massive star penetrates the inner magnetosphere of a neutron star.
As a result of the interaction of the wind with the dipole magnetic field of the NS, a strongly magnetized turbulent region is created (thick solid curve) in which the matter gains energy by being accelerated to the velocity of the rotating magnetic-field lines. Electrons (e) are accelerated in this turbulent transition region and cool by means of the synchrotron process and the Comptonization of thermal radiation (marked by X), emitted from the stellar surface around the magnetic-pole region. As a result, the first generation of IC |
| Open with DEXTER | |
We first consider the case of the NS in the phase of pure accretor.
The accretion rate of the matter onto the neutron star (
![]() g s-1) can be estimated from the observed (in some cases) thermal X-ray emission (
g s-1) can be estimated from the observed (in some cases) thermal X-ray emission (
![]() erg s-1).
erg s-1).
![]() and
and ![]() can by related to the known radius and mass of the NS (we assume
can by related to the known radius and mass of the NS (we assume
![]() cm and
cm and
![]() ),
),
This matter arrives onto the neutron star surface along the magnetic-field lines. The distance at which the magnetic field begins to dominate the dynamics of the matter (the Alfven radius) can be estimated by comparing the magnetic-field energy density with the kinetic-energy density of the matter,
where
where the magnetic field at the neutron-star surface is
We consider that the accretor scenario can occur provided the neutron star fulfills some conditions. First, the radius of the transition region must be inside the light cylinder radius of the neutron star, i.e.
Therefore, only relatively slowly rotating neutron stars can be considered.
Second, the rotational velocity of the magnetosphere at ![]() must then be lower than the Keplerian velocity of the accreting matter. The rotational velocity,
must then be lower than the Keplerian velocity of the accreting matter. The rotational velocity,
is lower than the Keplerian velocity,
for the NS with the periods,
This last condition separates the population of NS in the propeller phase (lower periods) from those in the accretor phase (larger periods). We note, that the scenario discussed below for acceleration of electrons can also be applied to the propeller stage of accretion onto the NS. However, in the propeller phase, the radiation field created by the matter accreting onto the NS is not uniquely defined. Part of the matter being accreted onto a NS cannot presently be linked to the basic parameters describing the model. We must introduce additional factor describing the amount of the matter that falls onto the NS surface and the total amount of the matter penetrating the inner NS magnetosphere (i.e accreting and being expelled from the vicinity of the NS).
The third condition relates the radius of the transition region, ![]() ,
to the capturing radius of the matter from the stellar wind. It is determined by the balance between the kinetic energy of the wind and its gravitational energy around the NS. The capturing radius is described by,
,
to the capturing radius of the matter from the stellar wind. It is determined by the balance between the kinetic energy of the wind and its gravitational energy around the NS. The capturing radius is described by,
where
For likely parameters of the neutron stars (classical and millisecond pulsars), this limit is not restrictive. We note that
Neutron stars of periods within the range defined by Eqs. (5) and (8) are in the propeller phase, those of period above that given by Eq. (8) are in the accretor phase, and those of period shorter than given by Eq. (5) are in the ejector phase. As already noted, the accretion rate can be linked directly to the thermal X-ray emission from the NS surface only in the accretor phase. In the propeller phase, the amount of the matter accreting onto the NS surface cannot be uniquely determined from the basic parameters of the model.
2.1 Acceleration of electrons
In the conditions expected for the transition region (a strongly magnetized and turbulent medium), particles should be efficiently accelerated. In this paper, we consider only the acceleration of electrons. The energy gain rate of electrons with energy E (and the Lorentz factor ![]() )
is often parametrized by the Larmor radius of electrons and the so-called acceleration parameter,
)
is often parametrized by the Larmor radius of electrons and the so-called acceleration parameter,
where
Electrons lose energy with the IC process in the Thomson (T) and the Klein-Nishina (KN) regimes. In general, this process can affect the stellar radiation and the thermal X-ray radiation from the surface of the polar cap on the NS. We estimate the photon energy densities from the star (
![]() )
and the polar cap (
)
and the polar cap (
![]() )
at the acceleration region to be,
)
at the acceleration region to be,
(where
where
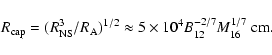 |
(14) |
The surface temperature of the polar cap is then,
 |
(15) |
We note that, the energy density of radiation from the polar cap at the distance of the turbulent region (
We also estimate the energy density of the magnetic field at the transition region (![]() given by Eq. (3)) to be,
given by Eq. (3)) to be,
The energy losses of electrons due to each of the considered process (synchrotron and IC in the T regime) can be calculated from,
where
The energy losses of electrons emitted as radiation from the NS surface can dominate over energy losses from other targets only at low energies, i.e. when the scattering occurs in the T regime for Lorentz factors of electrons equal to,
![]() .
In the KN regime, the energy losses can be estimated approximately by introducing into Eq. (17) the value of the Lorentz factor corresponding to the transition between the T and KN regimes,
.
In the KN regime, the energy losses can be estimated approximately by introducing into Eq. (17) the value of the Lorentz factor corresponding to the transition between the T and KN regimes,
![]() .
For the range of parameters defining the model, the IC energy losses of electrons in the KN regime becomes lower than the synchrotron energy losses for Lorentz factors about a factor of ten higher than
.
For the range of parameters defining the model, the IC energy losses of electrons in the KN regime becomes lower than the synchrotron energy losses for Lorentz factors about a factor of ten higher than
![]() (typically at
(typically at ![]() GeV energies). Therefore the maximum energies of accelerated electrons are determined by the balance between energy gains from the acceleration process (Eq. (11)) and energy losses due to synchrotron processes (Eq. (17)),
GeV energies). Therefore the maximum energies of accelerated electrons are determined by the balance between energy gains from the acceleration process (Eq. (11)) and energy losses due to synchrotron processes (Eq. (17)),
It is clear that electrons can reach even TeV energies (see Fig. 2a) for realistic parameters of the model. However, TeV
We can also estimate the characteristic energies of synchrotron photons expected in such a model by applying the approximate formula,
where
We note that the bremsstrahlung energy losses of relativistic electrons in the matter inside the transition region can be neglected since their energy-loss rate is relatively low,
where
| |
Figure 2:
The maximum energies of accelerated electrons a) and the maximum power that can be transferred to these electrons b) as a function of the accretion rate of the matter
from the massive star onto the neutron star. The results are shown for the neutron stars that have the surface magnetic field
B = 1012 G (solid line), and B = 109 G (dashed). The acceleration parameter is equal to
|
| Open with DEXTER | |
2.2 Energetics
The maximum power available for acceleration of electrons is limited by the energy
extracted from the rotating neutron star by the infalling matter. This matter from the stellar wind has to be accelerated to the velocity of the magnetic field lines at ![]() in order to accrete farther onto the neutron-star surface. The power that must be transferred from the rotating NS to the matter can be estimated from
in order to accrete farther onto the neutron-star surface. The power that must be transferred from the rotating NS to the matter can be estimated from
By using the limiting period given by Eq. (8), we derive the upper limit to the available power in the accretor stage,
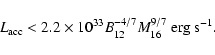 |
(22) |
This power is shown in Fig. 2b for two example surface magnetic-field strengths of the neutron star (classical NS:
The model discussed above for the accretor stage of the binary system is also applicable to the propeller stage in which only a fraction of the matter can eventually accrete onto the surface of the NS. However, in this case it is difficult to estimate the power transferable to relativistic particles due to the unknown observational signatures of matter accumulating close to the shock region.
In summary, electrons can be accelerated even to TeV energies in the case of neutron stars inside X-ray binaries with relatively weak thermal X-ray emission
from their surface, in contrast to the powerful X-ray binaries for which only a few tens GeV energy electrons are expected. However, the situation is the opposite concerning the maximum power transferred to these relativistic electrons. Sources in which electrons are accelerated only to GeV energies should be powerful enough to be observable by the ![]() -ray telescopes.
-ray telescopes.
3 Production of radiation
We assume that electrons are accelerated in the turbulent transition region with a power-law spectrum to maximum energies estimated from Eq. (18). Eventually, the spectrum of electrons can be strongly peaked at the highest possible energies due to the synchrotron energy losses during acceleration process (the so called pile-up mechanism: see e.g.
Protheroe 2004). As shown above, electrons lose energy by means of different radiation mechanisms of which the dominant ones are
the synchrotron process (dominates at the highest energies) and the ICS of thermal radiation from the NS polar cap (which contributes at the high energies in the KN regime and dominates at lower energies in the T regime).
We neglect the production of ![]() -rays by electrons in the acceleration region in the
scattering of stellar radiation since its energy density can be safely neglected with respect to the energy density of the magnetic field (at high energies) and the energy density of polar cap radiation (at low energies) (see Sect. 2.1).
To confirm whether electrons can lose energy efficiently already in the transition region, we estimate the convection timescale when matter is falling onto the NS surface along the open magnetic-field lines to be,
-rays by electrons in the acceleration region in the
scattering of stellar radiation since its energy density can be safely neglected with respect to the energy density of the magnetic field (at high energies) and the energy density of polar cap radiation (at low energies) (see Sect. 2.1).
To confirm whether electrons can lose energy efficiently already in the transition region, we estimate the convection timescale when matter is falling onto the NS surface along the open magnetic-field lines to be,
We compare this timescale with the radiation timescale, which (for electrons with sufficiently low energies) is determined by the IC losses (in T regime) in the radiation field from the polar cap of the NS,
From this comparison, we estimate the lower limit to the Lorentz factor of electrons losing energy efficiently before being convected onto the NS surface to be,
We conclude that relativistic electrons lose their energy close to the place of acceleration.
To calculate the ![]() -ray spectra produced by electrons inside the transition region, we simulate the energy-loss process of electrons in the radiation field of the polar cap and at the magnetic field of the transition region by applying the Monte Carlo method. It is assumed that the magnetic field is turbulent in the transition region
(the distribution of electrons is isotropic) and that the radiation field originates in the region of the polar cap. For some range of model parameters, IC
-ray spectra produced by electrons inside the transition region, we simulate the energy-loss process of electrons in the radiation field of the polar cap and at the magnetic field of the transition region by applying the Monte Carlo method. It is assumed that the magnetic field is turbulent in the transition region
(the distribution of electrons is isotropic) and that the radiation field originates in the region of the polar cap. For some range of model parameters, IC ![]() -rays can be absorbed farther into the radiation field of the polar cap. In this way the IC e
-rays can be absorbed farther into the radiation field of the polar cap. In this way the IC e![]() pair cascade initiates. To determine the conditions for the cascade process, we calculate the optical depths for
pair cascade initiates. To determine the conditions for the cascade process, we calculate the optical depths for ![]() -ray photons in the radiation of the polar cap in Sect. 4. We also calculate the optical depths of
-ray photons in the radiation of the polar cap in Sect. 4. We also calculate the optical depths of ![]() -rays in the radiation field of the massive companion to check whether this
-rays in the radiation field of the massive companion to check whether this ![]() -ray absorption process should also be taken into account when evaluating the
-ray absorption process should also be taken into account when evaluating the ![]() -ray spectra escaping from the binary system.
-ray spectra escaping from the binary system.
4 Optical depths for  -rays
-rays
As we argued above, the cooling of electrons in strong magnetic and radiation fields occurs efficiently. High energy ![]() -ray produced in the ICS of thermal photons from the polar cap can also be absorbed in this same radiation field
and, in principle, also in the radiation field of the close massive companion star. Below, we calculate the optical depths of the
-ray produced in the ICS of thermal photons from the polar cap can also be absorbed in this same radiation field
and, in principle, also in the radiation field of the close massive companion star. Below, we calculate the optical depths of the ![]() -ray photons in these two radiation fields. We demonstrate that for specific conditions (determined mainly by the accretion rate onto the NS and the parameters of the NS), the
-ray photons in these two radiation fields. We demonstrate that for specific conditions (determined mainly by the accretion rate onto the NS and the parameters of the NS), the ![]() -ray spectrum emerging from the binary system is in fact formed in the cascade process occurring in the radiation field of the polar cap.
-ray spectrum emerging from the binary system is in fact formed in the cascade process occurring in the radiation field of the polar cap.
4.1 Polar cap radiation
We calculate the optical depths for ![]() -rays by assuming that they are produced by electrons in the transition region at a distance
-rays by assuming that they are produced by electrons in the transition region at a distance ![]() from the stellar surface. In these calculations, we assume the diluted black-body spectrum for the polar-cap emission with the dilution factor
at the production site of
from the stellar surface. In these calculations, we assume the diluted black-body spectrum for the polar-cap emission with the dilution factor
at the production site of ![]() -rays estimated to be
-rays estimated to be
![]() .
The average optical depths (averaged isotropically for injected
.
The average optical depths (averaged isotropically for injected ![]() -rays) for different accretion rates onto the neutron star (i.e. equivalent to different X-ray luminosities, see Eq. (1)) are shown in Fig. 3.
It is clear that for low accretion rates (<1016 g s-1), when electrons can be accelerated to
-rays) for different accretion rates onto the neutron star (i.e. equivalent to different X-ray luminosities, see Eq. (1)) are shown in Fig. 3.
It is clear that for low accretion rates (<1016 g s-1), when electrons can be accelerated to ![]() TeV energies, the optical depths for
TeV energies, the optical depths for ![]() -ray photons are relatively low, i.e. they are below unity for energies above
-ray photons are relatively low, i.e. they are below unity for energies above ![]() 10 GeV. In this case, GeV-TeV
10 GeV. In this case, GeV-TeV ![]() -rays can escape from the radiation field of the polar cap without significant absorption.
-rays can escape from the radiation field of the polar cap without significant absorption.
On the other hand, for high accretion rates (>1016 g s-1), electrons are accelerated at most to a few tens of GeV. The ![]() -rays produced by these electrons should be efficiently absorbed by means of the radiation of the polar cap. Therefore, in this case the escaping
-rays produced by these electrons should be efficiently absorbed by means of the radiation of the polar cap. Therefore, in this case the escaping ![]() -ray spectra can be obtained only by calculating complicated IC e
-ray spectra can be obtained only by calculating complicated IC e![]() pair cascade within the radiation originating in the polar cap.
We conclude that for high accretion rates,
pair cascade within the radiation originating in the polar cap.
We conclude that for high accretion rates, ![]() -rays, produced in this model, could be observable by the satellite telescopes (
-rays, produced in this model, could be observable by the satellite telescopes (
![]() LAT and possibly AGILE).
LAT and possibly AGILE).
![\begin{figure}
\par\includegraphics[width=6.8cm,height=5cm,clip]{1063fi3a.eps}\p...
...{2mm}
\includegraphics[width=6.8cm,height=5.7cm,clip]{1063fi3b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg110.gif) |
Figure 3:
The optical depths for |
| Open with DEXTER | |
4.2 Massive-star radiation
![\begin{figure}
\par\includegraphics[width=6.8cm,height=5cm,clip]{1063fi4b.eps}\p...
...{2mm}
\includegraphics[width=6.8cm,height=5.7cm,clip]{1063fi4a.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg113.gif) |
Figure 4:
The optical depths as a function of |
| Open with DEXTER | |
The optical depths at ![]() -ray photons injected at an arbitrary distance from the surface of the massive star were calculated for the first time in the general case (including also dimensions of the star) by Bednarek (1997, 2000). The optical depths for
-ray photons injected at an arbitrary distance from the surface of the massive star were calculated for the first time in the general case (including also dimensions of the star) by Bednarek (1997, 2000). The optical depths for ![]() -rays close to the surface of other stars can be easily rescaled from those early calculations. For example,
-rays close to the surface of other stars can be easily rescaled from those early calculations. For example, ![]() -ray photons
with energies,
-ray photons
with energies,
![]() ,
propagating at specific
distances D and in directions (defined by the angle
,
propagating at specific
distances D and in directions (defined by the angle ![]() )
close to the star
with specific parameters (
)
close to the star
with specific parameters (![]() and
and ![]() )
are related to the optical depths
around arbitrary stars with
)
are related to the optical depths
around arbitrary stars with ![]() and
and ![]() in the following way,
in the following way,
where
5 Gamma-rays from the vicinity of an accreting neutron star
In the considered model, radiation is produced by electrons
accelerated to their maximum energies, estimated by Eq. (18) for the synchrotron and IC processes. Synchrotron energy losses dominate at the highest electron energies (close to
![]() ), and the IC process can dominate only at lower energies due to the KN cross section. However, as we have shown above, for high accretion rates,
), and the IC process can dominate only at lower energies due to the KN cross section. However, as we have shown above, for high accretion rates, ![]() -rays produced by electrons can be absorbed farther by the thermal radiation from the NS surface.
In Fig. 3 we show the average optical depths for the
-rays produced by electrons can be absorbed farther by the thermal radiation from the NS surface.
In Fig. 3 we show the average optical depths for the ![]() -rays in the thermal radiation from the NS polar cap in order to envisage for what parameters the cascading effects can become important.
Therefore, in these cases we must consider the production of the
-rays in the thermal radiation from the NS polar cap in order to envisage for what parameters the cascading effects can become important.
Therefore, in these cases we must consider the production of the ![]() -rays in the IC e
-rays in the IC e![]() pair cascade with additional synchrotron energy losses of primary electrons and secondary e
pair cascade with additional synchrotron energy losses of primary electrons and secondary e![]() pairs. On the other hand, for low accretion rates, the cascade does not develop, and
pairs. On the other hand, for low accretion rates, the cascade does not develop, and ![]() -rays are produced only as a result of the cooling of primary electrons. To follow the process of
-rays are produced only as a result of the cooling of primary electrons. To follow the process of ![]() -ray production, we developed a numerical code that simulates the
cooling process of electrons by taking into account not only the
-ray production, we developed a numerical code that simulates the
cooling process of electrons by taking into account not only the ![]() -ray production in the IC process but also the synchrotron-energy losses of primary electrons and secondary cascade e
-ray production in the IC process but also the synchrotron-energy losses of primary electrons and secondary cascade e![]() pairs. We note that the acceleration of electrons occurs inside the inner pulsar magnetosphere, where the magnetic field is relatively strong and depends on the distance of the turbulent transition region from the NS surface. Since the synchrotron process dominates over the IC process in the high energy part of the injected electron spectrum,
the
pairs. We note that the acceleration of electrons occurs inside the inner pulsar magnetosphere, where the magnetic field is relatively strong and depends on the distance of the turbulent transition region from the NS surface. Since the synchrotron process dominates over the IC process in the high energy part of the injected electron spectrum,
the ![]() -rays are rarely produced with energies comparable to the energies of primary electrons. Our IC e
-rays are rarely produced with energies comparable to the energies of primary electrons. Our IC e![]() pair cascade code with synchrotron-energy losses provides both the synchrotron and the IC spectra expected in such a model.
pair cascade code with synchrotron-energy losses provides both the synchrotron and the IC spectra expected in such a model.
Two models for injection of relativistic electrons are considered:
- 1.
- electrons injected with a power-law spectrum up to a maximum
Lorentz factor
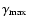 (see Eq. (18)), as expected in the
stochastic acceleration mechanism. The power-law spectrum of primary electrons
is normalized to correspond to a fraction,
(see Eq. (18)), as expected in the
stochastic acceleration mechanism. The power-law spectrum of primary electrons
is normalized to correspond to a fraction, 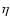 ,
of the kinetic power transferred from the rotating neutron star to the matter in the transition region;
,
of the kinetic power transferred from the rotating neutron star to the matter in the transition region;
- 2.
- electrons injected with the Lorentz factors
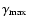 .
This injection spectrum provides a good approximation to the cases of acceleration processes occurring with large radiative-energy losses (the accumulation mechanism at the high end of accelerated power law spectrum of electrons; see e.g. Protheroe 2004).
.
This injection spectrum provides a good approximation to the cases of acceleration processes occurring with large radiative-energy losses (the accumulation mechanism at the high end of accelerated power law spectrum of electrons; see e.g. Protheroe 2004).
We investigate two general scenarios describing the cases of pure accretor phase (where all the matter arriving at the transition region falls onto the NS surface) and the intermediate accretor-propeller phase (where only part of the matter arriving at the transition region accretes onto the NS surface and the remainder is expelled from the vicinity of the NS by the propeller mechanism).
5.1 The accretor stage
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.2cm,clip]{1063fi5a.eps}...
...}
\includegraphics[width=7.4cm,height=5.8cm,clip]{1063fi5f.eps}
\par\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg124.gif) |
Figure 5:
The IC |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.8cm,clip]{1063fi6a.eps}...
...{4mm}
\includegraphics[width=7.5cm,height=5.8cm,clip]{1063fi6b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg125.gif) |
Figure 6:
As in Fig. 5 but for different spectral indexes of injected electrons:
s = 4 (dashed), 3 (dotted), 2.2 (solid), 1 (dot-dashed). The parameters describing the model are the following: |
| Open with DEXTER | |
The scenario for the accretion process onto a neutron star in the accretor stage is far more precisely defined, since the thermal radiation field from the NS surface (depending on the dimensions of the hot spot and its temperature) is uniquely determined by the parameters describing the model.
Therefore, the synchrotron and IC spectra produced by electrons depends on a relatively small number of free parameters, i.e. the accretion rate onto NS, the surface magnetic field of NS, and the acceleration rate ![]() .
The observed X-ray to
.
The observed X-ray to ![]() -ray power
depends additionally on the parameter,
-ray power
depends additionally on the parameter,
![]() ,
which combines the energy-conversion efficiency from the transition region to relativistic electrons,
,
which combines the energy-conversion efficiency from the transition region to relativistic electrons, ![]() ,
and the distance to the source D = 1D1 kpc.
At first, we performed calculations for the power-law spectrum of injected electrons
,
and the distance to the source D = 1D1 kpc.
At first, we performed calculations for the power-law spectrum of injected electrons
![]() between
between
![]() and
and
![]() ,
where A is the
normalization coefficient that equals
,
where A is the
normalization coefficient that equals
![]() .
We note, that only A depends weakly on
.
We note, that only A depends weakly on
![]() for the spectral indices of approximately 2. In our example calculations, we apply a spectral index equal to 2.2 and select
for the spectral indices of approximately 2. In our example calculations, we apply a spectral index equal to 2.2 and select
![]() MeV, since we reduce the energies of these electrons only to these minimum energies. Electrons with such energies are unable to produce
MeV, since we reduce the energies of these electrons only to these minimum energies. Electrons with such energies are unable to produce ![]() -rays detectable by the Fermi LAT.
The simulated spectra are also shown for different values of
-rays detectable by the Fermi LAT.
The simulated spectra are also shown for different values of ![]() ,
,
![]() ,
and B (see Fig. 5).
,
and B (see Fig. 5).
In Figs. 5a-d, we consider the case of a classical relatively young NS (![]() G), rotating with the limiting period defined by Eq. (8). When considering the sensitivity of the Fermi LAT telescope, it becomes clear that
G), rotating with the limiting period defined by Eq. (8). When considering the sensitivity of the Fermi LAT telescope, it becomes clear that ![]() -ray emission from these objects can be detected at energies below
-ray emission from these objects can be detected at energies below ![]() 1 GeV only in the case of high accretion rates (significantly above 1016 g s-1). The power-law synchrotron spectra corresponding to these accretion rates should also be easily detected by soft and hard X-ray detectors presently on the orbit. Note that due to strong magnetic field and large energies of primary electrons, the synchrotron spectra can extend in some cases also through the soft
1 GeV only in the case of high accretion rates (significantly above 1016 g s-1). The power-law synchrotron spectra corresponding to these accretion rates should also be easily detected by soft and hard X-ray detectors presently on the orbit. Note that due to strong magnetic field and large energies of primary electrons, the synchrotron spectra can extend in some cases also through the soft ![]() -ray energy range.
In Figs. 5e,f, we show the synchrotron and IC spectra for the case of a NS with a low surface magnetic field, characteristic of so-called millisecond pulsars. In the case of these slowly magnetized neutron stars,
-ray energy range.
In Figs. 5e,f, we show the synchrotron and IC spectra for the case of a NS with a low surface magnetic field, characteristic of so-called millisecond pulsars. In the case of these slowly magnetized neutron stars, ![]() -ray emission can also be detected by the Fermi LAT telescope, provided that the accretion rate onto the NS is above a few 1014 g s-1. We conclude that
-ray emission can also be detected by the Fermi LAT telescope, provided that the accretion rate onto the NS is above a few 1014 g s-1. We conclude that ![]() -ray telescopes presently in orbit should be able to detect
-ray telescopes presently in orbit should be able to detect ![]() -ray emission of energies of a few hundred MeV from the class of accreting NS. These NS are characterized by
thermal emission from its surface at a level of above
-ray emission of energies of a few hundred MeV from the class of accreting NS. These NS are characterized by
thermal emission from its surface at a level of above ![]()
![]() erg s-1 in the case of strongly magnetized neutron stars, and above a few 1034 erg s-1 in the case of a NS with a magnetic field characteristic of millisecond pulsars provided that the source is at a distance of 1 kpc. These limiting X-ray luminosities were derived by using the relation between the accretion rate and the thermal emission from the NS surface (see Eq. (1)).
erg s-1 in the case of strongly magnetized neutron stars, and above a few 1034 erg s-1 in the case of a NS with a magnetic field characteristic of millisecond pulsars provided that the source is at a distance of 1 kpc. These limiting X-ray luminosities were derived by using the relation between the accretion rate and the thermal emission from the NS surface (see Eq. (1)).
We also investigate how the detectability of these accreting NSs depends on the spectral index of the injected electrons. In Fig. 6 the synchrotron and IC ![]() -ray spectra are shown for the range of spectral indexes where s = 1-4 and other parameters describing the model have been fixed:
-ray spectra are shown for the range of spectral indexes where s = 1-4 and other parameters describing the model have been fixed:
![]() g s-1,
g s-1,
![]() ,
and
B = 1012 G. The electron spectrum must have a spectral index lower than
,
and
B = 1012 G. The electron spectrum must have a spectral index lower than ![]() 3 to produce IC
3 to produce IC ![]() -rays above the sensitivity of
-rays above the sensitivity of
![]() LAT telescope. These spectral indexes are expected in stochastic models
of particle acceleration in turbulent media.
LAT telescope. These spectral indexes are expected in stochastic models
of particle acceleration in turbulent media.
As already noted above, the acceleration of particles experiencing significant radiative energy losses may result in their accumulation at the highest energies depending on the balance between energy gains from the acceleration mechanism and energy losses (see e.g. Protheroe 2004).
In such cases, most of the energy is accumulated in particles with the highest possible energies. A first approximation, we can consider that the spectrum of particles is mono-energetic.
Therefore, in Fig. 7 we also show the photon spectra expected in the model for the case of mono-energetic injection of electrons. In such a case, IC ![]() -ray spectra are flat. Their detectability is more difficult than in the case of electrons injected with a power-law spectrum. This is due to the fact that electrons with maximum possible energies lose most of their energy with synchrotron processes. Therefore, the IC spectra are reduced in intensity and synchrotron spectra are enhanced (compare the corresponding cases shown in Figs. 5 and 7).
We conclude that an accreting NS, which has the highest probability of being detected by the Fermi LAT telescope, should have intermediate values of
-ray spectra are flat. Their detectability is more difficult than in the case of electrons injected with a power-law spectrum. This is due to the fact that electrons with maximum possible energies lose most of their energy with synchrotron processes. Therefore, the IC spectra are reduced in intensity and synchrotron spectra are enhanced (compare the corresponding cases shown in Figs. 5 and 7).
We conclude that an accreting NS, which has the highest probability of being detected by the Fermi LAT telescope, should have intermediate values of ![]() and B and high accretion rates (see Figs. 7c,d). These parameters enable the acceleration of electrons to energies of the order of a few tens of GeV, i.e. close to energies of which the ICS process begins to become of comparable efficiency to the synchrotron process.
and B and high accretion rates (see Figs. 7c,d). These parameters enable the acceleration of electrons to energies of the order of a few tens of GeV, i.e. close to energies of which the ICS process begins to become of comparable efficiency to the synchrotron process.
The ![]() -ray photons produced by electrons in the transition region of the accretion flow onto the NS, originate close to the massive companion star creating the strong radiation field. In Sect. 4.2, we show the optical depths for
-ray photons produced by electrons in the transition region of the accretion flow onto the NS, originate close to the massive companion star creating the strong radiation field. In Sect. 4.2, we show the optical depths for ![]() -rays in the radiation field of the massive star with parameters typical of massive binary systems (the example case of the massive binary IGR J19140+0951).
As we have shown above, primary electrons accelerated to the maximum energies
reduce their energies by means of the synchrotron process. Therefore,
-rays in the radiation field of the massive star with parameters typical of massive binary systems (the example case of the massive binary IGR J19140+0951).
As we have shown above, primary electrons accelerated to the maximum energies
reduce their energies by means of the synchrotron process. Therefore, ![]() -rays produced by them in the IC process have energies typically below
-rays produced by them in the IC process have energies typically below ![]() 10 GeV.
On the other hand, the optical depths of the massive star radiation (see Fig. 4) are quite high but at energies that are clearly above the energies of
10 GeV.
On the other hand, the optical depths of the massive star radiation (see Fig. 4) are quite high but at energies that are clearly above the energies of ![]() -rays produced in our model. Therefore, we conclude that for model considered here, the absorption of
-rays produced in our model. Therefore, we conclude that for model considered here, the absorption of ![]() -rays in the stellar radiation can be neglected.
-rays in the stellar radiation can be neglected.
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5cm,clip]{1063fi7a.eps}\h...
...{4mm}
\includegraphics[width=7.4cm,height=5.8cm,clip]{1063fi7f.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg135.gif) |
Figure 7:
As in Fig. 5 but for mono-energetic injection of electrons with energies
given by Eq. (18). The specific curves show the results obtained for these same parameters as in Fig. 5. The spectrum of thermal radiation emitted from the
neutron star surface is also shown for the typical accretion rate
|
| Open with DEXTER | |
In Figs. 7a,c,e, we also display the spectra of thermal radiation from the NS polar-cap
region for the example accretion rate of
![]() g s-1 and different values of the magnetic field on the NS surface (i.e.
B = 1012 G (a), 1011 G (c),
and 109 G (e). These spectra clearly dominate over the non-thermal synchrotron spectra
produced by relativistic electrons below a few keV. As we have already noted above,
these soft X-ray thermal excesses have been reported from some INTEGRAL hard X-ray massive binaries. In reality, this soft thermal X-ray emission may be modified significantly due to the interaction with the matter accreting onto the NS surface, the matter of the stellar
wind, and the matter on the surface of the close massive companion. In our calculations,
we are unable to take these possible modifications into account.
g s-1 and different values of the magnetic field on the NS surface (i.e.
B = 1012 G (a), 1011 G (c),
and 109 G (e). These spectra clearly dominate over the non-thermal synchrotron spectra
produced by relativistic electrons below a few keV. As we have already noted above,
these soft X-ray thermal excesses have been reported from some INTEGRAL hard X-ray massive binaries. In reality, this soft thermal X-ray emission may be modified significantly due to the interaction with the matter accreting onto the NS surface, the matter of the stellar
wind, and the matter on the surface of the close massive companion. In our calculations,
we are unable to take these possible modifications into account.
5.2 The intermediate accretor-propeller stage
As noted above, in the pure propeller stage the matter arriving in the transition region at the Alfven radius, ![]() ,
is expelled by the centrifugal source from the vicinity of the neutron star preferentially along the rotational axis.
Here we consider the intermediate case in which a small fraction of the accreting matter is able to penetrate the NS surface but majority is expelled outside the neutron star.
It is unclear whether this process remains stationary in time or is only non-stationary when the accretion rate onto the neutron star varies with time e.g. due to the clumpy wind or the elliptic orbit of the NS around the massive star.
To take account of the effects of only the partial accretion of matter onto the NS surface, we introduce the parameter,
,
is expelled by the centrifugal source from the vicinity of the neutron star preferentially along the rotational axis.
Here we consider the intermediate case in which a small fraction of the accreting matter is able to penetrate the NS surface but majority is expelled outside the neutron star.
It is unclear whether this process remains stationary in time or is only non-stationary when the accretion rate onto the neutron star varies with time e.g. due to the clumpy wind or the elliptic orbit of the NS around the massive star.
To take account of the effects of only the partial accretion of matter onto the NS surface, we introduce the parameter, ![]() ,
which is the ratio of the matter accreting onto the NS surface to the entire amount of matter arriving in the transition region (i.e.
the matter accreted onto the surface and expelled from the vicinity of NS).
In such an intermediate case, the temperature of the polar cap region on the NS surface (given by Eq. (23)) should be a factor of
,
which is the ratio of the matter accreting onto the NS surface to the entire amount of matter arriving in the transition region (i.e.
the matter accreted onto the surface and expelled from the vicinity of NS).
In such an intermediate case, the temperature of the polar cap region on the NS surface (given by Eq. (23)) should be a factor of
![]() lower than estimated in the case of complete accretion. However, in principle the power available for acceleration of electrons can be higher than expected from the period limiting of the accretor and propeller stage (given by Eq. (8)), and is in fact limited by Eq. (5).
In conclusion, as a result of only the partial accretion of matter from the transition region
onto the NS surface, the surface temperature of the polar cap is lower, and the power transferred to electrons can be higher than expected for the pure accretor stage.
lower than estimated in the case of complete accretion. However, in principle the power available for acceleration of electrons can be higher than expected from the period limiting of the accretor and propeller stage (given by Eq. (8)), and is in fact limited by Eq. (5).
In conclusion, as a result of only the partial accretion of matter from the transition region
onto the NS surface, the surface temperature of the polar cap is lower, and the power transferred to electrons can be higher than expected for the pure accretor stage.
In Fig. 8, we show the example ![]() -ray spectra obtained in the case of the
partial accretion of matter onto the NS surface, assuming different accretion rates defined by the factor
-ray spectra obtained in the case of the
partial accretion of matter onto the NS surface, assuming different accretion rates defined by the factor ![]() .
We also scale the power transferred to the relativistic electrons by the factor
.
We also scale the power transferred to the relativistic electrons by the factor
![]() ,
since in this case more energy can be extracted from the transition region. Based on these calculations, we expect that the
,
since in this case more energy can be extracted from the transition region. Based on these calculations, we expect that the ![]() -ray spectra
produced at the intermediate stage are steeper power-laws, although of higher luminosities. Therefore, they should be more easily detected by
-ray spectra
produced at the intermediate stage are steeper power-laws, although of higher luminosities. Therefore, they should be more easily detected by ![]() -ray telescopes (see Fig. 8 for a comparison at the sensitivity of the
-ray telescopes (see Fig. 8 for a comparison at the sensitivity of the
![]() LAT telescope for a source at the distance of 1 kpc).
LAT telescope for a source at the distance of 1 kpc).
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.6cm,clip]{1063fi8a.eps}...
...{4mm}
\includegraphics[width=7.4cm,height=5.6cm,clip]{1063fi8b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg139.gif) |
Figure 8:
As in Fig. 5 but for different rates describing the amount of the matter accreting onto the NS surface with respect to the entire amount of the matter
arriving in the transition region (accreting and expelled from the vicinity of the NS in propeller mechanism):
|
| Open with DEXTER | |
6 Discussion and conclusions
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.7cm,clip]{1063fi9a.eps}...
...{4mm}
\includegraphics[width=7.4cm,height=5.7cm,clip]{1063fi9b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg142.gif) |
Figure 9:
a) The comparison of the hard X-ray spectra detected by the INTEGRAL observatory from the massive binary IGR J19140+0951 with the synchrotron spectra expected from the vicinity of a neutron star for the pure accretor model with the parameters:
|
| Open with DEXTER | |
We have proposed that accreting neutron stars inside compact massive binary systems produce
![]() -ray fluxes that are detectable by the satellite telescope
-ray fluxes that are detectable by the satellite telescope
![]() LAT.
To demonstrate this, we have considered electron acceleration in the turbulent, strongly-magnetized, transition region in the inner neutron-star magnetosphere that appears as a result of the interaction between accreting matter and a rotating NS magnetosphere. Relativistic electrons
produce X-rays and
LAT.
To demonstrate this, we have considered electron acceleration in the turbulent, strongly-magnetized, transition region in the inner neutron-star magnetosphere that appears as a result of the interaction between accreting matter and a rotating NS magnetosphere. Relativistic electrons
produce X-rays and ![]() -rays as a result of synchrotron and IC processes corresponding to thermal radiation originating in the NS surface.
The cooling process of electrons is followed by applying the Monte Carlo method, since some of the
-rays as a result of synchrotron and IC processes corresponding to thermal radiation originating in the NS surface.
The cooling process of electrons is followed by applying the Monte Carlo method, since some of the ![]() -rays produced can be absorbed farther by the thermal radiation.
We have shown that synchrotron emission from primary electrons and secondary cascade e
-rays produced can be absorbed farther by the thermal radiation.
We have shown that synchrotron emission from primary electrons and secondary cascade e![]() pairs can extend in energy up to the MeV energy range and IC emission can extend up to a few GeV.
pairs can extend in energy up to the MeV energy range and IC emission can extend up to a few GeV.
A physical realization of this scenario may correspond to a class of obscured, massive, binary systems discovered by the INTEGRAL observatory, which exhibit:
(1) hard, power-law X-ray emission and; (2) evidence of a soft X-ray black-body component.
As an example, we considered here in more detail the high mass X-ray binary system, IGR J19140+0951, discovered by INTEGRAL (Hannikainen et al. 2003). A compact object in this system is likely to be a neutron star (Cabanac et al. 2005).
IGR J19140+0951 is at a distance of ![]() 2-3 kpc (Rahoui et al. 2008). A hard X-ray emission up to 100 keV with a spectral index
2-3 kpc (Rahoui et al. 2008). A hard X-ray emission up to 100 keV with a spectral index
![]() is observed from this source (Hannikainen et al. 2004). Its X-ray luminosity in the high state was
is observed from this source (Hannikainen et al. 2004). Its X-ray luminosity in the high state was ![]()
![]() erg s-1 (Rodriquez et al. 2005).
Unfortunately, the basic parameters of the neutron star in IGR J19140+0951 are unknown.
Therefore, we investigated the range of model parameters that are consistent with the hard power-law spectrum detected in the X-ray energy range by INTEGRAL.
Comparison of the observations with the example calculations were shown in Fig. 9.
It is clear that for some parameters the
erg s-1 (Rodriquez et al. 2005).
Unfortunately, the basic parameters of the neutron star in IGR J19140+0951 are unknown.
Therefore, we investigated the range of model parameters that are consistent with the hard power-law spectrum detected in the X-ray energy range by INTEGRAL.
Comparison of the observations with the example calculations were shown in Fig. 9.
It is clear that for some parameters the ![]() -ray flux predicted at a few hundred MeV is detectable by extensive Fermi LAT observations.
-ray flux predicted at a few hundred MeV is detectable by extensive Fermi LAT observations.
We performed calculations for neutron stars with parameters characteristic of the
classical radio pulsars (surface magnetic-field strength
![]() G and periods of
the order of seconds) and for the millisecond pulsars (
G and periods of
the order of seconds) and for the millisecond pulsars (
![]() G, periods of a few to several milliseconds). It is clear that to produce
G, periods of a few to several milliseconds). It is clear that to produce ![]() -ray fluxes observable by the
-ray fluxes observable by the
![]() LAT telescope, the neutron stars in binary systems at a distance of a few kpc should collect the matter from the wind with a relatively high accretion rates
(>1016 g s-1). However, in the case of millisecond pulsars these accretion rates can be significantly lower (just above a few 1014 g s-1). Therefore, in principle,
the millisecond pulsars appear to be the most probable
LAT telescope, the neutron stars in binary systems at a distance of a few kpc should collect the matter from the wind with a relatively high accretion rates
(>1016 g s-1). However, in the case of millisecond pulsars these accretion rates can be significantly lower (just above a few 1014 g s-1). Therefore, in principle,
the millisecond pulsars appear to be the most probable ![]() -ray sources. On the other hand, millisecond pulsars have only low mass companions, so high accretion rates are not expected for these binary systems.
-ray sources. On the other hand, millisecond pulsars have only low mass companions, so high accretion rates are not expected for these binary systems.
We note that both synchrotron X-ray and IC ![]() -ray emission are produced in the models
almost isotropically. As we have shown above, we do not expect any modulation of the
-ray emission are produced in the models
almost isotropically. As we have shown above, we do not expect any modulation of the ![]() -ray signal with the period of the binary system due to the selective absorption of the companion-star soft radiation, as expected in the case of TeV
-ray signal with the period of the binary system due to the selective absorption of the companion-star soft radiation, as expected in the case of TeV ![]() -ray binary systems (e.g. LS 5039 and LSI 61 303). However, the modulation might be related to the change in the accretion rate in the case of the elliptic orbit of the neutron star.
It is expected that the accretion rate should increase when the neutron star is closer to
the companion star. Therefore, we predict that the highest fluxes of X-rays and
-ray binary systems (e.g. LS 5039 and LSI 61 303). However, the modulation might be related to the change in the accretion rate in the case of the elliptic orbit of the neutron star.
It is expected that the accretion rate should increase when the neutron star is closer to
the companion star. Therefore, we predict that the highest fluxes of X-rays and ![]() -rays should be observed closer to the periastron passage of the neutron star.
Moreover, the X-ray emission should be correlated with the
-rays should be observed closer to the periastron passage of the neutron star.
Moreover, the X-ray emission should be correlated with the
![]() -ray emission (see spectra in Figs. 5-8).
-ray emission (see spectra in Figs. 5-8).
In the model considered here, we do not take into account the scattering of non-thermal
synchrotron radiation by the accelerated electrons. As we have shown in Fig. 7, the thermal
radiation clearly dominates at energies below a few keV over the non-thermal synchrotron radiation produced by accelerated electrons and secondary cascade e![]() pairs.
Since their energy densities at the acceleration site scales in a similar way with distance from
the NS, the energy losses by thermal radiation must dominate over the energy losses due to non-thermal radiation.
Therefore, we can safely neglect the cooling of electrons by this non-thermal radiation. We also note, that the scattering of non-thermal X-rays with energies above a few keV is inefficient since it occurs in the Klein-Nishina regime.
pairs.
Since their energy densities at the acceleration site scales in a similar way with distance from
the NS, the energy losses by thermal radiation must dominate over the energy losses due to non-thermal radiation.
Therefore, we can safely neglect the cooling of electrons by this non-thermal radiation. We also note, that the scattering of non-thermal X-rays with energies above a few keV is inefficient since it occurs in the Klein-Nishina regime.
Processes similar to these considered in this paper are also expected in the case of non-spherical accretion of matter onto a rotating neutron star. For example, in the case of disk accretion, the corresponding accretion rate should be scaled by a part of sphere that is intercepted by the accretion disk. Then, the turbulent region in the inner disk, in which acceleration of electrons occurs, is also limited to the corresponding part of the sphere. Only IC process may become more complicated in thiscase since thermal radiation from the hot spot on the neutron star surface, indicative of relativistic electrons, can be partially obscured by the neutron-star surface.
In conclusion, we predict that present satellite telescopes can discover a new class of ![]() -ray sources, i.e. accreting neutron stars inside binary systems. The emission from these sources should be characterized by a strong hard, synchrotron spectra and IC
-ray sources, i.e. accreting neutron stars inside binary systems. The emission from these sources should be characterized by a strong hard, synchrotron spectra and IC ![]() -rays limited to energies below
-rays limited to energies below ![]() 1 GeV, due to the significant synchrotron energy losses of relativistic electrons accelerated in the vicinity of neutron stars.
1 GeV, due to the significant synchrotron energy losses of relativistic electrons accelerated in the vicinity of neutron stars.
Acknowledgements
This work is supported by the Polish MNiSzW grant N N203 390834.
References
- Baan, W. A., & Treves, A. 1973, A&A, 22, 421 [NASA ADS] (In the text)
- Bednarek, W. 1997, A&A, 322, 523 (In the text)
- Bednarek, W. 2000, A&A, 363, 646 [NASA ADS] (In the text)
- Bednarek, W., & Giovannelli, F. 2007, A&A, 464, 437 [NASA ADS] [CrossRef] [EDP Sciences]
- Begelman, M. C., & Rees, M. J. 1984, MNRAS, 206, 209 [NASA ADS] (In the text)
- Chaty, S. 2008, Chin. J. Astron. Astrophys., 8, 197 (In the text)
- Cabanac, C., Rodriquez, J., Petrucci, P.-O., et al. 2005, Chin. J. Astron. Astrophys., 5, 93 [NASA ADS] (In the text)
- Corbet, R. H. D., Hannikainen, D. C., & Remillard, R. 2005, ATel, 269 [NASA ADS]
- Hannikainen, D. C., Rodriquez, J., & Pottschmidt, K. 2003, IAUC, 8088 [NASA ADS] (In the text)
- Hannikainen, D. C., Rodriquez, J., Cabanac, C., et al. 2004, A&A, 423, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hannikainen, D. C., Rawlings, M. G., Muhli, P., et al. 2007, MNRAS, 380, 665 [NASA ADS] [CrossRef]
- Lipunov, V. M. 1992, Astrophysics of neutron stars (Heidelberg: Springer-Verlag) (In the text)
- Protheroe, R. J. 2004, APh, 21, 415 [NASA ADS] (In the text)
- Rodriquez, J., & Bodaghee, A. 2008, in The Nature and Evolution of X-ray Binaries in Diverse Environments, ed. S. Bandyopadhyay, et al. [arXiv:0801.0961] (In the text)
- Rodriquez, J., Cabanac, C., Hannikainen, D. C., et al. 2005, A&A, 432, 235 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rahoui, F., Chaty, S., Lagage, P.-O., & Pantin, E. 2008, A&A, 484, 801 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sierpowska, A., & Bednarek, W. 2005, MNRAS, 356, 711 [NASA ADS] [CrossRef] (In the text)
- Tavani, M. 1991, ApJ, 379, L69 [NASA ADS] [CrossRef] (In the text)
- Tavani, M. 1993, A&AS, 97, 313 [NASA ADS] (In the text)
- Tavani, M., & Brookshaw, L. 1993, ApJ, 413, L39 [NASA ADS] [CrossRef] (In the text)
- Treves, A., Colpi, M., & Lipunov, V. M. 1993, A&A, 269, 319 [NASA ADS] (In the text)
- Zane, S., Turolla, R., & Treves, A. 2000, ApJ, 537, 387 [NASA ADS] [CrossRef] (In the text)
All Figures
| |
Figure 1:
Schematic representation of the model discussed in this paper.
The wind from a massive star penetrates the inner magnetosphere of a neutron star.
As a result of the interaction of the wind with the dipole magnetic field of the NS, a strongly magnetized turbulent region is created (thick solid curve) in which the matter gains energy by being accelerated to the velocity of the rotating magnetic-field lines. Electrons (e) are accelerated in this turbulent transition region and cool by means of the synchrotron process and the Comptonization of thermal radiation (marked by X), emitted from the stellar surface around the magnetic-pole region. As a result, the first generation of IC |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
The maximum energies of accelerated electrons a) and the maximum power that can be transferred to these electrons b) as a function of the accretion rate of the matter
from the massive star onto the neutron star. The results are shown for the neutron stars that have the surface magnetic field
B = 1012 G (solid line), and B = 109 G (dashed). The acceleration parameter is equal to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,height=5cm,clip]{1063fi3a.eps}\p...
...{2mm}
\includegraphics[width=6.8cm,height=5.7cm,clip]{1063fi3b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg110.gif) |
Figure 3:
The optical depths for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,height=5cm,clip]{1063fi4b.eps}\p...
...{2mm}
\includegraphics[width=6.8cm,height=5.7cm,clip]{1063fi4a.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg113.gif) |
Figure 4:
The optical depths as a function of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.2cm,clip]{1063fi5a.eps}...
...}
\includegraphics[width=7.4cm,height=5.8cm,clip]{1063fi5f.eps}
\par\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg124.gif) |
Figure 5:
The IC |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.8cm,clip]{1063fi6a.eps}...
...{4mm}
\includegraphics[width=7.5cm,height=5.8cm,clip]{1063fi6b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg125.gif) |
Figure 6:
As in Fig. 5 but for different spectral indexes of injected electrons:
s = 4 (dashed), 3 (dotted), 2.2 (solid), 1 (dot-dashed). The parameters describing the model are the following: |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5cm,clip]{1063fi7a.eps}\h...
...{4mm}
\includegraphics[width=7.4cm,height=5.8cm,clip]{1063fi7f.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg135.gif) |
Figure 7:
As in Fig. 5 but for mono-energetic injection of electrons with energies
given by Eq. (18). The specific curves show the results obtained for these same parameters as in Fig. 5. The spectrum of thermal radiation emitted from the
neutron star surface is also shown for the typical accretion rate
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.6cm,clip]{1063fi8a.eps}...
...{4mm}
\includegraphics[width=7.4cm,height=5.6cm,clip]{1063fi8b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg139.gif) |
Figure 8:
As in Fig. 5 but for different rates describing the amount of the matter accreting onto the NS surface with respect to the entire amount of the matter
arriving in the transition region (accreting and expelled from the vicinity of the NS in propeller mechanism):
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,height=5.7cm,clip]{1063fi9a.eps}...
...{4mm}
\includegraphics[width=7.4cm,height=5.7cm,clip]{1063fi9b.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11063-08/Timg142.gif) |
Figure 9:
a) The comparison of the hard X-ray spectra detected by the INTEGRAL observatory from the massive binary IGR J19140+0951 with the synchrotron spectra expected from the vicinity of a neutron star for the pure accretor model with the parameters:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.