| Issue |
A&A
Volume 495, Number 3, March I 2009
|
|
|---|---|---|
| Page(s) | 953 - 957 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361:200811034 | |
| Published online | 20 January 2009 | |
Signatures of Sweet-Parker magnetic reconnection in the solar chromosphere
Y. E. Litvinenko1 - J. Chae2
1 - Department of Mathematics, University of Waikato,
PB 3105, Hamilton, New Zealand
2 -
Astronomy Program, Department of Physics and Astronomy,
Seoul National University, Seoul 151-747, Korea
Received 25 September 2008 / Accepted 8 January 2009
Abstract
Aims. Predicted and observed signatures of magnetic reconnection in the solar chromosphere are discussed.
Methods. Compressible reconnection scalings for the Sweet-Parker current sheet in the chromosphere are derived, which generalize earlier treatments by including both the Lorentz force and the pressure gradient in the reconnection outflow as possible drivers of reconnection jets. The theoretical scalings were tested against the measured speed, density, and temperature of an extreme-ultraviolet jet, observed with TRACE. Model predictions for the reconnection jet parameters as functions of height above the solar photosphere were computed.
Results. The predicted variation of reconnection jet parameters with height appears to correspond to the observed wide range of parameters of chromospheric jet-like features.
Key words: Sun: activity - Sun: chromosphere - Sun: magnetic fields
1 Introduction
Transition-region explosive events and jets,
detected by ultraviolet (UV) and extreme-ultraviolet (EUV)
observations of the solar atmosphere, show that even
the ``quiet'' Sun is in fact strongly dynamic.
The observations are usually interpreted in terms of
magnetic reconnection at various heights in the solar atmosphere
(Dere et al. 1991;
Dere 1994;
Innes et al. 1997;
see Aschwanden 2006, for a review).
Reconnection in the photosphere is manifested as
the observed mutual cancellation of
photospheric magnetic fragments of opposite polarity
and the associated H![]() upflows
(e.g., Martin 1990;
Litvinenko & Martin 1999).
Ongoing convection-driven cancellation eventually
leads to chromospheric reconnection,
manifested as EUV explosive events
(Chae et al. 2003).
This interpretation gives a simple explanation for
the observed correlation between the transition-region
explosive events and the photospheric flux cancellation events
(Chae et al. 1998).
The interpretation could be strengthened though by computing
the expected variations of reconnection characteristics
with height and by comparing them with the observed signatures.
upflows
(e.g., Martin 1990;
Litvinenko & Martin 1999).
Ongoing convection-driven cancellation eventually
leads to chromospheric reconnection,
manifested as EUV explosive events
(Chae et al. 2003).
This interpretation gives a simple explanation for
the observed correlation between the transition-region
explosive events and the photospheric flux cancellation events
(Chae et al. 1998).
The interpretation could be strengthened though by computing
the expected variations of reconnection characteristics
with height and by comparing them with the observed signatures.
Photospheric reconnection has been quantitatively described using the Sweet-Parker model (Parker 1957, 1963), adapted for the conditions of the temperature minimum region of the solar photosphere (Litvinenko 1999; Litvinenko et al. 2007). Reconnection in the upper chromosphere and transition region occurs in a different parameter regime, and its observable characteristics are different as well. Notably, photospheric reconnection is approximately isothermal (Bellot Rubio & Beck 2005), whereas transition-region reconnection leads to significant plasma heating. Distinct features of chromospheric reconnection make it an interesting subject for a quantitative study.
Motivated by these considerations, in this paper we use the Sweet-Parker model for reconnection in a current sheet to describe chromospheric reconnection. First we present the model equations and derive reconnection scalings (Sect. 2). Next we test the theoretical scaling by applying them to the parameters of a well-observed EUV jet that appears to have been driven by magnetic reconnection in the upper chromosphere (Sect. 3). We compute the current sheet parameters as functions of height of the reconnection site in the chromosphere and relate them to expected observational signatures (Sect. 4). We use the results to argue that the lack of a preferred reconnection height leads to the observed wide range of parameters of chromospheric jet-like features (Sect. 5).
2 Compressible Sweet-Parker magnetic reconnection
Discussions of magnetic reconnection in the Sweet-Parker current sheet (Parker 1957, 1963) are typically based on a number of simplifying assumptions. It is assumed in particular that the plasma is accelerated in the reconnection outflow region either by the gas pressure gradient or by the Lorentz force in the sheet. For instance, Ji et al. (1998), motivated by the parameters of a reconnection experiment, analyzed the case when reconnection jets were driven by the pressure gradient in the outflow region. Oreshina & Somov (2000) quantified the effects of anomalous transport coefficients in the case of the pressure-driven outflows. Priest & Forbes (2000, see their Sect. 4.5) and Chae et al. (2003) explored compressible reconnection in the limit when the jets were accelerated by the Lorentz force. Litvinenko & Craig (2003) presented compressible reconnection scalings in both limiting cases. We are not aware of a model that would incorporate both acceleration mechanisms when plasma compression in the sheet cannot be neglected, although such general analysis has been presented for the incompressible case (Priest & Forbes 2000).
Here we generalize the earlier
treatments by considering reconnection jets that are driven
simultaneously by the Lorentz force and the pressure gradient.
Specifically, we consider a Sweet-Parker current sheet of width 2 L
and thickness 2 l. The goal is to determine the scalings that relate
the speed v, mass density ![]() ,
temperature T, pressure p, and
magnetic field B at the reconnection site. The subscripts
i and o refer to the inflow and outflow reconnection regions.
,
temperature T, pressure p, and
magnetic field B at the reconnection site. The subscripts
i and o refer to the inflow and outflow reconnection regions.
As in the standard approach
(Parker 1957; Priest & Forbes 2000),
the sought-after reconnection scalings follow from the balance
equations for the sheet. The mass balance equation is as follows:
| (1) |
For sub-Alfvénic inflows, the kinetic energy of the inflow is low, and the component of the momentum equation across the sheet reduces to the pressure balance:
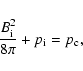 |
(2) |
where
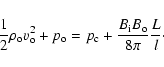 |
(3) |
The outflow magnetic field
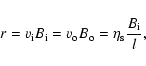 |
(4) |
where
(see the next section, however, for possible effects of the sheet cooling by conduction and radiation). Consistent with the momentum balance across the sheet, the kinetic energy flux is neglected in the inflow region, and the magnetic energy flux is neglected in the outflow region. Finally, the outflow pressure
| (6) |
The limiting case
The equations above relate the parameters of the current sheet
to those of the reconnection inflow region.
Note that the scaling
![]() ,
motivated
by the Maxwell equation
,
motivated
by the Maxwell equation
![]() ,
is sometimes
used to determine the magnetic field in the outflow region
(Priest & Forbes 2000;
Litvinenko & Craig 2003).
We do not employ this scaling in our analysis,
however, because its validity in the compressible case
has been questioned
(Chae et al. 2003;
Forbes 2007).
Our approach, based on the magnetic flux balance condition,
appears to go back to
Green (1965).
,
is sometimes
used to determine the magnetic field in the outflow region
(Priest & Forbes 2000;
Litvinenko & Craig 2003).
We do not employ this scaling in our analysis,
however, because its validity in the compressible case
has been questioned
(Chae et al. 2003;
Forbes 2007).
Our approach, based on the magnetic flux balance condition,
appears to go back to
Green (1965).
The resulting system of equations can be solved to determine
![]() and
and ![]() ,
as well as the parameters of the sheet
l,
,
as well as the parameters of the sheet
l,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
in terms of parameters
,
in terms of parameters ![]() and r, as well as
and r, as well as
![]() ,
,
![]() ,
and L.
While solving the model equations,
we retain the pressure
,
and L.
While solving the model equations,
we retain the pressure ![]() in the inflow region in both
the momentum equation and the energy equation, which is
important in the high-beta plasma of the lower chromosphere.
It is convenient to derive reconnection scalings in terms
of the inflow plasma beta
in the inflow region in both
the momentum equation and the energy equation, which is
important in the high-beta plasma of the lower chromosphere.
It is convenient to derive reconnection scalings in terms
of the inflow plasma beta
![]() rather than
rather than ![]() .
We use the mass density to take into account the height variation
of the mean molecular weight
.
We use the mass density to take into account the height variation
of the mean molecular weight ![]() .
For a given height above the photosphere,
an atmospheric model such as VAL-C
(Vernazza et al. 1981)
allows us to specify
.
For a given height above the photosphere,
an atmospheric model such as VAL-C
(Vernazza et al. 1981)
allows us to specify
![]() ,
,
![]() ,
and the resistive magnetic
diffusivity
,
and the resistive magnetic
diffusivity ![]() .
We allow for the possibility of an enhanced
effective diffusivity
.
We allow for the possibility of an enhanced
effective diffusivity
![]() that exceeds the standard
Spitzer value
that exceeds the standard
Spitzer value ![]() at the reconnection site.
Our analysis of flux pile-up magnetic reconnection
(Litvinenko et al. 2007)
shows that the enhancement factor
at the reconnection site.
Our analysis of flux pile-up magnetic reconnection
(Litvinenko et al. 2007)
shows that the enhancement factor
![]() scales
as the square of the magnetic field pile-up factor at the entrance
to sheet, suggesting that
scales
as the square of the magnetic field pile-up factor at the entrance
to sheet, suggesting that
![]() of a few tens is
not unreasonable.
of a few tens is
not unreasonable.
For the purpose of comparison with solar observations, the predicted
density, temperature, and speed of the reconnection jet
are of primary interest. The plasma compression ratio in the sheet
is given by
The reconnecting magnetic field is as follows:
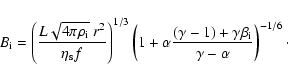 |
(8) |
Now the outflow and inflow speeds can be written in a compact form:
| (10) |
The temperature increase in the jet can be related to the jet speed as follows:
![\begin{displaymath}\Delta T \equiv T_{\rm o} - T_{\rm i} =
\frac{\gamma - 1} {...
...) \over 1 +
\alpha (1+\beta_{\rm i} - 2/\gamma) }\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/09/aa11034-08/img37.gif) |
(11) |
The corresponding temperature in the outflow is as follows:
The requirement that the plasma be compressed and heated in the sheet (
3 Interpretation of an EUV jet observed by TRACE
We test the model by applying it to the parameters of an EUV jet
that had been associated with photospheric
cancellation and presumably had been generated by magnetic
reconnection in the upper chromosphere. The jet had been detected
in the NOAA active region 8668, jointly observed by SOHO, TRACE, and
the Big Bear Solar Observatory in August 1999.
The following speed, density, and temperature of the jet
had been determined:
![]() cm s-1,
cm s-1,
![]() cm-3,
cm-3,
![]() K
(Chae 2003).
We begin by assuming that the observed parameters of the jet
coincide with those of the reconnection outflow,
K
(Chae 2003).
We begin by assuming that the observed parameters of the jet
coincide with those of the reconnection outflow,
![]() etc. Note from the outset that this assumption
neglects possible expansion of the jet as it travels away
from the reconnection site.
etc. Note from the outset that this assumption
neglects possible expansion of the jet as it travels away
from the reconnection site.
The theoretical scalings of the previous section
are simplified somewhat in the upper chromosphere
where the plasma is almost fully ionized.
In the approximation of a single-temperature fully ionized plasma,
the outflow pressure is given by
![]() and
and
![]() with
with ![]() .
The pressure in the inflow
.
The pressure in the inflow ![]() is assumed to be low, so that
is assumed to be low, so that
![]() .
Using the observed values of
.
Using the observed values of ![]() and
and ![]() in the case
in the case
![]() ,
Eq. (12) can be solved
to yield
,
Eq. (12) can be solved
to yield
![]() .
The key point is that not only the Lorentz force but also
the pressure force drives the reconnection jet. As a result,
the kinetic energy
flux exceeds the enthalpy flux in the outflow region:
.
The key point is that not only the Lorentz force but also
the pressure force drives the reconnection jet. As a result,
the kinetic energy
flux exceeds the enthalpy flux in the outflow region:
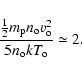 |
(13) |
If the pressure force were negligible,
For the observed parameters of the jet,
the density compression factor is found from
Eq. (7) to be
![]() ,
from which it follows that
,
from which it follows that
![]() cm-3.
This value is consistent
with plasma densities in the upper transition region,
corresponding to the densities at levels 3 and 4 of
the VAL-C model of the solar atmosphere
(Vernazza et al. 1981).
The corresponding temperatures in the VAL-C model
are between
cm-3.
This value is consistent
with plasma densities in the upper transition region,
corresponding to the densities at levels 3 and 4 of
the VAL-C model of the solar atmosphere
(Vernazza et al. 1981).
The corresponding temperatures in the VAL-C model
are between
![]() K and
K and
![]() K.
The neutral component of the gas at these temperatures
can contribute to the momentum and energy balance in the sheet,
yet taking the neutral component into consideration does not seem
to be justified, given the approximate nature of the model. Next,
Eq. (9) leads to the reconnecting magnetic field
K.
The neutral component of the gas at these temperatures
can contribute to the momentum and energy balance in the sheet,
yet taking the neutral component into consideration does not seem
to be justified, given the approximate nature of the model. Next,
Eq. (9) leads to the reconnecting magnetic field
![]() G. These parameters of the sheet can be used
to justify some assumptions of the model. Specifically,
the gas pressure in the inflow can indeed be neglected because
G. These parameters of the sheet can be used
to justify some assumptions of the model. Specifically,
the gas pressure in the inflow can indeed be neglected because
![]() and
and
![]() for
for
![]() K,
and the thermal energy flux into the sheet can be neglected because
K,
and the thermal energy flux into the sheet can be neglected because
![]() .
.
The derived value of ![]() is rather small for the transition region.
Notably, somewhat stronger magnetic fields had been derived
from the TRACE data on coronal loop oscillations
(e.g.,
is rather small for the transition region.
Notably, somewhat stronger magnetic fields had been derived
from the TRACE data on coronal loop oscillations
(e.g., ![]() G
in Nakariakov & Ofman 2001;
and 10-40 G
in Verwichte et al. 2004).
Note, however, that the observed EUV jets are believed
to represent a dynamic response of the upper chromosphere
to photospheric flux cancellation
(see, e.g., Chae 2003,
and references therein).
Hence significant density enhancement in the reconnection inflow
region can occur owing to the upflow of cool dense plasma,
driven by photospheric cancellation. Such enhancement
would be consistent with the reconnection jet expansion
that is neglected throughout this paper. Assume, for instance,
that
G
in Nakariakov & Ofman 2001;
and 10-40 G
in Verwichte et al. 2004).
Note, however, that the observed EUV jets are believed
to represent a dynamic response of the upper chromosphere
to photospheric flux cancellation
(see, e.g., Chae 2003,
and references therein).
Hence significant density enhancement in the reconnection inflow
region can occur owing to the upflow of cool dense plasma,
driven by photospheric cancellation. Such enhancement
would be consistent with the reconnection jet expansion
that is neglected throughout this paper. Assume, for instance,
that
![]() as a result of the jet expansion.
Then our model would lead to
as a result of the jet expansion.
Then our model would lead to
![]() cm-3 and
cm-3 and
![]() G.
New detailed measurements of the EUV jet parameters could
provide a test of the validity of the model.
G.
New detailed measurements of the EUV jet parameters could
provide a test of the validity of the model.
Our model, based on the adiabatic energy equation,
predicts relatively modest plasma compression in the sheet.
It is important, however, to verify the accuracy of
the assumption that the plasma in the outflow is not
significantly cooled by radiation or conduction.
Additional cooling could lead to a larger compression factor
![]() .
.
To achieve the energy balance by radiative losses,
the magnetic energy flux into the sheet (per unit length of the sheet)
would have to be equal to the radiation energy loss rate
![]() ,
where
,
where
![]() erg cm3 for the temperature
erg cm3 for the temperature
![]() K
(e.g., Hildner 1974).
Using the mass balance equation, the resulting sheet width
could be expressed as
K
(e.g., Hildner 1974).
Using the mass balance equation, the resulting sheet width
could be expressed as
![]() .
Numerically,
.
Numerically,
![]() cm, which would
exceed the thickness of the chromosphere. Hence
energy losses by radiation can be neglected
for current sheets in the upper chromosphere and corona
(Somov 1992).
cm, which would
exceed the thickness of the chromosphere. Hence
energy losses by radiation can be neglected
for current sheets in the upper chromosphere and corona
(Somov 1992).
Thermal conduction can be an efficient cooling mechanism
because of the steep temperature gradients that develop
at a localized reconnection site. The conditions required for
classical heat conduction, however, break down for
a high-temperature plasma, in which case the heat flux
is carried by a convective process rather than by a diffusive
one. The heat flux, carried by electrons, is then limited
to the value
![]() ,
where the subscript e refers to electrons, and
,
where the subscript e refers to electrons, and
![]() is an effective convective speed. This expression
for the saturated heat flux describes the highest possible rate
of heat transfer by conduction. Following theoretical
and numerical investigations for the laser fusion problem
(e.g., Manheimer & Klein 1975),
studies of reconnection in the solar atmosphere typically adopt
is an effective convective speed. This expression
for the saturated heat flux describes the highest possible rate
of heat transfer by conduction. Following theoretical
and numerical investigations for the laser fusion problem
(e.g., Manheimer & Klein 1975),
studies of reconnection in the solar atmosphere typically adopt
![]() (Craig & Davys 1984;
Somov & Titov 1985;
Oreshina & Somov 2000).
(Craig & Davys 1984;
Somov & Titov 1985;
Oreshina & Somov 2000).
The energy balance in the sheet with
![]() ,
generalized to incorporate the non-classical saturated heat flux,
is as follows:
,
generalized to incorporate the non-classical saturated heat flux,
is as follows:
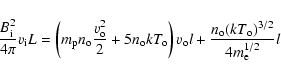 |
(14) |
(cf. Eq. (5)). Substitution of the observationally determined parameters of the reconnection jet leads to a slightly larger compression factor
We conclude that the TRACE data (Chae 2003) are consistent with the notion that magnetic reconnection in the solar chromosphere heats the plasma to EUV-emitting energies and generates fast jets. The parameters of the analyzed EUV jet are adequately described by compressible reconnection scalings for the Sweet-Parker current sheet with an adiabatic energy equation. One concern is a relatively weak reconnecting magnetic field, predicted by the model. Because the measured density in the jet only puts a lower bound on the reconnection outflow density, an interesting possibility remains that the density at the reconnection site is significantly enhanced relative to that in the transition region. These considerations strongly motivate new detailed observations of jet-like features in the chromosphere.
To get an insight into the physics of chromospheric reconnection and to guide the interpretation of the data, it is useful to summarize the predicted observational signatures of reconnection jets, as functions of height in the solar chromosphere. This is done in the next section.
4 Signatures of chromospheric magnetic reconnection at different heights
The observed variety of dynamic features, associated with photospheric flux cancellation, strongly suggests that magnetic reconnection can occur at different heights in the solar chromosphere, so that different parameter regimes lead to the wide range of observed reconnection signatures (Chae et al. 2003). In some cases a preferential location of the reconnection site can be suggested. For example, reconnection heights of photospheric canceling features are constrained by the sizes of the interacting magnetic bipoles, and reconnection is most likely to take place in the temperature minimum region in the photosphere, where the classical electric resistivity reaches a maximum (Litvinenko 1999; Sturrock 1999; Litvinenko et al. 2007). It appears, however, that generally reconnection heights are controlled by the magnetic geometry and characteristics of reconnection-driving flows. Hence no preferred reconnection height can be identified.
We calculate the expected parameters of the reconnection jet
as functions of height, using the compressible adiabatic
Sweet-Parker model, described in Sect. 2.
As an example, the flux cancellation rate is set to
the measured mean value in a previous statistical analysis
of photospheric cancelling features,
![]() G cm s-1
(Litvinenko et al. 2007).
The width of a vertically oriented current sheet is identified
with the local pressure scale height
(Litvinenko 1999).
The VAL-C atmospheric model is employed to specify
G cm s-1
(Litvinenko et al. 2007).
The width of a vertically oriented current sheet is identified
with the local pressure scale height
(Litvinenko 1999).
The VAL-C atmospheric model is employed to specify
![]() and
and ![]() (Vernazza et al. 1981).
The classical resistivity
(Vernazza et al. 1981).
The classical resistivity ![]() had been computed for the VAL-C model
(Kubat & Karlicky 1986).
Here a moderately enhanced value of effective diffusivity in the sheet
is assumed,
had been computed for the VAL-C model
(Kubat & Karlicky 1986).
Here a moderately enhanced value of effective diffusivity in the sheet
is assumed,
![]() ,
which is suggested by the analysis
by Chae et al. (2003).
Three values of
,
which is suggested by the analysis
by Chae et al. (2003).
Three values of ![]() (0, 0.5, and 0.9) illustrate
the relative role of the pressure force in the acceleration of the jet.
(0, 0.5, and 0.9) illustrate
the relative role of the pressure force in the acceleration of the jet.
Figures 1 and 2 show the results.
Notably, the predicted dependence on ![]() is
rather weak, especially compared with the height-related variations.
It is also interesting that the temperature-speed relationship,
originally derived for magnetically-driven jets
(Chae et al. 2003),
turns out to be a rather robust result.
Figures 1 and 2 demonstrate that the observed variety
of reconnection-driven jet-like features in the chromosphere - from
cool and slow jets in the photosphere to hot and fast jets
in the transition region - can be understood
in the framework of a single physical process:
magnetic reconnection at different heights, which is
ultimately driven by convective flows.
The geometry and dynamics of the driver determine
the reconnection height in each particular case.
is
rather weak, especially compared with the height-related variations.
It is also interesting that the temperature-speed relationship,
originally derived for magnetically-driven jets
(Chae et al. 2003),
turns out to be a rather robust result.
Figures 1 and 2 demonstrate that the observed variety
of reconnection-driven jet-like features in the chromosphere - from
cool and slow jets in the photosphere to hot and fast jets
in the transition region - can be understood
in the framework of a single physical process:
magnetic reconnection at different heights, which is
ultimately driven by convective flows.
The geometry and dynamics of the driver determine
the reconnection height in each particular case.
Our results also bring out a unique role played by the transition region as far as observational manifestations of reconnection are concerned. Figures 1 and 2 show that the reconnection jet temperature increases with height whereas the reconnection jet density decreases with height. The transition region is the location where the jets are particularly easy to observe because they are both sufficiently hot and sufficiently dense. This conclusion is consistent with an earlier result (Galsgaard 2002), showing a clear distinction between regimes of magnetic energy deposition below and above the transition region.
![\begin{figure}
\includegraphics[width=3.5in]{1034fig1.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11034-08/Timg83.gif) |
Figure 1:
Height variations of the current sheet
temperature and inflow and outflow speeds
for
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=3.5in]{1034fig2.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11034-08/Timg84.gif) |
Figure 2: Height variations of the current sheet density and magnetic field. The input parameters are as in Fig. 1. |
| Open with DEXTER | |
The dependence of the reconnection jet parameters on height can be used to interpret an observed jet as an outcome of reconnection at a certain level of the chromosphere. Limitations of the model should be kept in mind, however. The flux transfer rate r is basically a free parameter. The photospheric cancellation rate gives an upper estimate for r, yet the actual rate can be much lower in a chromospheric current sheet. This appears to be the case for the TRACE jet, analyzed in the previous section. Furthermore, the parameters of an observed chromospheric jet do not necessarily coincide with those of the reconnection outflow region. As discussed above, the primary reconnection jet can undergo expansion, leading to lower observed densities. The speed and temperature of the jet could also change as it expands, further complicating the interpretation of the data. More generally, description of interesting ways in which chromospheric and coronal reconnection is modulated by continual convective shuffling of the photospheric fibrils remains an unsolved problem (e.g., Parker 2007).
5 Discussion
Theoretical models
of magnetic reconnection in the solar photosphere
(e.g., Litvinenko 1999;
Litvinenko et al. 2007)
and in the corona
(e.g., Somov 1992;
Priest & Forbes 2000)
illustrate how different parameter regimes result in different observable
features of reconnection. Photospheric reconnection generates
H![]() jets but does not heat the photospheric plasma
(Bellot Rubio & Beck 2005),
whereas coronal reconnection generates X-ray jets
(Shimojo & Shibata 2000)
and can result in impulsive flare energy release.
Chromospheric reconnection, characterized by UV and EUV jets,
is an intermediate regime between these two extremes.
In this paper, we explore chromospheric reconnection using
the traditional Sweet-Parker reconnection model,
generalized to incorporate the effect of plasma
compression in a current sheet.
jets but does not heat the photospheric plasma
(Bellot Rubio & Beck 2005),
whereas coronal reconnection generates X-ray jets
(Shimojo & Shibata 2000)
and can result in impulsive flare energy release.
Chromospheric reconnection, characterized by UV and EUV jets,
is an intermediate regime between these two extremes.
In this paper, we explore chromospheric reconnection using
the traditional Sweet-Parker reconnection model,
generalized to incorporate the effect of plasma
compression in a current sheet.
Previous descriptions of compressible Sweet-Parker magnetic
reconnection assumed that the reconnection
jet is driven by either the Lorentz force
(e.g., Priest & Forbes 2000;
Litvinenko & Craig 2003;
Chae et al. 2003)
or the gas pressure
(e.g., Somov 1992;
Litvinenko & Craig 2003).
We are not aware of the general scalings in the literature,
which include both effects. Hence we derived these scalings
in this paper and used them to compute the expected
speeds and temperatures of reconnection jets at various levels
in the solar chromosphere.
We used the available TRACE data on the speed, density, and
temperature of an EUV jet
(Chae 2003)
to test the model. We showed that both the Lorentz
force and the pressure gradient contribute to the acceleration of
the observed jet. Notably, an earlier attempt to interpret the same data
(Chae et al. 2003)
did not incorporate the effect of the jet
acceleration by the pressure gradient in the sheet.
The model could only be reconciled with the data by postulating
an effective
![]() .
We achieved a more satisfactory
interpretation of the data by
incorporating the pressure acceleration effect into the model.
At the same time, the variation of the current sheet
parameters with height above the photosphere appears to be
more significant than the effect of the pressure gradient in
the outflow.
.
We achieved a more satisfactory
interpretation of the data by
incorporating the pressure acceleration effect into the model.
At the same time, the variation of the current sheet
parameters with height above the photosphere appears to be
more significant than the effect of the pressure gradient in
the outflow.
Observations suggest that chromospheric reconnection is ultimately driven by flux emergence and convective flows (Chae et al. 2003). Because of a strong variation of the chromospheric density with height, diverse observational features of reconnection are possible. Here we quantify this argument by computing the speeds and temperatures of chromospheric reconnection jets, which are shown to vary by several orders of magnitude for a fixed flux cancellation rate (Fig. 1).
Analysis of chromospheric magnetic reconnection is strongly motivated in a more general context of the coronal heating problem. It has been argued that plasma heating resulting from reconnection is more likely to occur in the transition region rather than at higher altitudes in the corona, in which case the observed multimillion-Kelvin temperatures in the corona result not from local coronal heating but rather from heating in the transition region and upper chromosphere, followed by chromospheric evaporation (Aschwanden et al. 2007). If this argument is correct, chromospheric reconnection is likely to be the energy release mechanism that results in the observed coronal temperatures.
Observations in the He II 304 Å passband of SOHO EIT show that the observed emission in the chromosphere and the lower corona occurs on the supergranular scale and the rate of occurrence correlates with the unsigned imbalance of the local magnetic field. These signatures of the emission suggest that chromospheric reconnection supplies the bulk of the energy and mass that are responsible for heating and mass loading of the solar corona (McIntosh 2007). While pioneering theoretical studies of coronal heating neglected the stratification of the solar atmosphere (Parker 1972, 1983), more recent numerical studies show that magnetic energy release should occur in different regimes below and above the transition region (Galsgaard 2002). Our results provide an independent argument in support of this notion.
A weakness of our model is the assumption that the magnetic field is annihilated completely in the current sheet. A nonreconnecting magnetic field component parallel to the sheet, however, is present in a general three-dimensional case. Hence the total magnetic field at the reconnection site is related to the reconnecting field component through a parameter that specifies the degree of nonplanarity of the magnetic field vector in the sheet. Moreover, the parallel field component gives rise to an additional magnetic pressure that modifies the pressure balance in the sheet, whereas a gradient of the parallel field corresponds to an additional resistive dissipation in the sheet (Somov & Titov 1985). This potentially important effects should be incorporated into the model. Its further development should also include a detailed analysis of the energy balance in the chromospheric current sheet.
Acknowledgements
Useful discussions with T. G. Forbes at the University of New Hampshire (USA) and H. Peter at the Kiepenheuer-Institut für Sonnenphysik (Freiburg, Germany) are gratefully acknowledged. This work was supported by NASA (grants NNX07AI04G and NNX08AG44G), NSF (grants ATM-0519249 and ATM-0734032), and by a research fellowship from the Alexander von Humboldt Foundation.
References
- Aschwanden, M. J. 2006, Physics of the Solar Corona (Berlin: Springer), Chap. 10.4 (In the text)
- Aschwanden, M. J., Winebarger, A., Tsiklauri, D., & Peter, H. 2007, ApJ, 659, 1673 [NASA ADS] [CrossRef] (In the text)
- Bellot Rubio, L. R., & Beck, C. 2005, ApJ, 626, L125 [NASA ADS] [CrossRef] (In the text)
- Chae, J. 2003, ApJ, 584, 1084 [NASA ADS] [CrossRef] (In the text)
- Chae, J., Wang, H., Lee, C.-Y., Goode, P. R., & Schuhle, U. 1998, ApJ, 497, L109 [NASA ADS] [CrossRef] (In the text)
- Chae, J., Moon, Y.-J., & Park, S.-Y. 2003, J. Korean Astron. Soc., 36, 13
- Craig, I. J. D., & Davys, J. W. 1984, Sol. Phys., 90, 343 [NASA ADS] (In the text)
- Dere, K. P. 1994, Adv. Space Res., 14, 13 [NASA ADS] [CrossRef] (In the text)
- Dere, K. P., Bartoe, J.-D. F., Brueckner, G. E., Ewing, J., & Lund, P. 1991, J. Geophys. Res., 96, 9399 [NASA ADS] [CrossRef] (In the text)
- Forbes, T. G. 2007, personal communication (In the text)
- Galsgaard, K. 2002, in SOLMAG: Magnetic Coupling of the Solar Atmosphere Euroconference and IAU Colloq. 188, ESA SP-505, 269 (In the text)
- Green, R. M. 1965, in Stellar and Solar Magnetic Fields, ed. R. Lust (Amsterdam: North-Holland), IAU Symp., 22, 398 (In the text)
- Hildner, E. 1974, Sol. Phys., 35, 123 [CrossRef] (In the text)
- Innes, D. E., Inhester, B., Axford, W. I., & Wilhelm, K. 1997, Nature, 386, 811 [CrossRef] (In the text)
- Ji, H., Yamada, M., Hsu, S., & Kulsrud, R. 1998, Phys. Rev. Lett., 80, 3256 [CrossRef] (In the text)
- Kubat, J., & Karlicky, M. 1986, Bull. Astron. Inst. Czechoslovakia, 37, 155 [NASA ADS] (In the text)
- Litvinenko, Y. E. 1999, ApJ, 515, 435 [CrossRef] (In the text)
- Litvinenko, Y. E., & Craig, I. J. D. 2000, ApJ, 544, 1101 [NASA ADS] [CrossRef] (In the text)
- Litvinenko, Y. E., & Craig, I. J. D. 2003, Sol. Phys., 218, 173 [NASA ADS] [CrossRef] (In the text)
- Litvinenko, Y. E., & Martin, S. F. 1999, Sol. Phys., 190, 45 [NASA ADS] [CrossRef] (In the text)
- Litvinenko, Y. E., Chae, J., & Park, S.-Y. 2007, ApJ, 662, 1302 [NASA ADS] [CrossRef] (In the text)
- Manheimer, W. M., & Klein, H. H. 1975, Phys. Fluids, 18, 1299 [CrossRef] (In the text)
- Martin, S. F. 1990, in Solar Photosphere: Structure, Convection, and Magnetic Fields, ed. J. O. Stenflo (Dordrecht: Kluwer), IAU Symp., 138, 129 (In the text)
- McIntosh, S. W. 2007, ApJ, 657, L125 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Oreshina, A. V., & Somov, B. V. 2000, Astron. Lett., 26, 750 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1957, J. Geophys. Res., 62, 509 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1963, ApJS, 8, 177 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1983, ApJ, 264, 642 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 2007, Conversations on Electric and Magnetic Fields in the Cosmos (Princeton: Princeton Univ. Press), Chap. 10 (In the text)
- Priest, E., & Forbes, T. 2000, Magnetic Reconnection (Cambridge: Cambridge Univ. Press), Chap. 4 (In the text)
- Shimojo, M., & Shibata, K. 2000, ApJ, 542, 1100 [NASA ADS] [CrossRef] (In the text)
- Somov, B. V. 1992, Physical Processes in Solar Flares (Dordrecht: Kluwer), Chap. 3 (In the text)
- Somov, B. V., & Titov, V. S. 1985a, Sol. Phys., 95, 141 [NASA ADS] [CrossRef] (In the text)
- Somov, B. V., & Titov, V. S. 1985b, Sol. Phys., 102, 79 [NASA ADS] [CrossRef] (In the text)
- Sturrock, P. A. 1999, ApJ, 521, 451 [CrossRef] (In the text)
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] (In the text)
- Verwichte, E., Nakariakov, V. M., Ofman, L., & DeLuca, E. E. 2004, Sol. Phys., 223, 77 [CrossRef] (In the text)
All Figures
![\begin{figure}
\includegraphics[width=3.5in]{1034fig1.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11034-08/Timg83.gif) |
Figure 1:
Height variations of the current sheet
temperature and inflow and outflow speeds
for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=3.5in]{1034fig2.eps}
\end{figure}](/articles/aa/full_html/2009/09/aa11034-08/Timg84.gif) |
Figure 2: Height variations of the current sheet density and magnetic field. The input parameters are as in Fig. 1. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



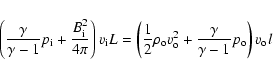
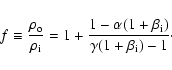
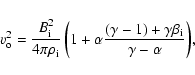
![\begin{displaymath}T_{\rm o} = \frac{1}{2}
\frac{\mu m_{\rm p} } {k} v_{\rm o}^...
...
\over 1 + \alpha (1+\beta_{\rm i} - 2/\gamma) }\right] \cdot
\end{displaymath}](/articles/aa/full_html/2009/09/aa11034-08/img38.gif)