Why did Comet 17P/Holmes burst out?

W. J. Altenhoff; E. Kreysa; K. M. Menten; A. Sievers; C. Thum; A. Weiss

doi:10.1051/0004-6361:200810458

Free Access

Issue		A&A Volume 495, Number 3, March I 2009


Page(s)		975 - 978
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361:200810458
Published online		20 January 2009

Nucleus splitting or delayed sublimation?

W. J. Altenhoff¹ - E. Kreysa¹ - K. M. Menten¹ - A. Sievers³ - C. Thum² - A. Weiss¹

1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - IRAM, University campus, 38406 St. Martin d'Herès, France
3 - IRAM, Pico Veleta, Granada, Spain

Received 25 June 2008 / Accepted 15 December 2008

Abstract
Based on millimeter-wavelength continuum observations we suggest that the recent ``spectacle'' of comet 17P/Holmes can be explained by a thick, air-tight dust cover and the effects of H₂O sublimation, which started when the comet arrived at the heliocentric distance $\le$ 2.5 AU. The porous structure inside the nucleus provided enough surface for additional sublimation, which eventually led to the break up of the dust cover and to the observed outburst. The magnitude of the particle burst can be explained by the energy provided by insolation, stored in the dust cover and the nucleus within the months before the outburst: the subliming surface within the nucleus is more than one order of magnitude larger than the geometric surface of the nucleus - possibly an indication of the latter's porous structure. Another surprise is that the abundance ratios of several molecular species with respect to H₂O are variable. During this apparition, comet Holmes lost about 3 $\%$ of its mass, corresponding to a ``dirty ice'' layer of 20 m.

Key words: comets: general - comets: individual: 17P/Holmes

1 Introduction

Comet 17P/Holmes was serendipitously discovered during an outbreak on 1892 November 6 by Holmes (reported by Plummer 1893) while he was observing the nearby Andromeda galaxy (M 31). Until early 1893 January, the comet faded from magnitude 4 to 9-10, after which a second eruption to $\approx$ 5 mag occurred. Obviously, this light curve is different in time dependence and amplitude from what was observed during the most recent apparition (2007/8). After the early observations, Comet Holmes was lost for some years, but later on recovered as an almost ``dead'' comet with magnitudes of $\approx$ 16-17 near every perihelion. Whipple (1986) analyzed the historic data again and explained the two outbursts by grazing encounters of a small hypothetical satellite with the nucleus: the first one on 1892 Nov. 4.6, 1892 and the second on 1893 January 16.3; even though these encounters could not be confirmed, his review of the historic observations allows this event to be discussed again in connection with the latest outburst discussed in this paper.

Montalto et al. (2008) report a significant disassembly of the nucleus, not even excluding a complete disintegration. Earlier, Sekanina (1982) had classified types of splitting comets: (a) single comets that break up into two or more; (b) comets that disintegrate or suddenly disappear; (c) and those with a pancake-shaped companion nucleus that disintegrates into microscopic dust grains. Recently, Sekanina (2008) summarized the optical observations of 17P/Holmes and some other comets for comparison. All types of splitting comets start in his hypothesis with a major outburst. The ``megaburst'' of 17P/Holmes is of type (c), starting with an exothermic reaction, resulting in a rapidly expanding cloud of microscopic dust particles. But not all major outbursts end in splitting: e.g., the one of comet Halley on 1991 February 12 at a heliocentric distance, r, of 14 AU (Sekanina et al. 1992).

2 The nucleus

2.1 Time line

The ``engine'' behind the cometary activity of Comet Holmes is the production of gaseous water as described by Delsemme (1982). Its production rate, Q(H₂O), is a function of heliocentric distance. It is $\propto$ 1/r²for low values of r, while for r $\ge1.5$ AU the dependence becomes highly nonlinear. Delsemme defines the limit of sublimation r₀, the heliocentric distance beyond which 97.5% of the energy received by insolation is re-radiated, and only $\le$ 2.5% are used for vaporization. For water ice, r₀ is about 2.5 AU.

Comet Holmes is a short-period comet in the Jupiter family (a JFC). Its average perihelion distance, q, over the last 6 apparitions was $\approx$ 2.2 AU (Marsden & Williams 1999), close to the limit of H₂O sublimation. But the perihelion distance of the most recent apparition was at a q of 2.05 AU. With the steepened production rate, mentioned above, the H₂O production is increased by a factor of 2. This is possibly responsible for the outburst.

The outburst happened according to Hsieh et al. (2007) on 2007 October 23.8, 173 days after perihelion passage, or 361 days after crossing r = 2.5 AU. Probably - because of the low-level cometary activity - the nuclear surface was free of ice and the icy nucleus was covered by some sort of a rubble pile (Jewitt 1992) or dust-particle mantle, causing the delay of visible cometary sublimation by months. During this period, the dust cover was ``air tight'', preventing the sublimated gas to escape. Sublimation inside the nucleus continued until the gas set free by this process broke up the dust mantle - the ``outburst''.

2.2 Model parameter

Dust cover. All accurately measured cometary nuclei show a geometric albedo, pbetween 0.02 and 0.05 (see e.g. Jewitt 2005), which is indicative of a dust cover. If closely packed, this material is thought to have a density, $\rho$ $\approx$ 1 g cm^-3, as inferred from numerous radar observations (Harmon 1999; Harmon et al. 2005). Information from the collision caused by the Deep Impact mission revealed that the nucleus of comet Tempel 1 had a devolatilized dust cover of about 1 m, with very little H₂O inside and none on the outside (Sunshine et al. 2007) - identical to what we assume for 17P/Holmes. Below the dust cover of comet Tempel 1, an at least 10 m thick layer of fine grained water ice particles was found, which appeared to be free of refractory impurities! This ``clean'' ice may originate from repeated sublimation and deposition inside the enclosed nucleus approaching and leaving the solar neighborhood. It is likely that comet Holmes has a similar layer. But for our model we neglect this detail and assume for the mass estimates ``dirty'' amorphous H₂O ice throughout the nucleus.

Diameter. Until recently, the resolution of optical telescopes was not high enough to directly measure the nuclear diameters of JFCs. Instead, absolute magnitudes of the nuclei were determined and nuclear diameters were calculated, assuming a geometric albedo p = 0.04, because observations constrain the albedo to $0.02 < p \le 0.05$ (see e.g. Jewitt 2005). For 17P/Holmes an absolute magnitude, H $_{\rm N}$ , of 16.6 (Tankredi 2006) was found and a median nuclear diameter, $d_{\rm N}$ , of 3.2 km derived within the limits of 4.6 and 2.9 km, corresponding to the albedo range. Meanwhile, Lamy et al. (2005) report a diameter $d_{\rm N} = 3.42$ km, obtained by a single snapshot by the Hubble space telescope (HST). We prefer this direct measurement, even though it might need a correction, if the nucleus is not spherical.

Bulk density, porosity. The bulk density may change from comet to comet, depending, e.g., on the outgassing history. For our model the value $\rho$ = 0.5 g cm^-3 was selected, derived by Rickman (1989) for the comet Halley data and from observations of 29 short period comets by Rickman et al. (1987). For the porosity (fraction of void volume/bulk volume) we assume a value 0.60. This provides ample storage for sublimated molecular gas inside the nucleus.

Equilibrium temperature. One needs to know the brightness temperature, $T_{\rm b}$ , of the nucleus and the dust grains to calculate their emission. In the absence of new data, we assume that they both will be close to the equilibrium temperature, $T_{\rm eq}$ . For a heliocentric distance of r $\approx$ 2.45 AU and an albedo p of 0.04, we assume $T_{\rm b}$ $\approx$ 175 K, i.e., identical to $T_{\rm eq}$ .

3 Observations

Table 1: Flux densities $S_\nu (250)$ at 250 GHz in a 11'' beam of 17P/Holmes. $\Delta$ and r are the comet's distance from Earth and Sun at time T after the outbreak.

The outburst of comet 17P/Holmes came at an unfavorable moment, when on Pico Veleta the MAx-Planck Millimeter BOlometer array (MAMBO) had not been installed on the 30 m telescope; in Effelsberg the 9 mm wavelength receiver was not operational at the 100 m telescope; and for the Atacama Pathfinder EXperiment (APEX) 12 m telescope, the comet was below the declination limit. About 25 days later, when MAMBO went back into operation, we started a series of maps and ON/OFF observations at its effective frequency of 250 GHz, trying to see the aftermath of the outburst. The observing and evaluation procedures of MAMBO observations are standard routines and have been frequently reported; see e.g. Altenhoff et al. (2000).

The results are collected in Table 1. Prior to our measurements, the comet had already been detected with the Plateau de Bure Interferometer (PdBI) near 90 GHz by Boissier et al. (2008, 2009). Their results, generously made available to us prior to publication, are included in our analysis. We have scaled the 90 GHz flux densities, obtained with a synthesized beam of 5.7 $\times$ 7.3 arcsec, to the angular resolution of our MAMBO data (11 arcsec), and we extrapolated the signal to 250 GHz with the canonical spectral index of comets SI = 2.7, reversing the procedure of Jewitt & Matthews (1999) to derive the spectral index of comet Hale-Bopp. This method was intensively tested by Altenhoff et al. (2008).

Each stage of the optical development has an equivalent one at millimeter (mm) wavelengths. The optical observations are summarized in Sekanina (2008), e.g. with the total magnitude m₁ as a function of time, ``the light curve''.

The mm data are compiled in Table 1 and Fig. 1. The extrapolation of the PdBI observations to 250 GHz is fairly accurate, and the combined errors of extrapolation and observation are indicated by the size of the symbols. The small beam broadening by the comet, reported by Boissier et al. (2008) shows that the source is optically thin. The two data sets are interpolated, suggesting a signal loss of 7% per day. The series of nuclear magnitudes m₂ shows a similar slope.

In a separate paper, Altenhoff et al. (2008) show that most cometary mm/radio light curves can be represented by the following equation:

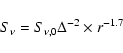
$\begin{displaymath}S_{\nu} = S_{\nu,0} \Delta^{-2} \times r^{-1.7} \end{displaymath}$

with $\Delta$ and r the geocentric and heliocentric distances in AU, respectively. The constant $S_{\nu,0}$ = 74.5 is derived from the last data points.

Thus the light curve is calculated and plotted in Fig. 1. It is obviously a reasonable fit for the time after day 33, when insolation and dust production (determining the intensity of the mm radiation) are apparently coming to equilibrium. For the first 30 days, this radio light curve is the baseline for the burst. As a further indicator of cometary activity, we use the nuclear magnitude, m₂, reported with the astrometric positions (Marsden 2007). These values with limited accuracy are averaged over three days (typically over 100 observations) to reduce the noise. These data also confirm increased nuclear activity in the first 30 days. Red circles show the H₂O production rates measured with the Solar Wind ANisotropy (SWAN) experiment on the SOlar Heliospheric Observatory (SOHO) reported by Combi (2007). This system has a beam of about one degree, probing the water production of about 4 days. This may be a crude guess, considering that we are using observing results obtained with very different resolutions. Even though we guess that, with the resulting smearing, the production rate might fit even better to our observed extended cometary activity.

Spectroscopic observations of HCN by Biver et al. (2008) at Pico Veleta and at the Caltech submillimeter observatory (CSO), and by Drahus et al. (2007, 2008) with the Arizona radio observatory (ARO), are shown for comparison. The data sets are consistent which each other and show a steeper decay than the cometary activity described before.

$\begin{figure} \includegraphics[angle=-90,width=8cm,clip]{0458fr.ps} \end{figure}$

Figure 1:

Comet 17P/Holmes: compilation of spectroscopic and continuum observations. The black dots and the black diamonds represent the mm continuum data at 250 GHz, taken with the 30 m and the PdBI, respectively. Dashed line: model of mm halo (see text). Red open circles: H₂O emission, observed with SWAN, light blue dots: HCN emission, blue squares: HCN emission. See text for references. The dotted magenta curve shows the optical nuclear magnitudes m₂, as an indicator of the nuclear activity. The spectroscopic data sets are normalized to their respective maximum.

Open with DEXTER

4 Mass determination

Fine dust. Optically, the scattered light by small dust particles is dominating the appearance of comets, even though the mass of these particles is low. Sekanina (1982) has estimated the mass of $2~\mu$ m sized fine dust in comet 17P/Holmes (see Table 2) near its outbreak. The size of the scattering particles is too small to detect with radio or mm telescopes. This dust is responsible for the optical appearance seen at magnitude m₁. The particulate dust and the bulk of the molecular gas are almost invisible optically.

Particulate dust. Radio and mm continuum observations measure the thermal emission of dust particles of size $\ge$ 10% of the observing wavelength, here $\ge$ 0.2 mm. Since the observed signal is proportional to the integrated particle cross sections, but the particle mass is proportional to its volume, the mass of big particles is underestimated, so observations at different wavelengths are needed for a more precise mass estimate. We estimate the dust mass with the photometric diameter to be the size of a disk at the distance of the comet with its equilibrium temperature, radiating as black body, yielding the same flux density as the radio/mm halo. For cometary dust, we find that the black body condition (emissivity $\approx$ 1) is fulfilled with a density of 1 g cm^-3 and a layer depth of 3 wavelengths (as confirmed by the rigorous halo evaluation for comets Hyakutake and Hale-Bopp (Altenhoff et al. 2000). This allows calculation of the dust mass in the halo for any observed signal.

Dust production rate. The average particle moves through the telescope's diffraction beam in about 60 h, and the resulting dust production rate and the dust mass in the beam are listed in Table 2.

Table 2: Mass budget.

Hypothetical pre-burst dust. The radio light curve, as defined above, can be extrapolated backwards over the whole apparition to calculate ``hypothetical'' signals and masses that would have been emitted in the absence of the dust cover. This total hypothetical mass is a factor 3-4 higher than the total mass released within 33 days after the outburst, i.e. the burst dust mass. Thus, we can safely assume that the insolation provided enough energy to start sublimation within the nucleus.

Accuracy estimate. Within our observing interval, the mass in the halo is approximately proportional to the observed flux density in the beam, thus to the observing accuracy. Therefore the relative accuracy from day to day and of the dust production rate is quite good. The absolute accuracy depends on our knowledge of the absorption coefficient $\kappa$ of cometary dust, whose uncertainty was estimated by Altenhoff et al. (2000) to be about a factor 2. The accuracies of the mass determinations of the small-grained dust (Sekanina 2007) and of water (Combi 2007) have unfortunately not been reported.

5 Interpretation

Start of the outburst. The nuclear structure of comets 9P/Tempel 1 and 17P/Holmes before the outbursts are probably alike, a densely packed dust cover ( $\approx$ 1 m) below a layer of pure water ice ( $\approx$ 10 m), below amorphous dirty H₂O ice, whose upper part is possibly free of highly volatile molecules. At 9P/Tempel 1 the impactor acted as the exothermic energy source to blow off the pancake-shaped dust cover, as the scheme of Sekanina (2007) suggests, making it a type (c) split nucleus. The development for 17P/Holmes is different. When H₂O sublimation started inside the porous nucleus, water vapor spread all over the nucleus, initiating more sublimation; deeper inside, and even other molecular ices with lower sublimation points were heated, stored there at lower temperatures. The effective sublimating surface inside the nucleus, estimated as excess over the emission after the burst on day 35 when it was near equilibrium with insolation, was more than 14 times the nuclear surface, corresponding roughly to the nuclear size of comet Hale-Bopp. The sum of the saturated partial pressures of all ice species was obviously breaking up the air tight dust mantle, allowing the cometary wind to start through the dust mantle and lifting dust particles, piece by piece, into the halo. The break up of the dust mantle is hardly spectacular, compared with the full start of cometary wind.

Time scale of the outburst. Different versions exist of the development of the outburst. Sekanina (2008, 2007) refers to an explosion and a single exothermic event, and Biver et al. (2008) and others report a water production rate, which almost ends after 3 days. In Fig. 1 the continuum observations are plotted, showing that the outburst-related increased continuum emission lasted for about 30 days, as did the increased nuclear magnitude m₂. Additional proof are the numerous photographs taken within the first month of the outburst; see e.g. Sekanina (2008), in which the comet appears as a filled Plerion rather than a shell, implying that the dust injection into the coma continued after the ``explosion'' for quite some time.

Molecular production rates. Production of gas-phase molecules is responsible for all the cometary activity. It is predominantly the cometary wind of the H₂O molecules, which lifts the dust particles from the nucleus, so a correlation between H₂O and dust production is expected. Usually the production of different molecules shows a fixed ratio, so that one can, e.g., predict the H₂O production rate from HCN observations. Not so for comet Holmes! Figure 1 shows that H₂O production, observed with the SWAN satellite, lasts at least for a month as does the enhanced mm continuum emission, while e.g. the spectral lines of HCN, CO, NH₃(Drahus et al. 2007; Biver et al. 2008; Menten 2007) had a big signal at the start, which apparently petered out dramatically after 3 days, as shown in Fig. 1. The reason may be the temperature/depth structure of the nucleus, because the near surface ice might be free of higher volatile molecules.

Mass comparison. All derived masses are collected in Table 2, where the total mass and the mass of the dust cover have been calculated with the model values. The mass of the 2 $\mu$ m sized dust, determined immediately after the outburst by Sekanina (2008), is surprisingly high, compared to the total mass of the dust layer! Even the total particulate dust mass (grains of size 0.2 to 7 mm) is smaller. Integrated over the 33 days of increased cometary activity, the dust mass produced by the outburst is $\approx$ 2% of the comet's total mass. Surprisingly low is also the H₂O mass released in the first part of the outburst, when we would have expected a mass comparable to the particulate dust mass. The hypothetical dust mass, calculated from the radio light curve backwards, is about a factor of 3-4 higher than the total mass in the burst. The energy released in the burst can be provided by the insolation before the burst, even allowing energy losses through re-radiation by the dust cover.

The total accounted mass loss during this apparition (mass of $2~\mu$ m sized dust, burst dust mass, burst H₂O mass) is in total $\le$ 3.5% of the total nuclear mass. If a bulk density of $\rho$ = 0.5 is assumed for the outer nucleus, this loss corresponds to a layer of 20 m thickness which is the same order of magnitude as found from observations of other comets.

5.1 Alternative models

Sekanina (2007, 1982) explained the outburst of comet 17P/Holmes as a splitting nucleus, whereby the secondary nucleus is a fragment of a jettisoned insulation mantle of debris. The splitting starts with an exothermic event. His model considers neither particulate dust with particles $\ge$ 0.2 mm and nor the H₂O production, both of which contribute at least as much mass, each seperately as doeshis ``secondary nucleus''.

6 Conclusion

The historic outbursts, as discussed by Whipple (1986), show several similarities to the present one, suggesting that they happened the same way, but in 2 steps. After all, comet 17 P/Holmes is a comet like many others whose appearance is determined by sublimation of cometary ices. What makes it peculiar is that it had a big dust cover and that it seldom comes close enough to the Sun to afford a great display of activity. Dust covers of cometary nuclei are standard (see model of Horanyi et al. 1984) and do not indicate a splitting comet. We think that the delayed sublimation, as explained above, is a viable alternative to the theory of splitting or sudden fragmentation of the cometary nucleus.

Acknowledgements

We are grateful to Dr. J. Boissier (IRAM) for communicating the 90 GHz results to us prior to publication. We thank the director of IRAM, Dr. P. Cox, for granting special observing time and the staff on Pico Veleta, Spain, for their support of the observing program.

References

Altenhoff, W. J., Bieging, J. H., Butler, B., et al. 1999, A&A, 348, 1020 (In the text)
Altenhoff, W. J., Bertoldi, F., Thum, C., et al. 2008, A&A, in preparation (In the text)
Biver, N., Bockelée-Morvan, D., Wiesemeyer, H., et al. 2008, Asteroids, Comets, Meteors 2008 held July 14-18, in Baltimore, Md. LPI Contribution No. 1405, paper 8146 (In the text)
Boissier, J., Bockelée-Morvan, D., Biver, N., et al. 2008, Asteroids, Comets, Meteors 2008 held July 14-18, in Balimore, Md. LPI Contribution No. 1405, paper 8081 (In the text)
Boissier, J., Bockelée-Morvan, D., Biver, N., et al. 2009, in preparation (In the text)
Combi, M. R., Maekinen, J. T. T., Bertaux, J.-L., et al. 2007, Central Bureau for Astronomical Telegrams, Cambridge, USA, IAU Circ., 8905 (In the text)
Delsemme, A. H. 1982, in Comets, Ed. L. L., Wilkening (Tucson: Univ. Arizona Press), 85 (In the text)
Drahus, M., Paganini, L., et al. 2007, Central Bureau for Astronomical Telegrams, Cambridge, USA, IAU Circular, 8891 (In the text)
Drahus, M., Paganini, L., et al. 2008, Asteroids, Comets, Meteors 2008 held July 14-18, in Baltimore, Md. LPI Contribution No. 1405, paper 8340 (In the text)
Fernández, Y. R., Jewitt, D. C., & Sheppard, S. S. 2001, ApJ, 553, L197 [NASA ADS] [CrossRef]
Gaillard, B., Lecacheux, J., & Colas, F. 2007, CBET, 1123 [NASA ADS], Central Bureau for Astronomical Telegrams, Cambridge, USA
Harmon, J. K., & Nolan, M. C. 2005, Icarus, 176, 175 [NASA ADS] [CrossRef] (In the text)
Harmon, J. K., Campbell, D. B., Ostro, S. J., & Nolan, M. C. 1999, Planet. Space Sci., 47, 1409 [NASA ADS] [CrossRef] (In the text)
Horanyi, M., Gombosi, T. I., Cravens, T. E., et al. 1984, ApJ 278, 449 [NASA ADS] (In the text)
Hsieh, H. H., Fitzsimmons, A., & Pollacco, D. L. 2007, Central Bureau for Astronomical Telegrams, Cambridge, USA, IAU Circ., 8897 (In the text)
Jewitt, D. C. 1992, in Observations and Physical Properties of Small Solar System Bodies, 30th Liege International Symp., Liège, 85 (In the text)
Jewitt, D. 2005, in Trans-Neptunian Objects and Comets, Saas-Fee Advanced Course, ed. K. Altwegg, W. Benz, & N. Thomas (Berlin: Springer-Verlag), 35, 1 (In the text)
Jewitt, D. C., & Matthews, H. 1999, AJ, 117, 1056 [CrossRef] (In the text)
Lamy, P. L., Toth, I., Fernández, Y. R., & Weaver, H. A. 2005, in Comets II, ed. H. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: Univ. Arizona Press), 223 (In the text)
Marsden, B. G. 2007, Observations of Comets. Bi-weekly listing in: Minor Planet Electronic Circulars, Minor Planet Center, Cambridge (In the text)
Marsden, B. G., Williams, & Gareth V. 1999, Catalogue of cometary orbits, 13th edition, Minor Planet Center, Cambridge, USA (In the text)
Menten, K. M. 2007, private communication (In the text)
Montalto, M., Riffeser, A., Hopp, U., et al. 2008, A&A, 479, L45 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Plummer, W. E. 1893, Report of the Council, MN, 53, 266 (In the text)
Rickman, H. 1989, Adv. Space Res., 9, 59 [NASA ADS] [CrossRef] (In the text)
Rickman, H., Kamel, L., Festou, M. C., & Froeschlé, C. 1987, in Symposium on the Diversity and Similarity of Comets, ed. E. J. Rolfe, & B. Battrick, ESA SP-278, Nordwijk, 471 (In the text)
Sekanina, Z. 1982, in Comets, ed. L. L. Wilkening (Tucson: Univ. Arizona Press), 251 (In the text)
Sekanina, Z. 1991, in Comets in the Post-Halley Era, ed. R. L. Newburn, M. Neugebauer, & J. Rahe (Dordrecht: Kluwer Academic Publisher), 2, 769
Sekanina, Z. 2007, Electronic Telegram, 1118 [NASA ADS], Central Bureau for Astronomical Telegrams, Cambridge, USA (In the text)
Sekanina, Z. 2008, ICQ, 30, 3 [NASA ADS] (In the text)
Sekanina, Z., Larson, S. M., Hainaut, O., et al. 1992, A&A, 263, 367 [NASA ADS] (In the text)
Sunshine, J. M., Groussin, O., Schultz, P. H., et al. 2007, Icarus, 191, 73 [NASA ADS] [CrossRef] (In the text)
Tancredi, G., Fernandes, J. A., Rickman, H., & Licandro, J. 2006, Icarus, 182, 527 [NASA ADS] [CrossRef] (In the text)
Whipple, F. 1984, Icarus, 60, 522 [NASA ADS] [CrossRef] (In the text)

All Tables

Table 1: Flux densities $S_\nu (250)$ at 250 GHz in a 11'' beam of 17P/Holmes. $\Delta$ and r are the comet's distance from Earth and Sun at time T after the outbreak.

Table 2: Mass budget.

All Figures

$\begin{figure} \includegraphics[angle=-90,width=8cm,clip]{0458fr.ps} \end{figure}$	Figure 1: Comet 17P/Holmes: compilation of spectroscopic and continuum observations. The black dots and the black diamonds represent the mm continuum data at 250 GHz, taken with the 30 m and the PdBI, respectively. Dashed line: model of mm halo (see text). Red open circles: H₂O emission, observed with SWAN, light blue dots: HCN emission, blue squares: HCN emission. See text for references. The dotted magenta curve shows the optical nuclear magnitudes m₂, as an indicator of the nuclear activity. The spectroscopic data sets are normalized to their respective maximum.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.