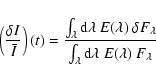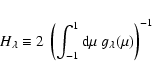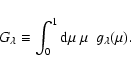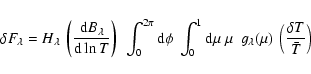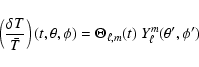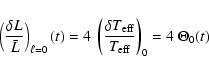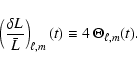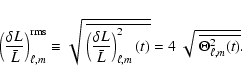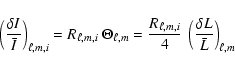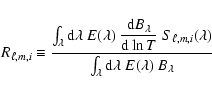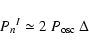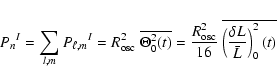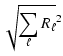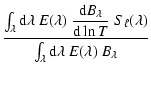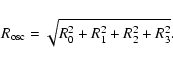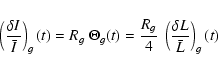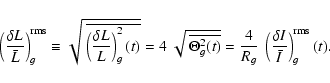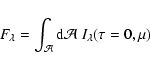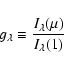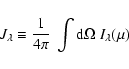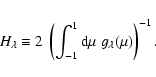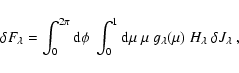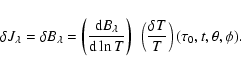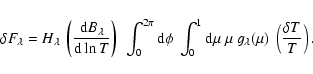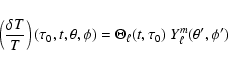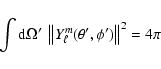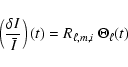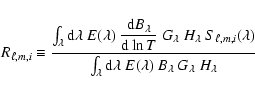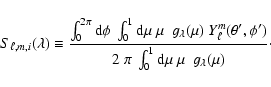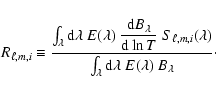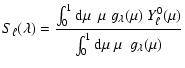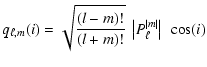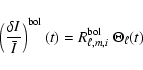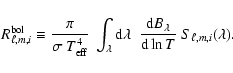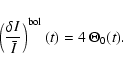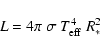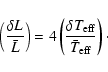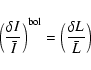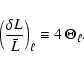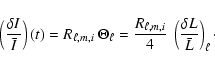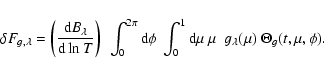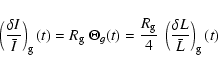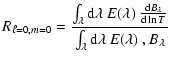Intrinsic photometric characterisation of stellar oscillations and granulation

E. Michel; R. Samadi; F. Baudin; C. Barban; T. Appourchaux; M. Auvergne

doi:10.1051/0004-6361:200810353

Free Access

Issue		A&A Volume 495, Number 3, March I 2009


Page(s)		979 - 987
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361:200810353
Published online		14 January 2009

Solar reference values and CoRoT response functions

E. Michel¹ - R. Samadi¹ - F. Baudin² - C. Barban¹ - T. Appourchaux² - M. Auvergne¹

1 - Observatoire de Paris-LESIA, CNRS (UMR 8109), Université Pierre et Marie Curie, Université Denis Diderot, Pl. J. Janssen, 92195 Meudon, France
2 - Institut d'Astrophysique Spatiale, UMR8617, Université Paris X, Bât.121, 91405 Orsay, France

Received 9 June 2008 / Accepted 6 December 2008

Abstract
Context. Measuring amplitudes of solar-like oscillations and the granulation power spectral density constitute two promising sources of information to improve our understanding and description of the convection in outer layers of stars. However, different instruments, using different techniques and different bandpasses, give measurements that cannot be directly compared to each other or to theoretical values.
Aims. In this work, we define simple response functions to derive intrinsic oscillation amplitudes and granulation power densities, from photometry measurements obtained with a specific instrument on a specific star.
Methods. We test this method on different photometry data sets obtained on the Sun with two different instruments in three different bandpasses.
Results. We show that the results are in good agreement and we establish reference intrinsic values for the Sun with photometry. We also compute the response functions of the CoRoT instrument for a range of parameters representative of the Main Sequence solar-like pulsators to be observed with CoRoT. We show that these response functions can be conveniently described by simple analytic functions of the effective temperature of the target star.

Key words: Sun: oscillations - Sun: granulation - stars: oscillations - techniques: photometric - convection

1 Introduction

Solar-like oscillations are being detected in a rapidely growing number of stars (see e.g. Bedding & Kjeldsen 2007). The excitation of these oscillations, first observed in the Sun, is attributed to the acoustic noise generated by convection in the outer layers of stars and the measurement of their amplitude is a source of information on the convection process (see e.g. Samadi et al. 2007a,b). The existing theoretical works generally consider parametric scaling laws calibrated on the Sun. However, as noticed by Kjeldsen et al. (2005), measurements made on different stars with different instruments using different techniques in velocimetry or photometry, in different spectral lines or bandpasses, have different sensitivity to the oscillations. They cannot be directly compared to each other, or to theoretical values. The comparison to the Sun is not straightforward either, since the different existing data sets obtained on the Sun have not been translated into a proper standard reference suitable for comparison with stars. Kjeldsen et al. (2005) initiated such a normalization work and a comparison between several stars. Kjeldsen et al. (2008) measured the solar oscillation amplitude with stellar techniques, aiming at setting up a consistent reference for stellar oscillation measurements. This was done with velocimetry, since until now the vast majority of solar-like oscillations measured in other stars has been obtained with this technique. However, CoRoT (Baglin et al. 2006) has started photometric measurements of oscillations in solar-like pulsators which will need to be measured quantitatively and compared with those of the Sun and with those obtained in velocimetry. In addition to oscillations, rapid photometry might allow us to measure, in approximately the same domain of frequency, the power density spectrum contribution associated with the stellar granulation. Granulation being a manifestation of the convective motion at the photosphere level, the profile of its power density spectrum is expected to reflect characteristic time scales and geometric scales associated with the convection process as described by heavy 3D numerical simulations (see e.g. Trampedach et al. 1998; Ludwig 2006) or by parametrized models (see e.g. Baudin et al. 2007).

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig1.eps} \end{figure}$

Figure 1:

Observational power density spectrum obtained for: SPM-blue a) and SPM-green b) data over 700 days; a moving mean is applied with a 4 ${\rm\mu }$ Hz boxcar (plain black line); the same spectrum highly smoothed with a 0.405 mHz boxcar (3 $\Delta$ ) is superimposed (plain light grey line [yellow]); individual powerlaws associated with granulation and mesogranulation are shown (dash lines [purple]); the white noise component (horizontal line [red]); the global fit of solar background + white noise components is represented (plain grey line [green]) but differs from the mean power density only in the domain of oscillations. Vertical error bars associated with the fit precision are illustrated at different frequencies for each component of the fit. For clarity, in the case of the white noise component, the error bar is represented only once at 1 mHz.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig2.eps} \end{figure}$	Figure 2: Same as Fig. 1 for, from top to bottom: SPM-blue ( a), SPM-green ( b), SPM-red ( c) data over 700 days and PMO6 ( d) data over 800 days, but here we forced C_i=4.
Open with DEXTER

In the present work, we consider measurements of solar photometric variations obtained with two different instruments in four different bandpasses (SOHO/VIRGO/PMO6 and SPM three channels). In the corresponding instrumental power density spectra, we fit contributions from the solar background and from the acoustic oscillations (Sect. 2). In Sect. 3, we establish a simple instrumental response function relating the instrumental power density measurement to the intrinsic bolometric luminosity relative variation. These response functions can be applied to infer the intrinsic (bolometric) power density of the solar background from specific photometry measurements. They also can be used to derive intrinsic amplitudes of solar radial oscillations from the same data. We discuss how they can be adapted for non-radial modes. Following Kjeldsen et al. (2005) and Kjeldsen et al. (2008), we also propose to relate the oscillation mean power density measurement to an intrinsic amplitude chosen here to be the bolometric amplitude for radial modes. In Sect. 4, we show that the results obtained with the different data sets considered here are consistent to a good approximation and allow us to produce a reference value of bolometric radial oscillation amplitude for the Sun observed as a star, and a reference bolometric power density spectrum for Solar granulation. Then (Sect. 5), we compute the response functions adapted to the CoRoT instrument for stars representative of potential solar-like pulsators on the Main Sequence in terms of effective temperatures, $\log ~ g$ values and chemical compositions. We show that to a great extent, the dependency on $\log ~ g$ and chemical composition can be neglected and that the CoRoT response functions can be conveniently described with good precision by analytic functions of $T_{\rm eff}$ .

2 Observational material and power density spectra

We consider four data sets obtained on the Sun with different techniques and different band pass by SOHO/VIRGO/PMO6 (essentially bolometric variations) and by SOHO/VIRGO/SPM (photon counting) in three narrow (5 nm) bands at 402 nm (blue), 500 nm (green) and 862 nm (red) (Frohlich et al. 1997). For each of these time series, we compute the power density spectrum shown in Figs. 1 and 2. Following the technique proposed by Kjeldsen et al. (2005) for stellar oscillation measurements, we smooth these spectra with a boxcar of width 405 $\mu$ Hz corresponding to 3 times the solar large separation (135 $\mu$ Hz).

Then, we perform a least square fit of each spectrum with three components: a flat white noise contribution essentially due to photon counting noise, the solar background contribution detailed hereafter, and on top, the stellar oscillation spectrum contribution. For the solar background contribution, following Harvey (1985) and Andersen et al. (1998a), we consider a sum of powerlaws: $P(\nu)= \Sigma_i P_i(\nu)$ , and $P_i(\nu)=a_i {\zeta_i}^2 {\tau}_i / (1+ (2 \pi \tau_i \nu)^{C_i})$ (also noted $P_i(\nu)=A_i / (1+ (B_i \nu)^{C_i})$ for convenience hereafter), with $\nu$ the frequency, $\tau_i$ the characteristic time scale and C_i the slope at high frequency associated with each powerlaw, and a_i a normalizing factor such as ${\zeta_i}^2 = \int P_i(\nu)$ d $\nu$ corresponding to the variance of the time series. Note that in the case of Harvey (1985), C_i being set to 2, a_i=2. This corresponds to a signal whose autocorrelation in time has a decreasing exponential behaviour. However, as mentioned by Harvey (1985), other values for the decay rate power over time might be found for different types of data probing the atmosphere at different heights (see e.g. Andersen et al. 1998a).

The physical processes most commonly considered in the solar background and represented by such power laws are: activity (predominant up to $\sim$ 10 $\mu$ Hz), supergranulation (up to $\sim$ 100 $\mu$ Hz), mesogranulation (up to $\sim$ 1 mHz), and granulation (see e.g. Aigrain et al. 2004; Andersen et al. 1998b; Anklin et al. 1998). In the present study, we will focus on the two latter processes showing significant contribution above 100 $\mu$ Hz, in the frequency domain where oscillations are found.

An estimate of the two first contributions (white noise and solar background) is obtained by a simultaneous fit of the spectrum outside the domain where the oscillation signal is seen with function $D+ \Sigma_i P_i(\nu)$ , where D represents the white noise contribution. After subtraction of these two components, we isolate the one due to stellar oscillations.

The two powerlaw components (7 parameters: A_i, B_i, C_i, and D) give a satisfactory fit of the background for our purpose and we do not find it necessary to include other components like supergranulation or activity.

As shown by error values in Table 1, the fit gives satisfactory results in the case of SPM data, especially for the blue and green channels. In the case of SPM/red channel, the coefficients are obtained with very large error bars and in the case of PMO6, the convergence precision is even worse, due to the larger white noise component. We note that these fits all suggest a value of C_i around 4, in agreement with the results obtained by Andersen et al. (1998a). We thus decided to fit again the previous function, but forcing the C_i coefficients to the value 4, thus reducing the number of free parameters to 5 and obtaining a more precise determination of them.

The results shown in Fig. 2 (see also Table 2) are very satisfactory, and we will refer to these values hereafter.

Table 1: Fit with seven parameters. Values of the parameters are given as well as the associated one-sigma error estimates.

Table 2: Fit with five parameters.

As could be expected, the level of the intensity components (A₁ and A₂) attributed to granulation and mesogranulation is very different in the measurements associated with different techniques and different bandpasses (see Fig. 3 top). The same is true for the contribution associated to the oscillations (Fig. 3 bottom), stressing the necessity to establish a reference independent of the instrument for the Sun oscillations and for comparison with other stars to be observed with other instruments.

$\begin{figure} \par\includegraphics[width=8cm,clip]{0353fig3a.eps}\\ [2.5mm] \includegraphics[width=8cm,clip]{0353fig3b.eps} \end{figure}$	Figure 3: a) Observational instrumental power density spectrum associated with the stellar background contribution and estimated as described in the text, for PMO6 data (plain black line), SPM-blue (dot [blue]), SPM-green (dash [green]), SPM-red (long dash [red]); b) same for the oscillation contribution.
Open with DEXTER

3 Instrumental response functions

In this section we establish a relation between intensity variation observed with a given instrument (hereafter ``instrumental flux variation'') and an intrinsic quantity defined as the ``bolometric luminosity variation''. This relation features a response function characteristic of the instrument.

We derive the response function for an individual non-radial mode (Sect. 3.2), then for a smoothed power density spectrum (Sect. 3.3), and finally for the granulation (Sect. 3.4).

This is done taking into account both the band-width of the instrument, the spectral energy distribution of the given star (approximated by a black body law) and the dependence of the stellar limb-darkening with the wavelength (given by stellar atmosphere models).

3.1 Instrumental flux variation and local temperature variation

Here, we express the relative instrumental flux variation $\delta I/\bar{I}$ as a function of the local relative variation of the temperature at the stellar photosphere $\delta T(\theta,\phi)/\bar{T}$ .

First we define the relative variation of the instrumental flux I:

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right ) (t) = { { \int_... ...ver { \int_\lambda {\rm d}\lambda ~ E(\lambda) ~ F_\lambda } } \end{displaymath}$

(3)

where $E(\lambda)$ is the global efficiency in terms of energy of the instrument at the wavelength $\lambda$ , $F_\lambda$ the flux received from the star at the wavelegth $\lambda$ and $\delta F_\lambda$ its variation.

Then, following the approach of Berthomieu & Provost (1990), we show (see Appendix A) that $F_\lambda$ and $\delta F_\lambda$ can be approximated as

$\begin{displaymath}F_\lambda = 2 \pi ~ H_\lambda ~ G_\lambda ~ {B}_\lambda \end{displaymath}$

(4)

where $B_\lambda$ is the black body law evaluated at the photosphere, i.e. at $T=T_{\rm eff}$ and where we have defined

$\begin{displaymath}H_\lambda \equiv 2 ~ \left (\int_{-1}^{1} {\rm d}\mu ~ g_\lambda(\mu) \right) ^{-1} \end{displaymath}$

(5)

and

$\begin{displaymath}G_\lambda \equiv \int_0^1 {\rm d} \mu ~ \mu ~ ~ g_\lambda(\mu). \end{displaymath}$

(6)

with $g_\lambda$ the limb-darkening function, $\mu=\cos(\theta)$ and $\theta$ and $\phi$ refer to the spherical coordinates for a z-axis pointing toward the observer (observer reference frame) and

$\begin{displaymath}\delta F_\lambda = H_\lambda ~ \left ( { {{\rm d} B_\lambda} ... ...u ~~ g_\lambda(\mu) ~ \left({{\delta T} \over \bar{T}} \right) \end{displaymath}$

(7)

where T is the temperature, $\delta T$ its variation, the meaning of other terms staying the same.

At this stage, we have expressed the instrumental flux relative variation $\delta I/\bar{I}$ as a function of $\delta T/\bar{T}$ the local ( $\mu$ , $\phi$ ) relative variation of the temperature at the photosphere.

3.2 Response function for an individual non-radial mode

Here, in the case of an individual oscillation mode, we show that we can relate $\delta T(\theta,\phi)/\bar{T}$ to a ``bolometric luminosity relative variation'' $(\delta L/\bar{L})_{\ell,m}$ , defined as an extension of the specific case of radial modes where $(\delta L/\bar{L}) = 4 \delta T_{\rm eff}/\bar{T}_{\rm eff}$ .

As detailed in Appendix A, we consider the relative temperature fluctuations associated with a mode with degree $\ell$ and azimuthal order m:

$\begin{displaymath}\left ( { {\delta T} \over \bar{T} } \right ) (t,\theta,\phi) = \Theta_{\ell,m}(t) ~ Y_\ell^m (\theta^\prime,\phi^\prime) \end{displaymath}$

(8)

where $\Theta_{\ell,m}(t)$ is the intrinsic and instantaneous mode amplitude in terms of temperature fluctuation, $Y_\ell^m$ is the spherical harmonic associated with the mode with degree $\ell$ and azimutal order m, and $(r,\theta^\prime,\phi^\prime)$ (resp. $(r,\theta,\phi)$ ) the spherical coordinate system in the pulsation frame (resp. in the observer frame). As discussed in Appendix A, $\left ( { {\delta T} / \bar{T} } \right )$ and hence $\Theta_{\ell,m}(t)$ are evaluated at the photosphere.

For a radial mode, the bolometric and instrinsic luminosity fluctuation is related to the relative instrinsic temperature fluctuation as:

$\begin{displaymath}\left (\delta L \over \bar{L} \right )_{\ell=0} (t) = 4 ~ \le... ...a T_{\rm eff} \over T_{\rm eff}} \right )_0 = 4 ~ \Theta_0 (t) \end{displaymath}$

(9)

where $T_{\rm eff}$ is the effective temperature and L the luminosity of the star. Then, by extension of the radial case, we define, in the general case, the bolometric and instrinsic mode amplitude in terms of luminosity:

$\begin{displaymath}\left (\delta L \over \bar{L} \right )_{\ell,m} (t) \equiv 4 ~ \Theta_{\ell,m}(t). \end{displaymath}$

(10)

Note that, in the present case, since the mode excitation is a random process, we rather consider the rms quantities

$\begin{displaymath}\left (\delta L \over \bar{L} \right )_{\ell,m}^{\rm rms} \e... ...,m}^2 (t)} } = 4~ \sqrt{~ \overline{ \Theta_{\ell,m}^2 (t)} }. \end{displaymath}$

(11)

The rms label will however be generally omitted in the following for conciseness of the notation.

Then, we establish the relation between $\left ( { {\delta I} / \bar{I} } \right )_{\ell,m,i}$ (the observed relative intensity fluctuations due to a given mode $(\ell,m)$ , for a given inclination i) and the instrinsic mode amplitude:

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right )_{\ell,m,i} = R... ...i} \over 4 } ~ \left (\delta L \over \bar{L} \right )_{\ell,m} \end{displaymath}$

(12)

with $R_{\ell,m,i}$ the instrumental response function associated with the mode with degree $\ell$ and azimuthal order m and inclination i. The expression for $R_{\ell,m,i}$ is:

$\begin{displaymath}R_{\ell,m,i} \equiv { {\int_\lambda {\rm d} \lambda ~ E(\lamb... ...ver { \int_\lambda {\rm d}\lambda ~ E(\lambda) ~ B_\lambda } } \end{displaymath}$

(13)

where $S_{\ell,m,i}(\lambda)$ is the so-called ``visibility'' coefficient associated with the mode.

The visibility coefficient, $S_{\ell,m,i}$ , measures the contribution of the mode integrated over the projected stellar surface, taking into account the effect of the limb-darkening (see e.g. Dziembowski 1977; Berthomieu & Provost 1990). An expression for $S_{\ell,m,i}$ is given in Eq. (A.19). Note that in the case of radial modes, S₀ is independent of $\lambda$ and S₀=1 by definition.

An interesting property of the visibility coefficients $S_{\ell,m,i}$ is that, assuming equipartition of energy among different modes of a same multiplet, the global visibility contribution of each multiplet (composed of modes of the same radial order n, same degree $\ell$ , and different azimuthal order m) is independent of the inclination i (Toutain & Gouttebroze 1993; Dziembowski 1977). It is thus possible to compute a global visibility function $S_{\ell} =\sqrt{\Sigma_m S^2_{\ell,m,i}}$ , which is independent of i for the different multiplets. This property will be useful in the next section.

3.3 Response function for smoothed oscillation power density spectrum

In the case of stellar observations, as remarked by Kjeldsen et al. (2005) the measurement of individual modes or even individual multiplets might be delicate and it might give more precise results to estimate oscillation amplitudes from the smoothed oscillation power density contribution as represented in Sect. 1. In this case, as suggested by Kjeldsen et al. (2005), the oscillation power density contribution ( $P_{\rm osc}$ , in ${\rm ppm}^2/\mu$ Hz) is smoothed over typically three or four times the large separation ( $\Delta$ ); then, once multiplied by the estimate of the large separation (in $\mu$ Hz), it is representative of P_n^I, the total power (in ${\rm ppm}^2$ ) concentrated in all modes present in one large separation (of order n). Accordingly, we have

$\begin{displaymath}\ {P_n}^I \simeq 2 ~ P_{\rm osc} ~ \Delta \end{displaymath}$

(14)

where $\Delta$ is the large separation and the factor 2 multiplying $P_{\rm osc}$ is introduced to take into account the power density spread in the negative part of the spectrum.

Let define $P_{\ell,m,i}$ as the observed power (in ${\rm ppm}^2$ ) associated with a mode $(\ell,m)$ , with inclination i. Assuming that $\Theta_{\ell,m}$ is the same for all the modes that are within the same separation and using Eq. (7), it can easily be shown that :

$\begin{displaymath}\ {P_n}^I=\sum_{l,m} {P_{\ell,m}}^I = R_{\rm osc}^2 ~ \overli... ...verline{ \left ({{\delta L } \over \bar{L}} \right)_{0}^2 (t)} \end{displaymath}$

(15)

with

$\displaystyle R_{\rm osc}$	$\textstyle \equiv$	$\displaystyle \sqrt { \sum_\ell R_\ell}^2$	(16)
$\displaystyle R_{\ell}$	$\textstyle \equiv$	$\displaystyle { {\int_\lambda {\rm d} \lambda ~ E(\lambda) ~ {\displaystyle{{{\... ...ell} (\lambda)} \over { \int_\lambda {\rm d} \lambda ~ E(\lambda)~ B_\lambda }}$	(17)

and $\overline{ \Theta_{0}^2 (t)}$ (resp. $\overline{ \left({{\delta L} \over \bar{L}} \right)_{0}^2 (t)}$ ) is the mean square value of $\Theta_0(t)$ (resp. $\left (\delta L / L \right)_0(t)$ ) for a radial mode. Note that in Eq. (13) the sum over $(\ell,m)$ is performed among all the multiplets within the same separation. The expression for the visibility coefficient $S_\ell$ is given by Eq. (A.22). The visibility factor associated with modes $\ell > 4$ can be neglected. Accordingly, Eq. (14) can be simplified as:

$\begin{displaymath}R_{\rm osc} = \sqrt{ R_0^2 + R_1^2 + R_2^2 + R_3^2 }. \end{displaymath}$

(18)

In practice, we consider $P_{\rm osc}$ , the smoothed power density component associated with oscillations derived from observations, as in Sect. 1. Using Eqs. (12), 13 and (9), one obtains the (rms) bolometric amplitude normalised to radial mode given by

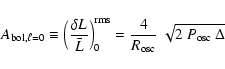$\begin{displaymath}A_{\rm bol,\ell=0} \equiv \left (\delta L \over \bar{L} \righ... ...R_{\rm osc} } ~ \sqrt{\displaystyle{2 ~ P_{\rm osc} ~ \Delta}} \end{displaymath}$

(19)

where $R_{\rm osc}$ is the response function given by Eq. (16) and computed for each data set using Eqs. (15) and (A.22).

In the present work, the $S_\ell(\lambda)$ coefficients (Eq. (A.22)) are computed taking into account monochromatic specific intensities derived from stellar atmosphere models (see Barban et al. 2003) with relevant $T_{\rm eff}$ , [Fe/H], and $\log g$ .

3.4 Response function for granulation

As detailed in Appendix A, since we are interested in rms values with time and assuming that these values are identical all over the stellar surface, the granulation component can be treated in a similar way as a radial mode. Accordingly, the relation between the observed relative intensity fluctuations and the associated intrinsic fluctuations is

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right )_g (t) = R_g ~ \... ...R_{g} \over 4 } ~ \left (\delta L \over \bar{L} \right )_g (t) \end{displaymath}$

(20)

where the quantities have the same meaning as previously for radial modes but subscript g refers to the granulation and

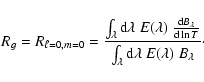$\begin{displaymath}R_{g} = R_{\ell=0,m=0} = {{\int_\lambda {\rm d}\lambda ~ E(\l... ...r { \int_\lambda {\rm d}\lambda ~ E(\lambda)~ B_\lambda}}\cdot \end{displaymath}$

(21)

As for the radial modes, we define the rms and instrinsic relative luminosity fluctuation due to granulation as the quantity

$\begin{displaymath}\left( \delta L \over \bar{L} \right)_g^{\rm rms} \equiv \sqr... ...g} } ~ \left (\delta I \over\bar{I} \right )_g^{\rm rms} (t) . \end{displaymath}$

(22)

If we consider the power density contribution associated with granulation (P_g) determined in Sect. 1, we can derive the corresponding bolometric power density spectrum according to

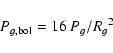$\begin{displaymath}P_{g,{\rm bol}}=16~P_g/{R_g}^2 \end{displaymath}$

(23)

which is expected to characterize granulation independently of the instrument considered. The application to the different data sets obtained on the Sun (R_g values are given in Table 3) with different instrumental techniques and with different bandpasses shows a good agreement (see Sect. 4).

Table 3: Response functions for different sets of solar data.

4 Results for different data sets

4.1 A reference solar bolometric oscillation amplitude

The resulting estimates of the bolometric amplitude per radial mode are shown in Fig. 4 ( $R_{\rm osc}$ values computed for the different data sets considered here are given in Table 3). We compare the curves obtained for each data set, with special attention to the value at maximum often taken as a convenient characteristic measurement of the oscillations amplitudes in stars (see also Table 4). Although some residuals of the initial difference seem to subsist (suggesting that our response function might be refined further), we notice a reasonable agreement of the different curves, within one-sigma error bar estimates. This allows us to propose as a reference for the Sun a $2.53 \pm 0.11$ ppm of maximum bolometric amplitude per radial mode (mean of the four values weighted by $1/{\sigma }_i$ ). We checked that this result was not affected significantly by changing the smoothing boxcar width from 2 times to 4 times $\Delta$ .

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig4.eps} \end{figure}$	Figure 4: Observational bolometric amplitude per radial mode estimated as described in the text, for PMO6 data (plain black line), SPM-blue (dot [blue]), SPM-green (dash [green]), SPM-red (long dash [red]). Error bars are given for the estimate of the maximum (boxcar: 3 times Large Separation taken as 135 $\mu$ Hz).
Open with DEXTER

4.2 A reference bolometric granulation power density spectrum

Table 4: Bolometric parameters. The last line corresponds to reference values resulting from a mean of the values given in the other lines, weighted by $1/{\sigma }_i$ .

The different mean profiles of bolometric background power density spectra are shown in Fig. 5. Here again, we notice the good agreement of the different curves. Coefficients characterizing the different curves are given in Table 4 as well as reference values proposed for the Sun background contribution. Here again, the influence of the size of the smoothing boxcar (between 0.1 to 4 times $\Delta$ ) has been tested and found negligible within the present error bars.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig5.eps} \end{figure}$	Figure 5: Observational bolometric power density spectrum estimated as described in the text, for PMO6 data (plain black line), SPM-blue (dot [blue]), SPM-green (dash [green]), SPM-red (long dash [red]). a): granulation+ mesogranulation components; b): granulation and mesogranulation individual components.
Open with DEXTER

5 Response functions of CoRoT for objects on the Main Sequence

Stellar atmosphere models are computed with the Atlas 9 code (Kurucz 1993) in a modified version including the CGM convection (see Heiter et al. 2002). Considering the CoRoT total efficiency shown in Fig. 6, we compute the CoRoT response functions for stellar atmosphere models characterized by different values of $T_{\rm eff}$ , $\log g$ and chemical compositions illustrative of possible solar-like candidates on the Main Sequence ( $-1<[{\rm Fe/H}]<+1$ , $3.9<\log g<4.5$ , $5800 < T_{\rm eff} < 6750$ K).

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig6.eps} \end{figure}$	Figure 6: CoRoT total efficiency.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig7.eps} \end{figure}$	Figure 7: Polynomial fit of the CoRoT response function $R_{\rm osc}$ (dash [red]) and $R_{\rm g}$ (plain [blue]) for different stellar atmosphere models mentioned in the text.
Open with DEXTER

As shown in Fig. 7, the dependency of the CoRoT response function $R_{\rm osc}$ on $\log g$ and chemical composition is small in the considered range. To a great extent (within 0.6%), it can be neglected and $R_{\rm osc}$ as $R_{\rm g}$ can be described as simple polynomial functions of $T_{\rm eff}$ only:

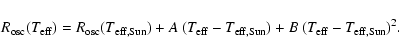
$\begin{displaymath}R_{\rm osc}(T_{\rm eff})= R_{\rm osc}(T_{\rm eff,Sun})+A~(T_{\rm eff}-T_{\rm eff,Sun})+B~(T_{\rm eff}-T_{\rm eff,Sun})^2.\end{displaymath}$

We proceed in the same way for $R_{\rm g}$ .

Values of the parameters obtained for the fit are given in Table 5.

6 Conclusions

Measurement of stellar oscillations or granulation provides instrumental values which depend on the instrumental technique and bandpass and on the star considered. In this work, with the purpose of helping future comparisons between stars observed in photometry,

1.: We propose a simple expression for response functions connecting specific instrumental photometric measurements with intrinsic bolometric values for oscillation amplitudes and granulation power density.
2.: We test and validate this expression on four sets of data obtained on the Sun, in four different bandpasses and with two different instrumental techniques.
3.: We establish reference bolometric measurements for the Solar oscillation amplitudes ( 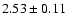$2.53 \pm 0.11$ ppm) and for the Solar granulation power density.
4.: We compute the response functions for the CoRoT instrument and give an analytic expression for it.

Table 5: Fit of CoRoT response functions.

Acknowledgements

SOHO is a mission of international collaboration between ESA and NASA.

Appendix A: Derivation of the instrumental response functions

Here we derive the relation between the observed flux fluctuation and the intrinsic temperature fluctuations induced by the presence of non-radial modes or granulation on the surface of the star. We proceed in the manner of Berthomieu & Provost (1990). We summarize the main steps and emphasize the approximations that we adopt in the present study. The flux, $F_\lambda$ , received from the star at the wavelength $\lambda$ is given by (see Berthomieu & Provost 1990):

$\begin{displaymath}F_\lambda = \int_{\cal A} {\rm d} {\cal A} ~ I_\lambda (\tau=0, \mu) \end{displaymath}$

(A.1)

where ${\cal A}$ is the total oberved surface, ${\rm d} {\cal A} = {\rm d} \vec A. \vec n$ the elementary observed surface around the direction of the observer, $\vec n$ a unit vector in the direction of the observer, ${\rm d} \vec A$ the differential surface element perpendicular to the stellar surface, $\tau$ the optical depth, $\mu=\cos(\theta)$ , and $I_\lambda(\mu)$ the specific intensity at the wavelength $\lambda$ . We adopt a spherical coordinate system with the z-axis pointing toward the observer. The specific intensity is assumed to be invariant with respect to any rotation along the z-axis; this is why here $I_\lambda$ depends only on $\mu$ . Note that the integral of Eq. (A.1) is evaluated at the optical depth $\tau=0$ .

We define the limb-darkening function, $g_\lambda$ , as

$\begin{displaymath}g_\lambda \equiv { I_\lambda(\mu) \over I_\lambda(1) } \end{displaymath}$

(A.2)

where $I_\lambda(1) \equiv I_\lambda(\mu=1)$ . Finally, we define the mean intensity as the quantity

$\begin{displaymath}J_\lambda \equiv {1 \over {4 \pi}} ~ \int {\rm d} \Omega ~ I_\lambda(\mu) \end{displaymath}$

(A.3)

where ${\rm d} \Omega$ is the elementary solid angle. Using Eqs. (A.2) and (A.3) we then derive the relation:

$\begin{displaymath}J_\lambda = I_\lambda(1) / H_\lambda \end{displaymath}$

(A.4)

where we have defined

$\begin{displaymath}H_\lambda \equiv 2 ~ \left ( \int_{-1}^{1} {\rm d} \mu ~ g_\lambda(\mu) \right) ^{-1}. \end{displaymath}$

(A.5)

According to Eqs. (A.1), (A.2) and (A.4), a small variation of $F_\lambda$ is given by

$\displaystyle \delta F_\lambda = \int_{\cal A} ~ {\rm d} {\cal A} ~ \left ( \ba... ... + \delta \left ( {\rm d} {\cal A} \right ) ~ \bar{J}_\lambda ~ \bar{g}_\lambda$

(A.6)

where $\overline{()}$ refers to the equilibrium quantity. The first term on the RHS of Eq. (A.6) corresponds to the perturbations of the mean intensity evaluated at an effective optical depth $\tau = \tau_0$ in the atmosphere. This effective optical depth corresponds to the layer that contributes predominantly to the variation of the emergent flux (see Berthomieu & Provost 1990). As in Berthomieu & Provost (1990), we assume that $g_\lambda$ and hence $H_\lambda$ do not depend on $\tau_0$ and are evaluated at $\tau=0$ .

The three last terms in RHS of Eq. (A.6) are the perturbation of the limb-darkening function and the surface distortion (for details see Berthomieu & Provost 1990). All these perturbuations are shown to have a negligible contribution to $\delta F_\lambda$ compared to that of $\delta J_\lambda$ . Accordingly, Eq. (A.6) can be simplified as:

$\begin{displaymath}\delta F_\lambda = \int_0^{2 \pi} {\rm d} \phi ~ \int_0^1 {\r... ... \mu ~ \mu ~ g_\lambda(\mu) ~ H_\lambda ~ \delta J_\lambda \;, \end{displaymath}$

(A.7)

where we have dropped $\overline{()}$ from $g_\lambda$ and $H_\lambda$ .

We place ourself in Local Thermodynamic Equilibrium and assume adiabatic perturbations for linearisation, accordingly $\delta J_\lambda = \delta B_\lambda$ where $B_\lambda$ is the black body law whose expression is

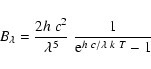$\begin{displaymath}B_\lambda = { {2 h~ c^2 } \over \lambda^5} ~ { 1 \over { {\rm e}^{ {h~c}/{\lambda ~ k ~ T}} - 1}} \end{displaymath}$

(A.8)

where T is the local temperature, c the speed of the light, h Planck's constant, and k Boltzmann's constant.

The local variation of $B_\lambda$ is induced by a local variation of T. Assuming small perturbations, we have

$\begin{displaymath}\delta J_\lambda = \delta B_\lambda = \left ( { {{\rm d} B_\l... ...left ( { {\delta T} \over T } \right ) (\tau_0,t,\theta,\phi). \end{displaymath}$

(A.9)

Using Eqs. (A.9) and (A.15), Eq. (A.7) can then be written as:

$\begin{displaymath}\delta F_\lambda = H_\lambda ~ \left ( { {{\rm d} B_\lambda} ... ...\mu ~ g_\lambda(\mu) ~ \left ( { {\delta T} \over T } \right). \end{displaymath}$

(A.10)

Finally, we approximate Eq. (A.1) as

$\begin{displaymath}F_\lambda = 2 \pi ~ H_\lambda ~ G_\lambda ~ {B}_\lambda, \end{displaymath}$

(A.11)

where $B_\lambda$ is evaluated at the photosphere, i.e. at $T=T_{\rm eff}$ and where we have defined

$\begin{displaymath}G_\lambda \equiv \int_0^1 {\rm d} \mu ~ \mu ~ ~ g_\lambda(\mu). \end{displaymath}$

(A.12)

The relative variation of the total flux I received by the instrument is finally given by

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right ) (t) = { { \int_... ...ver { \int_\lambda {\rm d}\lambda ~ E(\lambda) ~ F_\lambda } } \end{displaymath}$

(A.13)

where $E(\lambda)$ is the global efficiency in terms of energy of the instrument at a given wavelength. The function $E(\lambda)$ is normalised as

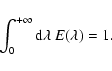$\begin{displaymath}\int_0^{ +\infty } {\rm d} \lambda~ E(\lambda) = 1. \end{displaymath}$

(A.14)

A.1 Non-radial oscillations

In the case of a non-radial spheroidal mode, ${\delta T} / T$ is by definition:

$\begin{displaymath}\left ( { {\delta T} \over T } \right) (\tau_0,t,\theta,\phi) = \Theta_\ell(t,\tau_0) ~ Y_\ell^m (\theta^\prime,\phi^\prime) \end{displaymath}$

(A.15)

where $\Theta_\ell(t,\tau_0)$ is the intrinsic and instantaneous mode amplitude in terms of temperature fluctuation, $Y_\ell^m$ is the spherical harmonic associated with the mode with a degree $\ell$ and azimutal order m, and $(r,\theta^\prime,\phi^\prime)$ the spherical coordinate system in the pulsation frame. The pulsation frame is chosen such that its polar axis coincides with the star rotation axis. The spherical harmonic, $Y_\ell^m$ , is normalized here as:

$\begin{displaymath}\int {\rm d} \Omega^\prime ~ \left \Vert Y_{\ell}^m (\theta^\prime,\phi^\prime) \right \Vert^2 = 4 \pi \end{displaymath}$

(A.16)

where $\Omega^\prime$ is the elementary solid angle associated with the pulsation coordinate system. Note that for low $\ell$ degree, $\Theta(t,\tau_0)$ is expected to negligibly depend on $\ell$ (Belkacem et al. 2008).

As shown by Berthomieu & Provost (1990), for low $\ell$ degree, $\tau_0$ marginally depends on $\ell$ . Furthermore, they show that - in the Sun - the optical depth $\tau_0$ is very close the the photosphere, which by definition corresponds to the layer $T=T_{\rm eff}$ and $\tau=2/3$ . Then, from here, we will assume that $\tau_0$ coincides with the photosphere ( $\tau=2/3$ ).

Using Eqs. (A.10), (A.11), (A.13), (A.12), and (A.15), we then derive the flux variation due to the mode:

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right ) (t) = R_{\ell,m,i} ~ \Theta_\ell (t) \end{displaymath}$

(A.17)

with

$\begin{displaymath}R_{\ell,m,i} \equiv { {\int_\lambda {\rm d} \lambda ~ E(\lamb... ...d} \lambda ~ E(\lambda) ~ B_\lambda ~ G_\lambda ~ H_\lambda} } \end{displaymath}$

(A.18)

where we have defined the ``visibility'' coefficient, $S_{\ell,m,i}$ , as the quantity:

$\begin{displaymath}S_{\ell,m,i} (\lambda) \equiv { { \int_0^{2 \pi} {\rm d} \phi... ...2 ~ \pi ~ \int_0^1 {\rm d} \mu ~ \mu ~ ~ g_\lambda(\mu)}}\cdot \end{displaymath}$

(A.19)

Note that, from the definition of $S_{\ell,m,i}$ , we have for a radial mode S₀=1.

By using stellar atmosphere models, we find that - in the domain of $T_{\rm eff}$ and gravity we are interested here - $G_\lambda ~ H_\lambda$ varies slowly with $\lambda$ compared to $B_\lambda$ and ${\rm d}B_\lambda~ / ~{\rm d} \ln T$ . Accordingly, Eq. (A.18) can be simplified as:

$\begin{displaymath}R_{\ell,m,i} \equiv { {\int_\lambda {\rm d} \lambda ~ E(\lamb... ...\int_\lambda {\rm d} \lambda ~ E(\lambda) ~ B_\lambda } }\cdot \end{displaymath}$

(A.20)

Following Dziembowski (1977), we can decompose $S_{\ell,m,i}(\lambda)$ as:

$\begin{displaymath}S_{\ell,m,i} = q_{\ell,m}(i) ~ S_{\ell} \end{displaymath}$

(A.21)

with

$\displaystyle S_{\ell} (\lambda) = { {\int_0^{1} {\rm d} \mu ~ ~\mu ~g_{\lambda}(\mu) ~ Y_\ell^0 (\mu) } \over {\int_0^1 {\rm d} \mu ~ \mu ~ ~ g_\lambda(\mu)}}$			(A.22)
$\displaystyle q_{\ell,m}(i) = \sqrt{{(l-m) ! } \over {(l+m) !} } ~ \left \vert P_{\ell}^{\vert m\vert} \right \vert ~ \cos(i)$			(A.23)

where i is the angle between the observer and the rotation axis and $P_{\ell}^{\vert m\vert}$ the associated Legendre function.

The bolometric flux variation, $\left ( { {\delta I} / \bar{I} } \right )^{\rm bol}$ , is obtained from Eq. (A.17) by assuming in Eq. (A.20) a constant $E(\lambda)$ , this gives

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right )^{\rm bol} (t) = R_{\ell,m,i}^{\rm bol} ~ \Theta_\ell (t) \end{displaymath}$

(A.24)

with

$\begin{displaymath}R_{\ell,m,i}^{\rm bol} \equiv { \pi \over {\sigma ~ T_{\rm ef... ...} B_\lambda} \over {{\rm d} \ln T} } ~ S_{\ell,m,i} (\lambda). \end{displaymath}$

(A.25)

For a radial mode, S_0,0=1 and $R_{{\rm bol},0,0}= 4$ . We have then for a radial mode:

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right )^{\rm bol} (t) = 4 ~\Theta_0 (t). \end{displaymath}$

(A.26)

By definition of the effective temperature ( $T_{\rm eff}$ ) and the stellar radius R_*, the total luminosity of the star, L, is given by Steffan's law:

$\begin{displaymath}L = 4 \pi ~ \sigma ~ T_{\rm eff}^4 ~ R_*^2 \; \end{displaymath}$

(A.27)

where $\sigma$ is Steffan's constant. Variation of the stellar radius due to the mode can be neglected. Accordingly, the relative variation of L due to a radial mode is given by the relation

$\begin{displaymath}\left (\delta L \over \bar{L} \right ) = 4 \left (\delta T_{\rm eff} \over {\bar{T}_{\rm eff}} \right )\cdot \end{displaymath}$

(A.28)

We have again for a radial mode:

$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right )^{\rm bol} = \left ( { {\delta L} \over \bar{L} } \right ) \end{displaymath}$

(A.29)

Then, according to Eqs. (A.26) and (A.28), we have

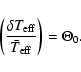$\begin{displaymath}\left ({ \delta T_{\rm eff} \over { \bar{T}_{\rm eff}} } \right ) = \Theta_0. \end{displaymath}$

(A.30)

Thus, for a radial mode, $\Theta_0$ (resp. $\left ( { {\delta I} / \bar{I} } \right )^{\rm bol}$ ) is then directly related to a variation of $T_{\rm eff}$ (resp. L). On the other hand, for a non-radial mode, $\left ( { {\delta I} / \bar{I} } \right )^{\rm bol}$ is related to the instrinsic mode amplitude in terms of temperature, $\Theta_\ell$ , through the coefficient given by Eq. (A.25) that depends on the mode geometry and the limb-darkening law. However, by extension of the radial case, we define, in the general case, the bolometric and instrinsic mode amplitude in terms of luminosity as the quantity:

$\begin{displaymath}\left (\delta L \over \bar{L} \right )_\ell \equiv 4 ~ \Theta_\ell. \end{displaymath}$

(A.31)

Now, according to Eqs. (A.17) and (A.31), we can writte:

$\begin{displaymath}\left ({{\delta I} \over \bar{I} } \right ) (t) = R_{\ell,m,i... ...} \over 4 } ~ \left (\delta L \over \bar{L} \right )_\ell\cdot \end{displaymath}$

(A.32)

Eq. (A.32) then relates the observed intensity fluctuations to the bolometric and instrinsic mode amplitude in terms of luminosity.

A.2 Granulation

We define $\left ( { {\delta T} / T} \right)_g = \Theta_g (t,\mu,\phi)$ as the relative temperature perturbation due to the granulation at the instant t and the position $(\theta,\phi)$ .

As for the mode, we derive the flux perturbation, $\delta I_{g,\lambda}$ , due to the granulation:

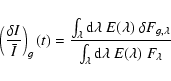$\begin{displaymath}\left ( { {\delta I} \over \bar{I} } \right )_g (t) = { { \in... ...ver { \int_\lambda {\rm d} \lambda ~ E(\lambda) ~ F_\lambda}}} \end{displaymath}$

(A.33)

with

$\begin{displaymath}\delta F_{g,\lambda} = \left ({{{\rm d} B_\lambda} \over {{\r... ... {\rm d} \mu ~ \mu ~ ~ g_\lambda(\mu) ~ \Theta_g (t,\mu,\phi). \end{displaymath}$

(A.34)

To go further, one needs to know how temperature fluctuations due to the granules are distributed along the star surface. We note that we are only interested in the time averaged intensity fluctuations. As a simplification, we assume that distribution of the temperature fluctuations is - in time average - homogeneous. Accordingly, we can ignore the dependence of $\Theta_g$ with $(\mu,\phi)$ . This is formally equivalent to assuming in Eq. (A.15) that $Y_\ell^m = 1$ , as for a radial mode ( $(\ell,m)=(0,0)$ ). Then, the expression for $\left (\delta I / \bar{I} \right)_{g}$ is derived from Eqs. (A.32) and (A.20) by assuming $(\ell,m)=(0,0)$ . Accordingly, $\delta \left ( I / \bar{I} \right )_g$ can be written as

$\begin{displaymath}\left ({{\delta I} \over \bar{I}} \right)_{\rm g} (t) = R_{\r... ...} \over 4} ~ \left (\delta L \over \bar{L} \right)_{\rm g} (t) \end{displaymath}$

(A.35)

with

$\displaystyle R_{\rm g}$	=	$\displaystyle R_{\ell=0,m=0} = {{\int_\lambda {\rm d} \lambda ~ E(\lambda)~ {{{... ...{\rm d} \ln T}}} \over { \int_\lambda {\rm d}\lambda ~ E(\lambda)~, B_\lambda}}$	(A.36)
$\displaystyle \quad\quad\left (\delta L \over \bar{L} \right )_g$	=	$\displaystyle 4 ~ \Theta_g.$	(A.37)

As for the radial modes, $\left (\delta L / \bar{L} \right )_g$ represents the bolometric and instrinsic luminosity variation due to the granulation.

References

Aigrain, S., Favata, F., & Gilmore, G. 2004, A&A, 414, 1139 [NASA ADS] [CrossRef] [EDP Sciences]
Andersen, B., Appourchaux, T., & Crommelnynck, D. 1998a, in Sounding solar and stellar interiors, ed. Provost, & F. Schmider, 181, 147 (In the text)
Andersen, B., Leifsen, T., Appourchaux, T., et al. 1998b, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, ed. S. Korzennik, ESA SP, 418, 83
Anklin, M., Frohlich, C., Wehrli, C., & Finsterle, W. 1998, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, ed. S. Korzennik, ESA SP, 418, 91
Baglin, A., Michel, E., Auvergne, M., & The COROT Team. 2006, in Proceedings of SOHO 18/GONG 2006/HELAS I, Beyond the spherical SunESA, Special Publication, 624, (In the text)
Barban, C., Goupil, M. J., Van't Veer-Menneret, C., et al. 2003, A&A, 405, 1095 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Baudin, F., Samadi, R., Appourchaux, T., & Michel, E. 2007, ArXiv e-prints, 710 (In the text)
Bedding, T. R., & Kjeldsen, H. 2007, in Unsolved Problems in Stellar Physics: A Conference in Honor of Douglas Gough, ed. R. J. Stancliffe, J. Dewi, G. Houdek, R. G. Martin, & C. A. Tout, Amer. Inst. Phys. Conf. Ser., 948, 117 (In the text)
Belkacem, K., Samadi, R., Goupil, M.-J., & Dupret, M.-A. 2008, A&A, 478, 163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Berthomieu, G., & Provost, J. 1990, A&A, 227, 563 [NASA ADS] (In the text)
Dziembowski, W. 1977, Acta Astron., 27, 203 [NASA ADS]
Frohlich, C., Andersen, B. N., Appourchaux, T., et al. 1997, Sol. Phys., 170, 1 [NASA ADS] [CrossRef] (In the text)
Harvey, J. 1985, in Future Missions in Solar, Heliospheric, & Space Plasma Physics, ed. E. Rolfe, & B. Battrick, ESA SP, 235, 199 (In the text)
Heiter, U., Kupka, F., van't Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kjeldsen, H., Bedding, T. R., Butler, R. P., et al. 2005, ApJ, 635, 1281 [NASA ADS] [CrossRef] (In the text)
Kjeldsen, H., Bedding, T. R., Arentoft, T., et al. 2008, ArXiv e-prints, 804 (In the text)
Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data (Kurucz CD-ROM, Cambridge, MA: Smithsonian Astrophysical Observatory) (In the text)
Ludwig, H.-G. 2006, A&A, 445, 661 [NASA ADS] [CrossRef] [EDP Sciences]
Samadi, R., Belkacem, K., Goupil, M.-J., Kupka, F., & Dupret, M.-A. 2007a, in IAU Symposium, ed. F. Kupka, I. Roxburgh, & K. Chan, 239, 349
Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007b, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences]
Toutain, T., & Gouttebroze, P. 1993, A&A, 268, 309 [NASA ADS]
Trampedach, R., Christensen-Dalsgaard, J., Nordlund, A., & Stein, R. F. 1998, in The First MONS Workshop: Science with a Small Space Telescope, held in Aarhus, Denmark, June 29-30, ed. H. Kjeldsen, T. R. Bedding, Aarhus Universitet, 59

All Tables

Table 1: Fit with seven parameters. Values of the parameters are given as well as the associated one-sigma error estimates.

Table 2: Fit with five parameters.

Table 3: Response functions for different sets of solar data.

Table 4: Bolometric parameters. The last line corresponds to reference values resulting from a mean of the values given in the other lines, weighted by $1/{\sigma }_i$ .

Table 5: Fit of CoRoT response functions.

All Figures

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig1.eps} \end{figure}$	Figure 1: Observational power density spectrum obtained for: SPM-blue a) and SPM-green b) data over 700 days; a moving mean is applied with a 4 ${\rm\mu }$ Hz boxcar (plain black line); the same spectrum highly smoothed with a 0.405 mHz boxcar (3 $\Delta$ ) is superimposed (plain light grey line [yellow]); individual powerlaws associated with granulation and mesogranulation are shown (dash lines [purple]); the white noise component (horizontal line [red]); the global fit of solar background + white noise components is represented (plain grey line [green]) but differs from the mean power density only in the domain of oscillations. Vertical error bars associated with the fit precision are illustrated at different frequencies for each component of the fit. For clarity, in the case of the white noise component, the error bar is represented only once at 1 mHz.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig2.eps} \end{figure}$	Figure 2: Same as Fig. 1 for, from top to bottom: SPM-blue ( a), SPM-green ( b), SPM-red ( c) data over 700 days and PMO6 ( d) data over 800 days, but here we forced C_i=4.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0353fig3a.eps}\\ [2.5mm] \includegraphics[width=8cm,clip]{0353fig3b.eps} \end{figure}$	Figure 3: a) Observational instrumental power density spectrum associated with the stellar background contribution and estimated as described in the text, for PMO6 data (plain black line), SPM-blue (dot [blue]), SPM-green (dash [green]), SPM-red (long dash [red]); b) same for the oscillation contribution.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig4.eps} \end{figure}$	Figure 4: Observational bolometric amplitude per radial mode estimated as described in the text, for PMO6 data (plain black line), SPM-blue (dot [blue]), SPM-green (dash [green]), SPM-red (long dash [red]). Error bars are given for the estimate of the maximum (boxcar: 3 times Large Separation taken as 135 $\mu$ Hz).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig5.eps} \end{figure}$	Figure 5: Observational bolometric power density spectrum estimated as described in the text, for PMO6 data (plain black line), SPM-blue (dot [blue]), SPM-green (dash [green]), SPM-red (long dash [red]). a): granulation+ mesogranulation components; b): granulation and mesogranulation individual components.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig6.eps} \end{figure}$	Figure 6: CoRoT total efficiency.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{0353fig7.eps} \end{figure}$	Figure 7: Polynomial fit of the CoRoT response function $R_{\rm osc}$ (dash [red]) and $R_{\rm g}$ (plain [blue]) for different stellar atmosphere models mentioned in the text.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.