---

VLT/NACO coronagraphic observations of fine structures in the disk of 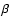 Pictoris

A. Boccaletti¹ - J.-C. Augereau² - P. Baudoz¹ - E. Pantin³ - A.-M. Lagrange²

1 - LESIA, Observatoire de Paris-Meudon, 92195 Meudon, France
2 - Laboratoire d'Astrophysique de Grenoble, Université Joseph Fourier, CNRS, UMR 5571, Grenoble, France
3 - Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France

Received 1 October 2008 / Accepted 19 December 2008

Abstract
Aims. We present ground-based observations of the disk around the A-type star  Pictoris to obtain scattered light images at the highest angular resolution (60 mas, equivalent to about 1 AU at the distance of the star) and the highest contrast in the very close environment of the star. The purpose of this program is to perform a close inspection of the inner disk morphology.
Methods. Images were collected with NACO, the AO-assisted near-IR instrument on the VLT (ESO) which includes two types of coronagraphs: classical Lyot masks and phase masks. In this program we took advantage of both types of coronagraphs in two spectral bands, H-band for the Lyot mask and Ks-band for the phase mask. The Lyot mask blocks a large central region around the star (radius <0.35 ) but allows deep integrations and hence good signal-to-noise ratio at large distances, while the phase mask allows imaging at very close separation (down to in theory) but conversely is more sensitive to residual aberrations. In addition, we simulated an extended object to understand the limitations in deconvolution of coronagraphic images.
Results. The reduced coronagraphic images allow us to carefully measure the structures of the debris disk and reveal a number of asymmetries of which some were not reported before (position, elevation and thickness of the warp). Our analysis also demonstrates the advantage of the phase mask coronagraph to explore the very close environment of stars. In this program, the circumstellar material is visible as close as 0.7 (13.5 AU) owing to the phase mask while the Lyot mask generates artifacts which hamper the detection of the dust at separations closer than 1.2 (23.2 AU). The point source detection limit is compared to recently published observations of a planet candidate. Finally, the simulations show that deconvolution of coronagraphic data may indeed produce artificial patterns within the image of a disk.

Key words: stars: individual: Pic - stars: pre-main sequence - stars: planetary systems: formation - stars: circumstellar matter - methods: observational - techniques: high angular resolution

1 Introduction

The young (<20 Myr) and nearby A-type star  Pictoris has been the subject of many investigations since the imaging by Smith & Terrile (1984) of the first circumstellar disk around a star. Over the last 25 years, the edge-on dusty disk was observed at many wavelengths, in scattered light and in thermal emission, from space and from the ground with the prime goal to understand the planet formation process, and ultimately to find evidence for planetary objects.

The discoverers, Smith & Terrile (1984), resolved the disk in the visible at projected separations larger than 5.2 (100 AU, adopting the Hipparcos distance of 19.3 pc), and, extrapolating the observed surface brightness profile to shorter distances, they proposed that the disk should be optically thick below 15 AU. About ten years latter, Kalas & Jewitt (1995) observed the disk down to 2.8 (54 AU) and identified morphological and brightness asymmetries between the north-east and south-west extensions of the edge-on disk. The WFPC2 instrument onboard the HST was used to observe the disk as close as 1.5 (29 AU) and confirms the asymmetrical structure. Mid-infrared imaging (Lagage & Pantin 1994) of the innermost regions of the disk (0-80 AU) showed that the inner disk (r<25 AU) is depleted by a factor of 100 with respect to the regions of peak density (  AU). Based on new datasets, this depletion was confirmed by Pantin et al. (1997) who proposed a two-component model to interpret both the visible/near-infrared and mid-infrared data. From modeling, Burrows et al. (1995) derived the presence of a relatively clear zone within 40 AU. In addition, they revealed a peculiar symmetrical structure, the so-called warp, at a distance <70 AU which should have disappeared in about 1 Myr. They interpreted this feature as the gravitational signature of a planetary object which would also cause the clearing of the inner disk regions. With the improvement of Adaptive Optics system (AO) on large ground-based telescopes, the warp was confirmed by Mouillet et al. (1997a) in the near-IR using the 3.6 m telescope at La Silla (ESO). To account for the presence of the warp Mouillet et al. (1997b) developed a model which concluded the presence of a planet on an inclined orbit (3-5) and located in the range 1-20 AU from the star. This warp was also observed in detail with the HST/STIS instrument at visible wavelengths (Heap et al. 2000). The small Lyot mask and the quality of the PSF subtraction process allow the detection of the disk as close to the star as 0.75 . According to Heap et al. (2000), the perturbing planet may have a mass of a few times that of Jupiter if located closer than 20 AU. The most recent analysis (Freistetter et al. 2007) based on numerical simulations constrained by the presence of planetesimal belts inferred from the observed temporal variations of metallic lines in the  Pictoris spectrum suggests a planet of 2 M_J at 12 AU. Note that high resolution spectra were also used to search for radial velocity variations of  Pictoris(Galland et al. 2006). The available data allowed them to detect pulsations (also seen in photometry) and to constrain the presence of planets with small periods (e.g. a few days). Longer periods planets are still poorly constrained with radial velocity data, with for example, at 1 AU, a limit of 9 M_J. While this paper was being reviewed, a candidate planet was discovered by Lagrange et al. (2008) taking advantage of a reduced contrast in L' band images. With an inferred mass of 8 M_J, at a projected distance of 8 AU it is significantly more massive than the Freistetter et al. (2007) predictions although more measurements would be needed to definitely rule on the mass of this candidate planet and confirm the companionship.

A detailled dynamical model of the  Pictoris dust disk was developed by Augereau et al. (2001) who simulate a disk of planetesimals and dust particles pertubed by a giant planet on an inclined orbit with respect to the disk midplane. The Kalas & Jewitt (1995) large scale asymmetries (at hundreds of AUs) and the warp observed in scattered light are well reproduced assuming a planet located at 10 AU about 10³ times less massive than the central star. The inferred surface density for the disk corresponds to a broad annulus peaked around 80-110 AU and smoothly declining inward within about 70 AU. Although the far-infrared thermal emission is correcty predicted by this model, it is shown that most of the mid-infrared emission is very likely produced by an additional hot population of small grains close to the star and not modeled. Recent high-resolution mid-IR images (Telesco et al. 2005) of the inner disk obtained with Gemini have revealed the presence of an asymmetric structure located at about 50 AU and which may correspond to a clump of particles differing in temperature and/or in size to the other particles in the disk. This observation supports the commonly shared hypothesis that the disk is replenished by short-lived dust originating from collisions of planetesimals but the mechanisms that can produce a clump of that size are still unclear.

The latest images of the  Pictoris disk were obtained by Golimowski et al. (2006) in the visible with ACS on the HST. Despite the very high sensitivity of the ACS, the large opaque Lyot mask does not allow them to probe the disk morphology at an angular separation less than about 1.5 to the star. Using a specific data reduction process to emphasize high spatial frequency structures in the disk, they suggest that the warp is in fact the result of a blend of a main disk with a much fainter, inclined secondary disk which can be separated from the main one from 80 AU up to about 150 AU in ACS images. However, the method used to separate the two disks is arguable (see Sect. 4.1 for a more detailled discussion) and it is therefore not clear if this secondary disk is a fully distinct component or originates in the main, twisted disk as supported by the work of Mouillet et al. (1997b) and Augereau et al. (2001). Golimowski et al. (2006) also showed an interesting color dependence of the disk in scattered light from which they inferred a typical minimum grain size of about m where the planetesimals lie (r<120 AU).

Improving the angular resolution in the first few tens of AU from  Pictoris is now clearly mandatory to access the planet forming regions. Optimal conditions are met either with large ground-based telescopes (providing the wavefront is corrected with high-order AO systems) or from space with the HST. In this paper, we present new coronagraphic images obtained with an 8 m telescope at the European Southern Observatory in the near-IR. Although the sensitivity is not sufficient to detect giant planets, the coronagraph we used is potentially sensitive to smaller separations than any previous observations. In Sect. 2 we describe the observations we carried out and the data reduction process. The analysis of the disk in terms of morphology, surface brightness profile, vertical flux and position of the midplane is presented in Sect. 3. We then discuss the hypothesis of a secondary disk (Sect. 4.1) and the contamination by PSF structures in coronagraphic images (Sect. 4.2).

2 Observations and data reduction

2.1 Observing strategy

Coronagraphic observations of  Pictoris were obtained on Nov. 5th, 2004 at ESO with NACO (Rousset et al. 2003) the IR AO system of the VLT.  Pictoris (V=3.86, H=3.54, K=3.53) was observed with 2 coronagraphs, a standard 0.7 diameter Lyot mask and a four quadrant phase mask (FQPM hereafter), in the H and Ks spectral bands, respectively. Seeing conditions and AO compensation were good but variable (Strehl ratios 30-50%). Although theoretical FWHMs are 42 mas and 56 mas in H and Ks filters, we measured respectively 61 mas and 66 mas resulting from both the actual Strehl ratios and the coronagraphic pupil stop (10% undersized).

The principle of the FQPM is discussed in Rouan et al. (2000). It uses a  phase shift in the focal plane resulting in a destructive interference inside the geometric pupil of a point-like object centered on the mask. A monochromatic FQPM operating at m was implemented in NACO on August 2003. Performance assessment of the FQPM is reported in Boccaletti et al. (2004). This coronagraph has no obscuration in the focal plane and therefore is able to reach the theoretical diffraction limit of the telescope. As a drawback, in actual observations (Strehl ratio <50%) the attenuation of the PSF peak is less than for a Lyot coronagraph (a factor of 10 instead of 200 depending on the level of the AO compensation). The chromatism of the FQPM is not a limitation on NACO as demonstrated in Boccaletti et al. (2004). Therefore, we decided to take advantage of both coronagraphs to get (i) a good signal to noise in the disk at large angular separations using the Lyot coronagraph; and (ii) to characterize the circumstellar dust at very close separations with the FQPM.

The reference star HD 45 291 (V=5.97, H=3.84, K=3.77), which was observed right after the target star, was chosen to have the same parallactic angle as  Pictoris in order to preserve the same pupil orientation. This way, the diffraction spikes of the reference star have about the same orientation as those of  Pictoris with respect to the field of view. The reference star has the same declination but a difference in right ascension which depends on the integration time (36 min here). We observed  Pictoris for a total of 800 s in the H band (Lyot coronagraph), and 700 s with the FQPM in the Ks band (but with a transmission of only 10% to avoid saturation of individual frames), and similarly for the reference star. In addition, the field of view was rotated by 45 when the FQPM is used to place the disk in a different direction than that of the phase transitions of the phase mask. The pixel sampling is 13 mas/pixel.

2.2 Data reduction

During the observations, the individual exposures (DIT = 1 s) are combined in long exposure images of 100 s each (NDIT = 100). Cosmetic reduction is applied on each image including flat fielding, bad pixel correction and sky subtraction. Images are then re-centered and co-added independently for the target star and the reference star.

Our procedure to remove the stellar residuals (unattenuated by the coronagraph) using a reference star is similar for the Lyot and the FQPM images. As described for example in Augereau et al. (1999) and Boccaletti et al. (2003), the image of the target is first divided by that of the reference (re-centered at a subpixel scale) to provide a map of the intensity ratio. The scaling factor is measured at a radial distance where the intensity ratio map is almost flat ( on the Lyot image and on the FQPM image) and is azimuthaly averaged in regions free of circumstellar material (perpendicularly to the disk midplane, in the north-west and south-east directions). The intensity ratio profiles are displayed in Fig. 1.

The reference star image is then normalized to the scaling factor and subtracted from the target star image. After this process, the Lyot subtracted image still has a diffraction pattern originating from the high frequency zonal polishing defects of the primary mirror (2). Similar patterns are observed in HST images of AU Mic (Krist et al. 2005) for instance. This feature was estimated in several sectors around the star and an azimuthaly averaged pattern was subtracted. However, a residual zonal pattern remains in the subtracted image and produces a modulation of the disk intensity in some particular regions. Nevertheless, the disk is clearly visible all across the field of view. The raw coronagraphic images and the subtracted images are displayed in Figs. 2 and in 3 for the Lyot and the FQPM.

For the photometric calibration, out-of-mask images of the star were collected, but with a different set-up than coronagraphic images. Indeed, these calibration data are obtained with a neutral density filter (attenuation of the intensity by factors of 80 in H-band and 90 in Ks-band) and of a full aperture stop (instead of a 10% undersized unobstructed circular stop). The procedure for photometric calibration of such data is fully described in Boccaletti et al. (2008). A detailed estimation of photometric uncertainties accounting for the differences between out-of-mask and on-mask data leads to error bars of 0.16 mag in both the H and Ks filters. The photometric error budget is actually driven by the flux extraction method of a point source (0.13 mag) rather than the scaling factors. The sources of errors being identical to those in Boccaletti et al. (2008), we will adopt the same photometric uncertainties.

2.3 Point source detection limit

Finally, we measured the point-source detection limits on the images of Figs. 2 and 3. The 5-sigma contrast is calculated as the standard deviation of all pixels located at a given radius and that for each radius. Once converted to absolute magnitude, the result displayed in Fig. 4 shows the detection limit for the H and Ks bands along the disk. Note that the 5-sigma detection level is taken here for convenience but does not rigorously correspond to a confidence level as usually defined for a Gaussian distribution. A detailed study of confidence level in the presence of diffraction residuals is given in Marois et al. (2008).

The FQPM image (Fig. 3) has a significantly worse detection limit in the background dominated region (>2 ) owing to the 10% transmission. However, the complementarity is clearly demonstrated in the limit of detection. The expected absolute magnitudes of giant planets (according to the DUSTY model of Chabrier et al. 2000) for 5, 8, 10 and 20 M_J were overplotted in Fig. 4.

At 0.4 , the 4QPM has the ability to pick out an object fainter than 8 M_J while this level of sensitivity is achieved at 0.5 in the Lyot image. The candidate planet reported by Lagrange et al. (2008) in Nov. 2003 data should have been detected at least in the K band image if located at the same position. However, our observations and those of Lagrange et al. (2008) are separated by nearly 1 year and hence orbital motion is to be expected.

The projected distance of the planet candidate was 8 AU ( mas) on Nov. 2003. We therefore re-analyze our data to look around this position but found no firm evidence of a companion. However, a suspicious point-like pattern is visible in the Lyot image at  mas i.e.  mas away from the discovery position (Fig. 5). It differs significantly from the Lagrange et al. (2008) observations. This pattern intensity is compatible with the DUSTY model ( ). But no counterpart is detectable in the 4QPM image ( ) while the DUSTY model does not predict an equivalent flux in the H and Ks bands. Given the proper motion of  Pictoris (about 82 mas/yr to the north) a background star would appear to move closer to the star between 2003 (Lagrange et al. 2008) and 2004 (this paper). The source, if real in both epochs of data, moves farther away from the star between 2003 and 2004. Despite a lack of constraints on the orbital parameters, a projected orbital motion of 107 mas can be consistent with an actual separation larger than 8 AU. However, the position angle of the suspicious point-like pattern differs by 4.5 with respect to the Lagrange et al. (2008) observations which appears inconsistent with an orbit aligned with the disk. We therefore favor a false positive detection as an interpretation of the presence of this pattern.

Two hypotheses can be drawn from our 4QPM detection limit at Ks:

1/

The physical separation in 2004 is less than 8 AU and then the planet candidate is at an angular separation less than 0.4 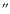which may account for the non detection in our data. In that case the motion is greater than 50 mas;

2/

the physical separation in 2004 is greater or equal to 8 AU and the planet candidate is fainter than the model prediction by almost 1 mag at Ks ( 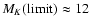). Parameters of the system (for instance age) must be reviewed and other models could be considered.

It is difficult with the available material to identify the most plausible situation and we will have to wait for a definitive confirmation of the companionship and then carry out additional observations in H and Ks with a more effective rejection of the speckles. Orbital motion, if observable, will be valuable to derive the actual mass of the candidate planet and hence will provide a calibration of evolutionary models.

3 Characterization of the dusty disk

3.1 Morphology of the disk

The  Pictoris disk is well detected in scattered light in the Lyot image (Fig. 6, top panel) up to 7.5 on the south-west (SW) side and 7 on the north-east (NE) side (actually limited by the detector field of view). At such distances, the surface brightness is lower than 15 mag/arcsec² (see Sect. 3.2). To avoid confusion from diffraction residuals either from the telescope or the coronagraph, most of the radial features visible in Fig. 2 have been masked by selecting a sector of about in the Lyot image about the position angle (PA) of the disk ( , measured from the north and counter-clockwise, see Sect. 3.3). The brightness asymmetry observed in the visible by Kalas & Jewitt (1995) is also seen in the near-IR (the NE side is brighter than the SW side). The warp is also seen when comparing the contour lines to the position of the midplane (dashed line in Fig. 6). The largest deviation from the midplane is observed in between 3 and 4 corresponding to a physical distance of 59-78 AU, in agreement with the measurement of HST/STIS (Heap et al. 2000). The innermost regions do not look aligned on the midplane but these regions are highly dominated by residual diffraction patterns, as explained in the next section. Indeed, unlike HST/STIS images, the image of the disk is not smooth but is perturbed by the radial diffraction pattern from the primary mirror. This diffraction residual produces ringed structures that we do not consider as real.

The FQPM image is displayed in the middle panel of Fig. 6 (a sector of 45 about the midplane was selected to avoid confusion with instrumental radial features). To better distinguish the large scale structures from the background noise we applied a Gaussian filtering to the image shown in Fig. 3 (right). As explained in Sect. 2, the signal to noise is worse than in the Lyot image, despite similar integration times, since the transmission is 10 times lower. The disk is detected down to a level of 12.5 mag/arcsec² at a radius of about 2 . Although the central field is not obscured as in the Lyot image, a discontinuity at 0.7 on both sides suggests that the patterns located below 0.7 are actually diffraction residuals. This is confirmed by the measurement of the surface brightness in Sect. 3.2. The warp is obviously not detected due to a lack of sensitivity at distances larger than 2 . However, a very pronounced pattern resembling a knot at about 1 is clearly visible on the SW side. It was not seen in the Lyot image owing to the presence of a diffraction spike and its origin remains unexplained. This feature surprisingly resembles the clump observed by Telesco et al. (2005) in the mid-IR although not located at the same position (52 AU in the SW side), while we are probing closer separations (1 is equivalent to about 20 AU). Other clumps (beyond 50 AU) reported by Wahhaj et al. (2003) and Weinberger et al. (2003) in the mid-IR are interpreted as the projection of rings since they are symmetrical. Such rings are also observed at much larger separations (>500 AU) in the visible by Kalas et al. (2000). However, in our near-IR data, the clump has no symmetrical couterpart in the NE side and the origin must be found elsewhere than in the presence of rings. The refinement of the planet candidate orbit (Lagrange et al. 2008) will certainly allows to perform more accurate dynamical simulations and possibly be helpful for the interpretation of such patterns.

A smooth contour of the Lyot image is overplotted on the FQPM image. The overlap is only partial because the usable field is different for each coronagraph (positions of the spikes and coronagraph signatures are different).

3.2 Surface brightness

The surface brightness (SB) of the disk was measured along the NE ( ) and SW ( ) sides and averaged over a sector (avoiding too many diffraction residuals). The SB radial profiles derived from the Lyot and the FQPM images are shown in Fig. 7 (left and right panels, respectively). The intensity variation versus radius is displayed with grey shades. The surface brightness of the disk is compared to the brightness measured in a similar sector but perpendicular to the disk axis (a region free of circumstellar material) to estimate an equivalent noise level. The modulus of this level is plotted in Fig. 7 as a dotted line. In the Lyot image, the region closer than 1.2 (23.2 AU) is totally dominated by diffraction residuals although the coronagraphic mask is only 0.35 in radius. In the FQPM image, the field is not obscured in the center but the diffraction residuals are clearly stronger than the disk brightness for separations closer than 0.7 (13.5 AU). At large distances (>2.2 ), the FQPM image is rapidly dominated by the background noise, as expected.

On the NE side, the two profiles are similar within the intensity range (grey shades), while on the SW side a small difference appears near 1.5 . However, it is difficult to interpret this difference as a color effect because the coronagraphs have different signatures and the overlap of the detected regions is only partial. Also, it is not sufficient to constrain the grain size distribution as we did for HD 141 569 in Boccaletti et al. (2003).

In both the Lyot and FQPM cases, the diffraction residuals in the center can probably be improved with a more careful matching of the star and reference images during the observation (better centering and better correction of the low order aberrations are needed). The advantage of the FQPM over the Lyot coronagraph, although less sensitive in the background dominated region, is clearly seen here and allows us to detect the disk at a separation which is almost half the size than on the Lyot image. This compares to the best distance reported in the literature and achieved with the HST/STIS instrument, where the disk is detected down to 0.75 (Heap et al. 2000). However, the exact signal-to-noise ratio at these distances cannot be estimated on the STIS images because Heap et al. (2000) do not compare the average brightness of the disk with the noise level.

3.3 Spine and thickness

The position angle of disk midplane is measured on the Lyot image by a line passing through the star and going from the edge of the NE side of the disk to that of the SW side. The disk PA is found to be , consistent with previous measurements (between and according to Kalas & Jewitt 1995, for separations larger than ).

In the inner disk regions, the known warp makes the disk not perfectly aligned with the midplane, but instead it appears twisted as shown for instance by Mouillet et al. (1997b) and Heap et al. (2000). Along cuts orthogonal to the midplane, the distance of the peak brightness position to the midplane defines the disk spine which is displayed in the left panel of Fig. 8 for our Lyot image and for a separation larger than . This figure was obtained in two steps. First, the image of the disk was convolved with a Gaussian function to account for the sole large-scale structures. Then, we measured the altitude of the peak brightness with respect to the midplane as a function of the distance from the star using two different methods: one consists of directly measuring the distance of the maximum intensity to the disk midplane, while in the second case, the spine position is obtained from a Gaussian fitting to the vertical profile. Both methods yield very similar results.

According to Fig. 8 (left panel), the position of the warp in the SW and NE sides appears to be not symmetrical with respect to the star. The warp extends to 3 on both sides but peaks at about 3.3 (65 AU) on the SW side and 4.0 (78 AU) on the NE side as measured with parabolic fits (overplotted on Fig. 8). This shift cannot be attributed to a mis-alignment of the star behind the mask, since the centering accuracy is better than 0.1 . The difference in the position of the warp with respect to the star is not reported in previous observations. It is reminiscent of the disk offset discovered in Fomalhaut by Kalas et al. (2005) and to a lesser extent in the disk around HD 141 569 (Boccaletti et al. 2003; Mouillet et al. 2001). The amplitude of this offset is physically almost identical in the cases of Fomalhaut and  Pictoris (about 15 AU), although the  Pictoris offset might be larger due to projection effects. It has been suggested that a planetary companion on an eccentric orbit (e=0.02) could create such asymmetries (e.g. HR 4796, Wyatt et al. 1999). However, it is noted that the mass of the pertubating planet is not very well constrained since several combinations of mass and semi-major axis are able to reproduce the observations. The recent detection of a planet around Fomalhaut (Kalas et al. 2008) confirms the relationship between the perturber and the eccentricity of the ring. The most stringent study in the case of  Pictoris is presented by Freistetter et al. (2007). To reproduce the planetesimal belt positions inferred from high-resolution mid-IR spectroscopy, a system with three planets is necessary, one of them being significantly more massive ( 2 ⁺³_-0.5 M_J) and located at 12 AU. A revised value of the  Pictoris age (12 Myr, Zuckerman et al. 2001) together with the reasoning of Heap et al. (2000) and an averaged position of 71 AU of the warp yield a mass of about 2 M_J, similar to that of Freistetter et al. (2007). Our detection limit presented in Fig. 4 is able to place an upper mass limit of 5-6 M_J at 10 AU for an hypothetic planet of 10 Myr. This is identical to the upper limit of Freistetter et al. (2007) and therefore not relevant to improve the mass constraint while the planet candidate from Lagrange et al. (2008) is actually more massive (8 M_J).

The altitude of the maximum deviation with respect to the midplane reaches 0.10 (1.96 AU) in the SW and 0.07 (1.37 AU) in the NE extension. Heap et al. (2000) also observed a higher altitude in the SW side although they did not discuss this point. Another deviation from the midplane is also visible at closer separations and is located at 1.1 and 1.5 respectively on the SW and NE sides. This inverse warp is likely an artifact since we do not detect it on the FQPM image which is more accurate than the Lyot image in this region. We suspect that the confusion near the center between circumstellar material and diffraction residuals from the on-axis star is responsible for such patterns which are enhanced by the use of a Lyot coronagraph. It might be the same kind of artifact that lead Heap et al. (2000) and Golimowski et al. (2006) to conclude that the two extensions in the inner disk do not intersect at the star.

The Gaussian fit also yields the full width at half maximum (FWHM) of the disk along the midplane. The maximum thickness occurs at about 4.5 and 4.0 from the center respectively for the SW and NE sides (Fig. 8, right). This asymmetry is opposite to that of the warp position. In addition, the SW side is marginally thinner than the NE side (at 1-sigma) a characteristic also reported at mid IR wavelengths (Pantin et al. 1997). The average thickness is about 0.9 (18 AU), in perfect agreement with Heap et al. (2000) and again with Pantin et al. (1997). There is a consensus for this parameter at visible, near IR and mid IR wavelengths. In Golimowski et al. (2006), the SW side appears thinner although error bars are missing to confirm this point. However, they claim that actual thicknesses are 30 less after PSF deconvolution. However, the narrow HST/ACS PSF ( ) cannot increase the apparent size of a pattern which is more than 15 times larger. With a simple numerical simulation, we measured that a disk of which the FWHM is 15 times larger than the PSF size undergoes an increase of only 0.5% in size once convolved with the PSF. Clearly, the impact of PSF-deconvolution in coronagraphic imaging is a very critical issue and will be discussed in Sect. 4.2.

A summary of the asymmetries we measured inside the disk is reported in Table 1.

Table 1:   Registration of asymmetries in the warp of  Pictoris.

3.4 Vertically integrated flux and normal optical thickness

We finally estimate the vertically integrated flux which is measured across the disk thickness (z-axis) and shown as a function of the radial distance to the star in Fig. 9. This flux is obtained by integrating the disk surface brightness over a  region centered on the disk midplane, and normalized to the integrating area. Residual patterns about the center are avoided with an appropriate mask which is adapted to each coronagraph. The vertically integrated flux is almost symmetrical for the NE and SW sides in the Lyot image. This is not the case with the FQPM. Again, the advantage of the Lyot is clearly seen at large separations (>2 ), but the FQPM image is still useful to rule out diffraction artifacts at separations closer than 2 and down to 0.7 . The same measurement performed at 90 from edge-on indicates the regions where we can be confident in the value of the vertically integrated flux. As we took the modulus of the residuals (to avoid negative values), a numerical effect makes the equivalent noise level sometimes larger than the flux measured inside the disk. This is particularly pronounced with the FQPM.

The disk being seen edge-on, the observed surface brightness profile at any given projected distance is the sum of the brightness contributions, modulated by the scattering phase function, of all the grains physically located at distances along the considered line of sight. Deriving the shape of the surface density profile from an edge-on disk brightness profile requires the use of a deprojection method, such the one employed by Augereau & Beust (2006) for AU Mic or the numerical one described in Pantin et al. (1997) for  PictorisIn this approach, the product of the dust surface density profile  and the mean scattering cross section of the grains is reconstructed from the outer disk edge down to the closest distance. For the inversion process to work properly, smooth profiles that extend to large distances where the disk brightness vanishes are required. It is therefore not well adapted to the FQPM profiles, but more suited to the Lyot surface brightness profiles which cover a much larger range of distances. Before performing the inversion, the Lyot profiles have nevertheless been extrapolated beyond 140 AU with a r^-4.5 radial profile and a Gaussian vertical profile (FWHM(r) taken from Golimowski et al. 2006), and then smoothed over 10 pixels.

Examples of deprojected normal disk profiles using the inversion technique of Augereau & Beust (2006) are displayed in Fig. 10 for the SW and NE sides. The figure shows the product of the mean scattering cross section of the grains in the H-band by the dust disk surface density for different scattering asymmetry factors |g| between 0 (isotropic scattering) and 0.5. The profiles are equivalent to normal dust disk optical thickness profiles multiplied by the mean albedo of the grains in the H-band. The  Pictoris disk appears 2 to 4 times less dense at the peak position than the 2.5 times more distant annulus about the F5/F6 V star HD 181 327 that peaks around 87 AU (Schneider et al. 2006).

Beyond 150 AU, the calculated profiles follow a r^-2.5power law as expected from the extrapolated surface brightness profiles at these distances. The SW profiles show a peak, whose exact position varies with |g|, but is situated in the range 80-90 AU. The global ring-shape of the SW dust disk is consistent with the normalized (to allow comparison) planetesimal surface density inferred by Augereau et al. (2001) (gray thick line in Fig. 10). The dust profiles in Fig. 10 appear more extended than the theoretical planetesimal belt because the radiation pressure force causes the grains produced through collisions to populate the outer disk regions as shown in Augereau et al. (2001). The NE  profiles below 100 AU do not mirror the SW profiles suggesting a non-axisymmetrical structure. The NE profiles indeed appear flatter than the SW profiles, and the peak at around 90 AU only becomes visible for very anisotropic scatterers (large |g| values). It is also noticeable that the observations in the mid-infrared deduced surface density profiles (Pantin et al. 1997) are consistent with |g|=0.5 profiles estimated here.

Although the exact shape of the disk cannot be derived uniquely (because of uncertainties in the observations and in the scattering properties in particular), both the NE and SW profiles point toward the presence of dust material inside the main 80-100 AU planetesimal belt, as previously suggested for example by mid-IR observations (Telesco et al. 2005, and ref. therein), and by the present FQPM images. Overall, the results tend to support the idea of a complex, structured and asymmetric system inside the apparent warp location, which led Freistetter et al. (2007) to conclude the presence of several planetary companions.

4 On the warp

The warp of  Pictoris has been the subject of many investigations and hypotheses especially regarding the presence of pertubing bodies like planets (Heap et al. 2000; Mouillet et al. 1997b; Freistetter et al. 2007; Augereau et al. 2001). Heap et al. (2000) and later Golimowski et al. (2006) have interpreted the warp as the blend of two distinct disks at slightly different position angles instead of a single distorted structure. To emphasize the presumed secondary disk, Golimowski et al. (2006) used a reduction process that we reproduce in Sect. 4.1 and critically discuss in Sect. 4.2.

4.1 The secondary disk

The coronagraphic images presented in Golimowski et al. (2006) were obtained with the HST/ACS instrument and classically subtracted with the image of a reference star. In this paper we adopted a similar approach for the data reduction (Sect. 2.2). This processing is extremely efficient in the case of the HST owing to the stability of the PSF compared to that of ground-based telescopes. Then, the HST/ACS subtracted coronagraphic image was deconvolved with a standard Lucy Richardson algorithm taking a synthetic Tiny Tim (Krist & Hook 2004) image as a PSF.

In classical imaging, the image results from the convolution of the object by the PSF. Deconvolution assumes that the PSF is stationary (independent of its position in the field). This is no longer the case in coronagraphy since the image variation is strongly non-linear especially near the center (Malbet 1996). The term PSF is no longer applicable. In a coronagraph, the convolution occurs in the pupil plane downstream of the mask where the pupil is convolved by the Fourier transform of the mask (Malbet 1996). A PSF defined for each point in the image might be necessary in this case for deconvolution. Golimowski et al. (2006) have worked around the problem by avoiding the inner region inside a 1.5 radius, but the effect of deconvolution on coronagraphic image is not further analyzed. At this stage, the warp is still visible as a structure in the main disk. To improve the visibility of fine structures, Golimowski et al. (2006) have divided the deconvolved with the non-deconvolved subtracted coronagraphic image. This procedure reinforces the high spatial frequencies of the images (as in unsharp masking) and reveals the warp as two separate disks. This hypothetic secondary disk can be distinguished from the main disk beyond 80 AU. Below that distance, the intrisic disk thickness prevents any partition of the two disks.

However, this structure is difficult to interpret. It could be a secondary disk fully separated from the main disk and centered on the star, or could instead originate from the main disk as for instance suggested by the inward extrapolation of NE secondary disk which intercepts the main NE disk at around 30 AU (Golimowski et al. 2006). The surface brightness profile of the secondary disk as measured by Golimowski et al. (2006) is very reminiscent of the brightness profile of the main disk beyond 125 AU. The latter distance is supposed to represent the outer edge of the main planetesimal belt from which the dust grains originate that populate the outer disk regions due to radiation pressure forces (e.g. Augereau et al. 2001, and ref. therein). Similarly, the secondary disk could represent the dusty tail of an inclined population of planetesimals located within 80 AU. It is noteworthy that the extrapolation inward of the secondary disk surface brightness measured by Golimowski et al. (2006) would make it brighter than the main disk below 70 AU, which would make the main disk brightness profile much steeper than actually observed. The rather flat surface brightness profile observed below 4 suggests that the secondary disk brightness profile breaks at around 70-80 AU and becomes flatter inside that distance. The reasoning developed for the main disk may thus also be valid for the secondary disk, which would then originate from parent bodies arranged in the form of an inclined belt with an outer edge close to 70-80 AU. It is remarkable that this distance matches the maximum extension for the warp produced by the inclined planet in the models of Mouillet et al. (1997a) and Augereau et al. (2001).

Our reduced coronagraphic images were deconvolved as in Golimowski et al. (2006) except that we were using an actual PSF image of  Pictoris (out of the coronagraph) and a maximum likelihood algorithm for the deconvolution. As a result of the deconvolution process, we marginally detect a radial structure with an inclination of with respect to the disk midplane and consistent with the secondary disk, but also one almost symmetrical structure about the disk midplane at from the main disk (Fig. 11, top panel). It is however difficult to measure the radial distance where these structures originate, although they are consistent with purely radial patterns intersecting the star unlike the secondary disk (at least on the NE side) observed with the ACS instrument. Here, we interpret the radial patterns revealed by the deconvolution process as PSF radial patterns instead of real patterns. These patterns are therefore different to those observed by Golimowski et al. (2006). Our emphasized FQPM image is presented in the bottom panel of Fig. 11 but does not show any features.

4.2 Deconvolution of coronagraphic images: simulation

To evaluate the significance and the nature of the PSF patterns that may appear after deconvolution of a coronagraphic image of a circumstellar disk, we produce synthetic HST/ACS-like coronagraphic observations of an edge-on disk that we afterwards deconvolve. Instead of using a Tiny Tim PSF, we produce a synthetic HST PSF image using our own diffraction code that we have developed to model the behavior and performance of coronagraphs, as well as to gauge the potential of several planet finding projects (Boccaletti et al. 2006; Boccaletti 2004; Boccaletti et al. 2005).

We consider a 2.4 m diameter telescope observing at m, with a bandwidth of 33%, and providing an angular resolution of 0.052 (similar to the ACS parameters). We generate the image of an edge-on circumstellar disk having a 4.5 diameter extension and a midplane surface brightness proportional to r^-1.5, r being the angular distance to the star. The disk extends vertically over 0.52 (10 times the angular resolution) with a Gaussian profile of FWHM = 0.17 (Fig. 12, top panel). The disk model is absolutely free of structures. Note that some of these parameters are arbitrary and are not intended to exactly model the  Pictoris disk. This object contains 8542points for which we have to calculate the image through a coronagraph (a Lyot mask of 1.8 diameter) and for several wavelengths so as to produce a realistic coronagraphic polychromatic image resembling that of the ACS instrument. To simulate realistic images, the model accounts for the phase aberrations using the measured phase map of the HST (Krist & Burrows 1995), and we assume similar static aberrations on the reference star but with an additional aberration in the form of a defocus (4 nm rms) to account for the so-called ``PSF breathing'' (the HST PSF is slightly evolving over time). This amount of defocus is taken arbitrarily as we are looking for qualitative results here. Another way to produce differences in the target star and reference star images would be to apply a different pointing for the two images with respect to the Lyot mask. The star to disk flux ratio is also arbitrary and is selected to have the residuals on the subtracted image of the order of the disk intensity. We suspect that this is precisely in this regime of contrast that deconvolution may generate artifacts. The synthetic images is then deconvolved as in Sect. 4.1.

Several images to illustrate the process of image formation are displayed in Fig. 12. The two top panels show the disk model alone (no star) and the disk convolved with the PSF. The two lower panels are coronagraphic images (reference star subtracted) before and after deconvolution. Several patterns like speckles, rings, and radial spikes which were not included in the disk model are seen and are clearly enhanced in the deconvolution process. For instance, the radial spikes mimic the splitting of the disk midplane into two parts but are obviously not real. These spikes are aligned here with the disk to depict a worse case but could be differently oriented.

We used these simulated data to measure the averaged radial profile and the disk thickness (Fig. 13), before and after deconvolution of the image. Despite the intensity fluctuations resulting from the PSF patterns the averaged radial profile is consistent with the model except near the mask edges. It is interesting to see how the deconvolution enhances the variations of the intensity profile (Fig. 13, left) especially at distances closer than 1.0-1.2 . As a confirmation of the discussion in Sect. 3.3 and contrary to what is proposed in Golimowski et al. (2006), the disk thickness is not affected by the deconvolution as long as it is thicker than the angular resolution (Fig. 13, right). In the simulation, the FWHM is only 0.17 which is about 3 times the angular resolution while in the actual data of  Pictoris, the disk thickness is about 0.87 (Fig. 8) so the PSF blurring should be even less visible. The vertical cut shown in Fig. 13 (right) is obtained at 1.5 (left side of the image). The shape of the blue line (deconvolved image) changes significantly at closer separations, so the FWHM of the disk must be measured in a region less affected by PSF patterns.

Although the simple simulation presented here reveals the production of artifacts, a more general analysis would be necessary to place quantitative limitations when using deconvolution with coronagraphic images of circumstellar disks. We note that the simulations presented here do not rule out the the reliability of the secondary disk shown in Golimowski et al. (2006). This secondary disk is clearly significant with respect to PSF patterns arising in deconvolution of coronagraphic images. In particular, it is symmetrical and originates in the main disk at a distance where PSF patterns are much less preponderant (see Sect. 4.1). The PSF patterns that may be confused with disks structures like spikes mostly originate from the star.

5 Conclusion

This paper reports on the observation of the  Pictoris disk in the near IR with NACO at the VLT using two coronagraphs in two different spectral bands. We have used a careful data reduction process to get rid as much as possible of the diffraction residuals and artifacts that arise in high contrast imaging with a coronagraph on ground-based telescopes. The resulting images reveal the dusty disk in preferential regions depending on the type of coronagraph: between 1.2 to 7.5 with the Lyot mask and between 0.7 to 2.5 for the FQPM image. These two sets of data are therefore complementary in terms of spectral bands and angular separations.

The Lyot mask coronagraph allows a very good characterization of the disk at large distances and especially of the famous warp. We have been able to precisely measure the position, elevation and thickness of the warp and we have shown geometric and photometric particular asymmetries that could eventually been used as inputs to dynamical modeling in order to better constrain the characteristics of the forming planetary system. Some of these asymmetries were reported in various spectral bands (visible and mid IR). The inversion of the surface brightness profiles have confirmed the presence of an asymmetric main planetesimal belt peaking at around 80-100 AU responsible for the dust material beyond that distance. The inversion further supports the presence of significant amounts of additional material inside the main planetesimal belt as suggested by other observations, depicting a complex planetary system.

The FQPM image reveals the presence of very close patterns very similar to what is observed in the mid-IR, a spectral regime that is sensitive to the dust emission. The interpretation of such structures would require further analysis possibly involving dynamical models to understand if the origin is similar to those observed in the mid-IR.

To understand the issue of deconvolution in coronagraphic imaging we have performed numerical simulations to mimic HST Lyot coronagraphic data. Assuming a disk with no structure, this qualitative work shows how the data reduction process may emphasize some PSF structures that reinforce the need for a thorough analytical study for this type of data.

These new images of the  Pictoris debris disk presented here demonstrate the interest of ground-based instruments to achieve high angular resolution at longer wavelengths than with the HST and motivate for even more accurate observations. The sub-arcsec region is now receiving most of the attention with the recent discovery of a planet candidate. Constraints on the characteristics of this object and possibly others could be inferred form the spatial distribution of the dust. Therefore, the precise registration of the inner structures we have performed if complemented with perturbation theory will help to better characterize this planetary system. To confirm the numerical simulations of Freistetter et al. (2007) the study of the disk and its structures near 12 AU is essential. This corresponds precisely to the limit reached in our data (0.62 ) and therefore the motivation is strong to perform more accurate observations. This is becoming possible at the VLT. The coronagraphic suite of NACO now implements other FQPMs tuned for the H and Ks bands with the ability to reach a better attenuation. Additional techniques also have been installed (Angular Differential Imaging, Spectral Differential Imaging) that may facilitate the calibration of the residual starlight and hence the registration of structures even closer to the star.

After more than 20 years of intensive studies, the dusty disk around  Pictoris is still the subject of many questions. Direct imaging observations are complementary to spectroscopy and photometry and are mandatory to better constrain the spatial distribution of the dust, planetesimals and hypothetical planets in order to contribute to the understanding of the planetary formation phase.

Acknowledgements

We are grateful to the ESO staff supporting observations with NACO at the VLT and to the referee for an objective report that help to improve the manuscript. This work also received the support of PHASE, the high angular resolution partnership between ONERA, Observatoire de Paris, CNRS and University Denis Diderot Paris 7.

References

• Augereau, J.-C., & Beust, H. 2006, A&A, 455, 987 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Augereau, J.-C., Lagrange, A.-M., Mouillet, D., & Ménard, F. 1999, A&A, 350, 51 (In the text)
• Augereau, J.-C., Nelson, R. P., Lagrange, A.-M., Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Boccaletti, A. 2004, in EAS Publ. Ser., 12, 165
• Boccaletti, A., Augereau, J.-C., Marchis, F., & Hahn, J. 2003, ApJ, 585, 494 [NASA ADS] [CrossRef] (In the text)
• Boccaletti, A., Riaud, P., Baudoz, P., et al. 2004, PASP, 116, 1061 [NASA ADS] [CrossRef] (In the text)
• Boccaletti, A., Baudoz, P., Baudrand, J., Reess, J.-M., & Rouan, D. 2005, Adv. Space Res., 36, 1099 [NASA ADS] [CrossRef]
• Boccaletti, A., Mouillet, D., Fusco, T., et al. 2006, in Direct Imaging of Exoplanets: Science Techniques, ed. C. Aime, & F. Vakili, IAU Coll., 200, 519
• Boccaletti, A., Chauvin, G., Baudoz, P., & Beuzit, J.-L. 2008, A&A, 482, 939 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Burrows, C. J., Krist, J. E., & Stapelfeldt, K. R. 1995, AAS 187, BAAS, 27, 1329 (In the text)
• Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] (In the text)
• Freistetter, F., Krivov, A., & Löhne, T. 2007, A&A, 466, 389 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Galland, F., Lagrange, A.-M., Udry, S., et al. 2006, A&A, 447, 355 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Golimowski, D., Ardila, D., Krist, J., et al. 2006, AJ, 131, 3109 [NASA ADS] [CrossRef] (In the text)
• Heap, S. R., Lindler, D. J., Lanz, T. M., et al. 2000, ApJ, 539, 435 [NASA ADS] [CrossRef] (In the text)
• Kalas, P., & Jewitt, D. 1995, AJ, 110, 794 [NASA ADS] [CrossRef] (In the text)
• Kalas, P., Larwood, J., Smith, B. A., & Schultz, A. 2000, ApJ, 530, L133 [NASA ADS] [CrossRef] (In the text)
• Kalas, P., Graham, J. R., & Clampin, M. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] (In the text)
• Kalas, P., Graham, J. R., Chiang, E., et al. 2008, ArXiv e-prints (In the text)
• Krist, J. E., & Burrows, C. J. 1995, Appl. Opt., 34, 4951 [NASA ADS] [CrossRef] (In the text)
• Krist, J. E., & Hook, R. 2004, The tiny Tim User's Guide, v6.3 (Baltimore STScI) (In the text)
• Krist, J. E., Ardila, D., Golimowski, D. A., et al. 2005, AJ, 129, 1008 [NASA ADS] [CrossRef] (In the text)
• Lagage, P. O., & Pantin, E. 1994, Nature, 369, 628 [NASA ADS] [CrossRef] (In the text)
• Lagrange, A., Gratadour, D., Chauvin, G., et al. 2008, ArXiv e-prints (In the text)
• Malbet, F. 1996, A&AS, 115, 161 [NASA ADS] (In the text)
• Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2008, ApJ, 673, 647 [NASA ADS] [CrossRef] (In the text)
• Mouillet, D., Lagrange, A.-M., Beuzit, J.-L., & Renaud, N. 1997a, A&A, 324, 1083 (In the text)
• Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A.-M. 1997b, MNRAS, 292, 1997 (In the text)
• Mouillet, D., Lagrange, A. M., Augereau, J. C., & Ménard, F. 2001, A&A, 372, L61 [NASA ADS] [CrossRef] [EDP Sciences]
• Pantin, E., Lagage, P. O., & Artymowicz, P. 1997, A&A, 327, 1123 (In the text)
• Rouan, D., Riaud, P., Boccaletti, A., Clenet, Y., & Labeyrie, A. 2000, PASP, 112, 1479 [NASA ADS] [CrossRef] (In the text)
• Rousset, G., Lacombe, F., Puget, P., et al. 2003, SPIE, 4839, 140 [NASA ADS] (In the text)
• Schneider, G., Silverstone, M. D., Hines, D. C., et al. 2006, ApJ, 650, 414 [NASA ADS] [CrossRef] (In the text)
• Smith, B., & Terrile, R. 1984, Science, 226, 1421 [NASA ADS] [CrossRef] (In the text)
• Telesco, C. M., Fisher, R. S., Wyatt, M. C., et al. 2005, Nature, 433, 133 [NASA ADS] [CrossRef] (In the text)
• Wahhaj, Z., Koerner, D. W., Ressler, M. E., et al. 2003, ApJ, 584 (In the text)
• Weinberger, A. J., Becklin, E. E., & Zuckerman, B. 2003, ApJ, 584, L33 [NASA ADS] [CrossRef] (In the text)
• Wyatt, M. C., Dermott, S. F., Telesco, C. M., et al. 1999, ApJ, 527, 918 [CrossRef] (In the text)
• Zuckerman, B., Song, I., Bessell, M. S., & Webb, R. A. 2001, ApJ, 562, L87 [NASA ADS] [CrossRef] (In the text)

All Tables

Table 1:   Registration of asymmetries in the warp of  Pictoris.

All Figures

---

Copyright ESO 2009