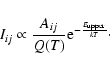| Issue |
A&A
Volume 495, Number 2, February IV 2009
|
|
|---|---|---|
| Page(s) | 655 - 661 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361:200810983 | |
| Published online | 14 January 2009 | |
Ab initio modeling of molecular IR spectra of astrophysical interest: application to CH4
R. Warmbier1 - R. Schneider1 - A. R. Sharma2 - B. J. Braams2 - J. M. Bowman2 - P. H. Hauschildt3
1 - Max-Planck-Institut für Plasmaphysik, Wendelsteinstr. 1, 17491 Greifswald, Germany
2 - Department of Chemistry and Cherry L. Emerson Center for Scientific Computation, Emory University, Atlanta,
Georgia 30322, USA
3 - Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 18 September 2008 / Accepted 19 December 2008
Abstract
Aims. We describe an ab initio-based numerical method of obtaining infrared spectroscopic data (line list) of polyatomic molecules that allows calculation of complete sets of lines for temperatures up to several thousand Kelvin. While the main focus is on completeness and consistency, not spectroscopic accuracy, the approach is in principle ``exact'' for line positions and, although not exact for line strengths, of sufficient accuracy to be of value, especially in wavelength regions where there are gaps in reliable experimental data.
Methods. Global potential energy and dipole moment hypersurfaces are fitted to the results of ab initio electronic structure calculations. The MULTIMODE software is then used to obtain rovibrational energy levels and dipole transition matrix elements. This information is used to calculate a complete set of Einstein coefficients of spontaneous emission A ij.
Results. The method is applied to obtain a spectroscopic database for methane containing over 1.4 million lines up to an upper state energy of 6200 cm-1 (![]() 9000 K). The emission spectrum of CH4 at 1000 K is calculated with the complete set of Einstein coefficients and compared with the one obtained from the HITRAN database. Gaps in the database are realistically filled in by the calculated spectrum.
9000 K). The emission spectrum of CH4 at 1000 K is calculated with the complete set of Einstein coefficients and compared with the one obtained from the HITRAN database. Gaps in the database are realistically filled in by the calculated spectrum.
Conclusions. Consistent and complete databases are important for astrophysical applications. Databases obtained by the method described here fulfill this requirement and are sufficiently accurate for astrophysical applications such as model atmosphere calculations and the corresponding synthetic spectra.
Key words: radiative transfer - molecular data
1 Introduction
Radiative transport calculations are used in astrophysics to model stellar and planetary atmospheres (e.g. Bean et al. 2006; Reiners et al. 2007; Hauschildt & Baron 1999; Leggett et al. 2007). These calculations need complete and consistent spectroscopic databases to avoid incomplete micro-physics and thus systematic errors in the computed model structures and the resulting synthetic spectra. Such problems may occur with inconsistent datasets, e.g., missing lines lead to false ``windows'' for radiation to escape, with some times catastrophic consequences for the computed atmospheric structure. The required accuracy for individual molecular lines is less important, because for such atmospheres no single lines are measured but conglomerates of lines from different molecules form the observed features.
We provide an approach to obtain spectroscopic data for polyatomic molecules that satisfies these requirements, using rigorous theoretical approaches. This paper briefly describes the methodology and presents a comparison of the calculated emission spectrum for methane with data from the HITRAN database over the wavenumber range up to 6200 cm-1 at 1000 K for rotational-vibrational transitions. A later paper will use the results to model radiative transport and compare the influence of different spectroscopic databases on the effective radiation transport and line opacities.
2 Method
The central quantity of interest is the spontaneous emission intensity. It is is given in terms of the well-known Einstein emission coefficient, A ij, defined as
i and j are the indices of the two rovibrational states involved. 2Ji+1 is the gJ-factor of the upper state and
The method adopted for numerically obtaining spectroscopic data of polyatomic molecules is shown schematically in Fig. 1. The two main steps are the calculation of electronic potential energy and dipole moment surfaces using high-level ab initio electronic structure methods and second the calculation of molecular rovibrational line positions (energies) and line strengths by solving the nuclear Schrödinger equation in the field of the electronic potential energy surface.
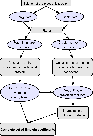 |
Figure 1: Flow chart of the algorithm for obtaining spectroscopic data from ab initio data as used. |
| Open with DEXTER | |
2.1 Potential energy and dipole moment surfaces
The starting point for computation of the (infrared) rovibrational molecular spectrum is the Born-Oppenheimer approximation, by which the electronic and the nuclear degrees of freedom are decoupled. Solution of the ground state electronic structure problem - described by the Schrödinger equation for the electronic degrees of freedom - provides a total energy and a dipole moment. When they are viewed as functions of the nuclear configuration then these are called the potential energy and the dipole moment surface (PES and DMS). The rovibrational spectrum is obtained by solving the Schrödinger equation for the nuclear degrees of freedom in the field of the Born-Oppenheimer PES, and the transition amplitudes follow from matrix elements of the DMS. Computation and analysis of the rovibrational spectrum requires the PES and DMS to be evaluated millions of times, meaning at millions of configurations, and therefore the necessary first step towards this goal is the construction of an analytic approximation to the PES and DMS, fitted to the results of ab initio electronic structure calculations for an appropriate sample of nuclear configurations.
For the PES the ab initio method used in the present work is the spin-restricted coupled cluster method with full iterative treatment of single and double excitations and perturbative treatment of triple excitations, RCCSD(T) (Hampel et al. 1992; Deegan & Knowles 1994; Knowles et al. 2000), using the augmented correlation consistent polarized valence-only triple-zeta (aug-cc-pvtz) basis set (Kendall et al. 1992). The ab initio method for the DMS is the averaged coupled pair functional method, ACPF (Gdanitz & Ahlrichs 1988), using the (non-augmented) cc-pvtz basis (Dunning 1989). All calculations were done using the Molpro program package (Werner 2006).
The ab initio calculations were carried out at a random
sample of configurations obtained iteratively. After an initial PES
was constructed based on a lower level of ab initio theory,
molecular dynamics trajectories were obtained using that surface at a
variety of total energies up to dissociation, configurations were
sampled from those trajectories, the nuclear coordinates in the sample
were additionally subjected to small random displacements, and the
RCCSD(T)/aug-cc-pvtz calculations were carried out for the
configurations obtained that way. Further configurations were sampled
by making random displacements to the global minimum geometry and by
sampling from additional molecular dynamics trajectories. In addition, data representing break-up into CH3 + H and CH2 + H2 were created by placing two fragments far apart and assigning as the energy the sum of energies of the separate fragments, and likewise for the dipole moment. The CH2 and CH3 fragment geometries were sampled from a collection obtained using similar procedures as for CH4 and the same ab initio method was used for energy and dipole moment as for CH4. For H we used the exact energy -0.5 hartree (![]() -13.605 eV),
for H2 the energy was calculated by full configuration interaction
(FCI) on the aug-cc-pvtz basis, and the dipole moment is 0 for both H
and H2 at any geometry. The final database used for the fit
contains 31 314 ab initio energies and 34473 ab initio dipole moments.
-13.605 eV),
for H2 the energy was calculated by full configuration interaction
(FCI) on the aug-cc-pvtz basis, and the dipole moment is 0 for both H
and H2 at any geometry. The final database used for the fit
contains 31 314 ab initio energies and 34473 ab initio dipole moments.
Given the database of ab initio electronic structure energies
and dipole moments the fitted analytical PES and DMS are constructed
following an approach developed and used extensively in the Bowman
group over the past five years for systems of up to 10 atoms
(e.g. Huang et al. 2005; Sharma et al. 2006; Jin et al. 2006; Wang et al. 2008a,b). In
this approach the potential energy surface is fitted in terms of
polynomials of exponential functions of the internuclear distances,
![]() where
where ![]() is a scale parameter and
i and j are nuclear indices. The polynomials are restricted to be
invariant under permutation of identical nuclei (hydrogens) and this
property is built into the basis. The dipole moment must transform
like a vector and is for that reason represented in the form
is a scale parameter and
i and j are nuclear indices. The polynomials are restricted to be
invariant under permutation of identical nuclei (hydrogens) and this
property is built into the basis. The dipole moment must transform
like a vector and is for that reason represented in the form
![]() where X denotes the nuclear
configuration,
where X denotes the nuclear
configuration,
![]() is the position of the i-th nucleus, and
the wi(X) are expanded as permutationally
is the position of the i-th nucleus, and
the wi(X) are expanded as permutationally
![]() functions
of the internuclear distances. An earlier paper on a PES and DMS for
the protonated water dimer (Huang et al. 2005) describes the dipole
moment representation more fully. The coefficients in the polynomial
expansion are determined by solving a weighted least squares system of
equations in which we assign to the k-th configuration a relative
weight
functions
of the internuclear distances. An earlier paper on a PES and DMS for
the protonated water dimer (Huang et al. 2005) describes the dipole
moment representation more fully. The coefficients in the polynomial
expansion are determined by solving a weighted least squares system of
equations in which we assign to the k-th configuration a relative
weight
![]() in which Ek is the ab initio energy of the configuration, E0 is the ab initio
energy at the global minimum, and
in which Ek is the ab initio energy of the configuration, E0 is the ab initio
energy at the global minimum, and ![]() is a parameter for which we
used 0.05 hartree.
is a parameter for which we
used 0.05 hartree.
The accuracy of the fitted PES is represented by a root mean square
deviation between PES and ab initio data, which we present here evaluated separately over three energy ranges. Of the 31 314 configurations there are 5299 that have energy in the range 0-0.05 hartree (0.05 hartree = 10 974
![]() )
relative to the global minimum, 7390 that have energy in the range 0.05-0.1 hartree, 11431 that have energy in the range 0.1-0.25 hartree, and the remainder have higher energy. Over the first
three ranges, the rms error for the energy is, respectively,
)
relative to the global minimum, 7390 that have energy in the range 0.05-0.1 hartree, 11431 that have energy in the range 0.1-0.25 hartree, and the remainder have higher energy. Over the first
three ranges, the rms error for the energy is, respectively,
![]() hartree =18.55
hartree =18.55
![]() ,
,
![]() hartree and
hartree and
![]() hartree, while for the dipole moment it is, respectively,
hartree, while for the dipole moment it is, respectively,
![]() ,
,
![]() and
and
![]() atomic units.
atomic units.
Other diagnostics of the accuracy of the fitted PES and DMS are of interest. Table 1 shows the harmonic frequencies evaluated on the PES at the global minimum in comparison with benchmark frequencies obtained from Molpro with RCCSD(T)/aug-cc-pvtz, while Table 2 gives additional information of PES properties. In Fig. 2 we show the ACPF/cc-pvtz ab initio dipole moment (crosses), the fitted dipole moment (lines), and a more accurate RCCSD(T)/aug-cc-pvtz ab initio dipole moment (pyramids) along the 7-th harmonic frequency displacement vector, which is the one that displays the largest dipole moment amplitude. There is an almost linear and a parabolic non-zero component of the dipole moment vector for this mode. The fitted curve for the parabolic one shows a significant large deviation from the ab initio data and is the worst case of the surface for the revelant range of configuration space. Still, this deviation is not serious for the calculation of transition data, because it delivers only small dipole transition elements for the energy range of interest, which is between -0.4 and 0.4 qi. The component of the dipole vector which is dominating is the one with the (almost) linear behavior. Here, the dipole transition element is one order of magnitude larger than for the other one. While the DMS fit properly covers the ab initio data for the linear component, the ACPF/cc-pvtz itself shows a 12% flatter slope than the more exact RCCSD(T)/aug-cc-pvtz leading to an underestimated transition probability.
Table 1: Normal mode frequencies [cm-1] of methane calculated at the global minimum on the PES compared with Molpro RCCSD(T)/aug-cc-pvtz normal mode frequencies at the ab initio optimized equilibrium geometry.
Table 2: Additional information of PES properties compared with experimental values (NIST 2006).
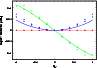 |
Figure 2: This figure provides an one dimensional cut through the dipole moment surface along the normal mode displacement of the IR active n3 mode. Each line respresents a component of the dipole moment vector, while the labeling of these components is arbitrary due to F2 degeneracy. The straight lines are DMS values, crosses the corresponding ab initio. For better comparison we included RCCSD(T) dipole moments (pyramids) as well. |
| Open with DEXTER | |
2.2 Calculation of energies
The next step is to calculate every rotational-vibrational energy level within a certain energy range up to a given value of the total angular momentum J. For this the MULTIMODE program package (see Carter et al. 1998; Carter & Bowman 1999) was used. Employing any user-defined potential it can calculate converged energies of the rigorous Watson Hamiltonian (Watson 1968) using the virtual configuration interaction (VCI) method (Carter & Bowman 1998,2000; Carter et al. 1998). The many-body VCI wave function is expanded in terms of the eigenstates of a vibrational self consistent field (VSCF) Hamiltonian (Bowman 1986; Carter et al. 1997), which are called virtual states. The expansion forms an orthonormal basis constructing a standard eigenvalue problem. This method delivers eigenstates and -functions which are true variational upper bounds of the exact values. The VSCF wave function assumes independent oscillators, while the vibrational modes of a molecule are coupled. A part of this coupling can be regained with the introduction of n-mode basis functions. The quality of the eigenvalues increases with a higher number of coupled modes. In theory, coupling all vibrational modes would deliver exact values. The expansion character of the VCI method does not allow a strict assignment of vibrational quantum numbers. Most often the state assignment can be made based on the dominant coefficient of the expansion, but this is not always the case. The assignment of each ``exact'' rovibrational energy level is important for the calculation of the intensities because this is done by an approximate method (described briefly below) which is exact for J = 0 but not for J > 0 and which needs to make a one-to-one correspondence with the exact energies. When these ambiguities occur (rarely) a band averaging approximation is done as described in detail in the next section.
To conclude this section we note that because the VCI energies obtained here are converged to within 10 or fewer wavenumbers, for a given PES, the deviations from experiment are mainly due to the small inaccuracies in the electronic energies used to obtain the PES, and in the present case we estimate these to contribute 5-30 cm-1 errors depending on the energy and modes involved, see Table 3. Thus the results presented here are consistent with the goals stated above, i.e., to calculate a low-resolution spectrum over a wide spectral range.
Table 3: Calculated fundamental vibrational energies [cm-1] compared with experimental values NIST (2006).
2.3 Calculation of dipole transition elements
The MULTIMODE program can also be used for the calculation of dipole matrix elements; however, at present this cannot be done exactly for arbitrary J. It can do these matrix elements rigorously for J=0and also in the so-called adiabatic rotation approximation (Carter & Bowman 1998). Here the vibrational Hamiltonian is extended with the classical rigid rotor energy. This simulates a part of the rotational dependence of the wave function, while the form of the wave function has not changed. This method is of adequate accuracy for low J and small Coriolis coupling, which is neglected here (Carter & Bowman 1998; Carter et al. 1999). We used this approximation, because it is compatible with the existing vibrational dipole moment matrix routine of Multimode. The quality of adiabatic rotation approximation results decrease with higher J's where the molecules are deformed stronger and the rigid rotor approach looses suitability. Still, we expect reasonable results within the surveyed energy range although a quantitative error estimation can not be given easily. An extension to full rotational treatment of the dipole elements is planned in the future, after modifications of the code are done and tested.
Since the energies and dipole matrix elements have to be calculated in
two independent calculations with different wave functions, a direct
identification of a state in both calculations can only be done via
the vibrational quantum numbers. For molecules with degenerated vibrational modes additional issues occur. Non-rotating methane has one doubly degenerate and two triply degenerate vibrational modes. The latter are split by Coriolis interactions for non-zero J.
In addition a splitting of overtones, and related to this of combination levels, appears![]() . Combination levels are states where more than one vibrational mode is excited. One can not obtain rigorous quantum state information out of the VCI method making this simple assignment problematic. Thus for both
parts of the calculations all states or transitions, respectively,
with the same quantum number assignments are collected and an average
of the mode energy or the transition dipole matrix element is done.
Later then the theoretical degeneracy factors can be used. With this
procedure we lose information about splitting of degenerated modes but
add certainty for the average and total band values.
. Combination levels are states where more than one vibrational mode is excited. One can not obtain rigorous quantum state information out of the VCI method making this simple assignment problematic. Thus for both
parts of the calculations all states or transitions, respectively,
with the same quantum number assignments are collected and an average
of the mode energy or the transition dipole matrix element is done.
Later then the theoretical degeneracy factors can be used. With this
procedure we lose information about splitting of degenerated modes but
add certainty for the average and total band values.
For J=0 energies and transition elements are calculated with the same wave function. Therefore, every transition element can be directly identified with the corresponding energies. This allows a quantitative comparison of exact and averaged spectroscopic information at least for the vibrational case. This is done later in this paper.
2.4 Einstein coefficients
Following Eq. (1) the Einstein coefficients, taking into account K-dependency and statistical factors for rotational radiation, are given by
where gi and gj are the degeneracy factors of the initial and final state respectively. This expression includes the standard Hönl-London factors SJK. (Hönl & London 1925; Hansson & Watson 2005) The dipole transition element
The final databases we produce are public and can be downloaded (www.ipp.mpg.de/~rbw/databases). They contain the wavenumber of the lines k [
![]() ], Einstein coefficients A ij [
], Einstein coefficients A ij [
![]() ], energies E [
], energies E [
![]() ], degeneracies g and the rotational (J, K) and vibrational (n) quantum
numbers for upper (i) and lower (j) states respectively. The available information differs from the HITRAN database, therefore, we have chosen a different format for the database file:
], degeneracies g and the rotational (J, K) and vibrational (n) quantum
numbers for upper (i) and lower (j) states respectively. The available information differs from the HITRAN database, therefore, we have chosen a different format for the database file:
| k | A ij | Ei | gi | Ej | gj | Ji | ... |
| F9.2 | E13.6 | F9.2 | I4 | F9.2 | I4 | I3 | ... |
| ... | Ki | ni | Jj | Kj | nj | ||
| ... | I3 | 1X | A15 | I3 | I3 | 1X | A15 |
3 Analysis
For practical calculations, also the partition function
has to be defined. The first term represents the I=1/2 nulcear spin degeneracy for the m=4 hydrogen atoms. Still, not all permutations are allowed by symmetry for all vibrations. It is common (Chakraborty et al. 2004) to use an averaged symmetry factor (
Table 4 shows partition functions up to T=1500 K. We also calculated partition functions of datasets truncated at
Table 4: Comparison of partition functions for the complete datasets (Col. 2) and two truncated datasets. In addition partition functions from (Chakraborty et al. 2004) (Col. 5) are listed.
The algorithm and method described in Sect. 2 limits the quality of the spectroscopic data. As mentioned, it is possible using MULTIMODE to obtain purely vibrational Einstein coefficients without any averaging. This allows a visual estimation of the quality of the averaging approach.
![\begin{figure}
\par\subfigure[no apparatus function]{\resizebox{7cm}{!}{\include...
...}$ ]{\resizebox{7cm}{!}{\includegraphics[angle=0]{0983fi3c.eps}} }\end{figure}](/articles/aa/full_html/2009/08/aa10983-08/Timg45.gif) |
Figure 3:
Relative intensity plots of methane at 1000 K with Lorentzian line broadening with broadening parameter
|
| Open with DEXTER | |
Figure 3 shows some example plots of the relative intensities for a section of the J=0 methane spectrum. The intensities I ij were calculated from Einstein coefficients multiplied with the Boltzman distribution function for
![]() ,
the partition function and a resolution of
,
the partition function and a resolution of
![]() .
.
The temperature was chosen so that the distribution function is negligible for energies higher than the
The figure compares the intensities of the band-averaged (dotted) and
not band-averaged (straight) calculations. In Fig. 3(a) the
effect on the line intensities and positions is shown. The averaging
causes a redistribution of intensities to the main line because the
minor sub-bands are added to them. Still, for complex systems as
stellar and planetary atmospheres the spectral lines are smeared out
by pressure broadening and instrumental resolution. This is simulated
in Figs. 3(b) and 3(c) with Gaussian apparatus
functions of different half widths ![]() .
For a resolution of the
measurement aperture worse than
.
For a resolution of the
measurement aperture worse than
![]() the composite
spectrum is of sufficient accuracy. The main effect is a loss of the
side bands and therefore a more pronouced main band.
the composite
spectrum is of sufficient accuracy. The main effect is a loss of the
side bands and therefore a more pronouced main band.
This proves, that our algorithm delivers spectroscopic databases with sufficient accuracy for the astrophysical application even for cases with strongly degenerated lines. The consistency and completeness of the data results in an advantage compared to common databases for the designed boundary conditions.
4 Comparison with HITRAN
We have built a spectroscopic database for methane using the method
described above, including over 1.2 million lines up to an upper
state energy of
![]() (
(
![]() ). We compare this database to the HITRAN
spectroscopic database (Brown et al. 2003; Rothman et al. 2005). Please note
that our database does not directly compete with HITRAN in terms of accuracy, for it was constructed
for a different purpose. Therefore, the present comparison does
by not have a quantitative message, but provides a proof-of-principle
for our approach.
). We compare this database to the HITRAN
spectroscopic database (Brown et al. 2003; Rothman et al. 2005). Please note
that our database does not directly compete with HITRAN in terms of accuracy, for it was constructed
for a different purpose. Therefore, the present comparison does
by not have a quantitative message, but provides a proof-of-principle
for our approach.
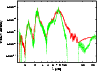 |
Figure 4: Relative intensities plot (same parameters as Fig. 3(a)) of our database (straight) and HITRAN (dotted) for methane. HITRAN does not contain continuous data, while our does. The main features of the HITRAN spectra are reproduced in our one, while intensity values deviate. |
| Open with DEXTER | |
Figure 4 shows relative intensity spectra built from HITRAN and our database, using the same parameters as in Fig. 3(a). Our database reproduces all main features of the HITRAN spectrum. The exact intensities show deviations which are caused by the band-averaging, the dipole transition matrix approximation and the different line densities of the databases. A quantitative assignment of the deviations to the sources can not be given. Therefore, a quantitative analysis of the quality of our data can not be achieved easily. However, some general arguments can be given. HITRAN is very reliable when one is looking at single lines, being more accurate than our database, but it includes only 187 000 lines. This lack of lines produces false empty regions in the spectrum; in particular at high temperatures. In addition, missing lines, independent of their intensity, produce windows allowing radiation energy to escape too easily. Our database is complete and, therefore, avoids these problems.
The common databases used for radiation transport calculations are
patched with data from different sources to achieve as much
completeness as possible but introducing systematic errors via the
combination of different databases. We have calculated synthetic
spectra for a fixed T dwarf model atmosphere with
![]() including only 12CH4 lines, all other lines from all other species are neglected to highlight the effects of 12CH4. This means that the same atmospheric structure was used for both cases, while the spectroscopic information is taken from different databases. Figure 5 shows the radiation flux
including only 12CH4 lines, all other lines from all other species are neglected to highlight the effects of 12CH4. This means that the same atmospheric structure was used for both cases, while the spectroscopic information is taken from different databases. Figure 5 shows the radiation flux
![]() emitted as a function of
the wavelength. In addition to our database (lower plot), fluxes for
the HITRAN (upper plot) database for CH4 are shown as a cloud of points. For better comparison we applied successive neighbor averaging until sufficient smooth lines could be drawn. The darker line represents the HITRAN based simulation. Both pictures
show the same general absorption characteristic. HITRAN has higher
absorption maxima and a broader characteristic than our database. The averaged values show less deviations. The interpretation of such data is delicate. Looking at a narrow spectral region the HITRAN calculation may show stronger maxima of absorption represented by very few data points, while the total absorption for the region is not necessarily larger than for our one. The
different maxima can be interpreted as a result of an underestimated
rotational dependence of the transition elements due to the adiabatic
approximation. For the high energy region the limited energy range of our calculations has to be taken into account. While we calculated all states up to 6200
emitted as a function of
the wavelength. In addition to our database (lower plot), fluxes for
the HITRAN (upper plot) database for CH4 are shown as a cloud of points. For better comparison we applied successive neighbor averaging until sufficient smooth lines could be drawn. The darker line represents the HITRAN based simulation. Both pictures
show the same general absorption characteristic. HITRAN has higher
absorption maxima and a broader characteristic than our database. The averaged values show less deviations. The interpretation of such data is delicate. Looking at a narrow spectral region the HITRAN calculation may show stronger maxima of absorption represented by very few data points, while the total absorption for the region is not necessarily larger than for our one. The
different maxima can be interpreted as a result of an underestimated
rotational dependence of the transition elements due to the adiabatic
approximation. For the high energy region the limited energy range of our calculations has to be taken into account. While we calculated all states up to 6200
![]() the line list can of course not be complete for this interval. The differences in the characteristics may result from
the better line density of our database compared to HITRAN. The radiative flux plots
show differences, which can be mapped to the characteristics of the
underlying databases. Analysis for more precise discussions of
specific databases will be done in a subsequent paper.
the line list can of course not be complete for this interval. The differences in the characteristics may result from
the better line density of our database compared to HITRAN. The radiative flux plots
show differences, which can be mapped to the characteristics of the
underlying databases. Analysis for more precise discussions of
specific databases will be done in a subsequent paper.
 |
Figure 5:
Radiative flux |
| Open with DEXTER | |
5 Conclusions
We presented a method to construct complete spectroscopic databases as needed for model atmospheres used in astrophysics. The method fulfills the accuracy requirements for this application and comparisons with the standard HITRAN show acceptable agreement.
Acknowledgements
We appreciate support for MULTIMODE by S. Carter. R. Warmbier and R. Schneider acknowledge funding of the work by the Intitiative and Networking Fund of the Helmholtz Association. The work of B.J.B. and A.R.S. was supported by the US Department of Energy under grant number #DE-FG02-07ER54914.
References
- Bean, J. L., Sneden, C., Hauschildt, P. H., Johns-Krull, C. M., & Benedict, G. F. 2006, ApJ, 652, 1604 [NASA ADS] [CrossRef]
- Bowman, J. M. 1986, Accounts of Chemical Research, 19, 202 [CrossRef]
- Brown, L. R., Benner, D. C., Champion, J. P., et al. 2003, Journal of Quantitative Spectroscopy & Radiative Transfer, 82, 219 [NASA ADS] [CrossRef]
- Carter, S., & Bowman, J. M. 1998, J. Chem. Phys., 108, 4397 [NASA ADS] [CrossRef]
- Carter, S., & Bowman, J. 1999, Manual for Multimode, 3rd edn., http://www.chemistry.emory.edu/faculty/bowman/multimode/
- Carter, S., & Bowman, J. M. 2000, J. Phys. Chem. A, 104, 2355 [CrossRef]
- Carter, S., Culik, S., & Bowman, J. 1997, J. Chem. Phys., 107, 10458 [NASA ADS] [CrossRef]
- Carter, S., Bowman, J., & Handy, N. 1998, Theoretical Chemistry Accounts, 100, 191
- Carter, S., Shnider, H. M., & Bowman, J. M. 1999, J. Chem. Phys., 110, 8417 [CrossRef]
- Chakraborty, A., Truhlar, D. G., Bowman, J. M., & Carter, S. 2004, J. Chem. Phys., 121, 2071 [NASA ADS] [CrossRef] (In the text)
- Deegan, M. J. O., & Knowles, P. J. 1994, Chem. Phys. Lett., 227, 321 [NASA ADS] [CrossRef]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] (In the text)
- Gdanitz, R., & Ahlrichs, R. 1988, Chem. Phys. Lett., 143, 413 [NASA ADS] [CrossRef] (In the text)
- Hampel, C., Peterson, K. A., & Werner, H. J. 1992, Chem. Phys. Lett., 190, 1 [NASA ADS] [CrossRef]
- Hansson, A., & Watson, J. 2005, Journal of Molecular Spectroscopy, 233, 169 [NASA ADS] [CrossRef]
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 109, 41 [CrossRef]
- Hönl, H., & London, F. 1925, Zeitschrift für Physik, 33
- Huang, X., Braams, B., & Bowman, J. 2005, J. Chem. Phys., 127, 099904 [NASA ADS]
- Jin, Z., Braams, B. J., & Bowman, J. M. 2006, J. Phys. Chem. A, 110, 1569 [CrossRef]
- Kendall, R. A., Dunning, T. H., & Harrison, R. J. 1992, J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef] (In the text)
- Knowles, P., Hampel, C., & Werner, H. 2000, J. Chem. Phys., 112, 3106 [NASA ADS] [CrossRef]
- Leggett, S., Marley, M., Freedman, R., et al. 2007, ApJ, 667, 537 [NASA ADS] [CrossRef]
- NIST. 2006, Computational Chemistry Comparsion and Benchmark Database, cccbdb.nist.gov, and references therein (In the text)
- Reiners, A., Homeier, D., Hauschildt, P. H., & Allard, F. 2007, A&A, 473, 245 [NASA ADS] [CrossRef] [EDP Sciences]
- Rothman, L., Jacquemart, D., Barbe, A., et al. 2005, Journal of Quantitative Spectroscopy & Radiative Transfer, 96, 139 [NASA ADS] [CrossRef]
- Sharma, A., Wu, J., Braams, B., et al. 2006, J. Chem. Phys., 125, 224306 [NASA ADS] [CrossRef]
- Wang, Y., Braams, B. J., Bowman, J. M., Carter, S., & Tew, D. P. 2008a, J. Chem. Phys., 128, 224314 [NASA ADS] [CrossRef]
- Wang, Y., Carter, S., Braams, B. J., & Bowman, J. M. 2008b, J. Chem. Phys., 128, 071101 [NASA ADS] [CrossRef]
- Watson, J. K. G. 1968, Molecular Phys., 15, 479 [NASA ADS] [CrossRef] (In the text)
- Werner, H.-J., K. P. E. A. 2006, Molpro, version 2006.1, a package of ab initio programs, see http://molpro.net (In the text)
Footnotes
- ... appears
![[*]](/icons/foot_motif.gif)
- A simple access to this problem, without touching quantum
mechanics, can be delivered by group theory. Here an example: Methane
belongs to the Td symmetry group. There a twofold degenerated mode
is of irreducible representation E. The first overtone is represented
by the direct product
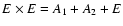 .
Realized are
A1 and E, representing the three possibilities to put two
marbles in two boxes.
.
Realized are
A1 and E, representing the three possibilities to put two
marbles in two boxes.
All Tables
Table 1: Normal mode frequencies [cm-1] of methane calculated at the global minimum on the PES compared with Molpro RCCSD(T)/aug-cc-pvtz normal mode frequencies at the ab initio optimized equilibrium geometry.
Table 2: Additional information of PES properties compared with experimental values (NIST 2006).
Table 3: Calculated fundamental vibrational energies [cm-1] compared with experimental values NIST (2006).
Table 4: Comparison of partition functions for the complete datasets (Col. 2) and two truncated datasets. In addition partition functions from (Chakraborty et al. 2004) (Col. 5) are listed.
All Figures
 |
Figure 1: Flow chart of the algorithm for obtaining spectroscopic data from ab initio data as used. |
| Open with DEXTER | |
| In the text | |
 |
Figure 2: This figure provides an one dimensional cut through the dipole moment surface along the normal mode displacement of the IR active n3 mode. Each line respresents a component of the dipole moment vector, while the labeling of these components is arbitrary due to F2 degeneracy. The straight lines are DMS values, crosses the corresponding ab initio. For better comparison we included RCCSD(T) dipole moments (pyramids) as well. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\subfigure[no apparatus function]{\resizebox{7cm}{!}{\include...
...}$ ]{\resizebox{7cm}{!}{\includegraphics[angle=0]{0983fi3c.eps}} }\end{figure}](/articles/aa/full_html/2009/08/aa10983-08/Timg45.gif) |
Figure 3:
Relative intensity plots of methane at 1000 K with Lorentzian line broadening with broadening parameter
|
| Open with DEXTER | |
| In the text | |
 |
Figure 4: Relative intensities plot (same parameters as Fig. 3(a)) of our database (straight) and HITRAN (dotted) for methane. HITRAN does not contain continuous data, while our does. The main features of the HITRAN spectra are reproduced in our one, while intensity values deviate. |
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
Radiative flux |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



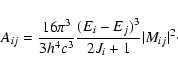
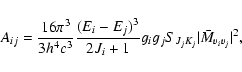
![$\displaystyle Q(T) = \frac{(2I+1)^m}{\sigma} \sum_J (2J+1) \sum_{K=-J}^{+J} \sum_{n_1,\ldots,n_N} g_{n_1,\ldots,n_N}
\quad {\rm exp}[-E(J,K,n_1,\ldots,n_N)/k_bT]$](/articles/aa/full_html/2009/08/aa10983-08/img36.gif)
![\begin{displaymath}
Q(T) = \frac{16}{12} \sum_i g_i \: {\rm exp}[-E_i/k_bT].
\end{displaymath}](/articles/aa/full_html/2009/08/aa10983-08/img39.gif)