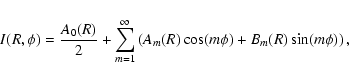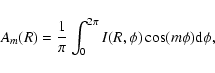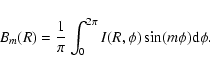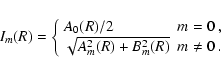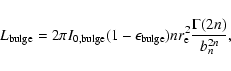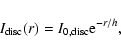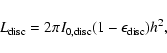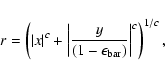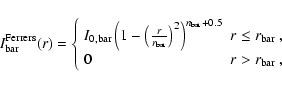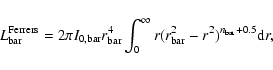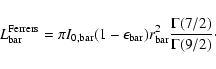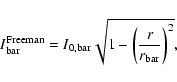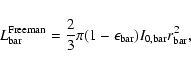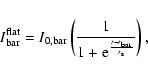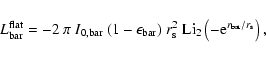The population of barred galaxies in the local universe

J. A. L. Aguerri; J. Méndez-Abreu; E. M. Corsini

doi:10.1051/0004-6361:200810931

Home

All issues

Volume 495 / No 2 (February IV 2009)

A&A, 495 2 (2009) 491-504

Full HTML

Free Access

Issue		A&A Volume 495, Number 2, February IV 2009


Page(s)		491 - 504
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361:200810931
Published online		14 January 2009

I. Detection and characterisation of bars

J. A. L. Aguerri¹ - J. Méndez-Abreu^2,3,4 - E. M. Corsini⁴

1 - Instituto de Astrofísica de Canarias, C/ Vía Láctea s/n, 38200 La Laguna, Spain
2 - INAF-Osservatorio Astronomico di Padova, vicolo dell'Osservatorio 5, 35122 Padova, Italy
3 - Universidad de La Laguna, Av. Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Spain
4 - Dipartimento di Astronomia, Università di Padova, vicolo dell'Osservatorio 3, 35122 Padova, Italy

Received 8 September 2008 / Accepted 16 December 2008

Abstract
Context. Bars are very common in the centre of the disc galaxies, and they drive the evolution of their structure. The state-of-the-art imaging and redshift surveys of galaxies allow us to study the relationships between the properties of the bars and those of their hosts in statistically significant samples.
Aims. A volume-limited sample of 2106 disc galaxies was studied to derive the bar fraction, length, and strength as a function of the morphology, size, local galaxy density, light concentration, and colour of the host galaxy. The sample galaxies were selected to not be strongly disturbed/interacting.
Methods. The bar and galaxy properties were obtained by analysing the r-band images of the sample galaxies available in the Sloan Digital Sky Survey Data Release 5.
Results. The bars were detected using the ellipse fitting method and Fourier analysis method. They were tested and calibrated with extensive simulations on artificial images. The ellipse fitting method was found to be more efficient in detecting bars in spiral galaxies. The fraction of barred galaxies turned out to be $45\%$ . A bar was found in $29\%$ of the lenticular galaxies, in $55\%$ and $54\%$ of the early- and late-type spirals, respectively. The bar length (normalised by the galaxy size) of late-type spirals is shorter than in early-type or lenticular ones. A correlation between the bar length and galaxy size was found with longer bars hosted by larger galaxies. The bars of the lenticular galaxies are weaker than those in spirals. Moreover, the unimodal distribution of the bar strength found for all the galaxy types argues against a quick transition between the barred and unbarred statues. There is no difference between the local galaxy density of barred and unbarred galaxies. Besides, neither the length nor strength of the bars are correlated with the local density of the galaxy neighbourhoods. In contrast, a statistical significant difference between the central light concentration and colour of barred and unbarred galaxies was found. Bars are mostly located in less concentrated and bluer galaxies.
Conclusions. These results indicate that the properties of bars are strongly related to those of their host galaxies, but do not depend on the local environment.

Key words: galaxies: elliptical and lenticular, cD - galaxies: evolution - galaxies: fundamental parameters - galaxies: kinematics and dynamics - galaxies: structure - galaxies: spiral

1 Introduction

Strong bars are observed in optical images of roughly half of all the nearby disc galaxies (Barazza et al. 2008; Marinova & Jogee 2007; Reese et al. 2007). This fraction rises to about $70\%$ when near-infrared images are analysed (Knapen et al. 2000; Menéndez-Delmestre et al. 2007; Eskridge et al. 2000). The presence of a bar can be found by visual inspection (e.g., de Vaucouleurs et al. 1991, hereafter RC3), by analysing the shape and orientation of the galaxy isophotes (e.g., Laine et al. 2002; Barazza et al. 2008; Wozniak et al. 1995; Marinova & Jogee 2007), or by studying the Fourier modes of the light distribution (e.g., Ohta et al. 1990; Elmegreen & Elmegreen 1985; Aguerri et al. 2000a,1998). Therefore, bars are a common feature in the central regions of disc galaxies of the local universe. But, this is also true at high redshift. In fact, the bar fraction apparently remains constant out to $z\approx 1$ (Jogee et al. 2004; Barazza et al. 2008; Elmegreen et al. 2004), although there are some claims that this is not the case (Sheth et al. 2008).

The presence of bars in the centre of lenticular and spiral galaxies make them ideal probes of the dynamics of the central regions of discs. In fact, bars are efficient agents of angular momentum, energy, and mass redistribution. They act on both luminous and dark matter components (Debattista & Sellwood 2000,1998; Athanassoula 2003; Weinberg 1985) driving the evolution of galaxy structure and morphology. In particular, the amount of angular momentum exchanged is related to specific properties of the galaxies, such as the bar mass, halo density, and halo velocity dispersion (Athanassoula 2003; Sellwood & Debattista 2006; Sellwood 2006) Moreover, they funnel material towards the galaxy centre building bulge-like structures (e.g., Kormendy & Kennicutt 2004), nuclear star-forming rings (e.g., Buta et al. 2003), and nuclear bars (e.g., Erwin 2004), and feeding the central black hole (e.g., Shlosman et al. 2000).

Bars play an important role in bulge formation. Major mergers or monolithic collapse are the classical theories for bulge formation in disc galaxies (e.g., Kormendy & Kennicutt 2004; Eggen et al. 1962). But bulges can be built via minor mergers (Eliche-Moral et al. 2006; Aguerri et al. 2001a) or secular evolution processes produced by bars. In fact, according with the results of N-body simulations, the inner parts of a bar inflate after a few bar rotations because of large-scale violent bending instabilities and settle with an increased thickness and vertical velocity dispersion (e.g., Combes et al. 1990; Athanassoula 2005; Debattista et al. 2004; Athanassoula 2003; Raha et al. 1991; Martinez-Valpuesta et al. 2006; Combes & Sanders 1981). This leads to the establishment of the connection between the bar-buckling mechanism and the formation of boxy/peanut bulges (Bureau & Athanassoula 1999; Bureau & Freeman 1999; Chung & Bureau 2004). The buckling instability does not destroy the bar and forms a central stellar condensation reminiscent of the bulges of late-type spirals (Athanassoula 2005; Debattista et al. 2004), in agreement with early findings by Hohl (1971). Observational evidences of secular bulge formation includes the near-exponential surface brightness profiles of some bulges (Méndez-Abreu et al. 2008a; de Jong 1996; Courteau et al. 1996; MacArthur et al. 2003; Carollo et al. 2001; Prieto et al. 2001; Andredakis et al. 1995; Aguerri et al. 2005; Fisher & Drory 2008), a correlation between bulge and disc scale length (Méndez-Abreu et al. 2008a; MacArthur et al. 2003; Aguerri et al. 2005), the similar colours of bulges and inner discs (Carollo et al. 2007; Courteau et al. 1996; Peletier & Balcells 1996), substantial rotation (Kormendy & Kennicutt 2004), and the presence of B/P-shaped bulges in $\approx$ $45\%$ of edge-on galaxies (Lütticke et al. 2000). Recently, the connection between B/P-shaped bulges and bars has also been confirmed in face-on barred galaxies (Méndez-Abreu et al. 2008b).

The most important parameters of bars are the length, strength, and pattern speed. Their evolution depends on the effectiveness of the angular momentum exchange between luminous and dark matter. Different methods have been proposed to measure bar properties.

The bar length can be obtained by eye estimates on galaxy images (Kormendy 1979; Martin 1995), locating the maximum ellipticity of the galaxy isophotes (Laine et al. 2002; Wozniak et al. 1995; Marinova & Jogee 2007), looking for variations of the isophotal position angle (Sheth et al. 2003; Erwin 2005) or of the phase angle of the Fourier modes of the galaxy light distribution (Aguerri et al. 2003; Quillen et al. 1994), analysing the bar-interbar contrast (Aguerri et al. 2003,2000a), or by photometric decomposition of the surface brightness distribution (Laurikainen et al. 2005; Prieto et al. 1997; Aguerri et al. 2005). The previous techniques reported that the typical bar length is about 3-4 kpc, and is correlated with the disc scale, suggesting that the two components are affecting each other (Marinova & Jogee 2007; Aguerri et al. 2005; Laurikainen et al. 2007).

The bar strength can be derived by measuring the bar torques (Buta & Block 2001), isophotal ellipticity (Aguerri 1999; Martinet & Friedli 1997; Marinova & Jogee 2007; Whyte et al. 2002), the maximum amplitude of the m=2Fourier mode (Laurikainen et al. 2005; Athanassoula & Misiriotis 2002), or integrating the m=2 Fourier mode in the bar region (Ohta et al. 1990; Aguerri et al. 2000a). The bar strength is almost constant with Hubble type (Marinova & Jogee 2007), but lenticular galaxies host weaker bars than spirals (Laurikainen et al. 2007).

The pattern speed of bars can be indirectly estimated by identifying rings with the location of the Lindblad resonances (e.g., Vega Beltrán et al. 1997; Jeong et al. 2007), matching the observed velocity and density fields with numerical models of the gas flows (e.g., Aguerri et al. 2001b; Weiner et al. 2001; Lindblad et al. 1996; Rautiainen et al. 2008), analysing the offset and shape of the dust lanes, which trace the location of shocks in the gas flows (e.g., Athanassoula 1992), looking for colour changes (Aguerri et al. 2000a) and minima in the star formation (Cepa & Beckman 1990) outside the bar region, or by adopting the Tremaine-Weinberg method (see Corsini 2008, for a review). The last is a model-independent way to measure the pattern speed (Tremaine & Weinberg 1984), which was successfully applied to single (Merrifield & Kuijken 1995; Debattista et al. 2002; Aguerri et al. 2003), double (Corsini et al. 2003) and dwarf barred galaxies (Corsini et al. 2007) too. Observed pattern speeds imply that barred galaxies host maximal discs (Debattista & Sellwood 2000,1998), since bars in dense dark matter halos are rapidly decelerated by dynamical friction (Weinberg 1985; Sellwood & Debattista 2006; Sellwood 2006).

Nowadays, the large galaxy surveys, such as the Sloan Digital Sky Survey (York et al. 2000, hereafter SDSS) allow us to study the bar properties in samples of thousands of galaxies, obtaining for the first time statistically significant results. By studying a volume-limited sample of $\sim$ 3000 galaxies in the local universe extracted from the SDSS, we plan to address three main issues: the first is to assess, by means of extensive tests on simulated galaxies, the advantages and drawbacks of the two more common methods used detecting bars: the ellipse fitting and the Fourier analysis. The second is to investigate the possible differences of the bar fraction and bar properties (length and strength) with the morphological type, ranging from S0 to late-type spirals. The third is to understand how the properties of the host galaxies affects the formation of the bar and its properties.

The paper is organised as follows. The galaxy sample is presented in Sect. 2; the methods we adopted to detect the bars in the sample galaxies are explained in Sect. 3; they are tested using artificial galaxy images in Sect. 4; the fraction of bars are given in Sect. 5; the bars properties (length, and strength) are reported in Sect. 6 and compared to galaxy properties in Sect. 7; conclusions are given in Sect. 8. Throughout this paper we assume H₀=100 km s^-1 Mpc^-1.

2 Sample selection and data reduction

The sample galaxies were selected in the spectroscopic catalogue of the SDSS Data Release 5 (SDSS-DR5, Adelman-McCarthy et al. 2007). From the $\sim$ 675 000 galaxies available in the catalogue, we took all the galaxies in the redshift range 0.01 < z < 0.04 and down to an absolute magnitude M_r < -20 ( $\approx$ M^*_r, Blanton et al. 2005). This represents a volume-limited sample, because the apparent magnitude of a galaxy with M_r = -20 at z=0.04 ( $m_{r} \sim 15.5$ ) is within the completeness limit ( m_r = 17.77) of the SDSS-DR5 spectroscopic catalogue.

In order to deal with projection effects, we restricted our sample to galaxies with b/a>0.5, a and b being the semi-major and semi-minor axis lengths of the galaxies. For disc galaxies, this is equivalent to say that we have selected objects with inclination $i<60^{\circ}$ . Although the cut in the observed axial ratio of the sample galaxies introduces a bias in the selection of the elliptical ones, this will not affect the results of the paper since we are interested only in the properties of disc galaxies.

Then, we rejected all galaxies with close neighbours. To this aim, we excluded all the galaxies with a companion which was closer than $2 \times r_{90}$ , where r₉₀ is defined as the radius which contains $90\%$ of the total galaxy light. In addition, the companion must be within $\pm$ 3 mag with respect to the magnitude of the target galaxy to be excluded. In this way, galaxies with faint companions or possibly contaminated by faint foreground/background objects are not discarded in our study. The resulting sample consisted of 3060 galaxies.

According to Marinova & Jogee (2007) the bar length of barred galaxies in the local universe ranges between about 0.5 and 5 kpc, with a mean value $\sim$ 3.5 kpc. At z=0.04 the shortest bar length ( $r_{\rm bar} = 0.5$ kpc) projects onto 2.17 pixel ( $0\hbox{$.\!\!^{\prime\prime}$ }86$ ) in the SDSS images, which have a scale of $0\hbox{$.\!\!^{\prime\prime}$ }3946$ arcsec pixel^-1. The PSF of the SDSS images can be modelled assuming a Moffat function (see e.g. Trujillo et al. 2001). We fit a bidimensional Moffat function of the form

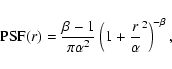$\begin{displaymath}{\rm PSF}(r)=\frac{\beta -1}{\pi \alpha^2}\left(1+\frac{r}{\alpha}^2\right)^{-\beta}, \end{displaymath}$

(1)

to several stars in each galaxy field obtaining a typical FWHM and $\beta$ parameter of $1\hbox{$.\!\!^{\prime\prime}$ }09$ (2.77 pixel) and 3.05, respectively. This means that the bars with a length of 0.5 kpc are not resolved. According to the tests on artificial galaxies we performed (see Sect. 4), the smallest bars that we are able to recover in the SDSS images have a length of $\sim$ 9 pixel. This corresponds to $\sim$ 0.5 kpc at z=0.01 and $\sim$ 2 kpc at z=0.04. Therefore, a value of 2 kpc is a more reliable limit on the actual resolution of the bar length throughout the range of distances covered by our sample galaxies.

The visual morphological classification given by the RC3 was available only for a subsample of 612 galaxies. Automatic galaxy morphological classifications divide galaxies according to some photometric observables. In particular, the light concentration is strongly correlated with the Hubble type (e.g., Abraham et al. 1996; Conselice et al. 2000; Conselice 2003). In fact, it is greater in early- than in late-type galaxies. We defined the light concentration as C=r₉₀/r₅₀, where r₅₀ and r₉₀ are the radii enclosing $50\%$ and $90\%$ of the total galaxy light, respectively. These radii are available in the SDSS database for all objects of our sample. We calculated the median values of C for the ellipticals ( $T \leq -4$ ), lenticulars ( $-3 \leq T \leq -1$ ), early-type spirals ( $0 \leq T \leq 3$ ), and late-type spirals ( $T \geq 4$ ) of the RC3 subsample. They are given in Table 1 and shown in Fig. 1. Although the dispersion of the data is large, the median value of the light concentration decreases with increasing Hubble type.

If the light traces mass, then we expect a relation between the mass concentration and morphological type too. The central mass concentration of a galaxy can be traced by the central velocity dispersion $\sigma _{0}$ . This was available in the SDSS for 298 of the sample galaxies listed in RC3. We calculated the median values of $\sigma _{0}$ for the different Hubble types, and they are given in Table 1 and shown in Fig. 1. The median velocity dispersion decreases with increasing Hubble type, too.

Figure 2 shows the relation between C and $\sigma _{0}$ for those galaxies in our sample with both the photometric and kinematic information. Each galaxy can be assigned to a morphological bin according to its values of C and $\sigma _{0}$ . They were assigned to the bin with closest median values listed in Table 1 by minimizing the following equation:

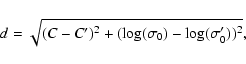$\begin{displaymath}d=\sqrt{(C-C')^{2}+(\log(\sigma_{0})-\log(\sigma_{0}'))^{2}}, \end{displaymath}$

(2)

where C' and $\sigma_{0}'$ are the median values of C and $\sigma _{0}$ reported in Table 1.

Galaxies, for which only the light concentration was available, were assigned to the morphological bin corresponding to the closest median value of C.

We found that $26\%$ , $29\%$ , $20\%$ , and $25\%$ of the selected galaxies turned to be ellipticals, lenticulars, early-type and late-type spirals, respectively. In this work, we focused on the 2166 disc galaxies which include the lenticulars and the early-type and late-type spirals. This represents our final sample. Among the disc galaxies $39\%$ , $28\%$ , and $33\%$ were classified as lenticulars, early-type and late-type spirals, respectively. Table 2 shows the comparison between the RC3 morphological classification and our automatic classification for the sample galaxies listed in RC3. It lists the fraction of elliptical, S0, S0/a-Sb and Sbc-Sm galaxies as classified by RC3 among the galaxies we classified as lenticular, early- and late-type spirals. It is worth noticing that for all the disc galaxies more than 50 $\%$ of the objects are assigned to the same morphological bin by both the RC3 and our automatic classification. The better agreement is shown by the early-type spiral galaxies. Nevertheless, the contamination between the different classes could be strong.

The r-band image of each galaxy was retrieved from the SDSS archive. All the images were bias subtracted, flat-field corrected, and sky subtracted according to the associated calibration information stored in the Data Archive Server (DAS).

Table 1: Median values of the light concentration and central velocity dispersion for the different galaxy types.

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{0931f1.ps} \end{figure}$	Figure 1: Values of the light concentration C ( top panel) and central velocity dispersion $\sigma _{0}$ ( bottom panel) as a function of the morphological parameter T. Only the sample galaxies in RC3 are plotted. Median values of C and $\sigma _{0}$ for ellipticals (diamond), lenticulars (asterisk), early-type spirals (triangle), and late-type spirals (square) are shown.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.7cm]{0931f2.ps} \end{figure}$

Figure 2:

Values of the light concentration C and central velocity dispersion $\sigma _{0}$ for the sample galaxies with $\sigma _{0}$ available in SDSS-DR5. They are colour coded according to our morphological classification: the red, magenta, green, and blue dots correspond to the ellipticals, lenticulars, early-type and late-type spirals, respectively. Median values for the ellipticals (diamond), lenticulars (asterisk), early-type spirals (triangle), and late-type spirals (square) plotted in Fig. 1 are also shown. The full lines represent the locus of equal distance between different galaxy morphological types.

Open with DEXTER

3 Methods for detecting and analysing bars

Three main methods have been proposed for detecting bars and analysing their properties (see for a review Erwin 2005; Michel-Dansac & Wozniak 2006). They are based on the ellipse fit of the galaxy isophotes (Sheth et al. 2003; Knapen et al. 2000; Laine et al. 2002; Wozniak et al. 1995; Jogee et al. 2004; Barazza et al. 2008; Marinova & Jogee 2007; Elmegreen et al. 2004), Fourier analysis of the azimuthal luminosity profile (Ohta et al. 1990; Buta et al. 2006; Elmegreen & Elmegreen 1985; Aguerri et al. 2000a; Laurikainen et al. 2007), and decomposition of the galaxy surface-brightness distribution (Laurikainen et al. 2005; Aguerri et al. 2005; Prieto et al. 2001).

In the present work, we have developed a fully automatic method for classifying barred and unbarred galaxies using the ellipse fitting (Sect. 3.1) and Fourier analysis (Sect. 3.2). This automatic procedure has several advantages with respect to the user-dependent visual classifications. In fact, it is reproducible, it can be implemented and applied to large data sets. We first tested it by means of extensive simulations on a large set of artificial disc galaxies (Sect. 4) and then we applied it to the images of the sample galaxies. In a forthcoming paper we will obtain the structural parameters for the bulge, disc, and bar of all the sample galaxies by applying a photometric decomposition of their surface-brightness distribution based on the technique developed by Méndez-Abreu (2008).

Table 2: Comparison between our and RC3 classification.

3.1 Ellipse fitting method

This method is based on the fit of the galaxy isophotes by ellipses.

As a first step, each image was cleaned of field stars and galaxies. This was done by rotating the image by 180 $^{\circ }$ with respect to the galaxy centre. Then, we subtract the rotated frame to the original one. The residual image was sigma-clipped to identify all the pixels with a number of counts lower than $1\sigma$ , where $\sigma$ is the rms of the image background after sky subtraction and calculated in regions free of sources and far from the galaxy to avoid contamination. The value of the deviant pixels was set to zero. Finally, the clipped image was subtracted to the original one to get the cleaned and symmetrized image to be used in the analysis.

The ellipses were fitted to the isophotes of the cleaned and symmetrized images of the 2166 disc galaxies using the IRAF task ELLIPSE (Jedrzejewski 1987).

In order to get a good fit at all radii out to an intensity level corresponding to the background rms, we implemented the fitting method described by Jogee et al. (2004) and Marinova & Jogee (2007). This is an iterative wrapped procedure, which runs the ellipse fitting several times changing the trial values at each fit iteration. At each fixed semi-major axis length, the coordinates of the centre of the fitting ellipse were kept fixed and corresponded to those of the galaxy centre. This was identified with the position of the intensity peak. The trial values for the ellipticity $\epsilon$ and position angle PA were randomly chosen between 0 and 1 and between $-90^\circ$ and $90^\circ$ , respectively. The fitting procedure stopped when either the convergence was reached or after 100 iterations. The ellipse fit failed for a small fraction (60/2166) of the sample galaxies. For all the galaxies with properly fitted isophotes, we obtained the radial profiles of $\epsilon$ and PA of the fitted ellipses.

The ellipticity radial profile in a bright and inclined unbarred galaxy usually shows a global increase from low values in the centre to a constant value at large radii. At large radii the PA radial profile is constant too. The constant values of $\epsilon$ and PA (on large radial scales) are related to the inclination and orientation of the line of nodes of the galactic disc. On the contrary, barred galaxies are characterised by the presence of a local maximum in the ellipticity radial profile and constant PA in the bar region (see e.g., Aguerri et al. 2000b; Wozniak et al. 1995). This is due to the shape and orientation of the stellar orbits of the bar (see Athanassoula 1992; Contopoulos & Grosbol 1989).

This allowed us to identify bars by analysing the radial profiles of $\epsilon$ and PA. We considered that a galaxy hosts a bar when: (1) the ellipticity radial profile shows a significant increase followed by a significant decrease ( $\Delta \epsilon \geq 0.08$ ), and (2) the PA of the fitted ellipses is roughly constant within the bar region ( $\rm\Delta PA \leq 20^\circ$ ).

The values adopted for $\Delta\epsilon$ and $\rm\Delta PA$ were determined by applying the method to artificial galaxies (see Sect. 4.2). The bar length was derived as the radius $r_{\rm bar}^{\epsilon }$ at which the maximum ellipticity was reached (e.g., Laine et al. 2002; Wozniak et al. 1995; Marinova & Jogee 2007) or as the radius $r_{\rm bar}^{\rm PA}$ at which the PA changes by $5^\circ$ with respect to the value corresponding to the maximum ellipticity (e.g, Sheth et al. 2003; Wozniak et al. 1995; Erwin & Sparke 2003; Erwin 2005; Michel-Dansac & Wozniak 2006).

This method has been already successfully applied by different authors both in the optical and near-infrared wavebands to detect bars in galaxies at low (Knapen et al. 2000; Laine et al. 2002; Marinova & Jogee 2007) and high redshift (Jogee et al. 2004; Sheth et al. 2008; Elmegreen et al. 2004).

3.2 Fourier analysis method

An alternative way to detect and characterise bars is with a Fourier analysis of the azimuthal luminosity profile (Ohta et al. 1990; Elmegreen & Elmegreen 1985; Aguerri et al. 2000a). The method starts by deprojecting the image of each sample galaxy by a flux-conserving stretch along the minor axis by the factor $1/\cos i$ , where i is the galaxy inclination. Therefore, we needed a good estimation of the inclination and major-axis PA of the galaxy. They were derived from the ellipticity and PA of the ellipses fitted to the five outermost isophotes, where the total luminosity is dominated by the disc contribution. For each galaxy, the intensity of the outermost isophote corresponds to a value of 1 $\sigma$ , where $\sigma$ is the rms of the sky-subtracted background of the image.

The deprojected luminosity profile, $I(R,\phi)$ , where $(R,\phi)$ are the polar coordinates in the galaxy frame, is decomposed into a Fourier series

$\begin{displaymath}I(R,\phi)=\frac{A_{0}(R)}{2}+ \sum_{m=1}^\infty \left(A_{m}(R) \cos(m\phi)+B_{m}(R)\sin(m\phi)\right) , \end{displaymath}$

(3)

where the coefficients are defined by

$\begin{displaymath}A_{m}(R)=\frac{1}{\pi}\int^{2\pi}_{0}I(R,\phi)\cos(m\phi){\rm d}\phi, \end{displaymath}$

(4)

and

$\begin{displaymath}B_{m}(R)=\frac{1}{\pi}\int^{2\pi}_{0}I(R,\phi)\sin(m\phi)\rm d\phi. \end{displaymath}$

(5)

The Fourier amplitude of the m-th component is defined as

$\begin{displaymath}I_{m}(R) = \left\{ \begin{array}{ll} A_{0}(R)/2 & \mbox{$m ... ...}(R)+B_{m}^{2}(R)} & \mbox{$m \neq 0$ }. \end{array} \right. \end{displaymath}$

(6)

The even ( m=2, 4, 6, ...) relative Fourier amplitudes I_m/I₀ of galaxies with bars are large, while the odd ( m=1, 3, 5, ...) ones are small. In particular, the bar is evidenced by a strong m=2 component. Similarly to the ellipse fitting method, we considered that a galaxy hosts a bar when: (1) the m=2 relative Fourier component shows a local maximum ( $\Delta(I_{2}/I_{0})\geq 0.2$ ); and (2) the phase angle of the m=2 mode $\phi_{2}$ is roughly constant within the bar region ( $\Delta \phi_{2} \leq 20^\circ$ ). The values adopted for $\Delta(I_{2}/I_{0})$ and $\Delta \phi_{2}$ were also determined by applying the method to artificial galaxies (see Sect. 4.3).

The bar length $r_{\rm bar}^{\rm Fourier}$ was calculated using the bar/interbar intensity ratio as in Aguerri et al. (2000a). The bar intensity, $I_{\rm b}$ , is defined as the sum of the even Fourier components, I₀+I₂+I₄+I₆, while the inter-bar intensity, $I_{\rm ib}$ , is given by I₀-I₂+I₄-I₆ (Ohta et al. 1990; Elmegreen & Elmegreen 1985; Aguerri et al. 2000a). Ohta et al. (1990) arbitrarily defined the bar length as the outer radius for which $I_{\rm b}/I_{\rm ib} = 2$ . However, Aguerri et al. (2000a) pointed out that a fixed value of $I_{\rm b}/I_{\rm ib}$ cannot account for the wide variety of bar luminosities present in galaxies. Instead, they defined the bar length as the FWHM of the curve of $I_{\rm b}/I_{\rm ib}$ . This method was applied by Athanassoula & Misiriotis (2002) to analytic models demonstrating its accuracy in measuring the bar length.

4 Test on artificial galaxies

4.1 Structural parameters of the artificial galaxies

Extensive simulations on a large set of artificial disc galaxies were carried out to test the reliability and accuracy of the ellipse fitting (Sect. 3.1) and Fourier analysis (Sect. 3.2) in detecting bars. Moreover, they were used to fine tune the free parameters of the two methods, i.e., $\Delta\epsilon$ and $\Delta {\rm PA}$ in the ellipse fitting, and $\Delta(I_{2}/I_{0})$ and $\Delta \phi_{2}$ in the Fourier analysis. The surface-brightness distribution of the artificial galaxies was assumed to be the sum of the contributions of three structural components: a bulge, a disc, and a bar (e.g., Laurikainen et al. 2005; Aguerri et al. 2003,2005; Prieto et al. 2001). The surface-brightness distribution of each individual component was assumed to follow a parametric law, which has to be strictly considered as an empirical fitting function.

The Sérsic law (Sérsic 1968) was assumed for the radial surface-brightness profile of the bulge

$\displaystyle I_{\rm bulge}(r)\;=\;I_{\rm0,bulge}\;10^{-b_{n}\left(r/r_{\rm e}\right)^{1/n}},$

(7)

where $r_{\rm e}$ , $I_{\rm0, bulge}$ , and n are the effective (or half-light) radius, the central surface-brightness, and the shape parameter describing the curvature of the profile, respectively. The value of b_n is coupled to n so that half of the total flux is always within $r_{\rm e}$ and can be approximated as b_n=0.868n-0.142 (Caon et al. 1993). The total luminosity of the bulge is given by

$\begin{displaymath}L_{\rm bulge} = 2 \pi I_{\rm0,bulge} (1-\epsilon_{\rm bulge}) n r_{\rm e}^{2}\frac{\Gamma(2n)}{b_{n}^{2n}}, \end{displaymath}$

(8)

where $\epsilon_{\rm bulge}$ is the observed ellipticity of the bulge and $\Gamma$ is the Euler gamma function.

The exponential law (Freeman 1970) was assumed to describe the radial surface-brightness profile of the disc

$\begin{displaymath}I_{\rm disc}(r)=I_{\rm0,disc} {\rm e}^{-r/h}, \end{displaymath}$

(9)

where h and $I_{\rm0,disc}$ are the scale length and central surface brightness of the disc, respectively. The total luminosity of the disc is given by

$\begin{displaymath}L_{\rm disc} = 2 \pi I_{\rm0,disc}(1-\epsilon_{\rm disc})h^{2}, \end{displaymath}$

(10)

where $\epsilon_{\rm disc}$ is the observed ellipticity of the disc.

Several parametric laws have been adopted in literature to describe the surface-brightness distribution of bars. Ferrers (Laurikainen et al. 2005), Freeman (Freeman 1966), and flat bars (Prieto et al. 1997) were considered for the artificial galaxies.

The surface-brightness distribution was assumed to be axially symmetric with respect to a generalised ellipse (Athanassoula et al. 1990). When the principal axes of the ellipse are aligned with the coordinate axes, the radial coordinate is defined as

$\begin{displaymath}r= \left( \vert x\vert^c + \left\vert \frac{y}{(1-\epsilon_{\rm bar})}\right\vert^c \right)^{1/c}, \end{displaymath}$

(11)

where $\epsilon_{\rm bar}$ is the ellipticity and c controls the shape of the isophotes. A bar with pure elliptical isophotes has c=2. It is c>2 if the isophotes are boxy, and c<2 if they are discy. The parameters $\epsilon_{\rm bar}$ and c are assumed to be constant as a function of radius.

The radial surface-brightness profile of a Ferrers ellipsoid (Ferrers 1877) is given by

$\begin{displaymath}I_{\rm bar}^{\rm Ferrers}(r) = \left\{ \begin{array}{ll} I_... ...$ }, \\ 0 & \mbox{$r > r_{\rm bar}$ } , \end{array} \right. \end{displaymath}$

(12)

where $I_{\rm0,bar}$ , $r_{\rm bar}$ , and $n_{\rm bar}$ are the central surface brightness, length, and a shape parameter of the bar, respectively. The total luminosity for a perfect ellipse is given by

$\begin{displaymath}L_{\rm bar}^{\rm Ferrers} = 2 \pi I_{\rm0, bar} r_{\rm bar}^{... ...^{\infty}r (r_{\rm bar}^{2}-r^{2})^{n_{\rm bar}+0.5} {\rm d}r, \end{displaymath}$

(13)

where $\epsilon_{\rm bar}$ is the ellipticity of the bar. The simulated bars were generated by adopting $n_{\rm bar}=2$ following Laurikainen et al. (2005). In this particular case, the total luminosity of the bar for a perfect ellipse is given by

$\begin{displaymath}L_{\rm bar}^{\rm Ferrers}= \pi I_{\rm0,bar} (1-\epsilon_{\rm bar}) r_{\rm bar}^{2}\frac{\Gamma(7/2)}{\Gamma(9/2)}\cdot \end{displaymath}$

(14)

The radial surface-brightness profile of a Freeman bar is

$\begin{displaymath}I_{\rm bar}^{\rm Freeman} = I_{\rm0,bar} \sqrt{1-\left(\frac{r}{r_{\rm bar}}\right)^{2}}, \end{displaymath}$

(15)

where $I_{\rm0,bar}$ and $r_{\rm bar}$ are the central surface brightness and length of the bar, respectively (Freeman 1966). The total luminosity of a Freeman bar for a perfect ellipse is

$\begin{displaymath}L_{\rm bar}^{\rm Freeman} = \frac{2}{3} \pi(1-\epsilon_{\rm bar}) I_{\rm0,bar} r_{\rm bar}^{2}, \end{displaymath}$

(16)

where $\epsilon_{\rm bar}$ is the ellipticity of the bar.

Finally, the radial surface-brightness profile of a flat bar is

$\begin{displaymath}I_{\rm bar}^{\rm flat} = I_{\rm0,bar} \left( \frac{1}{1+{\rm e}^{\frac{r-r_{\rm bar}}{r_{\rm s}}}} \right), \end{displaymath}$

(17)

where $I_{\rm0,bar}$ and $r_{\rm bar}$ are the central surface brightness and length of the bar. For radii larger than $r_{\rm bar}$ the surface-brightness profile falls off with a scale length $r_{\rm s}$ (Prieto et al. 1997). The total luminosity is

$\begin{displaymath}L_{\rm bar}^{\rm flat}= -2~ \pi~ I_{\rm0,bar}~ (1-\epsilon_{\... ...{2}~ {\rm Li}_2\left(-{\rm e}^{r_{\rm bar}/r_{\rm s}} \right), \end{displaymath}$

(18)

where $\epsilon_{\rm bar}$ is the ellipticity of the bar and ${\rm Li}_2$ is the dilogarithm function (also know as the Jonquiere function).

We generated a set of 8000 images of artificial galaxies with a Sérsic bulge and an exponential disc. Among these galaxies, 2000 have a Ferrers bar, 2000 a Freeman bar, 2000 a flat bar, and 2000 do not posses a bar.

The apparent magnitudes of the artificial galaxies were randomly chosen in the range

10 < m_r < 16,

(19)

corresponding to that of the sample galaxies. To redistribute the total galaxy luminosity among the three galaxy components, the bulge-to-total $L_{\rm bulge}/L_{\rm tot}$ and bar-to-disc $L_{\rm bar}/L_{\rm disc}$ luminosity ratio were taken into account. They were considered to be

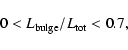$\begin{displaymath}0<L_{\rm bulge}/L_{\rm tot}<0.7, \end{displaymath}$

(20)

and

$\begin{displaymath}0<L_{\rm bar}/L_{\rm disc}<0.3, \end{displaymath}$

(21)

following Laurikainen et al. (2005). The adopted ranges for the effective radius of the bulge, scale-length of the disc, and bar length were selected according to the values measured for spiral galaxies by Möllenhoff & Heidt (2001), MacArthur et al. (2003), Möllenhoff (2004), Laurikainen et al. (2007), and Méndez-Abreu et al. (2008a). They are

$\begin{displaymath}0.5 < r_{\rm e} < 3\ \mbox{kpc}, \end{displaymath}$

(22)

$\begin{displaymath}1 < h < 6 \ \mbox{kpc}, \end{displaymath}$

(23)

and

$\begin{displaymath}0.5 < r_{\rm bar} < 5\ \mbox{kpc}, \end{displaymath}$

(24)

respectively. The ellipticities of the structural components were also selected to mimic those measured in real galaxies (e.g, Marinova & Jogee 2007). They are

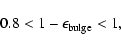$\begin{displaymath}0.8 < 1-\epsilon_{\rm bulge} < 1, \end{displaymath}$

(25)

$\begin{displaymath}0.5 < 1-\epsilon_{\rm disc} < 1, \end{displaymath}$

(26)

and

$\begin{displaymath}0.2 < 1-\epsilon_{\rm bar} <0.7, \end{displaymath}$

(27)

with

$\begin{displaymath}\epsilon_{\rm bulge} < \epsilon_{\rm disc} <\epsilon_{\rm bar}. \end{displaymath}$

(28)

Finally, the position angles of the three components were selected randomly between $0^\circ$ and $180^\circ$ to allow each component to be independently oriented with respect to the others.

In each pixel of the resulting images noise was added to yield a signal-to-noise ratio (S/N) similar to that of the available SDSS images. It was given by the Poisson noise associated to the photon counts due to both the galaxy and sky background and read-out noise (RON) of the CCD. The pixel scale, CCD gain and RON were 0 $.\!\!^{\prime\prime}$ 3946 arcsec pixel^-1, 4.72 e^- ADU^-1, and 5.52 e^-, respectively. They mimic the instrumental setup of the SDSS images. In order to account for seeing effects, the images of the artificial galaxies were convolved with a Moffat PSF with ${\it FWHM}=2.77$ pixels and $\beta=3.05$ (see Sect. 2).

The artificial galaxies do not match the sample galaxies since we did not account for their redshift distribution. Due to this issue, the fractions given in Tables 3 and 4 do not represent at all estimations of the absolute bar fraction lost in real galaxies. However, they are useful to test the efficiency of the two proposed methods for detecting bars, in order to fine tune their free parameters and understand possible biases in the results. The artificial galaxies were sized in pixels. In this way, the images are somewhat ``dimensionless'' and the performances of two methods can be assessed by converting the scale lengths from pixel to physical units according to the distance of the objects. In order to cover the full range of bar lengths and redshifts, the shortest bars ( $r_{\rm bar} = 0.5$ kpc) were scaled assuming a redshift z=0.04, while the largest ones ( $r_{\rm bar} = 5$ kpc) were placed at z=0.01.

4.2 Testing the ellipse fitting method

The ellipse fitting method has two free parameters, $\Delta\epsilon$ and $\rm\Delta PA$ . Laine et al. (2002) adopted $\Delta \epsilon =0.1$ and $\rm\Delta PA = 20^\circ$ , Marinova & Jogee (2007), Menéndez-Delmestre et al. (2007), and Barazza et al. (2008) adopted $\Delta \epsilon =0.1$ and $\rm\Delta PA=10^\circ$ .

We applied the ellipse fitting method to the artificial galaxies by adopting $\Delta \epsilon = 0.1, 0.08, 0.05$ and $\rm\Delta PA = 10^\circ, 20^\circ, 30^\circ$ to find the best combination of $\Delta\epsilon$ and $\rm\Delta PA$ maximising the bar identifications and minimising the bad and/or spurious detections. The results are given in Table 3.

Table 3: Percentage of galaxies classified as barred and unbarred galaxies erroneously found to be barred by applying the ellipse fitting method to the sample of artificial galaxies.

Table 4: Percentage of galaxies classified as barred and unbarred galaxies erroneously found to be barred by applying the Fourier analysis method to the sample of artificial galaxies.

The flat and Freeman bars are the most difficult and easiest bars to be detected, respectively. This means that the ellipse fitting method detects more efficiently the bars with sharp ends than those characterised by a smooth transition to the disc. Moreover, adopting $\rm\Delta PA = 20^\circ$ instead of $\rm\Delta PA=10^\circ$ increases the fraction of bar detections by $10\%$ for all the bar types, while the increment between $\rm\Delta PA = 20^\circ$ and $\rm\Delta PA = 30^\circ$ is only about $4\%$ .

Spurious detections correspond to unbarred galaxies which are erroneously found to be barred. In order to estimate their fraction, we applied the method to the sample of unbarred artificial galaxies we built to this aim. The results for the different values of $\Delta\epsilon$ and $\rm\Delta PA$ are also given in Table 3. Bad detections correspond to barred galaxies for which we obtained a bad measurement of the bar length. In order to estimate this fraction (which is not reported in Table 3), we compared the bar lengths known for the artificial galaxies with the $r_{\rm bar}^{\epsilon }$ derived by applying the ellipse fitting method. We derived the median and standard deviation of the relative error between the known and measured bar length using a 3 $\sigma$ clipping iterative procedure. We considered as bad detections the measurements with a relative error larger than 3 $\sigma$ with respect to the median.

The fraction of galaxies classified as barred versus the bad/spurious detections are shown in Fig. 3 as a function of $\Delta\epsilon$ and $\rm\Delta PA$ . The optimal configuration is $\Delta \epsilon=0.08$ and $\rm\Delta PA = 20^\circ$ since the fraction of detections increases by more than $10\%$ with respect to $\Delta \epsilon =0.1$ and $\rm\Delta PA=10^\circ$ , while the fraction of bad/spurious detections is always lower than $10\%$ . It is worth noticing that for $\Delta_\epsilon=0.08$ and $\rm\Delta PA = 30^\circ$ the fraction of bar detections rises by about $3\%$ with respect to $\Delta_\epsilon=0.08$ and $\rm\Delta PA = 20^\circ$ . But the fraction of bad/spurious detections increases too. For example, for the Ferrers bars such a fraction is even larger than $10\%$ .

The bar lengths we measured as $r_{\rm bar}^{\epsilon }$ and $r_{\rm bar}^{\rm PA}$ in the artificial galaxies are shown in Fig. 4. The bar length is underestimated when $r_{\rm bar}^{\epsilon }$ is used, as found by Michel-Dansac & Wozniak (2006) too. This is particularly true for the Ferrers bars where the measured bar lengths are 51 $\%$ shorter than the real ones. In contrast, Freeman and flat bars were better determined, their measurements being shorter by 30 $\%$ and 19 $\%$ , respectively. The bar length is underestimated when $r_{\rm bar}^{\rm PA}$ is used for the Ferrers bars (11 $\%$ ), but it is overestimated for the Freeman (8 $\%$ ) and flat bars (28 $\%$ ). These results show the possibility of define an empirical correction to the bar length, knowing the bar type in advance.

$\begin{figure} \par\includegraphics[width=9cm]{0931f3.ps} \end{figure}$

Figure 3:

Fraction of artificial galaxies correctly classified as barred vs fraction of bad/spurious bar detections using the ellipse fitting method with $\Delta$ PA = 10 $^{\circ }$ (asterisks), 20 $^{\circ }$ (filled circles), and 30 $^{\circ }$ (squares) and $\Delta \epsilon =0.1$ (black symbols), 0.08 (red symbols), and 0.05 (blue symbols). The large, medium, and small symbols correspond to Ferrers, Freeman, and flat bars, respectively.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=15cm]{0931f4.ps} \end{figure}$

Figure 4:

Bar length measured with the maximum ellipticity ( top panels), position angle ( middle panels), and Fourier analysis method ( bottom panels) for Ferrers ( left panels), Freeman ( central panels), and flat bars ( right panels) in artificial galaxies. Mean relative error (defined as the difference between input and measured values) and standard deviation for the measurements are given in each panel.

Open with DEXTER

4.3 Testing the Fourier analysis method

The deprojection of the galaxy image is a crucial step in applying the Fourier method, which has two free parameters, $\Delta(I_{2}/I_{0})$ and $\rm\Delta \phi_{2}$ . The inclination and major-axis position angle of the galaxy disc can be obtained by either fitting ellipse to the outermost galaxy isophotes (e.g., Aguerri et al. 2003) or minimising the m=2 Fourier mode in the outermost regions of the galaxy (e.g., Grosbol 1985). We applied these two methods to the artificial galaxies and found that ellipse fitting gave lower errors (about $3^\circ$ ) on both i and PA.

We applied the Fourier method to the artificial galaxies by adopting $\Delta (I_{2}/I_{0}) =0.2, 0.1, 0.08, 0.05$ and $\rm\Delta \phi_{2} = 10^\circ, 20^\circ, 30^\circ$ to find the best combination of $\Delta(I_{2}/I_{0})$ and $\rm\Delta \phi_{2}$ , maximising the bar identification and minimising the bad and/or spurious detections. The results are given in Table 4 and in Fig. 5.

In general, the Fourier method is less efficient in detecting bars than the ellipse fitting method. We found that $\Delta (I_2/I_0)=0.2$ has to be adopted to have a fraction of bad/spurious detections lower than $10\%$ . We also adopted $\Delta \phi_{2} = 20^\circ$ because it increases detections by more than $10\%$ and gives less bad/spurious detections with respect to $\Delta \phi_{2} = 30^\circ$ . The bar lengths we measured as $r_{\rm bar}^{\rm Fourier}$ in the artificial galaxies are shown in Fig. 4. The method recovers the bar length with the best accuracy for the Ferrers bars (3 $\%$ error), while the bar length is over estimated for the Freeman (28 $\%$ ) and flat bars (46 $\%$ ).

$\begin{figure} \par\includegraphics[width=9cm]{0931f5.ps} \end{figure}$

Figure 5:

Fraction of artificial galaxies correctly classified as barred and fraction of bad/spurious bar detections using the Fourier analysis method with $\Delta \phi _2=10^{\circ }$ (asterisks), 20 $^{\circ }$ (filled circles), and 30 $^{\circ }$ (squares) and $\Delta (I_2/I_0)=0.2$ (green symbols), 0.1 (black symbols), 0.08 (red symbols), and 0.05 (blue symbols). The large, medium, and small symbols correspond to Ferrers, Freeman, and flat bars, respectively.

Open with DEXTER

5 Bar fraction

Both the ellipse fitting and Fourier method were applied to our sample of 2106 disc galaxies. We found that the fraction of galaxies classified as barred depends strongly on the technique adopted for the analysis: it is $45\%$ with the ellipse fitting method and $26\%$ with the Fourier method. Although the Fourier method was demonstrated to be less efficient than ellipse fitting in detecting bars, this difference is larger than that expected from the analysis of the artificial galaxies. To investigate this issue, we took into account the morphological classification of the galaxies found to be barred. According to the ellipse fit method $29\%$ , $55\%$ , and $54\%$ of the lenticular, early-type and late-type spiral galaxies, respectively, are barred. They are $29\%$ , $33\%$ , and $17\%$ , respectively, with the Fourier method. Therefore, both methods obtained a similar of fraction of barred lenticular galaxies, while the Fourier method is less efficient in detecting bars in spirals, and particularly in late-type spiral galaxies.

An example is shown in Fig. 6. The early-type spiral SDSSJ031947.01+003504.4 and the late-type spiral SDSSJ020159.33-081441.9 are analysed by both methods. The bar of the early-type spiral was detected by both methods and the measured bar lengths are in agreement. In fact, the radial profiles of $\epsilon$ and I₂/I₀ show a local maximum at about $5\hbox{$^{\prime\prime}$ }$ , where the PA and $\phi_{2}$ are constant. On the contrary, the bar of the late-type spiral was detected only by the ellipse fit method. The radial profiles of $\epsilon$ and I₂/I₀ show a local maximum at different radii (about 10''). The I₂/I₀ maximum is located in the spiral arm region, where $\phi_{2}$ is not constant. Therefore, the bar of this galaxy was not detected by the Fourier method. We conclude that bars with sharp ends are detected by both ellipse fitting and Fourier methods. But, the bars of galaxies with lenses or strong spiral arms are more easily detected with the ellipse fitting method. This kind of bars is usually found in late-type spirals. These large differences in the bar fractions between the two methods could bias our conclusions. For this reason, we will study the photometrical parameters of the bars by adopting only the ellipse fitting method.

$\begin{figure} \par\includegraphics[width=9cm]{0931f6.ps} \end{figure}$	Figure 6: The r-band images ( left panels), ellipticity ( central panels), and m=2 Fourier amplitude radial profiles ( right panels) of the early-type spiral SDSSJ031947.01+003504.4 ( top panels) and the late-type spiral SDSSJ020159.33-081441.9 are analysed by both methods ( bottom panels). For each galaxy the vertical dotted line corresponds to the value of $r_{\rm bar}^{\epsilon }$ .
Open with DEXTER

As an additional check, we visually classified all galaxies in barred and unbarred. The visual classification was done by two of us (JALA and JMA). Both the classifications were in close agreement and only their mean is reported. No attempt to classify the galaxies according to their Hubble type was done. The difference between the bar fractions found with the visual and the automatic classification ( $\sim$ $7\%$ ) is our best estimate of the fraction of undetected bars in the galaxy sample. We obtained that the global fraction of barred galaxies in our sample was 38 $\%$ . Taking into account the different morphological types we found that 22 $\%$ , 52 $\%$ and 48 $\%$ of the lenticular, early-type and late-type spiral galaxies, respectively, were barred.

Our bar fraction ( $45\%$ ) of disc galaxies in the local universe is in good agreement with recent results obtained in optical bands by Marinova & Jogee (2007, 44% in the B band), Reese et al. (2007, 47% in the I band), and Barazza et al. (2008, 50% in the r band). In addition, our finding that early- and late-type spirals host a larger fraction of bars than lenticular galaxies, was also in agreement with Barazza et al. (2008) since they found that disc-dominated galaxies with low bulge-to-disc luminosity ratio display a higher bar fraction than galaxies with significant bulges. However, Marinova & Jogee (2007) did not find any difference in the bar fraction in the NIR as a function of the Hubble type, we argue that their result is biased by their smaller coverage of the Hubble sequence since neither lenticulars nor Sd/Sm galaxies were taken into account. The same consideration can be applied to the results found by Knapen et al. (2000) and Eskridge et al. (2000).

6 Bar properties

6.1 Bar length

The distributions of the bar lengths and normalised bar lengths were derived for the sample galaxies after deprojection on the galaxy plane. They are shown in Fig. 7. Both $r_{\rm bar}^{\epsilon }$ and $r_{\rm bar}^{\rm PA}$ were considered, and the galaxy size was defined as $r_{\rm gal} = 2 \times r_{\rm p}$ , where $r_{\rm p}$ is the Petrosian radius from SDSS. The median values derived for the different morphological bins are given in Table 5. The values of $r_{\rm bar}^{\epsilon }$ are systematically smaller than those of $r_{\rm bar}^{\rm PA}$ , as expected from the measurements of the artificial galaxies. The comparison of our results, with previous works where the $r_{\rm bar}^{\epsilon }$ values are reported, gives us a good agreement. For example, Erwin (2005) found a median bar length of 3.3 kpc, Marinova & Jogee (2007) calculate a mean value of 4 kpc and Menendez-Delmestre et al. (2007) obtain a median value of 3.5 kpc. These results hold even considering only the bars with a length larger than 2 kpc. This limit corresponds to minimum bar length we are able to resolve all throughout our range of distances.

$\begin{figure} \par\includegraphics[width=12cm,clip]{0931f7.ps} \end{figure}$	Figure 7: Distribution of the bar length ( left panels) and normalised bar length ( right panels) in lenticulars (full line), early-type spirals (dotted line), and late-type spirals (dashed line). The bar length was measured with both the maximum ellipticity (top panels) and PA method (bottom panels). Arrows mark the median values of the distributions.
Open with DEXTER

Since the bar length is strongly dependent on the method used to derive it, we can not conclude much about the correlation between the bar length and the morphological type. According to $r_{\rm bar}^{\epsilon }$ , the lenticulars host the shortest bars, while according to $r_{\rm bar}^{\rm PA}$ their bars are the longest ones. As far as the median bar length of the spirals concerns, the late-type spirals host shorter bars with respect to the early-type ones (Table 5). Nevertheless, a correlation between the bar length and galaxy size was found. Thus, larger bars are located in bigger galaxies (Fig. 8). The correlation is independent of the adopted method to measure the bar length. It holds for the different morphological bins too, being stronger for late-type spirals (r=0.52) and weaker for S0 galaxies (r=0.38). This relation could indicate a link between the formation and evolution processes between of bars and galaxy discs. A similar correlation was found by Marinova & Jogee (2007), although a quantitative comparison with them is not possible due to the different band-passes and different definition of the galaxy radius they adopted.

6.2 Bar strength

The bar strength represents the contribution of the bar to the total galaxy potential. Several methods have been developed to measure it (see Laurikainen et al. 2007, and references therein). Nowadays, the most commonly used parameter measuring the bar strength is $Q_{\rm g}$ defined by Buta & Block (2001). It can be accurately estimated by analysing near-infrared images (Buta et al. 2003; Block et al. 2004; Laurikainen et al. 2007), which are not available for our sample galaxies drawn from the SDSS. However, Abraham & Merrifield (2000) defined another bar strength parameter given by

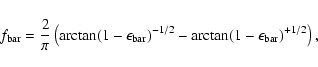$\begin{displaymath}f_{\rm bar} = \frac{2}{\pi} \left(\arctan (1-\epsilon_{\rm bar})^{-1/2} - \arctan (1-\epsilon_{\rm bar})^{+1/2} \right), \end{displaymath}$

(29)

where $\epsilon_{\rm bar}$ is the bar ellipticity measured at $r^{\epsilon}_{\rm bar}$ . It correlates with $Q_{\rm g}$ (e.g., Laurikainen et al. 2007) and was adopted for our sample galaxies.

We did not adopted any minimum value for the bar ellipticity. We found $\epsilon_{\rm bar, min}=0.16$ , which is close the minimum ellipticity adopted in other studies (e.g., $\epsilon_{\rm bar, min}=0.2$ , Marinova & Jogee 2007). The distributions of the bar strengths we derived for the different morphological types are shown in Fig. 9. The median values for the bar strengths of the lenticular, early-type, and late-type spiral galaxies are 0.16, 0.19, and 0.20, respectively. Indeed, we found a significant difference between the lenticular and spiral galaxies. They are characterised by different distributions, as confirmed at a high confidence level (> $95\%$ ) by a Kolmogorov-Smirnov (KS) test. Using four different methods to derive the bar strength, Laurikainen et al. (2007) also found that S0 galaxies host significantly weaker bars than the rest of disc galaxies, this result was hold also by (Das et al. 2003) and Barazza et al. (2008) using only the bar ellipticity. In contrast, Marinova & Jogee (2007) found that the ellipticity of the bar is practically independent of the Hubble type. But they not consider S0 galaxies which are those actually making the difference.

Table 5: Median values of the bar radius for the different galaxy types.

However, it could be possible that the presence of a large bulge could affect the measurement of the bar ellipticity, and therefore the calculation of the bar strength. In order to address this issue, we performed a further test. We fitted an exponential law to the outer parts of the surface-brightness profiles of our barred galaxies. Then, we computed the radius $r_{\rm bd}$ at which the galaxy surface brightness profile exceeds the fitted exponential. This radius represents an estimate of the extension of the region where the bulge contribution dominates the light of the galaxy. At this point, we selected a subsample of barred galaxies with $r_{\rm bar} > r_{\rm bd}$ . We recalculated the mean strength of these bars by splitting the sample in lenticulars, early- and late-type spirals. As expected, in the new subsample of galaxies we lost the weakest bars, especially in the lenticular galaxies. Nevertheless, the final result is the same: the lenticulars have weaker bars than the early- or the late-type spirals.

Some numerical simulations of bar formation and evolution propose that bars can be formed and destroyed fastly due to the accretion of gas towards the central regions of the galaxies (Bournaud et al. 2005; Bournaud & Combes 2002; Pfenniger & Norman 1990). In this framework, due to the fast destruction and re-formation of bars, we would expect a bimodal distribution of the bar strength at least for gas-rich galaxies like the late-type barred ones. The absent of this bimodality in the bar strength for all galaxy types showed in Fig. 9 could be against those bar formation and evolution scenarios.

$\begin{figure} \par\includegraphics[width=8cm,clip]{0931f8.ps} \end{figure}$	Figure 8: Galaxy radius $r_{\rm gal}$ versus bar length measured with the PA method ( top panel) and maximum ellipticity method ( bottom panel). The solid line represents the linear regression through all the data points. The Pearson correlation coefficient (r) and the result of the linear fit are given.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{0931f9.ps} \end{figure}$	Figure 9: Distribution of the bar strength in lenticulars (full line), early-type spirals (dotted line), and late-type spirals (dashed line) for the whole sample ( top panel) and for the galaxies with $r_{\rm bar} > r_{\rm bd}$ ( bottom panel). Arrows mark the median values of the distributions.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{0931f10.ps} \end{figure}$	Figure 10: Cumulative distribution of barred (solid black line) and unbarred (dashed black line) galaxies as function of the local galaxy density. Cumulative distribution of barred (long-dashed blue line) and unbarred (dashed-dotted blue line) galaxies after excluding those at less than 7 Mpc from the nearest edge of SDSS is also overplotted (see text for more details).
Open with DEXTER

7 Bars and galaxy properties

7.1 Galaxy local environment

Due to our selection criteria we excluded all the strongly disturbed/interacting galaxies. Nevertheless, we calculated for each sample galaxy the local density following the prescriptions of Balogh et al. (2004b,a) in order to investigate the relation between the bar properties and local environment of the host galaxy. The number density of local galaxies was computed using the distance d₅ of the galaxy to its fifth nearest neighbour galaxy. Thus, a projected galaxy density could be defined as

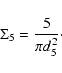$\begin{displaymath}\Sigma_5 = \frac{5}{\pi d_5^2} \cdot \end{displaymath}$

(30)

This was computed with those galaxies located in a velocity range of $\pm$ 1000 km s^-1 from the target galaxy to avoid background/foreground contamination. For sample galaxies without a measured redshift we imposed a luminosity constraint of $\pm$ 3 mag to derive the galaxy density as done by Balogh et al. (2004b,a).

Figure 10 shows the fraction of barred and unbarred galaxies in our sample as function of the local galaxy density. In the range of galaxy density covered by our sample, there is no relation between the presence of a bar and the environment of the host galaxy. The same is true even if the galaxies of different morphological type are considered independently. In addition, we did not find any correlation between the bar length or strength and the local galaxy density.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{0931f11.ps} \end{figure}$	Figure 11: Fraction of galaxies remaining in the sample after correcting for survey edge effects by removing all the galaxies with an edge of the survey closer than the measured fifth neighbour distance (blue squares), 2 Mpc (black diamonds), 5 Mpc (green triangles), and 7 Mpc (red asterisks). Poissonian errors are given. Horizontal lines show the width of the local density bins.
Open with DEXTER

However, a series of caveats must be taken into account when the distance neighbour method is applied.

The limited area of sky covered by the survey implies that usually the estimated density is lower than the true one. In fact, due to edges and holes in the survey, the value of d₅ could be overestimated and the derived density underestimated. Two methods were applied to our sample in order to test the robustness of our result against the edge effects. The first consists in removing all the galaxies whose distance to the survey edges is smaller than the measured fifth neighbour distance (Balogh et al. 2004b; Miller et al. 2003). In this way, we ensure that the remaining galaxies have an unbiased estimation of the local density. The fraction of galaxies we measured in each density bin after applying such a correction is shown in Fig. 11. It is worth noticing that no galaxy is available in the bin of lowest local density ( $\Sigma_5<0.01$ Mpc^-2). This means that such a low density can not be derived for any galaxy of the sample. On the contrary, the local density is correctly derived for all the sample galaxies with $\Sigma_5 > 1$ Mpc^-2.

Unfortunately, this method biases the distribution toward over-dense environments. This bias can be reduced by excluding all the galaxies within a given distance to the nearest edge (Cooper et al. 2005). We excluded the galaxies at less than 2, 5, and 7 Mpc from the nearest edge of SDSS (Fig. 11). If the lowest density bin is excluded, the method introduces only a weak contamination toward high density environments. An optimal given distance of 7 Mpc was found by calculating the maximum distance to the fifth neighbour in the bin of lowest density. In this way, the local density measurements are reliable and there is no bias toward the high-density environments, i.e. all the bins have almost the same number of galaxies. Figure 10 shows the fraction of barred and unbarred galaxies in our sample as function of the local galaxy density after excluding galaxies at less than 7 Mpc from the nearest edge of SDSS. They are about $40\%$ of the total. We do not find any difference between the environment of barred and unbarred galaxies.

Also the selected redshift range could lead to underestimate the local density. We circumvent this problem by defining a new volume-limited sample in a wider redshift range ( 0 < z < 0.06) taking into account the adopted velocity range.

Finally, the local density distribution could be biased by SDSS fiber collision which prevents to measured galaxies closer than $55\hbox{$^{\prime\prime}$ }$ with respect to each other. In SDSS-DR5 the net effect of fiber collision is a loss of $6\%$ of the galaxies in the photometric catalogue that would otherwise be in the spectroscopic catalogue (Cowan & Ivezic 2008). In our case, this value represents an upper limit since all the galaxies in photometric catalogue were taken into account in calculating the local density.

According to numerical simulations, galaxy mergers and interactions are mechanisms which should drive the formation of bars (Miwa & Noguchi 1998; Gerin et al. 1990; Mastropietro et al. 2005). Therefore, we could expect that fraction of barred galaxies increases with the local density. But, the observational proofs about the influence of the environment on bar formation and evolution are few. For example, Thompson (1981) suggested a link between bar formation and local galaxy environment by observing that the fraction of barred galaxies increases towards the core of Coma cluster. But, this is not case in the wide range of densities we explored ( $0.01 < \Sigma_5 < 100$ Mpc^-2, Fig. 10). For the lowest density bin our fraction of barred galaxies is even smaller than 60 $\%$ found by Verley et al. (2007) by analysing the optical images of 45 isolated galaxies. Recently, (Marinova et al. 2008) shows that the cluster environment does not strongly affect to the bar fraction. We argue that for non-interacting and undisturbed galaxies the environment do not play a major role in the formation and evolution of their bar.

Figure 10 shows that $80\%$ of the sample galaxies are located in very low-density environments ( $\Sigma_5 < 1$ Mpc^-2). The local density of the remaining $20\%$ (corresponding to more than 400 galaxies) covers mostly typical values measured for loose ( $\Sigma_5 > 1$ Mpc^-2) and compact galaxy groups ( $\Sigma_5 \sim 10$ Mpc^-2). Nevertheless, the fraction of barred galaxies does not depend on the local density also for these galaxies. Therefore, we conclude that the environment does not play an important role in the formation of bars, at least over the observed range of local densities. Moreover, it does not account for the variation of the central light concentration and galaxy colours discussed in Sects. 7.2 and 7.3, respectively. Similarly, low density environments, as those reported here, do not also account for variations in other galaxy properties, such as the blue galaxy fraction (e.g., Aguerri et al. 2007). However, we can not infer that close interactions do not affect bar formation and evolution, because we selected only non-strongly disturbed/interacting galaxies.

This result is in agreement with the numerical simulations by Heller et al. (2007); Romano-Diaz et al. (2008), who argue that there is no difference between the bar fraction for field and cluster galaxies. They claim that the bar evolution is mainly driven by the dark matter subhalos, which surround all the bright galaxies and do not depend of their environment. These subhalos could host faint galaxies, which are not visible in our images.

7.2 Central light concentration

Figure 12 shows the distribution of the Cparameter for the barred and unbarred sample galaxies and their cumulative distribution functions. Both types of galaxies are characterised by different distributions as confirmed at a high confidence level (> $99\%$ ) by a KS test. It is worth noting that the differences between both distributions is due to galaxies with higher central light concentration. This result holds even if we take into account the contamination of ellipticals into our sample of disc galaxies (Sect. 5).

Barazza et al. (2008) found that the fraction of barred galaxies is higher for the galaxies with a smaller value of the Sérsic parameter (i.e., the less-concentrated galaxies). We confirm their findings. Figure 12 shows that the number of barred and unbarred galaxies is clearly different for galaxies with high values of C, being the fraction of barred galaxies smaller than the unbarred ones.

Since light concentration is correlated with the central velocity dispersion, the previous result implies that, in some way, galaxies with higher central mass concentrations tend to inhibit the formation and/or evolution of bars. This is in agreement with the results of the numerical experiments by Debattista et al. (2006); Athanassoula & Misiriotis (2002); Norman et al. (1996); Pfenniger & Norman (1990), who showed that the presence of a large bulge weakens the bar.

$\begin{figure} \par\includegraphics[width=9cm]{0931f12.ps} \end{figure}$	Figure 12: Number of barred (full line) and unbarred disc galaxies (dotted line) as function of the light concentration ( upper panel). Cumulative distribution of barred (full line) and unbarred disc galaxies (dashed-line) as function of the light galaxy concentration ( lower panel).
Open with DEXTER

7.3 Galaxy colours

Figure 13 shows the cumulative distribution functions of the g-r colour for the sample galaxies. Barred and unbarred galaxies are characterised by different distributions as confirmed at a high confidence level (> $99\%$ ) by a KS test. Thus, barred galaxies are bluer than unbarred ones. We can explained this effect as due to the larger fraction of barred galaxies observed in the late-type systems, which are systematically bluer than the early-type ones. Similar colour difference between barred and unbarred galaxies was also reported by Barazza et al. (2008).

$\begin{figure} \par\includegraphics[width=8.7cm]{0931f13.ps} \end{figure}$	Figure 13: Cumulative distribution of barred (solid line) and unbarred (dashed line) as function of the g-r galaxy colour.
Open with DEXTER

8 Conclusions

We have studied the fraction and properties of bars in a sample of 2106 disc galaxies extracted from the SDSS-DR5. This is a volume-limited sample of undisturbed and non-interacting galaxies in the redshift range 0.01 < z < 0.04, with an absolute magnitude M_r < -20, and an inclination $i<60^{\circ}$ .

The sample galaxies have been classified lenticulars, early- (i.e, S0/a - Sb) or late-type spirals (i.e, Sbc - Sm) according to their light concentration. The light concentration was defined as C=r₉₀/r₅₀, where r₅₀ and r₉₀ are the radii enclosing $50\%$ and $90\%$ of the total galaxy light, respectively. These radii are available in the SDSS database for all objects of our sample. The correlation between the light concentration and morphological type was derived from a subsample of 612 galaxies listed in RC3, whose morphological classification was already known. We found that the fraction of lenticulars, early- and late-type spirals among the selected disc galaxies is $39\%$ , $28\%$ , and $33\%$ respectively.

We derived the fraction of barred galaxies by analysing the SDSS r-band images with the ellipse fitting and Fourier analysis methods. They consist in looking for a local maximum in the radial profile of ellipticity (associated to a constant position angle; e.g., Wozniak et al. 1995) and m=2 relative Fourier component (associated to a constant phase angle; e.g., Aguerri et al. 2000a), respectively.

The bar fraction depends strongly on the technique adopted for the analysis. By extensive testing on a large set of artificial galaxies, we concluded that the both methods are efficient in detecting the bars with sharp ends, such as the Ferrers and Freeman bars. On the contrary, the flat bars, which are characterised by a smooth transition to the disc, are more easily detected by the ellipse fitting method. The ellipse fitting method is more efficient in detecting bars in galaxies with lenses and spiral arms, where the m=2 relative Fourier component shows multiple maxima (but it is not associated to a constant phase angle). This is the case for late-type spiral galaxies. For this reason, we decided to rely only onto the results obtained with the ellipse fitting method. We found that $45\%$ of the selected disc galaxies host a bar in agreement with previous findings in optical wavebands (Marinova & Jogee 2007; Reese et al. 2007). The fraction of bars in the three different morphological bins is $29\%$ , $55\%$ , and $54\%$ for lenticulars, early- and late-type spirals, respectively. By classifying visually the galaxies in barred and unbarred we obtained similar bar fractions as those reported by the ellipse fitting method.

The bar length was obtained by measuring the radius $r_{\rm bar}^{\epsilon }$ at which the maximum ellipticity was reached and as the radius $r_{\rm bar}^{\rm PA}$ at which the PA changes by $5^\circ$ with respect to the value corresponding to the maximum ellipticity (e.g., Wozniak et al. 1995). According to the analysis of the artificial galaxies, the bar length is underestimated when $r_{\rm bar}^{\epsilon }$ is used, as found by Michel-Dansac & Wozniak (2006) too. This is particularly true for the Ferrers bars where the measured bar lengths are 51 $\%$ shorter than the real ones. In contrast, Freeman and flat bars were better determined, their measurements being shorter by 30 $\%$ and 19 $\%$ , respectively. The bar length is underestimated when $r_{\rm bar}^{\rm PA}$ is used for the Ferrers bars (11 $\%$ ), but it is overestimated for the Freeman (8 $\%$ ) and flat bars (28 $\%$ ). These results show the possibility of define an empirical correction to the bar length, knowing the bar type in advance. We obtained that the bar lengths (when normalised by the galaxy size) are larger in lenticular galaxies than those presented in early- and late-type ones. This finding is independent of the method used for measuring the bar length, and statistically significant according with the KS test. We also found a correlation between the bar length and galaxy size. This correlation is also independent of the method used for measuring the bar length. It holds for the different morphological bins, being stronger for late-type spirals (r=0.52) and weaker for lenticular galaxies (r=0.38). The larger bars are located in larger galaxies, indicating an interplay between the bar and disc in galaxy evolution.

The bar strength $f_{\rm bar}$ was estimated following the parametrisation by Abraham & Merrifield (2000) which requires the measurement of the bar ellipticity. The median values for the bar strengths of the lenticular, early-type, and late-type spiral galaxies are 0.16, 0.19, and 0.20, respectively. The bars of the lenticular galaxies were found to be weaker than those in spirals, as found by Laurikainen et al. (2007) too. The fact that the bar strength distribution are unimodal for all galaxy types argues against evolutionary models in which bars would be formed and destroyed in short timescales.

No difference between the local galaxy density was found between barred and unbarred galaxies in our sample. Thus, the local environment does not seem to influence bar formation. Moreover, neither the length nor strength of the bars are correlated with the local galaxy environment. The previous results are even true for the subsample of our galaxies located in the more dense environments (log( $\Sigma_5)>0$ Gal/Mpc². Those environments could be similar to those showed by galaxy groups or weak clusters of galaxies. Thus, we can say that even for the densest environments, the global environment do not play an important role in the bar formation. However, we can not exclude than close galaxy-galaxy encounters would trigger the bar formation, as they were excluded from our sample. These results indicate that formation and evolution of the bars in the studied sample depend mostly on internal galaxy processes rather than external ones.

A statistical significant difference between the central light concentration of barred and unbarred galaxies was found. The bars are mostly located in less concentrated galaxies. This difference could explain the lower fraction of bars detected in S0 galaxies with respect to spirals. Since the S0 galaxies host weaker bars than spirals, we conclude that central light concentration is an important factor driving the bar formation and evolution. In fact, according to the numerical simulations Debattista et al. (2006); Athanassoula & Misiriotis (2002); Norman et al. (1996); Pfenniger & Norman (1990), the bars are weakened by large bulges. Finally, bars are mainly hosted by bluer late-type spirals. We argue that this is due to late-type galaxies have larger bar fraction than early-type ones. Similar results were also found in previous works as Barazza et al. (2008).

The sample of galaxies presented in this study is one of the largest samples presented in the literature. This large number of studied galaxies makes that the conclusions reported in the present work about the different observational bar properties is stronger than those obtained with smaller number of galaxies. For this reason, the present work will be useful for constraining future theoretical works about formation and evolution of bars in disc galaxies.

Acknowledgements

We thank Victor P. Debattista, Lorenzo Morelli, Irina Marinova and Shardha Jogee for fruitful discussion. We also thank to the anonymous referee for helpful comments to this manuscript. J.A.L.A. is funded by the grant AYA2007-67965-C03-01 by the Spanish Ministerio de Educación y Ciencia. J.M.A. acknowledges support from the Istituto Nazionale di Astrofisica (INAF). E.M.C. receives support from the grant CPDA068415/06 by Padua University. J.M.A. and E.M.C. thank the Instituto de Astrofìsica de Canarias for hospitality while this paper was in progress. This research has made use of the NASA/IPAC Extragalactic Database (NED) and Sloan Digital Sky Survey (SDSS).

References

Abraham, R. G., & Merrifield, M. R. 2000, AJ, 120, 2835 [NASA ADS] [CrossRef] (In the text)
Abraham, R. G., Tanvir, N. R., Santiago, B. X., et al. 1996, MNRAS, 279, L47 [NASA ADS]
Adelman-McCarthy, J. K., Aguüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] (In the text)
Andredakis, Y. C., Peletier, R. F., & Balcells, M. 1995, MNRAS, 275, 874 [NASA ADS]
Aguerri, J. A. L. 1999, A&A, 351, 43
Aguerri, J. A. L., Beckman, J. E., & Prieto, M. 1998, AJ, 116, 2136 [NASA ADS] [CrossRef]
Aguerri, J. A. L., Muñoz-Tuñón, C., Varela, A. M., & Prieto, M. 2000a, A&A, 361, 841 [NASA ADS]
Aguerri, J. A. L., Varela, A. M., Prieto, M., & Muñoz-Tuñón, C. 2000b, AJ, 119, 1638 [NASA ADS] [CrossRef]
Aguerri, J. A. L., Balcells, M., & Peletier, R. F. 2001a, A&A, 367, 428 [NASA ADS] [CrossRef] [EDP Sciences]
Aguerri, J. A. L., Hunter, J. H., Prieto, M., et al. 2001b, A&A, 373, 786 [NASA ADS] [CrossRef] [EDP Sciences]
Aguerri, J. A. L., Debattista, V. P., & Corsini, E. M. 2003, MNRAS, 338, 465 [NASA ADS] [CrossRef]
Aguerri, J. A. L., Elias-Rosa, N., Corsini, E. M., & Muñoz-Tuñón, C. 2005, A&A, 434, 109 [NASA ADS] [CrossRef] [EDP Sciences]
Aguerri, J. A. L., Sánchez-Janssen, R., & Muñoz-Tuñón, C. 2007, A&A, 471, 17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Athanassoula, E. 1992, MNRAS, 259, 328 [NASA ADS] (In the text)
Athanassoula, E. 2003, MNRAS, 341, 1179 [NASA ADS] [CrossRef]
Athanassoula, E. 2005, MNRAS, 358, 1477 [NASA ADS] [CrossRef]
Athanassoula, E., & Misiriotis, A. 2002, MNRAS, 330, 35 [NASA ADS] [CrossRef]
Athanassoula, E., Morin, S., Wozniak, H., et al. 1990, MNRAS, 245, 130 [NASA ADS] (In the text)
Balogh, M. L., Baldry, I. K., Nichol, R., et al. 2004a, ApJ, 615, L101 [NASA ADS] [CrossRef]
Balogh, M., Eke, V., Miller, C., et al. 2004b, MNRAS, 348, 1355 [NASA ADS] [CrossRef]
Barazza, F. D., Jogee, S., & Marinova, I. 2008, ApJ, 675, 1194 [NASA ADS] [CrossRef]
Blanton, M. R., Lupton, R. H., Schlegel, D. J., et al. 2005, ApJ, 631, 208 [NASA ADS] [CrossRef] (In the text)
Block, D. L., Buta, R., Knapen, J. H., et al. 2004, AJ, 128, 183 [NASA ADS] [CrossRef]
Bournaud, F., & Combes, F. 2002, A&A, 392, 83 [NASA ADS] [CrossRef] [EDP Sciences]
Bournaud, F., Combes, F., & Semelin, B. 2005, MNRAS, 364, L18 [NASA ADS]
Bureau, M., & Athanassoula, E. 1999, ApJ, 522, 686 [CrossRef]
Bureau, M., & Freeman, K. C. 1999, AJ, 118, 126 [CrossRef]
Buta, R., & Block, D. L. 2001, ApJ, 550, 243 [NASA ADS] [CrossRef] (In the text)
Buta, R., Block, D. L., & Knapen, J. H. 2003, AJ, 126, 1148 [NASA ADS] [CrossRef] (In the text)
Buta, R., Laurikainen, E., Salo, H., Block, D. L., & Knapen, J. H. 2006, AJ, 132, 1859 [NASA ADS] [CrossRef]
Caon, N., Capaccioli, M., & D'Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] (In the text)
Carollo, C. M., Stiavelli, M., de Zeeuw, P. T., Seigar, M., & Dejonghe, H. 2001, ApJ, 546, 216 [NASA ADS] [CrossRef]
Carollo, C. M., Scarlata, C., Stiavelli, M., Wyse, R. F. G., & Mayer, L. 2007, ApJ, 658, 960 [NASA ADS] [CrossRef]
Cepa, J., & Beckman, J. E. 1990, ApJ, 349, 497 [NASA ADS] [CrossRef] (In the text)
Chung, A., & Bureau, M. 2004, AJ, 127, 3192 [NASA ADS] [CrossRef]
Combes, F., & Sanders, R. H. 1981, A&A, 96, 164 [NASA ADS]
Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS]
Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef]
Conselice, C. J., Bershady, M. A., & Jangren, A. 2000, ApJ, 529, 886 [NASA ADS] [CrossRef]
Contopoulos, G., & Grosbol, P. 1989, A&AR, 1, 261 [NASA ADS]
Cooper, M. C., Newman, J. A., Madgwick, D. S., et al. 2005, ApJ, 634, 833 [NASA ADS] [CrossRef] (In the text)
Corsini, E. M. 2008, in Formation and Evolution of Galaxy Bulges, ed. M. Bureau (Cambridge: Cambridge Univ. Press), IAU Symp., 245, 145 (In the text)
Corsini, E. M., Debattista, V. P., & Aguerri, J. A. L. 2003, ApJ, 599, L29 [NASA ADS] [CrossRef] (In the text)
Corsini, E. M., Aguerri, J. A. L., Debattista, V. P., et al. 2007, ApJ, 659, L121 [NASA ADS] [CrossRef] (In the text)
Courteau, S., de Jong, R. S., & Broeils, A. H. 1996, ApJ, 457, L73 [NASA ADS]
Cowan, N. B., & Ivezic, Z. 2008, ApJ, 674, L13 [NASA ADS] [CrossRef] (In the text)
Das, M., Teuben, P. J., Vogel, S. N., et al. 2003, ApJ, 582, 190 [NASA ADS] [CrossRef] (In the text)
Debattista, V. P., & Sellwood, J. A. 1998, ApJ, 493, L5 [NASA ADS] [CrossRef]
Debattista, V. P., & Sellwood, J. A. 2000, ApJ, 543, 704 [NASA ADS] [CrossRef]
Debattista, V. P., Corsini, E. M., & Aguerri, J. A. L. 2002, MNRAS, 332, 65 [NASA ADS] [CrossRef]
Debattista, V. P., Carollo, C. M., Mayer, L., & Moore, B. 2004, ApJ, 604, L93 [NASA ADS] [CrossRef]
Debattista, V. P., Mayer, L., Carollo, C. M., et al. 2006, ApJ, 645, 209 [NASA ADS] [CrossRef]
de Jong, R. S. 1996, A&A, 313, 45 [NASA ADS]
de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G. Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (Berlin: Springer-Verlag) (In the text)
Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef]
Eliche-Moral, M. C., Balcells, M., Aguerri, J. A. L., & González-García, A. C. 2006, A&A, 457, 91 [NASA ADS] [CrossRef] [EDP Sciences]
Elmegreen, B. G., & Elmegreen, D. M. 1985, ApJ, 288, 438 [NASA ADS] [CrossRef]
Elmegreen, B. G., Elmegreen, D. M., & Hirst, A. C. 2004, ApJ, 612, 191 [NASA ADS] [CrossRef]
Erwin, P. 2004, A&A, 415, 941 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Erwin, P. 2005, MNRAS, 364, 283 [NASA ADS] [CrossRef]
Erwin, P., & Sparke, L. S. 2003, ApJS, 146, 299 [NASA ADS] [CrossRef]
Eskridge, P. B., Frogel, J. A., Pogge, R. W., et al. 2000, AJ, 119, 536 [NASA ADS] [CrossRef]
Ferrers, N. M. 1877, Quart. J. Pure and Appl. Math., 14, 1 (In the text)
Fisher, D. B., & Drory, N. 2008, AJ, 136, 773 [NASA ADS] [CrossRef]
Freeman, K. C. 1966, MNRAS, 133, 47 [NASA ADS] (In the text)
Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] (In the text)
Gerin, M., Combes, F., & Athanassoula, E. 1990, A&A, 230, 37 [NASA ADS]
Grosbol, P. J. 1985, A&AS, 60, 261 (In the text)
Heller, C. H., Shlosman, I., & Athanassoula, E. 2007, ApJ, 671, 226 [NASA ADS] [CrossRef]
Hohl, F. 1971, ApJ, 168, 343 [NASA ADS] [CrossRef] (In the text)
Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [NASA ADS] (In the text)
Jeong, H., Bureau, M., Yi, S. K., Krajnovic, D., & Davies, R. L. 2007, MNRAS, 376, 1021 [NASA ADS] [CrossRef]
Jogee, S., Barazza, F. D., Rix, H.-W., et al. 2004, ApJ, 615, L105 [NASA ADS] [CrossRef]
Knapen, J. H., Shlosman, I., & Peletier, R. F. 2000, ApJ, 529, 93 [NASA ADS] [CrossRef]
Kormendy, J. 1979, ApJ, 227, 714 [NASA ADS] [CrossRef]
Kormendy, J., & Kennicutt, R. C., Jr. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] (In the text)
Laine, S., Shlosman, I., Knapen, J. H., & Peletier, R. F. 2002, ApJ, 567, 97 [NASA ADS] [CrossRef]
Laurikainen, E., Salo, H., & Buta, R. 2005, MNRAS, 362, 1319 [NASA ADS] [CrossRef]
Laurikainen, E., Salo, H., Buta, R., & Knapen, J. H. 2007, MNRAS, 381, 401 [NASA ADS] [CrossRef]
Lindblad, P. A. B., Lindblad, P. O., & Athanassoula, E. 1996, A&A, 313, 65 [NASA ADS]
Lütticke, R., Dettmar, R.-J., & Pohlen, M. 2000, A&AS, 145, 405 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
MacArthur, L. A., Courteau, S., & Holtzman, J. A. 2003, ApJ, 582, 689 [NASA ADS] [CrossRef]
Marinova, I., & Jogee, S. 2007, ApJ, 659, 1176 [NASA ADS] [CrossRef]
Marinova, I., et al. 2008, ApJ, submitted (In the text)
Martin, P. 1995, AJ, 109, 2428 [NASA ADS] [CrossRef]
Martinet, L., & Friedli, D. 1997, A&A, 323, 363
Martinez-Valpuesta, I., Shlosman, I., & Heller, C. 2006, ApJ, 637, 214 [NASA ADS] [CrossRef]
Mastropietro, C., Moore, B., Mayer, L., et al. 2005, MNRAS, 364, 607 [NASA ADS]
Méndez-Abreu, J. 2008, Ph.D. Thesis, Univ. La Laguna and Univ. Padova (In the text)
Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008a, A&A, 478, 353 [NASA ADS] [CrossRef] [EDP Sciences]
Méndez-Abreu, J., Corsini, E. M., Debattista, V. P., et al. 2008b, ApJ, 679, L73 [NASA ADS] [CrossRef] (In the text)
Menéndez-Delmestre, K., Sheth, K., Schinnerer, E., et al. 2007, ApJ, 657, 790 [NASA ADS] [CrossRef]
Merrifield, M. R., & Kuijken, K. 1995, MNRAS, 274, 933 [NASA ADS]
Michel-Dansac, L., & Wozniak, H. 2006, A&A, 452, 97 [NASA ADS] [CrossRef] [EDP Sciences]
Miller, C. J., Nichol, R. C., Gómez, P. L., Hopkins, A. M., & Bernardi, M. 2003, ApJ, 597, 142 [NASA ADS] [CrossRef]
Miwa, T., & Noguchi, M. 1998, ApJ, 499, 149 [NASA ADS] [CrossRef]
Möllenhoff, C. 2004, A&A, 415, 63 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Möllenhoff, C., & Heidt, J. 2001, A&A, 368, 16 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Norman, C. A., Sellwood, J. A., & Hasan, H. 1996, ApJ, 462, 114 [NASA ADS] [CrossRef]
Ohta, K., Hamabe, M., & Wakamatsu, K.-I. 1990, ApJ, 357, 71 [NASA ADS] [CrossRef]
Peletier, R. F., & Balcells, M. 1996, AJ, 111, 2238 [NASA ADS] [CrossRef]
Pfenniger, D., & Norman, C. 1990, ApJ, 363, 391 [NASA ADS] [CrossRef]
Prieto, M., Gottesman, S. T., Aguerri, J.-A. L., & Varela, A.-M. 1997, AJ, 114, 1413 [CrossRef]
Prieto, M., Aguerri, J. A. L., Varela, A. M., & Muñoz-Tuñón, C. 2001, A&A, 367, 405 [NASA ADS] [CrossRef] [EDP Sciences]
Quillen, A. C., Frogel, J. A., & Gonzalez, R. A. 1994, ApJ, 437, 162 [NASA ADS] [CrossRef]
Raha, N., Sellwood, J. A., James, R. A., & Kahn, F. D. 1991, Nature, 352, 411 [NASA ADS] [CrossRef]
Rautiainen, P., Salo, H., & Laurikainen, E. 2008, MNRAS, 388, 1803 [NASA ADS] [CrossRef]
Reese, A. S., Williams, T. B., Sellwood, J. A., Barnes, E. I., & Powell, B. A. 2007, AJ, 133, 2846 [NASA ADS] [CrossRef]
Romano-Diaz, E., Shlosman, I., Hoffman, Y., & Heller, C. 2008, ApJ, 685, 105 [NASA ADS] [CrossRef]
Sellwood, J. A. 2006, ApJ, 637, 567 [NASA ADS] [CrossRef]
Sellwood, J. A., & Debattista, V. P. 2006, ApJ, 639, 868 [NASA ADS] [CrossRef]
Sérsic, J. L. 1968, Atlas de Galaxias Australes (Córdoba, Observatorio Astronomico) (In the text)
Sheth, K., Regan, M. W., Scoville, N. Z., & Strubbe, L. E. 2003, ApJ, 592, L13 [NASA ADS] [CrossRef]
Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [NASA ADS] [CrossRef] (In the text)
Shlosman, I., Peletier, R. F., & Knapen, J. H. 2000, ApJ, 535, L83 [NASA ADS] [CrossRef] (In the text)
Thompson, L. A. 1981, ApJ, 244, L43 [NASA ADS] [CrossRef] (In the text)
Tremaine, S., & Weinberg, M. D. 1984, ApJ, 282, L5 [NASA ADS] [CrossRef] (In the text)
Trujillo, I., Aguerri, J. A. L., Cepa, J., & Gutiérrez, C. M. 2001, MNRAS, 328, 977 [NASA ADS] [CrossRef] (In the text)
Vega Beltrán, J. C., Corsini, E. M., Pizzella, A., & Bertola, F. 1997, A&A, 324, 485
Verley, S., Combes, F., Verdes-Montenegro, L., Bergond, G., & Leon, S. 2007, A&A, 474, 43 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Weinberg, M. D. 1985, MNRAS, 213, 451 [NASA ADS]
Weiner, B. J., Sellwood, J. A., & Williams, T. B. 2001, ApJ, 546, 931 [NASA ADS] [CrossRef]
Whyte, L. F., Abraham, R. G., Merrifield, M. R., et al. 2002, MNRAS, 336, 1281 [NASA ADS] [CrossRef]
Wozniak, H., Friedli, D., Martinet, L., Martin, P., & Bratschi, P. 1995, A&AS, 111, 115 [NASA ADS]
York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] (In the text)

Footnotes

... IRAF: IRAF is distributed by NOAO, which is operated by AURA Inc., under contract with the National Science Foundation.
... $\rm\Delta PA \leq 20^\circ$ ): We have considered that a global maximum in the ellipticity profile is produced by a bar when it is located at more than 3.5 pixels from the galaxy centre. This radial distance correspond to more than 3 times the FWHM/2 of the images.

All Tables

Table 1: Median values of the light concentration and central velocity dispersion for the different galaxy types.

Table 2: Comparison between our and RC3 classification.

Table 3: Percentage of galaxies classified as barred and unbarred galaxies erroneously found to be barred by applying the ellipse fitting method to the sample of artificial galaxies.

Table 4: Percentage of galaxies classified as barred and unbarred galaxies erroneously found to be barred by applying the Fourier analysis method to the sample of artificial galaxies.

Table 5: Median values of the bar radius for the different galaxy types.

All Figures

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{0931f1.ps} \end{figure}$	Figure 1: Values of the light concentration C ( top panel) and central velocity dispersion $\sigma _{0}$ ( bottom panel) as a function of the morphological parameter T. Only the sample galaxies in RC3 are plotted. Median values of C and $\sigma _{0}$ for ellipticals (diamond), lenticulars (asterisk), early-type spirals (triangle), and late-type spirals (square) are shown.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.7cm]{0931f2.ps} \end{figure}$	Figure 2: Values of the light concentration C and central velocity dispersion $\sigma _{0}$ for the sample galaxies with $\sigma _{0}$ available in SDSS-DR5. They are colour coded according to our morphological classification: the red, magenta, green, and blue dots correspond to the ellipticals, lenticulars, early-type and late-type spirals, respectively. Median values for the ellipticals (diamond), lenticulars (asterisk), early-type spirals (triangle), and late-type spirals (square) plotted in Fig. 1 are also shown. The full lines represent the locus of equal distance between different galaxy morphological types.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0931f3.ps} \end{figure}$	Figure 3: Fraction of artificial galaxies correctly classified as barred vs fraction of bad/spurious bar detections using the ellipse fitting method with $\Delta$ PA = 10 $^{\circ }$ (asterisks), 20 $^{\circ }$ (filled circles), and 30 $^{\circ }$ (squares) and $\Delta \epsilon =0.1$ (black symbols), 0.08 (red symbols), and 0.05 (blue symbols). The large, medium, and small symbols correspond to Ferrers, Freeman, and flat bars, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=15cm]{0931f4.ps} \end{figure}$	Figure 4: Bar length measured with the maximum ellipticity ( top panels), position angle ( middle panels), and Fourier analysis method ( bottom panels) for Ferrers ( left panels), Freeman ( central panels), and flat bars ( right panels) in artificial galaxies. Mean relative error (defined as the difference between input and measured values) and standard deviation for the measurements are given in each panel.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0931f5.ps} \end{figure}$	Figure 5: Fraction of artificial galaxies correctly classified as barred and fraction of bad/spurious bar detections using the Fourier analysis method with $\Delta \phi _2=10^{\circ }$ (asterisks), 20 $^{\circ }$ (filled circles), and 30 $^{\circ }$ (squares) and $\Delta (I_2/I_0)=0.2$ (green symbols), 0.1 (black symbols), 0.08 (red symbols), and 0.05 (blue symbols). The large, medium, and small symbols correspond to Ferrers, Freeman, and flat bars, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0931f6.ps} \end{figure}$	Figure 6: The r-band images ( left panels), ellipticity ( central panels), and m=2 Fourier amplitude radial profiles ( right panels) of the early-type spiral SDSSJ031947.01+003504.4 ( top panels) and the late-type spiral SDSSJ020159.33-081441.9 are analysed by both methods ( bottom panels). For each galaxy the vertical dotted line corresponds to the value of $r_{\rm bar}^{\epsilon }$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{0931f7.ps} \end{figure}$	Figure 7: Distribution of the bar length ( left panels) and normalised bar length ( right panels) in lenticulars (full line), early-type spirals (dotted line), and late-type spirals (dashed line). The bar length was measured with both the maximum ellipticity (top panels) and PA method (bottom panels). Arrows mark the median values of the distributions.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0931f8.ps} \end{figure}$	Figure 8: Galaxy radius $r_{\rm gal}$ versus bar length measured with the PA method ( top panel) and maximum ellipticity method ( bottom panel). The solid line represents the linear regression through all the data points. The Pearson correlation coefficient (r) and the result of the linear fit are given.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0931f9.ps} \end{figure}$	Figure 9: Distribution of the bar strength in lenticulars (full line), early-type spirals (dotted line), and late-type spirals (dashed line) for the whole sample ( top panel) and for the galaxies with $r_{\rm bar} > r_{\rm bd}$ ( bottom panel). Arrows mark the median values of the distributions.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0931f10.ps} \end{figure}$	Figure 10: Cumulative distribution of barred (solid black line) and unbarred (dashed black line) galaxies as function of the local galaxy density. Cumulative distribution of barred (long-dashed blue line) and unbarred (dashed-dotted blue line) galaxies after excluding those at less than 7 Mpc from the nearest edge of SDSS is also overplotted (see text for more details).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{0931f11.ps} \end{figure}$	Figure 11: Fraction of galaxies remaining in the sample after correcting for survey edge effects by removing all the galaxies with an edge of the survey closer than the measured fifth neighbour distance (blue squares), 2 Mpc (black diamonds), 5 Mpc (green triangles), and 7 Mpc (red asterisks). Poissonian errors are given. Horizontal lines show the width of the local density bins.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0931f12.ps} \end{figure}$	Figure 12: Number of barred (full line) and unbarred disc galaxies (dotted line) as function of the light concentration ( upper panel). Cumulative distribution of barred (full line) and unbarred disc galaxies (dashed-line) as function of the light galaxy concentration ( lower panel).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.7cm]{0931f13.ps} \end{figure}$	Figure 13: Cumulative distribution of barred (solid line) and unbarred (dashed line) as function of the g-r galaxy colour.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.