The VVDS-VLA deep field

S. Bardelli; E. Zucca; M. Bolzonella; P. Ciliegi; L. Gregorini; G. Zamorani; M. Bondi; A. Zanichelli; L. Tresse; D. Vergani; I. Gavignaud; A. Bongiorno; D. Bottini; B. Garilli; V. Le Brun; O. Le Fèvre; D. Maccagni; R. Scaramella; M. Scodeggio; G. Vettolani; C. Adami; S. Arnouts; A. Cappi; S. Charlot; T. Contini; S. Foucaud; P. Franzetti; L. Guzzo; O. Ilbert; A. Iovino; F. Lamareille; H. J. McCracken; B. Marano; C. Marinoni; A. Mazure; B. Meneux; R. Merighi; S. Paltani; R. Pellò; A. Pollo; L. Pozzetti; M. Radovich; U. Abbas; J. Brinchmann; O. Cucciati; S. de la Torre; L. de Ravel; P. Memeo; E. Perez-Montero; Y. Mellier; P. Merluzzi; S. Temporin; H. R. De Ruiter; P. Parma

doi:10.1051/0004-6361:200810567

Home

All issues

Volume 495 / No 2 (February IV 2009)

A&A, 495 2 (2009) 431-446

Full HTML

Free Access

Issue		A&A Volume 495, Number 2, February IV 2009


Page(s)		431 - 446
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361:200810567
Published online		04 December 2008

IV. Radio-optical properties

S. Bardelli¹ - E. Zucca¹ - M. Bolzonella¹ - P. Ciliegi¹ - L. Gregorini^2,6 - G. Zamorani¹ - M. Bondi² - A. Zanichelli² - L. Tresse³ - D. Vergani¹ - I. Gavignaud⁵ - A. Bongiorno⁶ - D. Bottini⁴ - B. Garilli⁴ - V. Le Brun³ - O. Le Fèvre³ - D. Maccagni⁴ - R. Scaramella^2,8 - M. Scodeggio⁴ - G. Vettolani² - C. Adami³ - S. Arnouts³ - A. Cappi¹ - S. Charlot^9,10 - T. Contini⁷ - S. Foucaud¹¹ - P. Franzetti⁴ - L. Guzzo¹² - O. Ilbert¹³ - A. Iovino¹² - F. Lamareille^1,3 - H. J. McCracken^10,14 - B. Marano⁶ - C. Marinoni¹⁵ - A. Mazure³ - B. Meneux^4,12 - R. Merighi¹ - S. Paltani^16,17 - R. Pellò⁷ - A. Pollo^1,18 - L. Pozzetti¹ - M. Radovich¹⁹ - U. Abbas³ - J. Brinchmann²⁰ - O. Cucciati^12,21 - S. de la Torre³ - L. de Ravel³ - P. Memeo⁴ - E. Perez-Montero⁷ - Y. Mellier^10,14 - P. Merluzzi¹⁹ - S. Temporin¹² - H. R. De Ruiter¹ - P. Parma²

1 - INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
2 - IRA-INAF, via Gobetti 101, 40129, Bologna, Italy
3 - Laboratoire d'Astrophysique de Marseille, (UMR 6110) CNRS-Université de Provence, 38 rue Frederic Joliot-Curie, 13388 Marseille Cedex 13, France
4 - IASF-INAF, via Bassini 15, 20133 Milano, Italy
5 - Astrophysical Institute Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
6 - Università di Bologna, Dipartimento di Astronomia, via Ranzani 1, 40127 Bologna, Italy
7 - Laboratoire d'Astrophysique de Toulouse/Tarbes (UMR 5572) CNRS, 14 Av. E. Belin, 31400 Toulouse, France
8 - INAF-Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
9 - Max Planck Institut fur Astrophysik, 85741 Garching, Germany
10 - Institut d'Astrophysique de Paris, UMR 7095, 98bis Bd Arago, 75014 Paris, France
11 - School of Physics & Astronomy, University of Nottingham, University Park, Nottingham NG72RD, UK
12 - INAF-Osservatorio Astronomico di Brera, via Brera 28, Milan, Italy
13 - Institute for Astronomy, 2680 Woodlawn Dr., University of Hawaii, Honolulu, Hawaii, 96822, USA
14 - Observatoire de Paris, LERMA, 61 avenue de l'Observatoire, 75014 Paris, France
15 - Centre de Physique Théorique, UMR 6207 CNRS-Université de Provence, 13288 Marseille, France
16 - Integral Science Data Centre, ch. d'Écogia 16, 1290 Versoix, Switzerland
17 - Geneva Observatory, ch. des Maillettes 51, 1290 Sauverny, Switzerland
18 - Astronomical Observatory of the Jagiellonian University, ul Orla 171, 30-244 Kraków, Poland
19 - INAF-Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
20 - Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
21 - Universitá di Milano-Bicocca, Dipartimento di Fisica, Piazza delle Scienze 3, 20126 Milano, Italy

Received 11 July 2008 / Accepted 5 November 2008

Abstract
Aims. The availability of wide angle and deep surveys, both in the optical and the radio band, allows us to explore the evolution of radio sources with optical counterparts up to redshift $z\sim 1.1$ in an unbiased way using large numbers of radio sources and well defined control samples of radio-quiet objects.
Methods. We use the 1.4 GHz VIMOS-VLA Deep Survey, the optical VIMOS-VLT Deep Survey and the CFHT Legacy Survey to compare the properties of radio-loud galaxies with respect to the whole population of optical galaxies. The availability of multiband photometry and high quality photometric redshifts allows us to derive rest-frame colors and radio luminosity functions to a limit of a B rest-frame magnitude of M_B=-20. We derive spectrophotometric types, following the classification of Zucca et al. (2006, A&A, 455, 879), in order to have a priori knowledge of the optical evolution of different galaxy classes.
Results. Galaxy properties and luminosity functions are estimated up to $z\sim 1$ for radio-loud and radio-quiet early and late type galaxies. Radio-loud late type galaxies show significantly redder colors than radio-quiet objects of the same class and this is related to the presence of more dust in stronger star forming galaxies. We estimate the optical luminosity functions, stellar masses and star formation rate distributions for radio sources and compare them with those derived for a well defined control sample, finding that the probability of a galaxy to be a radio emitter significantly increases at high values of these parameters. Radio-loud early type galaxies exhibit luminosity evolution in their bivariate radio-optical luminosity function, due to evolution in the radio-optical ratio. The lack of evolution of the mass function of radio-loud early type galaxies means that no new AGN are formed at redshift z<1. In contrast, radio-loud late type objects exhibit a strong evolution, both in luminosity and density, of the radio luminosity function for z>0.7. This evolution is a direct effect of the strong optical evolution of this class and no significant change with redshift in the radio-optical ratio is required. With the knowledge of the radio-optical ratio and the optical and radio luminosity functions for late type galaxies, we show that it is possible to estimate the star formation history of the Universe up to redshift $z\sim 1.5$ , using optical galaxies as tracers of the global radio emission.

Key words: galaxies: fundamental parameters - galaxies: general - galaxies: luminosity function, mass function - radio continuum: galaxies

1 Introduction

Deep 1.4 GHz counts exhibit an upturn below a few millijansky (mJy), which corresponds to a rapid increase in the number of faint sources (Windhorst et al. 1985). First results of the spectroscopic follow-up of relatively bright counterparts (B<22) identified many of them as blue galaxies with spectra showing evidence of intense star formation (Benn et al. 1993; Franceschini et al. 1988). However, with increasing depth of the optical follow-up programs, it resulted that an increasing number of sub-mJy sources was associated with earlier type galaxies (Gruppioni et al. 2003; Prandoni et al. 2001; Hammer et al. 1995; Afonso et al. 2006).

The relative fractions of the various populations contributing to the sub-mJy radio counts (AGN, starburst, late, and early type galaxies) are still a matter of debate, with different surveys providing different results (Smolcic et al. 2008, and references therein).

In fact, the photometric and spectroscopic work required in the optical identification process is demanding in terms of telescope time, since a significant fraction of the faint radio sources has also faint optical counterparts. It is therefore clear that to investigate the nature and evolution of the sub-mJy population, it is neces sary to couple deep radio and optical (both imaging and spectroscopic) observations over a reasonably large area of the sky.

The properties of radio sources in the local Universe were studied extensively by Best et al. (2005) using the NVSS/FIRST radio surveys coupled with the optical Sloan Digital Sky Survey and by Magliocchetti et al. (2002) using the same radio data and the 2dF galaxy redshift survey for the optical part. These optical surveys permit a spectral classification for the optical counterparts of radio sources, by dividing the sample mainly in to early and late type galaxies (broadly representative of passive and star-forming galaxies) on the basis of spectral features such as the 4000 $\AA$ break or colors. The results, represented by the bivariate radio-optical luminosity functions, demostrate that the luminosity function of early type galaxies (presumably hosting an AGN) can be described by a power law function flatter than for late type galaxies.

Moving to higher redshift, the Phoenix Deep survey allowed the study of the evolution of the radio luminosity function (Afonso et al. 2005) and showed that the radio emission of star-forming galaxies strongly evolved from $z\sim 0.1$ up to $z\sim 0.5$ . Later surveys explored the star formation density evolution at even higher redshifts (Seymour et al. 2008; Barger et al. 2007; Ivison et al. 2007; Smolcic et al. 2008) finding typical trend of rapidly increasing star formation from redshift zero to $\sim$ 0.8-1.0 and then a plateau (or a decrease) at higher redshifts.

When one wants to study radio sources as a function of redshift, it is necessary to go through the radio-optical identification process. For this reason, it is critical to know as accurately as possible the properties of the optical counterparts in order to discriminate the contribution to the evolution of the radio sources of the the optical host galaxies or of the radio emitting process.

The VIMOS-VLT Deep Survey (Le Fèvre et al. 2005), complemented with photometric data from the CFHT Legacy Survey, provides a unique opportunity to study the evolution of optical galaxies with redshift. In fact, it offers the availability of a large sample of reference redshifts obtained from a deep spectroscopic survey, a large set of photometric bands and high quality photometric redshifts over a wide area. This allows us to study the properties of the counterparts of an associated 1.4 GHz VLA survey (Bondi et al. 2003; Ciliegi et al. 2005) by using the rest-frame colors and therefore avoiding the use of redshift-dependent quantities.

The aim of this paper is to compare the optical properties of galaxies hosting a radio source with those of a well defined control sample of galaxies, for which selection effects and evolutionary behaviour are known a priori, to understand the relations between the radio and optical properties. For this reason, in this paper we define as ``radio galaxies'' or ``radio-loud galaxies'' all galaxies with detected radio emission: our definition is therefore based only on observed quantities.

The advantage of this work is the simultaneous availability of a deep radio survey, a multiwavelength optical band coverage over a relatively large area, accurate photometric redshifts and absolute magnitudes which minimize the model dependency, but the most important point is the availability of a control sample with well studied luminosity and stellar mass functions as a function of redshift and galaxy type, from which it is possible in a completely homogeneus way to extract galaxies that host a radio source.

The plan of the paper is the following: in Sect. 2 we present the data and definition of our samples; in Sect. 3 we compare the redshift distribution of the radio galaxy subsample with the sample of all galaxies; in Sect. 4 we present the results of the color distributions and in Sect. 5 the bivariate luminosity functions. The radio-optical ratio distribution for our sample is presented in Sect. 6, while the stellar mass and star formation rate distributions are shown in Sect. 7. In Sect. 8 we estimate the star formation density evolution and in Sect. 9 we present the conclusions.

Throughout the paper we adopt a flat $\Omega_{\rm m} = 0.3$ and $\Omega_\Lambda = 0.7$ cosmology, with $H_{\rm0} = 70$ km s^-1 Mpc^-1. Absolute magnitudes are given in the AB system and are expressed in the five standard bands U (Bessel), B and V (Johnson), R and I(Cousins). Errors are estimated as poissonian fluctuations and refer to $1\sigma$ confidence level.

2 The data

Table 1: Numbers of objects in our samples. The low/high redshift bins are [0-0.5]/[0.5-1.1] for all galaxies and type 3+4 galaxy samples and [0-0.7]/[0.7-1.0] for type 1+2 galaxy sample.

The radio data were obtained with the Very Large Array (VLA) in B configuration (NRAO code AB925): a one square degree mosaic map with an approximately uniform noise of $\sim$ $17.5~ \mu$ Jy (1 $\sigma$ ) and with a $6 \times 6$ arcsec FWHM Gaussian resolution beam was obtained. This map (centered on $\alpha_{2000} = 02$ :26:00 $\delta_{2000} = -$ 04:30:00) was used to extract a catalogue of 1054 radio sources to a completeness limit of $80 ~\mu$ Jy. A detailed description of the radio observations, data reduction, sources extraction and radio source counts is reported in Bondi et al. (2003), while the radio-optical correlation (done with a likelihood ratio technique) and the properties of radio objects with optical counterparts are presented in Ciliegi et al. (2005), who detected 718 radio sources with an optical counterpart brighter than $I_{\rm AB}=25$ . The percentage of optical identifications of the radio sources varies from $\sim$ $70\%$ , for fluxes between 0.08 and 0.2 mJy, to $\sim$ $65\%$ , for fluxes between 0.2 and 0.1 mJy, and decreases to $58\%$ for brighter sources. Bondi et al. (2007) performed a 610 MHz survey with the Giant Meterwave Radio Telescope (GMRT), finding that the median spectral index of faint radio sources (below 0.5 mJy at 1.4 GHz) is significantly flatter than that of brighter sources. This fact is probably due to a significant contribution below 0.5 mJy from a population of flat spectrum low luminosity compact AGN and radio-quiet QSO.

The optical data are part of both the F02 deep field of the VIMOS-VLT Deep Survey (VVDS) and the D1 field of the MEGACAM CFHT Legacy Survey (CFHT-LS). The first set consists of data for the B, V, R and I bands (McCracken et al. 2003), obtained with the CFHT wide-field 12 K mosaic camera for the entire field. The completeness limits are $\sim$ 26 for the B, V and R bands and $\sim$ 25 for the I band.

The second set comprises data for the u^*, g',r',i' and z' bands (McCracken et al. 2009) and covers an area of 1 deg² centered on the VVDS F02 deep field; the completeness limits are 26.0, 25.8, 24.3, 25.1 and 24.5, respectively. We used also the UKIDSS J and K data (complete to a limit of $K\sim 18$ , Warren et al. 2007), which covers the entire area.

Starting from the VVDS photometric catalogue, a deep spectroscopic survey was conducted for galaxies with $I_{\rm AB}\le24$ (Le Fèvre et al. 2005), with a sampling rate of $\sim$ $33\%$ over an area of 0.6 deg² and a spectral resolution of $\sim$ $33~ \AA$ at $7500~ \AA$ . Due to this sampling rate and area covered, only 53 radio sources (among the 718 with optical counterparts) have a spectroscopic redshift. To increase the number of studied objects, we decided to use the VVDS photometric redshift sample. The VVDS photometric redshift catalogue and the method to estimate redshifts and their quality were presented by Ilbert et al. (2006). The typical error is $\sigma(\Delta z / (1+z))\sim 0.029$ and the reliability is maximum in the redshift range [0.2-1.5]. We analysed the differences between the photometric and spectroscopic redshifts of the 28 galaxies in the Radio Sample (see below), finding that the zero-point is consistent with zero (at $0.05 \sigma$ ) and the error is 0.034. Therefore, the properties of the photometric redshifts of radio galaxies are consistent with those of the optical sample.

Absolute magnitudes are computed following the method described in the Appendix of Ilbert et al. (2005): the K-correction is computed using a set of templates and all the photometric information available. However, to reduce the template dependency, the rest-frame absolute magnitude in each band is derived using the apparent magnitude in the closest observed band, shifted to the redshift of the galaxy. With this method, the applied K-correction is as small as possible.

Following the procedure adopted in Zucca et al. (2006), for each galaxy the rest-frame magnitudes were matched with an empirical set of SEDs, consisting of four observed spectra (CWW Coleman et al. 1980) and two starburst SEDs computed with GISSEL (Bruzual & Charlot 1993). The match is performed by minimizing a $\chi^2$ variable on these templates at the redshift of each galaxy. Note that this method for the galaxy classification is more refined than a simple color division because of the simultaneous use of all available photometric data, which minimizes the influence of errors in a single band.

Galaxies were divided into four types, corresponding to the E/S0 template (type 1), early spiral template (type 2), late spiral template (type 3) and irregular template (type 4); type 4 also includes the starburst templates. Franzetti et al. (2007) have shown that there is a good correspondence between this classification and that obtained from spectral features, such as the 4000 $\AA$ break to $z\sim 1.4$ .

By studying the luminosity function of these photometric types for the spectroscopic survey, Zucca et al. (2006) found that type 1 (corresponding to early type galaxies) and type 4 galaxies (corresponding to star forming late blue galaxies) exhibit the most extreme behaviour regarding evolution in the luminosity function, with the former class showing little evolution and the latter showing a strong evolution. The other two classes (2 and 3) could be regarded as intermediate types in the sense that their properties are less extreme.

The accurate knowledge of the behaviour of these classes encouraged us to use the same classification. We assume that the results for the spectroscopic subsample holds also for the entire, photometric redshift-based sample. This assumption is confirmed by the comparison of the luminosity functions from the two datasets (Ilbert, private communication).

From the 718 original radio-optical identifications (the ``Original Sample''), we consider only objects with M_B<-20 in the redshift interval [0-1.1] (or the interval [0-1.0] when considering type 1 alone), where we have reliable photometric redshifts and well studied optical luminosity functions. We refer to this sub-sample as the ``Complete Sample''. The magnitude limit assures that the considered galaxies are visible within the entire adopted redshift range and our sample therefore has the same properties as a volume limited sample. The different redshift limit for type 1 galaxies is due to their higher K-correction, which influences their absolute magnitude limit (see the discussion of Zucca et al. 2006).

The sample of all galaxies from the CFHT-LS/VVDS catalogue was divided by the same limits to obtain the ``Control Sample''. In the upper panel of Fig. 1 we show the apparent I-band magnitude distribution of the Original Sample (empty histogram) and of the Complete Sample (shaded histogram). This histogram allows us to define a further cut in the Control and Complete Samples at $I_{\rm AB}<24$ . This ensures that the two samples are cleaner because at fainter magnitudes the estimated photometric redshifts are less precise and the fraction of unreliable or uncorrect redshift increases. This apparent magnitude limit is the same of that of the VVDS spectroscopic survey and we are therefore in the same framework as Zucca et al. (2006) work on the luminosity functions.

Within these limits there are 430 radio sources. It is clear from the figure that the majority of the objects not present in the Complete Sample have magnitudes of $I_{\rm AB}>22$ . Among the radio sources not selected by our limits, 133 have M_B>-20 and 154 match our absolute magnitude criterion but have z>1.1, while the 35 $I_{\rm AB}<18$ objects are too faint to be included in the Complete Sample.

Considering the frequency of types in the Complete Sample, 169 objects are of type 1 (149 within z<1.0), 134 are of type 2, while 74 and 53 are of type 3 and type 4, respectively. Given the relatively low number of type 4 galaxies, we consider as a single class (hereafter type 3+4) the late type galaxies. The Control Sample is formed by 4332 type 1 (3775 z<1.0), 3082 type 2 and 10 466 type 3+4 objects (see Table 1). Therefore, in our sample the percentage of radio emitting sources is $\sim$ $4 \%$ , $\sim$ $3\%$ and $\sim$ $1\%$ for the three considered classes, respectively. Here, we assume that the emission mechanism of type 1 and type 2 radio galaxies is due mainly to AGN (thus selecting the ``absorption line AGN'' of Best et al. 2005), while for type 3 and type 4 it is induced by star formation.

This assumption is reasonable in the light of the classification in Fig. 9 of Best et al. (2005), which shows the plot log $L_{\rm radio}/M_*$ versus D_n (4000), where $L_{\rm radio}$ is the radio luminosity, M_* is the stellar mass and D_n (4000) is the measure of the $4000~\AA$ break. In this plot, there are two well separated clumps, which do not depend on log $L_{\rm radio}/M_*$ , one at $D_n (4000)\sim 1.25$ populated almost completely by star forming galaxies, and another at $D_n (4000)\sim 2.0$ dominated by galaxies with AGN induced emission and LINERS. For the 31 radio galaxies in our sample with measured D_n (4000) our classification agrees with that of Best et al. (2005). Considering the entire sample, almost all our radio sources ( $\sim$ $93\%$ ) have a ratio $11.5<\log L_{\rm radio}/M_* < 14$ , and this implies that the division between star forming and AGN induced radio emission spans the range [1.3-1.6] in D_n (4000): this value roughly corresponds to the division between type 1+2 and type 3+4 for the Control Sample.

$\begin{figure} \par\includegraphics[width=9cm]{0567fig1a.ps} \includegraphics[width=9cm]{0567fig1b.ps} \end{figure}$

Figure 1:

Upper panel: shaded histogram: distribution of I magnitude for radio galaxies with M_B<-20 and $z_{\rm phot}<1.1$ (the Complete Sample). Empty histogram: all identified radio galaxies (the Original Sample). Lower panel: dotted histogram corresponds to the radio flux for all radio galaxies (the Original Sample), solid line represents the Complete Sample, dot-dashed line the type 3+4 objects, long dashed line the type 1 objects.

Open with DEXTER

Another way of testing our classification is by looking at the upper panel of Fig. 11 (see Sect. 7): all radio galaxies with star formation rates (as estimated in the optical) of less than $1{-}2~ M_{\odot}~\rm yr^{-1}$ (all of type 1+2) are far from the correlation between SFR(optical) and SFR(radio) seen at higher rates, meaning that the AGN component of the radio luminosity is dominant. Moreover, we checked our classification using the spectra from the zCOSMOS 10 K sample (Lilly et al. 2007), limiting the data set at M_B<-20 and z<0.9, due to the different depths of the surveys. Only $6 \%$ of the type 1+2 objects are beneath the dividing line (i.e. classified as star forming) of Best et al. (2005) and $30 \%$ of type 3+4 are just above the dividing line (Bardelli et al. 2009).

In the lower panel of Fig. 1 we display the 1.4 GHz flux histogram of the Original Sample and the Complete Sample, in which the long dashed line corresponds to type 1 galaxies and the dot-dashed line corresponds to type 3+4 objects. There is no significant trend of types with flux: the fraction of type 1 galaxies decreases from $46\%$ in the flux range [0.2-0.45] mJy to $32\%$ in the range [0.08-0.2], while the fraction of type 3+4 galaxies increases from $22\%$ to $31\%$ . In our case, no dramaticly increasing percentage of star-forming galaxies is present at low fluxes, in contrast to early results (see the discussion in Gruppioni et al. 1999). This conclusion would be similar if we adopt a fainter I magnitude limit or relax all of our restrictions, in particular that at high redshift: in this case the fraction of type 3+4 increases from $37\%$ to $41\%$ . Only type 1 galaxies show a decrease from $34\%$ to $25 \%$ , possibly due to the blueing of ellipticals at higher redshifts, which could shift radio galaxies from type 1 to type 2. However, as shown by Seymour et al. (2008), our adopted flux limit is just above the upturn of the star forming galaxy counts.

2.1 Contribution from optically identified AGN

In the optical spectroscopy, the emission of an active nucleus is revealed by the presence of typical features of emission lines, leading to the definition of two broad classes: the Broad Line AGN (BLAGN) and Narrow Line AGN (NLAGN). These AGN are known to be sometimes radio-loud. These objects are expected to be relatively rare within our limits and have spectral energy distributions that could be misclassified within our classification scheme (AGN induced radio emission associated with early type galaxies and star formation induced emission with late type galaxies). For this reason, we consider as ``contamination'' the presence of these objects in both the Complete and Control samples.

We estimate the significance of the possible contamination in our sample by these objects: unfortunately, a direct estimation is not possible due to a the lack of spectroscopy for most of our radio sample.

The presence of optical AGN in the spectroscopic VVDS survey was studied by Bongiorno et al. (2007), Gavignaud et al. (2006), and Paltani et al. (2009), finding a sample of 333 NLAGN and 63 BLAGN. Within our limits in redshift and absolute magnitude the ratio between type 1+2 objects versus type 3+4 is 1/6 for BLAGN and 1/3 for NLAGN. Among these objects, 4 BLAGN and 2 NLAGN have radio counterparts in the Original Sample and 2 BLAGN and 2 NLAGN are part of our Complete Sample.

The NLAGN optical counterparts were assigned to the type 1+2 sample, and the BLAGN to the type 3+4 sample. The radio luminosities are log P(W Hz^-1) = 23.19 and log P(W Hz^-1) = 22.52 for NLAGN and log P(W Hz^-1) = 23.84 and log P(W Hz^-1) = 24.54 for BLAGN. These numbers come from the common area between the CFHT-LS survey and the spectroscopic VVDS survey, which is approximately $28 \%$ of our survey. In addition, we corrected for the VVDS survey sampling rate ( $33\%$ ). With the assumption that the contamination estimate obtained in this sub-area is representative of the entire area sampled, in our sample we expect $21 \pm 15$ AGN objects in the power range log P(W Hz^-1) = 23-24.

As an independent way to estimate the contamination, we cross-correlated the positions of SWIRE survey sources (Lonsdale et al. 2003) with our Complete Sample. For the sample containing type 3+4, we have 85 galaxies in common and in a clear relation between redshift and the ratio of flux in the 24 $\mu$ m to radio bands. Only 9 objects are significantly shifted towards lower values of the ratio, indicating the possible presence of an AGN. If the ratio between all galaxies and AGN is representative, we expect a contamination in the sample of $15 \pm 5$ AGN, which is well consistent with the previous result. This approach is impossible for early type galaxies because the AGN and star forming populations are inseparable.

Considering the color distribution of all NLAGN, we find that for type 1 objects the B-I colors are more similar to those of radio emitting objects, while the U-B colors have a flatter distribution, with a small peak at $U-B\sim 0.7$ . Also for type 4 galaxies, colors distributions have a similar behaviour.

3 The redshift distributions

In Figs. 2 and 3 the redshift distribution of the radio galaxies in our Complete Sample (solid lines) is compared with the Control Sample (dashed lines) for all galaxy types and for type 1 and 3+4. Although not used in the following analysis, we also show in the figures objects with redshift higher than 1.1. Note that the Control Sample histograms have been rescaled by the ratio of the number of objects in the two samples. In principle, the two histograms are not expected to be identical because the radio sample have limits both in optical magnitude and radio flux, while the Control Sample has only the first limit. The most important peak in both the Control and Complete Sample is at $z\sim 0.9$ and is due mostly to early type galaxies. This peak is the result of the combination of the presence of a huge large-scale structure at that redshift (see Le Fèvre et al. 2005) and the increasing incompleteness of our Complete Sample beyond z=1.1 (or z=1.0 for type 1 galaxies) due to our absolute magnitude limit. At lower redshifts, the shape of the the histogram of the Control Sample is determined only by the increasing volume sampled.

The other significant bump visible in the Complete Sample is centered on $z \sim 0.3$ and is primarly due to the radio flux limit. Within our limits, the radio sample is complete for radio powers of log P(W Hz^-1) > 22 and z<0.2. At lower redshifts, the distribution is dependen only by the increasing volume, while at higher redshifts the histogram is a combination of the losses due to the radio flux limit and the larger number of optical galaxies. However, after a visual check, no obvious $\alpha -\delta$ segregation of radio galaxies corresponding to this bump is evident. A clump at the same redshift is present in the Control Sample and in this case we detected the presence of a cluster (visible as a two-dimensional galaxy distribution) centered on $\alpha_{2000}=2^{\rm h} 24^{\rm m} 32^{\rm s}$ and $\delta_{2000}=-4^{\rm o} 14\hbox{$^\prime$ }54\hbox{$^{\prime\prime}$ }$ . Two radio sources have redshifts consistent with that of the cluster, one being at its centre.

Another difference between the Control Samples and Complete Samples is an excess of radio galaxies at $z\sim 0.6$ , which is the only one clearly related to a physical structure, because of its narrow redshift width. By plotting the $\alpha -\delta$ distribution of early type radio galaxies (which are expected to better delineate clusters and large scale structure) in the [0.5-0.65] redshift range, it is clear that they are located in the lower left (South-East) quadrant of the field (Fig. 4). By plotting the adaptively smoothed isodensity contours of all galaxies in this bin, we found that the overdensity coincides with two galaxy clumps close to each other ( $\sim$ 4 Mpc). This fact is consistent with the claim of Owen et al. (1999) that cluster merging triggers radio emission (see also Giacintucci et al. 2004). Unfortunately, no velocity dispersion estimate is possible because the two clumps are located just outside the region covered by the spectroscopic survey.

Finally, we note that the effect of cosmic variance on these plots is of the order of $15 \%$ , as estimated with similar samples, the same data (CFHT-LS) and the same classification method by McCracken et al. (2008) and more specifically for the VVDS survey by Vergani et al. (2009). The expected variance in the radio source sample is of the same order because the correlation functions in the Control and Radio samples are similar (see Sect. 3.1).

$\begin{figure} \par\includegraphics[width=9cm]{0567fig2.ps} \end{figure}$	Figure 2: Redshift histogram of the radio galaxies in the Complete Sample (solid line) compared with galaxies in the Control Sample (dashed line). The Control Sample histogram has been rescaled by the ratio of the numbers of objects in the two samples.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{0567fig3a.ps} \includegraphics[width=9cm]{0567fig3b.ps} \end{figure}$	Figure 3: Upper panel: same as Fig. 2 but for type 1 galaxies. Lower panel: same as upper panel but for type 3+4 galaxies.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{0567fig4CMYK.eps} \end{figure}$	Figure 4: Isodensity contours are the adaptive kernel smoothed $\alpha -\delta$ distibution of early type galaxies in the redshift range [0.5-0.65]. Points show the positions of the optical counterparts of the radio sources in the same redshift bin.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{0567fig5a.ps} \includegraphics[width=9cm]{0567fig5b.ps} \end{figure}$

Figure 5:

Upper panel: B-I color distribution of the radio emitting early type galaxies (solid line) compared with the same distribution of the Control Sample (dashed line). The latter has been rescaled to take into account the different number of objects. Lower panel: U-B color distribution of the radio emitting early type galaxies and of the Control Sample. Symbols are the same as in the upper panel.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{0567fig6a.ps} \includegraphics[width=9cm]{0567fig6b.ps} \end{figure}$	Figure 6: Same as Fig. 5 but for type 3+4 objects.
Open with DEXTER

3.1 Correlation function

An unresolved problem about the properties of the radio galaxies is related to their clustering properties. For this reason we computed the angular correlation function of all galaxies and radio-loud objects divided into type 1 and type 3+4 galaxies. We detect no significant difference between the various populations; it is present only a weak signal considering the bright and faint type 1 radio galaxies, the ones fainter than log P(W Hz^-1) < 23.5 being more clustered than the brighter ones.

4 Color distributions

The advantage of using redshifts is that one ia then able to use the rest-frame colors, and avoid all ambiguities caused by type dependent K-corrections when adopting observed colors. Moreover, in order to disentangle real effects due to the presence of the radio source from the evolution of the optical host galaxy, it is necessary to make a relative comparison between radio galaxies of a given type with their ``parent'' population (in our case the Control Sample).

The rest-frame B-I color distribution of early type galaxies (type 1) that exhibit radio emission is significantly different from that of the parent sample of early type galaxies (the K-S probability of its having been extracted from the same population being $\sim$ 10^-7), the first showing an evident peak at $B-I \sim 1.4$ (see Fig. 5 upper panel), and the second having broader distibution, with approximately the same mode.

The color distribution difference between radio emitting and parent sample early type galaxies is present only at higher redshifts (0.5<z<1.0), while the distributions are statistically indistinguishable for z<0.5. The colors of early type powerful radio galaxies (log P(W Hz^-1) > 23.5) do not differ from those of the Control Sample, while a significant difference (K-S probability of $\sim$ 10^-11) is evident between the color distribution of faint sources (with log P(W Hz^-1) < 23.5) and that of all early type galaxies. In all of these cases the difference is due to a more peaked and narrower distribution of radio sources than for the general population of early type galaxies. The redshift and luminosity effects are related to each other in the sense that the higher redshift bin is populated mainly by the most powerful radio galaxies, while at lower redshifts the dominant population is that of the weakest radio galaxies.

Although marginally significant, the U-B color distributions do differ (Fig. 5 lower panel), with the significance of the difference between the radio faint or bright galaxies with the Control Sample is $98 \%$ and $95\%$ , respectively.

Considering the relative color distributions, powerful radio sources tend to be bluer in B-I and redder in U-B than faint radio sources. This appears to be caused to a relatively lower B band flux for radio faint objects.

The difference between the B-I colors of the radio-loud and Control Sample is far more evident for type 3+4 objects, with a strong segregation of radio sources toward red colors in relation to the Control Sample (Fig. 6 upper panel): this difference is present, although with far less significance, also in the U-B colors (KS probability of 0.01). In this case, the variable causing this difference appears to be the redshift, because galaxies with redshifts lower than 0.5 differs less significantly (KS probability of 0.01) than those of higher redshift (KS probability $\sim$ 10^-12) from their Control Samples. This is due to the fact that at higher redshift the Control Sample contains more blue galaxies in the B-I colors than the Complete Sample. The converse behaviour is found for the U-B color, for which no difference between radio-loud and parent sample is found at higher redshifts, while a difference with a K-S probability of $\sim$ 0.0007 is present at lower redshifts.

An interesting question is whether the color difference of type 3+4 radio-loud galaxies is due to some interaction between radio emission and optical spectrum or simply because redder galaxies tend to be more luminous at optical wavelengths (due to the well known color-magnitude relation for galaxies) and, given a radio-optical ratio value, also in the radio wavelengths. To investigate this point, we taken the Control Sample of type 3+4 galaxies (10 466 objects) and randomly assigned to each galaxy a radio-optical ratio extracted from the observed distribution (see Sect. 6). With this value and given the optical luminosity of the chosen galaxy, we computed its radio power. We then removed all objects with simulated flux below the limit of the VVDS-VLA radio survey and verified that the power distribution was similar to that observed. The resulting number of expected radio sources was 140 compared with the observed 143. We note that in this procedure we assumed the null hypothesis that the radio power is independent from the galaxy color but depends only on the optical luminosity. As a result, the fraction of type 3+4 mock galaxies with B-I<0.5 is $\sim$ $26 \%$ , significantly higher than the observed $\sim$ $8\%$ . This implies that, at a given optical luminosity, only the redder late type galaxies tend to have higher radio power, possibly indicating a larger amount of dust. In other words, higher star formation rates (which ensures thst a late type galaxy is detectable at radio wavelengths) appear to occur in objects richer in dust (which causes galaxies redder in optical colors).

5 The radio luminosity function

Luminosity functions are a powerful tool for investigating the evolution of astronomical objects. However, in the case of radio sources it is more correct to refer to a bivariate luminosity function, i.e. the composite distribution of optical and radio luminosities. Therefore, one has to face the possible physical evolution of the sources and biases induced by the flux limits in the two bands. This latter problem is particularly severe in the optical bands and at high redshift. As shown by Ilbert et al. (2004), in a magnitude limited sample a pure K-correction effect can induce a variation of the population mix of red and blue galaxies, even in the absence of evolution. Moreover, at different redshifts any single photometric band records different regions of the galaxy spectra making the interpretation of the results more difficult.

To overcome these difficulties, we choose to limit our optical sample to a B rest frame luminosity, i.e a quantity independent from redshift. The M_B=-20 limit enables a galaxy to be observed over the entire redshift range eliminating the optical constraint in the estimation of the observable maximum volume. The luminosity function was estimated with a standard $1/V_{\rm max}$ method (Schmidt 1968) in the redshift range [0-1.1] ([0-1.0] for early type galaxies). The radio K-correction was estimated by assuming that the radio spectrum is a power law function (defined by $S \propto \nu^{\alpha}$ ) with a slope $\alpha=-0.7$ . As a check, we recomputed the luminosity functions with the observed 610 MHz-1.4 GHz indexes (for 310 objects within our limits) presented by Bondi et al. (2007) and the results remain unchanged. We present the results without considering the completeness correction determined in Table 3 of Bondi et al. (2003), which corrects statistically for radio sources lost at low fluxes. However, we also repeated the analysis by weighting the $1/V_{\rm max}$ of each radio galaxy by the corresponding flux-dependent correction factor: the resulting corrections had the effect of increasing on average the luminosity functions by $\sim$ $10 \%$ for log P(W Hz^-1) < 23 in each redshift bin. For higher powers the corrections were larger (between 20 and $60 \%$ ) but are in the same directions for all redshift bins and therefore our conclusions are not changing.

In Fig. 7 the radio luminosity functions of the Complete Sample (upper left panel), of early type (upper right panel ) and late type (lower right panel) galaxies are compared with the corresponding low redshift results from (Best et al. 2005, dashed lines). In particular, in the early type panel the red curve correponds to type 1 galaxies, while the green curve represents the combined type 1+2 sample; in the late type panel, the blue curve represents the combined type 3+4 sample.

The Complete Sample and the early type luminosity functions are in reasonable agreement with the Best et al. (2005) estimate, considering that their optical classification is differs slightly, i.e. based on lines present in the galaxy spectra. The small systematicdifference between our type 1 luminosity function and the corresponding Best et al. (2005) curve could be due to differentes in the limiting optical magnitude, since the SDSS was sample limited to M_B<-19.

To determine the effect of different optical luminosity limits, we derived luminosity functions for the Complete Sample using two different absolute magnitude limits, M_B>-19 and M_B>-21. In this test, we restricted the redshift range to z<0.7 to maintain the full visibility of the optical galaxies. We found that the two luminosity functions were almost identical for log P(W Hz^-1) > 22.7, with the optically bright radio luminosity function loosing $\sim$ $20 \%$ of objects in the range of log P(W Hz^-1) [22-22.7]. Therefore, we can conclude that all differences between our estimates and those of Best et al. (2005) are due to the redshift evolution of radio sources.

The type 3+4 galaxies luminosity function is flatter than the corresponding luminosity function of star forming galaxies frm Best et al. (2005), and this remains true also when considering only the most extreme population (type 4 galaxies).

Assuming a power law shape for the radio luminosity functions, we measured a slope of -1.78^+0.07_-0.07for type 1+2 galaxies and -1.84^+0.12_-0.11 for type 3+4 objects.

The lower left panel of the Fig. 7, we show the comparison between the optical luminosity function of radio emitting galaxies and the corresponding luminosity function of all galaxies in the same redshift bin (obtained following Zucca et al. 2006). Black curves correspond to all galaxies, red curves to type 1 objects, and blue to type 3+4 galaxies. Connected points are the $1/V_{\rm max}$ estimates for the radio samples, while solid curves are Schechter luminosity functions for optical galaxies, obtained with the standard parametric STY method for estimating optical luminosity functions (Sandage Tammann & Yahil 1979). For clarity, the curves for various samples have been shifted vertically, by a value of +2 for type 1 and -1 for type 3+4.

Working with luminosity functions means that the ratio between the two curves for a given type in this panel is directly related to the probability of a galaxy to be radio emitter. For luminous galaxies (M_B<-22.5), the probability is higher than for fainter ones and this apperas to be independent of galaxy type. The probability for faint (M_B>-21) objects is $\sim$ $7\times 10^{-2}$ and $1.7\times 10^{-2}$ for type 3+4 and type 1, respectively, and increases by more than a factor of 3-4 for brighter galaxies. Note the flattening of the radio luminosity functions at low powers: this effect is outlined by Cara & Lister (2008) in estimating the luminosity function with the $1/V_{\rm max}$ in the presence of evolving parent populations.

$\begin{figure} \par\includegraphics[width=17cm]{0567fig7.ps} \end{figure}$

Figure 7:

The radio luminosity functions of the Complete Sample for different galaxy types (points connected by solid lines) compared with NVSS/FIRST/SDSS survey results (Best et al. 2005), represented by a dashed line. Upper left panel: all galaxies. Upper right panel: early type galaxies; in red the type 1 sample and in green the type 1+2 sample. Lower right panel: late type galaxies; in blue: type 3+4 sample. Lower left panel: optical luminosity function of radio emitting galaxies (connected points) compared with the luminosity function of the optical galaxies in the Control Sample in the same redshift bin (solid curves). Black: all galaxies; red: type 1 galaxies; blue: type 3+4 galaxies. The curves of the various samples have been vertically shifted for clarity (+2 for early type and -1 for type 1+2).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=17cm]{0567fig8.ps} \end{figure}$

Figure 8:

Upper left panel: radio luminosity function of all radio emitting galaxies with redshift below 0.5 (red curve) and in the range [0.5-1.1] (black curve). Upper right panel: the same but for type 1+2 sample and in the redshift intervals [0-0.7] and [0.7-1.0]. Blue dashed line is the de-evolved'' luminosity functions (see text). Lower right panel: the same but for type 3+4 sample and in the redshift intervals [0-0.5] and [0.5-1.0]. Blue dashed line is the de-evolved'' luminosity functions (see text). Lower left panel: optical luminosity functions for the Control Sample divided into the same types and in the same redshift intervals as previous panels. Dashed lines correspond to the high redshifts bins, while solid lines are the lower redshift samples. Color codes are the following: black for the Complete Sample, green for type 1+2, and blue for type 3+4 samples. For clarity, the curves of the various samples have been shifted along the magnitude axis (M_B+1 for type 3+4 and M_B-2 for type 1+2 samples).

Open with DEXTER

In Fig. 8, we show the evolution of the luminosity function as a function of redshift. In the upper left panel, the black curve represents radio galaxies of our Complete Sample in the [0.5-1.1] redshift interval, while the red one corresponds to the [0-0.5] bin. A significant evolution is evident It is evident a significant evolution in the common range of radio luminosities, reaching more than a factor of 10 in the range log P(W Hz^-1) [24-25]. In the upper right and lower right panels, the same is reported for type 1+2 and type 3+4 samples, respectively. Given the different K-correction effect on absolute magnitudes, we recall that the type 1+2 sample is limited to redshift <1.0. The limit between high and low redshift range is set to 0.7 for type 1+2 and to 0.5 for type 3+4 sample, to ensure reasonable numbers of galaxies per bin (see Table 1). These different limits have the advantage of showing the maximum difference between samples. In order to increase the statistics, we show the type 1+2 sample instead of only type 1 galaxies. By considering the most extreme early type objects, the results do not change but the significance decreases. The evolution of early type galaxies is mild, althought present, and corresponds to a density increase of a factor of $\sim$ 5 in the log P(W Hz^-1) range [23.5-24], while the evolution of type 3+4 sources is stronger. This strong evolution is consistent with that of Afonso et al. (2005), found for z<0.5, and Smolcic et al. (2008) for the deeper VLA-COSMOS sample. Assuming luminosity and density evolution of the form $(1+z)^{\beta}$ and (1+z)^k respectively, we found that the best fit to data were $\beta=2.76$ and k=0.04 for type 1+2 and $\beta=2.63$ and k=0.43 for type 3+4 objects. These values are consistent with those in literature (Hopkins 2004; Haarsma et al. 2000; Brown et al. 2001). Although he errors are quite large and the $\beta$ and k parameters are strongly correlated each other our aim is only to show that the early type galaxies undergo luminosity evolution and small amount of density evolution, while late type galaxies exhibit both types of evolution. These results, obtained using a sample with a wide redshift range and with high statistics, are still consistent with the very early estimates of Colla et al. (1975) and Auriemma et al. (1977).

The measured evolution could have two different origins: a) the evolution of the corresponding optical luminosity functions, i.e. one has more objects and/or more optically luminous ones, which would translate into more luminous radio sources in the case of a constant radio-optical ratio; b) the evolution with redshift of the radio optical ratios; or a combination of both a) and b).

In order to give an idea of the behaviour of the optical luminosity functions, which enter in point a), we show in Fig. 8 (lower left panel) the STY estimates (computed following Zucca et al. 2006), for all galaxies (black), type 1+2 (green) and type 3+4 (blue) samples in the same redshift bins used for the radio samples. The curves have been shifted for clarity in the magnitude axis by +1 for type 1+2 and by -2 for the type 3+4 class.

The main difference evident in this panel is a brightening by one magnitude and a small steepening of the slope from low to high redshifts for type 3+4 objects. For type 1+2 objects, the main difference is that at high redshift the galaxies are 0.2 mag brighter (from the best fit of M^* in the Schechter function) and $\sim$ $30 \%$ less numerous than today. These results are consistent with those published for the VVDS survey (see Zucca et al. 2006, Table 3).

In the next section, we estimate the second important parameter entering in studying the radio luminosity function evolution, i.e. the radio-optical ratio (which regards point b).

We ``de-evolved'' the high redshift radio luminosity functions taking into account our conclusion regarding the optical luminosity function and the radio-optical ratio for the two classes. This exercise aims to verify whether the detected evolution of the bivariate radio-optical luminosity function is the mirror of the evolution of both the optical luminosity function and the radio-optical ratio.

To ``de-evolve'' the bivariate luminosity function of type 3+4 sample, we cut the higher redshift bin at M_B=-21, assuming an average one-magnitude evolution of the corresponding optical function (limited at M_B<-20 at z=0) and no evolution in the radio-optical ratio. The luminosity function cut eliminates all optical galaxies entered in the radio sample at high redshifts, which are not bright enough at lower redshift, and therefore responsible of the radio density evolution.

For type 1+2 galaxies, we corrected for density and luminosity evolution detected for the optical luminosity function, and a variation of $\sim$ 1.4 in the radio-optical ratio (see Sect. 6).

The resulting ``de-evolved'' luminosity functions are represented by blue points in the right panels of Fig. 8. The remaining discrepancy between these functions and the low redshift luminosity functions is likely due to contamination of BLAGN and NLAGN (see Sect. 2.1).

Therefore, we estimated whether the difference between the ``de-evolved'' high redshift and the low redshift radio luminosity function of type 3+4 objects is consistent with the expected AGN contamination, assuming that all AGN are in the high redshift bin. The number excess of the ``de-evolved'' luminosity function with respect to the low redshift one is 12, which is consistent again with the expected contamination of $15 \pm 5$ (see Sect. 2.1).

6 The radio-optical ratio

In the previous section we evaluated the radio luminosity distribution for a sample with an optical absolute magnitude limit. A related way of showing the relationship between the radio and optical emission is by means of the radio-optical ratio. Classically, it has benn estimated by using the quantity $S_{({\rm mJy})} \times 10^{(m-12.5)/2.5}$ , where S is the radio flux and m is the apparent magnitude of a radio galaxy. In our case, this formula is unsatisfactory because it does not take account of the shift between the observed and the rest frame fluxes, which is important in our sample because of its wide range in redshift. For this reason we compute the ratio between the radio luminosity (L_R) and the optical B band luminosity given by

$\begin{displaymath}L_{R}/L_B = L_R /\left[5.08\times 10^{0.4(5.48-M_{B})} \times 10^{29}\right]\end{displaymath}$

which represents a rest-frame radio-optical ratio with both L_R and L_B in $\rm erg~ s^{-1}$ . However, this is insufficient for estimating the correct radio-optical ratio distribution. In fact, the cut in radio power as a function of redshift imposed by the flux limit of the survey introduces a Malmquist bias in the ratio distribution, a problem that is not present for the optical data. For this reason, a given radio galaxy with an optical luminosity L_B ' and radio luminosity L_R' is visible to its maximum redshift $z_{\rm max}'$ determined by its radio luminosity and the limiting flux of the survey: the corresponding radio-optical ratio is therefore observable only within the corresponding $V_{\rm max}'$ . If one wants to compare the frequency of different radio-optical ratios within a fixed volume V, the radio-optical ratio of each single radio galaxy must to be weighted by the factor $V / V_{\rm max}$ . Comparing frequencies requires that the histograms must be divided by the expected $\sum V / V_{\rm max}$ and not simply by the number of radio sources.

$\begin{figure} \par\includegraphics[width=9cm]{0567fig9.ps} \end{figure}$	Figure 9: Frequency of the radio-optical Ratio in our sample. Solid line is the Complete Sample, dashed line corresponds to type 1+2 galaxies and dotted line to type 3+4 galaxies.
Open with DEXTER

The radio-optical distributions derived in this way for the Complete Sample and type 1+2 and type 3+4 samples are shown in Fig. 9. The distributions are broadened significantly around the mean. For late type galaxies, this is probably due to different dust contents (seen as distribution of blue luminosity) corresponding to a given radio power, which is directly related to the star formation rate. For early type objects, this is a measure of the AGN power variance, presumably related to the accretion efficiency, at a given optical luminosity.

The radio-optical distribution of early type galaxies is shifted towards higher values with respect to that of late type objects. To study the evolution in the radio-optical ratio for the same redshift bins of the luminosity function, it is necessary to consider only radio luminosity ranges always observable in the considered redshift range. For this reason, we cut the type 1+2 sample at log P(W Hz^-1) > 23.1 and the type 3+4 at log P(W Hz^-1)> 22.8, because the two classes have different high redshift limits. Although the number statistics are significantly reduced by these cuts, it is possible to say that no significant evolution is present for type 3+4 objects. This result is not surprising because if the shape of the initial mass function remains constant with redshift, the number of resulting radio emitting supernova remnants depends only on the total number of stars formed. However, we detected a slight dependence of the radio-optical ratio on optical magnitude, the radio-optical distribution presenting a tail toward higher ratios for galaxies with M_B<-21.5 (Fig. 10, lower panel). We checked whether the increasing in the radio-optical ratio for bright galaxies is due to the presence of an AGN, using the upper panel of Fig. 11 (see Sect. 7). The star formation values for bright galaxies are consistent with the log SFR(radio)-log SFR(optical) relation.

For type 1+2 objects (Fig. 10, upper panel), the situation appears to be more complicated. It seems that there is a shift of a factor $\sim$ 1.4 between the low redshift and high redshift bins. This would imply that the efficiency in feeding the central black hole was slightly higher in the past. We used the reported factor of 1.4 in deriving the ``de-evolved'' luminosity function described in Sect. 5.

$\begin{figure} \par\includegraphics[width=9cm]{0567fig10a.ps}\par\includegraphics[width=9cm]{0567fig10b.ps} \end{figure}$

Figure 10:

Upper panel: frequency of radio-optical ratio as a function of redshift for type 1+2 galaxies. Solid line represents low redshift (z<0.7) galaxies, while dasehd line refers to high redshift galaxies. To be comparable, the samples have been limited at log P(W Hz^-1) > 23.1 Lower panel: the radio-optical ratio for type 3+4 galaxies is plotted for objects with M_B<-21.5(red dashed line) and M_B>-21.5 (blue solid line).

Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{0567fig11a.ps} \includegraphics[width=9cm]{0567fig11b.ps} \end{figure}$

Figure 11:

Upper panel: star formation rate computed from the optical versus the star formation rate determined from the radio emission. Red and blue points correspond to type 1+2 and 3+4 objects, respectively. The vertical dashed line corresponds to the value of $2~M_{\odot}~\rm yr^{-1}$ , while the solid line corresponds to log SFR(optical) = log SFR(radio) and is plotted for reference. Lower panel: stellar masses versus star formation rate derived from the radio emission for type 3+4 galaxies; squares represent the low redshift (z<0.5) objects.

Open with DEXTER

7 Star formation rate and stellar mass

Star formation rates (SFR) and stellar masses for galaxies were computed from the photometric quantities, following a method described in detail in Pozzetti et al. (2007). In this method by matching the data were matched to a set of synthetic templates computed with various star formation histories and dust absorption. The star formation rates and stellar masses were calculated using the Chabrier (2003) initial mass function, while the equations used in the literature to compute SFR from the radio power use the Salpeter (1955) initial mass function. This implies that the SFR vlues derived from the radio and optical band data may therefore be slightly different. For consistency, we converted our quantities by applying the median difference of log (SFR $_{\rm Salpeter}$ ) - log (SFR $_{\rm Chabrier}$ ) $\sim$ 0.186. For onsistency with other optical papers, when comparing the SFR and stellar mass distributions of radio-loud galaxies with those of the Control Sample we used the original Chabrier (2003) initial mass function estimates. In the upper panel of Fig. 11 we show the star formation rate computed for the Complete Sample following this procedure based on the optical spectral distribution and compare this with the star formation rate estimated with the formula of Haarsma et al. (2000) ( ${\it SFR}({\rm radio})=L_{1.4 ~\rm GHz} / 8.36 \times 10^{20}~ M_{\odot}~\rm yr^{-1}$ ), which uses only radio powers at 1.4 GHz (see Condon 1992). In the literature, there are other formulae to estimate the star formation rate with different assumptions, as for example that of Bell (2003) and Cram et al. (1998), which give rates a factor 2.16 and 4.35 lower than that of Haarsma et al. (2000), respectively.

The majority of early type galaxies ( $\sim$ $70\%$ ) are localized into a region with SFR(optical) < $2~M_{\odot}~\rm yr^{-1}$ and this fraction increases to $\sim$ $82 \%$ when considering only the extreme type 1 objects. On the other hand, almost all ( $\sim$ $86\%$ ) late type galaxies have star formation rates higher than $2~M_{\odot}~\rm yr^{-1}$ . This is unsurprising because both the star formation rate and type classification depend on the difference between red and blue-UV colors (which is mainly controlled by the 4000 $\AA$ break). The early type galaxies with ${\it SFR} >2 ~M_{\odot}~\rm yr^{-1}$ have similar M_B with respect to the low star formation rate counterparts, but a brighter ultraviolet color. This UV excess, which is responsible for the high star formation rate, has little, if any, impact on the classification.

There are some weak trends in the SFR(radio)-SFR(optical) plot for the two galaxy classes, type 1+2 exhibiting an anticorrelation, while type 3+4 appear to be correlated. To evaluate the significance of the correlations, we applied the Spearman rank test finding the values of $\rho_{1+2}=-0.173$ and $\rho_{3+4}=0.474$ with a probability of the null hypothesis (no-correlation) of 0.002 in both cases. However, we assumed that the radio emission for type 1+2 objects is AGN-induced and therefore this relationship should be regarded as radio power versus star formation rate. We note that the type 3+4 objects are not symmetrically distributed about the relation log SFR(radio) = log SFR(optical), only $\sim$ $19 \%$ of the points being below the equality line. This result can be explained by an increasing role of dust with increasing star formation rates. We note that the factor between radio power and star formation rate that maximize the fraction of objects with log SFR(radio) < log SFR(optical) is that of Cram et al. (1998), leading to $34\%$ .

The lower panel of Fig. 11 is analogous to Fig. 3 of Cram et al. (1998). The diagonal lines correspond to the characteristic time scales $\tau= 10^{8}$ , 10⁹ and 10¹⁰ yr defined by Cram et al. as $M_{\odot}/{\it SFR}_{1.4~ \rm GHz}$ . Cram et al. (1998) claimed that there is a tendency for galaxies that have already formed many stars to support a higher current star formation rate; this effect was also present in our sample if we ignored the effect of different redshifts. Dividing the sample in two redshift bins (above and below 0.5), we find that at the same stellar mass the star formation rate as estimated from the radio band is higher at higher redshifts. We checked this result by also considering all radio galaxies with log P(W Hz^-1) > 22.8 to avoid biases due to different power ranges in different redshift ranges: we found the same result i.e. that there is no correlation between the star formation rate and stellar mass, but the mean value of the star formation rate distribution was higher in the past. This means that the specific star formation rate decreases with both redshift and stellar mass (see Vergani et al. 2009).

As for the radio-optical ratio, in Figs. 12 and 13 we plot the stellar masses and the star formation rate distribution weighted by $V_{\rm max}$ : after correcting stellar masses with the maximum volumes is equal to estimate the mass function. Our mass functions are not fitted by a Schechter function because the effect of increasing mass incompleteness with increasing redshift is important for our wide redshift ranges. However, we are interested in the comparison between the radio and Control Sample and we assumed that the mass incompleteness is not a function of the radio properties and the same argument holds also for the star formation rate.

As found for the optical luminosity function of the radio emitting galaxies also for the stellar masses of type 1+2 objects the fraction of radio-loud objects increases with mass and almost all galaxies with M> 10¹¹ $M_\odot$ are radio-loud (upper panel of Fig. 12).

In the lower panel of Fig. 12 we present the stellar mass functions in the two redshift bins used to estimatet he luminosity functions. It is clear that the number density of radio sources does not vary with cosmic time, although the overall number of massive galaxies increases (see Pozzetti et al. 2007). This probably implies that the AGN is already active at high redshift and no new activity started in between. Concerning the star formation rate, the distributions of radio-loud and radio-quiet type 1+2 objects are similar for ${\it SFR} >1~ M_\odot$ yr^-1. The two curves are only shifted by a factor less than 2.

The distributions for late type galaxies differs significantly, such that the SFR of radio emitting objects is always lower than that of the Control Sample, although the differences decreases with increasing star formation. This is true when using star formation rates estimated in the optical bands. When we use the star formation rates based on radio power, we obtain the blue line of Fig. 13, which is more similar to the distribution of star formation rates of the Control Sample. Note that the behaviour of late type galaxies in Fig. 13 is similar to the relations found by (Seymour et al. 2008, see their Fig. 4).

$\begin{figure} \par\includegraphics[width=8.7cm]{0567fig12a.ps} \includegraphics[width=8.7cm]{0567fig12b.ps} \end{figure}$	Figure 12: Upper panel: stellar mass functions of the type 1+2 radio sample (black solid line) and the type 1+2 control sample (red dashed curve). Lower panel: in red the low redshift ([0-0.7]) subsample for type 1+2 galaxies and in black the high redshift sample ([0.7-1.0]). Dashed curves correspond to the control samples, solid curves to radio-loud objects.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm]{0567fig13a.ps}\par\includegraphics[width=8.8cm]{0567fig13b.ps} \end{figure}$	Figure 13: Upper panel: stellar mass functions of the type 3+4 radio Sample (black solid line) and the type 3+4 Control Sample (red dashed line). Lower panel: star formation rates distribution of the radio rample (red solid line) and the Control Sample (black dashed line) for type 3+4 galaxies. The blue line corresponds to star formation rate computed from the radio emission.
Open with DEXTER

Table 2: Parameters of the optical luminosity function and value of the star formation rate. The symbol ^* means that errors are underestimated.

8 Star formation density evolution

By assuming that radio emission from late type galaxies is entirely due to star formation, the estimation of the evolution of the star formation density follows in a natural way. The most direct and used method is the determination of the radio luminosity function and its integral in different redshift bins. The integral of the radio luminosity function is directly related to the actual star formation rate. The drawbacks of this method are essentially the poor statistics (few hundred of radio objects at most are observed over the entire redshift range) and the fact that at different redshifts the sampled galaxies are different, being optically more luminous at higher redshift.

Another way of approaching the problem is to consider the optical sample as a tracer of radio emission. In this case, the star formation density could be written as

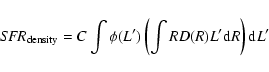
$\begin{displaymath}{\it SFR}_{\rm density} = C \int \phi(L') \left( \int R D(R) L' {\rm d}R \right) {\rm d}L' \end{displaymath}$

where R and D(R) are the radio-optical ratio and its probability distribution (derived as radio-optical distribution in Sect. 6), respectively, L is the blue absolute luminosity (see Sect. 2), $\phi(L)$ is the optical luminosity function and C is the factor converting the radio luminosity density to star formation density (assumed to be that of Haarsma et al. 2000, see Sect. 7).

We note that all quantities in this equation were estimated above. In particular, we take into account the difference between the optical luminosity function of the Control Sample and that of radio emitting galaxies, and the dependence of the radio-optical ratio on optical magnitude.

We refitted the optical luminosity function in the B-band from the same sample and using the method of Zucca et al. (2006) but considering together type 3 and type 4 galaxies. For $\phi(L)$ , we used the fitted Schechter function, which depends on three parameters ( $\alpha$ , M^*, and $\phi^*$ ). Errors are estimated by considering the variance in the fit of the optical luminosity function and considering the poissonian error in the radio-optical distibution function. We computed various Schechter functions at the border of the one sigma error ellipses, and considered the maximum and minimum functions as part of the error induced by the optical luminosity function. Similarly, we considered as upper and lower limits for the radio-optical distribution function the one sigma fluctuations in the histogram of Fig. 9 and again assumed the maximum and minimum of the computed star formation density as errors induced by the radio-optical distribution. Finally, we added in quadrature these values to the previous ones.

For the highset two redshift bins, for which the slope $\alpha$ of the optical luminosity function was not constrained, we fixed the value of the slope to $\alpha=-1.33$ , which is the fitted value of the two bins considered together. Therefore, for the highest two bins the errors given by our procedure are underestimated. The values are reported in Table 2. In Fig. 14, the estimated star formation density is compared with values found in the literature both from radio and other bands. The radio data was converted to the formula of Haarsma et al. (2000).

There is an overall consistency between all the estimators, even if our star formation density in the lowest redshift bin is higher than the other estimates. However, considering that the true error bars could become larger by taking account of sources of statistical variation other than error in the optical luminosity function fit alone, our point at z=0.1 could be regarded as still consistent with other estimators. Moreover, also the first bin of Smolcic et al. (2008), whose data in term of limiting radio flux are similar to ours, is high. By comparing our values with the VVDS dust uncorrected values found by Tresse et al. (2007) using ultraviolet data, we find that at all redshifts there is an approximately constant shift of $\Delta$ log SFR $_{\rm density} = 0.73\pm 0.02$ . There is also a weak indication of a $\sim$ $10 \%$ increase in this correction with redshift. We note that the value is similar to the correction of $\sim$ 0.74by (Hopkins et al. 2001, see Eq. (7)) required for the FUV $1500 ~ \AA$ (for which the Tresse et al. 2007, SFR densities are computed) and a star formation rate of log ${\it SFR}\sim 1$ .

Our star formation density is fitted by an evolution of (1+z)^2.15, consistent with the ultraviolet light density evolution of Tresse et al. (2007).

The main conclusion is that the optical light can be used as tracer of radio emission at high redshift, provided that no significant variation of the radio-optical ratio is present. We note that we checked this point because our radio sample cover, even if with small statistics, a large fraction of the range over which the star formation history was estimated.

$\begin{figure} \par\includegraphics[width=8.5cm]{0567fig14.ps} \end{figure}$

Figure 14:

Star formation rate density as a function of the reddshift. The red points are our estimates, the black points those of Haarsma et al. (2000) as corrected by Hopkins (2004), the green solid line is the fit of Hopkins (2004), the black dot-dashed line is from Cram et al. (1998). The blue squares are the points of Smolcic et al. (2008) and crosses are the estimates of Seymour et al. (2008). Large black squares with error bars correspond to the VVDS dust uncorrected values, while red and blue dashed lines correspond to the star formation rate density estimated from near-IR and H $\alpha$ data as reported by Tresse et al. (2007).

Open with DEXTER

9 Conclusions

In this paper we analyzed the rest frame properties of radio-loud galaxies in the VVDS-VLA Deep Field survey. To avoid all difficulties intrinsic to samples containing both optical and radio limits, we have chosen to a) work using rest-frame quantities; b) limit the sample to an absolute magnitude of M_B<-20and c) consider only objects with z<1.1 ( $\rm or<1.0$ in the case of early type galaxies). The two last points correspond to having an optical volume-limited sample, i.e. no loss of optical galaxies with redshift. Therefore, the only limit that remains is the radio flux limit ( $\sim$ $80 ~\rm\mu Jy$ ). In this way, we can control the optical properties of radio galaxies, although paying the price of smaller statistics and losoing all optically faint objects.

Following Zucca et al. (2006), we divided the galaxies into four spectrophotometric classes corresponding to early type (types 1 and 2) and late type (types 3 and 4) galaxies. Furthermore, we assumed that early type galaxies have AGN-induced radio emission and late type galaxies have star-formation induced radio emission. The aim of this work was to investigate the possible evolution of radio galaxies knowing a priori the optical behaviour of all galaxies with our cuts in the entire CFHT-LS/VVDS survey (taken as Control Sample).

From the redshift distribution of radio sources, we detected an overdensity corresponding to two interacting clusters at redshift $z\sim 0.6$ , while the other redshift peaks appear to be associated with a large-scale structure (a superclusters). It has been impossible to investigate this point further because of the relatively small number of spectroscopic redshifts and the smoothing effect due to the use of photometric redshifts. The angular two points correlation function of radio-loud galaxies does not differs significantly frm that of optical galaxies, suggesting that these objects are not living in the most extreme environments. By estimating the distribution of blue luminosities, stellar masses, and star formation rates, the probability of a galaxy to be a radio emitter increases significantly at high values of all of these parameters.

Early type (type 1) radio-loud galaxies differ from their radio-quiet counterparts in terms of the colors distributions. In particular, radio-faint galaxies exhibit a peak in B-I color at $B-I\sim 1.45$ , while radio bright galaxies do no differ from the Control Sample. This class of radio sources shows evolution in the bivariate radio-optical luminosity function, mainly due to luminosity evolution. By studying the radio-optical ratio distribution, for redshifts above 0.7 at fixed blue luminosity, the galaxies resulted more radio luminous. This effect is somehow compensated in the bivariate luminosity function by the simultaneous decrease in the type 1+2 optical luminosity function. This luminosity evolution is probably due to a variation in efficiency in feeding the central black hole and not to an increased contribution by star formation in the radio band. This is also evident in Fig. 11 (upper panel) divided into redshift bins: the fraction of galaxies with star formation rates (as computed in the optical band) lower than $2~M_{\odot}~\rm yr^{-1}$ is the same at high and low redshifts. This means that, unless dust extinction and star formation exactly compensate each other, no significantly increased star formation for this galaxy type is present.

Type 3 and type 4 radio-loud objects are significantly redder than the control population. These galaxies exhibit a significant evolution in the bivariate luminosity function both in luminosity and density: this behaviour can be explained if we take into account the one-magnitude evolution of this class of objects detected in the optical, without invoking large variations in the radio emission properties (such as the radio-optical ratio). In fact, the only dependence of the radio-optical ratio is, in this case, on the optical luminosity. Using the estimated radio-optical ratio, we conclude that the difference in colors between radio-loud and radio-quiet objects is physical, and not induced by statistical effects. We aspeculated that radio-loud star forming galaxies contain on average more dust.

The star formation rate computed from both radio power and optical colors shows a significant correlation similar to the relation betwen radio and UV-based SFR shown in Cram et al. (1998). By plotting the star formation rate computed from radio luminosities and the stellar mass, we show that, at higher redshift, the population has a higher instantaneous star formation rate at fixed stellar mass. In other words, the specific star formation rate is decreasing with redshift.

With the knowledge of the parameters for the radio-loud types 3 and 4 galaxies, we show that it is possible to use optical galaxies as tracers of radio emission at various redshifts. This permits us to derive an estimate of the star formation history, which was found to be consistent with results of other bands and methods.

In summary, according to our data, the AGN induced radio emission increases with redshift because the host galaxies increased their radio-optical ratios, with the AGN already in place at high redshifts. On the contrary, the evolution of late type radio sources is a direct consequence of the strong evolution seen the in optical band and is due to the evolution of the star formation rate with redshift.

Acknowledgements

S.B. thanks C. Gruppioni, I. Prandoni, F. Pozzi for useful discussions. This research has been developed within the framework of the VVDS consortium. The authors thank the referee for the careful reading of the manuscript and for the comments, which improved the paper. This work has been partially supported by the CNRS-INSU and its Programme National de Cosmologie (France), by Italian Ministry (MIUR) grants COFIN2000 (MM02037133) and COFIN2003 (num.2003020150), by INAF (contract PRIN-2007/1.06.10.08) and by an ASI (grant ASI/COFIS I/026/07/0). The VLT-VIMOS observations have been carried out on guaranteed time (GTO) allocated by the European Southern Observatory (ESO) to the VIRMOS consortium, under a contractual agreement between the Centre National de la Recherche Scientifique of France, heading a consortium of French and Italian institutes, and ESO, to design, manufacture and test the VIMOS instrument. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.

References

Afonso, J., Georgakakis, A., Almeida, C., et al. 2005, ApJ, 624, 135 [NASA ADS] [CrossRef] (In the text)
Afonso, J., Mobasher, B., Koekemoer A., Norris, R. P., & Cram, L. 2006, AJ, 131, 1230 [NASA ADS]
Auriemma, C., Perola, G. C., Ekers, R., et al. 1977, A&A, 57, 41 [NASA ADS] (In the text)
Barger, A. J., Cowie, L. L., & Wang, W. H. 2007, ApJ, 654, 764 [NASA ADS] [CrossRef]
Bardelli, S., et al. 2009, A&A, in preparation (In the text)
Bell, E. F. 2003, ApJ, 586, 794 [NASA ADS] [CrossRef] (In the text)
Benn, C. R., Rowan-Robinson, M., McMahon, R. G., Broadhurst, T. J., & Lawrence, A. 1993, MNRAS, 263, 98 [NASA ADS]
Best, P. N., Kauffmann, G., Heckman, T. M., & Ivezic, Z. 2005, MNRAS, 362, 9 [NASA ADS] [CrossRef] (In the text)
Bondi, M., Ciliegi, P., Zamorani, G., et al. 2003, A&A, 403, 857 [NASA ADS] [CrossRef] [EDP Sciences]
Bondi, M., Ciliegi, P., Venturi, T., et al. 2007, A&A, 463, 519 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Bongiorno, A., Zamorani, G., Gavignaud, I., et al. 2007, A&A, 472, 443 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Brown, M. J., Webster, R. L., & Boyle, B. J. 2001, AJ, 121, 2381 [NASA ADS] [CrossRef]
Bruzual, G., & Charlot, S. 1993, ApJ, 405, 538 [NASA ADS] [CrossRef] (In the text)
Cara, M., & Lister, M. L. 2008 ApJ, 686, 148 (In the text)
Chabrier, G. 2003, PASP, 115, 763 [CrossRef] (In the text)
Ciliegi, P., Zamorani, G., Bondi, M., et al. 2005, A&A, 441, 879 [NASA ADS] [CrossRef] [EDP Sciences]
Coleman, G. D., Wu, C. C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] (In the text)
Colla, G., Fanti, C., Fanti, R., et al. 1975, A&A, 38, 209 (In the text)
Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] (In the text)
Cram, L., Hopkins, A., Mobasher, B., & Rowan-Robinson, M. 1998, ApJ, 507, 155 [NASA ADS] [CrossRef] (In the text)
Franceschini, A., Danese, L., Toffolatti, L., & de Zotti, G. 1988, MNRAS, 233, 157 [NASA ADS]
Franzetti, P., Scodeggio, M., Garilli, B., et al. 2007, A&A, 465, 711 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gavignaud, I., Bongiorno, A., Paltani, S., et al. 2006, A&A, 457, 79 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Giacintucci, S., Venturi, T., Bardelli, S., Dallacasa, D., & Zucca, E. 2004, A&A, 419, 71 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gruppioni, C., Mignoli, M., & Zamorani, G. 1999, MNRAS, 305, 297 [NASA ADS] [CrossRef] (In the text)
Gruppioni, C., Pozzi, F., Zamorani, G., et al. 2003, MNRAS, 341, L1 [NASA ADS] [CrossRef]
Haarsma, D. B., Partridge, R. B., Windhorst, R. A., & Richards, E. A. 2000, ApJ, 544, 641 [NASA ADS] [CrossRef]
Hammer, F., Crampton, D., Lilly, S. J., Le Fèvre, O., & Kenet, T. 1995, MNRAS, 276, 1085 [NASA ADS]
Hopkins, A. M. 2004, ApJ, 615, 209 [NASA ADS] [CrossRef]
Hopkins, A. M., Connoly, A. J, Haarsma, D. B., & Cram, L. E. 2001, AJ, 122, 288 [NASA ADS] [CrossRef] (In the text)
Ilbert, O., Tresse, L., Arnouts, S., et al. 2004, MNRAS, 351, 541 [NASA ADS] [CrossRef] (In the text)
Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Ilbert, O., Arnout, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Ivison, R. J., Chapman, S. C., Faber, S. M., et al. 2007, ApJ, 660, L77 [NASA ADS] [CrossRef]
Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] (In the text)
Lonsdale, C. J., Smith, H. E., Rowan Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] (In the text)
Magliocchetti, M., Maddox, S. J., Jackson, C. A., et al. 2002, MNRAS, 333, 100 [NASA ADS] [CrossRef] (In the text)
McCracken, H. J., Radovich, M., Bertin, E., et al. 2003, A&A, 410, 17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
McCracken, H. J., Ilbert, O., Mellier, Y., et al. 2008, A&A, 479, 321 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
McCracken, H. J., et al. 2009, A&A, in preparation (In the text)
Owen, F. M., Ledlow, M. J., Keel, W. C., & Morrison, G. E. 1999, AJ, 118, 633 [CrossRef] (In the text)
Paltani, S., et al. 2009, A&A, in preparation (In the text)
Pozzetti, L., Bolzonella, M., Lamairelle, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Prandoni, I., Gregorini, L., Parma, P., et al. 2001, A&A, 369, 787 [NASA ADS] [CrossRef] [EDP Sciences]
Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
Sandage, A., Tammann, G. A., & Yahil, A. 1979, ApJ, 232, 352 [NASA ADS] [CrossRef] (In the text)
Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] (In the text)
Seymour, N., Dwelly, T., Moss, D., et al. 2008, MNRAS, 368, 1695 [NASA ADS]
Smolcic, V., Schinnerer, E., Zamorani, G., et al. 2008, ApJ, in press[arXiv:0808.0493]
Smolcic, V., Schinnerer, E., Scodeggio, M., et al. 2008, ApJS, 177, 14 [NASA ADS] [CrossRef] (In the text)
Tresse, L., Ilbert, O., Zucca, E., et al. 2007, A&A, 472, 403 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Vergani, D., et al. 2009, A&A, in preparation (In the text)
Warren, S. J., Cross, N. J. G., Dye, S., et al. 2007 [arXiv:astro-ph/0703037] (In the text)
Windhorst, R. A., Miley, G. K., Owen, F., et al. 1985, ApJ, 289, 494 [NASA ADS] [CrossRef] (In the text)
Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)

All Tables

Table 1: Numbers of objects in our samples. The low/high redshift bins are [0-0.5]/[0.5-1.1] for all galaxies and type 3+4 galaxy samples and [0-0.7]/[0.7-1.0] for type 1+2 galaxy sample.

Table 2: Parameters of the optical luminosity function and value of the star formation rate. The symbol ^* means that errors are underestimated.

All Figures

$\begin{figure} \par\includegraphics[width=9cm]{0567fig1a.ps} \includegraphics[width=9cm]{0567fig1b.ps} \end{figure}$	Figure 1: Upper panel: shaded histogram: distribution of I magnitude for radio galaxies with M_B<-20 and $z_{\rm phot}<1.1$ (the Complete Sample). Empty histogram: all identified radio galaxies (the Original Sample). Lower panel: dotted histogram corresponds to the radio flux for all radio galaxies (the Original Sample), solid line represents the Complete Sample, dot-dashed line the type 3+4 objects, long dashed line the type 1 objects.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig2.ps} \end{figure}$	Figure 2: Redshift histogram of the radio galaxies in the Complete Sample (solid line) compared with galaxies in the Control Sample (dashed line). The Control Sample histogram has been rescaled by the ratio of the numbers of objects in the two samples.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig3a.ps} \includegraphics[width=9cm]{0567fig3b.ps} \end{figure}$	Figure 3: Upper panel: same as Fig. 2 but for type 1 galaxies. Lower panel: same as upper panel but for type 3+4 galaxies.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig4CMYK.eps} \end{figure}$	Figure 4: Isodensity contours are the adaptive kernel smoothed $\alpha -\delta$ distibution of early type galaxies in the redshift range [0.5-0.65]. Points show the positions of the optical counterparts of the radio sources in the same redshift bin.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig5a.ps} \includegraphics[width=9cm]{0567fig5b.ps} \end{figure}$	Figure 5: Upper panel: B-I color distribution of the radio emitting early type galaxies (solid line) compared with the same distribution of the Control Sample (dashed line). The latter has been rescaled to take into account the different number of objects. Lower panel: U-B color distribution of the radio emitting early type galaxies and of the Control Sample. Symbols are the same as in the upper panel.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig6a.ps} \includegraphics[width=9cm]{0567fig6b.ps} \end{figure}$	Figure 6: Same as Fig. 5 but for type 3+4 objects.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm]{0567fig7.ps} \end{figure}$	Figure 7: The radio luminosity functions of the Complete Sample for different galaxy types (points connected by solid lines) compared with NVSS/FIRST/SDSS survey results (Best et al. 2005), represented by a dashed line. Upper left panel: all galaxies. Upper right panel: early type galaxies; in red the type 1 sample and in green the type 1+2 sample. Lower right panel: late type galaxies; in blue: type 3+4 sample. Lower left panel: optical luminosity function of radio emitting galaxies (connected points) compared with the luminosity function of the optical galaxies in the Control Sample in the same redshift bin (solid curves). Black: all galaxies; red: type 1 galaxies; blue: type 3+4 galaxies. The curves of the various samples have been vertically shifted for clarity (+2 for early type and -1 for type 1+2).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm]{0567fig8.ps} \end{figure}$	Figure 8: Upper left panel: radio luminosity function of all radio emitting galaxies with redshift below 0.5 (red curve) and in the range [0.5-1.1] (black curve). Upper right panel: the same but for type 1+2 sample and in the redshift intervals [0-0.7] and [0.7-1.0]. Blue dashed line is the de-evolved'' luminosity functions (see text). Lower right panel: the same but for type 3+4 sample and in the redshift intervals [0-0.5] and [0.5-1.0]. Blue dashed line is the de-evolved'' luminosity functions (see text). Lower left panel: optical luminosity functions for the Control Sample divided into the same types and in the same redshift intervals as previous panels. Dashed lines correspond to the high redshifts bins, while solid lines are the lower redshift samples. Color codes are the following: black for the Complete Sample, green for type 1+2, and blue for type 3+4 samples. For clarity, the curves of the various samples have been shifted along the magnitude axis (M_B+1 for type 3+4 and M_B-2 for type 1+2 samples).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig9.ps} \end{figure}$	Figure 9: Frequency of the radio-optical Ratio in our sample. Solid line is the Complete Sample, dashed line corresponds to type 1+2 galaxies and dotted line to type 3+4 galaxies.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig10a.ps}\par\includegraphics[width=9cm]{0567fig10b.ps} \end{figure}$	Figure 10: Upper panel: frequency of radio-optical ratio as a function of redshift for type 1+2 galaxies. Solid line represents low redshift (z<0.7) galaxies, while dasehd line refers to high redshift galaxies. To be comparable, the samples have been limited at log P(W Hz^-1) > 23.1 Lower panel: the radio-optical ratio for type 3+4 galaxies is plotted for objects with M_B<-21.5(red dashed line) and M_B>-21.5 (blue solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{0567fig11a.ps} \includegraphics[width=9cm]{0567fig11b.ps} \end{figure}$	Figure 11: Upper panel: star formation rate computed from the optical versus the star formation rate determined from the radio emission. Red and blue points correspond to type 1+2 and 3+4 objects, respectively. The vertical dashed line corresponds to the value of $2~M_{\odot}~\rm yr^{-1}$ , while the solid line corresponds to log SFR(optical) = log SFR(radio) and is plotted for reference. Lower panel: stellar masses versus star formation rate derived from the radio emission for type 3+4 galaxies; squares represent the low redshift (z<0.5) objects.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.7cm]{0567fig12a.ps} \includegraphics[width=8.7cm]{0567fig12b.ps} \end{figure}$	Figure 12: Upper panel: stellar mass functions of the type 1+2 radio sample (black solid line) and the type 1+2 control sample (red dashed curve). Lower panel: in red the low redshift ([0-0.7]) subsample for type 1+2 galaxies and in black the high redshift sample ([0.7-1.0]). Dashed curves correspond to the control samples, solid curves to radio-loud objects.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm]{0567fig13a.ps}\par\includegraphics[width=8.8cm]{0567fig13b.ps} \end{figure}$	Figure 13: Upper panel: stellar mass functions of the type 3+4 radio Sample (black solid line) and the type 3+4 Control Sample (red dashed line). Lower panel: star formation rates distribution of the radio rample (red solid line) and the Control Sample (black dashed line) for type 3+4 galaxies. The blue line corresponds to star formation rate computed from the radio emission.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm]{0567fig14.ps} \end{figure}$	Figure 14: Star formation rate density as a function of the reddshift. The red points are our estimates, the black points those of Haarsma et al. (2000) as corrected by Hopkins (2004), the green solid line is the fit of Hopkins (2004), the black dot-dashed line is from Cram et al. (1998). The blue squares are the points of Smolcic et al. (2008) and crosses are the estimates of Seymour et al. (2008). Large black squares with error bars correspond to the VVDS dust uncorrected values, while red and blue dashed lines correspond to the star formation rate density estimated from near-IR and H $\alpha$ data as reported by Tresse et al. (2007).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.