| Issue |
A&A
Volume 495, Number 1, February III 2009
|
|
|---|---|---|
| Page(s) | 15 - 26 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361:200811043 | |
| Published online | 22 December 2008 | |
Internal dynamics of the galaxy cluster Abell 959
W. Boschin1,2 - R. Barrena3 - M. Girardi2,4
1 - Fundación Galileo Galilei - INAF, Rambla José Ana
Fernández Perez 7, 38712 Breña Baja (La Palma),
Canary Islands, Spain
2 -
Dipartimento di Astronomia of the Università degli
Studi di Trieste, via Tiepolo 11, 34143 Trieste,
Italy
3 -
Instituto de Astrofísica de Canarias,
C/Vía Láctea s/n, 38205 La Laguna (Tenerife),
Canary Islands, Spain
4 -
INAF - Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143
Trieste, Italy
Received 26 September 2008 / Accepted 16 November 2008
Abstract
Context. The connection of cluster mergers with the presence of extended, diffuse radio sources in galaxy clusters is still being debated.
Aims. We aim to obtain new insights into the internal dynamics of Abell 959, showing evidence of a diffuse radio source, analyzing velocities and positions of member galaxies.
Methods. Our analysis is based on redshift data for 107 galaxies in the cluster field acquired at the Telescopio Nazionale Galileo. We also use photometric data from the Sloan Digital Sky Survey (Data Release 6). We combine galaxy velocities and positions to select 81 galaxies recognized as cluster members and determine global dynamical properties. We analyze the cluster searching for substructures by using the weighted gap analysis, the KMM method and the Dressler-Shectman statistics. We also study the 2D galaxy distribution in the field of the cluster. We compare our results with those from X-ray and gravitational lensing analyses.
Results. We estimate a cluster redshift of
![]() .
We detect an NE high velocity group at 5
.
We detect an NE high velocity group at 5
![]() from the cluster center with a relative line-of-sight (LOS) velocity of
from the cluster center with a relative line-of-sight (LOS) velocity of
![]() km s
km s![]() with respect to the main system. We also detect a central, dense structure elongated along the SE-NW direction likely connected with the two dominant galaxies and their surrounding cores. This elongated central structure is probably the trace of an old cluster merger. The LOS velocity dispersion of galaxies is very high. By excluding the NE clump we obtain
with respect to the main system. We also detect a central, dense structure elongated along the SE-NW direction likely connected with the two dominant galaxies and their surrounding cores. This elongated central structure is probably the trace of an old cluster merger. The LOS velocity dispersion of galaxies is very high. By excluding the NE clump we obtain
![]() km s
km s![]() and a virial mass
and a virial mass
![]()
![]() .
Our results suggest that this cluster is forming along two main directions of mass accretion.
.
Our results suggest that this cluster is forming along two main directions of mass accretion.
Conclusions. Abell 959 is confirmed to show the typical characteristics of radio clusters; i.e., it is very massive and shows a young dynamical state. However, deeper radio observations are needed to clarify the nature of the diffuse radio emission in Abell 959 and its connection with the cluster internal dynamics.
Key words: galaxies: clusters: individual: Abell 959 - galaxies: clusters: general - galaxies: distances and redshifts
1 Introduction
In the hierarchical scenario for large-scale structure formation,
clusters of galaxies are known to be unrelaxed structures. Instead, as
the cosmic time flows clusters are interested by perturbing merging
processes that constitute an essential ingredient of their
evolution. Much progress has been made in the past decade in the
observations of the signatures of merging processes (see Feretti
et al. 2002, for a general review). A recent aspect of these
investigations is the possible connection of cluster mergers with the
presence of extended, diffuse radio sources: halos and relics. The
synchrotron radio emission of these sources demonstrates the existence
of large-scale cluster magnetic fields and of widespread relativistic
particles. It has been suggested that cluster mergers provide the
large amount of energy necessary for electron reacceleration up to
relativistic energies and for magnetic field amplification (Feretti
1999; Feretti 2002; Sarazin 2002). However,
the precise radio halos/relics formation scenario is still being
debated since the diffuse radio sources are quite uncommon and only
recently can we study these phenomena on the basis of sufficient
statistics (few dozen clusters up to ![]() ,
e.g., Giovannini
et al. 1999; see also Giovannini & Feretti 2002; Feretti
2005).
,
e.g., Giovannini
et al. 1999; see also Giovannini & Feretti 2002; Feretti
2005).
There is growing evidence of the connection between diffuse radio emission and cluster merging based on X-ray data (e.g., Böhringer & Schuecker 2002; Buote 2002). Studies based on a large number of clusters have found a significant relation between the radio and the X-ray surface brightness (Govoni et al. 2001a,b) and connections between the presence of radio-halos/relics and irregular and bimodal X-ray surface brightness distribution (Schuecker et al. 2001).
Optical data are a powerful way to investigate the presence and the
dynamics of cluster mergers (e.g., Girardi & Biviano 2002),
too. The spatial and kinematical analysis of member galaxies allow us
to detect and measure the amount of substructures and to identify and
analyze possible pre-merging clumps or merger remnants. This optical
information is really complementary to X-ray information since
galaxies and intracluster medium react on different time scales
during a merger (see, e.g., numerical simulations by Roettiger
et al. 1997). In this context we are conducting an intensive
observational and data analysis program to study the internal dynamics
of radio clusters by using member galaxies. Our program concerns both
massive clusters, where diffuse radio emissions are more frequently
found (e.g., Girardi et al. 2008, and refs. therein), and
low-mass galaxy systems (Boschin et al. 2008![]() ).
).
During our observational program we conducted an intensive study of
the cluster Abell 959 (hereafter A959). It is a fairly rich,
X-ray luminous, hot and massive Abell cluster: Abell richness
class = 1 (Abell et al. 1989); ![]() (0.1-2.4 keV) =
(0.1-2.4 keV) =
![]() erg s-1 (Popesso
et al. 2004, but correcting for our
erg s-1 (Popesso
et al. 2004, but correcting for our
![]() ,
see below);
,
see below);
![]() keV (ASCA data, Mushotzky &
Scharf 1997); a projected 2D aperture mass within a radius of
440
keV (ASCA data, Mushotzky &
Scharf 1997); a projected 2D aperture mass within a radius of
440
![]()
![]()
![]() (Dahle et al. 2002, in
their cosmology).
(Dahle et al. 2002, in
their cosmology).
Optically, the cluster center is not dominated by any single galaxy - it is classified as Bautz-Morgan class III (Abell et al. 1989) - but it has a core region consisting of many early-type galaxies of similar brightness (Dahle et al. 2002). The general SE-NW elongation of the A959 cluster galaxy distribution is matched in X-rays (ROSAT/PSPC data; Dahle et al. 2003). Perpendicularly, the NE-SW direction is defined by a clear NE external extension and a likely SW extension in the X-ray emission (Dahle et al. 2003) and by a possible very central bimodal structure (Ota & Mitsuda 2004).
A highly significant mass peak (with some evidence of substructure) is
seen in the weak lensing mass map (Dahle et al. 2002;
2003), and the mass distribution again indicates two
directions for the cluster elongation (SE-NW and NE-SW) roughly
resembling the galaxy light distribution, although the agreement is
not perfect in the central region (see Fig. 1, for a
multiwavelength view of this cluster). Moreover, there is a dark
matter concentration at ![]() 6
6
![]() SW of the cluster center, which
does not correspond to any peak in the luminosity distribution and
is connected by a mass bridge with A959 (WL 1017.3+5931). To date the
nature of this object is unknown and WL 1017.3+5931 remains a good
candidate for an optically ``dark'' subcluster (Dahle et al. 2003).
SW of the cluster center, which
does not correspond to any peak in the luminosity distribution and
is connected by a mass bridge with A959 (WL 1017.3+5931). To date the
nature of this object is unknown and WL 1017.3+5931 remains a good
candidate for an optically ``dark'' subcluster (Dahle et al. 2003).
The presence of a radio extended emission in A959 has been reported by
Cooray et al. (1998). Owen et al. (1999) lists A959
among clusters showing a detectable diffuse radio source with a flux
density of 3 mJy (at 1.4 GHz) and a size of ![]() 3
3![]() (
(![]() 0.8
h70-1 Mpc
0.8
h70-1 Mpc![]() in our cosmology). The measurements of this preliminary study are
rough and more observations of this radio source are needed to clarify
the possible connection with the cluster. However, we note that this
source shows the typical sizes of radio halos and radio relics/gischt
(see Kempner et al. 2004; Ferrari et al. 2008). Moreover, its radio power (
in our cosmology). The measurements of this preliminary study are
rough and more observations of this radio source are needed to clarify
the possible connection with the cluster. However, we note that this
source shows the typical sizes of radio halos and radio relics/gischt
(see Kempner et al. 2004; Ferrari et al. 2008). Moreover, its radio power (![]()
![]() W/Hz) closely matches the relation log P (1.4 GHz) - log
W/Hz) closely matches the relation log P (1.4 GHz) - log ![]() found by Cassano et al. (2006, see their Fig. 3b)
for radio halos.
found by Cassano et al. (2006, see their Fig. 3b)
for radio halos.
![\begin{figure}
\par\includegraphics[width=18cm]{1043f01.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg39.gif) |
Figure 1:
Multiwavelength image of A959 (north at the top and east to
the left). The contour levels (thin levels) of a smoothed archival
ROSAT/PSPC X-ray image are superimposed on the SDSS |
| Open with DEXTER | |
Poor spectroscopical data exist for A959. The value usually quoted in the literature for the cluster redshift is z=0.353, but Irgens et al. (2002) determined z=0.286 using four galaxies. We carried out spectroscopic observations at the Telescopio Nazionale Galileo (TNG) giving new redshift data for 107 galaxies in the field of A959 and finding z=0.288.
This paper is organized as follows. We present our new spectroscopical data and the cluster catalog in Sect. 2. We present our results about the cluster structure in Sect. 3. We briefly discuss our results and give our conclusions in Sect. 4.
Unless otherwise stated, we give errors at the 68% confidence level
(hereafter c.l.). Throughout this paper, we use H0=70 km s-1 Mpc-1 in a flat cosmology with
![]() and
and
![]() .
In the adopted cosmology, 1
.
In the adopted cosmology, 1
![]() corresponds
to
corresponds
to ![]() 260
h70-1 kpc
260
h70-1 kpc ![]() at the cluster redshift.
at the cluster redshift.
![\begin{figure}
\par\includegraphics[width=18cm]{1043f02.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg42.gif) |
Figure 2:
SDSS |
| Open with DEXTER | |
2 New data and galaxy catalog
Multi-object spectroscopic observations of A959 were carried out at
the TNG telescope in December 2006. We used DOLORES/MOS with the LR-B
Grism 1, yielding a dispersion of 187 Å/mm, and the Loral CCD of
![]() pixels (pixel size of 15
pixels (pixel size of 15 ![]() m). This combination of
grating and detector results in a dispersion of 2.8 Å/pix. We
observed four MOS masks for a total of 130 slits. We acquired three
exposures of 1800 s for each mask. Wavelength calibration was
performed using helium-argon lamps. Reduction of spectroscopic data
was carried out with the IRAF
m). This combination of
grating and detector results in a dispersion of 2.8 Å/pix. We
observed four MOS masks for a total of 130 slits. We acquired three
exposures of 1800 s for each mask. Wavelength calibration was
performed using helium-argon lamps. Reduction of spectroscopic data
was carried out with the IRAF![]() package.
package.
Radial velocities were determined using the cross-correlation
technique (Tonry & Davis 1979) implemented in the RVSAO
package (developed at the Smithsonian Astrophysical Observatory
Telescope Data Center). Each spectrum was correlated against six
templates for a variety of galaxy spectral types: E, S0, Sa, Sb, Sc,
Ir (Kennicutt 1992). The template producing the highest value
of ![]() ;
i.e., the parameter given by RVSAO and related to the
signal-to-noise of the correlation peak, was chosen. Moreover, all
spectra and their best correlation functions were examined visually to
verify the redshift determination. The median value of
;
i.e., the parameter given by RVSAO and related to the
signal-to-noise of the correlation peak, was chosen. Moreover, all
spectra and their best correlation functions were examined visually to
verify the redshift determination. The median value of ![]() of our
successfully measured galaxy redshifts is
of our
successfully measured galaxy redshifts is ![]() 7.5. In 4 cases (IDs 76, 79, 84, and 90; see Table 1) we took the EMSAO
redshift as a reliable estimate of the redshift. Our spectroscopic
survey in the field of A959 consists of 119 spectra with a median
nominal error on cz of 56 km s-1. The nominal errors as given by the
cross-correlation are known to be smaller than the true errors (e.g.,
Malumuth et al. 1992; Bardelli et al. 1994; Ellingson
& Yee 1994; Quintana et al. 2000). Double redshift
determinations for the same galaxy allowed us to estimate real
intrinsic errors in data of the same quality taken with the same
instrument (Barrena et al. 2007a,b). Here we
applied a similar correction to our nominal errors; i.e., hereafter we
assume that true errors are larger than nominal cross-correlation
errors by a factor 1.4. Thus the median error on cz is
7.5. In 4 cases (IDs 76, 79, 84, and 90; see Table 1) we took the EMSAO
redshift as a reliable estimate of the redshift. Our spectroscopic
survey in the field of A959 consists of 119 spectra with a median
nominal error on cz of 56 km s-1. The nominal errors as given by the
cross-correlation are known to be smaller than the true errors (e.g.,
Malumuth et al. 1992; Bardelli et al. 1994; Ellingson
& Yee 1994; Quintana et al. 2000). Double redshift
determinations for the same galaxy allowed us to estimate real
intrinsic errors in data of the same quality taken with the same
instrument (Barrena et al. 2007a,b). Here we
applied a similar correction to our nominal errors; i.e., hereafter we
assume that true errors are larger than nominal cross-correlation
errors by a factor 1.4. Thus the median error on cz is ![]() 78 km s-1.
78 km s-1.
We also used public photometric data from the Sloan Digital Sky Survey
(SDSS, Data Release 6). In particular, we used ![]() ,
,
![]() ,
,
![]() magnitudes, already corrected for the Galactic extinction,
and considered galaxies within a radius of 30
magnitudes, already corrected for the Galactic extinction,
and considered galaxies within a radius of 30
![]() from the cluster
center. Our spectroscopic sample is
from the cluster
center. Our spectroscopic sample is ![]() 70% complete down to
70% complete down to
![]() within 4
within 4![]() from the cluster center.
from the cluster center.
Table 1 lists the velocity catalog (see also
Fig. 2): identification number of each galaxy, ID
(Col. 1); right ascension and declination, ![]() and
and ![]() (J2000, Col. 2); SDSS
(J2000, Col. 2); SDSS ![]() magnitudes (Col. 3); heliocentric radial
velocities,
magnitudes (Col. 3); heliocentric radial
velocities,
![]() (Col. 4) with errors,
(Col. 4) with errors,
![]() (Col. 5).
(Col. 5).
Table 1: Velocity catalog of 107 spectroscopically measured galaxies in the field of A959.
3 Analysis and results
3.1 Member selection and global properties
To select cluster members out of 107 galaxies having redshifts, we
follow a two-steps procedure. First, we perform the 1D
adaptive-kernel method (hereafter DEDICA, Pisani 1993, 1996; see also Fadda et al. 1996; Girardi et al. 1996; Girardi & Mezzetti 2001). We search for
significant peaks in the velocity distribution at >99% c.l. This
procedure detects A959 as a peak at
![]() populated by 94
galaxies considered as candidate cluster members (see
Fig. 3). Out of 13 non members, nine and four are
foreground and background galaxies, respectively.
populated by 94
galaxies considered as candidate cluster members (see
Fig. 3). Out of 13 non members, nine and four are
foreground and background galaxies, respectively.
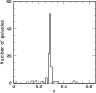 |
Figure 3: Redshift galaxy distribution. The solid line histogram refers to (94) galaxies assigned to the cluster according to the DEDICA reconstruction method. |
| Open with DEXTER | |
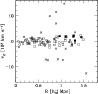 |
Figure 4: Rest frame velocity vs. projected clustercentric distance for the 94 galaxies in the main peak (Fig. 3) showing galaxies detected as interlopers by our ``shifting gapper'' procedure (crosses). Solid squares indicate cluster members detected as the northeastern substructure in the Dressler-Shectman test (DS-NE). |
| Open with DEXTER | |
All the galaxies assigned to the A959 peak are analyzed in the second
step, that uses the combination of position and velocity information:
the ``shifting gapper'' method by Fadda et al. (1996). This
procedure rejects galaxies that are too far in velocity from the main
body of galaxies and within a fixed bin that shifts along the distance
from the cluster center. The procedure is iterated until the number
of cluster members converges to a stable value. Following Fadda
et al. (1996) we use a gap of 1000 km s![]() - in the cluster
rest frame - and a bin of 0.6
h70-1 Mpc, or large enough to include 15 galaxies.
- in the cluster
rest frame - and a bin of 0.6
h70-1 Mpc, or large enough to include 15 galaxies.
The choice of the cluster center is not obvious. No evident dominant
galaxy is present, but rather there are two luminous galaxies (IDs. 53
and 82, hereafter I and II dominant galaxies) defining the SE-NW
direction already shown by X-rays (Dahle et al. 2003). Moreover, the gravitational lensing analysis brings
out several mass peaks (Dahle et al. 2003). As the cluster
center, hereafter we assume the position of the peak of X-ray
emission as listed by Popesso et al. (2004)
(RA =
![]() ,
Dec. =
,
Dec. =
![]() (J2000.0)) which is very close to the I dominant
galaxy. After the ``shifting gapper'' procedure, we obtain a sample of
81 fiducial cluster members (see Fig. 4).
(J2000.0)) which is very close to the I dominant
galaxy. After the ``shifting gapper'' procedure, we obtain a sample of
81 fiducial cluster members (see Fig. 4).
The 2D galaxy distribution analyzed through the 2D DEDICA method only
shows one peak (at RA =
![]() ,
Dec. =
,
Dec. =
![]() (J2000.0)), which is very close
to the I dominant galaxy (ID. 53), too. Using this alternative cluster
center, we verify the robustness of our member selection obtaining the
same sample of fiducial members as above.
(J2000.0)), which is very close
to the I dominant galaxy (ID. 53), too. Using this alternative cluster
center, we verify the robustness of our member selection obtaining the
same sample of fiducial members as above.
By applying the biweight estimator to the 81 cluster members (Beers
et al. 1990), we compute a mean cluster redshift of
![]() ,
i.e.
,
i.e.
![]() km s-1. We estimate the LOS velocity
dispersion,
km s-1. We estimate the LOS velocity
dispersion,
![]() ,
by using the biweight estimator and
applying the cosmological correction and the standard correction for
velocity errors (Danese et al. 1980). We obtain
,
by using the biweight estimator and
applying the cosmological correction and the standard correction for
velocity errors (Danese et al. 1980). We obtain
![]() km s-1, where errors are estimated through a
bootstrap technique.
km s-1, where errors are estimated through a
bootstrap technique.
To evaluate the robustness of the
![]() estimate, we
analyze the velocity dispersion profile (Fig. 5). The
integral profile is roughly flat suggesting that the value of
estimate, we
analyze the velocity dispersion profile (Fig. 5). The
integral profile is roughly flat suggesting that the value of
![]() is quite robust. However we notice a slight
increasing in the external cluster regions confirmed by the behavior
of the differential velocity dispersion profile that increases, rather
than decreases, going to larger and larger radii. The
is quite robust. However we notice a slight
increasing in the external cluster regions confirmed by the behavior
of the differential velocity dispersion profile that increases, rather
than decreases, going to larger and larger radii. The
![]() enhancement is likely due to the NE structure we detect and discuss in
the following section. A more reliable estimate of the global
enhancement is likely due to the NE structure we detect and discuss in
the following section. A more reliable estimate of the global
![]() then seems the value within 0.8
h70-1 Mpc
then seems the value within 0.8
h70-1 Mpc![]() where
where
![]() km s-1.
km s-1.
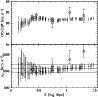 |
Figure 5:
Differential (big circles) and integral (small points) profiles of
mean velocity ( upper panel) and LOS velocity dispersion (
lower panel). For the differential profiles we plot the values for
five annuli from the center of the cluster, each of 0.3
h70-1 Mpc |
| Open with DEXTER | |
Making the usual assumptions (cluster sphericity, dynamical
equilibrium and galaxy distribution tracing the mass distribution), we
can compute global virial quantities using our estimate of
![]() .
Following the prescriptions of Girardi & Mezzetti
(2001), we assume for the radius of the quasi-virialized
region
.
Following the prescriptions of Girardi & Mezzetti
(2001), we assume for the radius of the quasi-virialized
region
![]() h70-1 Mpc
h70-1 Mpc![]() - see
their Eq. (1) after introducing the scaling with H(z) (see also Eq. (8)
of Carlberg et al. 1997 for R200). Thus the cluster is
sampled out to a large fraction of R200. We compute the virial
mass (Limber & Mathews 1960; see also, e.g., Girardi et al. 1998):
- see
their Eq. (1) after introducing the scaling with H(z) (see also Eq. (8)
of Carlberg et al. 1997 for R200). Thus the cluster is
sampled out to a large fraction of R200. We compute the virial
mass (Limber & Mathews 1960; see also, e.g., Girardi et al. 1998):
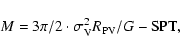 |
(1) |
where SPT is the surface pressure term correction (The & White 1986), and
Since A959 is not sampled out to
![]() and the sample is not
magnitude complete we decide to use an alternative estimate of
and the sample is not
magnitude complete we decide to use an alternative estimate of
![]() based on the knowledge of the galaxy distribution. Following
Girardi et al. 1998 (see also Girardi & Mezzetti
2001), we assume a King-like distribution with parameters
typical of nearby/medium-redshift clusters: a core radius
based on the knowledge of the galaxy distribution. Following
Girardi et al. 1998 (see also Girardi & Mezzetti
2001), we assume a King-like distribution with parameters
typical of nearby/medium-redshift clusters: a core radius
![]() and a slope-parameter
and a slope-parameter
![]() ;
i.e., the galaxy volume density at large radii goes as
;
i.e., the galaxy volume density at large radii goes as
![]() .
We obtain
.
We obtain
![]() h70-1 Mpc, where a
h70-1 Mpc, where a ![]() error is expected (Girardi et
al. 1998). We obtain
error is expected (Girardi et
al. 1998). We obtain
![]()
![]() ,
which rescaled using the above
model gives
,
which rescaled using the above
model gives
![]()
![]() ,
in good agreement with the
direct mass estimate given in the previous paragraph.
,
in good agreement with the
direct mass estimate given in the previous paragraph.
3.2 Velocity distribution
We analyze the velocity distribution to look for possible deviations from Gaussianity that might provide important signatures of complex dynamics. For the following tests the null hypothesis is that the velocity distribution is a single Gaussian.
We estimate three shape estimators, i.e. the kurtosis, the skewness,
and the scaled tail index (see, e.g., Beers et al. 1991).
According to the value of the kurtosis (2.319), the velocity
distribution is light-tailed and marginally differs from a Gaussian
at the ![]() c.l. (see Table 2 of Bird & Beers 1993).
c.l. (see Table 2 of Bird & Beers 1993).
Then we investigate the presence of gaps in the velocity distribution.
A weighted gap in the space of the ordered velocities is defined as
the difference between two contiguous velocities, weighted by the
location of these velocities with respect to the middle of the
data. We obtain values for these gaps relative to their average size,
precisely the midmean of the weighted-gap distribution. We look for
normalized gaps larger than 2.25, since in random draws of a Gaussian
distribution they arise at most in about ![]() of the cases,
independent of the sample size (Wainer and Schacht 1978; see
also Beers et al. 1991). We detect two significant gaps (at
the
of the cases,
independent of the sample size (Wainer and Schacht 1978; see
also Beers et al. 1991). We detect two significant gaps (at
the ![]() c.l.) that separate the main cluster in three groups of 20,
37 and 24 galaxies (see Fig. 6), hereafter named V1, V2,
and V3, respectively (see Table 2 for their main kinematical
properties).
c.l.) that separate the main cluster in three groups of 20,
37 and 24 galaxies (see Fig. 6), hereafter named V1, V2,
and V3, respectively (see Table 2 for their main kinematical
properties).
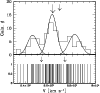 |
Figure 6: Upper panel: rest frame velocity histogram for the 81 cluster members. The bigger and smaller arrows indicate the velocities of the I and II dominant galaxies. The three Gaussians correspond to the three groups (V1, V2, and V3, from left to right) found in the velocity distribution (see Table 2). Lower panel: stripe density plot where the arrows indicate the positions of the significant gaps. |
| Open with DEXTER | |
Table 2: Kinematical properties of galaxy subclumps.
When compared two by two through the 2D Kolmogorov-Smirnov test
(Fasano & Franceschini 1987), these groups differ in spatial
distribution: the V1 group marginally differs both from the V2 and V3
groups (at the ![]() and
and ![]() c.l., respectively); the V2 group
differs from the V3 group (at the
c.l., respectively); the V2 group
differs from the V3 group (at the ![]() c.l.). In particular, the V2
group forms a dense elongated group around the cluster center and
hosts both dominant galaxies. The V3 galaxies are mostly located in
the northeastern part of the sampled region. For each of the these
groups, Fig. 7 shows the spatial distribution of
galaxies. The contours of the three galaxy distributions as recovered
using the 2D DEDICA method (one for each distribution) are shown in
Fig. 1. The V1 and V2 groups define the SE-NW direction
and, in particular, the V2 group shows a bimodal 2D distribution where
the two peaks correspond to the two dominant galaxies. The V3 group
defines the NE-SW direction.
c.l.). In particular, the V2
group forms a dense elongated group around the cluster center and
hosts both dominant galaxies. The V3 galaxies are mostly located in
the northeastern part of the sampled region. For each of the these
groups, Fig. 7 shows the spatial distribution of
galaxies. The contours of the three galaxy distributions as recovered
using the 2D DEDICA method (one for each distribution) are shown in
Fig. 1. The V1 and V2 groups define the SE-NW direction
and, in particular, the V2 group shows a bimodal 2D distribution where
the two peaks correspond to the two dominant galaxies. The V3 group
defines the NE-SW direction.
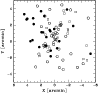 |
Figure 7: Spatial distribution on the sky of the 81 member galaxies showing the groups recovered by the weighted gap analysis. Open squares, open circles and solid circles indicate V1, V2 and V3 groups. The larger and smaller crosses indicate the positions of the I and II dominant galaxies, respectively. |
| Open with DEXTER | |
Finally, we notice that the luminous galaxies are preferentially
located in the V2 group tracing, in particular, the cluster core.
When comparing the magnitude distribution of V2 galaxies with that of
V1+V3 galaxies, we find a difference at the ![]() c.l. according to
the 1D Kolmogorov-Smirnov test (see, e.g., Ledermann 1982).
c.l. according to
the 1D Kolmogorov-Smirnov test (see, e.g., Ledermann 1982).
3.3 ``3D'' substructure analysis
The existence of correlations between positions and velocities of cluster galaxies is a footprint of real substructures. Here we use different approaches to analyze the structure of A959 combining velocity and position information.
We analyze the presence of a velocity gradient performing a multiple
linear regression fit to the observed velocities with respect to the
galaxy positions in the plane of the sky (e.g, Boschin et al. 2004, and refs. therein). We find a position angle on the
celestial sphere of
![]() degrees (measured
counter-clockwise from north), i.e. higher-velocity galaxies lie
in the western region of the cluster (see Fig. 8). To
assess the significance of this velocity gradient, we perform
1000 Monte Carlo simulations by randomly shuffling the galaxy velocities,
and for each simulation we determine the coefficient of multiple
determination (RC2, see e.g., NAG Fortran Workstation Handbook
1986). We define the significance of the velocity gradient as
the fraction of times in which the RC2 of the simulated data is
smaller than the observed RC2. We find that the velocity gradient
is significant at the
degrees (measured
counter-clockwise from north), i.e. higher-velocity galaxies lie
in the western region of the cluster (see Fig. 8). To
assess the significance of this velocity gradient, we perform
1000 Monte Carlo simulations by randomly shuffling the galaxy velocities,
and for each simulation we determine the coefficient of multiple
determination (RC2, see e.g., NAG Fortran Workstation Handbook
1986). We define the significance of the velocity gradient as
the fraction of times in which the RC2 of the simulated data is
smaller than the observed RC2. We find that the velocity gradient
is significant at the ![]() c.l.
c.l.
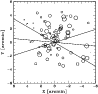 |
Figure 8: Spatial distribution on the sky of 81 cluster members. The larger the symbol, the smaller the radial velocity. The plot is centered on the cluster center. The solid and faint lines indicate the position angle of the cluster gradient and relative errors, respectively. |
| Open with DEXTER | |
We combine galaxy velocity and position information to compute the
![]() -statistics devised by Dressler & Shectman (1988).
This test is sensitive to spatially compact subsystems that have
either an average velocity that differs from the cluster mean or a
velocity dispersion that differs from the global one, or both. We
find
-statistics devised by Dressler & Shectman (1988).
This test is sensitive to spatially compact subsystems that have
either an average velocity that differs from the cluster mean or a
velocity dispersion that differs from the global one, or both. We
find
![]() for the value of the parameter that gives the
cumulative deviation. This value is a significant indication of
substructure (at the
for the value of the parameter that gives the
cumulative deviation. This value is a significant indication of
substructure (at the ![]() c.l.) as assessed by computing
1000 Monte Carlo simulations, randomly shuffling the galaxy velocities.
Figure 9 shows the distribution on the sky of all galaxies,
each marked by a circle: the larger the circle, the larger the
deviation
c.l.) as assessed by computing
1000 Monte Carlo simulations, randomly shuffling the galaxy velocities.
Figure 9 shows the distribution on the sky of all galaxies,
each marked by a circle: the larger the circle, the larger the
deviation ![]() of the local parameters from the global cluster
parameters, i.e. the greater the evidence for substructure.
of the local parameters from the global cluster
parameters, i.e. the greater the evidence for substructure.
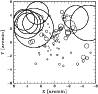 |
Figure 9:
Spatial distribution of the 81 cluster members, each marked by a
circle: the larger the circle, the larger the deviation |
| Open with DEXTER | |
To better point out galaxies belonging to substructures, we resort to
the technique developed by Biviano et al. (2002, see also
Boschin et al. 2006; Girardi et al. 2006), who used
the individual ![]() -values of the Dressler-Shectman
method. The critical point is to determine the value of
-values of the Dressler-Shectman
method. The critical point is to determine the value of ![]() that optimally indicates galaxies belonging to substructure. To this
aim we consider the
that optimally indicates galaxies belonging to substructure. To this
aim we consider the ![]() -values of all 1000 Monte Carlo
simulations used above. The resulting distribution of
-values of all 1000 Monte Carlo
simulations used above. The resulting distribution of ![]() is
compared with the observed one finding a difference at the
is
compared with the observed one finding a difference at the ![]() c.l. according to the 1D Kolmogorov-Smirnov test. The ``simulated''
distribution is normalized to produce the observed number of galaxies
and compared with the observed distribution in Fig. 10:
the latter shows a tail at high values. The inspection of
Fig. 10 suggests that galaxies with
c.l. according to the 1D Kolmogorov-Smirnov test. The ``simulated''
distribution is normalized to produce the observed number of galaxies
and compared with the observed distribution in Fig. 10:
the latter shows a tail at high values. The inspection of
Fig. 10 suggests that galaxies with
![]() likely are in substructures. These galaxies are indicated with heavy
circles in Fig. 9. The six galaxies located in the
northeastern region of the cluster are likely to form a subclump,
hereafter DS-NE (see Table 2 and Fig. 4).
likely are in substructures. These galaxies are indicated with heavy
circles in Fig. 9. The six galaxies located in the
northeastern region of the cluster are likely to form a subclump,
hereafter DS-NE (see Table 2 and Fig. 4).
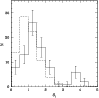 |
Figure 10:
The distribution of |
| Open with DEXTER | |
We also use here the Kaye's mixture model (KMM) test to find a
possible group partition of the velocity distribution (as implemented
by Ashman et al. 1994). The KMM algorithm fits a
user-specified number of Gaussian distributions to a dataset and
assesses the improvement of that fit over a single Gaussian. In
addition, it provides the maximum-likelihood estimate of the unknown
n-mode Gaussians and an assignment of objects into groups. This
algorithm is usually used to analyze the velocity distribution where
theoretical and/or empirical arguments indicate that the Gaussian
model is reasonable. Here the 1D KMM test fails in confirming the
three groups detected by the weighted gap method. However, since in
this case there is a significant correlation between galaxy velocities
and positions we have decided to use KMM as a 3D diagnostic. We use
the three-group galaxy assignment given by the weighted gap analysis
to determine the first guess when fitting three groups. The algorithm
fits a three-group partition at the ![]() c.l. according to the
likelihood ratio test (hereafter KMM1, KMM2, KMM3 groups of 24, 40,
and 17 galaxies from low to high mean velocities). The results for the
three groups are shown in Table 2 and Fig. 11.
Although there are some differences between the group memberships
recovered with the two different methods (cf. Fig. 11 with
Fig. 7), there are important common features: the
NE region is populated by the high-velocity galaxies while the cluster
core, elongated in the SE-NW direction, is formed by the medium
velocity galaxies. The main difference is that the SE-NW bimodal
structure is now somehow split, with KMM1 and KMM2 tracing the SE and
NW peaks better, respectively. However, note that the two dominant
galaxies are both contained in the medium velocity group
KMM2. Moreover, the galaxies in SW region are now assigned primarily
to the low velocity group.
c.l. according to the
likelihood ratio test (hereafter KMM1, KMM2, KMM3 groups of 24, 40,
and 17 galaxies from low to high mean velocities). The results for the
three groups are shown in Table 2 and Fig. 11.
Although there are some differences between the group memberships
recovered with the two different methods (cf. Fig. 11 with
Fig. 7), there are important common features: the
NE region is populated by the high-velocity galaxies while the cluster
core, elongated in the SE-NW direction, is formed by the medium
velocity galaxies. The main difference is that the SE-NW bimodal
structure is now somehow split, with KMM1 and KMM2 tracing the SE and
NW peaks better, respectively. However, note that the two dominant
galaxies are both contained in the medium velocity group
KMM2. Moreover, the galaxies in SW region are now assigned primarily
to the low velocity group.
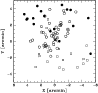 |
Figure 11: Spatial distribution on the sky of the 81 galaxies of the whole cluster showing the groups recovered by the weighted gap analysis. Open squares, open circles, and solid circles indicate KMM1, KMM2, and KMM3 groups. The larger and smaller crosses indicate the positions of the I and II dominant galaxies, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1043f12.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg99.gif) |
Figure 12:
i'-z' vs. r'-i' diagram for galaxies with available
spectroscopy is shown by small crosses. The faint box is centered
on the median value for colors of member galaxies (circles) and
encloses galaxies having colors in the range of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{1043f13.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg100.gif) |
Figure 13:
Spatial distribution on the sky and relative isodensity contour map
of likely cluster members (according to the selection in the
color-color plane) with |
| Open with DEXTER | |
3.4 2D galaxy distribution
When applying the DEDICA method to the 2D distribution of the 81 galaxy members, we find only one significant peak. However, our spectroscopic data suffer from magnitude incompleteness, and the sampled region does not cover the whole virial region. To overcome these limits we use the photometric catalog extracted from the SDSS (Data Release 6).
In the SDSS photometric catalog, we select likely members on the base
of the (r'-i') - (i'-z') color-color plane (see
e.g. Goto et al. 2002; Boschin et al. 2008). Out of
our photometric catalog, we consider galaxies (here objects with r'phototype parameter =3) lying within ![]() 0.08 mag from the median
values of r'-i'=0.49 and i'-z'=0.35 colors of the
spectroscopically cluster members (see Fig. 12). The value of
0.08 mag is two times the typical scatter reported by Goto
et al. (2002) for the corresponding color-magnitude relations
r'-i' vs. r' and i'-z' vs. r'. By adopting this
alternative selection method in a region within 30
0.08 mag from the median
values of r'-i'=0.49 and i'-z'=0.35 colors of the
spectroscopically cluster members (see Fig. 12). The value of
0.08 mag is two times the typical scatter reported by Goto
et al. (2002) for the corresponding color-magnitude relations
r'-i' vs. r' and i'-z' vs. r'. By adopting this
alternative selection method in a region within 30
![]() (almost 4
(almost 4
![]() )
from the cluster center we select a sample of likely
cluster members with r'<21. The result of the application of DEDICA
to this sample is shown in Fig. 13. The galaxy distribution
shows a shape elongated along the SE-NW direction in the central
regions. The most significant peaks (at the >
)
from the cluster center we select a sample of likely
cluster members with r'<21. The result of the application of DEDICA
to this sample is shown in Fig. 13. The galaxy distribution
shows a shape elongated along the SE-NW direction in the central
regions. The most significant peaks (at the >![]() c.l.)
correspond to the I dominant galaxy, the II dominant galaxy, a western
peak well outside of
c.l.)
correspond to the I dominant galaxy, the II dominant galaxy, a western
peak well outside of
![]() (hereafter ``W'' peak), the NE peak
at
(hereafter ``W'' peak), the NE peak
at ![]() 5
5![]() and a far NE peak at
and a far NE peak at ![]() 18
18
![]() from the
cluster center (hereafter ``far NE'' peak).
from the
cluster center (hereafter ``far NE'' peak).
To probe the robustness of these detections, we also apply the Voronoi
tessellation and percolation (VTP) technique (see Ramella
et al. 2001; Barrena et al. 2005). This technique is
non-parametric and does not smooth the data. As a consequence, it
identifies galaxy structures irrespective of their shapes. In
particular, we run VTP in a region within 30
![]() from the cluster
center selecting galaxies with r'<22 and the same color constraints
as above. The result of the application of VTP is shown in
Fig. 14. VTP is run 4 times adopting four detection
thresholds: galaxies identified as belonging to structures at the
95
from the cluster
center selecting galaxies with r'<22 and the same color constraints
as above. The result of the application of VTP is shown in
Fig. 14. VTP is run 4 times adopting four detection
thresholds: galaxies identified as belonging to structures at the
95![]() ,
98
,
98![]() ,
99
,
99![]() ,
and
,
and ![]() c.ls. VTP reveals the elongation
of A959 in the SE-NW direction and confirms the NE peak, the W, and
far NE peaks.
c.ls. VTP reveals the elongation
of A959 in the SE-NW direction and confirms the NE peak, the W, and
far NE peaks.
![\begin{figure}
\par\includegraphics[width=9cm]{1043f14.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg102.gif) |
Figure 14:
Galaxies belonging to structures as detected by the Voronoi
tessellation and percolation technique. The algorithm is run on a
sample of galaxies with |
| Open with DEXTER | |
4 Discussion and conclusions
Our analysis based on member galaxies shows that A959 is a strongly
substructured cluster. In particular, we detect an NE clump, at
![]() 5
5
![]() from the cluster center, using the weighted gap analysis
(V3 group), the Dressler-Shectman statistics (DS-NE group), the
3D KMM analysis (KMM3 group) and the 2D analysis of the galaxy
distribution. This clump has a rest frame velocity of
from the cluster center, using the weighted gap analysis
(V3 group), the Dressler-Shectman statistics (DS-NE group), the
3D KMM analysis (KMM3 group) and the 2D analysis of the galaxy
distribution. This clump has a rest frame velocity of
![]() km s
km s![]() and is the likely cause of the velocity gradient we
observe in A959. The NE clump is also detected in ROSAT/PSPC X-ray
data and in the lensing gravitational map by Dahle et al. (2003). This clump is also aligned with the SW mass
concentration WL 1017.3+5931 whose nature is very intriguing.
and is the likely cause of the velocity gradient we
observe in A959. The NE clump is also detected in ROSAT/PSPC X-ray
data and in the lensing gravitational map by Dahle et al. (2003). This clump is also aligned with the SW mass
concentration WL 1017.3+5931 whose nature is very intriguing.
The central cluster region is not well relaxed, too. We find evidence of a central, dense structure elongated along the SE-NW direction as shown by the the weighted gap analysis (V2 group), the 3D KMM analysis (KMM2 group) and the 2D analysis of the galaxy distribution. The SE-NW central structure has an intermediate velocity and hosts more luminous cluster galaxies; thus it likely represents the main part of the cluster still showing the trace of a past merger. The apparent elongation of this structure is connected with the presence of the two dominant galaxies and some galaxies surrounding them, as shown by the two peaks detected by DEDICA and VTP in the 2D galaxy distributions. Close couples of dominant galaxies having different velocities are often observed in clusters (Boschin et al. 2006; Barrena et al. 2007a) and are the likely tracers of a previous cluster merger. Indeed cluster merger is thought to be the cause of the formation of dumbbell galaxies (e.g., Beers et al. 1992; Flores et al. 2000). With respect to other cases we have studied (e.g., clusters Abell 773 and Abell 2744; see Barrena et al. 2007a and Boschin et al. 2006, respectively), the two dominant galaxies are closer in the velocity space and more distant in sky positions suggesting that the direction of the old, past merger is almost parallel to the plane of the sky.
Table 3: Properties of structures not listed in Table 2.
The SE-NW elongation is also shown by gravitational lensing and ROSAT X-ray data (Dahle et al. 2003). The ellipticity of the X-ray surface brightness appears less pronounced than those of mass and galaxy distributions, in agreement with the collisional component of the cluster having already had some time to relax.
The above discussion suggests that A959 is forming along two main
directions of mass accretion (SE-NW and NE-SW). Indeed, the region
around this cluster is quite complex and deserves a brief
discussion. By running the VTP technique and DEDICA on the 2D galaxy
distribution we find two significant galaxy concentrations: a group at
![]() 13
13
![]() W of A959 and a far NE one at
W of A959 and a far NE one at ![]() 18
18
![]() from the
core of the cluster. These two groups were first detected by Koester
et al. (2007) using the maxBCG red-sequence method in SDSS
photometric data. They computed photometric redshifts of
from the
core of the cluster. These two groups were first detected by Koester
et al. (2007) using the maxBCG red-sequence method in SDSS
photometric data. They computed photometric redshifts of ![]() 0.281
and
0.281
and ![]() 0.284 for the W and NE groups, respectively. Thus, they are
at the same redshift of A959, at projected distances from it of
0.284 for the W and NE groups, respectively. Thus, they are
at the same redshift of A959, at projected distances from it of
![]() 3.4
h70-1 Mpc
3.4
h70-1 Mpc![]() (W group) and
(W group) and ![]() 4.7
h70-1 Mpc
4.7
h70-1 Mpc![]() (NE group), possibly
representing the most important knots of the filamentary large-scale
structure around the cluster, after A959 itself. Closer to A959 (at
(NE group), possibly
representing the most important knots of the filamentary large-scale
structure around the cluster, after A959 itself. Closer to A959 (at
![]() 6
6
![]() WSW from the cluster center), ROSAT archival data reveal
a diffuse X-ray emission probably associated to a small galaxy
group. Unfortunately, we have no redshift in this region, but at the
center of the X-ray emission there is a brilliant galaxy (only
slightly less luminous than the I and II dominant galaxies) showing
the typical colors of the early-type galaxies of A959. This galaxy
(known as NVSS J101642+592222) is an evident pointlike radio source in
NVSS (Condon et al. 1998) archival data, too. We suspect that
this radio galaxy is at the center of a galaxy group falling in the
gravitational well of A959. In Table 3 we summarize the
properties of the WSW group, the W group and other structures not
listed in Table 2.
WSW from the cluster center), ROSAT archival data reveal
a diffuse X-ray emission probably associated to a small galaxy
group. Unfortunately, we have no redshift in this region, but at the
center of the X-ray emission there is a brilliant galaxy (only
slightly less luminous than the I and II dominant galaxies) showing
the typical colors of the early-type galaxies of A959. This galaxy
(known as NVSS J101642+592222) is an evident pointlike radio source in
NVSS (Condon et al. 1998) archival data, too. We suspect that
this radio galaxy is at the center of a galaxy group falling in the
gravitational well of A959. In Table 3 we summarize the
properties of the WSW group, the W group and other structures not
listed in Table 2.
As for the global properties of the cluster, the value we find for the
velocity dispersion of all A959 cluster members is very high,
![]() km s-1. When considering a more
central region to avoid the NE subclump we still obtain a high value
km s-1. When considering a more
central region to avoid the NE subclump we still obtain a high value
![]() km s-1. This value is in
good agreement with the average X-ray temperature (Mushotzky &
Scharf 1997) when assuming the energy density equipartition
between gas and galaxies (i.e.
km s-1. This value is in
good agreement with the average X-ray temperature (Mushotzky &
Scharf 1997) when assuming the energy density equipartition
between gas and galaxies (i.e.
![]()
![]() , see Fig. 5) and leads to a virial mass of
, see Fig. 5) and leads to a virial mass of
![]()
![]() .
We compare our mass
estimate with that derived from the gravitational lensing
analysis. Dahle et al. (2002) obtained a projected mass
.
We compare our mass
estimate with that derived from the gravitational lensing
analysis. Dahle et al. (2002) obtained a projected mass
![]()
![]() (in our cosmology). To
rescale and project our mass, we assume two alternative mass
distributions: a King-like mass distribution (see above) or an NFW
profile where the mass-dependent concentration parameter c is taken
from Navarro et al. (1997) and rescaled by the factor 1+z(Bullock et al. 2001; Dolag et al. 2004). Our
projected mass estimate is
(in our cosmology). To
rescale and project our mass, we assume two alternative mass
distributions: a King-like mass distribution (see above) or an NFW
profile where the mass-dependent concentration parameter c is taken
from Navarro et al. (1997) and rescaled by the factor 1+z(Bullock et al. 2001; Dolag et al. 2004). Our
projected mass estimate is
![]()
![]() ,
where the projection is done assuming that the cluster mass
distribution is truncated at one or at two virial radii. The lensing
mass is consistent with our projected estimate within their errors,
even if the former is likely to be a bit higher, possibly due to the
young dynamical state of the cluster.
,
where the projection is done assuming that the cluster mass
distribution is truncated at one or at two virial radii. The lensing
mass is consistent with our projected estimate within their errors,
even if the former is likely to be a bit higher, possibly due to the
young dynamical state of the cluster.
In conclusion, A959 shows the typical features of most clusters
hosting halo/relic radio sources, i.e. a high mass (higher than
0.7
![]() within 2
h70-1 Mpc; see Giovannini & Feretti 2002) and
a young dynamical state (diffuse radio sources appear in
clusters possessing substructures, i.e. experiencing large departures
from a virialized state; see, e.g., Buote 2001). This makes
of this cluster a good candidate for deep radio studies. More
observations of the diffuse radio source will allow to clarify its
connection with the internal dynamics of this cluster. Moreover, deep
X-ray observations will be useful for determining the merging phase of
the NE clump.
within 2
h70-1 Mpc; see Giovannini & Feretti 2002) and
a young dynamical state (diffuse radio sources appear in
clusters possessing substructures, i.e. experiencing large departures
from a virialized state; see, e.g., Buote 2001). This makes
of this cluster a good candidate for deep radio studies. More
observations of the diffuse radio source will allow to clarify its
connection with the internal dynamics of this cluster. Moreover, deep
X-ray observations will be useful for determining the merging phase of
the NE clump.
Acknowledgements
This publication is based on observations made on the island of La Palma with the Italian Telescopio Nazionale Galileo (TNG), operated by the Fundación Galileo Galilei - INAF (Istituto Nazionale di Astrofisica), in the Spanish Observatorio of the Roque de Los Muchachos of the Instituto de Astrofisica de Canarias. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the galaxy catalog of the Sloan Digital Sky Survey (SDSS). Funding for the SDSS has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This work was partially supported by a grant from the Istituto Nazionale di Astrofisica (INAF, grant PRIN-INAF2006 CRA ref number 1.06.09.06).
References
- Abell, G. O., Corwin, H. G. Jr., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] (In the text)
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] (In the text)
- Bardelli, S., Zucca, E., Vettolani, G., et al. 1994, MNRAS, 267, 665 (In the text)
- Barrena, R., Ramella, M., Boschin, W., et al. 2005, A&A, 444, 685 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Barrena, R., Boschin, W., Girardi, M., & Spolaor, M. 2007a, A&A, 467, 37 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Barrena, R., Boschin, W., Girardi, M., & Spolaor, M. 2007b, A&A, 469, 861 [NASA ADS] [CrossRef] [EDP Sciences]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Forman, W., Huchra, J. P., Jones, C., & Gebhardt, K. 1991, AJ, 102, 1581 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Gebhardt, K., Huchra, J. P., et al. 1992, ApJ, 400, 410 [NASA ADS] [CrossRef] (In the text)
- Bird, C. M. 1994, ApJ, 422, 480 [NASA ADS] [CrossRef]
- Bird, C. M., & Beers, T. C. 1993, AJ, 105, 1596 [NASA ADS] [CrossRef] (In the text)
- Biviano, A., Katgert, P., Thomas, T., & Adami, C. 2002, A&A, 387, 8 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Böhringer, H., & Schuecker, P. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.) (In the text)
- Boschin, W., Girardi, M., Barrena, R., et al. 2004, A&A, 416, 839 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boschin, W., Barrena, R., Girardi, M., & Spolaor, M. 2008, A&A, 487, 33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boschin, W., Girardi, M., Spolaor, M., & Barrena, R. 2006, A&A, 449, 461 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [NASA ADS] [CrossRef] (In the text)
- Buote, D. A. 2001, ApJ, 553, 15 [NASA ADS] [CrossRef] (In the text)
- Buote, D. A. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.) (In the text)
- Carlberg, R. G., Yee, H. K. C., & Ellingson, E. 1997, ApJ, 478, 462 [NASA ADS] [CrossRef] (In the text)
- Cassano, R., Brunetti, G., & Setti, G. 2006, MNRAS, 369, 1577 [NASA ADS] [CrossRef] (In the text)
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] (In the text)
- Cooray, A. R., Grego, L., Holzapfel, W. L., Joy, M., & Carlstrom, J. E. 1998, AJ, 115, 1388 [NASA ADS] [CrossRef] (In the text)
- Dahle, H., Kaiser, N., Irgens, R. J., Lilje, P. B., & Maddox, S. J. 2002, ApJS, 139, 313 [NASA ADS] [CrossRef] (In the text)
- Dahle, H., Pedersen, K., Lilje, P. B., Maddox, S. J., & Kaiser, N. 2003, ApJ, 591, 662 [NASA ADS] [CrossRef] (In the text)
- Danese, L., De Zotti, C., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] (In the text)
- Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dressler, A., & Shectman, S. A. 1988, AJ, 95, 985 [NASA ADS] [CrossRef] (In the text)
- Ellingson, E., & Yee, H. K. C. 1994, ApJS, 92, 33 [NASA ADS] [CrossRef] (In the text)
- Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] (In the text)
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] (In the text)
- Feretti, L. 1999, MPE Report, 271 [CrossRef] (In the text)
- Feretti, L. 2002, The Universe at Low Radio Frequencies, held 30 Nov. - 4 Dec. 1999, Pune, India, ed. A. Pramesh Rao, G. Swarup, & Gopal-Krishna, Proc. IAU Symp., 199, 133 (In the text)
- Feretti, L. 2005, X-Ray and Radio Connections ed. L. O. Sjouwerman, & K. K. Dyer, Published electronically by NRAO, http://www.aoc.nrao.edu/events/xraydio, Held 3-6 February 2004 in Santa Fe, New Mexico, USA (In the text)
- Feretti, L., Gioia, I. M., & Giovannini, G. 2002, Merging Processes in Galaxy Clusters (The Netherlands: Kluwer Academic Publisher), Ap&SS Library, 272 (In the text)
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] (In the text)
- Flores, R. A., Quintana, H., & Way, M. J. 2000, ApJ, 532, 206 [NASA ADS] [CrossRef] (In the text)
- Giovannini, G., & Feretti, L. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands, Kluwer Ac. Pub.) (In the text)
- Giovannini, G., Tordi, M., & Feretti, L. 1999, New Astron., 4, 141 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., & Mezzetti, M. 2001, ApJ, 548, 79 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., & Biviano, A. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), Optical Analysis of Cluster Mergers (In the text)
- Girardi, M., Biviano, A., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1993, ApJ, 404, 38 [NASA ADS] [CrossRef]
- Girardi, M., Fadda, D., Giuricin, G., et al. 1996, ApJ, 457, 61 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Giuricin, G., Mardirossian, F., Mezzetti, M., & Boschin, W. 1998, ApJ, 505, 74 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Boschin, W., & Barrena, R. 2006, A&A, 455, 45 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Girardi, M., Barrena, R., Boschin, W., & Ellingson, E. 2008, A&A, 491, 379 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Goto, T., Sekiguchi, M., Nichol, R. C., et al. 2002, AJ, 123, 1807 [NASA ADS] [CrossRef] (In the text)
- Govoni, F., Ensslin, T. A., Feretti, L., & Giovannini, G. 2001a, A&A, 369, 441 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Govoni, F., Feretti, L., Giovannini, G., et al. 2001b, A&A, 376, 803 [NASA ADS] [CrossRef] [EDP Sciences]
- Irgens, R. J., Lilje, P. B., Dahle, H., & Maddox, S. J. 2002, 579, 227 (In the text)
- Kempner, J. C., Blanton, E. L., Clarke, T. E., et al. 2004, in The Riddle of Cooling Flows in Galaxies and Clusters of Galaxies, ed. T. Reiprich, J. Kempner, & N. Soker (Charlottesville: Univ. Virginia), 335 (In the text)
- Kennicutt, R. C. 1992, ApJS, 79, 225 (In the text)
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] (In the text)
- Ledermann, W. 1982, Handbook of Applicable Mathematics (New York: Wiley), 6 [NASA ADS] (In the text)
- Limber, D. N., & Mathews, W. G. 1960, ApJ, 132, 286 [NASA ADS] [CrossRef] (In the text)
- Malumuth, E. M., Kriss, G. A., Dixon, W. Van Dyke, Ferguson, H. C., & Ritchie, C. 1992, AJ, 104, 495 [NASA ADS] [CrossRef] (In the text)
- Mushotzky, R. F., & Scharf, C. A. 1997, ApJ, 482, L13 [NASA ADS] [CrossRef] (In the text)
- NAG Fortran Workstation Handbook 1986 (Downers Grove, IL: Numerical Algorithms Group) (In the text)
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] (In the text)
- Ota, N., & Mitsuda, K. 2004, A&A, 428, 757 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Owen, F., Morrison, G., & Voges, W. 1999, proceedings of the workshop Diffuse Thermal and Relativistic Plasma in Galaxy Clusters, ed. H. Böhringer, L. Feretti, & P. Schuecker, MPE Report, 271, 9 (In the text)
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] (In the text)
- Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] (In the text)
- Popesso, P., Böhringer, H., Brinkmann, J., Voges, W., & York, D. 2004, A&A, 423, 449 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Quintana, H., Carrasco, E. R., & Reisenegger, A. 2000, AJ, 120, 511 [NASA ADS] [CrossRef] (In the text)
- Ramella, M., Boschin, W., Fadda, D., & Nonino, M. 2001, A&A, 368, 776 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Roettiger, K., Loken, C., & Burns, J. O. 1997, ApJS, 109, 307 [NASA ADS] [CrossRef] (In the text)
- Sarazin, C. L. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), The Physics of Cluster Mergers (In the text)
- Schuecker, P., Böhringer, H., Reiprich, T. H., & Feretti, L. 2001, A&A, 378, 408 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- The, L. S., & White, S. D. M. 1986, AJ, 92, 1248 [NASA ADS] [CrossRef] (In the text)
- Tonry, J., & Davis, M. 1979, ApJ, 84, 1511 [NASA ADS] (In the text)
- Wainer, H., & Schacht, S. 1978, Psychometrika, 43, 203 [CrossRef] (In the text)
Footnotes
- ...2008
![[*]](/icons/foot_motif.gif)
- Please visit the web site of the DARC (Dynamical Analysis of Radio Clusters) project: http://adlibitum.oat.ts.astro.it/girardi/darc
- ... IRAF
![[*]](/icons/foot_motif.gif)
- IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
- ...
![[*]](/icons/foot_motif.gif)
-
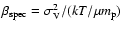 with
with 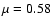 the mean molecular weight and
the mean molecular weight and 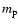 the
proton mass.
the
proton mass.
All Tables
Table 1: Velocity catalog of 107 spectroscopically measured galaxies in the field of A959.
Table 2: Kinematical properties of galaxy subclumps.
Table 3: Properties of structures not listed in Table 2.
All Figures
![\begin{figure}
\par\includegraphics[width=18cm]{1043f01.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg39.gif) |
Figure 1:
Multiwavelength image of A959 (north at the top and east to
the left). The contour levels (thin levels) of a smoothed archival
ROSAT/PSPC X-ray image are superimposed on the SDSS |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{1043f02.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg42.gif) |
Figure 2:
SDSS |
| Open with DEXTER | |
| In the text | |
 |
Figure 3: Redshift galaxy distribution. The solid line histogram refers to (94) galaxies assigned to the cluster according to the DEDICA reconstruction method. |
| Open with DEXTER | |
| In the text | |
 |
Figure 4: Rest frame velocity vs. projected clustercentric distance for the 94 galaxies in the main peak (Fig. 3) showing galaxies detected as interlopers by our ``shifting gapper'' procedure (crosses). Solid squares indicate cluster members detected as the northeastern substructure in the Dressler-Shectman test (DS-NE). |
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
Differential (big circles) and integral (small points) profiles of
mean velocity ( upper panel) and LOS velocity dispersion (
lower panel). For the differential profiles we plot the values for
five annuli from the center of the cluster, each of 0.3
h70-1 Mpc |
| Open with DEXTER | |
| In the text | |
 |
Figure 6: Upper panel: rest frame velocity histogram for the 81 cluster members. The bigger and smaller arrows indicate the velocities of the I and II dominant galaxies. The three Gaussians correspond to the three groups (V1, V2, and V3, from left to right) found in the velocity distribution (see Table 2). Lower panel: stripe density plot where the arrows indicate the positions of the significant gaps. |
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Spatial distribution on the sky of the 81 member galaxies showing the groups recovered by the weighted gap analysis. Open squares, open circles and solid circles indicate V1, V2 and V3 groups. The larger and smaller crosses indicate the positions of the I and II dominant galaxies, respectively. |
| Open with DEXTER | |
| In the text | |
 |
Figure 8: Spatial distribution on the sky of 81 cluster members. The larger the symbol, the smaller the radial velocity. The plot is centered on the cluster center. The solid and faint lines indicate the position angle of the cluster gradient and relative errors, respectively. |
| Open with DEXTER | |
| In the text | |
 |
Figure 9:
Spatial distribution of the 81 cluster members, each marked by a
circle: the larger the circle, the larger the deviation |
| Open with DEXTER | |
| In the text | |
 |
Figure 10:
The distribution of |
| Open with DEXTER | |
| In the text | |
 |
Figure 11: Spatial distribution on the sky of the 81 galaxies of the whole cluster showing the groups recovered by the weighted gap analysis. Open squares, open circles, and solid circles indicate KMM1, KMM2, and KMM3 groups. The larger and smaller crosses indicate the positions of the I and II dominant galaxies, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1043f12.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg99.gif) |
Figure 12:
i'-z' vs. r'-i' diagram for galaxies with available
spectroscopy is shown by small crosses. The faint box is centered
on the median value for colors of member galaxies (circles) and
encloses galaxies having colors in the range of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{1043f13.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg100.gif) |
Figure 13:
Spatial distribution on the sky and relative isodensity contour map
of likely cluster members (according to the selection in the
color-color plane) with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{1043f14.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa11043-08/Timg102.gif) |
Figure 14:
Galaxies belonging to structures as detected by the Voronoi
tessellation and percolation technique. The algorithm is run on a
sample of galaxies with |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


