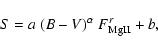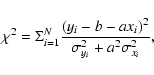EDP Sciences
Home All issues Volume 495 / No 1 (February III 2009) A&A, 495 1 (2009) 287-295 Full HTML
Free Access
Issue
A&A
Volume 495, Number 1, February III 2009
Page(s) 287 - 295
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361:200810985
Published online 14 January 2009

Long-term chromospheric activity of non-eclipsing RS CVn-type stars

A. P. Buccino - P. J. D. Mauas

Instituto de Astronomía y Física del Espacio (CONICET), C.C. 67 Sucursal 28, 1428-Buenos Aires, Argentina

Received 18 September 2008 / Accepted 19 December 2008

Abstract
Context. The IUE database provides several UV high and low-resolution spectra of RS CVn-type stars from 1978 to 1996. In particular, many of these stars were monitored continuously during several seasons by IUE.
Aims. Our main purpose is to study the short and long-term chromospheric activity of the RS CVn systems most observed by IUE: HD 22 468 (V711 Tau, HR 1099, K1IV+G5V), HD 21 242 (UX Ari, K0IV+G5V), and HD 224 085 (II Peg, K2IV).
Methods. We first obtained the Mount Wilson index S from the IUE high and low-resolution spectra. Secondly, we used the Lomb-Scargle periodogram to analyse the mean annual index $\langle S\rangle$ and the amplitude of the rotational modulation of the index S.
Results. For HD 22 468 (V711 Tau, HR 1099), we find a possible chromospheric cycle with a period of $\sim$18 years and a shorter cycle with a period of $\sim$3 years, which could be associated to a chromospheric ``flip-flop'' cycle. The data of HD 224 085 (II Peg) also suggest a chromospheric cycle of $\sim$21 years and a flip-flop cycle of $\sim$9 years. Finally, we obtained a possible chromospheric cycle of $\sim$7 years for HD 21 242 (UX Ari).

Key words: stars: activity - stars binaries: spectroscopic - ultraviolet: stars

1 Introduction

One of the principal diagnostics for solar and stellar chromospheric activity is the emission in the Ca II H and K resonance lines (at 3968 and 3934 Å). In particular, the largest dataset of activity measurements available at present, comprising observations of over 2000 stars, is the one obtained with the Mount Wilson HK spectrophotometers, which have been used since 1966 to measure high-precision Ca  II H+K fluxes. As an indicator of stellar activity, an index S has been defined as the ratio between the line-core fluxes and the flux in the continuum nearby.

Since the Mg II h and k lines (at 2803 and 2796 Å) are formed in a similar way to the Ca  II lines, they are also good indicators of the thermal structure of stellar atmospheres, especially from the high photosphere to the upper part of the chromospheric plateau.

The International Ultraviolet Explorer (IUE) provides a large database of low and high-resolution UV spectra in the band 1150-3350 Å, from 1978 to 1996, which can be used to study long-term stellar activity through the Mg  II  lines.

In a previous work (Buccino & Mauas 2008, hereafter Paper I) we obtained a colour dependent relation between the Mount Wilson index S and Mg  II  line-core surface fluxes derived from IUE high-resolution spectra for F5 to K3 main sequence stars. As an application of this calibration, we computed the Mount Wilson index for all the dF to dK stars which have high-resolution IUE spectra. In that paper we also combined IUE observations with those obtained by Henry et al. (1996), and by our group (see Cincunegui & Mauas 2004; Cincunegui et al. 2007a). For some of the most frequently observed main sequence stars, we combined the Mount Wilson index S from the IUE spectra, together with the ones derived from visible spectra, covering the period between 1978 and 2005. Analysing the data with the Lomb-Scargle periodogram, we were able to confirm the chromospheric activity cycle of $\epsilon$ Eri (HD 22 049) and $\beta$ Hydri (HD 2151) with periods of $\sim$5 and $\sim$12 years respectively, and we found a magnetic cycle in $\alpha$ Cen B (HD 128 621) of $\sim$8 years.

Similarly, the purpose of the present study is to calibrate IUE low-resolution observations of Mg  II h+k lines with the Mount Wilson index S, as a complement of the work presented in Paper I, and to apply this calibration to study the activity in RS CVn stars.

RS CVn-type stars are well known due to their strong chromospheric plages, coronal X-ray, and microwave emissions, as well as strong flares in the optical, UV, radio, and X-ray. These stars belong to a class of close detached binaries where the more massive primary component is a G-K giant or subgiant and the secondary is a subgiant or dwarf of spectral classes G to M. The magnetic activity signatures are generally dominated by the primary star of the system. Since these stars are fast rotators enforced by tidal synchronization, they are, in general, more active than single stars of similar mass and age.

The remarkable activity and high luminosity of these stars make them favourite targets for light curve modeling (Rodonò et al. 1986; Donati et al. 1995; Berdyugina et al. 1999; Berdyugina & Henry 2007), Doppler imaging (Donati et al. 1992; Donati 1999; Kitchatinov et al. 2000; Donati et al. 1997) and spectral line analysis (Walter et al. 1987; Dempsey et al. 1996; Pagano et al. 2001; Montes et al. 2000). In general, most long-term stellar activity studies of RS CVn-type stars are based on easily detected optical photometric variations produced by their long-lived large spots. Recently, Messina (2008) presented the results of a long-term photometric monitoring project, where he carefully studied the magnetic activity of 14 late-type active components of close binary systems and its evolution on different time scales. Lanza et al. (2006,1998) and Berdyugina & Henry (2007) presented similar long-term studies for individual RS CVn stars.

In general, these studies concluded that the mean activity level of RS CVn-type stars presents cyclic variations similar to the 11-year solar cycle. Moreover, they found that large starspots tend to appear always at particular longitudes, called ``active longitudes'' (ALs), which are generally separated by 180$^\circ$ on average and differ in their level of activity. Berdyugina & Tuominen (1998) found that the dominant activity switches periodically from one active longitude to the other in most RS CVn stars. This type of stellar activity cycle, known as ``flip-flop cycle'', is mainly related to the non-axisymmetric redistribution of the spotted area.

The IUE database provides a large number of UV high and low-resolution spectra of RS CVn-type stars. Furthermore, IUE monitored these stars continuously during several seasons. In most cases, the observations were aimed at uniform coverage with respect to orbital phase over more than one rotation period in each season (e.g. Dempsey et al. 1996; Busà et al. 1999). In this work we analyse the short and long-term chromospheric activity of the non-eclipsing RS CVn stars most observed by IUE and we compare the chromospheric and photospheric patterns of variability.

In particular, in Sect. 2, we derive a relation to determine the Mount Wilson index from the Mg  II  line-core fluxes measured on IUE low-resolution spectra. As an application of this calibration, in Sect. 3 we study the Mount Wilson indices we derived from both IUE high and low-resolution spectra of the RS CVn stars HD 22468 (V711 Tau, HR 1099), HD 21 242 (UX Ari) and HD 224 085 (II Peg).

2 Mg II lines and Mount Wilson index

In Paper I we inter-calibrated the index S and Mg  II fluxes using quasi-simultaneous IUE high-resolution observations for a set of dwarf stars with spectral types F to K. Since in the present work we intend to use this calibration to study the activity of RS CVn systems, which have sub-giants as their primary star, we check the accuracy of applying this calibration to cool sub-giants. To do so, we obtained the IUE Mg  II  fluxes for those cool sub-giant stars also observed at Mount Wilson Observatory. In Fig. 1 we show the calibration of Paper I, and we include these sub-giants. It can be seen that these stars follow this calibration within the statistical errors.

 \begin{figure} \par\includegraphics[width=8.5cm]{0985fig1.eps} \end{figure} Figure 1:

S vs. $F_{\rm Mg II}(B-V)^{3}$ for the set of 117 nearly simultaneous observations of Mount Wilson index and IUE high-resolution Mg  II h and k fluxes for dwarfs we used in Paper I ( $\blacksquare $). We considered errors of 10% for $F_{\rm Mg{\scriptsize{II} \normalsize}}$ and 6% for S. The least square fit (solid line) has a correlation coefficient of 0.95. The dotted lines indicate $\pm $3$\sigma $ from the fit. The triangles ( $\blacktriangle $) represent non-simultaneous Mount Wilson indices and IUE high-resolution Mg  II fluxes of cool sub-giant stars, not used in the calibration.
Open with DEXTER

Since the IUE database also provides a large number of low-resolution spectra of late-type stars, in particular RS CVn stars, it is important to incorporate these spectra to the systematic studies of magnetic activity. To this end, in what follows we analyse the relation between the Mg  II  line-core fluxes derived from IUE low-resolution spectra and the Mount Wilson index.

2.1 Observations

In Fig. 2 we present some examples of IUE low-resolution spectra of three F, G and K main sequence stars. These spectra present a resolution of R=400 at 2700 Å, they are available from the IUE public library (at http://sdc.laeff.esa.es/cgi-ines/IUEdbsMY), and have been calibrated using the NEWSIPS (New Spectral Image Processing System) algorithm (Garhart et al. 1997). The internal accuracy of the low-resolution flux calibration is 10-15% (Massa & Fitzpatrick 2000).

 \begin{figure} \par\includegraphics[width=8.5cm]{0985fig2.eps} \end{figure} Figure 2:

IUE low-resolution spectra of three representative stars: HD 22 049 (K2V), HD 1835 (G3V) and HD 1581 (F9V). Surface flux is obtained according to Eq. (1). The windows used to integrate the line-core emission (2790-2810 Å) are marked on each spectrum.
Open with DEXTER

The observed flux f in the IUE spectra was transformed to the surface flux F using Schrijver et al.'s (1992) relation:

\begin{displaymath}\log~(F/f)=0.35+0.4(m_V+BC)+4~~\log~T_{\rm eff}, \end{displaymath} (1)

where mV is the visual apparent magnitude (from the Hipparcos and Thycho Catalogue Perryman et al. 1997; Hoeg et al. 1997), BC is the bolometric correction (from Flower 1996) and $T_{\rm eff}$ is the effective temperature (from Boehm-Vitense 1981).

In Fig. 2 we also show the windows used to integrate the Mg  II  line-core fluxes, which are 10 Å-wide and are centred at 2795 Å. The position and the width of these windows were chosen to guarantee that the contribution of the integrated flux is predominantly chromospheric, beyond the basal contribution. However, it can be seen in the figure that the Mg  II  line-core emission can only be detected in stars of late spectral type, in which the level of phostospheric continuum is low. Therefore, the Mg  II line-core fluxes derived from IUE low-resolution spectra could be only considered as an activity indicator in stars cooler than G3.

On the other hand, the ``IUE Newly Extracted Spectra'' (INES) system provides a rebinned spectrum for each high-resolution image, which is obtained by re-sampling the high-resolution spectrum into the low-resolution wavelength domain. The re-sampling has been performed so that the total flux is conserved. However, the rebinned spectra have not been convolved with the low-resolution Point Spread Function (PSF) and, in consequence, have a better spectral resolution than low-dispersion spectra (González-Riestra et al. 2000).

 \begin{figure} \par\includegraphics[width=8cm]{0985fig3.eps} \end{figure} Figure 3:

IUE low-dispersion (dashed line) and rebinned (solid line) spectra of HD 22 049, both observed on January, 14 th 1984 with a time difference of 1 h.

Open with DEXTER

In Fig. 3 we plot two quasi-simultaneous rebinned and low-dispersion spectra of the star HD 22 049 (K2V). We can see that both spectra are similar but not equal. However, the Mg  II  line-core fluxes integrated between 2790 and 2810 Å (dotted rectangle) on both spectra only differ by 1-2%. Therefore, in order to calculate the Mount Wilson index from the IUE spectra, we can consider the low-resolution and the rebinned spectra indistinguishable.

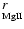
2.2 Calibration of S vs. F $^{\textit {{r}}}_{\rm {Mg II}}$

To intercalibrate the Mount Wilson index S and the Mg  II  line-core surface fluxes derived from the IUE low-resolution spectra, we used the same set of quasi-simultaneous observations used in Paper I (see Fig. 1). In particular, we measured the Mg  II  fluxes on the IUE rebinned spectra ( $F^r_{\rm Mg~II}$) corresponding to the high-resolution spectra used in our previous work.

Table 1:   Stars used in the Mg II - and the index S calibration.

As mentioned before, the Mg II line-core fluxes can be considered as an activity indicator only in late-type stars, where the line-core emission is remarkably larger than the contribution of the continuum nearby. Therefore, we reduced our set of calibration stars to those with B-V>0.65, listed in Table 1.

We proposed a calibration for S vs. $F^r_{\rm MgII}$ analogous to the one obtained in Paper I for the Mg  II  fluxes derived from IUE high-resolution spectra:

\begin{displaymath}S = a~(B-V)^\alpha~F^r_{\rm Mg II}+b, \end{displaymath} (2)

with $F^r_{\rm Mg\scriptsize {II} \normalsize }$ expressed in erg cm-2 s-1. We found that the best correlation coefficient R=0.82 is obtained for $\alpha=(5.65 \pm 0.20)$.

 \begin{figure} \par\includegraphics[width=8.2cm]{0985fig4.eps} \end{figure} Figure 4:

S vs. $F^r_{\rm Mg II}(B-V)^{5.65}$ for the stars listed in Table 1. We considered errors of 10% for $F^r_{\rm Mg\scriptsize {II} \normalsize }$ and 6% for S. The least square fit (solid line) has a correlation coefficient of 0.82. The dotted lines indicate the points that apart $\pm $$\sigma $ from the fit. The triangles ( $\blacktriangle $) represent non-simultaneous Mount Wilson indices and IUE high-resolution Mg  II fluxes of cool sub-giant stars with B-V>0.65, not used in the calibration.

Open with DEXTER

Table 2:   Long and short term variability records of the RS CVn-type stars most observed by IUE.

The uncertainties in the determination of the effective temperature and the bolometric correction of the star may introduce a $\sim$10% error in the Mg  II surface fluxes obtained with Eq. (1) (Schrijver et al. 1992). On the other hand, the dispersion in $F^r_{\rm Mg\scriptsize {II} \normalsize }$, due to the fact that there is a single value of S for IUE spectra differing in less than 36 h, has a standard deviation that can be up to 5%. The standard deviations of the Mount Wilson indices S obtained from Duncan et al. (1991) do not exceed 10% of its mean value. Therefore, we varied the error of $F^r_{\rm Mg\scriptsize {II} \normalsize }$ and S near the maximum standard deviation (15% for $F^r_{\rm Mg\scriptsize {II} \normalsize }$ and 10% for S) in order to minimize the $\chi ^2$-statistic.

Considering errors in both coordinates and minimizing the expression:

\begin{displaymath}\chi^{2}=\Sigma_{i=1}^N\frac{(y_i-b-ax_{i})^{2}}{\sigma_{y_{i}}^{2}+a^{2}\sigma_{x_{i}}^{2}}, \end{displaymath} (3)

where $y\equiv S$ and $x\equiv F^r_{\rm Mg\scriptsize {II} \normalsize }(B-V)^\alpha$, we obtained that the best parameters are $a=(2.76\pm0.18)\times 10^{-7}$ and $b=-0.155\pm 0.041$, which give a reduced $\chi^2=1.27$ for uncertainties of 10% and 6% in the $F^r_{\rm Mg\scriptsize {II} \normalsize }$and S values respectively.

In Fig. 4 we plot the Mount Wilson index Svs. the Mg II line-core surface fluxes for dwarf stars and the best linear fit given by Eq. (2). As in Fig. 1, we also included the index S and the Mg  II  fluxes for cool sub-giant stars with B-V>0.65. We can see that these sub-giants follow the calibration obtained in Eq. (2) within the statistical errors.

3 RS CVn stars

The IUE database provides a large number of UV high and low-resolution spectra of RS CVn-type stars. In this section, we analyse the long and short-term chromospheric activity of three RS CVn stars observed many times by IUE. In particular, we analysed the activity signatures, which mainly correspond to the primary star, of the system: HD 22 468 (V711 Tau, HR 1099), HD 21 242 (UX Ari, HD 21 242) and HD 224 085 (II Peg).

Most observations were performed at high-resolution. To add to these observations the low-resolution ones, we transform the Mg  II  fluxes to S, following the calibrations obtained here and in Paper I. We note that the values obtained from low-resolution observations have larger uncertainties since they include an extra activity component related to the continuum nearby, whose variation could be up to 30% for very active stars (see Sect. 2 in Paper I). We also note that, for a given star, the error in the transformation to surface fluxes (Eq. (1)) is common to all the observations and, therefore, does not affect our results regarding stellar variability, although it might affect the mean level of activity.

In this way, our observations cover the period between 1978 and 1996. Even if, in several cases, the density of measurements along the years is low, we can infer the average level of activity and its variability for the whole period and during a few short intervals of time.

For the stars mentioned above, we list in Table 2 the average, maximum and minimum level of activity reached along decades (Cols. 4 and 5) and the variations recorded in particular years (Col. 6).

In what follows we plot the index S vs. time and we analyse the stellar magnetic behaviour of each system in detail.

3.1 HD 22 468 - V711 Tau - HR 1099

HD 22 468 is one of the most active RS CVn non-eclipsing spectroscopic binary systems, consisting of a K1 subgiant primary and a G5 dwarf secondary in a 2.837-day orbit.

In RS CVn stars the activity contribution of the secondary star is another source of error for determining the Mg  II  line-core emission of the primary star. To estimate this contribution, we fitted the Mg II h and k lines with two Gaussian functions to approximate the line-core emission of the primary and the secondary star in each line, using the IRAF task splot (see Fig. 5).

 \begin{figure} \par\includegraphics[width=8.2cm]{0985fig5.eps} \end{figure} Figure 5:

HD 22 468-V711 Tau-HR 1099. Mg II k line fitted with two Gaussian functions, the dashed and solid curves represent the contribution of the primary and secondary star of the system respectively.
Open with DEXTER

For all the IUE high-resolution spectra of HD 22 468, we integrated the fluxes under these curves and we found that the Mg  II  h+k line-core fluxes emitted by the G star do not exceed 10% of the total flux, which is within the standard deviation we assumed for the measured flux. Therefore, the Mg  II  h+k line-core fluxes derived from the IUE high and low-resolution spectra of HD 22 468 can be considered as an activity indicator of the K star of the system.

In Fig. 6 we plot the indices S for this star, for which we obtained a mean Mount Wilson index $\langle S \rangle=1.864$from 1978 to 1995.

 \begin{figure} \par\includegraphics[width=8.5cm]{0985fig6.eps} \end{figure} Figure 6:

HD 22 468 - V711 Tau - HR 1099. We indicate the Mount Wilson index Sobtained from the IUE high and low-resolution spectra with triangles ($\triangle $) and circles ($\bigcirc $) respectively. We indicate with arrows the sets of data for which we analysed the short-term variability.
Open with DEXTER

Cerruti-Sola et al. (1992) reported that HD 22 468 had fluxes comparable to those of the brightest solar regions and even approaching those observed in solar flares. In fact, several flares were observed with IUE, and can be noticed in Fig. 6. In particular, Linsky et al. (1989) reported a flare on 1981, October 3 rd, which released a total energy of $\sim$1032 erg. Using our calibration, we obtain that S increased 21% in a few hours during that event. Brown et al. (1994) reported another flare on 1994, August 24 th. During that date, the Mount Wilson index presented a 60% variation in six hours. In December 1992, Neff (1995) also reported a flare observed by IUE, during which S increased by 50% in half an hour. In Fig. 7 we plot the values of S obtained from the IUE spectra during these three flares.

    \begin{figure} \par\subfigure[]{\includegraphics[width=2.7cm]{0985fig7.eps} }\hs... ...igure[]{\includegraphics[width=2.7cm]{0985fig9.eps} }\hspace*{2mm}\end{figure} Figure 7:

HD 22 468 - V711 Tau - HR 1099. Three flares on 1981, Oct. 3rd; 1992, Dec. 14th and 1994, Aug. 24th.
Open with DEXTER
   \begin{figure} \par\subfigure[]{\includegraphics[width=4.3cm]{0985fig10.eps} }\h... ...*{1mm} \subfigure[]{\includegraphics[width=4.5cm]{0985fig11.eps} }\end{figure} Figure 8:

HD 22 468 - V711 Tau - HR 1099. Left: Lomb-Scargle periodogram of the mean annual $\langle S\rangle$ of the data plotted in Fig. 6. The False Alarm Probability (FAP) levels of 1, 10, 50 and 90% are indicated. Right: the mean annual $\langle S\rangle$ of the data plotted in Fig. 6 phased with the period of 6589 days. The solid line shows the harmonic curve that best fits the data with a reduced $\chi ^2=1.5$ and the dashed lines indicate the points that apart $\sigma $ from that fit.
Open with DEXTER

On the other hand, long-term time series of optical photometry were extensively analysed for this star (Henry et al. 1995; Lanza et al. 2006). Recently, Berdyugina & Henry (2007) analysed photometric observations of HD 22 468 in the V-band for the years 1975-2006 and they confirmed an activity cycle with a period of 15-16 years, first found in this star by Henry et al. (1995). Also from photometric observations obtained between 1975 and 2001, Lanza et al. (2006) found a long-term activity cycle with a period of $19.5 \pm 2.0$ years.

In order to search for long-term periodic chromospheric variations, we obtained the mean annual $\langle S\rangle$ of the indices plotted in Fig. 6, excluding those points related to the flares mentioned above. The uncertainties of each point S were obtained considering a 10% and a 25% error for the high and low-resolution fluxes respectively.

We analysed the indices $\langle S\rangle$as a function of time with the Lomb-Scargle periodogram (Scargle 1982; Horne & Baliunas 1986), using the algorithm given by Press et al. (1992). This periodogram is shown in Fig. 8a, where it can be seen that there is, indeed, a peak at 6589 days ($\pm $1170 days) with power $P_{\rm LS}=4.56$ and a False Alarm Probability (FAP) of 11%. This FAP was computed following Horne & Baliunas (1986), who assumed a strictly periodic signal with Gaussian noise. This condition, however, is not actually met in this case.

Therefore, we also computed the FAP of this period with a Monte Carlo simulation, with an algorithm similar to the one used by Herbst et al. (2002). We built 10 000 random series from our dataset and we computed the Lomb-Scargle periodogram for each random series. Only in 110 of these periodograms a period was ``detected'' with a power $P>P_{\rm LS}=4.56$. Therefore, in this way we obtained a FAP = 1.1% for the peak of 6589 days in Fig. 8a. In this figure we also show the 10, 50 and 90% FAP levels computed with this method.

This period of $18.05\pm 3.21$ years is in concordance, within the statistical error, with the ones found by the authors cited above.

In Fig. 8b, we plot the mean annual $\langle S\rangle$ phased with the period obtained and we found that a harmonic function fits these points with a reduced $\chi ^2=1.5$, which corroborates the period found.

Berdyugina & Henry (2007) also found a 5-year flip-flop cycle, derived from the cyclic pattern of the peak-to-peak V magnitude which reflects the non-axisymmetric redistribution of the spotted area. The photometric observations analysed by Lanza et al. (2006) also reflected this short-term oscillation with a period of 3-5 years superposed on the long-term spot activity cycle.

To search for a chromospheric flip-flop cycle, we analysed the peak-to-peak Mount Wilson index for several seasons of measurements, since these variations are proportional to the difference of the area of plages between opposite hemispheres of HD 22 468. To do this, we built individual light curves for the sets of data indicated with arrows in Fig. 6, which are shown in Fig. 9. We excluded from these datasets those points associated with flares. Following Díaz et al. (2007), we phased each light-curve with the 2.837-day rotation period and we fitted the data of each light-curve with a harmonic function expressed as:

\begin{displaymath}a_0+a_1 \cos(2\pi\phi)+a_2 \sin(2\pi\phi), \end{displaymath} (4)

where the amplitude A of the curve and its error $\sigma_A$ were computed with these expressions:
$\displaystyle A=\sqrt{a_1^2+a_2^2}~,$     (5)
$\displaystyle \sigma_A=A^{-1}\left[a_1^2\sigma_{a_1}^2+a_2^2\sigma_{a_2}^2+2a_1a_2cov(a_1,a_2)\right]^{1/2},$     (6)

where $\sigma_{a_{1,2}}$ is the standard deviations of a1,2 and ${\rm cov}(a_1,a_2)$is the non-diagonal term of the covariance matrix of a1 and a2.

 \begin{figure} \par\includegraphics[width=8.5cm]{0985fig12.eps} \end{figure} Figure 9:

Variability on HD 22 468 - V711 Tau - HR 1099. Light curves S vs. $\phi $ of the datasets indicated with arrows in Fig. 6. We plotted the harmonic curve that best fit the data, the number in each plot refers to the reduced $\chi ^2$ of the fit.

Open with DEXTER

We analysed the variation of the amplitude against time, using the Lomb-Scargle periodogram, and we obtained that the variability of Spresents a cyclic behaviour with a period of $1207\pm 45$ days ($\sim$3.3 years) with a 5% Monte Carlo FAP, which is consistent with the period obtained by Lanza et al. (2006).

3.2 HD 21 242 - UX Ari

HD 21 242 is a RS CVn-type system composed of a K0IV star and a G5V companion in a 6.483-day orbit (Duemmler & Aarum 2001). There is also a third component, probably in a longer-period orbit around the central binary system (Vogt & Hatzes 1991), which is weakly present in the spectrum (Duemmler & Aarum 2001).

By separating the Ca II K line-core contributions due to each component of the HD 21 242 system, Aarum Ulvås & Engvold (2003) concluded that the secondary star does show signatures of chromospheric activity, but this activity does not influence the average photospheric line-depth. To corroborate if this conclusion is also valid for chromospheric UV lines, we estimated the Mg  II  line-core contributions of the primary and secondary stars to the total flux by fitting each line with two Gaussian functions, as we did for HD 22 468 (Fig. 5). In this case, however, we found that the contribution of the G star is larger and can be up to 20%. Since we could not separate the contribution of both stars in all spectra, we included the total flux in the analysis of this system.

In Fig. 10 we plot the index S obtained from all the IUE rebinned and low-resolution spectra between 1978 and 1996 for both primary and secondary stars. The mean annual Mount Wilson index is $\langle S\rangle=1.28$ during this period.

 \begin{figure} \par\includegraphics[width=8.5cm]{0985fig13.eps} \end{figure} Figure 10:

HD 21 242 - UX Ari. Symbols as in Fig. 6.

Open with DEXTER

We also observe in this figure appreciable short-scale ($\sim$months) variations from 15% to 80%. In particular, during the large flare of 1979, January 1 st (Simon et al. 1980) the S-index reached a value $\sim$300% greater than the mean. From our data, we also obtained that the index S increased $\sim$60% during the flares of 1987, January 6 th (Lang & Willson 1988) and 1991, September 14 th (Sanz-Forcada et al. 2002).

In order to search for a long-term periodic chromospheric pattern, we first obtained the mean annual $\langle S\rangle$ of the indices plotted in Fig. 10, excluding those points related to the flares mentioned above. We analysed the indices $\langle S\rangle$as a function of time with the Lomb-Scargle periodogram, which is shown in Fig. 11a. It can be seen that there is a peak at 2529 days ($\sim$7 years) with a FAP of 18%, computed with the Monte Carlo method explained in the previous section.

To our knowledge, this period has not been reported in the literature before. However, Aarum Ulvås & Henry (2003) analysed several series of photometric observations obtained between 1987 and 2002 by different authors and found that the mean magnitude presents a cyclic behaviour with a period of 25 years and a significance of 99%. Note that a peak at 25 years is also observed in Fig. 11a, although with a FAP > 70%. Conversely, in Fig. 2 of Aarum Ulvås & Henry's paper it can be found a peak at $\sim$5.5 years consistent with our result with a significance close to 90%. On the other hand, the activity cycle we obtained present a minimum between 1980 and 1982 and a maximum between 1993 and 1995 in agreement with Aarum Ulvås & Henry's photometric observations.

   \begin{figure} \par\subfigure[]{\includegraphics[width=4.5cm]{0985fig14.eps} }\hfill \subfigure[]{\includegraphics[width=4.3cm]{0985fig15.eps} }\end{figure} Figure 11:

HD 21 242 - UX Ari. Left: Lomb-Scargle periodogram of the mean annual $\langle S\rangle$ of the data plotted in Fig. 10. The False Alarm Probability (FAP) levels of 20, 50 and 80% are indicated. Right: the mean annual $\langle S\rangle$ of the data plotted in Fig. 10 phased with the period of $2529 \pm 101$ days ( $6.95\pm 0.5$ years). The solid line shows the harmonic curve that best fits the data with a reduced $\chi ^2=3$ and the dashed lines indicate the points that apart $\sigma $ from that fit.
Open with DEXTER

Given the discrepancy between both periods, we analysed whether the IUE observations cover an interval too short and/or too sparse to detect a cycle 25 years long. To do it, taking into account that stellar cycles are not perfect harmonic functions, we assumed that the star has a quasi-periodic cycle similar in shape to the solar one, with a period of 25 years.

Following Cincunegui et al. (2007b), we used the sunspot number $S_{\rm N}$ from the National Geophysical Data Center between 1900 and 2000 and rescaled the series in time to the period P=25 years. To consider data with the same signal-to-noise as ours, we also rescaled the $S_{\rm N}$ values to obtain a time series of the same mean value and standard deviation as our data in Fig. 11b. Then, we took a sample of the rescaled solar data with the same phase intervals as in the IUE observations, and we computed the Lomb-Scargle periodogram. We repeated this procedure 1000 times with random starting dates.

 \begin{figure} \par\includegraphics[width=8.3cm]{0985fig16.eps} \end{figure} Figure 12:

Histogram of the detected periods (with maximum significance) for sample of 1000 different sets the sunspot number re-scaled to 25 years.

Open with DEXTER

For each periodogram, we considered the period with the maximum significance as the detected period. In Fig. 12 we plot the histogram of the 1000 detected periods. In this figure it can be seen that in 556 cases the ``correct'' period between 20 and 27 years has been detected. Of the 444 cases where a ``false'' period is detected, 125 cases correspond to the period 18 years ($\pm $10%), which is the time length of the dataset. In 89 cases we detected a period between 4 and 8 years. Therefore, this test seems to suggest that our data in Fig. 12 are not compatible with a 25-year period with a significance >90%.

Unfortunately, we are not able to detect a flip-flop cycle from the data plotted in Fig. 10, which are insufficient to obtain a significant period in this case.

3.3 II Peg - HD 224 085

HD 224 085 (II Peg) is a single-lined RS CVn-binary system composed by a K2IV star and an unseen companion of an estimated spectral class M0-M3V (Berdyugina et al. 1998).

In Fig. 13 we plot the Mount Wilson index S derived from the IUE high and low-resolution spectra obtained between 1979 and 1995. From these data, we obtained a mean level of activity given by $\langle S\rangle= 1.694$ during this period with a 35% annual variation.

 \begin{figure} \par\includegraphics[width=8.5cm]{0985fig17.eps} \end{figure} Figure 13:

HD 224 085 - II Peg. Symbols as in Fig. 6.
Open with DEXTER

On the other hand, HD 224 085 is a well-known source of flares. These type of events are evident in Fig. 13 as appreciable short-scale variations of the index S. In particular, during the flare of 1981 October (Byrne et al. 1987), the index S increased 40% in 18 h. During the large flares of 1983, February 2 nd (Andrews et al. 1988) and 1992, September 5 th (Byrne et al. 1998), the index S reached a value 105% and 94% larger than the mean respectively.

By analysing 34 years of photometric observations, Rodonò et al. (2000) concluded that the spot pattern of HD 224 085 could be subdivided in two components, which present different cyclic behaviours. They found that one component is uniformly distributed in longitude and seems to be possibly modulated by a $\sim$13.5-year activity cycle; the other component is unevenly distributed and mainly concentrated in three active longitudes. One of these longitudes is characterised by persistent spot activity, but the other two active longitudes are not continuously active, and the spot activity switches cyclically back and forth between them. The duration of the phase when only one longitude is predominantly active is on average $\sim$4.7 years. This result is consistent with the 9.30-year flip-flop cycle previously reported by Berdyugina & Tuominen (1998) for this star.

   \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=4.3cm]{0985fig18.ep... ...hfill \subfigure[]{\includegraphics[width=4.5cm]{0985fig19.eps} }}\end{figure} Figure 14:

HD 224 085 - II Peg. Left: Lomb-Scargle periodogram of the mean annual $\langle S\rangle$ of the data plotted in Fig. 13. The False Alarm Probability (FAP) levels of 10, 50 and 90% are indicated. Right: the mean annual $\langle S\rangle$ of the data plotted in Fig. 13 phased with the period of $7740\pm 207$ days ( $21.21 \pm \rm years$ 0.57 ). The solid line shows the harmonic curve that best fits the observations and the dashed lines indicate the points that apart $\sigma $ from that fit.
Open with DEXTER

To search for cyclic chromospheric patterns, we first studied the mean annual index $\langle S\rangle$ of the data plotted in Fig. 13 as a function of time with the Lomb-Scargle periodogram. In Fig. 14a we observe that the periodogram has a maximum at 7740 days ($\sim$21 years) with a Monte Carlo FAP of 10%. In Fig. 14b we show the mean annual indices $\langle S\rangle$ phased with this period. Although the 7740-day peak is not sharp, only two points (with $\langle S \rangle=1.083$ and $\langle S\rangle=1.778$) apart more than 1$\sigma $ from the harmonic curve in Fig. 14b. Therefore, we can only affirm that the data of HD 224 085 suggest a chromospheric cycle of near 21 years. As far as we know, this period has not been reported in the literature before, but an activity cycle was previously detected in this star (Rodonò et al. 2000; Henry et al. 1995).

 \begin{figure} \par\includegraphics[width=8.3cm]{0985fig20.eps} \end{figure} Figure 15:

Histogram of the detected periods for a sample of 1000 different sets of sunspots number re-sampled with a period of 12 years.
Open with DEXTER

To check if these periods reported in the literature are compatible with the IUE observations, we repeated the analysis done in the previous section. We first rescaled the sunspot number to obtain series with the same mean value and the same standard deviation as our data, and with a period P=12 years, which is the mean period reported in the literature. Then, we calculated the Lomb-Scargle periodogram for 1000 subsets of $S_{\rm N}$ with the same phase intervals as our data plotted in Fig. 14(b).

In Fig. 15 we plot the histogram of the 1000 periods detected and we found that in 602 cases the period detected is 12 years ($\pm $15%). In the histogram there is also a peak for the period $\sim$15 years, which is the time length of the dataset. Only in 89 of the cases a $P'\ge 16$ years ($\pm $10%) is detected, which is the range that include the period we obtained in Fig. 14a. Therefore, this test suggests that the data of HD 224 085 in Fig. 14b are not compatible with a period P=12 years, with a confidence level >90%.

 \begin{figure} \par\includegraphics[width=8.3cm]{0985fig21.eps}\small { } \end{figure} Figure 16:

Variability on HD 224 085- II Peg. Light curves S vs. $\phi $ of the datasets indicated with arrows in Fig. 13. We plotted the harmonic curve that best fit the data, the number in each plot refers to reduced $\chi ^2$ of the fit.

Open with DEXTER

To search for cyclic patterns of shorter periods, we finally analysed the rotational modulation of the index S during the seasons indicated with arrows in Fig. 13. Similarly to the analysis done for HD 22 468, we phased each season's light-curve Svs. time with the 6.724-day rotation period and we fitted each set of data with the harmonic function given in Eq. (4). We analysed the amplitude A (see Eq. (5)) against time with the Lomb-Scargle periodogram and we obtained a period of $3310\pm 253$ days ( $9.07 \pm 0.69$ years) with a Monte Carlo FAP of 7%. This cyclic behaviour seems to be well correlated with the flip-flop cycle of period 9.30 years obtained by Berdyugina & Tuominen (1998) for the spot activity.

4 Conclusions

The main purpose of this paper is to study the short and long-term chromospheric activity of the RS CVn-type stars most observed by IUE.

In the first part of this work we calibrate the Mg II  fluxes observed in low-resolution spectroscopic observations available in the IUE archives with the Mount Wilson index S, which allows us to use these observations for systematic studies of magnetic activity in late-type stars. In particular, we found that the Mg II  line-core fluxes derived from IUE low-resolution spectra could be only considered as an activity indicator in stars cooler than G3.

To complement the calibration between the Mount Wilson index S and the IUE high-resolution Mg  II  line-core fluxes we obtained in Paper I, we analysed a set of 96 nearly simultaneous observations, which belong to 11 G3 to K3 main sequence stars, of the index S and the Mg  II  fluxes derived from IUE high-resolution spectra re-sampled into the low-resolution wavelength domain. We obtained a B-V colour dependent relation between the index S and the IUE low-resolution Mg  II  line-core fluxes.

In the second part of this work, we studied the long and short-term chromospheric activity of the non-eclipsing RS CVn stars most observed by IUE: HD 22 468 (V711 Tau, HR 1099, K1IV+G5V), HD 21 242 (UX Ari, K0IV+G5V) and HD 224 085 (II Peg, K2IV). To do so, we analysed with the Lomb-Scargle periodogram the mean annual index $\langle S\rangle$and the amplitude of the rotational modulation of S of each star.

We obtained a possible chromospheric activity cycle in HD 22 468 with a period of $\sim$18 years and a chromospheric flip-flop cycle of period $\sim$3 years. We also found a flip-flop like cycle with a period of $\sim$9 years in the HD 224 085 data. These results are in agreement with the ones reported in the literature. On the other hand, we also detected a cyclic chromospheric pattern in the mean annual index of HD 224 085 and HD 21 242 with periods of $\sim$21 and $\sim$7 years respectively.

Acknowledgements

We thank the referee Dr. Sergio Messina, for his useful comments and observations.

References

All Tables

Table 1:   Stars used in the Mg II - and the index S calibration.

Table 2:   Long and short term variability records of the RS CVn-type stars most observed by IUE.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm]{0985fig1.eps} \end{figure} Figure 1:

S vs. $F_{\rm Mg II}(B-V)^{3}$ for the set of 117 nearly simultaneous observations of Mount Wilson index and IUE high-resolution Mg  II h and k fluxes for dwarfs we used in Paper I ( $\blacksquare $). We considered errors of 10% for $F_{\rm Mg{\scriptsize{II} \normalsize}}$ and 6% for S. The least square fit (solid line) has a correlation coefficient of 0.95. The dotted lines indicate $\pm $3$\sigma $ from the fit. The triangles ( $\blacktriangle $) represent non-simultaneous Mount Wilson indices and IUE high-resolution Mg  II fluxes of cool sub-giant stars, not used in the calibration.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{0985fig2.eps} \end{figure} Figure 2:

IUE low-resolution spectra of three representative stars: HD 22 049 (K2V), HD 1835 (G3V) and HD 1581 (F9V). Surface flux is obtained according to Eq. (1). The windows used to integrate the line-core emission (2790-2810 Å) are marked on each spectrum.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm]{0985fig3.eps} \end{figure} Figure 3:

IUE low-dispersion (dashed line) and rebinned (solid line) spectra of HD 22 049, both observed on January, 14 th 1984 with a time difference of 1 h.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.2cm]{0985fig4.eps} \end{figure} Figure 4:

S vs. $F^r_{\rm Mg II}(B-V)^{5.65}$ for the stars listed in Table 1. We considered errors of 10% for $F^r_{\rm Mg\scriptsize {II} \normalsize }$ and 6% for S. The least square fit (solid line) has a correlation coefficient of 0.82. The dotted lines indicate the points that apart $\pm $$\sigma $ from the fit. The triangles ( $\blacktriangle $) represent non-simultaneous Mount Wilson indices and IUE high-resolution Mg  II fluxes of cool sub-giant stars with B-V>0.65, not used in the calibration.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.2cm]{0985fig5.eps} \end{figure} Figure 5:

HD 22 468-V711 Tau-HR 1099. Mg II k line fitted with two Gaussian functions, the dashed and solid curves represent the contribution of the primary and secondary star of the system respectively.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{0985fig6.eps} \end{figure} Figure 6:

HD 22 468 - V711 Tau - HR 1099. We indicate the Mount Wilson index Sobtained from the IUE high and low-resolution spectra with triangles ($\triangle $) and circles ($\bigcirc $) respectively. We indicate with arrows the sets of data for which we analysed the short-term variability.
Open with DEXTER
In the text

     \begin{figure} \par\subfigure[]{\includegraphics[width=2.7cm]{0985fig7.eps} }\hs... ...igure[]{\includegraphics[width=2.7cm]{0985fig9.eps} }\hspace*{2mm}\end{figure} Figure 7:

HD 22 468 - V711 Tau - HR 1099. Three flares on 1981, Oct. 3rd; 1992, Dec. 14th and 1994, Aug. 24th.
Open with DEXTER
In the text

    \begin{figure} \par\subfigure[]{\includegraphics[width=4.3cm]{0985fig10.eps} }\h... ...*{1mm} \subfigure[]{\includegraphics[width=4.5cm]{0985fig11.eps} }\end{figure} Figure 8:

HD 22 468 - V711 Tau - HR 1099. Left: Lomb-Scargle periodogram of the mean annual $\langle S\rangle$ of the data plotted in Fig. 6. The False Alarm Probability (FAP) levels of 1, 10, 50 and 90% are indicated. Right: the mean annual $\langle S\rangle$ of the data plotted in Fig. 6 phased with the period of 6589 days. The solid line shows the harmonic curve that best fits the data with a reduced $\chi ^2=1.5$ and the dashed lines indicate the points that apart $\sigma $ from that fit.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{0985fig12.eps} \end{figure} Figure 9:

Variability on HD 22 468 - V711 Tau - HR 1099. Light curves S vs. $\phi $ of the datasets indicated with arrows in Fig. 6. We plotted the harmonic curve that best fit the data, the number in each plot refers to the reduced $\chi ^2$ of the fit.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{0985fig13.eps} \end{figure} Figure 10:

HD 21 242 - UX Ari. Symbols as in Fig. 6.

Open with DEXTER
In the text

    \begin{figure} \par\subfigure[]{\includegraphics[width=4.5cm]{0985fig14.eps} }\hfill \subfigure[]{\includegraphics[width=4.3cm]{0985fig15.eps} }\end{figure} Figure 11:

HD 21 242 - UX Ari. Left: Lomb-Scargle periodogram of the mean annual $\langle S\rangle$ of the data plotted in Fig. 10. The False Alarm Probability (FAP) levels of 20, 50 and 80% are indicated. Right: the mean annual $\langle S\rangle$ of the data plotted in Fig. 10 phased with the period of $2529 \pm 101$ days ( $6.95\pm 0.5$ years). The solid line shows the harmonic curve that best fits the data with a reduced $\chi ^2=3$ and the dashed lines indicate the points that apart $\sigma $ from that fit.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.3cm]{0985fig16.eps} \end{figure} Figure 12:

Histogram of the detected periods (with maximum significance) for sample of 1000 different sets the sunspot number re-scaled to 25 years.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm]{0985fig17.eps} \end{figure} Figure 13:

HD 224 085 - II Peg. Symbols as in Fig. 6.
Open with DEXTER
In the text

    \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=4.3cm]{0985fig18.ep... ...hfill \subfigure[]{\includegraphics[width=4.5cm]{0985fig19.eps} }}\end{figure} Figure 14:

HD 224 085 - II Peg. Left: Lomb-Scargle periodogram of the mean annual $\langle S\rangle$ of the data plotted in Fig. 13. The False Alarm Probability (FAP) levels of 10, 50 and 90% are indicated. Right: the mean annual $\langle S\rangle$ of the data plotted in Fig. 13 phased with the period of $7740\pm 207$ days ( $21.21 \pm \rm years$ 0.57 ). The solid line shows the harmonic curve that best fits the observations and the dashed lines indicate the points that apart $\sigma $ from that fit.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.3cm]{0985fig20.eps} \end{figure} Figure 15:

Histogram of the detected periods for a sample of 1000 different sets of sunspots number re-sampled with a period of 12 years.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.3cm]{0985fig21.eps}\small { } \end{figure} Figure 16:

Variability on HD 224 085- II Peg. Light curves S vs. $\phi $ of the datasets indicated with arrows in Fig. 13. We plotted the harmonic curve that best fit the data, the number in each plot refers to reduced $\chi ^2$ of the fit.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.