| Issue |
A&A
Volume 495, Number 1, February III 2009
|
|
|---|---|---|
| Page(s) | 83 - 112 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361:200810764 | |
| Published online | 14 January 2009 | |
VLT/ISAAC spectra of the H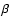 region in intermediate-redshift
quasars
region in intermediate-redshift
quasars![[*]](/icons/foot_motif.gif)
III. H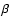 broad-line profile analysis and inferences about BLR structure
broad-line profile analysis and inferences about BLR structure
P. Marziani1 - J. W. Sulentic2 - G. M. Stirpe3 - S. Zamfir2 - M. Calvani1
1 - INAF, Osservatorio Astronomico di Padova,
Vicolo dell' Osservatorio 5, 35122 Padova, Italy
2 -
Department of Physics and Astronomy, University of
Alabama, Tuscaloosa, AL 35487, USA
3 -
INAF, Osservatorio Astronomico di Bologna,
via Ranzani 1, 40127 Bologna, Italy
Received 7 August 2008 / Accepted 18 November 2008
Abstract
Aims. We present new VLT ISAAC spectra for 30 quasars, which we combine with previous data to yield a sample of 53 intermediate-redshift (
![]() -3.0) sources. The sample is used to explore properties of prominent lines in the H
-3.0) sources. The sample is used to explore properties of prominent lines in the H![]() spectral region of these very luminous quasars.
spectral region of these very luminous quasars.
Methods. We compare this data with two large low-redshift (z<0.8) samples in a search for trends over almost 6dex in source luminosity.
Results. We find two major trends: (1) a systematic increase in minimum FWHM H![]() with luminosity (discussed in a previous paper). This lower FWHM envelope is best fit by assuming that the narrowest sources radiate near the Eddington limit, show line emission from a virialized cloud distribution, and obey a well-defined broad line region size vs. luminosity relation. (2) A systematic decrease in equivalent width of [OIII]
with luminosity (discussed in a previous paper). This lower FWHM envelope is best fit by assuming that the narrowest sources radiate near the Eddington limit, show line emission from a virialized cloud distribution, and obey a well-defined broad line region size vs. luminosity relation. (2) A systematic decrease in equivalent width of [OIII]
![]() 4959, 5007 (from
4959, 5007 (from
![]() to
to ![]() 1 Å) with increasing source bolometric luminosity (from
1 Å) with increasing source bolometric luminosity (from
![]() to
to
![]() ). Other identified trends require differntiating between so-called Population A and Bsources. We generate median composite spectra in six luminosity bins to maximize S/N. Population A sources show reasonably symmetric Lorentzian H
). Other identified trends require differntiating between so-called Population A and Bsources. We generate median composite spectra in six luminosity bins to maximize S/N. Population A sources show reasonably symmetric Lorentzian H![]() profiles at all luminosities, while Pop. B sources require two component fits involving an unshifted broad and a redshifted very broad component. Very broad H
profiles at all luminosities, while Pop. B sources require two component fits involving an unshifted broad and a redshifted very broad component. Very broad H![]() increases in strength with increasing
increases in strength with increasing
![]() ,
while the broad component remains constant, resulting in an apparent ``Baldwin effect'' with equivalent width decreasing from
,
while the broad component remains constant, resulting in an apparent ``Baldwin effect'' with equivalent width decreasing from ![]() to
to ![]() 20 Å over our sample luminosity range. The roughly constant equivalent width shown by the H
20 Å over our sample luminosity range. The roughly constant equivalent width shown by the H![]() very broad component implies production in optically-thick, photoionized gas. The onset of the redshifted very broad component appears to be a critical change that occurs near the Pop. A-B boundary at FWHM H
very broad component implies production in optically-thick, photoionized gas. The onset of the redshifted very broad component appears to be a critical change that occurs near the Pop. A-B boundary at FWHM H![]()
![]() 4000 km s-1, which we relate to a critical Eddington ratio (
4000 km s-1, which we relate to a critical Eddington ratio (
![]() ).
).
Key words: galaxies: quasars: general - galaxies: quasars: emission lines - black hole physics - line: profiles
1 Introduction
Much remains to be defined in quasar research even if restricting
attention to the broad emission lines often used to define them.
Their broad line spectra show considerable diversity complicating
attempts to generate composite spectra and making estimates of
intrinsic properties such as black hole mass unreliable. In
addition, the relationship between broad line emitting active galactic nuclei
(type 1 AGN) and various classes of sources that do not show broad
lines (e.g. type 2 AGN, LINERs, Blazars, NLRGs) is still uncertain.
It is difficult to imagine how advances in physical understanding
can come until source phenomenology is clarified. We have focused on
clarifying the phenomenology of type 1 sources because of their
relatively unambiguous broad line signature. Leaving aside
reverberation studies that make use of source variability,
observational advances can be expected to come from two areas of
spectroscopic investigation: (1) inter-line comparisons (from Ly![]() to H
to H![]() )
in terms of relative intensity and profile shape
(e.g., Shang et al. 2007), and (2) moderate dispersion and high S/Nstudies of the H
)
in terms of relative intensity and profile shape
(e.g., Shang et al. 2007), and (2) moderate dispersion and high S/Nstudies of the H![]() spectral region in quasars with
spectral region in quasars with
![]() .
There is a long history of infrared spectroscopy of the Balmer lines
in high-redshift AGN (e.g.,
Carswell et al. 1991; Elston et al. 1994; Murayama et al. 1999; Kuhr et al. 1984; Hill et al. 1993; Espey et al. 1989; Murayama et al. 1998; Baker et al. 1994; Evans et al. 1998), but only
recently has it become possible to obtain spectra with resolution
and S/N comparable to those for optical spectra of low z sources.
The IR spectroscopy of H
.
There is a long history of infrared spectroscopy of the Balmer lines
in high-redshift AGN (e.g.,
Carswell et al. 1991; Elston et al. 1994; Murayama et al. 1999; Kuhr et al. 1984; Hill et al. 1993; Espey et al. 1989; Murayama et al. 1998; Baker et al. 1994; Evans et al. 1998), but only
recently has it become possible to obtain spectra with resolution
and S/N comparable to those for optical spectra of low z sources.
The IR spectroscopy of H![]() at
at ![]() enables one to use the same
line (H
enables one to use the same
line (H![]() ), the same rest-frame determination ([OIII]
), the same rest-frame determination ([OIII]
![]() 4959, 5007 or narrow component of H
4959, 5007 or narrow component of H![]() )
and the same reduction procedures for estimating the central black
hole mass (
)
and the same reduction procedures for estimating the central black
hole mass (
![]() ). Even so, observations of the most numerous and most
luminous quasars at
). Even so, observations of the most numerous and most
luminous quasars at
![]() can only be made when the optical
lines are redshifted into one of the IR bands of high atmospheric
transmission.
can only be made when the optical
lines are redshifted into one of the IR bands of high atmospheric
transmission.
Spectrographs of HST have provided UV coverage of higher ionization
broad lines in low-z type 1 sources (Seyfert 1 and quasars) with
![]() 150 sources having useful measures of CIV
150 sources having useful measures of CIV![]() 1549 (e.g., Marziani et al. 1996; Brotherton et al. 1994; Baskin & Laor 2005; Sulentic et al. 2007).
Almost all of these sources now have matching optical spectroscopic
measures of the H
1549 (e.g., Marziani et al. 1996; Brotherton et al. 1994; Baskin & Laor 2005; Sulentic et al. 2007).
Almost all of these sources now have matching optical spectroscopic
measures of the H![]() region (e.g.,
Marziani et al. 2003a; Baskin & Laor 2005; Shang et al. 2007). Continuing a
litany of difficulties, we note that even some of these UV
observations show marginal S/N, while many do not cover the full
range from Ly
region (e.g.,
Marziani et al. 2003a; Baskin & Laor 2005; Shang et al. 2007). Continuing a
litany of difficulties, we note that even some of these UV
observations show marginal S/N, while many do not cover the full
range from Ly![]() to 3500 Å. Optical coverage is usually not synoptical.
This makes detailed
intercomparisons of the strongest high and low ionization broad
lines possible for only a few dozen objects at best. The lack of
spectra covering the rest frame from Ly
to 3500 Å. Optical coverage is usually not synoptical.
This makes detailed
intercomparisons of the strongest high and low ionization broad
lines possible for only a few dozen objects at best. The lack of
spectra covering the rest frame from Ly![]() to H
to H![]() is
unfortunate since line intensity and profile ratios provide a wealth
of physical constraints. The ability to compare lines from ions of
widely different ionization potentials has helped elucidating for two main
emitting regions within the broad line region (BLR): (a) one
responsible for the production of low-ionization lines (LIL) like
FeII, H
is
unfortunate since line intensity and profile ratios provide a wealth
of physical constraints. The ability to compare lines from ions of
widely different ionization potentials has helped elucidating for two main
emitting regions within the broad line region (BLR): (a) one
responsible for the production of low-ionization lines (LIL) like
FeII, H![]() as well as MgII
as well as MgII![]() 2800, and (b) one that emits mainly lines
(CIV
2800, and (b) one that emits mainly lines
(CIV![]() 1549, He II
1549, He II![]() 4686) from ions of high ionization potential (HIL; e.g.,
Collin-Souffrin et al. 1988). Meaningful line profile studies begin with
observations of CIV
4686) from ions of high ionization potential (HIL; e.g.,
Collin-Souffrin et al. 1988). Meaningful line profile studies begin with
observations of CIV![]() 1549and H
1549and H![]() as the most typical HIL and LIL.
as the most typical HIL and LIL.
Our attempt at clarifying type 1 AGN phenomenology involves the
Eigenvector 1 formalism of Boroson & Green (1992) and was later
expanded into 4 dimensions (4DE1). The latter focused on four
parameters including measures of H![]() and FeII (Sulentic et al. 2000a,2007,2000b). Changes
in the width and relative strength of H
and FeII (Sulentic et al. 2000a,2007,2000b). Changes
in the width and relative strength of H![]() and FeII lines
appear to be primarily related to the Eddington ratio convolved with
source orientation (Boroson 2005; Shang et al. 2003; Yip et al. 2004; Collin et al. 2006; Marziani et al. 2003b).
The 4DE1 studies also introduced the concept of two quasar populations A
and B that maximize phenomenological differences and possibly
identify sources with higher and lower Eddington ratios,
respectively. The width of broad H
and FeII lines
appear to be primarily related to the Eddington ratio convolved with
source orientation (Boroson 2005; Shang et al. 2003; Yip et al. 2004; Collin et al. 2006; Marziani et al. 2003b).
The 4DE1 studies also introduced the concept of two quasar populations A
and B that maximize phenomenological differences and possibly
identify sources with higher and lower Eddington ratios,
respectively. The width of broad H![]() (FWHM or 2
(FWHM or 2![]() profile
moment
profile
moment ![]() )
have been widely used as measures of velocity
dispersion in the line-emitting gas (see
e.g. Peterson et al. 2004; Vestergaard & Peterson 2006; Sulentic et al. 2006),
allowing what are thought to be the most reliable estimates of black
hole mass in low z quasars. This approach has motivated us to seek
similar measures in sources with the highest possible redshift
rather than using other lines as H
)
have been widely used as measures of velocity
dispersion in the line-emitting gas (see
e.g. Peterson et al. 2004; Vestergaard & Peterson 2006; Sulentic et al. 2006),
allowing what are thought to be the most reliable estimates of black
hole mass in low z quasars. This approach has motivated us to seek
similar measures in sources with the highest possible redshift
rather than using other lines as H![]() surrogates.
surrogates.
In this paper we leave aside inter-line comparisons and focus on
the H![]() spectral range in low and in intermediate-to-high z quasars (
spectral range in low and in intermediate-to-high z quasars (![]() ). Near IR spectra of the latter were obtained
with the infrared spectrometer ISAAC on ESO VLT Unit 1. The high S/N and resolution
of the new observations allow a meaningful comparison with
measures obtained for low z sources. Low z measures come from two
samples: (1) an atlas of bright sources with
). Near IR spectra of the latter were obtained
with the infrared spectrometer ISAAC on ESO VLT Unit 1. The high S/N and resolution
of the new observations allow a meaningful comparison with
measures obtained for low z sources. Low z measures come from two
samples: (1) an atlas of bright sources with
![]() (Marziani et al. 2003a, hereafter, ATLAS sample) and (2)
a magnitude-limited sample of 321 SDSS quasars (m
(Marziani et al. 2003a, hereafter, ATLAS sample) and (2)
a magnitude-limited sample of 321 SDSS quasars (m
![]() ,
z<0.7 from Zamfir et al. 2008, hereafter SDSS sample).
,
z<0.7 from Zamfir et al. 2008, hereafter SDSS sample).
In two previous papers we focused on a search for luminosity
effects involving H![]() ,
FeII
,
FeII
![]() ,
and [OIII]
,
and [OIII]
![]() 4959, 5007 (Sulentic et al. 2004, hereafter
Paper I), as well as on the use of H
4959, 5007 (Sulentic et al. 2004, hereafter
Paper I), as well as on the use of H![]() as a virial
black hole mass estimator (Sulentic et al. 2006, hereafter Paper
II). This paper presents observations and reductions
for 30 additional sources (
z= 1.08- 3.09; Sect. 2). We
briefly discuss the H
as a virial
black hole mass estimator (Sulentic et al. 2006, hereafter Paper
II). This paper presents observations and reductions
for 30 additional sources (
z= 1.08- 3.09; Sect. 2). We
briefly discuss the H![]() ,
FeII, and narrow-line measures (Sect. 3) and then show that the addition of 27 new sources to the
VLT sample reinforces the luminosity trends described in Paper I
(Sect. 4). We then consider the distribution of VLT sources in
the optical plane of 4DE1. Median 4DE1 and luminosity-binned
composite spectra are discussed in the context of the 4DE1
Population A-B concept (Sulentic et al. 2008,2000a).
In Sect. 5 we use the binned composite
spectra to decompose H
,
FeII, and narrow-line measures (Sect. 3) and then show that the addition of 27 new sources to the
VLT sample reinforces the luminosity trends described in Paper I
(Sect. 4). We then consider the distribution of VLT sources in
the optical plane of 4DE1. Median 4DE1 and luminosity-binned
composite spectra are discussed in the context of the 4DE1
Population A-B concept (Sulentic et al. 2008,2000a).
In Sect. 5 we use the binned composite
spectra to decompose H![]() and make estimates of black hole mass
and make estimates of black hole mass
![]() and Eddington ratio
and Eddington ratio
![]() for Pop. A and B sources.
for Pop. A and B sources.
Table 1: Basic properties of sources and log of observations
2 Observations and data reduction
Spectra for intermediate-high redshift sources were obtained
between 07/2004 and 07/2006 in service mode with the infrared
spectrometer ISAAC mounted on VLT1 (ANTU) at the European Southern
Observatory. Table 1 summarizes the new
observations. The basic format is given below the table, following
almost exactly Table 1 of Paper II. In addition to the format
provided below Table 1, we note that Col. (3) lists
the blue apparent magnitude taken from Hamburg-ESO survey papers
(Wisotzki et al. 2000; Reimers et al. 1996), while Col. (4) lists the
source redshift z computed as described in Sect. 2.2.
Column 8 lists the radio-loudness parameter ![]() defined as the
ratio between the specific flux at 6 cm and 4400 Å in the rest
frame. We applied a k-correction for both the radio and optical
data. In the case of the radio data:
defined as the
ratio between the specific flux at 6 cm and 4400 Å in the rest
frame. We applied a k-correction for both the radio and optical
data. In the case of the radio data:
![]() where the radio spectral-index
is
where the radio spectral-index
is
![]() .
Only 14 of the sources have radio detections, and
1.4 GHz upper limits were derived for undetected sources from the
NVSS detection threshold or the Sydney University Molonglo Sky
Survey (SUMSS, Bock et al. 1999). Two sources are formally
radio-loud following our definitions (Zamfir et al. 2008).
.
Only 14 of the sources have radio detections, and
1.4 GHz upper limits were derived for undetected sources from the
NVSS detection threshold or the Sydney University Molonglo Sky
Survey (SUMSS, Bock et al. 1999). Two sources are formally
radio-loud following our definitions (Zamfir et al. 2008).
Each spectrum corresponds to a wavelength range (IR windows sZ, J,
sH, sK; Col. (10) of Table 1) that covers all or part of
the region involving H![]() Fe II
Fe II![]() 4570 and/or Fe
II
4570 and/or Fe
II![]() 5130. Reduction of quasar spectra and standard stars
followed exactly the same procedures as described in Papers I and II.
Wavelength calibration yielded rms residuals of 0.4, 0.6, and
0.9 Å in the sZ, J, and sH windows, respectively. Absolute flux
measures will be inaccurate because atmospheric seeing almost
always exceeded the slit width (
5130. Reduction of quasar spectra and standard stars
followed exactly the same procedures as described in Papers I and II.
Wavelength calibration yielded rms residuals of 0.4, 0.6, and
0.9 Å in the sZ, J, and sH windows, respectively. Absolute flux
measures will be inaccurate because atmospheric seeing almost
always exceeded the slit width (![]() 0
0
![]() 6), resulting in
significant light loss. Small offsets were present in the
wavelength calibration because the arc lamp frames were obtained
in daytime and therefore usually after grism movement. A
correction for these shifts was obtained by measuring the
centroids of 2-3 OH sky lines against the arc calibration and
calculating the average difference.
6), resulting in
significant light loss. Small offsets were present in the
wavelength calibration because the arc lamp frames were obtained
in daytime and therefore usually after grism movement. A
correction for these shifts was obtained by measuring the
centroids of 2-3 OH sky lines against the arc calibration and
calculating the average difference.
2.1 Sample considerations
All 53 sources in the VLT-ISAAC sample were selected from the
Hamburg-ESO (HE) quasar survey, which was a color-selected and
magnitude-limited (
![]() )
quasar survey
(Wisotzki et al. 2000). Thirty-one new spectra are presented for
30 sources in Sect. 1 with 27 sources not previously
observed. They are merged with Papers I and II measures to
yield a total sample of 53 sources. Two of the new observations
involve previously observed sources that were discussed in Paper
I. The independent pairs of measures provide a valuable
consistency check and are treated as independent data points in
our statistical analysis of Sect. 4. Two new spectra
obtained for HE 1505+0212 are listed in Table 1 with
average values used in the analysis. HE 0353-3919 (Paper I) has
been excluded from quantitative analysis because its H
)
quasar survey
(Wisotzki et al. 2000). Thirty-one new spectra are presented for
30 sources in Sect. 1 with 27 sources not previously
observed. They are merged with Papers I and II measures to
yield a total sample of 53 sources. Two of the new observations
involve previously observed sources that were discussed in Paper
I. The independent pairs of measures provide a valuable
consistency check and are treated as independent data points in
our statistical analysis of Sect. 4. Two new spectra
obtained for HE 1505+0212 are listed in Table 1 with
average values used in the analysis. HE 0353-3919 (Paper I) has
been excluded from quantitative analysis because its H![]() profile is compromised by a gap in coverage between the sZ and Z bands (see Fig. 2 of Paper I). The resulting sample of 52 sources
(and 54 data points) is henceforth referred to as the ISAAC
sample.
profile is compromised by a gap in coverage between the sZ and Z bands (see Fig. 2 of Paper I). The resulting sample of 52 sources
(and 54 data points) is henceforth referred to as the ISAAC
sample.
The samples of Marziani et al. (2003a, ATLAS) and
Zamfir et al. (2008, SDSS) are used as low-z spectroscopic
comparison samples. SDSS is more complete, involving the 321 brightest g-band selected (![]() 17.0) in SDSS DR5 with
17.0) in SDSS DR5 with ![]() ,
while the ATLAS sample involves a more heterogeneous
selection of 215 quasars largely brighter than
,
while the ATLAS sample involves a more heterogeneous
selection of 215 quasars largely brighter than
![]() .
We make wide use of the SDSS sample in this study because of
its higher level of completeness, larger number of sources, and
because results from the ATLAS sample have been already presented in
Papers I and II. Both the SDSS and ATLAS data enable (1) accurate
measurements of H
.
We make wide use of the SDSS sample in this study because of
its higher level of completeness, larger number of sources, and
because results from the ATLAS sample have been already presented in
Papers I and II. Both the SDSS and ATLAS data enable (1) accurate
measurements of H![]() and FeII
and FeII
![]() emission, (2) decomposition of
the broad H
emission, (2) decomposition of
the broad H![]() profile, and (3) measures of the narrow H
profile, and (3) measures of the narrow H![]() component (H
component (H
![]() )
and [OIII]
)
and [OIII]
![]() 4959, 5007 lines.
The SDSS sample suffers a
strong Malmquist bias. The ATLAS sample shows a more uniform
luminosity distribution making a correlation analysis less biased.
It will be used in the analysis of luminosity trends involving FWHM
H
4959, 5007 lines.
The SDSS sample suffers a
strong Malmquist bias. The ATLAS sample shows a more uniform
luminosity distribution making a correlation analysis less biased.
It will be used in the analysis of luminosity trends involving FWHM
H![]() (Sect. 5).
(Sect. 5).
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.3cm,clip]{0764f01a.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg53.gif) |
Figure 1:
Calibrated VLT-ISAAC spectra for 30 new
intermediate-redshift quasars. Abscissæ are rest-frame
wavelength in Å, ordinates are rest-frame specific flux in units
of 10-15 erg s-1 cm-1 Å-1. The spectrum behavior of HE 0035-2853, HE 0043-2300, HE 0058-3231 is fully unreliable beyond |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.3cm,clip]{0764f01b.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg54.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.3cm,clip]{0764f01c.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg55.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.8cm,height=16.8cm,clip]{0764f02a.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg56.gif) |
Figure 2:
Continuum-subtracted spectra. Lefthand panels: the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.4cm,clip]{0764f02b.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg57.gif) |
Figure 2: continued. |
| Open with DEXTER | |
| Figure 2: continued. |
|
| Open with DEXTER | |
Table 2: Measurements of fluxes, equivalent qidths and FWHM of strongest lines.
Table 3: Measurements of fluxes and equivalent widths of narrow lines
Table 4:
H![]() Line profile measurements.
Line profile measurements.
Table 5:
H![]() Line centroids at different fractional heights
Line centroids at different fractional heights
![\begin{figure}
\par\hspace*{2mm}
\includegraphics[width=7.8cm,height=7.8cm, angl...
...}\includegraphics[width=7.8cm,height=7.8cm, angle=0]{0764f03d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg254.gif) |
Figure 3:
FWHM(H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f04.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg255.gif) |
Figure 4:
The optical plane of Eigenvector 1 with the VLT sources presented in this paper and in Papers I and II (large filled circles, red in the online version of the paper), and the SDSS sample of Zamfir et al. 2008, small gray circles). Circled data points identify RL sources. Abscissa is Fe II |
| Open with DEXTER | |
2.2 Data analysis
Analysis of ISAAC spectra made use of IRAF tasks to
accomplish continuum and FeII
![]() modeling, as well as
subtraction. The specfit task was employed to make a
reliable model of the H
modeling, as well as
subtraction. The specfit task was employed to make a
reliable model of the H![]() spectral region. The
simultaneous fitting of continuum and FeII should
be less dependent on subjective evaluations by the
observer. We assume that the continuum underlying the H
spectral region. The
simultaneous fitting of continuum and FeII should
be less dependent on subjective evaluations by the
observer. We assume that the continuum underlying the H![]() spectral region is a power law of variable slope. Continuum
subtraction has severe limitations due to the small bandwidth of
our spectra and to (unknown) internal reddening effects. However,
specfit usually found a plausible continuum (see Fig. 1). Estimation of continuum subtraction
uncertainty due to S/N involves choosing continuum fluxes at about
-3
spectral region is a power law of variable slope. Continuum
subtraction has severe limitations due to the small bandwidth of
our spectra and to (unknown) internal reddening effects. However,
specfit usually found a plausible continuum (see Fig. 1). Estimation of continuum subtraction
uncertainty due to S/N involves choosing continuum fluxes at about
-3![]() (minimum) and +3
(minimum) and +3![]() (maximum) levels where
(maximum) levels where ![]() is the standard deviation of the most likely continuum
choice. Uncertainties of continuum placement were empirically
defined from the difference between extreme high/low continua and
the most probable one derived by specfit.
is the standard deviation of the most likely continuum
choice. Uncertainties of continuum placement were empirically
defined from the difference between extreme high/low continua and
the most probable one derived by specfit.
The FeII
![]() emission was modeled using a scaled and broadened template
as previously employed by Marziani et al. (2003a). An important
change was introduced to the FeII template emission underlying
H
emission was modeled using a scaled and broadened template
as previously employed by Marziani et al. (2003a). An important
change was introduced to the FeII template emission underlying
H![]() as described below (Sect. 2.3). We stress again that a
notable advantage of specfit is that the scaled and broadened
template can be simultaneously fit over
as described below (Sect. 2.3). We stress again that a
notable advantage of specfit is that the scaled and broadened
template can be simultaneously fit over ![]() 1000 Å with a
power-law continuum, the H
1000 Å with a
power-law continuum, the H![]() profile and the narrow lines (H
profile and the narrow lines (H
![]() ,
[OIII]
,
[OIII]
![]() 4959, 5007, Fe VII
4959, 5007, Fe VII![]() 5160, Fe VII
5160, Fe VII![]() 5177). The strong
FeII blue blend (4450-4680 Å: Fe II
5177). The strong
FeII blue blend (4450-4680 Å: Fe II![]() 4570) was measured as an estimator of the FeII
4570) was measured as an estimator of the FeII
![]() strength. The Gaussian broadening factor from the best-fitting template yields an
estimate of FWHM FeII. A careful estimate of minimum and maximum
plausible broadening factors was made to derive
strength. The Gaussian broadening factor from the best-fitting template yields an
estimate of FWHM FeII. A careful estimate of minimum and maximum
plausible broadening factors was made to derive ![]()
![]() uncertainties. The blue side of the spectrum including
Fe II
uncertainties. The blue side of the spectrum including
Fe II![]() 4570 is missing or only marginally covered in several sources. In
these cases the best template fit was achieved for the red blend
(Fe II
4570 is missing or only marginally covered in several sources. In
these cases the best template fit was achieved for the red blend
(Fe II![]() 5130 in the range 5200-5600 Å) and Fe II
5130 in the range 5200-5600 Å) and Fe II![]() 4570 was estimated assuming a fixed ratio between the red and blue
blends. Figure 2 shows the estimated FeII emission.
4570 was estimated assuming a fixed ratio between the red and blue
blends. Figure 2 shows the estimated FeII emission.
The H![]() profile was modeled with (1a) a core Lorentzian component plus a
weaker/broader Gaussian on the blue (usually) or on the red side of
the core or, alternatively, (1b) the sum of two Gaussians one always very broad
and showing non-negligible velocity shift relative to a narrower
core component; (2) a narrow component (H
profile was modeled with (1a) a core Lorentzian component plus a
weaker/broader Gaussian on the blue (usually) or on the red side of
the core or, alternatively, (1b) the sum of two Gaussians one always very broad
and showing non-negligible velocity shift relative to a narrower
core component; (2) a narrow component (H
![]() ). We do not attribute any physical meaning to the ``blind'' decompositions performed with specfit in the case of
the double Gaussian fits for individual sources. The two types of
fit provide the simplest empirical description of broad H
). We do not attribute any physical meaning to the ``blind'' decompositions performed with specfit in the case of
the double Gaussian fits for individual sources. The two types of
fit provide the simplest empirical description of broad H![]() profiles in the majority of sources. The H
profiles in the majority of sources. The H![]() profile was fit with a
high-order spline function (IRAF task sfit), in a few
cases where the model fits showed significant deviations from the
actual profile. Spline functions do not yield a model fit but only
an empirical fit that smooths noise and reproduces the main features
and inflections in H
profile was fit with a
high-order spline function (IRAF task sfit), in a few
cases where the model fits showed significant deviations from the
actual profile. Spline functions do not yield a model fit but only
an empirical fit that smooths noise and reproduces the main features
and inflections in H![]() .
The spline fit approach was the one used in
our previous work (Marziani et al. 2003a) where sources with FWHM
H
.
The spline fit approach was the one used in
our previous work (Marziani et al. 2003a) where sources with FWHM
H![]()
![]() and
and ![]() 4000 km s-1 favored Lorentzian and double
Gaussian fits respectively. Systematic differences in flux and W measurements as well as in line profile parameters between the
empirical and specfit approach occur since the extended wings
of Gaussian and especially Lorentzian profiles lead to a lower
continuum placement. The effect however is within the estimated
measurement uncertainty.
4000 km s-1 favored Lorentzian and double
Gaussian fits respectively. Systematic differences in flux and W measurements as well as in line profile parameters between the
empirical and specfit approach occur since the extended wings
of Gaussian and especially Lorentzian profiles lead to a lower
continuum placement. The effect however is within the estimated
measurement uncertainty.
The [OIII]
![]() 4959, 5007 lines were also simultaneously modeled with the
following conditions strictly enforced during the fitting procedure:
(1) the flux ratio between [ OIII]
4959, 5007 lines were also simultaneously modeled with the
following conditions strictly enforced during the fitting procedure:
(1) the flux ratio between [ OIII]![]() 5007 and [ OIII]
5007 and [ OIII]![]() 4959
4959
![]() 3, (2) both lines should show identical profiles. It was
often necessary to include a ``semi-broad'' and/or blueshifted
component to model the [OIII]
3, (2) both lines should show identical profiles. It was
often necessary to include a ``semi-broad'' and/or blueshifted
component to model the [OIII]
![]() 4959, 5007 profile since evidence of a strong
blue asymmetry was observed in several cases. This approach yields
a satisfactory reproduction of the observed [OIII]
4959, 5007 profile since evidence of a strong
blue asymmetry was observed in several cases. This approach yields
a satisfactory reproduction of the observed [OIII]
![]() 4959, 5007 profiles
within our resolution and S/N limits. It is again an empirical
method to properly estimate the total [OIII]
4959, 5007 profiles
within our resolution and S/N limits. It is again an empirical
method to properly estimate the total [OIII]
![]() 4959, 5007 strength and
describe the line profile shape. We do not make any assumptions
about the actual nature of [OIII]
4959, 5007 strength and
describe the line profile shape. We do not make any assumptions
about the actual nature of [OIII]
![]() 4959, 5007 emission, which will be the
subject of a separate paper.
4959, 5007 emission, which will be the
subject of a separate paper.
2.3 The Fe II
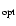 template
template
Considerable attention has been given to theoretical and empirical
estimations of FeII
![]() emission in the spectral region of H
emission in the spectral region of H![]() ,
for a number of scientific (i.e., obtain a diagnostic of the BLR)
and technical goals. Theoretical calculations of FeII emission,
assuming the predominance of photoionization in the broad line
region have greatly improved in the past decade
(Sigut & Pradhan 2003; Sigut et al. 2004; Verner et al. 1999) with a 371-level model of the
Fe+ ion presently included in the photionization code CLOUDY v. 07.01 (Ferland et al. 1998). A detailed analysis of the
FeII emission in I Zw 1 (Véron-Cetty et al. 2004) reveals rich
and complex emission from several line systems, each associated
with a well-defined redshift and FWHM. In the case of sources with
larger FWHM and data with intermediate resolution, as well as
average S/N, an analysis as detailed as that made for I Zw 1
(Véron-Cetty et al. 2004) cannot be done. The FeII
,
for a number of scientific (i.e., obtain a diagnostic of the BLR)
and technical goals. Theoretical calculations of FeII emission,
assuming the predominance of photoionization in the broad line
region have greatly improved in the past decade
(Sigut & Pradhan 2003; Sigut et al. 2004; Verner et al. 1999) with a 371-level model of the
Fe+ ion presently included in the photionization code CLOUDY v. 07.01 (Ferland et al. 1998). A detailed analysis of the
FeII emission in I Zw 1 (Véron-Cetty et al. 2004) reveals rich
and complex emission from several line systems, each associated
with a well-defined redshift and FWHM. In the case of sources with
larger FWHM and data with intermediate resolution, as well as
average S/N, an analysis as detailed as that made for I Zw 1
(Véron-Cetty et al. 2004) cannot be done. The FeII
![]() template
approach works satisfactorily for the heterogeneous variety of
type-1 AGN (Zamfir et al. 2008; Marziani et al. 2003a; Boroson & Green 1992) with the probable
exception of some outliers and extremely strong FeII emitters.
template
approach works satisfactorily for the heterogeneous variety of
type-1 AGN (Zamfir et al. 2008; Marziani et al. 2003a; Boroson & Green 1992) with the probable
exception of some outliers and extremely strong FeII emitters.
There is, however, a major problem associated with the empirical
template: it is difficult to estimate the FeII emission under
the H![]() line. Our empirical template differs from that of Boroson & Green (1992)
because of lower FeII emission under H
line. Our empirical template differs from that of Boroson & Green (1992)
because of lower FeII emission under H![]() and from
Véron-Cetty et al. (2004) for the opposite reason. The new analysis
of the I Zw 1 spectrum by Véron-Cetty et al. (2004), coupled with
photoionization models, suggests that emission under H
and from
Véron-Cetty et al. (2004) for the opposite reason. The new analysis
of the I Zw 1 spectrum by Véron-Cetty et al. (2004), coupled with
photoionization models, suggests that emission under H![]() should
not be very strong. Therefore, the strength of the FeII lines
underlying H
should
not be very strong. Therefore, the strength of the FeII lines
underlying H![]() has been computed with an appropriate
photoionization model. In the context of photoionization the
present understanding of the FeIIemitting region suggests low
ionization and high electron density
(Bruhweiler & Verner 2008; Verner et al. 1999). We assumed an ionization
parameter
has been computed with an appropriate
photoionization model. In the context of photoionization the
present understanding of the FeIIemitting region suggests low
ionization and high electron density
(Bruhweiler & Verner 2008; Verner et al. 1999). We assumed an ionization
parameter
![]() ,
and electron density [cm-3]
,
and electron density [cm-3]
![]() .
This model provides an intensity
ratio between FeII m29 and H
.
This model provides an intensity
ratio between FeII m29 and H![]() consistent with that measured
in I Zw1. These improvements in the template do not significantly
affect our
consistent with that measured
in I Zw1. These improvements in the template do not significantly
affect our
![]() = F(Fe II
= F(Fe II![]() 4570)/F(H
4570)/F(H![]() )
) ![]() W(Fe II
W(Fe II![]() 4570)/W(H
4570)/W(H![]() )
measurements. Even in the strongest FeII emitters (
)
measurements. Even in the strongest FeII emitters (
![]()
![]() ),
the change in H
),
the change in H![]() intensity is much lower than the associated
uncertainty. The effect on H
intensity is much lower than the associated
uncertainty. The effect on H![]() profile is to lower the FeII
profile is to lower the FeII
![]() subtraction on the red side of H
subtraction on the red side of H![]() ,
making it stronger. The change
with respect to the previous template is negligible in the case of
weak emission but may not be so if FeII is strong and relatively
narrow (see Sect. 4.2). A blueshifted, broad component ascribed
to a wind (Marziani et al. 2008; Sulentic et al. 2002) is affected
qualitatively by the new FeII
,
making it stronger. The change
with respect to the previous template is negligible in the case of
weak emission but may not be so if FeII is strong and relatively
narrow (see Sect. 4.2). A blueshifted, broad component ascribed
to a wind (Marziani et al. 2008; Sulentic et al. 2002) is affected
qualitatively by the new FeII
![]() subtraction, although there are
several examples of individual
ISAAC sources (HE 0248-3628, HE 0512-3329 in Paper II) that
unambiguously confirm the existence of such a component, which is obvious in
Ly
subtraction, although there are
several examples of individual
ISAAC sources (HE 0248-3628, HE 0512-3329 in Paper II) that
unambiguously confirm the existence of such a component, which is obvious in
Ly![]() and especially CIV
and especially CIV![]() 1549 for several low-z sources (Marziani et al. 2008).
1549 for several low-z sources (Marziani et al. 2008).
3 Reduced spectra and line measures
3.1 Redshift determination and rest-frame corrections
Determining the rest frame is important in quasar spectroscopy
because both broad and narrow emission lines are known to show
velocity displacements relative to one another. We followed our
standard procedure (Marziani et al. 2003a) and adopted the H![]() peak redshift (
peak redshift (
![]() Å) as rest frame for our new
sources. The [OIII]
Å) as rest frame for our new
sources. The [OIII]
![]() 4959, 5007 lines (
4959, 5007 lines (
![]() ,
5006.85 Å) were only
used when they gave the same value as H
,
5006.85 Å) were only
used when they gave the same value as H![]() (see Col. (6) of
Table 1). They sometimes show a blueshift relative to
the H
(see Col. (6) of
Table 1). They sometimes show a blueshift relative to
the H![]() peak and are designated as ``blue outliers'' in extreme
cases (Boroson 2005; Aoki et al. 2005; Komossa et al. 2008; Zamanov et al. 2002; Marziani et al. 2003b). Blue
outliers usually show FWHM H
peak and are designated as ``blue outliers'' in extreme
cases (Boroson 2005; Aoki et al. 2005; Komossa et al. 2008; Zamanov et al. 2002; Marziani et al. 2003b). Blue
outliers usually show FWHM H![]() < 2000 km s-1. but caution should be used
when adopting [ OIII]
< 2000 km s-1. but caution should be used
when adopting [ OIII]![]() 5007 or H
5007 or H![]() for rest-frame determination
(see also Hu et al. 2008a, who suggest a systematic FeII
for rest-frame determination
(see also Hu et al. 2008a, who suggest a systematic FeII
![]() redshift with respect to the quasar rest frame). The adopted
z estimates were used to de-redshift the spectra while the IRAF dopcor task applied a (1+z)3 correction to convert
observed specific fluxes into rest-frame values.
Figure 1 shows the flux and wavelength calibrated
spectra.
redshift with respect to the quasar rest frame). The adopted
z estimates were used to de-redshift the spectra while the IRAF dopcor task applied a (1+z)3 correction to convert
observed specific fluxes into rest-frame values.
Figure 1 shows the flux and wavelength calibrated
spectra.
3.2 Optical Fe II lines
Figure 2 shows the continuum-subtracted spectra (left
panels) with the adopted FeII
![]() template model superimposed.
Table 2 provides flux and equivalent width of H
template model superimposed.
Table 2 provides flux and equivalent width of H![]() ,
as well as flux and FWHM of Fe II
,
as well as flux and FWHM of Fe II![]() 4570. The data format is explained
in the footnotes of each table. Care should be applied in using
the FWHM values for Fe II
4570. The data format is explained
in the footnotes of each table. Care should be applied in using
the FWHM values for Fe II![]() 4570. These values were obtained through a
4570. These values were obtained through a
![]() minimization in the specfit procedure and
therefore should at least be free of any subjective bias.
Uncertainties were estimated by superimposing a sequence of
templates with different FWHM values on the optimal Fe II
minimization in the specfit procedure and
therefore should at least be free of any subjective bias.
Uncertainties were estimated by superimposing a sequence of
templates with different FWHM values on the optimal Fe II![]() 4570 spectrum and estimating the
4570 spectrum and estimating the ![]()
![]() confidence levels where
FWHM FeII became unacceptably large or small. We find that
FWHM(Fe II
confidence levels where
FWHM FeII became unacceptably large or small. We find that
FWHM(Fe II![]() 4570) is systematically smaller than FWHM(H
4570) is systematically smaller than FWHM(H![]() )
and that
the median value is
)
and that
the median value is ![]() 4000 km s-1. Uncertainties of
the individual FeIImeasurements are quite large, allowing only
statistical inferences to be made.
4000 km s-1. Uncertainties of
the individual FeIImeasurements are quite large, allowing only
statistical inferences to be made.
3.3 Narrow lines
Table 3 reports the flux and equivalent widths
values for H
![]() and [ OIII]
and [ OIII]![]() 5007. The narrow component of H
5007. The narrow component of H![]() is weak/marginal in most
sources and undetected in 4 sources.
The
total flux values for [ OIII]
is weak/marginal in most
sources and undetected in 4 sources.
The
total flux values for [ OIII]![]() 5007 often include narrow and semi-broad
components that are required to adequately fit the [OIII]
5007 often include narrow and semi-broad
components that are required to adequately fit the [OIII]
![]() 4959, 5007 line
profiles using specfit. Differences between the H
4959, 5007 line
profiles using specfit. Differences between the H
![]() and
[OIII]
and
[OIII]
![]() 4959, 5007 profiles indicate that crude intensity ratios [ OIII]
4959, 5007 profiles indicate that crude intensity ratios [ OIII]![]() 5007/H
5007/H
![]() may not be meaningful. The ratio [ OIII]
may not be meaningful. The ratio [ OIII]![]() 5007/H
5007/H
![]() has a clear meaning
only if there is a redshift and FWHM consistency between [OIII]
has a clear meaning
only if there is a redshift and FWHM consistency between [OIII]
![]() 4959, 5007 and H
4959, 5007 and H![]() .
.
3.4 H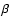 line profiles
line profiles
Measurements of the broad H![]() profile including FWHM and other
important line parameters such as asymmetry index, kurtosis and line
centroid at various fractional intensities were obtained using a
FORTRAN program developed for the purpose. These parameters
are the same as defined in Paper I and are given in Tables 4
and 5. The righthand panels of
Fig. 2 emphasize the shape of H
profile including FWHM and other
important line parameters such as asymmetry index, kurtosis and line
centroid at various fractional intensities were obtained using a
FORTRAN program developed for the purpose. These parameters
are the same as defined in Paper I and are given in Tables 4
and 5. The righthand panels of
Fig. 2 emphasize the shape of H![]() for each source.
Table 5 lists measurements of the H
for each source.
Table 5 lists measurements of the H
![]() centroid
at various fractional intensities (in km s-1). Each line measurement
in Tables 4 and 5 is followed in the
next column by its appropriate uncertainty at the
centroid
at various fractional intensities (in km s-1). Each line measurement
in Tables 4 and 5 is followed in the
next column by its appropriate uncertainty at the ![]() confidence level. The uncertainties on line profile parameters were
estimated by changing the fractional height by
confidence level. The uncertainties on line profile parameters were
estimated by changing the fractional height by ![]() 0.05. All of
these measures are affected by the compositeness of the broad H
0.05. All of
these measures are affected by the compositeness of the broad H![]() profile, which frequently shows unambiguous evidence of at least two
distinct components: a broad component proper (H
profile, which frequently shows unambiguous evidence of at least two
distinct components: a broad component proper (H
![]() )
and very
broad component (H
)
and very
broad component (H
![]() presumably from a very broad line region, VBLR). In
the following, we continue to refer to H
presumably from a very broad line region, VBLR). In
the following, we continue to refer to H![]() as the total broad
emission excluding H
as the total broad
emission excluding H
![]() ,
and to H
,
and to H
![]() as to the H
as to the H![]() emission
after H
emission
after H
![]() (and of course also H
(and of course also H
![]() )
removal.
)
removal.
4 Results
4.1 Luminosity effects
H![]() - Fig. 3 shows the distribution
of H
- Fig. 3 shows the distribution
of H![]() profile measures as a function of bolometric luminosity
where
profile measures as a function of bolometric luminosity
where
![]() (
(
![]() Å) for the SDSS data. Bolometric luminosity was
computed from z and
Å) for the SDSS data. Bolometric luminosity was
computed from z and ![]() for the ISAAC sample because
of the spectra uncertain flux scale. Figure 3a (upper left
panel) shows the distribution of FWHM(H
for the ISAAC sample because
of the spectra uncertain flux scale. Figure 3a (upper left
panel) shows the distribution of FWHM(H![]() )
measures as a function of
log
)
measures as a function of
log
![]() where low z measures come from the SDSS
sample (Zamfir et al. 2008) and the ISAAC sample. The only obvious,
well-defined FWHM trend found over
where low z measures come from the SDSS
sample (Zamfir et al. 2008) and the ISAAC sample. The only obvious,
well-defined FWHM trend found over ![]() 5 decades of source luminosity involves an increase
in the minimum FWHM H
5 decades of source luminosity involves an increase
in the minimum FWHM H![]() with luminosity as previously reported in
Paper I. Figure 3a shows a systematic increase with
with luminosity as previously reported in
Paper I. Figure 3a shows a systematic increase with
![]() of mean/median FWHM H
of mean/median FWHM H![]() from mean/median
3200/2550 km s-1 to 5075/4900 km s-1, which is likely driven by the
minimum FWHM trend. No trend is observed, for example, among sources
with
from mean/median
3200/2550 km s-1 to 5075/4900 km s-1, which is likely driven by the
minimum FWHM trend. No trend is observed, for example, among sources
with
![]() km s-1. The excess of sources with
km s-1. The excess of sources with
![]() km s-1 in the range
km s-1 in the range
![]() -46.5 simply
reflects Malmquist bias amplified by the increase of sources above
-46.5 simply
reflects Malmquist bias amplified by the increase of sources above
![]() due to the onset of strong
source evolution in the range z = 0.5-0.7. The correlation of
FWHM H
due to the onset of strong
source evolution in the range z = 0.5-0.7. The correlation of
FWHM H![]() with source luminosity is weak (cf. Paper I) but
statistically significant for the increased samples of this paper,
with Pearsson's correlation coefficient
with source luminosity is weak (cf. Paper I) but
statistically significant for the increased samples of this paper,
with Pearsson's correlation coefficient
![]() (
(
![]() ).
).
Figure 3b (upper right) shows the distribution of
asymmetry index (A.I.) as a function of luminosity. An excess of red
asymmetric profiles is seen at all luminosities but does not show up
well in the mean or median values that lie in the range
0.03-0.06 because of the strong SDSS source concentration between
A.I. = ![]() 0.05. The ISAAC sample shows the highest (reddest) mean and
median values with A.I. = 0.11 and 0.09. If we focus
on the sources with more extreme A.I. values, then we find the
largest difference between the ``strips'' -0.4 < A.I. < - 0.2 and
0.2 < A.I. < 0.4: red asymmetries outnumber blue ones by a factor of seven. Only 17 SDSS
sources (zero ISAAC) show blue asymmetries greater than -0.2, while
0.05. The ISAAC sample shows the highest (reddest) mean and
median values with A.I. = 0.11 and 0.09. If we focus
on the sources with more extreme A.I. values, then we find the
largest difference between the ``strips'' -0.4 < A.I. < - 0.2 and
0.2 < A.I. < 0.4: red asymmetries outnumber blue ones by a factor of seven. Only 17 SDSS
sources (zero ISAAC) show blue asymmetries greater than -0.2, while
![]() 85 show red asymmetries greater than +0.2 (17 ISAAC). No
luminosity correlation is detected with the red asymmetric excess
visible at all luminosities.
85 show red asymmetries greater than +0.2 (17 ISAAC). No
luminosity correlation is detected with the red asymmetric excess
visible at all luminosities.
Figures 3c (lower left) and 3d (lower right) show the
distributions of H
![]() ``peak''
``peak''
![]() and ``base''
and ``base''
![]() profile velocity displacements (line shifts), respectively. The centroid
profile velocity displacements (line shifts), respectively. The centroid
![]() shows a strong source concentration around zero (unshifted profile
base) but a significant excess of redshifts at all luminosities.
There is evidence for a trend toward mean/median values increasing
from 56/57 km s-1 in the lowest luminosity decade to 671/292 km s-1 for the ISAAC sample. Thirteen sources (7 ISAAC) show base
redshifts between 2000-4000 km s-1. while no sources show blueshifts
in that range. Clearly the red excess in Figs. 3b
and 3d are related. If we distinguish between radio quiet (RQ)
and radio loud (RL) sources (Zamfir et al. in preparation),
we find the striking absence of a RL source
concentration near zero. Radio-loud sources span the full range
of observed red and blueshifts, however, with a preference for
redshifts. The concentration around zero is a pure RQ effect.
shows a strong source concentration around zero (unshifted profile
base) but a significant excess of redshifts at all luminosities.
There is evidence for a trend toward mean/median values increasing
from 56/57 km s-1 in the lowest luminosity decade to 671/292 km s-1 for the ISAAC sample. Thirteen sources (7 ISAAC) show base
redshifts between 2000-4000 km s-1. while no sources show blueshifts
in that range. Clearly the red excess in Figs. 3b
and 3d are related. If we distinguish between radio quiet (RQ)
and radio loud (RL) sources (Zamfir et al. in preparation),
we find the striking absence of a RL source
concentration near zero. Radio-loud sources span the full range
of observed red and blueshifts, however, with a preference for
redshifts. The concentration around zero is a pure RQ effect.
The centroid
![]() shows only a small number of sources with
shifts above
shows only a small number of sources with
shifts above ![]() 1000 km s-1 (4 red and 7 blue and 0 ISAAC). The
approximately 2 for 1 preference for blueshifts is confirmed in
the range
1000 km s-1 (4 red and 7 blue and 0 ISAAC). The
approximately 2 for 1 preference for blueshifts is confirmed in
the range
![]() = 600-1000 km s-1 with 8 red and 15 blueshifted
sources. Mean values are slightly blue for lower luminosities
(-20 to -40 km s-1 for
= 600-1000 km s-1 with 8 red and 15 blueshifted
sources. Mean values are slightly blue for lower luminosities
(-20 to -40 km s-1 for
![]() )
and become slightly red in the highest luminosity
SDSS and ISAAC bins (+35 km s-1). The simplest accretion disk models
predict redshifted profile bases and blueshifted peaks
(Chen et al. 1989; Eracleous & Halpern 2003)
leaving open the possibility that an
underlying disk signature is present in all sources. Later
discussion, however, does not support that conclusion for redshifted
and red asymmetric profiles. The absence of strong luminosity
correlations in Fig. 3 is confirmed by Pearson
and Spearman correlation coefficients.
)
and become slightly red in the highest luminosity
SDSS and ISAAC bins (+35 km s-1). The simplest accretion disk models
predict redshifted profile bases and blueshifted peaks
(Chen et al. 1989; Eracleous & Halpern 2003)
leaving open the possibility that an
underlying disk signature is present in all sources. Later
discussion, however, does not support that conclusion for redshifted
and red asymmetric profiles. The absence of strong luminosity
correlations in Fig. 3 is confirmed by Pearson
and Spearman correlation coefficients.
[OIII]
![]() 4959, 5007 -
Perhaps the most striking difference between the
SDSS and ISAAC samples involves the relative weakness of narrow line
emission in
4959, 5007 -
Perhaps the most striking difference between the
SDSS and ISAAC samples involves the relative weakness of narrow line
emission in ![]() 80% of the latter. Table 3
shows only three ISAAC sources with W([ OIII]
80% of the latter. Table 3
shows only three ISAAC sources with W([ OIII]![]() 5007)
5007) ![]() 13 Å. We
previously found (Sulentic et al. 2000b) mean values for low z sources in the range W([ OIII]
13 Å. We
previously found (Sulentic et al. 2000b) mean values for low z sources in the range W([ OIII]![]() 5007) = 23-27 Å with standard
deviations for various subsamples in the range 10-30 Å (see also Netzer et al. 2006,2004). Only
one source in the ISAAC sample shows W([ OIII]
5007) = 23-27 Å with standard
deviations for various subsamples in the range 10-30 Å (see also Netzer et al. 2006,2004). Only
one source in the ISAAC sample shows W([ OIII]![]() 5007) greater than the
mean of the low z sample: HE 0109-3518 with W([ OIII]
5007) greater than the
mean of the low z sample: HE 0109-3518 with W([ OIII]![]() 5007)
5007) ![]() 38.5 Å, an extremely high value especially considering the high
luminosity of this
38.5 Å, an extremely high value especially considering the high
luminosity of this
![]() quasar. This is the
ISAAC source (Fig. 1) that most closely resembles
a low z quasar. Twelve blue outliers identified by
Marziani et al. (2003b) show W([ OIII]
quasar. This is the
ISAAC source (Fig. 1) that most closely resembles
a low z quasar. Twelve blue outliers identified by
Marziani et al. (2003b) show W([ OIII]![]() 5007)
5007) ![]() 7.5 Å, which is
the same as the mean value for the sources listed in Table 3. There is a high fraction of sources in the ISAAC
sample that may show a systematic blueshift with respect to H
7.5 Å, which is
the same as the mean value for the sources listed in Table 3. There is a high fraction of sources in the ISAAC
sample that may show a systematic blueshift with respect to H
![]() ,
making several ISAAC sources similar to the blue outliers in terms
of the [OIII]
,
making several ISAAC sources similar to the blue outliers in terms
of the [OIII]
![]() 4959, 5007 properties. The issue will be discussed in
a separate paper.
4959, 5007 properties. The issue will be discussed in
a separate paper.
4.2 4DE1 parameters
A previously defined 4DE1 spectroscopic parameter space (Sulentic et al. 2007,2000b) involves measures of FWHM(H
We used the 4DE1 optical plane to see if the higher luminosity ISAAC
sample shows any difference in source distribution that might hint
at a luminosity trend. ISAAC sources are shown as large dots with
error bars in Fig. 4. The largest distribution
differences involve (a) the absence of ISAAC sources below
![]() km s-1 and (b) an apparent displacement of almost
half of the ISAAC sample towards higher values of FWHM H
km s-1 and (b) an apparent displacement of almost
half of the ISAAC sample towards higher values of FWHM H
![]() and
and
![]() :
on average by
:
on average by ![]() 1-2000 km s-1 in FWHM H
1-2000 km s-1 in FWHM H
![]() and by
0.1-0.2 in
and by
0.1-0.2 in
![]() .
Difference (a) involves the previously discussed
increase in minimum FWHM H
.
Difference (a) involves the previously discussed
increase in minimum FWHM H
![]() with luminosity and can be described
as a zone of avoidance for high-luminosity sources in the 4DE1
optical plane. Difference (b) requires more detailed study in the
next section.
with luminosity and can be described
as a zone of avoidance for high-luminosity sources in the 4DE1
optical plane. Difference (b) requires more detailed study in the
next section.
4.3 4DE1 spectral types and composite profiles
Further analysis of 4DE1 and source luminosity trends are best
accomplished using composite spectra. This avoids confusion
introduced by details in individual spectra and optimizes
S/N. Composite spectra in the context of the optical 4DE1 plane have
special value because FeII
![]() prominence is one of the key
parameters and FWHM H
prominence is one of the key
parameters and FWHM H![]() is arguably the most reliable virial
estimator of black hole mass. Figure 4 is subdivided into
bins of
is arguably the most reliable virial
estimator of black hole mass. Figure 4 is subdivided into
bins of ![]() FWHM(H
FWHM(H![]() )
)
![]() km s-1 and
km s-1 and
![]()
![]()
![]() ,
following Sulentic et al. (2002).
,
following Sulentic et al. (2002).
Spectral types (bins) B1+, B4, and A3 each contain a single ISAAC
source. A reexamination of the single B4 source HE 1505+0212 suggests
that Fe II![]() 4570 emission is unusually strong with no reasonable
continuum adjustment capable of moving it further to the left than
bin B3. This source is either a genuine outlier or an extreme Pop. A
source (following the luminosity-dependent boundary between Pops. A
and B discussed in Sect. 4.5.1). Many ISAAC sources are
located in bin B2 while SDSS sources are apparently rarer there and
much more concentrated toward the lower left corner of the bin. The ratio
4570 emission is unusually strong with no reasonable
continuum adjustment capable of moving it further to the left than
bin B3. This source is either a genuine outlier or an extreme Pop. A
source (following the luminosity-dependent boundary between Pops. A
and B discussed in Sect. 4.5.1). Many ISAAC sources are
located in bin B2 while SDSS sources are apparently rarer there and
much more concentrated toward the lower left corner of the bin. The ratio
![]() is relatively insensitive to small
changes in the adopted continuum leading us to conclude that the
displacement of ISAAC sources towards higher
is relatively insensitive to small
changes in the adopted continuum leading us to conclude that the
displacement of ISAAC sources towards higher
![]() cannot be
attributed only to an effect of the data reduction. This supports the
reality of distribution difference (b) discussed above.
cannot be
attributed only to an effect of the data reduction. This supports the
reality of distribution difference (b) discussed above.
4.3.1 Decomposition and fitting of ISAAC spectra in the optical plane of 4DE1
Median composite ISAAC spectra were computed for sources
in 4DE1 bins A1, A2, B1, B2 (Fig. 5) using calibrated and de-redshifted
spectra normalized to specific flux of unity at 5100 Å. The
first two composites show broader FWHM(H![]() ), and the second two
show stronger
), and the second two
show stronger
![]() compared to ATLAS (Sulentic et al. 2002) or
SDSS composites for the same bins.
compared to ATLAS (Sulentic et al. 2002) or
SDSS composites for the same bins.
Population A sources can usually be modeled with a single unshifted
Lorentzian component. This is also true for bin A1 and A2 ISAAC
sources. Population B sources usually require a double Gaussian
(unshifted broad H
![]() and redshifted very broad H
and redshifted very broad H
![]() components: Sulentic et al. 2002). The H
components: Sulentic et al. 2002). The H![]() profiles in bin B1 and
B2 sources are best fit with a double Gaussian model implying that both
unshifted H
profiles in bin B1 and
B2 sources are best fit with a double Gaussian model implying that both
unshifted H
![]() and redshifted H
and redshifted H
![]() components seen in low z quasars are also present in high luminosity sources (Fig. 6). The decomposition is not always unique and it can
therefore be difficult to estimate the relative contributions of the
two components. An important clue about the proper decomposition
comes from profile variations in the source PG1416-129 (Sulentic et al. 2000c, see
also 3C 206 in Corbin & Smith 2000) where the H
components seen in low z quasars are also present in high luminosity sources (Fig. 6). The decomposition is not always unique and it can
therefore be difficult to estimate the relative contributions of the
two components. An important clue about the proper decomposition
comes from profile variations in the source PG1416-129 (Sulentic et al. 2000c, see
also 3C 206 in Corbin & Smith 2000) where the H
![]() almost disappeared
following a continuum decline, while the
H
almost disappeared
following a continuum decline, while the
H
![]() showed less variation and was revealed much more
clearly as very broad and redshifted. The highest S/N inflected
spectra in the ISAAC sample (e.g. HE 0109-3518) also clearly favor
this decomposition, which is adopted throughout our analysis.
showed less variation and was revealed much more
clearly as very broad and redshifted. The highest S/N inflected
spectra in the ISAAC sample (e.g. HE 0109-3518) also clearly favor
this decomposition, which is adopted throughout our analysis.
4.4 Luminosity binned spectra
Comparing mean or median spectra for random samples of quasars
observed in different luminosity ranges is unlikely to yield
meaningful results. Any difference would be obscured by the
intrinsic dispersion of spectral properties at any given apparent
luminosity. As stressed in much of our previous work (see
especially the review by Sulentic et al. 2000a) and illustrated again
in Fig. 5, all quasar spectra are not self-similar.
Figure 3a reinforces this point in one dimension by
showing that FWHM H![]() spans a very wide range from
spans a very wide range from ![]() 500 km s-1 to
500 km s-1 to
![]() 20 000 km s-1. We suggest that a minimum
requirement for physically meaningful comparisons among low-z samples involves distinguishing between 4DE1 Pops. A and B sources.
More refined comparisons become possible by
generating composite spectra for individual Pops. A and B bins: e.g.
A1, A2, A3, ...and B1, B2, B1+, etc. The population A-B
concept was perhaps the most controversial part of our 4DE1
formalism where sources were arbitrarily divided into populations A
and B based on FWHM H
20 000 km s-1. We suggest that a minimum
requirement for physically meaningful comparisons among low-z samples involves distinguishing between 4DE1 Pops. A and B sources.
More refined comparisons become possible by
generating composite spectra for individual Pops. A and B bins: e.g.
A1, A2, A3, ...and B1, B2, B1+, etc. The population A-B
concept was perhaps the most controversial part of our 4DE1
formalism where sources were arbitrarily divided into populations A
and B based on FWHM H![]() profile measures above and below
profile measures above and below
![]() 4000 km s-1, respectively. However, we find a multitude of differences
when we distinguish sources this way (Sulentic et al. 2007). Most RL
sources belong to Pop. B, and about 25-30% of RQ sources also
belong to Pop. B, but the Pop. A/B distinction appears to be more
effective than more traditional RQ vs. RL comparisons in terms of
BLR structure.
4000 km s-1, respectively. However, we find a multitude of differences
when we distinguish sources this way (Sulentic et al. 2007). Most RL
sources belong to Pop. B, and about 25-30% of RQ sources also
belong to Pop. B, but the Pop. A/B distinction appears to be more
effective than more traditional RQ vs. RL comparisons in terms of
BLR structure.
Figure 7 shows median composite spectra in six luminosity
intervals using 321 SDSS and 53 ISAAC sources. Composites were
generated separately for Pop. A and B sources in decades of
![]() -44 to 48-49. All ISAAC sources lie in the
interval
-44 to 48-49. All ISAAC sources lie in the
interval
![]() -49 with a small number
creating the highest
-49 with a small number
creating the highest
![]() bin (48-49). Population A and B
quasars show parallel trends with increasing luminosity: [OIII]
bin (48-49). Population A and B
quasars show parallel trends with increasing luminosity: [OIII]
![]() 4959, 5007 and H
4959, 5007 and H
![]() systematically decrease in equivalent width but H
systematically decrease in equivalent width but H![]() at the same time increasingly becomes redward asymmetric. The strong decrease in
narrow line strength is expected from standard nebular theory
(see e.g. Netzer 1990, with the caveats of
Sulentic et al. 2007). The Eigenvector 2
anti-correlation between strength of He II
at the same time increasingly becomes redward asymmetric. The strong decrease in
narrow line strength is expected from standard nebular theory
(see e.g. Netzer 1990, with the caveats of
Sulentic et al. 2007). The Eigenvector 2
anti-correlation between strength of He II![]() 4686 and luminosity
(Boroson & Green 1992) is also seen. No obvious trend involving
FeII
4686 and luminosity
(Boroson & Green 1992) is also seen. No obvious trend involving
FeII
![]() is seen that reflects the orthogonality of luminosity
with respect to Eigenvector 1 measures using principal component
analysis (PCA). The ISAAC sample median spectra are most similar to
the highest luminosity SDSS bin composite. The change in H
is seen that reflects the orthogonality of luminosity
with respect to Eigenvector 1 measures using principal component
analysis (PCA). The ISAAC sample median spectra are most similar to
the highest luminosity SDSS bin composite. The change in H![]() towards high luminosity appears to be concentrated in the strength
of the red side of the line, which was already anticipated as a red
asymmetry and line base
towards high luminosity appears to be concentrated in the strength
of the red side of the line, which was already anticipated as a red
asymmetry and line base
![]() red shift in Figs. 3b
and 3c.
red shift in Figs. 3b
and 3c.
4.4.1 Decomposition of luminosity binned spectra
The next logical step is to decompose and quantify individual lines
and line components in different Pop. A and B luminosity bins.
Earlier attempts revealed one of the most obvious differences among
low redshift H![]() profiles and provided one of the motivations for
the population A-B concept
(Sulentic et al. 2007,2002; Marziani et al. 2003b).
Figure 8 shows Pops. A and B median spectra binned in luminosity
after continuum subtraction. Table 6 provides line
equivalent width measures and FWHM FeII values for various
spectral bins discussed in the text. Table 7 tabulates
line profile measures and Table 8 provides H
profiles and provided one of the motivations for
the population A-B concept
(Sulentic et al. 2007,2002; Marziani et al. 2003b).
Figure 8 shows Pops. A and B median spectra binned in luminosity
after continuum subtraction. Table 6 provides line
equivalent width measures and FWHM FeII values for various
spectral bins discussed in the text. Table 7 tabulates
line profile measures and Table 8 provides H![]() centroid measures and estimated uncertainties for the same bins.
Formats appear as footnotes below each table. The first seven lines
present various 4DE1 bin values for ISAAC sources, while the
remainder provide luminosity bin values following the
designations in Fig. 4. Measures in these tables
reflect the results of simultaneous fits to all lines and components
in each median composite spectrum. Attempts at a sequential
line-by-line decomposition yielded very similar results. Numbers
quoted in the discussion of Fig. 3 are averages or
medians based on individual source measures, while Tables 6, 7, and 8 give values derived
from composite spectra. There are no
significant discrepancies between measures estimated in these two
ways.
Source codes for
centroid measures and estimated uncertainties for the same bins.
Formats appear as footnotes below each table. The first seven lines
present various 4DE1 bin values for ISAAC sources, while the
remainder provide luminosity bin values following the
designations in Fig. 4. Measures in these tables
reflect the results of simultaneous fits to all lines and components
in each median composite spectrum. Attempts at a sequential
line-by-line decomposition yielded very similar results. Numbers
quoted in the discussion of Fig. 3 are averages or
medians based on individual source measures, while Tables 6, 7, and 8 give values derived
from composite spectra. There are no
significant discrepancies between measures estimated in these two
ways.
Source codes for
![]() bins use the first two digits of
the
bins use the first two digits of
the
![]() bin followed by A or B for the population (e.g. values for
line 43A correspond to measures of the Pop. A luminosity composite
for log
bin followed by A or B for the population (e.g. values for
line 43A correspond to measures of the Pop. A luminosity composite
for log
![]() -44). Narrow line changes with
luminosity will be discussed in a separate paper so that we can
concentrate on the properties of H
-44). Narrow line changes with
luminosity will be discussed in a separate paper so that we can
concentrate on the properties of H
![]() and H
and H
![]() .
The FWHM H
.
The FWHM H![]() in Pop. A
sources shows a systematic increase with
in Pop. A
sources shows a systematic increase with
![]() from 2000 km s-1 to 4100 km s-1 across the six luminosity bins likely driven by the
increase in minimum FWHM H
from 2000 km s-1 to 4100 km s-1 across the six luminosity bins likely driven by the
increase in minimum FWHM H![]() with
with
![]() shown in
Fig. 3a.
shown in
Fig. 3a.
Population B shows no clear FWHM trend with
![]() ,
but we find that W(H
,
but we find that W(H![]() )
decreases systematically with increasing
luminosity. Population A does not show an obvious trend, although W(H
)
decreases systematically with increasing
luminosity. Population A does not show an obvious trend, although W(H![]() )
is smallest in the most luminous Pop. A bins. The Pop. B
``Baldwin Effect'' shows W(H
)
is smallest in the most luminous Pop. A bins. The Pop. B
``Baldwin Effect'' shows W(H![]() )
decreasing from 143 Å to 82 Å with increasing
)
decreasing from 143 Å to 82 Å with increasing
![]() .
Population B sources show 6-7 times larger asymmetry indices at
the highest source luminosities, as well as evidence of a redshift
near the base (
.
Population B sources show 6-7 times larger asymmetry indices at
the highest source luminosities, as well as evidence of a redshift
near the base (
![]() )
of the line. The mean velocity redshift
increases by 9 times from the lowest to highest luminosity bin.
Figure 9 shows the increase with source luminosity of the
fraction of
)
of the line. The mean velocity redshift
increases by 9 times from the lowest to highest luminosity bin.
Figure 9 shows the increase with source luminosity of the
fraction of
![]() redshifts for Pop. B sources. The excess flux in
the red wing of H
redshifts for Pop. B sources. The excess flux in
the red wing of H![]() is revealed in Fig. 8
decompositions to be a real H
is revealed in Fig. 8
decompositions to be a real H![]() flux excess and not due to
FeII
flux excess and not due to
FeII
![]() contamination (see also Netzer & Trakhtenbrot 2007, who found a similar result).
contamination (see also Netzer & Trakhtenbrot 2007, who found a similar result).
Conversely FeII
![]() subtraction reveals that H
subtraction reveals that H![]() shows little
evidence of profile shifts and asymmetries in Pop. A sources. The
apparent Pop. A red asymmetry appears to increase with luminosity in
Fig. 7; however, Fig. 8 suggests that it
is mainly due to FeII
shows little
evidence of profile shifts and asymmetries in Pop. A sources. The
apparent Pop. A red asymmetry appears to increase with luminosity in
Fig. 7; however, Fig. 8 suggests that it
is mainly due to FeII
![]() and [OIII]
and [OIII]
![]() 4959, 5007 contamination on the red
side of H
4959, 5007 contamination on the red
side of H![]() .
Table 6 shows that W(Fe II
.
Table 6 shows that W(Fe II![]() 4570) does
not increase with luminosity, but H
4570) does
not increase with luminosity, but H
![]() decreases somewhat making
red FeII
decreases somewhat making
red FeII
![]() contamination appear to grow in strength, even if some redward, very broad emission cannot be excluded at a low flux level in the highest luminosity bins.
contamination appear to grow in strength, even if some redward, very broad emission cannot be excluded at a low flux level in the highest luminosity bins.
The quantification in Tables 6, 7, and 8, and the two components required to model Pop. B
sources, reenforce past evidence
(Sulentic et al. 2002,2000c; Corbin 1995) of
a redshifted very broad line component in H![]() .
The H
.
The H
![]() is the most obvious profile difference between Pops. A and B, as
well as between high and low luminosity sources in Pop. B. As noted
earlier, both RL and RQ sources are found in Pop. B and both Pop. B
RL and Pop. B RQ sources show the H
is the most obvious profile difference between Pops. A and B, as
well as between high and low luminosity sources in Pop. B. As noted
earlier, both RL and RQ sources are found in Pop. B and both Pop. B
RL and Pop. B RQ sources show the H
![]() .
This provides a
strong spectroscopic argument in favor of the importance of the
Pop. A-B concept compared to comparisons on the basis of radio loudness.
The effect of the VBLR component is to produce a broader, more red
asymmetric, and more redshifted H
.
This provides a
strong spectroscopic argument in favor of the importance of the
Pop. A-B concept compared to comparisons on the basis of radio loudness.
The effect of the VBLR component is to produce a broader, more red
asymmetric, and more redshifted H![]() profile with the amplitude of these
effects dependent on the relative strengths of the BLR and VBLR
components. HE 0109-3518 in Fig. 1 is an example of
a source with a weak/moderate VBLR component, while HE 1039-0724
shows one of the strongest VBLR components in the ISAAC sample.
Tables 7, 8, Fig. 9, and the profile
decompositions in Fig. 8 show evidence of uniform
increase of H
profile with the amplitude of these
effects dependent on the relative strengths of the BLR and VBLR
components. HE 0109-3518 in Fig. 1 is an example of
a source with a weak/moderate VBLR component, while HE 1039-0724
shows one of the strongest VBLR components in the ISAAC sample.
Tables 7, 8, Fig. 9, and the profile
decompositions in Fig. 8 show evidence of uniform
increase of H
![]() strength with luminosity.
strength with luminosity.
![\begin{figure}
\par\includegraphics[angle=0,scale=0.48]{0764f05.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg287.gif) |
Figure 5:
Median spectra for bins A1, B1, A2, B2, as defined in Fig. 4. Original spectral have been normalized to unity at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9.0cm,height=9.0cm, angle=0]{0764f06a....
...}\includegraphics[width=9.0cm,height=9.0cm, angle=0]{0764f06d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg288.gif) |
Figure 6:
Analysis of the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[scale=0.7,angle=0]{0764f07.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg290.gif) |
Figure 7:
Luminosity effects in the median spectra of Pop. A and Pop. B sources, binned in decades of luminosity in the luminosity ranges
|
| Open with DEXTER | |
4.5 Luminosity dependence of spectral types
The lefthand panel of Fig. 10 shows the bolometric
luminosity distributions for ISAAC sources showing H![]() profile
best fit with single Lorentzian and double Gaussian models.
Ambiguous sources are excluded. A K-S test confirms that the two
source luminosity distributions are not significantly different. The
right panel shows the distribution of profile fits in an FWHM H
profile
best fit with single Lorentzian and double Gaussian models.
Ambiguous sources are excluded. A K-S test confirms that the two
source luminosity distributions are not significantly different. The
right panel shows the distribution of profile fits in an FWHM H![]() vs. bolometric luminosity plane with Lorentzian, double-Gaussian, and
ambiguous sources denoted L, G, and U respectively. No strong
luminosity preference is seen for L or G sources. The difference
between FWHM distributions for L and G profiles is highly
significant with a K-S test suggesting that
vs. bolometric luminosity plane with Lorentzian, double-Gaussian, and
ambiguous sources denoted L, G, and U respectively. No strong
luminosity preference is seen for L or G sources. The difference
between FWHM distributions for L and G profiles is highly
significant with a K-S test suggesting that
![]() for
sources with different profile shapes are drawn from the same
parent population. This can be taken as an independent confirmation
of the Pop. A-B dichotomy.
for
sources with different profile shapes are drawn from the same
parent population. This can be taken as an independent confirmation
of the Pop. A-B dichotomy.
4.5.1 Spectral types: a refinement
The Pop. A-B FWHM(H
![]() ) = 4000 km s-1 boundary was adopted using a
low z and low luminosity sample. There is no strong evidence that
it has a direct physical meaning even if it is better motivated
empirically than the limit at FWHM(H
) = 4000 km s-1 boundary was adopted using a
low z and low luminosity sample. There is no strong evidence that
it has a direct physical meaning even if it is better motivated
empirically than the limit at FWHM(H![]() ) = 2000 km s-1 used to
separate ``narrow; ine'' Seyfert 1s (NLSy1s) from the rest of broad
line AGN.
) = 2000 km s-1 used to
separate ``narrow; ine'' Seyfert 1s (NLSy1s) from the rest of broad
line AGN.
Figure 11 presents a reprise of Fig. 3a
with a much expanded low-redshift sample including (a) SDSS DR5
quasars brighter than g=17.0 within z=0.7, (b) FIRST radio detected
SDSS DR5 quasars between
g=17.0-17.5 within z=0.7(Zamfir et al. 2008) and (c) the ATLAS sample of low redshift
quasars (Marziani et al. 2003a). This provides a somewhat better
mapping of the low z source distribution in the FWHM -
![]() plane. The SDSS quasar sample does not include
sources with FWHM H
plane. The SDSS quasar sample does not include
sources with FWHM H![]() < 1000 km s-1 that were classified in SDSS as
galaxies. The narrowest of these ``broad line'' sources can be
confirmed as type 1 AGN (NLSy1) by the presence of Fe II
< 1000 km s-1 that were classified in SDSS as
galaxies. The narrowest of these ``broad line'' sources can be
confirmed as type 1 AGN (NLSy1) by the presence of Fe II![]() 4570 emission
in their spectra. Among the 400+ highest S/N SDSS quasars that we
have studied in detail (Zamfir et al. 2008), all but five show
detectable FeII
4570 emission
in their spectra. Among the 400+ highest S/N SDSS quasars that we
have studied in detail (Zamfir et al. 2008), all but five show
detectable FeII
![]() emission suggesting that the presence of
optical FeII
emission suggesting that the presence of
optical FeII
![]() emission is an ubiquitous property of type 1 AGN.
A recent survey (Zhou et al. 2006) of NLSy1s using SDSS DR3 provides
a representative census of these sources. They found 41 sources
(
emission is an ubiquitous property of type 1 AGN.
A recent survey (Zhou et al. 2006) of NLSy1s using SDSS DR3 provides
a representative census of these sources. They found 41 sources
(![]() )
brighter than g = 17.5 between FWHM H
)
brighter than g = 17.5 between FWHM H![]() = 450-2000 km s-1. The old Pop. A-B and NLSy1-rest of type-1 AGN
``boundaries'' at 4000 and 2000 km s-1, respectively, are indicated.
Figure 11 provides us with a better defined lower edge to the FWHM
H
= 450-2000 km s-1. The old Pop. A-B and NLSy1-rest of type-1 AGN
``boundaries'' at 4000 and 2000 km s-1, respectively, are indicated.
Figure 11 provides us with a better defined lower edge to the FWHM
H![]() distribution. We superpose curves corresponding to exponents
a=0.52 (Bentz et al. 2006) and 0.67 (Paper II) in the Kaspi
relation, which will be considered in the discussion.
Figure 11 also shows a revised Pop. A-B boundary following
the form of an a = 0.67 Kaspi relation as done in Paper I.
distribution. We superpose curves corresponding to exponents
a=0.52 (Bentz et al. 2006) and 0.67 (Paper II) in the Kaspi
relation, which will be considered in the discussion.
Figure 11 also shows a revised Pop. A-B boundary following
the form of an a = 0.67 Kaspi relation as done in Paper I.
Figures 10 and 11 suggest a modified 4DE1 Pop.
A/B boundary is required for high-luminosity quasars. We define
modified 4DE1 spectral types MA1, MA2, MB1, MB2, etc. where the
boundary between the MA and MB populations is now
luminosity-dependent and given by
![]() (a = 0.67; analogous to Paper I).
Composite line H
(a = 0.67; analogous to Paper I).
Composite line H![]() profiles for the revised 4DE1 bins are similar
to those obtained with the fixed FWHM definition
(Figs. 5 and 6) and are therefore
not shown.
profiles for the revised 4DE1 bins are similar
to those obtained with the fixed FWHM definition
(Figs. 5 and 6) and are therefore
not shown.
To decide whether the fixed (4000 km s-1) or luminosity
dependent boundary is more significant we defined three samples: (1)
the old Pop. A; (2) an intermediate population between 4000 km s-1 and new luminosity-dependent limit; and (3) a modified Pop. B MB
![]()
![]() .
We can also consider a modified Pop. A,
MA
.
We can also consider a modified Pop. A,
MA ![]()
![]() .
The H
.
The H![]() spectral region before and after
continuum subtraction for the median spectra of A, M, and MB are
shown in Figs. 12 and 13
respectively. The M median most closely resembles the Pop. A median
rather than MB (or B). Figures 12 and 13 show that the M H
spectral region before and after
continuum subtraction for the median spectra of A, M, and MB are
shown in Figs. 12 and 13
respectively. The M median most closely resembles the Pop. A median
rather than MB (or B). Figures 12 and 13 show that the M H![]() spectral region
resembles the one of Pop. A and that the H
spectral region
resembles the one of Pop. A and that the H![]() fit is well fit by a
Lorentzian function, as is the case for Pop. A sources. This
suggests that the luminosity-dependent limit
fit is well fit by a
Lorentzian function, as is the case for Pop. A sources. This
suggests that the luminosity-dependent limit
![]() might be more appropriate. The distribution of G and L sources in
the FWHM(H
might be more appropriate. The distribution of G and L sources in
the FWHM(H
![]() )
vs. luminosity plane (Fig. 10) also
supports this result. Although individual fits should be treated
with caution we see that the shapes are predominantly Lorentzian in
the Pop. A and M areas of the plane. while they are Gaussian in the MB area.
)
vs. luminosity plane (Fig. 10) also
supports this result. Although individual fits should be treated
with caution we see that the shapes are predominantly Lorentzian in
the Pop. A and M areas of the plane. while they are Gaussian in the MB area.
4.6 Black hole mass and Eddington ratio
The FWHM of H![]() has been used as a virial estimator of
has been used as a virial estimator of
![]() (Vestergaard & Peterson 2006) at low redshift. The problem is what
to use above redshift
(Vestergaard & Peterson 2006) at low redshift. The problem is what
to use above redshift
![]() .
The use of CIV
.
The use of CIV![]() 1549 as an H
1549 as an H![]() surrogate involves problems that seriously reduce the reliability of
high z
surrogate involves problems that seriously reduce the reliability of
high z
![]() estimates (Netzer et al. 2007; Sulentic et al. 2007). We have
chosen instead to follow H
estimates (Netzer et al. 2007; Sulentic et al. 2007). We have
chosen instead to follow H![]() out to the highest possible redshifts
via infrared spectroscopy. We use the updated relationships linking
FWHM(H
out to the highest possible redshifts
via infrared spectroscopy. We use the updated relationships linking
FWHM(H
![]() ), specific luminosity at 5100 Å and BLR radial
distance
), specific luminosity at 5100 Å and BLR radial
distance
![]() from Vestergaard & Peterson (2006, their Eq. (5)). We do not enter into the caveats of
black hole mass and Eddington ratio determinations (see
e.g. Marconi et al. 2008; Collin et al. 2006; Shen et al. 2008; Sulentic et al. 2006)
noting only that
from Vestergaard & Peterson (2006, their Eq. (5)). We do not enter into the caveats of
black hole mass and Eddington ratio determinations (see
e.g. Marconi et al. 2008; Collin et al. 2006; Shen et al. 2008; Sulentic et al. 2006)
noting only that
![]() values are uncertain by a factor 2-3 at 1
values are uncertain by a factor 2-3 at 1![]() confidence level if derived from single-epoch observations. It is also possible to infer
bolometric luminosity from the specific continuum flux assuming a
constant bolometric correction. One can therefore also estimate the
luminosity-to-mass ratio (
confidence level if derived from single-epoch observations. It is also possible to infer
bolometric luminosity from the specific continuum flux assuming a
constant bolometric correction. One can therefore also estimate the
luminosity-to-mass ratio (
![]() /
/
![]() ). This approach is
very crude (see e.g. Kelly et al. 2008; Hopkins et al. 2007) but a
bolometric correction is still relatively stable across RQ and most
RL sources with the obvious exception of core-dominated (beamed)
sources.
). This approach is
very crude (see e.g. Kelly et al. 2008; Hopkins et al. 2007) but a
bolometric correction is still relatively stable across RQ and most
RL sources with the obvious exception of core-dominated (beamed)
sources.
Table 6: Measurements on the broad lines of median spectra.
Table 7:
H![]() Line profile measurements on spectral types.
Line profile measurements on spectral types.
Table 8:
H![]() Line centroids at different fractional heights of spectral types.
Line centroids at different fractional heights of spectral types.
The distribution of ISAAC quasars with L- and G-type fits as a
function of
![]() and
and
![]() are shown in the left- and righthand
panels of Fig. 14 respectively. Figure 15
shows all ISAAC sources (including U H
are shown in the left- and righthand
panels of Fig. 14 respectively. Figure 15
shows all ISAAC sources (including U H
![]() profiles) in the
profiles) in the
![]() vs.
vs.
![]() plane. We derive quite high masses in the range
log
plane. We derive quite high masses in the range
log
![]() = 8.5-10.0 with a range of log
= 8.5-10.0 with a range of log
![]() = -1.0 to 0.0. L
(assumed Pop. A) and G (assumed Pop. B) profiles favor lower/higher
log
= -1.0 to 0.0. L
(assumed Pop. A) and G (assumed Pop. B) profiles favor lower/higher
log
![]() and higher/lower log
and higher/lower log
![]() values, respectively, as
previously found for our ATLAS sample (Marziani et al. 2003b).
The difference in the distribution is significant for both
values, respectively, as
previously found for our ATLAS sample (Marziani et al. 2003b).
The difference in the distribution is significant for both
![]() and
and
![]() ,
with a low probability that sources with L- and
G-type profiles come from the same parent distribution of
,
with a low probability that sources with L- and
G-type profiles come from the same parent distribution of
![]() and
and
![]() :
K-S tests indicate a probability
:
K-S tests indicate a probability ![]() 10-3. However,
there is a range of
10-3. However,
there is a range of
![]() (
(
![]() )
where L- and G-
type sources are almost equally represented. The absence of a sharp
)
where L- and G-
type sources are almost equally represented. The absence of a sharp
![]() boundary can be understood in terms of error effects, as well
as of systemic biases. Typical uncertainty in
boundary can be understood in terms of error effects, as well
as of systemic biases. Typical uncertainty in ![]()
![]() is
is
![]() 0.1, if one assumes that the bolometric luminosity is
uncertain by 50% and that the FWHM(H
0.1, if one assumes that the bolometric luminosity is
uncertain by 50% and that the FWHM(H![]() )
has a typical error of 10%.
However, this estimate neglects the scatter in the size-luminosity
relationship for the BLR. In addition, orientation effects - which
are established among radio = loud quasars (see
e.g., Rokaki et al. 2003; Sulentic et al. 2003) - may well raise the
)
has a typical error of 10%.
However, this estimate neglects the scatter in the size-luminosity
relationship for the BLR. In addition, orientation effects - which
are established among radio = loud quasars (see
e.g., Rokaki et al. 2003; Sulentic et al. 2003) - may well raise the
![]() of several sources of Pop. B. They are not considered in the
of several sources of Pop. B. They are not considered in the
![]() and
and
![]() estimates presented here. Moreover, the magnitude limit of
our ISAAC sample makes it possible that we can detect only those Pop. B
sources with the highest
estimates presented here. Moreover, the magnitude limit of
our ISAAC sample makes it possible that we can detect only those Pop. B
sources with the highest
![]() values (cf. Fig. 7 of Paper II).
values (cf. Fig. 7 of Paper II).
Figure 16 shows the dependence of
![]() and A.I.
on
and A.I.
on
![]() and
and
![]() .
Significant correlations between
.
Significant correlations between
![]() and both
A.I. and
and both
A.I. and
![]() are found, while no significant correlations are
found involving
are found, while no significant correlations are
found involving
![]() .
The A.I. vs.
.
The A.I. vs.
![]() correlation is marginally
significant (
correlation is marginally
significant (
![]() )
if Pop. B sources are
considered alone; in this case,
)
if Pop. B sources are
considered alone; in this case,
![]() and
and
![]() are not
significantly correlated. This is perhaps not surprising considering
the small number of sources, the typical errors, the
are not
significantly correlated. This is perhaps not surprising considering
the small number of sources, the typical errors, the
![]() ``segregation'' between Pops. A and B. Median spectra in bins of
``segregation'' between Pops. A and B. Median spectra in bins of
![]() and
and
![]() point toward the origin of the correlation with
point toward the origin of the correlation with
![]() (Fig. 17). The bin labeled as
(Fig. 17). The bin labeled as ![]()
![]() < 9.5 actually covers masses in the range
< 9.5 actually covers masses in the range
![]()
![]() < 9.5, and
for
< 9.5, and
for ![]()
![]()
![]() corresponds to the bin
corresponds to the bin
![]() /
/
![]()
![]() in Fig. 9 of
Marziani et al. (2003b). The remaining three bins represent the
extension to higher masses and
in Fig. 9 of
Marziani et al. (2003b). The remaining three bins represent the
extension to higher masses and
![]() that were not sampled at
that were not sampled at ![]() .
We see a trend, as observed at low-z, that for fixed
.
We see a trend, as observed at low-z, that for fixed
![]() the redward component is stronger for larger
the redward component is stronger for larger
![]() .
This result is
discussed in Sect. 5.4.
.
This result is
discussed in Sect. 5.4.
![\begin{figure}
\par\includegraphics[width=8.9cm,height=7.8cm, angle=0]{0764f08a....
...cludegraphics[width=8.9cm,height=7.8cm, angle=0]{0764f08f.eps}\par
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg360.gif) |
Figure 8:
Median spectra analysis of the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9.0cm,height=8.0cm, angle=0]{0764f08g....
...s}\includegraphics[width=9.0cm,height=8.0cm, angle=0]{0764f08l.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg361.gif) |
Figure 8: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0764f09-coul.ps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg363.gif) |
Figure 9:
Distribution of unshifted and shifted H |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.3cm,height=8.3cm, angle=0]{076...
...\includegraphics[width=7.9cm,height=8cm, angle=0]{0764f10b.eps} }
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg364.gif) |
Figure 10:
Left: distribution of the ISAAC sources whose H
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,height=12cm,clip]{0764f11.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg365.gif) |
Figure 11:
FWHM(H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,scale=0.4]{0764f12.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg366.gif) |
Figure 12: Median spectra for Pop. A, intermediate spectra in region M, and modified Population B (BM), as defined in Fig. 10. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f13a.eps}...
...raphics[width=9cm,height=9cm, angle=0]{0764f13c.eps}\hspace*{9cm}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg367.gif) |
Figure 13:
Median spectra analysis of the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.0cm,height=8cm, angle=0]{0764f14a.eps}\includegraphics[width=8.0cm,height=8cm, angle=0]{0764f14b.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg368.gif) |
Figure 14:
Distribution of sources whose H
|
| Open with DEXTER | |
5 Discussion
5.1 Luminosity trends
One of the motivations for the ISAAC survey was to search for
trends, or even correlations, between emission line properties and
source luminosity. Another motivation was to compare high and low
luminosity source properties in the 4DE1 context. The PCA of a bright
quasar sample (Boroson & Green 1992) found source luminosity to be
orthogonal to all line measures except W( He II![]() 4686). An [ OIII]
4686). An [ OIII]![]() 5007 measure
was included among the original Eigenvector 1 parameters
(Boroson & Green 1992) showing a large scatter likely due to the
strong
5007 measure
was included among the original Eigenvector 1 parameters
(Boroson & Green 1992) showing a large scatter likely due to the
strong
![]() dependence that we find with ISAAC. We did
not adopt an [OIII] measure in our 4DE1 formalism because we
preferred to avoid narrow = line considerations as much as possible
(Sulentic et al. 2000b). Subsequent 4DE1 studies at low z (e.g.,
Paper I and references) found no luminosity dependence on broad line
LIL measures. What was thought to be the most significant (inverse)
correlation between luminosity and broad line HIL measures
(especially CIV
dependence that we find with ISAAC. We did
not adopt an [OIII] measure in our 4DE1 formalism because we
preferred to avoid narrow = line considerations as much as possible
(Sulentic et al. 2000b). Subsequent 4DE1 studies at low z (e.g.,
Paper I and references) found no luminosity dependence on broad line
LIL measures. What was thought to be the most significant (inverse)
correlation between luminosity and broad line HIL measures
(especially CIV![]() 1549, Baldwin et al. 1978) is now known to be present in
quasar samples with small redshift/luminosity dispersion
(Xu et al. 2008) and is likely related to intrinsic source
properties such as Eddington ratio (Bachev et al. 2004).
1549, Baldwin et al. 1978) is now known to be present in
quasar samples with small redshift/luminosity dispersion
(Xu et al. 2008) and is likely related to intrinsic source
properties such as Eddington ratio (Bachev et al. 2004).
Only one luminosity trend was found over the 5-6 luminosity decades
covered in this study (without Pop. A/B discrimination). Profile
parameter distributions (Fig. 3) are essentially
the same at all luminosities. The one exception involves an increase
in minimum FWHM H![]() with
with
![]() visible in
Fig. 3a (see also Paper I). Low-luminosity (
visible in
Fig. 3a (see also Paper I). Low-luminosity (
![]() )
sources show FWHM H
)
sources show FWHM H
![]() values as low as
500-750 km s-1, while the minimum value at
values as low as
500-750 km s-1, while the minimum value at
![]() appears to be FWHM H
appears to be FWHM H![]()
![]() 3000 km s-1. The lower FWHM H
3000 km s-1. The lower FWHM H![]() limit
is expected if broad Balmer line emission arises in a virialized
cloud distribution (or accretion disk) that obeys a Kaspi (see
e.g. Kaspi et al. 2005) relation. We can think of the minimum
FWHM-
limit
is expected if broad Balmer line emission arises in a virialized
cloud distribution (or accretion disk) that obeys a Kaspi (see
e.g. Kaspi et al. 2005) relation. We can think of the minimum
FWHM-
![]() trend as the boundary for sources
radiating sub-Eddington. NLSy1s defined (at low z) as sources
with FWHM H
trend as the boundary for sources
radiating sub-Eddington. NLSy1s defined (at low z) as sources
with FWHM H![]() < 2000 km s-1 are absent from the ISAAC sample.
< 2000 km s-1 are absent from the ISAAC sample.
It is unclear if a Kaspi relation (
![]() )
is valid above redshifts of a few tenths. There
has been much discussion about the correct exponent in the Kaspi
relation with values between a = 0.5-0.7 favored
(Bentz et al. 2006; Kaspi et al. 2005,2000). Figure 11
provides an empirical representation of the minimum FWHM H
)
is valid above redshifts of a few tenths. There
has been much discussion about the correct exponent in the Kaspi
relation with values between a = 0.5-0.7 favored
(Bentz et al. 2006; Kaspi et al. 2005,2000). Figure 11
provides an empirical representation of the minimum FWHM H![]() trend.
Note that the expected trend has been quadratically combined with
the instrumental resolution (assumed to be 200 km s-1 at FWHM,
appropriate for the SDSS). Superposed curves corresponding to
a =0.52 (Bentz et al. 2006), and 0.67 (Kaspi et al. 2005, Paper II)
show that distinguishing between these values becomes possible above
trend.
Note that the expected trend has been quadratically combined with
the instrumental resolution (assumed to be 200 km s-1 at FWHM,
appropriate for the SDSS). Superposed curves corresponding to
a =0.52 (Bentz et al. 2006), and 0.67 (Kaspi et al. 2005, Paper II)
show that distinguishing between these values becomes possible above
![]() .
A first impression is that
a = 0.52 is not supported by the ISAAC data unless a considerable number
of these sources are super-Eddington radiators. Thus values in the
range a = 0.6-0.7 are favored. However, a complicating factor
involves the dependence of FWHM H
.
A first impression is that
a = 0.52 is not supported by the ISAAC data unless a considerable number
of these sources are super-Eddington radiators. Thus values in the
range a = 0.6-0.7 are favored. However, a complicating factor
involves the dependence of FWHM H![]() on source orientation, which is
especially important if one accepts the paradigm of a line-emitting
accretion disk. Some low-redshift sources with small FWHM H
on source orientation, which is
especially important if one accepts the paradigm of a line-emitting
accretion disk. Some low-redshift sources with small FWHM H![]() (extreme NLSy1 sources) show rapid high-amplitude X-ray variability
(e.g. Brinkmann et al. 2003) or blue-shifted narrow lines (blue
outliers) that have been argued to signal near face-on orientation. In a
previous paper (Marziani et al. 2003b), we attempted inclination
corrections for blue outliers assuming a
(extreme NLSy1 sources) show rapid high-amplitude X-ray variability
(e.g. Brinkmann et al. 2003) or blue-shifted narrow lines (blue
outliers) that have been argued to signal near face-on orientation. In a
previous paper (Marziani et al. 2003b), we attempted inclination
corrections for blue outliers assuming a ![]() dependence of
FWHM. Using a tentative correction that increases black hole mass by
dependence of
FWHM. Using a tentative correction that increases black hole mass by
![]()
![]()
![]() 0.4, we were able to move many apparently
superEddington NLSy1 radiators (sources with
0.4, we were able to move many apparently
superEddington NLSy1 radiators (sources with
![]() that lie below the a = 0.5 curve in Fig. 11)
below
that lie below the a = 0.5 curve in Fig. 11)
below
![]() = 1. It seems unlikely that more than a very few ISAAC
sources involve preferred orientation (5 are nominally
super-Eddington) given the distribution of observed FWHM H
= 1. It seems unlikely that more than a very few ISAAC
sources involve preferred orientation (5 are nominally
super-Eddington) given the distribution of observed FWHM H![]() values,
even if optical luminosity is orientation dependent. It is also
possible that orientation becomes increasingly less important in
higher
values,
even if optical luminosity is orientation dependent. It is also
possible that orientation becomes increasingly less important in
higher
![]() sources because of radiative instabiliy in
the accretion disk (Blaes 2007). A value as high as a = 0.67would imply that all quasars radiate well below the Eddington limit.
We conclude that there is no strong evidence for a population of super-Eddington
radiators in our low z and ISAAC samples.
sources because of radiative instabiliy in
the accretion disk (Blaes 2007). A value as high as a = 0.67would imply that all quasars radiate well below the Eddington limit.
We conclude that there is no strong evidence for a population of super-Eddington
radiators in our low z and ISAAC samples.
5.2 4DE1 populations A and B
This study suggests that, in order to isolate luminosity effects
and other fundamental trends in quasar samples, one should work in
the context of the 4DE1 formalism and take advantage of the
Population A-B concept. The empirical evidence continues to grow
in favor of two distinct populations of quasars. We recently summarized
the multitude of empirical differences between the two populations
(Sulentic et al. 2008,2007). If luminosity trends exist for
only one of the populations then, the lack of a trend in the other might
obscure the effect in a mixed sample, such as the one displayed
in Fig. 11. The Pop. A-B boundary was
empirically defined, after noting a discontinuity between the
sources whose FWHM(H![]() )
lies in the range 2000-4000 km s-1 and
those of Pop. B (also because almost all RL sources are Pop. B).
The similarity in emission line parameters between those sources
and the NLSy1s then suggested a single population for the entire
0-4000 km s-1 range. In analogy with the minimum FWHM H
)
lies in the range 2000-4000 km s-1 and
those of Pop. B (also because almost all RL sources are Pop. B).
The similarity in emission line parameters between those sources
and the NLSy1s then suggested a single population for the entire
0-4000 km s-1 range. In analogy with the minimum FWHM H![]() trend,
which corresponds to a fixed Eddington ratio of 1, we can expect
that the limit between Pops. A and B will also be luminosity
dependent (Paper I).
trend,
which corresponds to a fixed Eddington ratio of 1, we can expect
that the limit between Pops. A and B will also be luminosity
dependent (Paper I).
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f15.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg375.gif) |
Figure 15:
Distribution of the ISAAC sources in the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f16a.eps}...
....eps}\includegraphics[width=9cm,height=9cm, angle=0]{0764f16d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg376.gif) |
Figure 16:
Dependence on black hole
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f17a.eps}...
....eps}\includegraphics[width=9cm,height=9cm, angle=0]{0764f17d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg379.gif) |
Figure 17:
H |
| Open with DEXTER | |
We have previously suggested that the Pop. A-B FWHM H
![]() boundary
might reflect a critical accretion rate/Eddington ratio
(
boundary
might reflect a critical accretion rate/Eddington ratio
(
![]()
![]() ). We note that a number of recent studies have
independently arrived at a similar ``critical'' FWHM or
). We note that a number of recent studies have
independently arrived at a similar ``critical'' FWHM or
![]() value (Kelly et al. 2008; Hu et al. 2008b; Bonning et al. 2007; Marziani et al. 2003b; Collin et al. 2006).
Such a critical value might signal a significant change in disk
structure/kinematics that is reflected in systematically larger FWHM
H
value (Kelly et al. 2008; Hu et al. 2008b; Bonning et al. 2007; Marziani et al. 2003b; Collin et al. 2006).
Such a critical value might signal a significant change in disk
structure/kinematics that is reflected in systematically larger FWHM
H![]() ,
the demise of a CIV
,
the demise of a CIV![]() 1549 wind as well as weaker soft X-ray and
FeII emission. It is interesting to point out that the thin
accretion disk approximation is expected to break down at
1549 wind as well as weaker soft X-ray and
FeII emission. It is interesting to point out that the thin
accretion disk approximation is expected to break down at
![]()
![]() 0.3 with the development of an inner thick structure
(Hubeny et al. 2000). This kind of change might well affect the
spectroscopic signature of the BLR.
0.3 with the development of an inner thick structure
(Hubeny et al. 2000). This kind of change might well affect the
spectroscopic signature of the BLR.
It is probably naïve to expect a luminosity dependence as
strong as the one predicted by a fixed
![]() (Fig. 11). The Pop. A/B boundary is found to be close to 4000 km s-1, following four lines of evidence: (1) the median spectrum for
Pop. A in the luminosity bin
(Fig. 11). The Pop. A/B boundary is found to be close to 4000 km s-1, following four lines of evidence: (1) the median spectrum for
Pop. A in the luminosity bin
![]() shows
that the H
shows
that the H![]() is Lorentzian; (2) between constant FWHM(H
is Lorentzian; (2) between constant FWHM(H![]() ) = 4000 km s-1 and the
) = 4000 km s-1 and the
![]() = 0.15 line, and for
= 0.15 line, and for
![]() ,
most ATLAS sources show typical Pop. A properties. A
minority of core-dominated radio-loud sources are located there
since they are expected to be observed almost pole-on, at minimum
FWHM. If
,
most ATLAS sources show typical Pop. A properties. A
minority of core-dominated radio-loud sources are located there
since they are expected to be observed almost pole-on, at minimum
FWHM. If
![]() ATLAS sources are
mainly located within -500 km s-1 of FWHM = 4000 km s-1, their H
ATLAS sources are
mainly located within -500 km s-1 of FWHM = 4000 km s-1, their H![]() profiles are similar to but not exactly the same as the ones of Pop. A. In the
present paper we consider the luminosity dependence of the boundary
to follow Paper I assuming a
profiles are similar to but not exactly the same as the ones of Pop. A. In the
present paper we consider the luminosity dependence of the boundary
to follow Paper I assuming a ![]() 0.67. It is assumed constant
corresponding to
0.67. It is assumed constant
corresponding to
![]() km s-1 below
km s-1 below
![]() .
.
5.3 An H
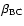 ``Baldwin effect'' is present only in population B
``Baldwin effect'' is present only in population B
The Pop. A/B concept provides a useful alternate way to evaluate
luminosity properties. When we separate by source population, we
immediately find possible luminosity trends between FWHM and
W(H![]() )
for Pops. A and B respectively. The former trend sees a
mean FWHM H
)
for Pops. A and B respectively. The former trend sees a
mean FWHM H![]() increase with luminosity from
increase with luminosity from ![]() 2000 km s-1 up
to
2000 km s-1 up
to ![]() 4000 km s-1. This is very likely driven by the minimum FWHM
H
4000 km s-1. This is very likely driven by the minimum FWHM
H![]() trend already discussed, as well as by the Malmquist bias since all
of the highest luminosity sources lie at higher redshifts and are
preferentially selected in a flux-limited sample. Assuming an
underlying correlation between black hole mass and source luminosity,
we expect systematically higher black hole masses for the ISAAC
sources, as observed.
trend already discussed, as well as by the Malmquist bias since all
of the highest luminosity sources lie at higher redshifts and are
preferentially selected in a flux-limited sample. Assuming an
underlying correlation between black hole mass and source luminosity,
we expect systematically higher black hole masses for the ISAAC
sources, as observed.
Population B sources show a decrease in W(H![]() )
by almost a factor of two
over our source luminosity range. This H
)
by almost a factor of two
over our source luminosity range. This H![]() Baldwin effect is
difficult to interpret because H
Baldwin effect is
difficult to interpret because H![]() is a composite feature
(H
is a composite feature
(H
![]() + H
+ H
![]() ). Table 6 presents an attempt at quantitatively
separating BLR and VBLR components for the six Pop. B luminosity
binned composite spectra. The same can be done for Pop. A, but the
BLR component always dominates H
). Table 6 presents an attempt at quantitatively
separating BLR and VBLR components for the six Pop. B luminosity
binned composite spectra. The same can be done for Pop. A, but the
BLR component always dominates H![]() in all luminosity bins. The
BLR component in Pop. B ranges from 60% of H
in all luminosity bins. The
BLR component in Pop. B ranges from 60% of H![]() at low
luminosity to 25% at
at low
luminosity to 25% at
![]() -48. Correction
for the VBLR component yields a ``super''
Baldwin effect where W(H
-48. Correction
for the VBLR component yields a ``super''
Baldwin effect where W(H
![]() )
decreases by a factor of four
over our luminosity range. At the same time we find considerable
scatter but no obvious trend in the strength of FeII emission as
measured in the Fe II
)
decreases by a factor of four
over our luminosity range. At the same time we find considerable
scatter but no obvious trend in the strength of FeII emission as
measured in the Fe II![]() 4570 blend. The highest luminosity Pop. B
sources with smallest W(H
4570 blend. The highest luminosity Pop. B
sources with smallest W(H
![]() )
show an apparently more prominent H
)
show an apparently more prominent H
![]() ,
while its contribution in low-luminosity sources seems
modest because H
,
while its contribution in low-luminosity sources seems
modest because H
![]() dominates.
dominates.
The simplest interpretation of these results involves changes in
the physical conditions of the BLR emitting region due to: (1) source
luminosity and (2) the Pop. A-B dichotomy. As alluded to above, the
first may involve changes related to radiation pressure dominance in
the accretion disk at higher source luminosity and the second
changes related to a critical Eddington ratio.
The tendency for FWHM(FeII) to follow FWHM H
![]() in BLR-dominated
Pop. A sources can be taken as evidence of an FeII - H
in BLR-dominated
Pop. A sources can be taken as evidence of an FeII - H![]() BLR commonality. The inferred lower density of the VBLR (e.g., Sulentic et al. 2000c) in (less BLR-dominated) Pop. B sources
speaks against an FeII/VBLR emission region commonality
(Marziani et al. 2008). W(H
BLR commonality. The inferred lower density of the VBLR (e.g., Sulentic et al. 2000c) in (less BLR-dominated) Pop. B sources
speaks against an FeII/VBLR emission region commonality
(Marziani et al. 2008). W(H
![]() )
is found to be approximately
constant in the six luminosity bins, suggesting that it arises
largely in optically thick gas photoionized by the central
continuum. The strongest challenge is to explain the fourfold decrease
in H
)
is found to be approximately
constant in the six luminosity bins, suggesting that it arises
largely in optically thick gas photoionized by the central
continuum. The strongest challenge is to explain the fourfold decrease
in H
![]() strength observed only Pop. B sources. The simplest
interpretation involves a change in Pop. B physical conditions that
suppresses H
strength observed only Pop. B sources. The simplest
interpretation involves a change in Pop. B physical conditions that
suppresses H
![]() .
Since H
.
Since H
![]() and FeII are thought to arise in
the same region, this might point toward collisional quenching of
H
and FeII are thought to arise in
the same region, this might point toward collisional quenching of
H![]() BLR emission as originally suggested by Gaskell (1985).
Another, even simpler possibility involves different-sized annuli
for FeII and H
BLR emission as originally suggested by Gaskell (1985).
Another, even simpler possibility involves different-sized annuli
for FeII and H
![]() emitting regions. If we correct W(H
emitting regions. If we correct W(H![]() )
measures for H
)
measures for H
![]() and recalculate
and recalculate
![]() parameters,
we find that many/most Pop. B sources will move towards higher
parameters,
we find that many/most Pop. B sources will move towards higher
![]() values
values ![]() 1 in the 4DE1 optical plane. The similar
1 in the 4DE1 optical plane. The similar
![]() ratios observed in Pop. A luminosity bins (using only H
ratios observed in Pop. A luminosity bins (using only H
![]() )
also suggest a similarity in physical conditions. In other words, we
would have a similar low-ionization BLR in both Pops. A and B
sources plus a second VBLR only in Pop. B sources.
)
also suggest a similarity in physical conditions. In other words, we
would have a similar low-ionization BLR in both Pops. A and B
sources plus a second VBLR only in Pop. B sources.
5.4 Black hole mass and Eddington ratio
Table 6 presents FWHM H
![]() estimates for Pop. B
luminosity bins. The H
estimates for Pop. B
luminosity bins. The H
![]() of Table 6 is related to
the ``reverberating'' component almost equivalent to the entire
H
of Table 6 is related to
the ``reverberating'' component almost equivalent to the entire
H![]() profile in Pop. A sources. We note that the decomposition
H
profile in Pop. A sources. We note that the decomposition
H
![]() - H
- H
![]() of Pop. B sources assumes two Gaussians, while the intrinsic shapes of
H
of Pop. B sources assumes two Gaussians, while the intrinsic shapes of
H
![]() and H
and H
![]() ,
especially in the radial velocity range where
they overlap is, unknown. The origin of the redward asymmetry often
seen in the H
,
especially in the radial velocity range where
they overlap is, unknown. The origin of the redward asymmetry often
seen in the H![]() profile is also unclear. It seems too high to be
due to gravitational redshift associated with line emission from
increasingly shorter distances from the central black hole (under
the assumption that the motion is predominantly virial). A likely
possibility is non-virial motion associated with gas infall toward
the central black hole (see e.g. Hu et al. 2008a; Gaskell & Goosmann 2008, who provide renewed support for the hypothesis of infalling emitting regions), but alternatives like Compton scattering have also been considered
(e.g. Kallman & Krolik 1986). However, if the
VBLR is mainly made of optically thick gas the radial velocity
range underlying the H
profile is also unclear. It seems too high to be
due to gravitational redshift associated with line emission from
increasingly shorter distances from the central black hole (under
the assumption that the motion is predominantly virial). A likely
possibility is non-virial motion associated with gas infall toward
the central black hole (see e.g. Hu et al. 2008a; Gaskell & Goosmann 2008, who provide renewed support for the hypothesis of infalling emitting regions), but alternatives like Compton scattering have also been considered
(e.g. Kallman & Krolik 1986). However, if the
VBLR is mainly made of optically thick gas the radial velocity
range underlying the H
![]() is especially ambiguous. Note also that
the width re-estimation is not the same as using the 2
is especially ambiguous. Note also that
the width re-estimation is not the same as using the 2![]() moment of
the H
moment of
the H![]() profile:
profile: ![]() (Peterson et al. 2004; Collin et al. 2006)
may have little meaning for a composite line since it is measured on
the whole H
(Peterson et al. 2004; Collin et al. 2006)
may have little meaning for a composite line since it is measured on
the whole H![]() profile. The re-estimation leads to a more extreme
reduction than suggested in Paper II; actually, all VBLR corrected
FWHM values decrease to within 1000 km s-1 of the Pop. A-B
boundary (4-5000 km s-1). In fact, the highest luminosity bins show
FWHM(H
profile. The re-estimation leads to a more extreme
reduction than suggested in Paper II; actually, all VBLR corrected
FWHM values decrease to within 1000 km s-1 of the Pop. A-B
boundary (4-5000 km s-1). In fact, the highest luminosity bins show
FWHM(H
![]() )
within the revised Pop. A range as defined in Fig. 10.
)
within the revised Pop. A range as defined in Fig. 10.
An important implication of this correction involves its effect on
![]() and
and
![]() estimation for Pop. B sources. Population B sources
would essentially cease to exist as a separate population in the
context of
estimation for Pop. B sources. Population B sources
would essentially cease to exist as a separate population in the
context of
![]() estimation. All
estimation. All
![]() values for Pop B would
decrease from the previous range (Paper II) log
values for Pop B would
decrease from the previous range (Paper II) log
![]() = 7.5-9.5 to
7.0-9.0, which is more like the Pop. A range but still
consistent with the view (Sulentic et al. 2000a) that Pop. B quasars
are radiating at lower
= 7.5-9.5 to
7.0-9.0, which is more like the Pop. A range but still
consistent with the view (Sulentic et al. 2000a) that Pop. B quasars
are radiating at lower
![]() ,
as discussed below.
,
as discussed below.
Considering the uncertain and somewhat speculative nature of the corrections applied to Pop. B sources, FWHM H![]() in Pop. A sources appears to provide more
direct and reliable black hole mass estimates yielding a range in
log
in Pop. A sources appears to provide more
direct and reliable black hole mass estimates yielding a range in
log
![]() = 6.0-8.5 at low z and 9.0-10.0 at
= 6.0-8.5 at low z and 9.0-10.0 at ![]() (see
figures in Paper II). The major source of uncertainty involves the
inclination correction that depends on the BLR geometry. A weak
VBLR component and/or blue asymmetry are present in an uncertain
number of sources, which might lead to slight overestimates of
(see
figures in Paper II). The major source of uncertainty involves the
inclination correction that depends on the BLR geometry. A weak
VBLR component and/or blue asymmetry are present in an uncertain
number of sources, which might lead to slight overestimates of
![]() when assuming that the virial line component is a symmetric
Lorentzian. Gaussian fits to Pop. A profiles
(e.g. Shen et al. 2008) lead to significant overestimates of
when assuming that the virial line component is a symmetric
Lorentzian. Gaussian fits to Pop. A profiles
(e.g. Shen et al. 2008) lead to significant overestimates of
![]() .
Median values from our luminosity composite profiles (assuming
mean FWHM H
.
Median values from our luminosity composite profiles (assuming
mean FWHM H![]() and
and
![]() for sources in that bin) show a
clear luminosity correlation ranging from
for sources in that bin) show a
clear luminosity correlation ranging from ![]()
![]()
![]() 6-10
for the most luminous ISAAC sources. Estimates corrected for H
6-10
for the most luminous ISAAC sources. Estimates corrected for H![]() asymmetries are slightly lower but only for the SDSS bins.
asymmetries are slightly lower but only for the SDSS bins.
The
![]() values in Table 6 increase from 0.02 to
values in Table 6 increase from 0.02 to ![]() 0.6 in the highest luminosity bins of Pop. B. We note that the
0.6 in the highest luminosity bins of Pop. B. We note that the
![]() value for the most luminous bin (
value for the most luminous bin (![]() 1) is especially uncertain because of the limited number of sources and the large correction amplitude (FWHM(H
1) is especially uncertain because of the limited number of sources and the large correction amplitude (FWHM(H![]() )
) ![]() 9300 km s-1; FWM(H
9300 km s-1; FWM(H
![]() )
) ![]() 4300 km s-1). The
4300 km s-1). The
![]() values obtained using
FWHM (H
values obtained using
FWHM (H![]() )
without removing H
)
without removing H
![]() (Table 7) range from
(Table 7) range from ![]() 0.02 to 0.27. Similar values are obtained if FWHM(Fe II
0.02 to 0.27. Similar values are obtained if FWHM(Fe II![]() 4570) is used as a virial estimator to compute
4570) is used as a virial estimator to compute
![]() .
The corresponding
.
The corresponding
![]() estimates for Pop. A luminosity composites also show an increase ranging from
estimates for Pop. A luminosity composites also show an increase ranging from
![]()
![]() 0.2 (lowest luminosity) to 1.3 in the highest luminosity bin. Ranges for Pop A from Paper II were
0.2 (lowest luminosity) to 1.3 in the highest luminosity bin. Ranges for Pop A from Paper II were
![]() = 0.05-1.0 at low z and
0.5-1.0 at
= 0.05-1.0 at low z and
0.5-1.0 at ![]() assuming that sources above
assuming that sources above
![]() > 1.0 are the result of face-on orientation. The luminosity trend is expected for both Pops. A and B since we are sampling preferentially higher
> 1.0 are the result of face-on orientation. The luminosity trend is expected for both Pops. A and B since we are sampling preferentially higher
![]() radiators with increasing
radiators with increasing
![]() (as shown in Paper II). Without H
(as shown in Paper II). Without H
![]() correction the difference between the
correction the difference between the
![]() of Pops. A and B is
of Pops. A and B is
![]()
![]()
![]() 0.6 for the SDSS luminosity bin, decreasing to
0.6 for the SDSS luminosity bin, decreasing to ![]() 0.3 for the ISAAC luminosity bins
(47 and 48). If we consider the width of H
0.3 for the ISAAC luminosity bins
(47 and 48). If we consider the width of H
![]() alone,
alone,
![]()
![]()
![]() 0.5, even if this difference becomes rather small in the ISAAC bins, probably because of the extreme amplitude of the correction and of the caveats listed at the beginning of this section. At any rate, from the SDSS sample we can conclude that Pop. B appears to be a population of lower Eddington ratio than Pop. A. Population B is likely to be an older and more evolved quasar population than
Pop A, since black holes seem to reside in hosts with large
spheroidal components, often elliptical galaxies (Woo et al. 2005).
In contrast, the morphology of NLSy1 hosts (i.e., in many ways
the ``extreme Pop. A'' sources) in the local Universe often involves
high surface brightness star-forming galaxies
(Ohta et al. 2007; Krongold et al. 2001). They are often barred and/or
remarkably perturbed suggesting that they may be young systems
sustained by a strong flow of matter toward their central black holes
(see e.g. the review by Sulentic et al. 2008).
0.5, even if this difference becomes rather small in the ISAAC bins, probably because of the extreme amplitude of the correction and of the caveats listed at the beginning of this section. At any rate, from the SDSS sample we can conclude that Pop. B appears to be a population of lower Eddington ratio than Pop. A. Population B is likely to be an older and more evolved quasar population than
Pop A, since black holes seem to reside in hosts with large
spheroidal components, often elliptical galaxies (Woo et al. 2005).
In contrast, the morphology of NLSy1 hosts (i.e., in many ways
the ``extreme Pop. A'' sources) in the local Universe often involves
high surface brightness star-forming galaxies
(Ohta et al. 2007; Krongold et al. 2001). They are often barred and/or
remarkably perturbed suggesting that they may be young systems
sustained by a strong flow of matter toward their central black holes
(see e.g. the review by Sulentic et al. 2008).
5.5 Occupation of spectral type B2
ISAAC sources are found in the B2 bin of the 4DE1 optical plane
(FWHM = 4-8000 km s-1 and
![]() = 0.5-1.0. The low z ATLAS sample
included only 11 sources (
= 0.5-1.0. The low z ATLAS sample
included only 11 sources (![]() 5%) in that bin, but the more
complete SDSS sample involves 40 B2 sources (
5%) in that bin, but the more
complete SDSS sample involves 40 B2 sources (![]() 10%). Bin B2
may involve sources with the highest black hole masses (several
times 109
10%). Bin B2
may involve sources with the highest black hole masses (several
times 109 ![]() ). The highest masses are expected to fall in the
region of bin B2 (Zamanov & Marziani 2002), but such massive black
holes are not observed at low z (see, for example, the
). The highest masses are expected to fall in the
region of bin B2 (Zamanov & Marziani 2002), but such massive black
holes are not observed at low z (see, for example, the
![]() distribution as a function of z in Paper II). In the ISAAC sample
we derive
distribution as a function of z in Paper II). In the ISAAC sample
we derive
![]() values as high as
values as high as
![]() (Sulentic et al. 2006). According to the grid in Fig. 2 of
Zamanov & Marziani (2002), the B2 bin is expected to be occupied by
sources with
(Sulentic et al. 2006). According to the grid in Fig. 2 of
Zamanov & Marziani (2002), the B2 bin is expected to be occupied by
sources with
![]()
![]()
![]() .
The expected
.
The expected
![]()
![]() ratio is modest with
ratio is modest with
![]()
![]() .
B2 sources therefore expected to share physical properties that are thought to be
typical of Pop. B. The H
.
B2 sources therefore expected to share physical properties that are thought to be
typical of Pop. B. The H![]() line profile is also described well by a
double Gaussian decomposition if we restrict our attention to
revised bin MB2. This result is consistent with the conclusion that
most sources in bin B2 are similar to those in B1, although with
stronger
line profile is also described well by a
double Gaussian decomposition if we restrict our attention to
revised bin MB2. This result is consistent with the conclusion that
most sources in bin B2 are similar to those in B1, although with
stronger
![]() .
The H
.
The H![]() line profiles imply that both types may fall on
the Pop. B side of a critical
line profiles imply that both types may fall on
the Pop. B side of a critical
![]() that separates the Pop. A and
Pop. B boundary.
that separates the Pop. A and
Pop. B boundary.
6 Conclusions
We presented VLT-ISAAC spectroscopic observations for 30 intermediate z and high-luminosity HE quasars. Combined with
previous data we have a sample of 53 objects (z = 0.9-3.0) that we
compare with two large low-z samples
(Zamfir et al. 2008; Marziani et al. 2003a). We find few
correlations/trends between broad emission line properties and
the source luminosity. We previously proposed an empirical limit at
FWHM(H![]() )
)
![]() km s-1 to distinguish between two
populations A-B of quasars with very different spectroscopic
properties. Sources with FWHM(H
km s-1 to distinguish between two
populations A-B of quasars with very different spectroscopic
properties. Sources with FWHM(H![]() ) < 4000 km s-1 show Lorentzian
H
) < 4000 km s-1 show Lorentzian
H![]() profiles while those above this limit are best fit with double
Gaussian models. This low z/ low luminosity dichotomy is also
found for the high luminosity ISAAC sources. Elementary
profiles while those above this limit are best fit with double
Gaussian models. This low z/ low luminosity dichotomy is also
found for the high luminosity ISAAC sources. Elementary
![]() computations suggest that the dichotomy may be explained if a
critical
computations suggest that the dichotomy may be explained if a
critical
![]() is associated with a BLR structure change, but the
issue of the Pop. A/B boundary deserves further scrutiny. Once the
population A/B dichotomy is taken into account the phenomenology of
the H
is associated with a BLR structure change, but the
issue of the Pop. A/B boundary deserves further scrutiny. Once the
population A/B dichotomy is taken into account the phenomenology of
the H
![]() emitting region, as well as inferences about BLR structure are quite similar over a 5 dex luminosity range that
includes some of the most luminous known quasars. This overall
scenario is described in more detail by the following results of
the present paper:
emitting region, as well as inferences about BLR structure are quite similar over a 5 dex luminosity range that
includes some of the most luminous known quasars. This overall
scenario is described in more detail by the following results of
the present paper:
- 1.
- A minimum requirement for quantifying and interpreting BLR
properties in type 1 AGN involves the Pop. A-B dichotomy.
If we do not separate type 1 AGN in this way, then spectroscopic averaging appears to be equivalent to discussing stellar properties without considering the OBAFGKM spectroscopic sequence
- 2.
- Population A sources show a minimum FWHM H
 that increases with
source luminosity from
that increases with
source luminosity from  500-1000 km s-1 to 3000-3500 km s-1. The
best boundary to this lower envelope favors an exponent a
500-1000 km s-1 to 3000-3500 km s-1. The
best boundary to this lower envelope favors an exponent a
 0.67 in the Kaspi relation. Population A sources span a FWHM H
0.67 in the Kaspi relation. Population A sources span a FWHM H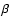 range of
range of  4000 km s-1 driven by source orientation and virial motions in an
accretion disk. The virial assumption implies a
4000 km s-1 driven by source orientation and virial motions in an
accretion disk. The virial assumption implies a
 range of 4 dex
(
range of 4 dex
(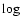
 = 6-10) for this high accreting population. In
the ISAAC sample studied in this paper Pop. A sources show
= 6-10) for this high accreting population. In
the ISAAC sample studied in this paper Pop. A sources show
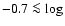
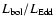
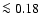 .
.
- 3.
- The H
 emission in Pop. B sources involves both unshifted
broad (H
emission in Pop. B sources involves both unshifted
broad (H
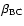 )
and redshifted very broad line (H
)
and redshifted very broad line (H
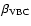 )
components.
Population B shows a ``super'' Baldwin effect with W(H
)
components.
Population B shows a ``super'' Baldwin effect with W(H
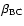 )
decreasing
by a factor 4 with increasing
)
decreasing
by a factor 4 with increasing
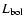 .
At the same time
W(H
.
At the same time
W(H
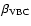 )
remains almost constant, implying that it arises in a
photo-ionized optically thick medium. The FWHM(H
)
remains almost constant, implying that it arises in a
photo-ionized optically thick medium. The FWHM(H
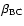 )
shows no
luminosity dependence after correction for H
)
shows no
luminosity dependence after correction for H
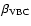 broadening. This
yields an
broadening. This
yields an
 range similar to that for Pop. A. Population B is a
lower accreting population with
range similar to that for Pop. A. Population B is a
lower accreting population with
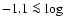
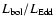
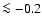 for the objects of this paper. One should bear in mind the caveats of
Sect. 4.6 in analyzing the
for the objects of this paper. One should bear in mind the caveats of
Sect. 4.6 in analyzing the
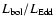 limits and recall that 80% of
Pop. B sources of the ISAAC sample show
limits and recall that 80% of
Pop. B sources of the ISAAC sample show 
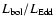
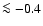 .
Considering the
blurring by errors in
.
Considering the
blurring by errors in
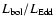 estimates, and results of previous
papers, intrinsic
estimates, and results of previous
papers, intrinsic
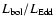 ranges could be
ranges could be  0.01-0.2
(Pop. B) and
0.01-0.2
(Pop. B) and 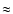 0.2-1 (Pop. A), with a separation at
0.2-1 (Pop. A), with a separation at
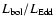
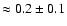 .
Population B sources in the SDSS sample seem to remain a population of lower Eddington ratio even if the extreme correction to FWHM implied by removal of the H
.
Population B sources in the SDSS sample seem to remain a population of lower Eddington ratio even if the extreme correction to FWHM implied by removal of the H
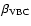 is applied (Sect. 5.4).
is applied (Sect. 5.4).
- 4.
- Most type 1 AGN do not show broad line profiles consistent with
simple accretion disk models. Perhaps Lorentzian Pop. A profiles can
be accommodated with thin/slim disk emission models (if disk
emission is very extended), but Pop. B cannot. The redshifted H
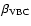 in Pop. B sources can not be considered part of a double
peak signature since the asymmetry and the centroid shift at
in Pop. B sources can not be considered part of a double
peak signature since the asymmetry and the centroid shift at
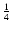 intensity (near the profile base is usually too large
to be attributed to a gravitational redshift. Arp 102B - the
prototypical ``double-peaked'' Balmer line emitter - shows a redshift
at line base that is modest, and consistent with the value expected
for gravitational redshift at the inner emitting radius of the
accretion disk according to the model of Chen et al. (1989). This is
however not the case for many Pop. B objects that have been
included in so-called double-peaked source compilations (i.e. as accretion disk candidates: e.g., Strateva et al. 2003).
intensity (near the profile base is usually too large
to be attributed to a gravitational redshift. Arp 102B - the
prototypical ``double-peaked'' Balmer line emitter - shows a redshift
at line base that is modest, and consistent with the value expected
for gravitational redshift at the inner emitting radius of the
accretion disk according to the model of Chen et al. (1989). This is
however not the case for many Pop. B objects that have been
included in so-called double-peaked source compilations (i.e. as accretion disk candidates: e.g., Strateva et al. 2003).
- 5.
- H
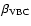 is the dominant broad line component at high luminosity
(from
is the dominant broad line component at high luminosity
(from  25% to 60% of the H
25% to 60% of the H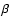 flux over our
flux over our
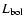 range) for Pop. B sources. The geometry and kinematics of the VBLR are
still unclear. The H
range) for Pop. B sources. The geometry and kinematics of the VBLR are
still unclear. The H
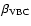 redshift
redshift
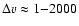 km s-1 is
unlikely to be gravitational in nature. The increase in dominance
with redshift favors a connection to the hypothesized infall
involved with the
km s-1 is
unlikely to be gravitational in nature. The increase in dominance
with redshift favors a connection to the hypothesized infall
involved with the
 growth.
Another possibility involves photon downshifting via some form of
scattering (e.g. Laor 2006, and references
therein).
growth.
Another possibility involves photon downshifting via some form of
scattering (e.g. Laor 2006, and references
therein).
Acknowledgements
Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Aoki, K., Kawaguchi, T., & Ohta, K. 2005, ApJ, 618, 601 [NASA ADS] [CrossRef]
- Bachev, R., Marziani, P., Sulentic, J. W., et al. 2004, ApJ, 617, 171 [NASA ADS] [CrossRef] (In the text)
- Baker, A. C., Carswell, R. F., Bailey, J. A., et al. 1994, MNRAS, 270, 575
- Baldwin, J. A., Burke, W. L., Gaskell, C. M., & Wampler, E. J. 1978, Nature, 273, 431 [NASA ADS] [CrossRef] (In the text)
- Baskin, A., & Laor, A. 2005, MNRAS, 356, 1029 [NASA ADS] [CrossRef]
- Bentz, M. C., Peterson, B. M., Pogge, R. W., Vestergaard, M., & Onken, C. A. 2006, ApJ, 644, 133 [NASA ADS] [CrossRef] (In the text)
- Blaes, O. 2007, The Central Engine of Active Galactic Nuclei, 373, 75 [NASA ADS] (In the text)
- Bock, D. C.-J., Large, M. I., & Sadler, E. M. 1999, AJ, 117, 1578 [CrossRef] (In the text)
- Bonning, E. W., Cheng, L., Shields, G. A., Salviander, S., & Gebhardt, K. 2007, ApJ, 659, 211 [NASA ADS] [CrossRef]
- Boroson, T. 2005, AJ, 130, 381 [NASA ADS] [CrossRef]
- Boroson, T. A. 2002, ApJ, 565, 78 [NASA ADS] [CrossRef]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [NASA ADS] [CrossRef] (In the text)
- Brinkmann, W., Grupe, D., Branduardi-Raymont, G., & Ferrero, E. 2003, A&A, 398, 81 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brotherton, M. S., Wills, B. J., Steidel, C. C., & Sargent, W. L. W. 1994, ApJ, 423, 131 [NASA ADS] [CrossRef]
- Bruhweiler, F., & Verner, E. 2008, ApJ, 675, 83 [NASA ADS] [CrossRef]
- Carswell, R. F., Mountain, C. M., Robertson, D. J., et al. 1991, ApJ, 381, L5 [NASA ADS] [CrossRef]
- Chen, K., Halpern, J. P., & Filippenko, A. V. 1989, ApJ, 339, 742 [NASA ADS] [CrossRef]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences]
- Collin-Souffrin, S., Dyson, J. E., McDowell, J. C., & Perry, J. J. 1988, MNRAS, 232, 539 [NASA ADS] (In the text)
- Corbin, M. R. 1995, ApJ, 447, 496 [NASA ADS] [CrossRef]
- Corbin, M. R., & Smith, P. S. 2000, ApJ, 532, 136 [NASA ADS] [CrossRef]
- Elston, R., Thompson, K. L., & Hill, G. J. 1994, Nature, 367, 250 [NASA ADS] [CrossRef]
- Eracleous, M., & Halpern, J. P. 2003, ApJ, 599, 886 [NASA ADS] [CrossRef]
- Espey, B. R., Carswell, R. F., Bailey, J. A., Smith, M. G., & Ward, M. J. 1989, ApJ, 342, 666 [NASA ADS] [CrossRef]
- Evans, A. S., Sanders, D. B., Cutri, R. M., et al. 1998, ApJ, 506, 205 [NASA ADS] [CrossRef]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [CrossRef] (In the text)
- Fine, S., et al. 2008, ArXiv e-prints, 807 [arXiv:0807.1155]
- Hill, G. J., Thompson, K. L., & Elston, R. 1993, ApJ, 414, L1 [NASA ADS] [CrossRef]
- Gaskell, C. M. 1985, ApJ, 325, 114 [NASA ADS] [CrossRef] (In the text)
- Gaskell, C. M., & Goosmann, R. W. 2008 [arXiv:0805.4258]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef]
- Hu, C., Wang, J.-M., Ho, L. C., Bian, W.-H., & Xue, S.-J. 2008b, ApJ, 683, L11
- Hu, C., Wang, J.-M., Ho, L. C., et al. 2008a, ApJ, 687, 78 [NASA ADS] [CrossRef] (In the text)
- Hubeny, I., Agol, E., Blaes, O., & Krolik, J. H. 2000, ApJ, 533, 710 [NASA ADS] [CrossRef] (In the text)
- Kallman, T. R., & Krolik, J. H. 1986, ApJ, 308, 805 [NASA ADS] [CrossRef] (In the text)
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef]
- Kaspi, S., Maoz, D., Netzer, H., et al. 2005, ApJ, 629, 61 [NASA ADS] [CrossRef] (In the text)
- Kelly, B. C., Bechtold, J., Trump, J. R., Vestergaard, M., & Siemiginowska, A. 2008, [arXiv:0801.2383]
- Komossa, S., Xu, D., Zhou, H., Storchi-Bergmann, T., & Binette, L. 2008, ApJ, 680, 926 [NASA ADS] [CrossRef]
- Krongold, Y., Dultzin-Hacyan, D., & Marziani, P. 2001, AJ, 121, 702 [NASA ADS] [CrossRef]
- Kuhr, H., McAlary, C. W., Rudy, R. J., Strittmatter, P. A., & Rieke, G. H. 1984, ApJ, 284, L5 [NASA ADS] [CrossRef]
- Laor, A. 2006, ApJ, 643, 112 [NASA ADS] [CrossRef] (In the text)
- Marconi, A., Axon, D. J., Maiolino, R., et al. 2008, ApJ, 678, 693 [NASA ADS] [CrossRef]
- Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS, 104, 37 [NASA ADS] [CrossRef]
- Marziani, P., Sulentic, J. W., Zamanov, R., et al. 2003a, ApJS, 145, 199 [NASA ADS] [CrossRef]
- Marziani, P., Zamanov, R., Sulentic, J. W., & Calvani, M. 2003b, MNRAS, 345, 1133 [NASA ADS] [CrossRef]
- Marziani, P., Dultzin, D., & Sulentic, J. W. 2008, Rev. Mex. Astron. Astrofis. Conf. Ser., 32, 103 [NASA ADS]
- Murayama, T., Taniguchi, Y., Evans, A. S., et al. 1998, AJ, 115, 2237 [NASA ADS] [CrossRef]
- Murayama, T., Taniguchi, Y., Evans, A. S., et al. 1999, AJ, 117, 1645 [CrossRef]
- Nazarova, L. S., Bochkarev, N. G., & O'Brien, P. T. 2007, Astron. Astrophys. Trans., 26, 401 [NASA ADS] [CrossRef]
- Netzer, H. 1990, in Active Galactic Nuclei, Saas-Fee Advanced Course 20. Lecture Notes, Swiss Society for Astrophysics and Astronomy, XII, ed. R. D. Blandford, H. Netzer, L. Woltjer, T. J.-L. Courvoisier, & M. Mayor (Berlin Heidelberg New York: Springer-Verlag) (In the text)
- Netzer, H., & Trakhtenbrot, B. 2007, ApJ, 654, 754 [NASA ADS] [CrossRef] (In the text)
- Netzer, H., Shemmer, O., Maiolino, R., et al. 2004, ApJ, 614, 558 [NASA ADS] [CrossRef]
- Netzer, H., Mainieri, V., Rosati, P., & Trakhtenbrot, B. 2006, A&A, 453, 525 [NASA ADS] [CrossRef] [EDP Sciences]
- Netzer, H., Lira, P., Trakhtenbrot, B., Shemmer, O., & Cury, I. 2007, ApJ, 671, 1256 [NASA ADS] [CrossRef]
- Ohta, K., Aoki, K., Kawaguchi, T., & Kiuchi, G. 2007, ApJS, 169, 1 [NASA ADS] [CrossRef]
- Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166 [NASA ADS] [CrossRef]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef]
- Reimers, D., Koehler, T., & Wisotzki, L. 1996, AApS, 115, 235 [NASA ADS]
- Rokaki, E., Lawrence, A., Economou, F., & Mastichiadis, A. 2003, MNRAS, 340, 1298 [NASA ADS] [CrossRef]
- Shang, Z., Wills, B. J., Robinson, E. L., et al. 2003, ApJ, 586, 52 [NASA ADS] [CrossRef]
- Shang, Z., Wills, B. J., Wills, D., & Brotherton, M. S. 2007, AJ, 134, 294 [NASA ADS] [CrossRef] (In the text)
- Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., & Schneider, D. P. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef]
- Sigut, T. A. A., & Pradhan, A. K. 2003, ApJS, 145, 15 [NASA ADS] [CrossRef]
- Sigut, T. A. A., Pradhan, A. K., & Nahar, S. N. 2004, ApJ, 611, 81 [NASA ADS] [CrossRef]
- Strateva, I. V., Strauss, M. A., Hao, L., et al. 2003, AJ, 126, 1720 [NASA ADS] [CrossRef] (In the text)
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000a, ARA&A, 38, 521 [NASA ADS] [CrossRef]
- Sulentic, J. W., Marziani, P., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2000b, ApJ, 536, L5 [NASA ADS] [CrossRef]
- Sulentic, J. W., Marziani, P., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2000c, ApJ, 545, L15 [NASA ADS] [CrossRef] (In the text)
- Sulentic, J. W., Marziani, P., Zamanov, R., et al. 2002, ApJ, 566, L71 [NASA ADS] [CrossRef] (In the text)
- Sulentic, J. W., Zamfir, S., Marziani, P., et al. 2003, ApJ, 597, L17 [NASA ADS] [CrossRef]
- Sulentic, J. W., Stirpe, G. M., Marziani, P., et al. 2004, A&A, 423, 121 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
- Sulentic, J. W., Repetto, P., Stirpe, G. M., et al. 2006, A&A, 456, 929 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II)
- Sulentic, J. W., Bachev, R., Marziani, P., Negrete, C. A., & Dultzin, D. 2007, ApJ, 666, 757 [NASA ADS] [CrossRef]
- Sulentic, J. W., Zamfir, S., Marziani, P., & Dultzin, D. 2008, Rev. Mex. Astron. Astrofis. Conf. Ser., 32, 51 [NASA ADS]
- Tsuzuki, Y., Kawara, K., Yoshii, Y., et al. 2006, ApJ, 650, 57 [NASA ADS] [CrossRef]
- Verner, E. M., Verner, D. A., Korista, K. T., et al. 1999, ApJS, 120, 101 [CrossRef]
- Véron-Cetty, M.-P., Joly, M., & Véron, P. 2004, A&A, 417, 515 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [NASA ADS] [CrossRef]
- Wisotzki, L., Christlieb, N., Bade, N., et al. 2000, A&A, 358, 77 [NASA ADS]
- Woo, J.-H., Urry, C. M., van der Marel, R. P., Lira, P., & Maza, J. 2005, ApJ, 631, 762 [NASA ADS] [CrossRef] (In the text)
- Xu, Y., Bian, W.-H., Yuan, Q.-R., & Huang, K.-L. 2008, [arXiv:0806.1787] (In the text)
- Yip, C. W., Connolly, A. J., Vanden Berk, D. E., et al. 2004, AJ, 128, 2603 [NASA ADS] [CrossRef]
- Zamanov, R., & Marziani, P. 2002, ApJ, 571, L77 [NASA ADS] [CrossRef] (In the text)
- Zamanov, R., Marziani, P., Sulentic, J. W., et al. 2002, ApJ, 576, L9 [NASA ADS] [CrossRef]
- Zamfir, S., Sulentic, J. W., & Marziani, P. 2008, MNRAS, 387, 856 [NASA ADS] [CrossRef] (In the text)
- Zhou, H., Wang, T., Yuan, W., et al. 2006, ApJS, 166, 128 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
quasars
![[*]](/icons/foot_motif.gif)
- Based on observations made with ESO Telescopes at the Paranal Observatory under programme ID 073.B-0398(A) and 075.B-0171(A).
All Tables
Table 1: Basic properties of sources and log of observations
Table 2: Measurements of fluxes, equivalent qidths and FWHM of strongest lines.
Table 3: Measurements of fluxes and equivalent widths of narrow lines
Table 4:
H![]() Line profile measurements.
Line profile measurements.
Table 5:
H![]() Line centroids at different fractional heights
Line centroids at different fractional heights
Table 6: Measurements on the broad lines of median spectra.
Table 7:
H![]() Line profile measurements on spectral types.
Line profile measurements on spectral types.
Table 8:
H![]() Line centroids at different fractional heights of spectral types.
Line centroids at different fractional heights of spectral types.
All Figures
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.3cm,clip]{0764f01a.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg53.gif) |
Figure 1:
Calibrated VLT-ISAAC spectra for 30 new
intermediate-redshift quasars. Abscissæ are rest-frame
wavelength in Å, ordinates are rest-frame specific flux in units
of 10-15 erg s-1 cm-1 Å-1. The spectrum behavior of HE 0035-2853, HE 0043-2300, HE 0058-3231 is fully unreliable beyond |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.3cm,clip]{0764f01b.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg54.gif) |
Figure 1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.3cm,clip]{0764f01c.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg55.gif) |
Figure 1: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.8cm,height=16.8cm,clip]{0764f02a.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg56.gif) |
Figure 2:
Continuum-subtracted spectra. Lefthand panels: the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.4cm,height=16.4cm,clip]{0764f02b.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg57.gif) |
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm}
\includegraphics[width=7.8cm,height=7.8cm, angl...
...}\includegraphics[width=7.8cm,height=7.8cm, angle=0]{0764f03d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg254.gif) |
Figure 3:
FWHM(H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f04.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg255.gif) |
Figure 4:
The optical plane of Eigenvector 1 with the VLT sources presented in this paper and in Papers I and II (large filled circles, red in the online version of the paper), and the SDSS sample of Zamfir et al. 2008, small gray circles). Circled data points identify RL sources. Abscissa is Fe II |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,scale=0.48]{0764f05.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg287.gif) |
Figure 5:
Median spectra for bins A1, B1, A2, B2, as defined in Fig. 4. Original spectral have been normalized to unity at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.0cm,height=9.0cm, angle=0]{0764f06a....
...}\includegraphics[width=9.0cm,height=9.0cm, angle=0]{0764f06d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg288.gif) |
Figure 6:
Analysis of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.7,angle=0]{0764f07.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg290.gif) |
Figure 7:
Luminosity effects in the median spectra of Pop. A and Pop. B sources, binned in decades of luminosity in the luminosity ranges
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,height=7.8cm, angle=0]{0764f08a....
...cludegraphics[width=8.9cm,height=7.8cm, angle=0]{0764f08f.eps}\par
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg360.gif) |
Figure 8:
Median spectra analysis of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.0cm,height=8.0cm, angle=0]{0764f08g....
...s}\includegraphics[width=9.0cm,height=8.0cm, angle=0]{0764f08l.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg361.gif) |
Figure 8: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0764f09-coul.ps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg363.gif) |
Figure 9:
Distribution of unshifted and shifted H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.3cm,height=8.3cm, angle=0]{076...
...\includegraphics[width=7.9cm,height=8cm, angle=0]{0764f10b.eps} }
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg364.gif) |
Figure 10:
Left: distribution of the ISAAC sources whose H
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,height=12cm,clip]{0764f11.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg365.gif) |
Figure 11:
FWHM(H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,scale=0.4]{0764f12.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg366.gif) |
Figure 12: Median spectra for Pop. A, intermediate spectra in region M, and modified Population B (BM), as defined in Fig. 10. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f13a.eps}...
...raphics[width=9cm,height=9cm, angle=0]{0764f13c.eps}\hspace*{9cm}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg367.gif) |
Figure 13:
Median spectra analysis of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.0cm,height=8cm, angle=0]{0764f14a.eps}\includegraphics[width=8.0cm,height=8cm, angle=0]{0764f14b.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg368.gif) |
Figure 14:
Distribution of sources whose H
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f15.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg375.gif) |
Figure 15:
Distribution of the ISAAC sources in the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f16a.eps}...
....eps}\includegraphics[width=9cm,height=9cm, angle=0]{0764f16d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg376.gif) |
Figure 16:
Dependence on black hole
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,height=9cm, angle=0]{0764f17a.eps}...
....eps}\includegraphics[width=9cm,height=9cm, angle=0]{0764f17d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10764-08/Timg379.gif) |
Figure 17:
H |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


