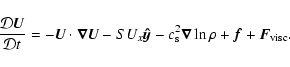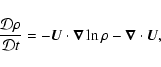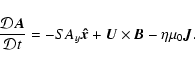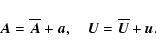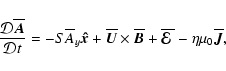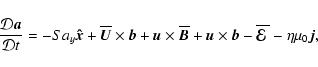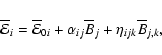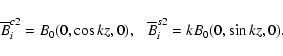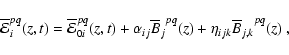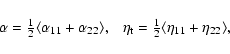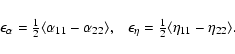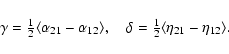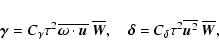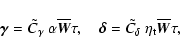| Issue |
A&A
Volume 495, Number 1, February III 2009
|
|
|---|---|---|
| Page(s) | 1 - 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361:200810359 | |
| Published online | 11 December 2008 | |
Alpha effect and diffusivity in helical turbulence with shear
D. Mitra1 - P. J. Käpylä2 - R. Tavakol1 - A. Brandenburg3
1 - Astronomy unit, School of Mathematical Sciences, Queen Mary University of London,
Mile End Road, London E1 4NS, UK
2 -
Observatory, Tähtitorninmäki (PO Box 14), 00014
University of Helsinki, Finland
3 -
NORDITA, Roslagstullsbacken 23, 10691 Stockholm, Sweden
Received 10 June 2008 / Accepted 28 November 2008
Abstract
Aims. We study the dependence of turbulent transport coefficients, such as the components of the ![]() tensor (
tensor (
![]() )
and the turbulent magnetic diffusivity tensor (
)
and the turbulent magnetic diffusivity tensor (![]() ), on shear and magnetic Reynolds number in the presence of helical forcing.
), on shear and magnetic Reynolds number in the presence of helical forcing.
Methods. We use three-dimensional direct numerical simulations with periodic boundary conditions and measure the turbulent transport coefficients using the kinematic test field method. In all cases the magnetic Prandtl number is taken as unity.
Results. We find that with increasing shear the diagonal components of
![]() quench, whereas those of
quench, whereas those of ![]() increase. The antisymmetric parts of both tensors increase with increasing shear. We also propose a simple expression for the turbulent pumping velocity (or
increase. The antisymmetric parts of both tensors increase with increasing shear. We also propose a simple expression for the turbulent pumping velocity (or ![]() effect). This pumping velocity is proportional to the kinetic helicity of the turbulence and the vorticity of the mean flow. For negative helicity, i.e. for a positive trace of
effect). This pumping velocity is proportional to the kinetic helicity of the turbulence and the vorticity of the mean flow. For negative helicity, i.e. for a positive trace of
![]() ,
it points in the direction of the mean vorticity, i.e. perpendicular to the plane of the shear flow. Our simulations support this expression for low shear and magnetic Reynolds number. The transport coefficients depend on the wavenumber of the mean flow in a Lorentzian fashion, just as for non-shearing turbulence.
,
it points in the direction of the mean vorticity, i.e. perpendicular to the plane of the shear flow. Our simulations support this expression for low shear and magnetic Reynolds number. The transport coefficients depend on the wavenumber of the mean flow in a Lorentzian fashion, just as for non-shearing turbulence.
Key words: magnetohydrodynamics (MHD) - hydrodynamics - turbulence - magnetic fields
1 Introduction
Understanding the origin of non-uniform large-scale magnetic fields in stars, galaxies, and accretion discs continues to pose important challenges. Such fields are commonly thought to be the result of dynamo action that converts the kinetic energy of turbulent motions and large-scale shear into magnetic energy. The usual framework for studying such dynamo actions is mean field electrodynamics (e.g. Krause & Rädler 1980). Over the years, however, the applicability of this framework has been questioned (Piddington 1981; Vainshtein & Cattaneo 1992). In particular, an important debate in this connection revolves around the role played by magnetic helicity (Gruzinov & Diamond 1994). Magnetic helicity is conserved for ideal (non-dissipative) magnetohydrodynamics (MHD) and also in the limit of large magnetic Reynolds numbers. This conservation places severe constraints on the growth of the mean magnetic field and may regulate the quenching of the
Several studies have recently looked at various
aspects of this problem (see, e.g., Rüdiger & Kitchatinov 2006; Rogachevskii & Kleeorin 2003,2004; Brandenburg 2005;
Leprovost & Kim 2008; Rädler & Stepanov 2006;Brandenburg et al. 2008a). These works employ different tools and make different
assumptions and are often applicable to limited regions of the parameter space.
As a consequence, care must be taken in comparing these results.
For example, using semi-analytical tools, which treat the
nonlinear Lorentz force feedback perturbatively, Leprovost & Kim (2008) have found that
shear can reduce ![]() in helically forced turbulence.
This is analogous to the ``rotational quenching'' of turbulent transport
coefficients with increasing Coriolis or inverse Rossby numbers
(Kitchatinov et al. 1994; Pipin et al. 1996).
There are also other related cases in which the presence of
shear enhances the growth rate of the dynamo. For example;
using direct numerical simulations of
the MHD equations in the presence of shear
and non-helical forcing, Yousef et al. (2008a,b) have found
large-scale dynamos whose growth rate increases linearly with shear.
Such scaling has also been found for
in helically forced turbulence.
This is analogous to the ``rotational quenching'' of turbulent transport
coefficients with increasing Coriolis or inverse Rossby numbers
(Kitchatinov et al. 1994; Pipin et al. 1996).
There are also other related cases in which the presence of
shear enhances the growth rate of the dynamo. For example;
using direct numerical simulations of
the MHD equations in the presence of shear
and non-helical forcing, Yousef et al. (2008a,b) have found
large-scale dynamos whose growth rate increases linearly with shear.
Such scaling has also been found for ![]() -shear dynamos where the
-shear dynamos where the
![]() effect is due to stratified convection with shear
(Käpylä et al. 2008a).
Furthermore, using the kinematic test field method
(described below), Brandenburg et al. (2008a) have studied the dynamo
coefficients in the presence of shear, but in the absence of helicity,
and they find that Gaussian fluctuations of
effect is due to stratified convection with shear
(Käpylä et al. 2008a).
Furthermore, using the kinematic test field method
(described below), Brandenburg et al. (2008a) have studied the dynamo
coefficients in the presence of shear, but in the absence of helicity,
and they find that Gaussian fluctuations of ![]() about
zero are strong enough to drive an incoherent
about
zero are strong enough to drive an incoherent
![]() -shear dynamo (Vishniac & Brandenburg 1997; Proctor 2007).
The significance of the incoherent
-shear dynamo (Vishniac & Brandenburg 1997; Proctor 2007).
The significance of the incoherent ![]() effect has also been stressed
by Hughes & Proctor (2009), although their system may have also had a net
effect has also been stressed
by Hughes & Proctor (2009), although their system may have also had a net ![]() effect.
They dismissed this on the grounds that for an imposed uniform magnetic
field
effect.
They dismissed this on the grounds that for an imposed uniform magnetic
field ![]() is very small.
However, this result disagrees with recent calculations of
is very small.
However, this result disagrees with recent calculations of ![]() using the test field method (Käpylä et al. 2008b).
using the test field method (Käpylä et al. 2008b).
In this paper we use three-dimensional direct numerical simulations of the kinematic test field equations with helical forcing in order to study the dependence of turbulent transport coefficients on shear and magnetic Reynolds number. In Sect. 2 we give a brief account of our model. Section 3 contains our results and finally we conclude in Sect. 4.
2 The model
We use the test field method (Schrinner et al. 2005,2007) to calculate the turbulent transport coefficients. This method and its modification in the presence of large-scale shear are described in Brandenburg et al. (2008a). Here we just point out the essence of the method and elaborate only on those aspects where our treatment differs from their paper.
In the presence of large-scale shear, the equations of magnetohydrodynamics
are treated in the following way. Writing the velocity as the
sum
![]() ,
where the large-scale shear
velocity
,
where the large-scale shear
velocity
![]() with a constant shear S,
and assuming an isothermal equation of state characterised by the sound
speed
with a constant shear S,
and assuming an isothermal equation of state characterised by the sound
speed ![]() ,
the momentum equation becomes
,
the momentum equation becomes
Here
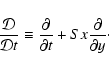 |
(2) |
As our external forcing
and the uncurled induction equation in the Weyl gauge,
Here the magnetic field is
The equations satisfied by the mean and fluctuating parts of the magnetic vector potential are given by
and
where
where
In our simulations we employ averages over x and
y directions to define our mean fields, which are therefore functions
of z and t only. Thus, all other components
of
![]() except
except
![]() and
and
![]() vanish, and the
vanish, and the
![]() and
and ![]() tensors can be written as rank two tensors
with
tensors can be written as rank two tensors
with
![]() and
and
![]() for i,j=(1,2)(Brandenburg et al. 2008a). Now consider, as an example, the following two test fields,
for i,j=(1,2)(Brandenburg et al. 2008a). Now consider, as an example, the following two test fields,
which we use to compute the two corresponding mean electromotive forces
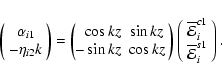 |
(11) |
The rest of the 2+2 components of the
In what follows we denote a test field by
such time dependence must be entirely due to
| |
Figure 1:
Root-mean-square velocity
|
| Open with DEXTER | |
In the following we shall, to begin with, use k=k1,
the wavenumber corresponding to the
box size, to study the dependence of
![]() and
and
![]() on shear and magnetic Reynolds number.
We shall discuss the dependence of the
on shear and magnetic Reynolds number.
We shall discuss the dependence of the
![]() and
and
![]() tensors on k in Sect. 3.3.
Note that the usual approach of using uniform applied fields for
calculating
tensors on k in Sect. 3.3.
Note that the usual approach of using uniform applied fields for
calculating ![]() (e.g., Courvoisier et al. 2006) corresponds to a
special case of the test field method for k=0.
However, dynamos generate large-scale fields with non-zero k,
so it is important to relax this restriction.
It is then also important to calculate
(e.g., Courvoisier et al. 2006) corresponds to a
special case of the test field method for k=0.
However, dynamos generate large-scale fields with non-zero k,
so it is important to relax this restriction.
It is then also important to calculate ![]() .
The test
field method allows the simultaneous calculation of all the components of
the
.
The test
field method allows the simultaneous calculation of all the components of
the
![]() and
and ![]() tensors for arbitrary values of k.
tensors for arbitrary values of k.
The test field method has recently been criticised by Cattaneo & Hughes (2008) on the grounds that the test fields are arbitrary predetermined mean fields. They argue that the resulting turbulent transport coefficients will only be approximations to the true values unless the test fields are close to the actual mean fields - a criticism equally applicable to other methods using arbitrary uniform fields. This concern has been addressed by Tilgner & Brandenburg (2008), who argue that Eq. (7) can instead be applied to any mean field. This statement has been numerically verified in three cases that we describe below.
Firstly, the test field method correctly reproduces a vanishing growth
rate in saturated nonlinear cases (Brandenburg et al. 2008b).
Secondly, in the time-dependent case, the test field method
correctly reproduces also a non-vanishing growth rate, but
in that case it is no longer permissible to express
![]() in terms of
a multiplication of turbulent transport coefficients with the mean field
and its spatial derivatives.
One must therefore write Eq. (8) as a convolution in time
(Hubbard & Brandenburg 2008).
Finally, the success of the test field method becomes particularly clear
when it is applied to a passive vector field that obeys a separate
induction equation with a velocity field from a saturated dynamo (Tilgner & Brandenburg 2008).
This question was originally posed by Cattaneo & Tobias (2008).
In particular for the Roberts flow with a mean field of Beltrami type,
e.g. one that is proportional to
in terms of
a multiplication of turbulent transport coefficients with the mean field
and its spatial derivatives.
One must therefore write Eq. (8) as a convolution in time
(Hubbard & Brandenburg 2008).
Finally, the success of the test field method becomes particularly clear
when it is applied to a passive vector field that obeys a separate
induction equation with a velocity field from a saturated dynamo (Tilgner & Brandenburg 2008).
This question was originally posed by Cattaneo & Tobias (2008).
In particular for the Roberts flow with a mean field of Beltrami type,
e.g. one that is proportional to
![]() ,
the
,
the
![]() tensor is anisotropic and has an additional component
proportional to
tensor is anisotropic and has an additional component
proportional to
![]() that tends
to quench the components of the isotropic part of
that tends
to quench the components of the isotropic part of
![]() .
The fastest growing passive vector field is then
proportional to
.
The fastest growing passive vector field is then
proportional to
![]() .
This result has been confirmed both numerically and
using weakly nonlinear theory (Tilgner & Brandenburg 2008).
.
This result has been confirmed both numerically and
using weakly nonlinear theory (Tilgner & Brandenburg 2008).
In the following we ignore the complications involving time-dependent
mean fields and restrict ourselves
to transport coefficients that apply strictly speaking only to the
time-independent or marginally excited case.
For our numerical simulations we use the
PENCIL CODE![]() ,
where the test field algorithm has already been implemented.
All our numerical simulations are performed in a periodic cubic box.
The forcing scale is chosen to have the wavenumber
,
where the test field algorithm has already been implemented.
All our numerical simulations are performed in a periodic cubic box.
The forcing scale is chosen to have the wavenumber
![]() .
This gives enough scale separation for a large-scale field to develop
(Haugen et al. 2004), and is still not too big to reduce the resulting
Reynolds numbers too much.
We use units such that
.
This gives enough scale separation for a large-scale field to develop
(Haugen et al. 2004), and is still not too big to reduce the resulting
Reynolds numbers too much.
We use units such that
![]() and arrange the forcing amplitude
so that the Mach number is around 0.1.
For the magnetic Prandtl number we choose
and arrange the forcing amplitude
so that the Mach number is around 0.1.
For the magnetic Prandtl number we choose
![]() ,
where
,
where ![]() lies
in the range
lies
in the range
![]() to
to
![]() (in units of
(in units of
![]() ).
We choose the shear S such that the parameter
).
We choose the shear S such that the parameter
| (14) |
takes values in the range -0.02 to -0.9, where
| (15) |
we obtain an exponential growth of small-scale magnetic field (see below). We interpret this as being associated with the
3 Results
Our principal aim in this paper is to study the effects of varying shear (![]() )
and magnetic Reynolds number (
)
and magnetic Reynolds number (
![]() )
on the components
of the
)
on the components
of the
![]() and
and ![]() tensors.
In the subsection below we summarize
our results concerning the different components of these tensors.
tensors.
In the subsection below we summarize
our results concerning the different components of these tensors.
3.1 Diagonal components of the transport tensors
The isotropic parts of the
![]() and
and ![]() tensors are respectively characterised as
tensors are respectively characterised as
where
Since
![]() enters the normalization of
enters the normalization of
![]() and
and ![]() ,
it is useful to first look at how it changes as a function of
,
it is useful to first look at how it changes as a function of
![]() (Fig. 1a) and
(Fig. 1a) and ![]() (Fig. 1b).
As can be seen,
(Fig. 1b).
As can be seen,
![]() increases as a function of
increases as a function of
![]() for small
for small
![]() and then reaches
a plateau for high
and then reaches
a plateau for high
![]() .
On the other hand,
.
On the other hand,
![]() is almost a constant as a function of shear except for high
is almost a constant as a function of shear except for high ![]() ,
where we observe excitation of the vorticity dynamo discussed further in
Sect. 3.4.
,
where we observe excitation of the vorticity dynamo discussed further in
Sect. 3.4.
In Fig. 2 we show ![]() as a function of shear for three
different values of the magnetic Reynolds number
as a function of shear for three
different values of the magnetic Reynolds number
![]() and 72. Figure 2b shows the corresponding
results for
and 72. Figure 2b shows the corresponding
results for
![]() .
We note that for small shear
the turbulent transport coefficients are close to their values for
zero shear.
As
.
We note that for small shear
the turbulent transport coefficients are close to their values for
zero shear.
As
![]() increases,
increases, ![]() decreases and
decreases and
![]() increases
up to four times
increases
up to four times
![]() .
As can be seen there is a clear reduction (quenching) of
.
As can be seen there is a clear reduction (quenching) of ![]() with
increasing shear in all these cases.
In order to examine the possible convergence of the results with
with
increasing shear in all these cases.
In order to examine the possible convergence of the results with
![]() we
plot
we
plot ![]() and
and
![]() as functions of
as functions of
![]() for three different values of the shear parameter
for three different values of the shear parameter
![]() ,
see Fig. 3.
For small
,
see Fig. 3.
For small
![]() we observe an increase in both
we observe an increase in both ![]() and
and
![]() with
with
![]() .
A similar initial increase of
.
A similar initial increase of ![]() and
and
![]() was also seen in
earlier simulations of helical turbulence without shear (Sur et al. 2008) and in
non-helical shear flow turbulence (Brandenburg et al. 2008a).
For higher values of
was also seen in
earlier simulations of helical turbulence without shear (Sur et al. 2008) and in
non-helical shear flow turbulence (Brandenburg et al. 2008a).
For higher values of
![]() and
and ![]() ,
both
,
both ![]() and
and
![]() show large variations.
In these kinematic simulations, however, we expect
them to tend to constant values asymptotically at high
show large variations.
In these kinematic simulations, however, we expect
them to tend to constant values asymptotically at high
![]() (Sur et al. 2008).
(Sur et al. 2008).
| |
Figure 2:
Turbulent transport coefficients a)
|
| Open with DEXTER | |
| |
Figure 3:
a)
|
| Open with DEXTER | |
In an earlier study of shear flow turbulence with non-helical forcing by
Brandenburg et al. (2008a), the diagonal components of ![]() were
found to be the same.
Obviously, in the absence of helicity
all the components of
were
found to be the same.
Obviously, in the absence of helicity
all the components of
![]() are zero.
It turns out that in the presence of helicity the two diagonal components
of
are zero.
It turns out that in the presence of helicity the two diagonal components
of ![]() are still the same, but those of
are still the same, but those of
![]() are now
non-zero and not equal to each other.
This is best shown by considering the quantities
are now
non-zero and not equal to each other.
This is best shown by considering the quantities
The results are shown in Fig. 4. Note that especially for large values of
| |
Figure 4:
Normalized
a)
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm]{0359fig5}
\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg131.gif) |
Figure 5:
Normalized off-diagonal components of
the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm]{0359fig6}
\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg133.gif) |
Figure 6:
Normalized off-diagonal components of the |
| Open with DEXTER | |
3.2 Off-diagonal components
We now consider the off-diagonal components of
![]() and
and ![]() .
The results are depicted in Figs. 5 and 6.
Of particular interest among these is the component
.
The results are depicted in Figs. 5 and 6.
Of particular interest among these is the component ![]() ,
whose dependence on
,
whose dependence on ![]() and
and
![]() is shown
in Figs. 5d and 6d, respectively.
This component can indicate the possible presence of a
shear-current dynamo that may operate when
is shown
in Figs. 5d and 6d, respectively.
This component can indicate the possible presence of a
shear-current dynamo that may operate when
![]() (Rogachevskii & Kleeorin 2003,2004). Here
(Rogachevskii & Kleeorin 2003,2004). Here
![]() is the total
(sum of turbulent and microscopic) magnetic diffusivity.
In our case we have S < 0,
which implies that the necessary condition for the shear-current dynamo
to operate is
is the total
(sum of turbulent and microscopic) magnetic diffusivity.
In our case we have S < 0,
which implies that the necessary condition for the shear-current dynamo
to operate is
![]() .
As can be seen from Fig. 6d,
for the range of
.
As can be seen from Fig. 6d,
for the range of
![]() values considered here
values considered here ![]() is positive for
small shear but becomes negative for strong shear and certain values of
is positive for
small shear but becomes negative for strong shear and certain values of
![]() .
Earlier work of Brandenburg et al. (2008a) without helicity did indicate a similar
sign change, although only for larger
.
Earlier work of Brandenburg et al. (2008a) without helicity did indicate a similar
sign change, although only for larger
![]() .
However, the error bars were so large that
this result could not be regarded as significant.
For the run with the strongest shear (
.
However, the error bars were so large that
this result could not be regarded as significant.
For the run with the strongest shear (
![]() )
and for
)
and for
![]() we now find
we now find ![]() to be more clearly negative, but for smaller
and larger values of
to be more clearly negative, but for smaller
and larger values of
![]() the results are again, at least within
error bars, compatible with zero.
Also, of course, the present results apply to the case with helicity
and are therefore not really comparable with those of Brandenburg et al. (2008a),
where the helicity is zero.
The antisymmetric contributions to the
the results are again, at least within
error bars, compatible with zero.
Also, of course, the present results apply to the case with helicity
and are therefore not really comparable with those of Brandenburg et al. (2008a),
where the helicity is zero.
The antisymmetric contributions to the
![]() and
and ![]() tensors
are characterised by the vectors
tensors
are characterised by the vectors
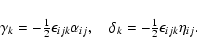 |
(18) |
Since our averages depend only on z, the z components of these tensors are irrelevant and therefore only the z components of the
A time series of both quantities is shown in Fig. 7 for positive and negative signs of the kinetic helicity. The results show that, in our case with S<0,
![\begin{figure}
\par\includegraphics[width=11cm]{0359fig7.ps}
\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg146.gif) |
Figure 7:
Normalized time series of turbulent transport coefficients,
a)
|
| Open with DEXTER | |
Some idea about the functional forms of ![]() and
and ![]() can be
obtained from symmetry considerations.
The vectors
can be
obtained from symmetry considerations.
The vectors
![]() and
and
![]() enter the electromotive force
thus
enter the electromotive force
thus
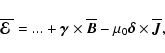 |
(20) |
so we see that
where we have introduced two non-dimensional quantities,
 |
(22) |
In the present case,
with new non-dimensional quantities,
The coefficient ![]() can be interpreted as turbulent pumping,
i.e. advection of the magnetic field by means other than the
mean velocity field.
In strongly stratified convection, turbulent pumping has been seen to be
directed from higher to lower turbulence intensity
(Käpylä et al. 2006; Tobias et al. 1998; Ossendrijver et al. 2002; Tobias et al. 2001),
which is usually in the downward direction.
Thus, turbulent pumping is likely
to play an important role in convection zones of stars where it can
overcome the buoyancy of the magnetic field. In the present case where
the turbulence is homogeneous, however, stratification does not play
a role and the pumping is just due to the combined action of shear and
helical turbulence.
can be interpreted as turbulent pumping,
i.e. advection of the magnetic field by means other than the
mean velocity field.
In strongly stratified convection, turbulent pumping has been seen to be
directed from higher to lower turbulence intensity
(Käpylä et al. 2006; Tobias et al. 1998; Ossendrijver et al. 2002; Tobias et al. 2001),
which is usually in the downward direction.
Thus, turbulent pumping is likely
to play an important role in convection zones of stars where it can
overcome the buoyancy of the magnetic field. In the present case where
the turbulence is homogeneous, however, stratification does not play
a role and the pumping is just due to the combined action of shear and
helical turbulence.
| |
Figure 8:
Normalized
a) |
| Open with DEXTER | |
| |
Figure 9:
Normalized a) |
| Open with DEXTER | |
3.3 Scale-dependence
So far we have confined the calculations of the| |
Figure 10:
a)
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{0359f11a}\includegraphics[width=6cm,clip]{0359f11b} }\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg180.gif) |
Figure 11:
Panel a) shows the root-mean-square values of the velocity for
one of our runs (with
|
| Open with DEXTER | |
3.4 Effects from the vorticity dynamo
In the runs with relatively high values of shear and Reynolds number, the root-mean-square velocity,
The vertical spikes in the inset of Fig. 11
come from resetting
![]() to zero
in regular time intervals; see the end of Sect. 2.
Note, however, that the mean values and also the upper envelope
trace the evolution of
to zero
in regular time intervals; see the end of Sect. 2.
Note, however, that the mean values and also the upper envelope
trace the evolution of
![]() reasonably well,
including the increased rise after t=300.
The late time behaviour is accompanied by the formation of large-scale
vortical structures, as seen in Fig. 11b,
which is a signature of the vorticity dynamo proposed by Elperin et al. (2003),
see also Yousef et al. (2008a,b). A detailed numerical study of the
vorticity dynamo has been performed by Käpylä et al. (2008).
reasonably well,
including the increased rise after t=300.
The late time behaviour is accompanied by the formation of large-scale
vortical structures, as seen in Fig. 11b,
which is a signature of the vorticity dynamo proposed by Elperin et al. (2003),
see also Yousef et al. (2008a,b). A detailed numerical study of the
vorticity dynamo has been performed by Käpylä et al. (2008).
The presence of the vorticity dynamo and the resulting
systematic variation in
![]() as well as
the turbulent transport coefficients
for late times limit the lengths of time
over which average values of the components of
the
as well as
the turbulent transport coefficients
for late times limit the lengths of time
over which average values of the components of
the
![]() and
and ![]() tensors
can be calculated. In the above case this interval lies between
the two arrows in Fig. 11a.
This limits the range of
tensors
can be calculated. In the above case this interval lies between
the two arrows in Fig. 11a.
This limits the range of ![]() and
and
![]() that we have
probed and explains the larger
error bars shown for example in Fig. 6,
and why they cannot be reduced by simply
running our simulations for longer times.
This problem would be avoided in the presence of magnetic fields, because
then the resulting Lorentz force would quench the vorticity dynamo
(Käpylä & Brandenburg 2008).
This is however beyond the scope of this paper.
that we have
probed and explains the larger
error bars shown for example in Fig. 6,
and why they cannot be reduced by simply
running our simulations for longer times.
This problem would be avoided in the presence of magnetic fields, because
then the resulting Lorentz force would quench the vorticity dynamo
(Käpylä & Brandenburg 2008).
This is however beyond the scope of this paper.
4 Conclusions
We have studied the effects of varying shear and magnetic Reynolds
number on the turbulent transport coefficients in the presence of helicity in
the kinematic limit. We have shown that for fixed
![]() ,
,
![]() is
reduced (quenched) with increasing shear. Despite the differences in the
assumptions made, this quenching is qualitatively similar to
the recent results obtained by Leprovost & Kim (2008).
To the best of our knowledge this is the first numerical study
to show quenching of
is
reduced (quenched) with increasing shear. Despite the differences in the
assumptions made, this quenching is qualitatively similar to
the recent results obtained by Leprovost & Kim (2008).
To the best of our knowledge this is the first numerical study
to show quenching of ![]() as a function of shear in helical turbulence.
We find that
as a function of shear in helical turbulence.
We find that
![]() increases
with increasing shear in the range of
increases
with increasing shear in the range of
![]() values that we have considered here. A similar behaviour
for
values that we have considered here. A similar behaviour
for
![]() was also seen in Brandenburg et al. (2008a) where the
forcing was non-helical.
was also seen in Brandenburg et al. (2008a) where the
forcing was non-helical.
We also compute the off-diagonal components of the
![]() and
and ![]() tensors.
The antisymmetric part of
tensors.
The antisymmetric part of
![]() corresponds to a turbulent
pumping velocity
corresponds to a turbulent
pumping velocity
![]() in the direction perpendicular to the
plane of the shear flow.
It shows a roughly linear increase with shear for small magnetic
Reynolds number. We propose simple expressions for
in the direction perpendicular to the
plane of the shear flow.
It shows a roughly linear increase with shear for small magnetic
Reynolds number. We propose simple expressions for ![]() and
and ![]() in Eq. (21) which show reasonable agreement with our
numerical results for small
in Eq. (21) which show reasonable agreement with our
numerical results for small ![]() and
and
![]() .
Our expression shows that for negative helicity,
.
Our expression shows that for negative helicity,
![]() points in the direction of the vorticity of the mean flow.
Regarding the component
points in the direction of the vorticity of the mean flow.
Regarding the component ![]() we find indications that, at least in
one or two cases, this component changes sign and becomes negative.
This could be of significance in connection with the shear-current effect.
we find indications that, at least in
one or two cases, this component changes sign and becomes negative.
This could be of significance in connection with the shear-current effect.
We also find that all the turbulent transport
coefficients depend on the wavenumber of the
mean flow in a Lorentzian fashion, just as in the case of non-shearing
turbulence (Brandenburg et al. 2008c).
This means that the kinematic values of ![]() and
and
![]() for k=k1 are close to the values obtained for
for k=k1 are close to the values obtained for ![]() .
This is not the case for certain non-turbulent flows such as
the Galloway-Proctor flow (Rädler & Brandenburg 2009; Courvoisier 2008).
In an earlier paper, Courvoisier et al. (2006) considered only the limiting case
k=0 for this flow.
.
This is not the case for certain non-turbulent flows such as
the Galloway-Proctor flow (Rädler & Brandenburg 2009; Courvoisier 2008).
In an earlier paper, Courvoisier et al. (2006) considered only the limiting case
k=0 for this flow.
Several aspects of the present investigations could
be of astrophysical relevance.
Turbulence in celestial bodies is helical and exhibits an ![]() effect.
In addition, shear (S) can be an important ingredient
in that the efficiency of large-scale dynamo action is determined by
the product of
effect.
In addition, shear (S) can be an important ingredient
in that the efficiency of large-scale dynamo action is determined by
the product of ![]() and S.
However, as S increases,
and S.
However, as S increases, ![]() itself becomes quenched when Sbecomes comparable with the inverse turnover time, i.e.
itself becomes quenched when Sbecomes comparable with the inverse turnover time, i.e.
![]() .
Furthermore, the turbulent diffusivity becomes enhanced, suppressing the
dynamo even further.
Finally, it is found that the combined action of helicity and shear
gives rise to a pumping velocity of mean magnetic field perpendicular
to the plane of the shear flow.
The existence of such a pumping velocity has not been emphasized before.
On the other hand, it is well known that
.
Furthermore, the turbulent diffusivity becomes enhanced, suppressing the
dynamo even further.
Finally, it is found that the combined action of helicity and shear
gives rise to a pumping velocity of mean magnetic field perpendicular
to the plane of the shear flow.
The existence of such a pumping velocity has not been emphasized before.
On the other hand, it is well known that
![]() (or rather
(or rather ![]() )
dynamos can have travelling wave solutions (Brandenburg et al. 2001).
When the product of
)
dynamos can have travelling wave solutions (Brandenburg et al. 2001).
When the product of ![]() and S is positive, these waves travel
in the positive z direction, which agrees with the direction of pumping.
In the near-surface shear layer of the Sun this pumping would therefore
support the equatorward migration in that layer.
and S is positive, these waves travel
in the positive z direction, which agrees with the direction of pumping.
In the near-surface shear layer of the Sun this pumping would therefore
support the equatorward migration in that layer.
It is important to understand the quenching of turbulent transport coefficients in the presence of shear beyond the kinematic approximation. In that case one needs to include the induction equation (in addition to the test field equations) and incorporate the resulting Lorentz force in the momentum equation (Brandenburg et al. 2008b). This would also help in alleviating problems of strong late-time fluctuations arising from the vorticity dynamo, because the vorticity dynamo tends to be suppressed by magnetic fields of equipartition strengths (Käpylä & Brandenburg 2008). Similarly, given their potential importance in allowing the escape of magnetic helicity, the effects of open boundary conditions also needs to be considered. These questions are under study and will be reported elsewhere.
Acknowledgements
The authors acknowledge the hospitality of Nordita during the programme ``Turbulence and Dynamos''. A.B. and P.J.K. thank Astronomy Unit, Queen Mary University of London, for hospitality. Computational resources were granted by CSC (Espoo, Finland), UKMHD, and QMUL HPC facilities purchased under the SRIF initiative. This work was supported by the the Leverhulme Trust (DM, RT), the Academy of Finland grant No. 121431 (PJK), and the Swedish Research Council (AB).
References
- Blackman, E., & Field, G. B. 2000, ApJ, 534, 984 [NASA ADS] [CrossRef]
- Blackman, E., & Brandenburg, A. 2002, ApJ, 579, 359 [NASA ADS] [CrossRef]
- Brandenburg, A. 2001, ApJ, 550, 824 [NASA ADS] [CrossRef] (In the text)
- Brandenburg, A. 2005, ApJ, 625, 539 [NASA ADS] [CrossRef]
- Brandenburg, A. 2008, ApJ, submitted [arXiv:0808.0961]
- Brandenburg, A., & Sandin, C. 2004, A&A, 427, 13 [NASA ADS] [CrossRef] [EDP Sciences]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] (In the text)
- Brandenburg, A., Bigazzi, A., & Subramanian, K. 2001, MNRAS, 325, 685 [NASA ADS] [CrossRef] (In the text)
- Brandenburg, A., Rädler, K.-H., Rheinhardt, M., & Käpylä, P. J. 2008a, ApJ, 676, 740 [NASA ADS] [CrossRef] (In the text)
- Brandenburg, A., Rädler, K.-H., Rheinhardt, M., & Subramanian, K. 2008b, ApJ, 687, L49 [NASA ADS] [CrossRef] (In the text)
- Brandenburg, A., Rädler, K.-H., & Schrinner, M. 2008c, A&A, 482, 739 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cattaneo, F., & Hughes, D. W. 2008 [arXiv:0805.2138] (In the text)
- Cattaneo, F., & Tobias, S. M. 2008, J. Fluid Mech. [arXiv:0809.1801] (In the text)
- Courvoisier, A. 2008, GAFD, 102, 217 [CrossRef]
- Courvoisier, A., Hughes, D. W., & Tobias, S. M. 2006, Phys. Rev. Lett., 96, 034503 [NASA ADS] [CrossRef] (In the text)
- Elperin, T., Kleeorin, N., & Rogachevskii, I. 2003, Phys. Rev. E, 68, 016311 [NASA ADS] [CrossRef] (In the text)
- Field, G., & Blackman, E. 2002, ApJ, 572, 685 [NASA ADS] [CrossRef]
- Gruzinov, A. V., & Diamond, P. H. 1994, Phys. Rev. Lett., 72, 1651 [NASA ADS] [CrossRef] (In the text)
- Haugen, N. E. L., Brandenburg, A., & Dobler, W. 2004, Phys. Rev. E 70, 016308 [NASA ADS]
- Hubbard, A., & Brandenburg, A. 2008 [arXiv:0811.2561] (In the text)
- Hughes, D. W., & Proctor, M. R. E. 2009, Phys. Rev. Lett. 102, 044501 (In the text)
- Käpylä, P. J., & Brandenburg, A. 2008, ApJ, submitted [arXiv:0810.2298] (In the text)
- Käpylä, P. J., Korpi, M. J., Ossendrijver, M., & Stix, M. 2006, A&A, 455, 401 [NASA ADS] [CrossRef] [EDP Sciences]
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2008a, A&A, 491, 353 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Käpylä, P. J., Korpi, M. J., & Brandenburg, A. 2008b, A&A, submitted [arXiv:0812.1792] (In the text)
- Käpylä, P. J., Mitra, D., & Brandenburg, A. 2008, Phys. Rev. E, 79, 016302 (In the text)
- Kitchatinov, L. L., Rüdiger, G., & Pipin, V. V. 1994, AN, 315, 157 [NASA ADS]
- Kleeorin, N., Moss, D., Rogachevskii, I., & Sokoloff, D. 2000, A&A, 361, L5 [NASA ADS]
- Krause, F., & Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) (In the text)
- Leprovost, N., & Kim, E.-J. 2008, Phys. Rev. Lett., 100, 144502 [NASA ADS] [CrossRef]
- Ossendrijver, M., Stix, M., Brandenburg, A., & Rüdiger, G. 2002, A&A, 394, 735 [NASA ADS] [CrossRef] [EDP Sciences]
- Piddington, J. H. 1981 ApJ, 247, 291
- Pipin, V. V., Rüdiger G., & Kitchatinov, L. L. 1996, GAFD, 83, 119 [CrossRef]
- Proctor, M. R. E. 2007, MNRAS, 382, L38 [NASA ADS]
- Rädler, K.-H., & Stepanov, R. 2006, Phys. Rev. E, 73, 056311 [NASA ADS] [CrossRef]
- Rädler, K.-H., & Brandenburg, A. 2009, MNRAS, 393, 113 [CrossRef]
- Rogachevskii, I., & Kleeorin, N. 2003, Phys. Rev. E, 68, 036301 [NASA ADS] [CrossRef]
- Rogachevskii, I., & Kleeorin, N. 2004, Phys. Rev. E, 70, 046310 [NASA ADS] [CrossRef]
- Rüdiger, G., & Kitchatinov, L. 2006, Astron. Nachr., 327, 298 [NASA ADS] [CrossRef]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. 2005, Astron. Nachr., 326, 245 [NASA ADS] [CrossRef]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. 2007, GAFD, 101, 81 [CrossRef]
- Subramanian, K., & Brandenburg, A. 2004, Phys. Rev. Lett., 93, 205001 [NASA ADS] [CrossRef]
- Sur, S., Brandenburg, A., & Subramanian, K. 2008, MNRAS, 385, L15 [NASA ADS] (In the text)
- Tilgner, A., & Brandenburg, A. 2008, MNRAS, 391, 1477 [NASA ADS] [CrossRef] (In the text)
- Tobias, S. M., Brummell, N. H., Clune, T. L., & Toomre, J. 1998, ApJ, 502, L177 [NASA ADS] [CrossRef]
- Tobias, S. M., Brummell, N. H., Clune, T. L., & Toomre, J. 2001, ApJ, 549, 1183 [NASA ADS] [CrossRef]
- Vishniac, E. T., & Brandenburg, A. 1997, ApJ, 584, L99
- Vishniac, E. T., & Cho, J. 2001, ApJ, 550, 752 [NASA ADS] [CrossRef]
- Vainshtein, E. T., & Cattaneo, J. 1992, ApJ, 393, 165 [NASA ADS] [CrossRef]
- Yousef, T. A., Heinemann, T., Schekochihin, A. A., et al. 2008a, Phys. Rev. Lett., 100, 184501 [NASA ADS] [CrossRef]
- Yousef, T. A., Heinemann, T., Rincon, F., et al. 2008b, AN, 329, 737 [NASA ADS]
Footnotes
All Figures
| |
Figure 1:
Root-mean-square velocity
|
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Turbulent transport coefficients a)
|
| Open with DEXTER | |
| In the text | |
| |
Figure 3:
a)
|
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
Normalized
a)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{0359fig5}
\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg131.gif) |
Figure 5:
Normalized off-diagonal components of
the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{0359fig6}
\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg133.gif) |
Figure 6:
Normalized off-diagonal components of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11cm]{0359fig7.ps}
\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg146.gif) |
Figure 7:
Normalized time series of turbulent transport coefficients,
a)
|
| Open with DEXTER | |
| In the text | |
| |
Figure 8:
Normalized
a) |
| Open with DEXTER | |
| In the text | |
| |
Figure 9:
Normalized a) |
| Open with DEXTER | |
| In the text | |
| |
Figure 10:
a)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm,clip]{0359f11a}\includegraphics[width=6cm,clip]{0359f11b} }\end{figure}](/articles/aa/full_html/2009/07/aa10359-08/Timg180.gif) |
Figure 11:
Panel a) shows the root-mean-square values of the velocity for
one of our runs (with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.