| Issue |
A&A
Volume 495, Number 1, February III 2009
|
|
|---|---|---|
| Page(s) | 243 - 248 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:200810238 | |
| Published online | 14 January 2009 | |
Evolution of long-period, white-dwarf binaries: application to GRO J1744-28 and type Ia supernovae
Xiao-Jie Xu - Xiang-Dong Li
Department of Astronomy, Nanjing University, Nanjing 210093, PR China
Received 22 May 2008 / Accepted 13 November 2008
Abstract
We calculated the evolution of long-period white dwarf binaries,
by accounting for thermally unstable accretion
during mass transfer. Under certain conditions we found that, the
accretion rates onto the white dwarf during dwarf
nova outbursts can be sufficiently high to allow steady nuclear burning of
the accreted matter and growth of the white dwarf mass.
If the Chandrasekhar mass is reached, the white dwarf may
collapse to be a neutron star, or explode as a type Ia supernova.
This scenario appears to account well for the formation of the bursting
pulsar GRO J1744-28, and probably type Ia supernovae with
delay times considerably longer than 1 Gyr.
Key words: accretion, accretion disks - stars: dwarf novae - stars: pulsars: individual: GRO J1744-28 - stars: supernovae: general
1 Introduction
Discovered in 1995, GRO J1744-28 is the only X-ray pulsar that
exhibitss type-II like X-ray bursts (Fishman et al. 1995; Kouveliotou et al. 1996; Finger et al. 1996).
With a spin period of 467 ms, the pulsar is in an 11.8-day binary
orbit with a remarkably small mass function
![]() (Finger et al. 1996), which indicates
that, unless we observe the system almost pole-on (inclination
angle <
(Finger et al. 1996), which indicates
that, unless we observe the system almost pole-on (inclination
angle <
![]() ), the companion has a mass <
), the companion has a mass <
![]() ,
implying that GRO J1744-28 is most likely to be a low-mass X-ray
binary (LMXB). Using VLT/ISAAC, Gosling et al. (2007) detected
two candidate counterparts to GRO J 1744-28, although it was unclear whether
one was the true counterpart.
,
implying that GRO J1744-28 is most likely to be a low-mass X-ray
binary (LMXB). Using VLT/ISAAC, Gosling et al. (2007) detected
two candidate counterparts to GRO J 1744-28, although it was unclear whether
one was the true counterpart.
From the observed pulse period and spin-up rate, the magnetic field
of GRO J1744-28 can be inferred to be of order 1011 G (Finger
et al. 1996; Daumerie et al. 1996). Observational evidence for the
``propeller'' effect in GRO J1744-28 also led to a similar
estimate of the pulsar's magnetic field (Cui 1997). Evolutionary
calculations by Rappaport & Joss (1997) implied that the donor star is
likely to be a low-mass giant of mass ![]()
![]() .
Thus,
this system is most likely to be in the final stages of losing its
hydrogen-rich envelope, and will become a recycled radio pulsar at
the end of the mass transfer.
.
Thus,
this system is most likely to be in the final stages of losing its
hydrogen-rich envelope, and will become a recycled radio pulsar at
the end of the mass transfer.
An important question related to the formation and evolution of
GRO J1744-28 is why it has a magnetic field of strength far higher than
those of low-mass binary millisecond pulsars, which are generally
thought to have evolved from LMXBs. Previous calculations of LMXB
evolution indicated that, to form an LMXB in a 12-day orbital period close to
the end of the mass-transfer stage, the neutron star (NS) is most likely to have
accreted at least several tenths of a solar mass (Li & Wang 1998, and references
therein), so that the NS's magnetic field has
decayed to ![]() 108-109 G
(van den Heuvel & Bitzaraki 1995; Urpin & Geppert 1995; Shibazaki et al. 1989; Taam & van den Heuvel 1986). To resolve this puzzle,
van Paradijs et al. (1997) proposed that the NS could originate from the
collapse of a white dwarf (WD) that was accreting from a normal
low-mass star, although, according to Li & Wang (1998) and Sutantyo & Li (2000), such a
NS would still have accreted too much matter after the
accretion-induced collapse (AIC) of the WD. The mass
transfer rate onto the WD is also far less than that required for steady
burning on top of the WD, so that most of the accreting matter would
have been expelled from the system during strong H-shell flashes
(Kovetz & Prialnik 1994).
108-109 G
(van den Heuvel & Bitzaraki 1995; Urpin & Geppert 1995; Shibazaki et al. 1989; Taam & van den Heuvel 1986). To resolve this puzzle,
van Paradijs et al. (1997) proposed that the NS could originate from the
collapse of a white dwarf (WD) that was accreting from a normal
low-mass star, although, according to Li & Wang (1998) and Sutantyo & Li (2000), such a
NS would still have accreted too much matter after the
accretion-induced collapse (AIC) of the WD. The mass
transfer rate onto the WD is also far less than that required for steady
burning on top of the WD, so that most of the accreting matter would
have been expelled from the system during strong H-shell flashes
(Kovetz & Prialnik 1994).
Li & Wang (1998) proposed a modified scenario for the formation of GRO
J1744-28 based on the AIC model. The progenitor system is assumed
to be a binary consisting of an O-Ne-Mg WD and a ![]()
![]() main-sequence secondary star in a
main-sequence secondary star in a ![]() 1 day orbit initially.
After several Gyr, the secondary fills its Roche-lobe (RL) due to
nuclear expansion. Along with mass transfer, the orbital period
increases, and the accretion disk becomes thermally and viscously
unstable giving rise to limit cycle behavior (Lasota 2001; King et al. 1997; ). As a result, the system appears as a dwarf
nova. The mass transfer rate during outbursts could rise to a few
times 10-8 to
1 day orbit initially.
After several Gyr, the secondary fills its Roche-lobe (RL) due to
nuclear expansion. Along with mass transfer, the orbital period
increases, and the accretion disk becomes thermally and viscously
unstable giving rise to limit cycle behavior (Lasota 2001; King et al. 1997; ). As a result, the system appears as a dwarf
nova. The mass transfer rate during outbursts could rise to a few
times 10-8 to
![]() yr-1, at which the WD could
burn the accreted matter steadily, while in quiescence, little
accretion occurs. Thus, the WD could steadily accumulate mass to
reach
yr-1, at which the WD could
burn the accreted matter steadily, while in quiescence, little
accretion occurs. Thus, the WD could steadily accumulate mass to
reach ![]()
![]() and collapse to become a high-field NS.
In the subsequent mass transfer, due to unstable disk
accretion the NS must have accreted hardly more than a few
hundredths of
and collapse to become a high-field NS.
In the subsequent mass transfer, due to unstable disk
accretion the NS must have accreted hardly more than a few
hundredths of
![]() ,
such that the magnetic field did not
decay significantly.
,
such that the magnetic field did not
decay significantly.
In this work, we attempt to examine the feasibility of the above scenario
with detailed numerical calculations of the evolutions of wide
WD binaries. However, our interest is not limited to the AIC formation
channel to GRO J1744-28 like objects, but extends to possible
progenitors of type Ia supernovae (SNe Ia) in old populations.
SNe Ia have been used as the most important standard candlelight
in cosmology (Perlmutter et al. 1999; Philips 1993; Riess et al. 2004,1998). It has long been
believed that SNe Ia originate from explosions of accreting WDs,
whose masses exceed the Chandrasekhar mass limit. However, the
nature of the progenitor systems remains unclear. Generally there are
two kinds of progenitor-system models:
the single degenerate (SD) model in which a WD accretes from a normal
binary companion (Nomoto 1982), and the double degenerate (DD) model
in which two WDs merge due to binary shrinkage (Iben & Tutukov 1984). The
SD model can be divided into two classes: (1) the WD accretes from a
main-sequence star more massive than ![]()
![]() with initial period
with initial period
![]() day (Han & Podsiadlowski 2004; Li & van den Heuvel 1997; Langer et al. 2000), and (2) the WD accretes from
a
day (Han & Podsiadlowski 2004; Li & van den Heuvel 1997; Langer et al. 2000), and (2) the WD accretes from
a ![]()
![]() red giant star with
red giant star with ![]() d
(Li & van den Heuvel 1997; Hachisu et al. 1996). Observations of the circumstellar material in the
type Ia SN 2006X inside the Virgo cluster spiral galaxy NGC 4321
strongly suggest that the WD was accreting material from a companion
star that was in the red giant phase at the time of the explosion
(Patat et al. 2007). It should be emphasized that mass transfer in the
evolution of long-period WD binaries is likely to be unstable (at least during
part of the mass-transfer lifetime), and
this important feature has been ignored practically in
previous theoretical work on SNe Ia apart from King et al. (2003), who
adopted a similar idea in Li & Wang (1998) to produce SNe Ia with
long-period dwarf novae in a semi-analytic approach. More
detailed work is obviously needed to investigate the influence of the input
parameters on the final results.
d
(Li & van den Heuvel 1997; Hachisu et al. 1996). Observations of the circumstellar material in the
type Ia SN 2006X inside the Virgo cluster spiral galaxy NGC 4321
strongly suggest that the WD was accreting material from a companion
star that was in the red giant phase at the time of the explosion
(Patat et al. 2007). It should be emphasized that mass transfer in the
evolution of long-period WD binaries is likely to be unstable (at least during
part of the mass-transfer lifetime), and
this important feature has been ignored practically in
previous theoretical work on SNe Ia apart from King et al. (2003), who
adopted a similar idea in Li & Wang (1998) to produce SNe Ia with
long-period dwarf novae in a semi-analytic approach. More
detailed work is obviously needed to investigate the influence of the input
parameters on the final results.
The structure of this paper is as follows. We describe the binary evolution code and input physics in Sect. 2. In Sects. 3 and 4, we present the calculated results for GRO J1744-28 and the progenitors of SNe Ia, respectively. We discuss the implications of the results and conclude in Sect. 5.
2 Binary calculations
2.1 Binary evolution code
We used an updated version of the stellar evolution code
developed by Eggleton (1971, see also Pols et al. 1995), to
calculate the detailed evolution of a binary containing initially a WD of mass M1 and a secondary star of mass M2. The opacities
were taken from Rogers & Iglesias (1992), and Alexander & Ferguson (1994) for temperatures
below 103.8 K. For the donor star, we assumed a solar chemical
composition (X=0.7, Y=0.28, and Z=0.02) and a mixing-length
parameter of
![]() .
The effective RL radius of the secondary
was calculated with Eggleton's equation (Eggleton 1983),
.
The effective RL radius of the secondary
was calculated with Eggleton's equation (Eggleton 1983),
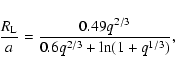 |
(1) |
where a is the orbital separation, and q=M2/M1 is the mass ratio. We use the following formula to calculate the mass-transfer rate from the donor star via RL-overflow
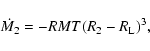 |
(2) |
where RMT is taken to be 500. We also included stellar-wind mass-loss from the donor with the rate suggested by Nieuwenhuijzen & de Jager (1990),
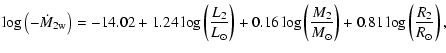 |
(3) |
where L2 and R2 are the luminosity and radius of the donor, respectively.
2.2 Accretion disk Instability & accretion rates
During RL-overflow mass transfer, the accreting material forms a
disk surrounding the WD, and the accretion disk may become thermally
unstable when the effective temperature in the disk falls below the
hydrogen ionization temperature ![]() 6500 K (Lasota 2001; King et al. 1997; ). This also corresponds to a critical mass-transfer
rate below which the disk is unstable. As to thermal
instability of the accretion disk, we set the critical mass-transfer
rate for a stable accretion disk to be
6500 K (Lasota 2001; King et al. 1997; ). This also corresponds to a critical mass-transfer
rate below which the disk is unstable. As to thermal
instability of the accretion disk, we set the critical mass-transfer
rate for a stable accretion disk to be
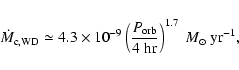 |
(4) |
for WD accretors, and
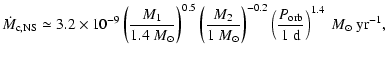 |
(5) |
for NS accretors with an irradiated accretion disk (Dubus et al. 1999; ). Here
2.3 Nuclear burning & WD mass growth
After the accumulation of fresh H and He on the WD, thermal nuclear
burning is likely to occur in certain circumstances. The
burning processes of the accreted material on the surface of a
WD includes the burning of both H to He and He to heavier elements. To
follow the mass growth during the burning processes, we adopted the
descriptions in Hachisu et al. (1999), Han & Podsiadlowski (2004), and Chen & Li (2007)
for H accumulation ratio
![]() ,
,
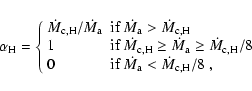 |
(6) |
where
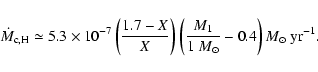 |
(7) |
If
During subsequent He burning, the WD mass also increases only if
the He accretion rate
![]() is within a narrow range. For He burning, we adopted the
accumulation ratio
is within a narrow range. For He burning, we adopted the
accumulation ratio
![]() in Kato & Hachisu (2004),
in Kato & Hachisu (2004),
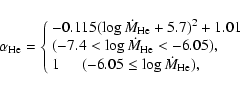 |
(8) |
for a
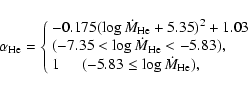 |
(9) |
for a
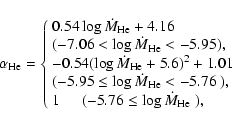 |
(10) |
for a
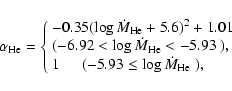 |
(11) |
for a
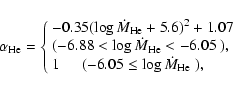 |
(12) |
for a
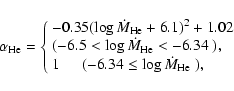 |
(13) |
for a
2.4 Mass and angular momentum loss
To follow the orbital momentum loss, we include the effects
of mass loss, magnetic braking (MB), and gravitational wave radiation. The
mass loss from the compact star includes those ejected from the
system both due to unstable H and He shell burning and due to
super-Eddington accretion. In the WD case, the mass-loss rate
can be expressed as
![]() ,
where
,
where
![]() is the Eddington accretion rate of a WD. We allow the ejected
matter to carry away the specific orbital angular momentum of the
compact star. For MB, we adopt the description of
angular momentum loss from Sills et al. (2000) and Andronov et al. (2003),
is the Eddington accretion rate of a WD. We allow the ejected
matter to carry away the specific orbital angular momentum of the
compact star. For MB, we adopt the description of
angular momentum loss from Sills et al. (2000) and Andronov et al. (2003),
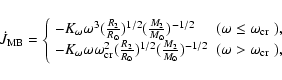 |
(14) |
where
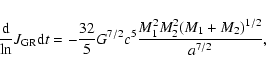 |
(15) |
where G and c are the gravitational constant and speed of light, respectively.
2.5 Conditions for AIC & SNe Ia
As proposed by Nomoto (1984), an accreting O-Ne-Mg WD of initial
mass higher than
![]() would collapse to a NS if its mass
exceeded the Chandrasekhar mass limit, otherwise the WD would end its life as
a SN Ia. In our calculations, we define the initial WD mass to be
would collapse to a NS if its mass
exceeded the Chandrasekhar mass limit, otherwise the WD would end its life as
a SN Ia. In our calculations, we define the initial WD mass to be
![]() for AIC systems, and
for AIC systems, and
![]() for SN Ia systems;
the WD is assumed to collapse to become a NS once its mass reaches
for SN Ia systems;
the WD is assumed to collapse to become a NS once its mass reaches
![]() ,
or trigger a SN Ia explosion when its mass reaches
,
or trigger a SN Ia explosion when its mass reaches
![]() ,
at which point we also terminate the calculation for SNe Ia systems.
For the AIC channel, we assume a
,
at which point we also terminate the calculation for SNe Ia systems.
For the AIC channel, we assume a ![]()
![]() mass loss
after collapse due to neutrino radiation, so the newborn NS has
a mass of
mass loss
after collapse due to neutrino radiation, so the newborn NS has
a mass of
![]() .
We also assume the initial magnetic field
of the NS to be
.
We also assume the initial magnetic field
of the NS to be
![]() G. As a result of the sudden
mass loss, the orbital period increases to a higher value, the system
becomes detached, and mass transfer pauses. Nuclear evolution will
drive the secondary to fill its RL again later, and resumes the mass
transfer. The following evolution of the system is similar to that of a
normal LMXB. We use Eq. (5) to determine if the accretion disk
experiences thermal instability. The evolution of the NS spin and
magnetic field caused by mass accretion is calculated according to
Li et al. (1998). Specifically, we use a phenomenological form of
field decay with accretion,
G. As a result of the sudden
mass loss, the orbital period increases to a higher value, the system
becomes detached, and mass transfer pauses. Nuclear evolution will
drive the secondary to fill its RL again later, and resumes the mass
transfer. The following evolution of the system is similar to that of a
normal LMXB. We use Eq. (5) to determine if the accretion disk
experiences thermal instability. The evolution of the NS spin and
magnetic field caused by mass accretion is calculated according to
Li et al. (1998). Specifically, we use a phenomenological form of
field decay with accretion,
![]() suggested by Shibazaki et al. (1989), where
suggested by Shibazaki et al. (1989), where
![]() is the mass accreted by the NS, and
is the mass accreted by the NS, and
![]() .
.
 |
Figure 1: The initial distribution of the donor masses and orbital periods for binaries evolving with an AIC. The duty cycle of outbursts due to unstable disk accretion is taken to be d=0.01. The open and filled dots refer to those with the donors on main sequence and being subgiants at the onset of mass transfer, respectively. The size of the dots indicates the mass that the NS accretes after AIC. |
| Open with DEXTER | |
 |
Figure 2: The end distribution of the companion masses and orbital periods for LMXBs. The filled dots are for LMXBs experienced an AIC from this work, and the solid line indicates the result for normal LMXBs given by Tauris & Savonije (1999). |
| Open with DEXTER | |
3 AIC formation channel to GRO J1744-28
We first investigate the evolution of a binary containing an
O-Ne-Mg WD. The initial WD mass is set to be
![]() to ensure that the
WD collapses to a NS rather than explodes as a SN Ia (Nomoto 1984).
The initial mass of the secondary is between
to ensure that the
WD collapses to a NS rather than explodes as a SN Ia (Nomoto 1984).
The initial mass of the secondary is between
![]() and
and
![]() .
We set the duty cycle d to be 0.01 for dwarf nova outbursts.
We calculated the evolution of 54 systems with a
successful AIC. Figure 1 shows the initial orbital periods and the
donor masses of these systems, where the open and filled dots are
for systems initiating mass transfer before and after the depletion
of central H of the companion, respectively. The dot size indicates
the amount of mass that the NS accreted during its
evolution after an AIC. The final distribution of the companion
mass (
.
We set the duty cycle d to be 0.01 for dwarf nova outbursts.
We calculated the evolution of 54 systems with a
successful AIC. Figure 1 shows the initial orbital periods and the
donor masses of these systems, where the open and filled dots are
for systems initiating mass transfer before and after the depletion
of central H of the companion, respectively. The dot size indicates
the amount of mass that the NS accreted during its
evolution after an AIC. The final distribution of the companion
mass (
![]() )
- orbital period (
)
- orbital period (
![]() )
at the end of mass transfer is shown in Fig. 2.
To compare with previous works we also plot the
)
at the end of mass transfer is shown in Fig. 2.
To compare with previous works we also plot the
![]() relation
given by Tauris & Savonije (1999), which reproduces well our calculated
results. Thus from the
relation
given by Tauris & Savonije (1999), which reproduces well our calculated
results. Thus from the
![]() relation, it appears impossible to
determine whether an LMXB system is primordial or originated from the AIC of a
WD binary.
relation, it appears impossible to
determine whether an LMXB system is primordial or originated from the AIC of a
WD binary.
Our calculations indicate that the minimum mass a NS accretes after
the AIC is ![]()
![]() when
when
![]() d, leaving the NS with a
weak magnetic field (
d, leaving the NS with a
weak magnetic field (![]() 108-109 G) (Shibazaki et al. 1989). To
solve this problem, we lowered the values of the duty cycle to
d=0.002 and 0.004, and found more suitable matches for GRO
J1744-28. One possible evolutionary path is given in Fig. 3. The
system initially contains a
108-109 G) (Shibazaki et al. 1989). To
solve this problem, we lowered the values of the duty cycle to
d=0.002 and 0.004, and found more suitable matches for GRO
J1744-28. One possible evolutionary path is given in Fig. 3. The
system initially contains a
![]() WD and a
WD and a
![]() main-sequence companion star with an orbital period of
main-sequence companion star with an orbital period of
![]() days. Mass
transfer initiates at
days. Mass
transfer initiates at
![]() Gyr when the companion is about to
evolve off the main sequence. The mass transfer rate is always below
Gyr when the companion is about to
evolve off the main sequence. The mass transfer rate is always below
![]() yr-1, and the accretion disk is thermally
unstable according to Eq. (4). In the first 1.6 Gyr, the mass
transfer rate is lower than
yr-1, and the accretion disk is thermally
unstable according to Eq. (4). In the first 1.6 Gyr, the mass
transfer rate is lower than
![]() yr-1 and almost
all of the accreted mass is lost from the WD due to unstable
H burning. In the next 0.8 Gyr, the mass accretion rate is sufficiently high
to allow stable H burning, the WD mass grows to
yr-1 and almost
all of the accreted mass is lost from the WD due to unstable
H burning. In the next 0.8 Gyr, the mass accretion rate is sufficiently high
to allow stable H burning, the WD mass grows to
![]() ,
and finally collapses to become a NS. During mass
transfer the companion loses
,
and finally collapses to become a NS. During mass
transfer the companion loses ![]()
![]() mass and the orbital
period increases to
mass and the orbital
period increases to ![]() 2 d. The AIC process further widens the
orbit to the one of period
2 d. The AIC process further widens the
orbit to the one of period
![]() d, and the system becomes detached. The
companion, now of mass
d, and the system becomes detached. The
companion, now of mass ![]()
![]() ,
evolves and fills its RL
to transfer mass once more at
,
evolves and fills its RL
to transfer mass once more at ![]() Gyr. For most of the
time, the mass transfer rate is still below
Gyr. For most of the
time, the mass transfer rate is still below
![]() yr-1, so the accretion disk is also thermally unstable, and
the binary becomes a soft X-ray transient. Since the mass
accretion rate during outbursts is substantially higher than the
Eddington limit accretion rate for a NS, most of the accreting
matter is expelled from the NS. The orbit expands to
yr-1, so the accretion disk is also thermally unstable, and
the binary becomes a soft X-ray transient. Since the mass
accretion rate during outbursts is substantially higher than the
Eddington limit accretion rate for a NS, most of the accreting
matter is expelled from the NS. The orbit expands to
![]() d at
d at
![]() Gyr, when the NS accumulates only
Gyr, when the NS accumulates only
![]() mass. The
system now contains a NS with a relatively strong magnetic field, and a
mass. The
system now contains a NS with a relatively strong magnetic field, and a
![]()
![]() companion. In the future, the mass transfer should
continue until the companion loses its entire H envelope and becomes
a WD.
companion. In the future, the mass transfer should
continue until the companion loses its entire H envelope and becomes
a WD.
A possible way of testing our model is to search for the counterpart
of GRO J1744-28 in other wavelengths, such as optical or infrared
band. We plot the evolutionary path of the companion star in the H-R diagram in Fig. 4, with the star, diamond, filled dot, and triangle
symbols indicating the positions of the companion when mass transfer
starts, AIC happens,
![]() d, and mass transfer terminates,
respectively. From the figure, the companion star appears to have
a surface temperature of
d, and mass transfer terminates,
respectively. From the figure, the companion star appears to have
a surface temperature of ![]() 4400 K and a luminosity of about
4400 K and a luminosity of about
![]() ,
which is characteristic of a K giant star. This appears to be
consistent with the properties of the bright counterpart detected by
Gosling et al. (2007). The fact that its spectrum does not exhibit
Brackett-
,
which is characteristic of a K giant star. This appears to be
consistent with the properties of the bright counterpart detected by
Gosling et al. (2007). The fact that its spectrum does not exhibit
Brackett-![]() emission implies that currently the source may not
be in an accreting phase, which is also consistent with our expectation of
its transient nature.
emission implies that currently the source may not
be in an accreting phase, which is also consistent with our expectation of
its transient nature.
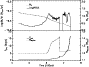 |
Figure 3: This figure shows an example of the evolution leading to the formation of GRO J1744-28. The solid and dotted lines show the evolution of the mass transfer rate and the donor mass in the upper panel, and the evolution of the orbital period and the accreting WD/NS mass in the lower panel, respectively. |
| Open with DEXTER | |
 |
Figure 4: The evolution of the companion star in H-R diagram. The star, diamond, filled dot and triangle indicate the start of mass transfer, the time of AIC, the present situation and the time when mass transfer terminates, respectively. |
| Open with DEXTER | |
4 Formation channel to SNe Ia
To explore possible progenitor systems of SNe Ia, we consider a
binary system containing a WD of initial mass
![]() and
and
![]() .
The mass of the companion star is taken to range from
.
The mass of the companion star is taken to range from
![]() to
to
![]() ,
the initial orbital period from
0.5 d to 10 d, and the duty cycle is set to be 0.01 for unstable disk
accretion.
,
the initial orbital period from
0.5 d to 10 d, and the duty cycle is set to be 0.01 for unstable disk
accretion.
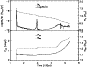 |
Figure 5: An example of the evolutionary path to SN Ia. The solid and dotted lines show the evolution of the mass transfer rate and the donor mass in the upper panel, and the evolution of the orbital period and the WD mass in the lower panel, respectively. |
| Open with DEXTER | |
We terminate the calculation when either of the following conditions
is satisfied: (1) the age of the binary exceeds 12 Gyr; (2) the
mass of the WD reaches
![]() within 12 Gyr when we assume
that it becomes a SN Ia; (3) the mass transfer becomes dynamically
unstable. In Fig. 5, we present an example of the evolutionary path
to become a SN Ia. The binary consists initially of a WD of mass
within 12 Gyr when we assume
that it becomes a SN Ia; (3) the mass transfer becomes dynamically
unstable. In Fig. 5, we present an example of the evolutionary path
to become a SN Ia. The binary consists initially of a WD of mass
![]() with a
with a
![]() companion in a
companion in a
![]() d orbit. The companion begins to fill its RL and trigger mass
transfer as its core H burning continues. During the whole
evolution, the mass-transfer rate is lower than the critical value
given by Eq. (4), and the accretion disk experiences thermal
instability. In the first
d orbit. The companion begins to fill its RL and trigger mass
transfer as its core H burning continues. During the whole
evolution, the mass-transfer rate is lower than the critical value
given by Eq. (4), and the accretion disk experiences thermal
instability. In the first ![]() 108 yr, mass transfer occurs on a
thermal timescale, since the mass ratio q>1 at this stage, which
produces a sharp increase in the mass-transfer rate curve and causes
the orbit to decrease in physical size. The mass-accretion rate of
the WD during outbursts lies above the critical value for stable
nuclear burning, and the WD mass increases to
108 yr, mass transfer occurs on a
thermal timescale, since the mass ratio q>1 at this stage, which
produces a sharp increase in the mass-transfer rate curve and causes
the orbit to decrease in physical size. The mass-accretion rate of
the WD during outbursts lies above the critical value for stable
nuclear burning, and the WD mass increases to ![]()
![]() .
After the mass ratio q becomes <1, the orbit starts to expand. The
mass transfer rate drops below
.
After the mass ratio q becomes <1, the orbit starts to expand. The
mass transfer rate drops below
![]() yr-1 in the
next 1.4 Gyr, and stable H burning is quenched, such that the mass
of the WD stops growing. At
yr-1 in the
next 1.4 Gyr, and stable H burning is quenched, such that the mass
of the WD stops growing. At
![]() Gyr, the mass transfer
rate increases again as the companion evolves off the main sequence
and expands, allowing stable nuclear burning, and the mass of the
WD increases further to
Gyr, the mass transfer
rate increases again as the companion evolves off the main sequence
and expands, allowing stable nuclear burning, and the mass of the
WD increases further to
![]() ,
triggering a SN Ia at
,
triggering a SN Ia at
![]() Gyr. At this time, the companion mass decreases to
Gyr. At this time, the companion mass decreases to
![]()
![]() ,
and the orbital period becomes
,
and the orbital period becomes
![]() d.
d.
Figure 6 summarizes the final results of our binary evolution
calculations, showing the initial distributions of the SN Ia
progenitors in the
![]() diagram. Open dots and
triangles in the left and right panel indicate the boundaries of
successful systems to produce SNe Ia with WDs of initial mass
diagram. Open dots and
triangles in the left and right panel indicate the boundaries of
successful systems to produce SNe Ia with WDs of initial mass
![]() and
and
![]() ,
respectively. Systems located inside
these regions are able to evolve to become SNe Ia, and those above
and below the dotted lines undergo phases of steady accretion and
outbursts with steady burning, respectively. For systems located
outside the regions, either mass transfer becomes dynamically
unstable, leading to a CE phase, or the WD is unable to accrete
sufficient matter to trigger a SN Ia explosion within 12 Gyr
because the mass transfer rates are too high (i.e., super-Eddington
accretion) or too low during outbursts, so that most of the
transferred material is lost from the binaries.
,
respectively. Systems located inside
these regions are able to evolve to become SNe Ia, and those above
and below the dotted lines undergo phases of steady accretion and
outbursts with steady burning, respectively. For systems located
outside the regions, either mass transfer becomes dynamically
unstable, leading to a CE phase, or the WD is unable to accrete
sufficient matter to trigger a SN Ia explosion within 12 Gyr
because the mass transfer rates are too high (i.e., super-Eddington
accretion) or too low during outbursts, so that most of the
transferred material is lost from the binaries.
The most striking difference between our results and previous work
is that we extend the lower boundary of donor masses to
![]()
![]() ,
because we include the effect of a thermally unstable
disk on the evolution of WD binaries. Observations of high-Z SNe Ia
suggest a bimodal delay time distribution, with at least
,
because we include the effect of a thermally unstable
disk on the evolution of WD binaries. Observations of high-Z SNe Ia
suggest a bimodal delay time distribution, with at least ![]() SNe
Ia having delay times longer than 1 Gyr (Dahlen et al. 2008; Mannucci et al. 2006).
These tardy SNe Ia are believed to be descendants of systems with
donors less massive than
SNe
Ia having delay times longer than 1 Gyr (Dahlen et al. 2008; Mannucci et al. 2006).
These tardy SNe Ia are believed to be descendants of systems with
donors less massive than
![]() .
In our calculations, we find
that the delay times are distributed across a rather wide range,
from several tenths Gyr to several Gyr. Systems with a
.
In our calculations, we find
that the delay times are distributed across a rather wide range,
from several tenths Gyr to several Gyr. Systems with a ![]() WD and relatively massive companion (
WD and relatively massive companion (
![]() )
generally
have delay times of
)
generally
have delay times of ![]() 1 Gyr, while those with less massive WDs
and/or companions have delay times of up to
1 Gyr, while those with less massive WDs
and/or companions have delay times of up to ![]() 6 Gyr.
6 Gyr.
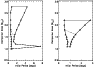 |
Figure 6:
The initial
|
| Open with DEXTER | |
5 Summary
Our numerical calculations imply that the properties of the NS in
GRO J1744-28 may be accounted for with a scenario involving both
AIC of an accreting WD and unstable disk accretion. For long-period
dwarf novae, the WD mass may increase during outbursts when the mass
accretion rate is sufficiently high to allow stable H burning, until
the Chandrasekhar mass limit is reached. During the subsequent mass
transfer after AIC, the newborn NS is also likely to be surrounded
by an unstable accretion disk and expels most of the transferred
matter, such that its magnetic field does not suffer a significant
decay. By including the effect of a thermally unstable accretion
disk, we have also explored the possible SNe Ia progenitor systems.
The calculated results confirm the suggestion by King et al. (2003) that
the disk instability could substantially increase the mass
accumulation efficiency for accreting WDs, and cause the possible
SNe Ia to occur also in systems with <
![]() donors.
donors.
Of course the results depend on the many input parameters adopted,
especially the mass accumulation ratios, the maximum mass-loss rate
allowed, and the duty cycles, which are all poorly known. However,
these factors influence the binary evolution in different ways. Mass
loss can stabilize rapid mass transfer when the donor star is a red
giant or more massive than the WD (Li & van den Heuvel 1997; Hachisu et al. 1996), and is
closely related to the upper limit to the donor masses. With higher
mass accumulation ratios, one may obtain lower mass donor stars in
successful systems evolved to AIC or SNe Ia. However, for acceptable
values of the mass accumulation ratios, standard binary evolution
calculations generally suggest a minimum mass ![]()
![]() for the main-sequence donor stars (with solar
composition) in SN Ia progenitors (e.g. Han & Podsiadlowski 2004; Li & van den Heuvel 1997; Langer et al. 2000).
In this respect, thermally unstable disk accretion seems to be a
reasonable choice to achieve a donor with mass low as
for the main-sequence donor stars (with solar
composition) in SN Ia progenitors (e.g. Han & Podsiadlowski 2004; Li & van den Heuvel 1997; Langer et al. 2000).
In this respect, thermally unstable disk accretion seems to be a
reasonable choice to achieve a donor with mass low as ![]()
![]() in SN Ia progenitors, if a novel mechanism for
driving rapid mass transfer in WD binaries with low-mass companions
does not exist. In this case, the main uncertainties lie in the fact
that the duty cycle varies from one system to another (Lasota 2001),
and may evolve with the orbital periods and mass transfer rates.
Finally, the duty cycles for accreting NS binaries are likely to
differ from those of the WD cases.
in SN Ia progenitors, if a novel mechanism for
driving rapid mass transfer in WD binaries with low-mass companions
does not exist. In this case, the main uncertainties lie in the fact
that the duty cycle varies from one system to another (Lasota 2001),
and may evolve with the orbital periods and mass transfer rates.
Finally, the duty cycles for accreting NS binaries are likely to
differ from those of the WD cases.
Acknowledgements
This work was supported by the Natural Science Foundation of China (under grant number 10873008) and the National Basic Research Program of China (973 Program 2009CB824800).
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] (In the text)
- Andronov, N., Pinsonneault, M., & Sills, A. 2003, ApJ, 582, 358 [NASA ADS] [CrossRef] (In the text)
- Chen, W.-C., & Li, X.-D. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef] (In the text)
- Cui, W. 1997, ApJ, 482, L163 [NASA ADS] [CrossRef]
- Dahlen, T., Strolger, L.-G., & Riess, A. G. 2008, ApJ, 681, 462 [NASA ADS] [CrossRef]
- Daumerie, P., Kalogera, V., Lamb, F. K., & Psaltis, D. 1996, Nature, 382, 141 [NASA ADS] [CrossRef]
- Dubus, G., Lasota, J. -P., Hameury, J. M., & Charles, P. 1999, MNRAS, 303, 139 [NASA ADS] [CrossRef]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] (In the text)
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] (In the text)
- Finger, M. H., Koh, D. T., Nelson, R. W., et al. 1996, Nature, 381, 291 [NASA ADS] [CrossRef]
- Fishman, G. J., Kouveliotou, C., van Paradijs, J., et al. 1995, IAU Circ., 6272
- Giles, A. B., Swank, J. H., Jahoda, K., Zhang, W., et al. 1996, ApJ, 469, L25 [NASA ADS] [CrossRef]
- Gosling, A. J., Bandyopadhyay, R. M., Miller-Jones, J. C. A., & Farrell, S. A. 2007, MNRAS, 380, 1511 [NASA ADS] [CrossRef] (In the text)
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef]
- Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999, ApJ, 519, 314 [CrossRef] (In the text)
- Hameury, J.-M., King, A. R., Lasota, J.-P., & Raison, F. 1993, A&A, 277, 81 [NASA ADS]
- Han, Z., & Podsiadlowski, Ph. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef]
- Iben, I. Jr., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] (In the text)
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] (In the text)
- King, A. R., Kolb, U., & Burderi, L. 1996, ApJ, 464, L127 [NASA ADS] [CrossRef]
- King, A. R., Frank, J., Kolb, U., & Titter, H. 1997, ApJ, 484, 844 [NASA ADS] [CrossRef]
- King, A. R., Rolfe, D. J., & Sshenker, K. 2003, MNRAS, 341, L35 [NASA ADS] [CrossRef] (In the text)
- Kouveliotou, C., van Paradijs, J., Fishman, G. J., et al. 1996, Nature, 379, 799 [NASA ADS] [CrossRef]
- Kovetz, A., & Prialnik, D. 1994, ApJ, 424, 319 [NASA ADS] [CrossRef] (In the text)
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS]
- Lasota, J.-P. 2001, NewAR, 45, 449 [NASA ADS] [CrossRef]
- Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9
- Li, X.-D., & Wang, Z.-R. 1998, ApJ, 500, 935 [NASA ADS] [CrossRef] (In the text)
- Li, X.-D., van den Heuvel, E. P. J., & Wang, Z.-R. 1998, ApJ, 497, 865 [NASA ADS] [CrossRef] (In the text)
- Mannucci, F., Helfand, A., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS]
- Nomoto, K. 1984, in Problems of Colalpse and Numerical Relativity, ed. D. Bancel, & M. Sifnore (Dordrecht: Reidel), 89 (In the text)
- Nomoto, K. 1982b, ApJ, 257, 780 [NASA ADS] [CrossRef] (In the text)
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] (In the text)
- Patat, F., Chandra, P., Chevalier, R., et al. 2007, Science, 317, 924 [NASA ADS] [CrossRef] (In the text)
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [CrossRef]
- Philips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef]
- Podsiadlowski, Ph., Rappaport, S., & Pfahl, E. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef]
- Rappaport, S., & Joss, P. C. 1997, ApJ, 486, 435 [NASA ADS] [CrossRef] (In the text)
- Rappaport, S., Podsiadlowski, Ph., Joss, P. C., Di Stefano, R., & Han, Z. 1995, MNRAS, 273, 731 [NASA ADS]
- Rapport, S. A., Vervunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef]
- Riess, A. G., Strolger, L.-G., Tonry, J., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] (In the text)
- Shibazaki, N., Murakami, T., Shaham, J., & Nomoto, K. 1989, Nature, 342, 656 [NASA ADS] [CrossRef]
- Sills, A., Pinsonneault, M. H., & Terndrup, D. M. 2000, ApJ, 534, 335 [NASA ADS] [CrossRef] (In the text)
- Sutantyo, W., & Li, X.-D. 2000, A&A, 360, 633 [NASA ADS] (In the text)
- Taam, R. E., & van den Heuvel, E. P. J. 1986, ApJ, 305, 235 [NASA ADS] [CrossRef]
- Tauris, T. M., & Savonije, G. J. 1999, A&A, 350, 928 (In the text)
- Urpin, V., & Geppert, U. 1995, MNRAS, 275, 1117 [NASA ADS]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1995, A&A, 297, L41 [NASA ADS]
- van Paradijs, J. 1996, ApJ, 464, L139 [NASA ADS] [CrossRef]
- van Paradijs, J., van den Heuvel, E. P. J., Kouveliotou, C., et al. 1997, A&A, 317, L9
All Figures
 |
Figure 1: The initial distribution of the donor masses and orbital periods for binaries evolving with an AIC. The duty cycle of outbursts due to unstable disk accretion is taken to be d=0.01. The open and filled dots refer to those with the donors on main sequence and being subgiants at the onset of mass transfer, respectively. The size of the dots indicates the mass that the NS accretes after AIC. |
| Open with DEXTER | |
| In the text | |
 |
Figure 2: The end distribution of the companion masses and orbital periods for LMXBs. The filled dots are for LMXBs experienced an AIC from this work, and the solid line indicates the result for normal LMXBs given by Tauris & Savonije (1999). |
| Open with DEXTER | |
| In the text | |
 |
Figure 3: This figure shows an example of the evolution leading to the formation of GRO J1744-28. The solid and dotted lines show the evolution of the mass transfer rate and the donor mass in the upper panel, and the evolution of the orbital period and the accreting WD/NS mass in the lower panel, respectively. |
| Open with DEXTER | |
| In the text | |
 |
Figure 4: The evolution of the companion star in H-R diagram. The star, diamond, filled dot and triangle indicate the start of mass transfer, the time of AIC, the present situation and the time when mass transfer terminates, respectively. |
| Open with DEXTER | |
| In the text | |
 |
Figure 5: An example of the evolutionary path to SN Ia. The solid and dotted lines show the evolution of the mass transfer rate and the donor mass in the upper panel, and the evolution of the orbital period and the WD mass in the lower panel, respectively. |
| Open with DEXTER | |
| In the text | |
 |
Figure 6:
The initial
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


