EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 495 / No 1 (February III 2009) A&A, 495 1 (2009) 183-188 Full HTML
Free Access
Issue
A&A
Volume 495, Number 1, February III 2009
Page(s) 183 - 188
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361:200810206
Published online 22 December 2008

Effects of accretion flow on the chemical structure in the inner regions of protoplanetary disks

H. Nomura1,[*] - Y. Aikawa2 - Y. Nakagawa2 - T. J. Millar1


1 - Astrophysics Research Centre, School of Mathematics & Physics, Queen's University Belfast, Belfast BT7 1NN, UK
2 - Department of Earth and Planetary Sciences, Kobe University, 1-1 Rokkodai-cho, Nada, Kobe 657-8501, Japan

Received 16 May 2008 / Accepted 22 October 2008

Abstract
Aims. We study the dependence of the profiles of molecular abundances and line emission on the accretion flow in the hot ($\ga100$ K) inner region of protoplanetary disks.
Methods. The gas-phase reactions initiated by evaporation of the ice mantle on dust grains are calculated along the accretion flow. We focus on methanol, a molecule that is formed predominantly by the evaporation of warm ice mantles, to demonstrate how its abundance profile and line emission depend on the accretion flow.
Results. Our results indicate that some evaporated molecules retain high abundances only when the accretion velocity is sufficiently high, and that methanol could be useful as a diagnostic of the accretion flow by means of ALMA observations at the disk radius of $\la10$ AU.

Key words: accretion, accretion disks - line: formation - molecular processes - planetary systems: protoplanetary disks

1 Introduction

Observations have detected a variety of molecular lines towards disks around T Tauri stars (e.g. Dutrey et al. 1997; Thi et al. 2004; Qi et al. 2008). Existing millimetre/sub-millimetre observations, which have relatively low spatial resolution, can trace only the outer region ($\ga$50 AU) of the disk, while near-infrared observations of high sensitivity or high spectral resolution probe molecular lines from the planet-forming region in the disks (Lahuis et al. 2006; Gibb et al. 2007; Carr & Najita 2008). The forthcoming Atacama Large Millimeter/sub-millimeter Array (ALMA), with both high sensitivity and high spatial resolution, will make it possible to observe various molecular lines from the inner regions of the disks.

Although many models of the chemical structure of young circumstellar disks focus on the outer disk (e.g. Aikawa et al. 2002; Willacy 2007), the chemistry in the inner disks has also been studied (e.g. Markwick et al. 2002). In cold pre-stellar cores, observations suggest that many gas-phase molecules, including CO, are frozen onto dust grains (e.g. Caselli et al. 1999). Young stars and circumstellar disks are understood to have formed as a result of the collapse of these molecular cloud cores. In addition, observations of molecular lines towards disks suggest that the gas-phase molecules are frozen onto grains close to the midplane of cold outer disks (e.g. Dutrey et al. 1997). However, in the inner region of the disk, the dust temperature is high due to the irradiation from the central star, and the ice mantles are expected to evaporate into the gas by analogy with the molecules observed towards star-forming cores, so-called hot molecular cores and hot corinos (e.g. Millar 1993; Ceccarelli et al. 2007), so that the chemistry in the inner disk will be characterized by this ice-mantle evaporation.

Accretion flow towards a central star is important for planet formation in the disk because it is a possible mechanism for dispersal of gas (e.g. Hollenbach et al. 2000). The amount of gas in the disk influences the coagulation and settling of dust grains, which lead to planetesimal formation, and also controls gaseous planet formation and the orbital motion of the planets (e.g. Nakagawa et al. 1986; Kominami & Ida 2002; Papaloizou et al. 2007). Meanwhile, theory has suggested that the planet forming region in the disks could be magnetorotationally stable, that is, there could be no driving source of the accretion flow (e.g. Sano et al. 2000). Therefore, it will be useful if we can identify observational evidence of the accretion flow in the inner disk and understand the planet formation processes.

If the gas and dust in the disks accrete towards the central star, the ice mantle molecules, which are frozen onto dust grains in the cold outer disk, will evaporate as they are transported into the hot inner disk. The evaporated molecules will be destroyed by chemical reactions as they migrate inwards along the accretion flow. Thus, the distributions of the molecules will trace the accretion velocity, depending on whether the timescale of the chemical reactions is shorter or longer than the accretion time. Hence, it will be possible to confirm the existence of accretion flows from observations of the molecular distributions in the inner disk.

In this work, we study the effect of the accretion flow on the chemical structure of the inner region of young disks by modelling the chemistry, initiated by the ice evaporation, along the accretion flow. We examine the effect on the observational properties, especially focusing on a transition line of methanol, which is an abundant ice molecule in many high- and low-mass star-forming cores (e.g. Gibb et al. 2004; Boogert et al. 2008). Methanol, which is difficult to form efficiently in the gas phase, is also known to be more abundant in the gas-phase around high and low mass young stars as well as comets (e.g. Macdonald et al. 1996; Schöier et al. 2002; Bockelee-Morvan et al. 1991) by more than orders of magnitude compared with cold dark clouds (e.g. Ohishi et al. 1992). In addition, laboratory experiments have shown that methanol can be formed in ice mantles on reasonably short timescales as a result of the hydrogenation of carbon monoxide (e.g. Watanabe et al. 2006). Therefore, methanol is understood to be one of the most probable components of grain mantle molecules.

In the following section, we introduce the physical and chemical models of the disk. We present the resulting molecular abundance profiles of the inner disk in Sect. 3, and the line emission of methanol in Sect. 4, using models with different accretion velocities. The influence of some assumptions on the results are discussed in Sect. 5, and the results are summarized in Sect. 6.

2 Models

We model an axisymmetric disk surrounding a central star of mass $M_*=1.5~M_{\odot}$, radius $R_*=2~R_{\odot}$, and temperature T*=6000 K, whose luminosity ($\sim $$5~L_\odot$) is relatively higher than the averaged luminosity of typical T Tauri stars ($\sim $$1~L_\odot$) (e.g. D'Alessio et al. 2005). It is known observationally that many T Tauri stars emit strong X-ray and UV radiation. We adopt a model with black body (T*=6000 K) plus thermal bremsstrahlung ( $T_{\rm br}=2.5$ $\times $ 104 K) emission for UV radiation ( $L_{\rm FUV}= 7$ $\times $ 1031 erg s-1; see Nomura & Millar 2005, hereafter NM05) and a simple thermal bremsstrahlung emission model with $T_{\rm X}=1$ keV and $L_{\rm X}=10^{30}$ erg s-1 for X-rays (Glassgold et al. 2004; Garmire et al. 2000).

The temperature and density distributions of gas and dust in the disk are obtained self-consistently as described in previous papers (see NM05 and Nomura et al. 2007, for details). Dust temperature is obtained by the iterative radiative transfer calculation (see Nomura 2002), where an initial dust temperature profile is calculated using the variable Eddington factor method (Dullemond et al. 2002) in this work. The disk is assumed to accrete towards the central star at a constant mass accretion rate, and the so-called $\alpha$-viscous model with $\alpha=0.01$ is adopted. The dust model that reproduces the observational extinction curve of dense clouds (see NM05) is adopted here. The resulting gas temperature and density profiles for a fiducial model of mass accretion rate $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1 are plotted in Fig. 1.

 \begin{figure} \par\includegraphics[width=8cm,clip]{0206fig1.eps} \end{figure} Figure 1:

Contour plots of the gas temperature (solid lines) and density (dotted lines) distributions in the z/x vs. x plane for the fiducial model with $\dot{M}=1.0$ $\times $  $10^{-8}~M_{\odot}$ yr-1.
Open with DEXTER

For the chemical model, we calculate the time-dependent, gas-phase reactions along stream lines of steady accretion flow to be

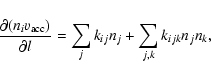\begin{displaymath}% \frac{\displaystyle{\partial (n_iv_{\rm acc})}}{\displaystyle{\partial l}}=\sum_{j}k_{ij}n_{j}+\sum_{j,k}k_{ijk}n_{j}n_{k}, \end{displaymath} (1)

where ni is the number density of the species, i, and the right-hand side of the equation describes the formation and destruction of the species, i, due to cosmic-ray/photo-chemistry (the first term) and two-body reactions (the second term). Three-body reactions are not included, since they will not affect our result significantly in the gas temperature range we treat in this work (e.g. Willacy et al. 1998). We assume that the stream lines, l, are described simply as z=sH, where $H={c_{\rm s}}_0/\Omega_{\rm K}$ is the disk scale height, and ${c_{\rm s}}_0$ the sound speed at the disk midplane, $\Omega_{\rm K}$ the Keplerian frequency. We set 60 grids for $0\leq s\leq 3$. The equations are solved with the continuity equation along the stream lines. The accretion velocity, $v_{\rm acc}$, is simply given by $v_{\rm acc}=\dot{M}/(2\pi\Sigma x)$, where $\dot{M}$ is the mass accretion rate, $\Sigma$ the surface density of the disk, and x the distance from the central star. Turbulent mixing is not taken into account in this paper (see discussions in Sect. 5).

The chemical network consists of 208 species connected by 2830 reactions, in which the reaction rate coefficients are taken from the UMIST RATE06 database[*] (Woodall et al. 2007). The X-ray ionisation is modelled simply by analogy with the cosmic-ray ionisation (see e.g. Aikawa et al. 1999, for a more detailed model). X-rays will ionise the gas and induce photoreactions, similar to cosmic-rays; we adopt the rates enhanced by $\zeta_{\rm X}/\zeta_{\rm CR}$ for the reactions, where the X-ray ionisation rate, $\zeta_{\rm X}$, is calculated using the X-ray flux at each position in the disk (see Nomura et al. 2007). The H2 cosmic-ray ionisation rate is set to be $\zeta_{\rm CR}=1.3$ $\times $ 10-17 s-1, and the attenuation is neglected since it is insignificant apart from close to the disk midplane at the disk radii of $x\sim 1$ AU in this model. As the initial conditions of the calculations, the fractional abundances of the species are taken from Nomura & Millar (2004, hereafter NM04), in which the initial ice mantle composition is fixed so as to be consistent with the infrared absorption features of ices observed towards young stellar objects and the line emission of gas-phase molecules observed towards a hot core, G34.3+0.15 (see Table 1).

Table 1:   Initial fractional abundances with respect to total hydrogen nuclei.

Since we focus in particular on the observational properties of a methanol line in Sect. 4, we simply develop calculations in the region where most methanol evaporates into the gas, that is, where the timescale of the thermal evaporation of methanol, $\tau_{\rm evap}$, becomes shorter than its adsorption timescale onto dust grains, $\tau_{\rm ads}$ (see Fig. 5). The evaporation time is given by $\tau_{\rm evap}=\nu_{0}^{-1}\exp(E_{\rm b}/kT_{\rm d})$, where $\nu_{0}$ is the vibrational frequency of the adsorbed species on the grain surface. The timescale is sensitive to the binding energy of the molecules onto the dust grains $E_{\rm b}$, and the thermal energy of the grains, $kT_{\rm d}$. The binding energy of methanol of $E_{\rm b}/k=4235$ K is used in this work, which is measured experimentally for pure methanol ice (Sandford & Allamandola 1993). We note that the binding energy of methanol onto methanol is equal to that of methanol onto water ice within the margins of error (Brown, private communication). The adsorption time is given by $\tau_{\rm ads}=(S\pi a^2 d_{\rm g}nv_{\rm th})^{-1}$, where S is the sticking probability, $\pi a^2d_{\rm g}n$ the grain surface area per unit volume ($d_{\rm g}$ is the abundance of the dust grains relative to total hydrogen nuclei), and $v_{\rm th}$ the thermal velocity of the molecule (e.g. Tielens & Allamandola 1987). Here, we use S=0.3, and the averaged grain surface area per total hydrogen nuclei of $\langle d_{\rm g}a^2 \rangle$ = 2.2 $\times $ 10-22 cm2, which is similar to that of the MRN dust model by Mathis et al. (1977) (see NM04 for details of the parameters; see also discussions in Sect. 5 about the effects of dust evolution). In this model, all the ice-mantle molecules evaporate at the same dust temperature of $T_{\rm d}\sim 85{-}100$ K, depending on the local density. The influence of this simple treatment of the ice-mantle evaporation is discussed briefly in Sect. 5.

3 Resulting molecular distributions

We calculate molecular abundances using the obtained density and temperature profiles. Figure 2 shows the resulting evolution of some molecular abundances relative to total hydrogen nuclei along the stream line of z=1.2H. The results for a fiducial model with the mass accretion rate of $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1 are plotted, in which the gas density and temperature are in the range $n\sim 3$ $\times $ 1011-1 $\times $ 1013 cm-3 and $T\sim 100{-}240$ K, respectively, along the flow. The gas density (n) and temperature (T) profiles, and distance from the central star (x) are also plotted in the figure at the bottom.

Figure 2 illustrates that the parent molecules that evaporate from grain surface, such as NH3, H2S, C2H2, and CH3OH in this model, are relatively stable, but are eventually destroyed by reactions with ionised species or atomic hydrogen producing daughter species, such as HCN, SO2, and CH3OCH3, on a timescale of $\tau_{\rm chem}\sim 10^4$ yr. The parent and a part of the daughter species become CO and small hydro-carbon molecules in the end. The timescales for the destruction of these parent molecules are almost independent of the total density, n. This is because the number densities of ionised species and atomic hydrogen, which are formed by cosmic-ray ionisation and induced photoreactions, respectively, are insensitive to n. OCS is destroyed on a longer timescale than other parent molecules since its main reactant is H3+, while many other molecules are destroyed mainly by H3O+, which is more abundant than H3+. OCS does not react with H3O+ because its proton affinity is lower than that of water. Since H2O and CH4 are produced efficiently in the gas-phase, their abundances are hardly altered, especially at high temperature in the case of H2O, which is formed by the endothermic reactions, O  $\stackrel{{\rm H}_2}{\longrightarrow}$ OH  $\stackrel{{\rm H}_2}{\longrightarrow}$ H2O. Methane is formed by the destruction of methanol, for which the formation processes are less temperature dependent. The abundances of NH3 and HCN increase at $t\sim 10^5$ yr in Fig. 2 due to endothermic reactions and the high temperature of the inner disk. The detailed gas-phase chemistry induced by the evaporated molecules is similar to that occurring in hot molecular cores, which is discussed in NM04. Along the stream line of z=1.2H, molecules are unaffected by UV and X-ray irradiation from the central star in this model (see also Sect. 4). We note that the timescales for destruction of these parent molecules by chemical reactions have uncertainties of about an order of magnitude due to uncertainties in the rate coefficients of the reactions (e.g. Wakalem et al. 2005).

 \begin{figure} \par\includegraphics[width=8cm,clip]{0206fig2.eps} \end{figure} Figure 2:

Evolution of molecular abundances relative to total hydrogen nuclei along the accretion flow, z=1.2H, for a model with the mass accretion rate of $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1. The figure at the bottom shows the gas density (n) and temperature (T) profiles and the distance from the central star (x). The molecules evaporated from ice mantles are destroyed by chemical reactions on the timescale of $\sim $104 yr.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8cm,clip]{0206f3a.eps}\hspace*{3mm} \includegraphics[width=8cm,clip]{0206f3b.eps} \end{figure} Figure 3:

Abundance profiles of some species relative to total hydrogen nuclei as a function of disk radius along the stream line of z=1.2H, for models with the mass accretion rates of $\dot{M}=$ a) 1.0 $\times $ 10-8 and b) 5.0 $\times $ $10^{-8}~M_{\odot}$ yr-1. Some molecules are abundant just around the region of the ice-mantle evaporation, when $\dot{M}$ is low and the accretion time ( $\tau _{\rm acc}$) is longer than the timescale of the chemical reactions that destroy the parent molecules, while they are abundant even close to the central star when $\dot{M}$ is high and $\tau _{\rm acc}$ is sufficiently short.
Open with DEXTER

In Fig. 3, we plot the abundance profiles of some species relative to total hydrogen nuclei as a function of disk radius along the stream line of z=1.2H, for models with mass accretion rates of $\dot{M}=$ (a) 1.0 $\times $ 10-8 and (b) 5.0 $\times $ $10^{-8}~M_{\odot}$ yr-1. In the steady accretion flow, a location of a fluid particle in the disk, x, is related to a time after the ice evaporation, t, by $t=\int_{x_{\rm evap}}^x \{v_{\rm acc}(x')\}^{-1}{\rm d}x'$ (where $x_{\rm evap}$ is the evaporation radius), as shown in the bottom of Fig. 2. The radial dependence of the accretion velocity is weak, and $v_{\rm acc}\sim 40$ cm s-1for the fiducial model with $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1. In this work, the accretion velocity is set to be proportional to the mass accretion rate ( $v_{\rm acc}\propto \dot{M}$) by fixing artificially the disk surface density to that of the fiducial model, for the purpose of understanding clearly the effect of accretion flow on the chemical structure of the disk.

Figure 3 shows that the molecular abundance profiles in the inner disk change dramatically depending on the velocity of the accretion flow. When the accretion velocity is low and the accretion time, $\tau_{\rm acc}\sim x/v_{\rm acc}$, is longer than the timescale of the chemical reactions that destroy the evaporated molecules, $\tau_{\rm chem}$, the parent molecules are transported only a small distance along the accretion flow before being destroyed by the chemical reactions. Therefore, some parent and daughter species are abundant only in the region where parent molecules are evaporated into the gas. On the other hand, if the accretion velocity is high and the accretion time is shorter than the chemical timescale, the parent molecules are transported to the central star before they are destroyed, and their abundances do not drop even close to the star. Some daughter species, such as HCN, become abundant gradually as the gas is transported inwards in this case. We note that the abundances of some daughter species are sensitive to the initial fractional abundances; for example, if atomic nitrogen is abundant initially, the maximum value of the HCN abundance increases by about two orders of magnitude compared with the model that we use here. Along the stream line of z=1.2H, C2H2 is destroyed by an endothermic reaction, C2H2 + O  $\rightarrow$ CO + CH2. Thus, the C2H2 abundance decreases, independent of the accretion rate, around $x\sim 4{-}5$ AU, at which the gas temperature becomes sufficiently high for the above reaction to proceed. Along stream lines in upper layers of the disk slightly above z=1.2H, where the gas density is relatively low, C2H2 is destroyed by reactions with molecular ions on a timescale of $\sim $104 yr, similar to that of other parent molecules.

4 Methanol line emission

Using the gas density and temperature as well as the molecular abundance profiles obtained in Sect. 3, we calculate the brightness temperature of the 145 GHz $J_{\rm K}=3_0{-}2_0$ transition of methanol. Figure 4 shows the resulting brightness temperature of the line along a single line of sight as a function of the disk radius for models with the mass accretion rates of $\dot{M}=1.0$ $\times $ 10-7 (solid line), 1.0 $\times $ 10-8 (dotted line), and 1.0 $\times $ 10-9 (dot-dashed line) $M_{\odot }$ yr-1. We assume that the molecules are in the local thermal equilibrium. The assumption is reasonable because the line is emitted from regions in which the density is much higher than the critical density for this transition, $n_{\rm cr}\sim 2$ $\times $ 105 cm-3 (e.g. Pavlychenkov et al. 2007). The disk is assumed to be face-on to an observer. The molecular data is taken from Leiden Atomic and Molecular Database[*] (Schöier et al. 2005), and a part of the RATRAN code[*] (Hogerheijde & van der Tak 2000) is used in line radiative transfer calculations (see NM05 for the detailed equations used in the calculations).

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{0206fig4.eps} \end{figure} Figure 4:

Brightness temperature of the 145 GHz $J_{\rm K}=3_0{-}2_0$ line of methanol calculated along a single line of sight as a function of the disk radius for models with mass accretion rates of $\dot{M}=1.0$ $\times $ 10-7 ( solid line), 1.0 $\times $ 10-8 ( dotted line), and 1.0 $\times $ 10-9 ( dot-dashed line) $M_{\odot }$ yr-1. The ALMA detection limit for the beam size of $\sim $14 AU is also plotted with a thin solid line, showing that the line emission will be detectable in the inner disk when the accretion rate and accretion velocity are high.
Open with DEXTER

The figure shows that the brightness temperature of the line, $T_{\rm B}$, is high over all the inner disk when the accretion velocity is high, while $T_{\rm B}$ becomes high just around the region in which the methanol is evaporated into the gas when the accretion velocity is low, since $T_{\rm B}$ traces the abundance of methanol (see Sect. 3). Methanol is destroyed mainly by chemical reactions with H3O+, on a timescale of around $\tau_{\rm chem}\sim (kn_{{\rm H}_3{\rm O}^+})^{-1}\sim 10^4$ yr. The rate coefficient is $k\sim 3$ $\times $ 10-9 cm3 s-1and the number density of H3O+ is $n_{{\rm H}_3{\rm O}^+}\sim 10^{-3}$ cm-3, which is almost independent of the total number density, n, since the formation process of H3O+ is related to cosmic-ray ionisation. The timescale of methanol destruction is affected slightly by the abundance of NH3, which helps recycle methanol by reacting with CH3OH2+ (e.g. Rodgers & Charnley 2001). When the accretion rate is high, $T_{\rm B}$ is high even in outer regions (x $\sim $ 7-9 AU) because the dust temperature is higher due to viscous heating.

At the disk surface, methanol is photodissociated by UV and X-ray irradiation from the central star. The timescales of the dissociation are given by $\tau_{\rm UV}\sim k_{\rm UV}^{-1}\sim 30G_{\rm FUV}^{-1}$ yr and $\tau_{\rm X}\sim k_{\rm X}^{-1}\sim 10^{-11}\zeta_{\rm X}^{-1}$ yr, respectively, where $G_{\rm FUV}$ is the FUV radiation field normalized by 1.6 $\times $ 10-3 erg s-1 cm-2 and $\zeta_{\rm X}$ is the total hydrogen ionisation rate by X-rays. Therefore, the photodissociation dominates the destruction of methanol, where $G_{\rm FUV}\ga 3$ $\times $ 10-3 or $\zeta_{\rm X}$ $\ga$ 10-15 s-1. In Fig. 5, the contour lines of $G_{\rm FUV}=10^{-3}$ and 10-10 (thin solid lines), and $\zeta _{\rm X}=10^{-15}$ and 10-17 s-1 (dashed lines) are plotted in a z versus x plane of the disk with the line of $\tau _{\rm evap}=\tau _{\rm ads}$ for methanol (thick solid line), which corresponds to $T_{\rm d}\sim 85{-}100$ K, and z=H (dot-dashed line) for the fiducial model. Figure 5 shows that the line brightness temperature at $x\ga 6{-}7.5$ AU in Fig. 4 is low because the methanol can evaporate from dust grains only in the surface layer of the disk, where it is dissociated very efficiently by strong X-ray and UV irradiation from the central star.

In Fig. 4, we also plot with a thin, solid line the ALMA detection limit for the methanol line, calculated using the ESO ALMA Sensitivity Calculator[*]. The detection limit of $\sim $17 K is achieved by observing for 600 s using 50 antennas of the 12 m Array, assuming a velocity resolution of 1 km s-1, and a beam size of 0.1 arcsec, which corresponds to $\sim $14 AU when the disk is located at the distance of nearby star-forming regions, $\sim $140 pc. The 145 GHz $J_{\rm K}=3_0{-}2_0$ transition of methanol has not been detected towards DM Tau (Dutrey 2001), and other methanol line searches towards some T Tauri and Herbig Ae stars (Thi et al. 2004; Semenov et al. 2005), have also been unsuccessful. Our results suggest that when the accretion velocity at $x\leq 10$ AU is sufficiently high, ALMA will be able to detect the methanol line, taking advantage of high spatial resolution to avoid beam dilution. When the accretion velocity is sufficiently low, line detection will be difficult even with ALMA. Thus, the observations of methanol by ALMA should be a useful tool in diagnosing the existence of accretion flows in inner disks.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{0206fig5.eps} \end{figure} Figure 5:

Line of $\tau _{\rm evap}=\tau _{\rm ads}$ inside which the icy methanol evaporates into the gas ( thick solid line), line of z=H ( dot-dashed line), and contour lines of $G_{\rm FUV}=10^{-3}$ and 10-10 ( thin solid lines), $\zeta _{\rm X}=10^{-15}$ and 10-17 s-1 ( dashed lines) for the fiducial model with $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1. The evaporated methanol is quickly dissociated due to strong UV photons or X-rays at $x\geq 7$ AU.
Open with DEXTER

5 Discussions

We discuss some possible effects of our assumptions on our results.

First, we discuss the influences of the simple treatment of the evaporation process we have taken in this work. Although we assume that all the species evaporate at the same dust temperature, the evaporation of ice mantle molecules may depend on the binding energy of each molecule and the morphology of water ice (e.g. Collings et al. 2004). Therefore, different parent molecules may evaporate at different positions (see e.g. Markwick et al. 2002), which will affect the spatial distributions of molecular abundances. In particular, CO and N2 are likely to evaporate at temperatures much lower than 85 K, particularly if they are abundant in the surface layers of the ice. However, given the chemical stability of these species, they are unlikely to affect the overall abundance of a molecule such as methanol. So, the timescales for the destruction of the parent molecules by chemical reactions, $\tau_{\rm chem}$, analysed in Sect. 3, will be insensitive to the treatment of the ice-mantle evaporation. In addition to the evaporation process, surface chemistry involving heavy radicals on warm dust grains may affect molecular abundances in both the solid- and gas-phase (e.g. Garrod & Herbst 2006; Aikawa et al. 2008). More detailed models including detailed evaporation processes and surface reactions on dust grains should be constructed in future work.

Next, if we take into account the effect of turbulent mixing in the vertical direction, the methanol abundance may increase close to the line, $\tau _{\rm evap}=\tau _{\rm ads}$, (see Fig. 5) when the diffusion time is shorter than the timescale of photodissociation (e.g. Willacy et al. 2006). In the inner disk ($x\la 6$ AU), the methanol abundance may decrease slightly by vertical mixing because of photodissociation at the disk surface. The turbulent mixing in the radial direction may enhance the gas-phase methanol abundance outside the evaporation radius if the timescale of the turbulent diffusion is shorter than the timescale of chemical reactions and adsorption onto dust grains. A detailed mixing model considering angular momentum transfer will be required in obtaining the diffusion timescale, and advance further discussion.

Finally, we note that the brightness temperature of the methanol line will reflect conditions other than the accretion velocity: the high-$T_{\rm B}$ region will become smaller if the central star is less luminous and the dust temperature in the disk is low. Also, $T_{\rm B}$ becomes low if the methanol abundance in the ice mantle is low. If the amount of small dust grains decreases due to dust coagulation and settling in the disk, FUV photons from the central star are attenuated ineffectively and methanol is photodissociated (e.g. Aikawa & Nomura 2006). Therefore, $T_{\rm B}$ drops, although the evaporation radius moves slightly outwards due to the decrease in the total grain surface area per unit volume, that is, the decrease in the adsorption rate (e.g. Aikawa 2007). Thus, some circumstances other than low accretion velocity can lead to low methanol abundance and the non-detection of the line. However, if the observed methanol abundance is high in the inner disk, then the accretion velocity must be high in the planet-forming region.

6 Conclusions

We have simulated gas-phase chemical reactions, initiated by ice-mantle evaporation, along the accretion flow in protoplanetary disks to show that the accretion velocity affects the abundance profiles of the evaporated molecules and their daughter species in the inner disk. We have obtained the brightness temperature profile of an emission line of methanol, and suggested that this could be useful as an indicator of accretion velocity in the planet-forming regions of disks using ALMA observations.

Acknowledgements
We are grateful to an anonymous referee and an editor, M. Walmsley, for their comments which improved the clarity of our discussion. H.N. is financially supported by the JSPS Postdoctoral Fellowships for Research Abroad. Astrophysics at QUB is supported by a grant from the STFC.

References

Footnotes

...[*]
Now at Department of Astronomy, Graduate School of Science, Kyoto University, Kyoto 606-8502, Japan.
... database[*]
http://www.udfa.net/
... Database[*]
http://www.strw.leidenuniv.nl/moldata/
... code[*]
http://www.sron.rug.nl/vdtak/ratran/ratran.html
... Calculator[*]
http://www.eso.org/sci/facilities/alma/observing/tools/etc/index.html

All Tables

Table 1:   Initial fractional abundances with respect to total hydrogen nuclei.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{0206fig1.eps} \end{figure} Figure 1:

Contour plots of the gas temperature (solid lines) and density (dotted lines) distributions in the z/x vs. x plane for the fiducial model with $\dot{M}=1.0$ $\times $  $10^{-8}~M_{\odot}$ yr-1.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{0206fig2.eps} \end{figure} Figure 2:

Evolution of molecular abundances relative to total hydrogen nuclei along the accretion flow, z=1.2H, for a model with the mass accretion rate of $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1. The figure at the bottom shows the gas density (n) and temperature (T) profiles and the distance from the central star (x). The molecules evaporated from ice mantles are destroyed by chemical reactions on the timescale of $\sim $104 yr.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{0206f3a.eps}\hspace*{3mm} \includegraphics[width=8cm,clip]{0206f3b.eps} \end{figure} Figure 3:

Abundance profiles of some species relative to total hydrogen nuclei as a function of disk radius along the stream line of z=1.2H, for models with the mass accretion rates of $\dot{M}=$ a) 1.0 $\times $ 10-8 and b) 5.0 $\times $ $10^{-8}~M_{\odot}$ yr-1. Some molecules are abundant just around the region of the ice-mantle evaporation, when $\dot{M}$ is low and the accretion time ( $\tau _{\rm acc}$) is longer than the timescale of the chemical reactions that destroy the parent molecules, while they are abundant even close to the central star when $\dot{M}$ is high and $\tau _{\rm acc}$ is sufficiently short.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0206fig4.eps} \end{figure} Figure 4:

Brightness temperature of the 145 GHz $J_{\rm K}=3_0{-}2_0$ line of methanol calculated along a single line of sight as a function of the disk radius for models with mass accretion rates of $\dot{M}=1.0$ $\times $ 10-7 ( solid line), 1.0 $\times $ 10-8 ( dotted line), and 1.0 $\times $ 10-9 ( dot-dashed line) $M_{\odot }$ yr-1. The ALMA detection limit for the beam size of $\sim $14 AU is also plotted with a thin solid line, showing that the line emission will be detectable in the inner disk when the accretion rate and accretion velocity are high.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{0206fig5.eps} \end{figure} Figure 5:

Line of $\tau _{\rm evap}=\tau _{\rm ads}$ inside which the icy methanol evaporates into the gas ( thick solid line), line of z=H ( dot-dashed line), and contour lines of $G_{\rm FUV}=10^{-3}$ and 10-10 ( thin solid lines), $\zeta _{\rm X}=10^{-15}$ and 10-17 s-1 ( dashed lines) for the fiducial model with $\dot{M}=1.0$ $\times $ $10^{-8}~M_{\odot}$ yr-1. The evaporated methanol is quickly dissociated due to strong UV photons or X-rays at $x\geq 7$ AU.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.