| Issue |
A&A
Volume 495, Number 1, February III 2009
|
|
|---|---|---|
| Page(s) | 335 - 352 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361:200810105 | |
| Published online | 14 January 2009 | |
Extrasolar planets and brown dwarfs around A-F type stars![[*]](/icons/foot_motif.gif)
VI. High precision RV survey of early type dwarfs with HARPS
A.-M. Lagrange1 - M. Desort1 - F. Galland1 - S. Udry2 - M. Mayor2
1 - Laboratoire d'Astrophysique de l'Observatoire de Grenoble,
Université Joseph Fourier, BP 53, 38041 Grenoble, France
2 -
Observatoire de Genève, 51 Ch. des Maillettes, 1290 Sauverny,
Switzerland
Received 30 April 2008 / Accepted 10 October 2008
Abstract
Context.
Aims. Systematic surveys to search for exoplanets have been mostly dedicated to solar-type stars sofar. We developed in 2004 a method to extend such searches to earlier A-F type dwarfs and started spectroscopic surveys to search for planets and quantify the detection limit achievable when taking the stars properties (Spectral Type, ![]() )
and their actual levels of intrinsic variations into account. We give here the first results of our southern survey with HARPS.
)
and their actual levels of intrinsic variations into account. We give here the first results of our southern survey with HARPS.
Methods. We observed 185 A-F (B-V in the range [-0.1; 0.6]) stars with HARPS and analysed them with our dedicated software. We used several criteria to probe different origins for the radial-velocity variations - stellar activity (spots, pulsations) or companions: bisector shape, radial-velocity variations amplitudes, and timescales.
Results. 1) Sixty-four percent of the 170 stars with enough data points are found to be variable. Twenty are found to be binaries or candidate binaries (with stars or brown dwarfs). More than 80![]() of the latest type stars (once binaries are removed), are intrinsically variable at a 2 m s
of the latest type stars (once binaries are removed), are intrinsically variable at a 2 m s![]() precision level. Stars with earlier spectral type (B-V
precision level. Stars with earlier spectral type (B-V ![]() 0.2) are either variable or associated to levels of uncertainties comparable to the RV rms observed on variable stars of the same B-V. 2) We detected one long-period planetary system (presented in another paper) around an F6IV-V star. 3) We quantified the jitter due to stellar activity and we show that when taking this jitter into account in addition to the stellar parameters (spectral type,
0.2) are either variable or associated to levels of uncertainties comparable to the RV rms observed on variable stars of the same B-V. 2) We detected one long-period planetary system (presented in another paper) around an F6IV-V star. 3) We quantified the jitter due to stellar activity and we show that when taking this jitter into account in addition to the stellar parameters (spectral type, ![]() ), it is still possible to detect planets with HARPS with periods of 3 days (resp. 10 days and 100 days) on 91
), it is still possible to detect planets with HARPS with periods of 3 days (resp. 10 days and 100 days) on 91![]() (resp. 83
(resp. 83![]() ,
61
,
61![]() )
of them. We show that even the earliest spectral type stars are accessible to this type of search, provided they have a low projected rotational velocity and low levels of activity. 4) Taking the present data into account, we computed the actually achieved detection limits for 107 targets and discuss the limits as a function of B-V. Given the data at hand, our survey is sensitive to short-period (few days) planets and to longer ones (100 days) to a lower extent (latest type stars). We derive first constrains on the presence of planets around A-F stars for these ranges of periods.
)
of them. We show that even the earliest spectral type stars are accessible to this type of search, provided they have a low projected rotational velocity and low levels of activity. 4) Taking the present data into account, we computed the actually achieved detection limits for 107 targets and discuss the limits as a function of B-V. Given the data at hand, our survey is sensitive to short-period (few days) planets and to longer ones (100 days) to a lower extent (latest type stars). We derive first constrains on the presence of planets around A-F stars for these ranges of periods.
Key words: techniques: radial velocities - stars: early-type - stars: planetary systems - stars: variables: general
1 Introduction
Since the discovery of the first exoplanet around a solar-like star in 1995, more than 250 planets have been found by radial-velocity (RV) surveys (Jean Schneider, http://exoplanet.eu). These surveys have generally focused on late-type stars (later than F8). However, knowing about the presence of planets or brown dwarfs (hereafter BDs) around more massive objects is mandatory if one wishes to investigate the impact of the mass of the central stars on the planetary formation and evolution processes.
There are theoretical indications that the mass of the planets increases with the mass of the parent star, at least for low-mass stars (Ida & Lin 2005) and that the frequency of giant planets increases linearly with the parent-star mass for stars between 0.4 and 3 ![]() (Kennedy & Kenyon 2008), with e.g., 6
(Kennedy & Kenyon 2008), with e.g., 6![]() frequency of giant planets around 1
frequency of giant planets around 1 ![]() and 10
and 10![]() frequency around 1.5
frequency around 1.5 ![]() .
More numerous and massive planets are consistent with what we could expect from a disk surface-density increasing with stellar mass. On the other hand, the shorter lifetimes of the systems, as well as the lack of solid material close to the star, could reduce the number of planets. Clearly, several parameters probably impact the occurrence and properties of planets around massive stars, and they have not been fully explored yet.
.
More numerous and massive planets are consistent with what we could expect from a disk surface-density increasing with stellar mass. On the other hand, the shorter lifetimes of the systems, as well as the lack of solid material close to the star, could reduce the number of planets. Clearly, several parameters probably impact the occurrence and properties of planets around massive stars, and they have not been fully explored yet.
The data to test the models are still quite limited, as the largest and earliest, now long-lasting surveys have focused on solar type, main-sequence (MS) stars. In recent years, some efforts have been made nevertheless to search for planets around stars with various masses: less massive, M-type stars, on the one hand, and more massive stars, on the other. The search for planets around M stars so far seems to confirm the previously mentioned expectations from theoretical works (see e.g., Bonfils et al. 2005; Butler et al. 2006). The available observations of massive stars are still very limited. Massive MS stars have been removed from early surveys, because it was generally thought that their spectra (few lines, usually broadened by stellar rotation) would not allow planet detection and, indeed, the classical RV measurements technique (based on the cross correlation of the actual spectra with a binary spectral mask corresponding to a star with an appropriate spectral type and ![]() = 0 km s
= 0 km s![]() )
fail to measure the RV of these stars. This has led some groups to study ``retired'' early-type instead, either low-mass (
)
fail to measure the RV of these stars. This has led some groups to study ``retired'' early-type instead, either low-mass (![]() 1.6
1.6 ![]() )
giants, intermediate-mass (1.6-2
)
giants, intermediate-mass (1.6-2 ![]() )
subgiants, or clump giants (1.7-3.9
)
subgiants, or clump giants (1.7-3.9 ![]() )
(see e.g., Hatzes et al. 2005; Niedzielski et al. 2007; Johnson et al. 2006, 2007; Lovis & Mayor 2007; Sato et al. 2008). These stars have indeed cooled down and also rotate more slowly due to coupling of stellar winds and magnetic fields. They therefore exhibit more numerous, narrower lines, which is adequate for classical RV measurements technique, and their level of activity (jitter) is relatively low (10-20 m s
)
(see e.g., Hatzes et al. 2005; Niedzielski et al. 2007; Johnson et al. 2006, 2007; Lovis & Mayor 2007; Sato et al. 2008). These stars have indeed cooled down and also rotate more slowly due to coupling of stellar winds and magnetic fields. They therefore exhibit more numerous, narrower lines, which is adequate for classical RV measurements technique, and their level of activity (jitter) is relatively low (10-20 m s![]() ,
Hekker et al. 2006) for giants and 10 m s
,
Hekker et al. 2006) for giants and 10 m s![]() for subgiants (Johnson et al. 2007, and ref. therein; Sato et al. 2008). The data available today are still more limited than for solar-type stars, and less than 20 planets have been found so far in total around these evolved stars. So far, the planets found around K subgiants stars with M
for subgiants (Johnson et al. 2007, and ref. therein; Sato et al. 2008). The data available today are still more limited than for solar-type stars, and less than 20 planets have been found so far in total around these evolved stars. So far, the planets found around K subgiants stars with M ![]() 1.5
1.5 ![]() are located at distances greater than 0.8 AU (Johnson et al. 2007), which has led these authors to conclude that close-in planets are rare, in agreement with some theoretical predictions on disk depletion timescales (Burkert & Ida 2007). However, the impact of the post MS evolution of the stars on closer-in planets has not been explored yet for these stars. All planets found so far around giant stars have relatively long periods, the closest ones being reported at less than 0.7 AU from 2 giants, in addition to a previously reported planet at 0.7 AU by Sato et al. (2003). Numerical simulations by the same authors suggest that planets with orbits inside 0.5-1 AU around 2-3
are located at distances greater than 0.8 AU (Johnson et al. 2007), which has led these authors to conclude that close-in planets are rare, in agreement with some theoretical predictions on disk depletion timescales (Burkert & Ida 2007). However, the impact of the post MS evolution of the stars on closer-in planets has not been explored yet for these stars. All planets found so far around giant stars have relatively long periods, the closest ones being reported at less than 0.7 AU from 2 giants, in addition to a previously reported planet at 0.7 AU by Sato et al. (2003). Numerical simulations by the same authors suggest that planets with orbits inside 0.5-1 AU around 2-3 ![]() stars could be engulfed by the central stars at the tip of RGB thanks to tidal torque from the central stars. According to them, if one then assumes that most of the clump giants are post RGB stars, there is then a risk that closer planets, if present before, had disappeared as the star evolved. In summary, even though there are some hints that hot Jupiters are not present around retired stars, it is recognized that data are still needed to definitely confirm this point. Also, because stellar evolutionary processes may have affected the presence of planets close to the stars, it is acknowledged that data are needed on A-F MS stars (see e.g., Burkert & Ida 2007; see also Li et al. 2008). We note finally that short-period planets have indeed been found around F5-F6 MS stars through transit observations (see http://exoplanet.eu).
stars could be engulfed by the central stars at the tip of RGB thanks to tidal torque from the central stars. According to them, if one then assumes that most of the clump giants are post RGB stars, there is then a risk that closer planets, if present before, had disappeared as the star evolved. In summary, even though there are some hints that hot Jupiters are not present around retired stars, it is recognized that data are still needed to definitely confirm this point. Also, because stellar evolutionary processes may have affected the presence of planets close to the stars, it is acknowledged that data are needed on A-F MS stars (see e.g., Burkert & Ida 2007; see also Li et al. 2008). We note finally that short-period planets have indeed been found around F5-F6 MS stars through transit observations (see http://exoplanet.eu).
A few years ago we developed a software dedicated to extracting the RV data around early type MS stars. The method consists in correlating, in the Fourier space, each spectrum and a reference spectrum built by summing-up all the available spectra for this star. We had shown earlier that with this approach and by taking the stars B-V and projected rotational velocities into account, it is possible to find planets around A-F type stars (Galland et al. 2005a). However, the price to pay is that more measurements are needed to find planets around A and early F dwarfs than for late F and G-K dwarfs, because of the relatively higher uncertainties in the RV measurements due to higher ![]() and higher effective temperature, and also because of the possible presence of pulsations or spots in the case of late F stars, the impact of which has not been quantified so far. (Spots or pulsations become also a limiting factor in the case of later-type stars, as well as pulsations, if one looks for low mass planets.) We then started systematic searches for low-mass companions to A-F type stars, with HARPS in the southern hemisphere and with ELODIE and then SOPHIE at OHP in the northern hemisphere. We have so far found a 9.1
and higher effective temperature, and also because of the possible presence of pulsations or spots in the case of late F stars, the impact of which has not been quantified so far. (Spots or pulsations become also a limiting factor in the case of later-type stars, as well as pulsations, if one looks for low mass planets.) We then started systematic searches for low-mass companions to A-F type stars, with HARPS in the southern hemisphere and with ELODIE and then SOPHIE at OHP in the northern hemisphere. We have so far found a 9.1
![]() (minimum mass) planet orbiting (a = 1.1 AU) an F6V star, with
(minimum mass) planet orbiting (a = 1.1 AU) an F6V star, with ![]() = 12 km s
= 12 km s![]() (Galland et al. 2005b). Very promisingly, we also detected a 21
(Galland et al. 2005b). Very promisingly, we also detected a 21
![]() brown dwarf orbiting (a = 0.2 AU) a pulsating A9V star with
brown dwarf orbiting (a = 0.2 AU) a pulsating A9V star with ![]() = 50 km s
= 50 km s![]() (Galland et al. 2006); noticeably, in that case, we could disentangle stellar pulsations from the presence of a low-mass companion.
(Galland et al. 2006); noticeably, in that case, we could disentangle stellar pulsations from the presence of a low-mass companion.
In parallel, we developed detailed simulations of stellar activity (spots) in order to estimate more quantitatively than what was available so far (Saar & Donahue 1997; Hatzes 2002) the impact of such stellar activity on RV data and other observables (bisectors, bisectors velocity-span, photometry). We showed that if the star ![]() is smaller than the spectrograph spectral resolution, depending on their location with respect to the line of sight, depending on their size, spots with realistic sizes can produce RV variations and bisector velocity-span variations that are quite similar to those of low-mass planets.
Hence, low amplitude (level of typically 20 m s
is smaller than the spectrograph spectral resolution, depending on their location with respect to the line of sight, depending on their size, spots with realistic sizes can produce RV variations and bisector velocity-span variations that are quite similar to those of low-mass planets.
Hence, low amplitude (level of typically 20 m s![]() or less) planetary-like RV and bisector velocity span variations alone cannot definitely prove the presence of planets around low
or less) planetary-like RV and bisector velocity span variations alone cannot definitely prove the presence of planets around low ![]() G-K stars (Desort et al. 2007), so additional criteria are mandatory for ruling out spots: photometry, activity evaluation down to levels relevent to explain the amplitude of RV variations, precise knowledge of the star rotaional period, etc. That situation is much more favorable in the case of earlier-type stars because they rotate statistically faster, so the bisector criteria can apply.
G-K stars (Desort et al. 2007), so additional criteria are mandatory for ruling out spots: photometry, activity evaluation down to levels relevent to explain the amplitude of RV variations, precise knowledge of the star rotaional period, etc. That situation is much more favorable in the case of earlier-type stars because they rotate statistically faster, so the bisector criteria can apply.
The present paper is devoted to our southern hemisphere survey. The sample, observations, measurements, and diagnostics are provided in Sect. 2. The results concerning the stellar variability and the quantitative impact on planet detectability around the early-type stars are presented in Sect. 3. Finally we give and discuss the detection limits obtained in the present survey in Sect. 4.
2 Sample, observations, and measurements
2.1 Sample
Our HARPS sample is limited to B8 to F7 dwarfs. The limit in spectral type (ST) at F7 is set because the surveys using the masking technique generally start with stars with ST later than F8. The limit at B8 is set by the precision that can be obtained with our method on stars, given their ST and their ![]() (Galland et al. 2005a): the detection limit of stars with ST earlier than B8 does not fall into the planet domain. Our survey is also volume-limited with an upper limit at 67 pc for the B8-A9 dwarfs and at 33 pc for the F0-F7 dwarfs. The distance was taken from Hipparcos catalog, and stars with distance uncertainties over 20
(Galland et al. 2005a): the detection limit of stars with ST earlier than B8 does not fall into the planet domain. Our survey is also volume-limited with an upper limit at 67 pc for the B8-A9 dwarfs and at 33 pc for the F0-F7 dwarfs. The distance was taken from Hipparcos catalog, and stars with distance uncertainties over 20![]() were removed. The difference in distance for both spectral types comes from our wanting to have roughly the same number of A and F stars. The dwarf nature was selected by selecting stars with absolute magnitudes within 2.5 mag from the main sequence.
were removed. The difference in distance for both spectral types comes from our wanting to have roughly the same number of A and F stars. The dwarf nature was selected by selecting stars with absolute magnitudes within 2.5 mag from the main sequence.
Spectroscopic binaries and close visual binaries with separations smaller than 5
![]() known at the beginning of the survey from Coravel or Hipparcos data were removed. Confirmed
known at the beginning of the survey from Coravel or Hipparcos data were removed. Confirmed ![]() Scuti (from Rodriguez et al. 2000) and
Scuti (from Rodriguez et al. 2000) and ![]() Doradus type stars (from Mathias et al. 2004 and http://astro.univie.ac.at/dsn/gerald/gdorlist.html) were also removed because they are known to produce RV variations over hours to a few days due to pulsations. Finally we also removed Ap and Am stars, which present spectral anomalies and are often associated to binary systems. This removes a number of late A - early F type stars, crossing the
Doradus type stars (from Mathias et al. 2004 and http://astro.univie.ac.at/dsn/gerald/gdorlist.html) were also removed because they are known to produce RV variations over hours to a few days due to pulsations. Finally we also removed Ap and Am stars, which present spectral anomalies and are often associated to binary systems. This removes a number of late A - early F type stars, crossing the ![]() Scuti and
Scuti and ![]() Doradus instability strip. We ended up with 207 stars with ST between B8 and F7, and B-V respectively ranging between -0.1 and 0.58, corresponding to mass ranging between 1.3 and 3.5
Doradus instability strip. We ended up with 207 stars with ST between B8 and F7, and B-V respectively ranging between -0.1 and 0.58, corresponding to mass ranging between 1.3 and 3.5 ![]() .
We have a relatively smaller number of stars in the [0.2; 0.4] B-V range (i.e., roughly, between 1.8 and 1.4
.
We have a relatively smaller number of stars in the [0.2; 0.4] B-V range (i.e., roughly, between 1.8 and 1.4 ![]() )
as we removed the known
)
as we removed the known ![]() Scuti and
Scuti and ![]() Doradus stars).
Doradus stars).
2.2 Observations
In all, 185 stars have been observed between August 2005 and January 2008. Figure 1 shows their position in the HR diagram. It can be seen that our survey fills a domain of the HR diagram that has not been covered yet.
We usually recorded 2 consecutive high-resolution (
![]() )
spectra each time we pointed to the star (each pointing is hereafter referred to as one epoch). The spectra cover a wavelength range between 3800 and 6900
)
spectra each time we pointed to the star (each pointing is hereafter referred to as one epoch). The spectra cover a wavelength range between 3800 and 6900 ![]() .
As far as possible, we tried to record data at two or three different times for a given object during one night, in order to identify possible high-frequency RV variations. We also tried whenever possible to record data on two or three consecutive nights. The time baseline for a given star varies between 5 days and more than 800 days. Only a few (11) stars have been observed during one night only, but for 15 stars we only got 4 good quality spectra or less (i.e., with a magnitude difference
.
As far as possible, we tried to record data at two or three different times for a given object during one night, in order to identify possible high-frequency RV variations. We also tried whenever possible to record data on two or three consecutive nights. The time baseline for a given star varies between 5 days and more than 800 days. Only a few (11) stars have been observed during one night only, but for 15 stars we only got 4 good quality spectra or less (i.e., with a magnitude difference![]() between the observation and the one that gives the best signal-to-noise ratio (SN) smaller than 2). We ended up with 170 dwarfs for which we recorded 6 or more good quality spectra. 45 have B-V
between the observation and the one that gives the best signal-to-noise ratio (SN) smaller than 2). We ended up with 170 dwarfs for which we recorded 6 or more good quality spectra. 45 have B-V ![]() 0.1; 72 have B-V between 0.1 and 0.4 and 53 have B-V
0.1; 72 have B-V between 0.1 and 0.4 and 53 have B-V ![]() 0.4. We hereafter limit our study to those stars.
0.4. We hereafter limit our study to those stars.
Typical exposure times ranged between 30 s and 15 min depending on the star magnitude and on the atmospheric conditions. Table 1 provides the 170 targets observed, together with several relevant pieces of information on the stars (ST, ![]() ,
B-V) and on the data obtained, as well as various measurements (see below).
,
B-V) and on the data obtained, as well as various measurements (see below).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figures/10105f1.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg20.gif) |
Figure 1: Observed stars in an HR diagram. We also plotted the dwarfs and/or (sub-) giants surveyed either with the Coralie spectrograph or by Johnson et al. (2006). Our targets cover a domain that has not been surveyed yet. Note the relative lack of objects in the [0.2; 0.4] B-V region, due to selection effects (see text). |
| Open with DEXTER | |
2.3 Measurements
2.3.1 Radial velocities
The extraction of the radial velocities is fully described in Galland et al. (2005a). Briefly, for each star, we built a first estimate of the reference spectrum that is the average of the spectra recorded and reduced via the STS HARPS pipeline. We then computed a first estimate of the RV for each spectrum, by correlating each spectrum and this first estimate of the reference spectrum in Fourier space. We then built a final reference spectrum by averaging the spectra once they had been shifted from their measured RV. For each spectrum we finally measured the RV velocity with respect to this reference spectrum. We also measured the uncertainties associated to each RV measurement.
To build up the reference we computed the ![]() of each spectrum compared to the first estimate of the reference spectrum. Most of the time, the
of each spectrum compared to the first estimate of the reference spectrum. Most of the time, the ![]() found was much less than 10. Whenever a higher
found was much less than 10. Whenever a higher ![]() was found, we checked the spectra. In such cases, either they were due to bad observing conditions or technical problems and were not kept to build the reference spectrum (this actually happened quite rarely as we already selected spectra with acceptable absorptions) or they were associated to line deformations indicative of a type-2 binary.
was found, we checked the spectra. In such cases, either they were due to bad observing conditions or technical problems and were not kept to build the reference spectrum (this actually happened quite rarely as we already selected spectra with acceptable absorptions) or they were associated to line deformations indicative of a type-2 binary.
2.3.2 CCFs, bisectors and bisectors velocity-span
Whenever possible (see below), we computed the resulting cross-correlation functions (CCFs) and the bisector's velocity-span for each target (see for their definition Galland et al. 2005a). Indeed, the bisector and bisectors' velocity span are very good diagnostics of stellar activity (spots, pulsations) provided 1) they can be measured (see below), and 2) the star projected rotational velocity is higher than the instrumental resolution (see Desort et al. 2007).
The uncertainty associated to the bisectors' velocity span depends directly on the projected rotational-velocity and/or their spectra type. Indeed, the number of lines used to compute the CCF depends on these two parameters (much more than on the signal-to-noise ratio). For stars with high ![]() (typ.
(typ. ![]() 150 km s
150 km s![]() )
and/or B-V
)
and/or B-V ![]() 0.1, the number of lines may be quite low (30-50) whereas for late-type stars with moderate
0.1, the number of lines may be quite low (30-50) whereas for late-type stars with moderate ![]() (10-20 km s
(10-20 km s![]() ), the number of lines used is a few hundreds (up to about 1000). When the bisectors had been computed, we then attributed quality flags to the bisectors' velocity-span measurements, respectively: Good, Acceptable, Bad, corresponding to numbers of lines respectively
), the number of lines used is a few hundreds (up to about 1000). When the bisectors had been computed, we then attributed quality flags to the bisectors' velocity-span measurements, respectively: Good, Acceptable, Bad, corresponding to numbers of lines respectively ![]() 100, 40-100, and
100, 40-100, and ![]() 40.
40.
Table 1: Stars properties and measurements.
2.4 Diagnostics for the classification of variable stars
Variable stars are defined as having an RV standard deviation (rms) more than twice the RV uncertainties and a total RV amplitude more than 6 times the RV uncertainties. The RV variations can a priori be due to the presence of a companion (star, brown dwarf, planet) or to intrinsic variations of the star (spots, pulsations). It can also be a combination of those different origins.
2.4.1 Binarity
We first checked those stars with high ![]() (
(![]() 10) and looked for line deformations indicative of spectroscopic binaries. Figure 2 provides an example of a binary SB2 identified on the basis of the
10) and looked for line deformations indicative of spectroscopic binaries. Figure 2 provides an example of a binary SB2 identified on the basis of the ![]() ,
HD 2885 (A2V;
,
HD 2885 (A2V; ![]() = 40 km s
= 40 km s![]() ). It has to be noted that, in such cases, the RV values measured are no longer valid, as our RV extraction method assumes that all lines in a given spectrum originate from the same object.
). It has to be noted that, in such cases, the RV values measured are no longer valid, as our RV extraction method assumes that all lines in a given spectrum originate from the same object.
For the rest of the variable stars, we tried to identify binary stars among the stars for which the RV amplitude can be explained by the presence of a stellar or BD companion. To do so, using rough estimations of the star masses via their B-V, we computed the RV amplitude 2 ![]()
![]() expected from the presence of a 13
expected from the presence of a 13
![]() body orbiting with a period of 2 days and the RV amplitude 2
body orbiting with a period of 2 days and the RV amplitude 2 ![]()
![]() expected in the case of a 200-day period and compared these quantities to the observed RV amplitudes, once corrected from the RV variations observed within a night (in practice, over a few hours), as the variations occuring within a few hours are assumed to stem from stellar origin, see below. Quantitatively we define the amplitude of the nightly RV variations as ``in-night'' RV amplitude for a given object. We then computed the following quantities:
expected in the case of a 200-day period and compared these quantities to the observed RV amplitudes, once corrected from the RV variations observed within a night (in practice, over a few hours), as the variations occuring within a few hours are assumed to stem from stellar origin, see below. Quantitatively we define the amplitude of the nightly RV variations as ``in-night'' RV amplitude for a given object. We then computed the following quantities:
![]() = (observed RV amplitude - ``in-night'' RV amplitude)/2
= (observed RV amplitude - ``in-night'' RV amplitude)/2 ![]()
![]() and
and
![]() = (observed RV amplitude - ``in-night'' RV amplitude)/2
= (observed RV amplitude - ``in-night'' RV amplitude)/2 ![]()
![]() ,
to be used as thresholds identifying the binaries. We chose 2 and 200-day periods as they are quite relevant given our temporal sampling and our average time baseline.
,
to be used as thresholds identifying the binaries. We chose 2 and 200-day periods as they are quite relevant given our temporal sampling and our average time baseline.
For those variable stars for which we could compute a CCF and test the relation between bisectors velocity-span and RV variations, we selected those that show a simple, flat bisector velocity span, i.e., values of bisectors velocity-span arranged horizontally in a (RV; bisector velocity-span) diagram (this corresponds to stars for which the ratio of the amplitude of the bisector velocity span to the RV amplitude is less than 0.2) and for which
![]()
![]() 2 or
2 or
![]()
![]() 2. We regard them as unambiguous binaries. Figure 3 provides an example of a variable star (HD 68456; F5V;
2. We regard them as unambiguous binaries. Figure 3 provides an example of a variable star (HD 68456; F5V; ![]() = 12 km s
= 12 km s![]() )
for which the bisector velocity span clearly indicates the presence of a companion, and the observed RV amplitude once corrected from in-night variations can be due to a
)
for which the bisector velocity span clearly indicates the presence of a companion, and the observed RV amplitude once corrected from in-night variations can be due to a ![]() 0.1
0.1 ![]() stellar companion (see below).
This star was also recently classified as a binary on the basis of astrometric data (see below; Goldin & Makarov 2007).
stellar companion (see below).
This star was also recently classified as a binary on the basis of astrometric data (see below; Goldin & Makarov 2007).
Some variable stars show a bisector velocity span that is either partly flat and partly vertical or partly flat and partly inclined, indicating that they are most probably binaries and at the same time pulsating or active (see below). We classify those objects with
![]() or
or
![]()
![]() 2 as strong binaries candidates. An example, HD 19545 (A3V;
2 as strong binaries candidates. An example, HD 19545 (A3V; ![]() = 80 km s
= 80 km s![]() ), is provided in Fig. 4. Figure 5 compares the case of a pulsating star for which we artificially simulated an additional companion star. The generated RV and span curves of the pulsating star and pulsating star plus stellar companion are comparable to those found in the case of HD 19545. We do not have quantitative criteria to identify those ``composite bisectors velocity spans'', which explains why we classify the candidates as strong candidates rather than unambiguous binaries.
), is provided in Fig. 4. Figure 5 compares the case of a pulsating star for which we artificially simulated an additional companion star. The generated RV and span curves of the pulsating star and pulsating star plus stellar companion are comparable to those found in the case of HD 19545. We do not have quantitative criteria to identify those ``composite bisectors velocity spans'', which explains why we classify the candidates as strong candidates rather than unambiguous binaries.
Finally, for the rest of the stars, we flagged those stars with
![]() or
or
![]()
![]() 4 as binary candidates. For these stars we conservatively adopted a more stringent threshold for
4 as binary candidates. For these stars we conservatively adopted a more stringent threshold for
![]() or
or
![]() as we lack any additional indication of companions, and we know that these stars may be intrinsically variable. We thus took into account that the actual amplitude RV variations due to the pulsations may be stronger than the one measured on our set of data. This ensures that most of the observed RV amplitudes are due to a perturbation by a BD or a star. Figure 6 gives an example of such a star where no CCF could be computed, and the binarity classification relies solely upon the RV curve.
as we lack any additional indication of companions, and we know that these stars may be intrinsically variable. We thus took into account that the actual amplitude RV variations due to the pulsations may be stronger than the one measured on our set of data. This ensures that most of the observed RV amplitudes are due to a perturbation by a BD or a star. Figure 6 gives an example of such a star where no CCF could be computed, and the binarity classification relies solely upon the RV curve.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f2.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg27.gif) |
Figure 2:
Example of an SB2 binary, HD 2885 (A2V; |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f3.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg28.gif) |
Figure 3:
Example of a binary identified by a flat bisector velocity-span diagram and large amplitude RV variations, HD 68456 (F5V; |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f4.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg29.gif) |
Figure 4:
Example of a star whose RV variations are most probably due to both pulsations and binarity, HD 19545 (A3V; |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4cm]{figures/10105f5a.eps}\hspace*{3mm...
...eps}\hspace*{3mm}
\includegraphics[width=4cm]{figures/10105f5d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg30.gif) |
Figure 5:
Simulation of a composite bisector velocity-span diagram produced when adding a 100-
|
| Open with DEXTER | |
| |
Figure 6:
Example of a star whose RV variations are most probably due to binarity, HD 200761 (A1V; |
| Open with DEXTER | |
2.4.2 Planets
Those stars that at the same time show signs of RV variability with low amplitudes and a flat bisector velocity span diagram are very good candidates for hosting planets. In some cases, stars showing composite bisector velocity span diagrams with
![]() or
or
![]() larger than 2 can still be ``proper'' candidates for hosting planets. In such cases, the total RV amplitude is not dominated by the planetary signatures but by stellar variability (e.g., spots).
larger than 2 can still be ``proper'' candidates for hosting planets. In such cases, the total RV amplitude is not dominated by the planetary signatures but by stellar variability (e.g., spots).
2.4.3 Intrinsically variable stars
In the case of spots, and provided the star ![]() is higher than the instrumental resolution, the bisector shape is very peculiar and the bisector velocity-span variations are correlated to the RV ones (see Desort et al. 2007). In a (RV; bisector velocity span) diagram, the bisector velocity-span values are arranged either as an inclined ``8'' shape, or along an inclined line (so called ``anti-correlation''). For these objects, the ratio of the bisector span amplitude to the RV amplitude is found to be in the range 1-3. Figure 7 provides an example of a star showing clear signatures of spots on the basis of the bisector velocity-span diagram (HD 25457; F5V;
is higher than the instrumental resolution, the bisector shape is very peculiar and the bisector velocity-span variations are correlated to the RV ones (see Desort et al. 2007). In a (RV; bisector velocity span) diagram, the bisector velocity-span values are arranged either as an inclined ``8'' shape, or along an inclined line (so called ``anti-correlation''). For these objects, the ratio of the bisector span amplitude to the RV amplitude is found to be in the range 1-3. Figure 7 provides an example of a star showing clear signatures of spots on the basis of the bisector velocity-span diagram (HD 25457; F5V; ![]() = 25 km s
= 25 km s![]() ). As another example, the very neat case of HD 138763 can also be found in Desort et al. (2007).
). As another example, the very neat case of HD 138763 can also be found in Desort et al. (2007).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f7.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg32.gif) |
Figure 7:
Example of a star with variable RV due to the presence of spots. HD 25457 (F5V; |
| Open with DEXTER | |
In the case of pulsations, the bisector velocity-span values are spread over a much wider range than the RV and their variations are not correlated to the RV ones. In a (RV; bisector velocity span) diagram, the bisector velocity-span values are spread vertically, and the ratio of the bisector span amplitude to the RV amplitude is large, typically ![]() 3. Figure 8 provides an example of a pulsating star (HD 159492; A7V;
3. Figure 8 provides an example of a pulsating star (HD 159492; A7V; ![]() = 60 km s
= 60 km s![]() ).
).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f8.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg33.gif) |
Figure 8:
Example of a star with variable RV due to pulsations. HD 159492 (A7V; |
| Open with DEXTER | |
3 Results
Given the variability criteria described above, 108 stars out of 170 are found to be variable in RV, and 62 are found to be constant in RV within our precision limits. Table 1 provides relevant measurements on these targets: RV amplitudes and uncertainties, bisector velocity-span rms and uncertainties.
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm,clip]{figures/10105f9a.eps...
...graphics[width=8.5cm,clip]{figures/10105f9c.eps}\hspace*{4.25cm}}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg34.gif) |
Figure 9: Radial velocity curves of the identified or strong candidates or probable binaries (see text). |
| Open with DEXTER | |
3.1 Variability classification
3.1.1 Stellar binaries
Twenty stars are identified as binaries or candidate binaries with the criteria given in the previous section. More precisely:
- 4 binaries are found on the basis of the
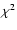 criterium, namely HD 99453, HD 209819, HD 2885 (Fig. 2), HD 142629.
criterium, namely HD 99453, HD 209819, HD 2885 (Fig. 2), HD 142629.
- 6 stars show mostly flat bisector velocity span in a (RV; bisector velocity span) diagram: HD 11262, HD 68456, HD 41742, HD 116568, HD 216627, HD 54834. Their RV amplitude varies between 1600 and 9200 m s
 .
.
- 4 stars have composite, flat+vertical bisector velocity span in a (RV; bisector velocity span) diagram, together with a total RV amplitude dominated by the binarity effect. These pulsating binaries are: HD 220729, HD 12311, HD 19545 (Fig. 4), and HD 112934.
- Finally, 6 stars are classified as probable binaries solely on the basis of their RV variations: HD 158352, HD 177756, HD 158094, HD 2834, HD 200761 (Fig. 6), HD 116160.
Notes follow on some individual binaries (and potential binaries):
- HD 11262 is associated to a ROSAT source by Suchkov et al. (2003).
- HD 54834: Koen & Eyer (2002) reported this star as a photometric Hipparcos variable at a level of 0.0046 mag and with a frequency of 0.802 day
 .
Our data do not either confirm or deny this frequency (not enough points, sampling not adapted).
.
Our data do not either confirm or deny this frequency (not enough points, sampling not adapted).
- HD 68456 (Fig. 3) was not reported as binary in the Hipparcos catalog from the photometric and astrometric points of view; it is classified by Adelman (2001) as one of the least variable Hipparcos stars. Goldin & Makarov (2007), however, provide an orbital solution to fit the Hipparcos astrometric data. The period found is 483
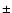 20 days, a0 = 9.6
+2.6-1.2 mas, eccentricity = 0.12
+0.25-0.15, inclination = 131
20 days, a0 = 9.6
+2.6-1.2 mas, eccentricity = 0.12
+0.25-0.15, inclination = 131 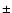 16
16
 ,
,
 = 103
+72-68
= 103
+72-68
 and
and 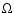 = 171
+164-83
= 171
+164-83
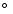 .
When fixing the period and eccentricity proposed by these authors, we tried to find a fit to our RV data. They happen to provide good fits assuming a mass of
.
When fixing the period and eccentricity proposed by these authors, we tried to find a fit to our RV data. They happen to provide good fits assuming a mass of 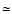 100
100
 for the companion.
for the companion.
- HD 99453: Baade & Kjeldsen (1997) questioned the previously suggested SB2 status of this object on the basis of their data; we do confirm the SB2 status for this star.
- HD 112934 (A9V;
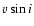 = 70 km s
= 70 km s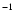 ): using Hipparcos photometry, Handler (1999) reports this star as a new possible
): using Hipparcos photometry, Handler (1999) reports this star as a new possible 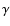 Doradus candidate but with a ``weak complicated signal'', associated to a 0.8-day period, and deCat et al. (2006) did not find clear line-profile variations in their CORALIE data. From our data, the star is both pulsating and a member of a binary system, which makes the line-profile variations indeed more complicated than for pulsating stars. Our limited number of data does not permit the high-frequency period to be characterized.
Doradus candidate but with a ``weak complicated signal'', associated to a 0.8-day period, and deCat et al. (2006) did not find clear line-profile variations in their CORALIE data. From our data, the star is both pulsating and a member of a binary system, which makes the line-profile variations indeed more complicated than for pulsating stars. Our limited number of data does not permit the high-frequency period to be characterized.
- HD 116160 was reported as an astrometric binary with accelerating proper motion by Makarov & Kaplan (2005).
- HD 116568 was classified as one of the least variable stars with Hipparcos by Adelman (2001). Baade & Kjeldsen (1997) report no variations in their
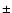 0.5 km s
0.5 km s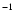 spectroscopic survey. The present data show that this star is a binary with an amplitude of at least 2750 m s
spectroscopic survey. The present data show that this star is a binary with an amplitude of at least 2750 m s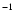 .
It is also reported as an unresolved Hipparcos problem star by Masson et al. (1999) and associated to a ROSAT source by Suchkov et al. (2003).
.
It is also reported as an unresolved Hipparcos problem star by Masson et al. (1999) and associated to a ROSAT source by Suchkov et al. (2003).
- HD 142629 is an astrometric Hipparcos binary. It was also recently reported for the first time as a spectroscopic binary by Antonello et al. (2006).
- HD 158352 was classified as a possible Herbig AeBe star by The et al. (1994). Corporon & Lagrange (1999) did not find variations to a 5-10 km s
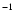 level in a survey of RV variations among Herbig AeBe stars. This star was reported as being surrounded by a dusty disk by Oudmaijer et al. (1992), and Moor et al. (2006) give an age of 750
level in a survey of RV variations among Herbig AeBe stars. This star was reported as being surrounded by a dusty disk by Oudmaijer et al. (1992), and Moor et al. (2006) give an age of 750 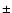 150 Myr for the system.
150 Myr for the system.
- HD 177756 was classified as a possible
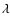 Bootis star, as well as a possible SB (Farragiana et al. 2004; Gerbaldi et al. 2003). It is reported as one of the Hipparcos least variable stars (Adelman 2001).
Bootis star, as well as a possible SB (Farragiana et al. 2004; Gerbaldi et al. 2003). It is reported as one of the Hipparcos least variable stars (Adelman 2001).
- HD 200761 was reported as one of the Hipparcos least variable stars (Adelman 2001).
- HD 209819 was also reported as one of the Hipparcos least variable stars (Adelman 2001).
- HD 220729 is associated to a ROSAT source by Suchkov et al. (2003).
3.1.2 Stars with planets
One star, HD60532 (F6IV-V; B-V = 0.52) clearly reveals low-amplitude RV variations and a flat bisector velocity span diagram at the same time, indicative of two Jupiter mass companions with a high confidence level. This star and the results of the fits of the RV curve is presented in Desort et al. (2008). Interestingly, in the frame of the present paper, the periods of the detected planets are long (![]() 100 days); hence, we get at least 1
100 days); hence, we get at least 1![]() of F stars with long-period planets in our sample. This is much less than the predicted rate of
of F stars with long-period planets in our sample. This is much less than the predicted rate of ![]()
![]() for 1.5
for 1.5 ![]() stars by Kennedy & Kenyon (2008); however, we are yet not sensitive to all ranges of masses and periods as shown in the last section.
stars by Kennedy & Kenyon (2008); however, we are yet not sensitive to all ranges of masses and periods as shown in the last section.
3.1.3 Single stars: intrinsic variability
We report in Table 1 the RV rms values obtained for each star, together with the associated uncertainties. For all the stars except those identified as binaries, Fig. 10 provides the measured RV rms as a function of their B-V, the ratio RV rms/uncertainties (E/I) as a function of their B-V as well, and the (B-V; ![]() )
diagram for the same objects. In the plots we have distinguished the 88 stars that are found to be variable according to the criteria defined above and those 62 found to be constant according to the same criteria.
)
diagram for the same objects. In the plots we have distinguished the 88 stars that are found to be variable according to the criteria defined above and those 62 found to be constant according to the same criteria.
The E/I ratio varies between 1.5 and a few tens. It is relatively less for stars with small B-V than for those with larger B-V. More quantitatively, the median value for this ratio computed on variable stars is 2.7 (resp. 4.4 and 5.2) for stars with B-V ![]() 0.2 (resp. 0.2
0.2 (resp. 0.2 ![]() B-V
B-V ![]() 0.4 and B-V
0.4 and B-V ![]() 0.4). Hence we detect more variable stars among stars with large B-V than stars with smaller B-V. We see, moreover, that the uncertainties generally increase with decreasing B-V.
These results are not surprising and illustrate that it is more difficult to identify variable stars when they have large uncertainties. In the frame of this study, it is important to keep in mind that our ability to detect variability generally decreases with decreasing B-V.
0.4). Hence we detect more variable stars among stars with large B-V than stars with smaller B-V. We see, moreover, that the uncertainties generally increase with decreasing B-V.
These results are not surprising and illustrate that it is more difficult to identify variable stars when they have large uncertainties. In the frame of this study, it is important to keep in mind that our ability to detect variability generally decreases with decreasing B-V.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figures/10105f10.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg42.gif) |
Figure 10:
Top: RV rms measured for all stars but binaries with more than 6 spectra available as a function of B-V. Middle: Ratio RV rms/uncertainty for the same stars. Bottom: (B-V; |
| Open with DEXTER | |
Table 2: Median values of RV rms and RV uncertainties for stars with more than 6 spectra (3 epochs) available.
The uncertainties increase with increasing ![]() .
We could actually verify that the uncertainties vary as
.
We could actually verify that the uncertainties vary as ![]() with a
with a
![]() law where
law where
![]()
![]() 0.1, as predicted in Galland et al. (2005a). The percentage of variable stars depends on B-V in the following way:
0.1, as predicted in Galland et al. (2005a). The percentage of variable stars depends on B-V in the following way:
- Most (85
 )
of the 58 stars with B-V greater than 0.4 are found to be variable and the RV uncertainty is 2 m s
)
of the 58 stars with B-V greater than 0.4 are found to be variable and the RV uncertainty is 2 m s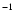 (median value). Even more, 90
(median value). Even more, 90 of the 46 stars with B-V over 0.45, i.e., well beyond the instability strip, are found to be variable and their uncertainty is 1.4 m s
of the 46 stars with B-V over 0.45, i.e., well beyond the instability strip, are found to be variable and their uncertainty is 1.4 m s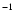 (median value). We conclude then that at a level of precision of 2 m s
(median value). We conclude then that at a level of precision of 2 m s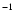 or less, most of the stars with B-V larger than 0.4 are RV variable.
or less, most of the stars with B-V larger than 0.4 are RV variable.
- Among the stars with B-V between 0.2 and 0.4, we found few variable stars, but this is due to a selection effect after known
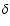 Scuti and
Scuti and 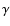 Doradus stars were removed from our sample (see above).
Doradus stars were removed from our sample (see above).
- Only 36
 of the 73 stars with B-V less than 0.2 are found to be variable. The percentage of variable decreases to 20
of the 73 stars with B-V less than 0.2 are found to be variable. The percentage of variable decreases to 20 if we consider the 40 stars with B-V under 0.1. For those stars with B-V between 0.1 and 0.2, we get as many variable stars as constant ones. The number of stars found to be constant according to our criteria increases then with decreasing B-V. However, we have seen that our ability to detect variable stars decreases with decreasing B-V. More quantitatively, the median uncertainty in the case of ``constant'' stars is
if we consider the 40 stars with B-V under 0.1. For those stars with B-V between 0.1 and 0.2, we get as many variable stars as constant ones. The number of stars found to be constant according to our criteria increases then with decreasing B-V. However, we have seen that our ability to detect variable stars decreases with decreasing B-V. More quantitatively, the median uncertainty in the case of ``constant'' stars is 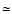 290 m s
290 m s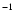 ,
whereas the median uncertainty in the case of stars found to be variable is
,
whereas the median uncertainty in the case of stars found to be variable is 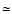 80 m s
80 m s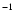 .
Furthermore, the median uncertainty of constant stars is comparable to the median value of the standard deviation of variable stars (265 m s
.
Furthermore, the median uncertainty of constant stars is comparable to the median value of the standard deviation of variable stars (265 m s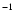 ). We may then stipulate that, in fact, most of the stars with B-V
). We may then stipulate that, in fact, most of the stars with B-V 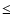 0.2 are probably RV variable.
0.2 are probably RV variable.
3.2 Variability of stellar origin and impact on planet detectability
The ``uncorrected'' jitters, as given directly by the measured RV rms are provided in Table 1 for each star, together with the associated uncertainties. We prefer not to use the jitters corrected from the uncertainties, as sometimes done, as our main aim is to evaluate the impact on planet detectabiliity rather than to make stellar studies. Table 2 gives the computed median ``uncorrected'' jitters per bins of B-V. Rows 7-9 give the median per bin of B-V of the achievable detection limits deduced from the measured rms for each star, expressed in Jupiter mass. Three periods are considered: 3, 10 and 100 days (see Sect. 3). We assumed that the planet, supposedly on a circular orbit, is detectable if the amplitude (2 ![]() K) of the RV variations is larger than 3
K) of the RV variations is larger than 3 ![]()
![]() ,
where RV rms is the ``uncorrected'' jitter actually measured. We will come back later to a validation of this assumption. Rows 7-9 give the percentage of stars for which the detection limit, given the measured RV rms, fall in the planetary domain.
,
where RV rms is the ``uncorrected'' jitter actually measured. We will come back later to a validation of this assumption. Rows 7-9 give the percentage of stars for which the detection limit, given the measured RV rms, fall in the planetary domain.
In Galland et al. (2005a) we showed that the detection limit strongly depends on the star ST and its projected rotational-velocity; more precisely, the detection limit increases with earlier ST and/or larger ![]() .
Thanks to the present data, we can in addition address the question of the impact of the stellar jitter.
.
Thanks to the present data, we can in addition address the question of the impact of the stellar jitter.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f11.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg46.gif) |
Figure 11: Achievable detection limits for all stars but binaries taking their actual ``uncorrected'' jitter (losanges) or the measured uncertainties (squares) into account, and assuming a planet on a circular 3-day orbit. |
| Open with DEXTER | |
Table 3:
Detection limits, either achievable or achieved with a 68.2![]() or a 99.7
or a 99.7![]() probability in the present survey (see text); only those detection limits less than 0.05 Jupiter mass are given with 2 digits.
probability in the present survey (see text); only those detection limits less than 0.05 Jupiter mass are given with 2 digits.
We give for each star in Table 3 the computed detectable limits assuming 3-day, 10-day, and 100-day periods. Figure 11 shows the detection limits for all stars for a 3-day period. For comparison, we also give the mass of the planet that would be detectable if the star is not active/pulsating (hence has no jitter), and the limit would then be set by the uncertainty (hypothesis 2K = 3![]() uncertainty). The ratio of the two values is E/I. As previously seen, this ratio is larger than 1.5 and may be quite high; the impact of the jitter on the detectable masses is therefore non negligible. Several comments can be made.
uncertainty). The ratio of the two values is E/I. As previously seen, this ratio is larger than 1.5 and may be quite high; the impact of the jitter on the detectable masses is therefore non negligible. Several comments can be made.
- The achievable limits fall into the planetary domain for a large number of stars: more precisely, in 137 out of 150 stars, i.e., 91
 ,
the detection limit for a 3-day period falls within the planetary domain. For the remaining, stars the limit falls well within the BD domain with masses up to 54
,
the detection limit for a 3-day period falls within the planetary domain. For the remaining, stars the limit falls well within the BD domain with masses up to 54
 .
When considering a 10-day (resp. 100-day) period, we find that we can reach the planetary mass domain for 124 stars, hence 83
.
When considering a 10-day (resp. 100-day) period, we find that we can reach the planetary mass domain for 124 stars, hence 83 (resp. 92 stars, hence 61
(resp. 92 stars, hence 61 ). For a 10-day period, the limit for all remaining stars but one fall into the BD regime; for the 100-day period, the limit for all remaining stars but 6 fall in the BD domain.
). For a 10-day period, the limit for all remaining stars but one fall into the BD regime; for the 100-day period, the limit for all remaining stars but 6 fall in the BD domain.
- As expected, the median of the detection limits generally improve with increasing B-V, from 10
 for B-V between -0.1 and 0, to 5
for B-V between -0.1 and 0, to 5
 for B-V between 0 and 0.3, to 0.05
for B-V between 0 and 0.3, to 0.05
 for B-V between 0.5 and 0.6 (for a 3-day period) (see Table 2). Noticeably, for stars with B-V
for B-V between 0.5 and 0.6 (for a 3-day period) (see Table 2). Noticeably, for stars with B-V 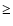 0.3, individual detection limits may be as low as 0.02
0.3, individual detection limits may be as low as 0.02
 and for stars with B-V
and for stars with B-V 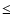 ,
0.3, individual detection limits may be as low as 0.5
,
0.3, individual detection limits may be as low as 0.5
 .
For a ten-day period, these numbers become respectively: 15, 7 and 0.08
.
For a ten-day period, these numbers become respectively: 15, 7 and 0.08
 ;
for a 100-day period, 31, 16, and 0.17
;
for a 100-day period, 31, 16, and 0.17
 .
Also, noticeably, the detection limits improve steeply at B-V = 0.3.
.
Also, noticeably, the detection limits improve steeply at B-V = 0.3.
- The ``uncorrected'' jitter varies a lot from one object to the next; therefore, the general conclusion that the detection limits improves with increasing B-V may not apply when considering individual objects. For instance, the two stars HD 50445 (A3V; B-V = 0.18) and HD 63847 (A9V; B-V = 0.3) have similar projected rotational-velocities (
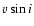
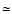 90 km s
90 km s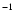 )
and very different levels of activity, with an RV rms of 66 m s
)
and very different levels of activity, with an RV rms of 66 m s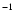 and 794 m s
and 794 m s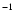 ,
respectively. When we take this ``uncorrected'' jitter into account, the detection limit is 1
,
respectively. When we take this ``uncorrected'' jitter into account, the detection limit is 1
 (P = 3 days) and 1.5
(P = 3 days) and 1.5
 (P = 10 days) around the A3V star, whereas the detection limit is about 10 times higher for the A9V star.
(P = 10 days) around the A3V star, whereas the detection limit is about 10 times higher for the A9V star.
We note that, of course, the measured ``uncorrected'' jitter provides a reliable limit to planet detection only when this jitter is due to stellar activity in general and not to companions. Were a companion present, its contribution to the RV variability would have to be removed in order to estimate the impact of the stellar activity.
4 Planet detection limits of the present survey
4.1 Estimation of the achieved detection limits
We now try to estimate the detection limits reached by the present survey, taking the actual RV curve into account. For each star, we then compute the detection limit (companion mass) as a function of its period. To do so, we consider a planet with a given mass and with a given period (the orbit is assumed to be circular). For any couple (mass; period) we generate a large number of Keplerian orbits, assuming different times of passage at periastron (T0). For each orbit, we compute the expected radial velocities at the times of the actual observations. We add a noise (random value between +- RV uncertainty), where RV uncertainty is the uncertainty measured on the RV data. We then get a virtual set of RVs, which takes the star properties into account (in particular, its ST and rotational velocity, through the uncertainties and SN). We then compute the standard deviation of the virtual RVs points. For a given (mass; period), the distribution of all the standard deviations (corresponding to different T0) obtained is Gaussian. We then compute the average value of the distribution of the virtual standard deviations. We consider that a planet with a given (mass; period) is detectable if the standard deviation of the real RV values is less than the average value of the virtual standard deviations. We determine the confidence level (or detection probability) associated to such an orbit by comparing the standard deviation of the virtual distribution with the difference between the standard deviation of the real RV measurements and the average value of the virtual standard deviations.
In practice, for a given object, we explored 200 periods in the range 0.5 to 1000 days, and 100 planet masses in the range (Mmin; 100
![]() )
where Mmin corresponds to the achievable mass given the measured uncertainty. For a given (mass; period), we explored 1000 T0. We checked that increasing the number of periods, planet masses, and/or initial T0 do not significantly affect the results.
)
where Mmin corresponds to the achievable mass given the measured uncertainty. For a given (mass; period), we explored 1000 T0. We checked that increasing the number of periods, planet masses, and/or initial T0 do not significantly affect the results.
For each (mass; period) couple, we thus obtain a detection probability. In a (mass; period) diagram, we can then identify the domain where a planet with a given mass and period should be detectable if present, with a given level of confidence. This defines a domain in which we can exclude the presence of a planet with a given level of confidence. We consider two levels of confidence: 1![]() (i.e., a 68.2
(i.e., a 68.2![]() probability) and 3
probability) and 3![]() (i.e., 99.7
(i.e., 99.7![]() probability).
probability).
4.2 Sensitivity of the survey and first constraints on early type stars
The sensitivity of our survey is a consequence of the number of data available and on the temporal sampling of the data. We kept only those stars (107 objects) found to be either constant or variable, for which we got more than 12 data points (6 epochs). Also, given the data at hand, we limited the range of periods investigated between 1 day and a few hundred days. We report in
Table 3 the achieved limits (68.2![]() and 99.7
and 99.7![]() probabilities) obtained for each of the 107 stars considering three periods: 3, 10, and 100 days.
probabilities) obtained for each of the 107 stars considering three periods: 3, 10, and 100 days.
We also give in Fig. 12 examples of the detection limits achieved (68.2![]() and 99.7
and 99.7![]() probabilities) as estimated with the previously described simulations. We also plotted the achievable detection limits taking the jitter into account, as defined in the previous section, as well as the detection limits corresponding to the measured uncertainties. We recall that the last two cases (achievable limits) do not take the actual temporal sampling of the data into account, conversely to the detection limits computed with our virtual realizations.
probabilities) as estimated with the previously described simulations. We also plotted the achievable detection limits taking the jitter into account, as defined in the previous section, as well as the detection limits corresponding to the measured uncertainties. We recall that the last two cases (achievable limits) do not take the actual temporal sampling of the data into account, conversely to the detection limits computed with our virtual realizations.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{figures/10105f12.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg48.gif) |
Figure 12:
Detection limits. X-axis: periods (days). Y-axis: detection limit (M/
|
| Open with DEXTER | |
When enough data are available, the actual detection limits fall close to the achievable limits obtained assuming the
![]() rms threshold for the amplitude of RV variations, as can be seen in Fig. 12. This justifies the choice of the threshold adopted in the previous section to estimate the achievable limits.
rms threshold for the amplitude of RV variations, as can be seen in Fig. 12. This justifies the choice of the threshold adopted in the previous section to estimate the achievable limits.
We sometimes endup with high detection limits that fall outside the investigated range of masses, i.e., ![]() 100
100
![]() when we consider a period of 100 days, whereas the detection limits for a 3- or 10-day period are close to the achievable limits. This corresponds to cases where the temporal sampling is not adapted to exploring such a long period (see for instance the case of HD 33256, in Fig. 12). Sometimes, but much less frequently, the detection limit for a 10-day fall outside the investigated range of masses, whereas the detection limits for a 3-day period is close to the achievable limit. In fact, our survey searches mostly for short-period planets (typ. a few days). Ten to 100-day periods are not always sampled often enough to get interesting results (especially on early-type stars) and
when we consider a period of 100 days, whereas the detection limits for a 3- or 10-day period are close to the achievable limits. This corresponds to cases where the temporal sampling is not adapted to exploring such a long period (see for instance the case of HD 33256, in Fig. 12). Sometimes, but much less frequently, the detection limit for a 10-day fall outside the investigated range of masses, whereas the detection limits for a 3-day period is close to the achievable limit. In fact, our survey searches mostly for short-period planets (typ. a few days). Ten to 100-day periods are not always sampled often enough to get interesting results (especially on early-type stars) and ![]() 100-day periods are not properly sampled to get interesting results. We therefore discuss only periods
100-day periods are not properly sampled to get interesting results. We therefore discuss only periods ![]() 100 days. Finally, one has to note that, in some cases, we get a 99.7
100 days. Finally, one has to note that, in some cases, we get a 99.7![]() probability detection limit out of the investigated range, whereas the 68.2
probability detection limit out of the investigated range, whereas the 68.2![]() limit falls well into the investigated range. This happens generally when the number of data is the lowest: 12 or 14.
limit falls well into the investigated range. This happens generally when the number of data is the lowest: 12 or 14.
Table 4:
Percentage of stars for which the achieved detection ![]() or
or ![]() limits fall in the planetary or BD/planet domains. Median values of the achieved detection limits, expressed in Jupiter mass, per bin of B-V.
limits fall in the planetary or BD/planet domains. Median values of the achieved detection limits, expressed in Jupiter mass, per bin of B-V.
To study the impact of B-V on the present results, we computed the percentage of stars for which the achieved detection limits (68.2![]() and 99.7
and 99.7![]() probabilities) fall in the planetary or BD domains per bin of B-V, considering a 3-day, a 10-day, and a 100-day period. We also computed the median of the achieved detection limits (considering 68.2
probabilities) fall in the planetary or BD domains per bin of B-V, considering a 3-day, a 10-day, and a 100-day period. We also computed the median of the achieved detection limits (considering 68.2![]() and 99.7
and 99.7![]() probabilities) per bin of B-V for such periods. The results are given in Table 4. In order to allow comparison between the limits obtained with these two probabilities and with the achievable ones, we considered only those stars for the computation of the median values for which both the 68.2
probabilities) per bin of B-V for such periods. The results are given in Table 4. In order to allow comparison between the limits obtained with these two probabilities and with the achievable ones, we considered only those stars for the computation of the median values for which both the 68.2![]() and 99.7
and 99.7![]() probability detection limits fall within the investigated range of masses. Finally, one has to note that, for the earliest type stars, there are few objects per bin is quite small, so one has to be very cautious with the associated statistics. We can see that
probability detection limits fall within the investigated range of masses. Finally, one has to note that, for the earliest type stars, there are few objects per bin is quite small, so one has to be very cautious with the associated statistics. We can see that
- if we consider a 3-day period, the achieved limit at 1
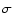 (resp. 3
(resp. 3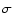 )
falls within the planetary domain for 90
)
falls within the planetary domain for 90 (resp. 81
(resp. 81 )
of the stars. This percentage is comparable to the one found in Sect. 3. It increases from 75
)
of the stars. This percentage is comparable to the one found in Sect. 3. It increases from 75 (resp. 25
(resp. 25 )
for the earliest type stars to 100
)
for the earliest type stars to 100 (resp. 100
(resp. 100 )
for stars with B-V greater than 0.3. Also, the median of the achieved limits at 1
)
for stars with B-V greater than 0.3. Also, the median of the achieved limits at 1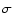 (resp. 3
(resp. 3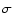 )
decreases from 7
)
decreases from 7
 (resp. 7
(resp. 7
 )
for the earliest-type stars to 0.08
)
for the earliest-type stars to 0.08
 (resp. 0.3
(resp. 0.3
 )
for the latest-type stars. Moreover, the steep step seen in Sect. 3 in the detectable masses at B-V = 0.3 is also clear.
)
for the latest-type stars. Moreover, the steep step seen in Sect. 3 in the detectable masses at B-V = 0.3 is also clear.
- if we consider a 10-day period, the achieved limit at 1
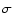 (resp. 3) fall in the planetary domain for 82
(resp. 3) fall in the planetary domain for 82 (resp. 67
(resp. 67 )
of the stars. This percentage increases from 50 (resp. 25)
)
of the stars. This percentage increases from 50 (resp. 25) for the earliest type stars to 100
for the earliest type stars to 100 (resp. 100
(resp. 100 )
for stars with B-V larger than 0.4, however, with an exception in the [0.2; 0.3] range where it decreases back to 50
)
for stars with B-V larger than 0.4, however, with an exception in the [0.2; 0.3] range where it decreases back to 50 .
Also, the median of the achieved limits at 1
.
Also, the median of the achieved limits at 1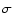 (resp. 3
(resp. 3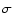 )
decreases from 12
)
decreases from 12
 (resp. 24
(resp. 24
 )
for the earliest-type stars to 0.1 (resp. 0.7) for the latest-type stars, with however an exception in the range [0.2; 0.3] range as regards the 99.7
)
for the earliest-type stars to 0.1 (resp. 0.7) for the latest-type stars, with however an exception in the range [0.2; 0.3] range as regards the 99.7 probability. Again the steep step is observed at B-V = 0.3.
probability. Again the steep step is observed at B-V = 0.3.
- if we finally consider a 100-day period, the achieved limit at 1
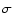 (resp. 3
(resp. 3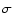 )
falls within the planetary domain for 54
)
falls within the planetary domain for 54 (resp. 35
(resp. 35 )
of the stars. We note that this percentage is lower than the one obtained in Sect. 3, so we attribute the discrepancy to the actual temporal sampling and the relatively small amount of targets investigated yet. The median of the achieved limits at 1
)
of the stars. We note that this percentage is lower than the one obtained in Sect. 3, so we attribute the discrepancy to the actual temporal sampling and the relatively small amount of targets investigated yet. The median of the achieved limits at 1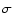 (resp. 3
(resp. 3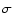 )
decreases from 19
)
decreases from 19
 (resp. 34
(resp. 34
 )
for stars with B-V
)
for stars with B-V 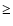 0.0 to 1
0.0 to 1
 (resp. 1.9
(resp. 1.9
 )
for the latest-type stars. Again this steep step is observed at B-V = 0.3.
)
for the latest-type stars. Again this steep step is observed at B-V = 0.3.
Finally, we give the probability of not detecting planets of a given mass and with a given period (3, 10, 200, 500 days) around stars with a given spectral type and ![]() .
The results are summarized in Table 5. We see that as expected, for a given probability, the limits globally decrease with increasing B-V and decreasing
.
The results are summarized in Table 5. We see that as expected, for a given probability, the limits globally decrease with increasing B-V and decreasing ![]() .
.
Table 5:
Detection limit for 50![]() and 90
and 90![]() for different periods.
for different periods.
Obviously, the statistics provided by our survey are still poor on early type stars, and still very limited on the latest type stars. Concerning the latter, we note that, if we consider the 41 objects with B-V ![]() 0.4, i.e., well beyond the instability strip, we find that less than 24
0.4, i.e., well beyond the instability strip, we find that less than 24![]() of stars host planets with masses equal to 0.5
of stars host planets with masses equal to 0.5
![]() or more; less than 5
or more; less than 5![]() host planets with masses equal to 1
host planets with masses equal to 1
![]() or more on a 3-day period. For a 10-day period, we find that less than 42
or more on a 3-day period. For a 10-day period, we find that less than 42![]() host planets with masses
host planets with masses ![]() 0.5
0.5
![]() ,
and less than 20
,
and less than 20![]() )
host planets with masses
)
host planets with masses ![]() 1
1
![]() .
The comparison between achieved and achievable detection limits shows that there is still room to significantly improve those statistics (thanks to new data points).
.
The comparison between achieved and achievable detection limits shows that there is still room to significantly improve those statistics (thanks to new data points).
The present statistics certainly do not allow quantitative comparisons with late type dwarfs, which have been surveyed by several groups for more than 10 years, or with giant or subgiant stars, because in that case of the lack of data for both massive dwarfs and (sub-)giants.
Concerning the presence or absence of hot Jupiters around massive stars, we note that the planets found so far in our survey are located at about 0.7 AU or more from a 1.4 ![]() star. This separation corresponds to what is found for the closest planet around giant stars. We have also recently detected a planet orbiting at 0.6 AU from a dwarf with a similar mass in the northern hemisphere (Desort et al. 2009). Because of the still limited amount of data available, it should not, however, be concluded that there are no planets closer to massive dwarfs. We also recall that a few short-period planets have been found around 1.4
star. This separation corresponds to what is found for the closest planet around giant stars. We have also recently detected a planet orbiting at 0.6 AU from a dwarf with a similar mass in the northern hemisphere (Desort et al. 2009). Because of the still limited amount of data available, it should not, however, be concluded that there are no planets closer to massive dwarfs. We also recall that a few short-period planets have been found around 1.4 ![]() stars through transits.
stars through transits.
5 Conclusion
Based on the observation of a large number of A-F type stars (170), we have been able to measure their jitters and, for the first time, derive estimations of the detection limits that can be expected on average on those stars with B-V in that range [-0.1; 0.6] (once previously known ![]() Scuti and
Scuti and ![]() Doradus stars are removed) for 3 periods: 3, 10, and 100 days. We have shown that, at the precision provided by HARPS, most of the stars are variable in RV, and the impact of the RV jitter, due to either spots or pulsations, is generally not negligible on planet detectability. However, assuming that planets are detectable if the amplitude of the induced RV variation is greater than
Doradus stars are removed) for 3 periods: 3, 10, and 100 days. We have shown that, at the precision provided by HARPS, most of the stars are variable in RV, and the impact of the RV jitter, due to either spots or pulsations, is generally not negligible on planet detectability. However, assuming that planets are detectable if the amplitude of the induced RV variation is greater than
![]() (this threshold defines the achievable detection limits, which depends on the star and the spectrograph used), we have shown that, even when taking into account the jitter, giant planets can still be found around these stars in most cases.
This is not only true for the stars with B-V
(this threshold defines the achievable detection limits, which depends on the star and the spectrograph used), we have shown that, even when taking into account the jitter, giant planets can still be found around these stars in most cases.
This is not only true for the stars with B-V ![]() 0.3, for which we can find either short- or long-period planets, with masses as low as 0.02
0.3, for which we can find either short- or long-period planets, with masses as low as 0.02
![]() (case of short period) for the latest type stars, but also for dwarfs with B-V
(case of short period) for the latest type stars, but also for dwarfs with B-V ![]() 0.3. For such stars, short-period planets can still be found around those with relatively low projected rotational velocity and low level of activity, with masses down to 0.5
0.3. For such stars, short-period planets can still be found around those with relatively low projected rotational velocity and low level of activity, with masses down to 0.5
![]() (best case). This survey has identified for the first time those stars that are best-suited to further searches for planets around massive dwarfs.
(best case). This survey has identified for the first time those stars that are best-suited to further searches for planets around massive dwarfs.
We have also shown that, given the data available, the present survey is sensitive to short-period planets (hot Jupiters) and only partially sensitive to longer periods (up to 100 days). We found in particular one 2-planet system with periods longer than 100 days around one late-type star. Whenever possible (107 stars), we computed the detection limits actually achieved for each star and showed that when enough data are available, the achieved detection limit is set by the
![]() threshold. We indeed reached such limits for early-type, as well as for late-type stars. We finally derived first estimates of the presence of short-period planets around these A-F stars. We showed for instance that fewer than 5
threshold. We indeed reached such limits for early-type, as well as for late-type stars. We finally derived first estimates of the presence of short-period planets around these A-F stars. We showed for instance that fewer than 5![]() of the latest-type stars (B-V
of the latest-type stars (B-V ![]() 0.4) host P=3 day-period planets with masses 1
0.4) host P=3 day-period planets with masses 1
![]() or more. Such statistics are not constraining enough to allow interesting comparisons with later type stars or with model predictions, but as soon as more data become available, the statistics can be improved straightforwardy.
or more. Such statistics are not constraining enough to allow interesting comparisons with later type stars or with model predictions, but as soon as more data become available, the statistics can be improved straightforwardy.
Finally, we note that to compute these detection limits, we did not try to average out the spectra over timescales associated to the frequencies of intrinsic stellar variations. This approach would of course allow a significant decrease in the detectable masses. As it would require lots of telescope time, it should probably be kept for stars with the highest scientific interest.
Acknowledgements
We acknowledge financial support from the French Programme National de Planétologie ( PNP, INSU). We also acknowledge support from the French National Research Agency (ANR) through project grant NT05-4_44463.
These results have made use of the SIMBAD database, operated at the CDS, Strasbourg, France.
We also thank Gérard Zins and Sylvain Cètre for their help in implementing the SAFIR interface, Sylvain Cètre also for performing some of the observations, and P. Rubini for his help on the layout of the paper.
References
- Adelman, S. J. 2001, A&A, 367, 297 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Antonello, E., Mantegazza, L., Rainer, M., & Miglio, A. 2006, A&A, 445, L15 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baade, D., & Kjeldsen, H. 1997, A&A, 323, 429 (In the text)
- Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Burkert, A., & Ida, S. 2007, ApJ, 660, 845 [NASA ADS] [CrossRef] (In the text)
- Butler, R. P., Johnson, J. A., Marcy, G. W., et al. 2006, PASP, 118, 1685 [NASA ADS] [CrossRef] (In the text)
- Corporon, P., & Lagrange, A.-M. 1999, A&A, 136, 429 [CrossRef] (In the text)
- De Cat, P., Eyer, L., Cuypers, J., et al. 2006, A&A, 449, 281 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Desort, M., Lagrange, A.-M., Galland, F., et al. 2007, A&A, 473, 893 [NASA ADS] (In the text)
- Desort, M., Lagrange, A.-M., Galland, F., et al. 2008, A&A, 491, 883 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Desort, M., Lagrange, A.-M., Galland, F., et al. 2009, A&A, in preparation (In the text)
- Farragiana, R., & Bonifacio, G. 2004, A&A, 349, 521 (In the text)
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005a, A&A, 443, 337 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005b, A&A, 444, L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2006, A&A, 452, 709 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gerbaldi, M., Farragiana, R., & Lai, O. 2003, A&A, 412, 447 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Goldin, A., & Makarov, V. V. 2007, ApJS, 173, 137 [NASA ADS] [CrossRef] (In the text)
- Ida, S., & Lin, D. N. C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] (In the text)
- Handler, G. 1999, MNRAS, 309, L19 [NASA ADS] [CrossRef] (In the text)
- Hatzes, A. P. 2002, Astron. Nachr., 323, 3 [CrossRef]/4, 392 (In the text)
- Hatzes, A. P., Guenther, E. W., Endl, M., et al. 2005, A&A, 437, 743 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hekker, S., Reffert, S., Quirrenbach, A., et al. 2006, A&A, 454, 943 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- ESA 1997, The Hipparcos and Tycho Cat, ESA SP-1200
- Johnson, J.A., Marcy, G.W., Fisher, D.A., et al. 2006, ApJ, 652, 1724 [NASA ADS] [CrossRef] (In the text)
- Johnson, J.A., Butler, R.P., Marcy, G.W., et al. 2007, ApJ, 665, 785 [NASA ADS] [CrossRef] (In the text)
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] (In the text)
- Koen, C., & Eyer, L. 2002, MNRAS, 331, 45 [NASA ADS] [CrossRef] (In the text)
- Li, S. L., Lin, D. N. C., & Liu, X. W. 2008, ApJ, 685, 1210 [NASA ADS] [CrossRef] (In the text)
- Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Makarov, V. V., & Kaplan, G. H. 2005, AJ, 129, 2420 [NASA ADS] [CrossRef] (In the text)
- Masson, B. D., Martin, C., Hartkopf, W. I., et al. 1999, AJ, 117, 1890 [CrossRef] (In the text)
- Mathias, P., Le Contel, J.-M., & Le Chapellier, E. 2004, A&A, 417, 189 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moor, A., Abraham, P., derekas, A., et al. 2006, ApJ, 644, 525 [NASA ADS] [CrossRef] (In the text)
- Niedzielski, A., Konacki, M., Wolszcan, A., et al. 2007, ApJ, 669, 1354 [NASA ADS] [CrossRef] (In the text)
- Rodriguez, E., Lopez-Gonzales, M. J., & Lopez de Coca, P. 2000, A&A, 144, 469 [NASA ADS] [CrossRef] (In the text)
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] (In the text)
- Sato, B., Ando, H., Takeda, Y., et al. 2003, ApJ, 597, L157 [NASA ADS] [CrossRef] (In the text)
- Sato, B., Izumiura, H., Toyota, E., et al. 2008, PASJ, 60, 539 [NASA ADS] (In the text)
- Suchkov, A. A., Makarov, V. V., & Voges, W. 2003, ApJ, 595, 1206 [NASA ADS] [CrossRef] (In the text)
- The, P. S., de Winter, D., & Perez, M. R. 1994, A&AS, 104, 315 [NASA ADS] (In the text)
- Oudmaijer, R. D., et al. 1992, A&AS, 96, 625 [NASA ADS] (In the text)
Footnotes
- ... stars
![[*]](/icons/foot_motif.gif)
- Based on observations collected at the European Southern Observatory, Chile, ESO 075.C-0689, 076.C-0279, 077.C-0295, 078.C-0209, 080.C-0664, 080.C-0712.
- ... difference
![[*]](/icons/foot_motif.gif)
-
![$\Delta m(i) = 6\log_{10}[ \epsilon_{{\rm rv}}(i) / \min(\epsilon_{{\rm rv}})]$](/articles/aa/full_html/2009/07/aa10105-08/img17.gif) ,
where
,
where
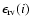 stands for the uncertainty associated to the measurement of the observation (i) for the considered object, and
stands for the uncertainty associated to the measurement of the observation (i) for the considered object, and
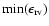 is the lowest value of uncertainty obtained for this object; the measured uncertainties (cf. Galland et al. 2005a) take the photon noise + instrumental uncertainties into account.
is the lowest value of uncertainty obtained for this object; the measured uncertainties (cf. Galland et al. 2005a) take the photon noise + instrumental uncertainties into account.
All Tables
Table 1: Stars properties and measurements.
Table 2: Median values of RV rms and RV uncertainties for stars with more than 6 spectra (3 epochs) available.
Table 3:
Detection limits, either achievable or achieved with a 68.2![]() or a 99.7
or a 99.7![]() probability in the present survey (see text); only those detection limits less than 0.05 Jupiter mass are given with 2 digits.
probability in the present survey (see text); only those detection limits less than 0.05 Jupiter mass are given with 2 digits.
Table 4:
Percentage of stars for which the achieved detection ![]() or
or ![]() limits fall in the planetary or BD/planet domains. Median values of the achieved detection limits, expressed in Jupiter mass, per bin of B-V.
limits fall in the planetary or BD/planet domains. Median values of the achieved detection limits, expressed in Jupiter mass, per bin of B-V.
Table 5:
Detection limit for 50![]() and 90
and 90![]() for different periods.
for different periods.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{figures/10105f1.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg20.gif) |
Figure 1: Observed stars in an HR diagram. We also plotted the dwarfs and/or (sub-) giants surveyed either with the Coralie spectrograph or by Johnson et al. (2006). Our targets cover a domain that has not been surveyed yet. Note the relative lack of objects in the [0.2; 0.4] B-V region, due to selection effects (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f2.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg27.gif) |
Figure 2:
Example of an SB2 binary, HD 2885 (A2V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f3.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg28.gif) |
Figure 3:
Example of a binary identified by a flat bisector velocity-span diagram and large amplitude RV variations, HD 68456 (F5V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f4.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg29.gif) |
Figure 4:
Example of a star whose RV variations are most probably due to both pulsations and binarity, HD 19545 (A3V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm]{figures/10105f5a.eps}\hspace*{3mm...
...eps}\hspace*{3mm}
\includegraphics[width=4cm]{figures/10105f5d.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg30.gif) |
Figure 5:
Simulation of a composite bisector velocity-span diagram produced when adding a 100-
|
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
Example of a star whose RV variations are most probably due to binarity, HD 200761 (A1V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f7.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg32.gif) |
Figure 7:
Example of a star with variable RV due to the presence of spots. HD 25457 (F5V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f8.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg33.gif) |
Figure 8:
Example of a star with variable RV due to pulsations. HD 159492 (A7V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm,clip]{figures/10105f9a.eps...
...graphics[width=8.5cm,clip]{figures/10105f9c.eps}\hspace*{4.25cm}}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg34.gif) |
Figure 9: Radial velocity curves of the identified or strong candidates or probable binaries (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{figures/10105f10.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg42.gif) |
Figure 10:
Top: RV rms measured for all stars but binaries with more than 6 spectra available as a function of B-V. Middle: Ratio RV rms/uncertainty for the same stars. Bottom: (B-V; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{figures/10105f11.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg46.gif) |
Figure 11: Achievable detection limits for all stars but binaries taking their actual ``uncorrected'' jitter (losanges) or the measured uncertainties (squares) into account, and assuming a planet on a circular 3-day orbit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{figures/10105f12.eps}
\end{figure}](/articles/aa/full_html/2009/07/aa10105-08/Timg48.gif) |
Figure 12:
Detection limits. X-axis: periods (days). Y-axis: detection limit (M/
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


