| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 1025 - 1030 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:200810743 | |
| Published online | 22 December 2008 | |
Two  35 day clocks in Hercules X-1: evidence for neutron star free precession
35 day clocks in Hercules X-1: evidence for neutron star free precession
R. Staubert1 - D. Klochkov1 - K. Postnov2 - N. Shakura2 - J. Wilms3 - R. E. Rothschild4
1 - Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1, 72076 Tübingen, Germany
2 -
Sternberg Astronomical Institute, 13 Universitetskii pr., 119992 Moscow, Russia
3 -
Dr. Karl Remeis-Sternwarte, Astronomisches Institut der
Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
4 -
Center for Astrophysics and Space Sciences, University of
California at San Diego, La Jolla, CA 92093-0424, USA
Received 4 August 2008 / Accepted 13 November 2008
Abstract
We present evidence for the existence of two ![]() 35 day clocks in the
Her X-1/HZ Her binary system.
35 day clocks in the
Her X-1/HZ Her binary system. ![]() 35 day modulations are observed
1) in the Turn-On cycles with two on- and two off-states
and 2) in the changing shape of the pulse profiles which
re-appears regularly. The two ways of counting the 35 day cycles are generally
in synchronization. This synchronization did apparently break down temporarily
during the long Anomalous Low (AL3), which Her X-1 experienced in
1999/2000, in the sense that there must have been one extra Turn-On cycle.
Our working hypothesis is that there are two clocks in the system,
both with a period of about
35 day modulations are observed
1) in the Turn-On cycles with two on- and two off-states
and 2) in the changing shape of the pulse profiles which
re-appears regularly. The two ways of counting the 35 day cycles are generally
in synchronization. This synchronization did apparently break down temporarily
during the long Anomalous Low (AL3), which Her X-1 experienced in
1999/2000, in the sense that there must have been one extra Turn-On cycle.
Our working hypothesis is that there are two clocks in the system,
both with a period of about ![]() 35 days: precession of the accretion disk (the less
stable ``Turn-On clock'') and free precession of the neutron star (the more stable
``Pulse profile clock''). We suggest that free precession of the
neutron star is the master clock and that the precession of the accretion disk is
basically synchronized to that of the neutron star through a feedback mechanism
in the binary system. However, the Turn-On clock can slip against its master
when the accretion disk has a very low inclination, as is observed to be the case
during AL3. We take the apparent correlation between the histories of the Turn-Ons,
of the Anomalous Lows and of the pulse period evolution, with a 5 yr quasi-periodicity,
as evidence for strong physical interaction and feedback between the major
components in the system. We speculate that the 5 yr (10 yr) period is
due either to a corresponding activity cycle of HZ Her or a natural
ringing period of the physical system of coupled components. The question of whether
free precession really exists in neutron stars is very important for understanding
matter with supra-nuclear density.
35 days: precession of the accretion disk (the less
stable ``Turn-On clock'') and free precession of the neutron star (the more stable
``Pulse profile clock''). We suggest that free precession of the
neutron star is the master clock and that the precession of the accretion disk is
basically synchronized to that of the neutron star through a feedback mechanism
in the binary system. However, the Turn-On clock can slip against its master
when the accretion disk has a very low inclination, as is observed to be the case
during AL3. We take the apparent correlation between the histories of the Turn-Ons,
of the Anomalous Lows and of the pulse period evolution, with a 5 yr quasi-periodicity,
as evidence for strong physical interaction and feedback between the major
components in the system. We speculate that the 5 yr (10 yr) period is
due either to a corresponding activity cycle of HZ Her or a natural
ringing period of the physical system of coupled components. The question of whether
free precession really exists in neutron stars is very important for understanding
matter with supra-nuclear density.
Key words: stars: binaries: general - accretion, accretion disks - stars: neutron - X-rays: general - X-rays: binaries - X-rays: individuals: Her X-1
1 Introduction
The binary X-ray pulsar Her X-1 shows a number of periodic modulations of its
X-ray flux: the 1.24 s pulse period, the 1.70 d orbital period (through eclipses and
the Doppler modulation of the pulse period), a 1.62 d dip period, and a 35 d
super-orbital period. The last period is observed first through an on-off cycle with a
10 d Main-On and a 5 d Short-On, separated by two 10 d
Off-states (Tananbaum et al. 1972), and second through a reproduced change
in the shape of the 1.24 s pulse profile (Trümper et al. 1986; Deeter et al. 1998; Scott et al. 2000). With
respect to these modulations, we argue that there are two ![]() 35 d clocks in the
system that are generally synchronized, but that were observed to temporarily
lose synchronization during the long Anomalous Low in 1999/2000.
Anomalous Lows seem to appear quasi-periodically about every 5 yrs
(Staubert et al. 2006) and are believed to be connected with episodes of a low
tilt of the accretion disk, which is then blocking the line of sight to the X-ray source.
35 d clocks in the
system that are generally synchronized, but that were observed to temporarily
lose synchronization during the long Anomalous Low in 1999/2000.
Anomalous Lows seem to appear quasi-periodically about every 5 yrs
(Staubert et al. 2006) and are believed to be connected with episodes of a low
tilt of the accretion disk, which is then blocking the line of sight to the X-ray source.
The 35 day modulation of the X-ray flux is generally explained by the precession of the accretion disk, which regularly blocks the line of sight to the X-ray emitting regions near the magnetic poles of the neutron star (Gerend & Boynton 1976; Schandl et al. 1994). With regard to the systematic variation in the shape of the X-ray pulse profiles, we follow Trümper et al. (1986), Shakura et al. (1998), and Ketsaris et al. (2000) in assuming that the responsible physical mechanism is free precession of the neutron star.
Free precession may appear as a fundamental physical property of rigid non-spherical spinning bodies. The simplest case is a spheroid with some small oblateness (a ``two-axial'' body) in which the axis of angular velocity is not aligned with any principle axis of inertia (e.g., Klein & Sommerfeld 1910). It has been suggested as the underlying reason for the long-period variations, both in timing and spectral properties, observed in several neutron stars (Jones & Anderson 2001; Cutler et al. 2002; Link & Epstein 2001; Haberl et al. 2006). The candidate objects are mostly radio pulsars (including the Crab and Vela pulsars), the isolated X-ray pulsar RX J0720.4-3125(Haberl et al. 2006) and the accreting binary X-ray pulsar Her X-1. The existence of free precession in neutron stars and its consequences for our understanding of the physics of the interior of neutron stars is extensively discussed in the literature (Anderson & Itoh 1975; Shaham 1977; Alpar & Ögelman 1987; Sedrakian et al. 1999; Wasserman 2003; Levin & D'Angelo 2004; Link 2007). Recently, Link (2007) has emphasized that the question of the reality of free precession in neutron stars has strong implications for our understanding of the properties of matter at supra-nuclear densities.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig1.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg3.gif) |
Figure 1: Pulse profiles of Her X-1 as observed by RXTE/PCA (3-20 keV) during the Main-On of November 2002 (35 d cycle No. 3231, according to the pulse profile counting) as a function of 35 d phase. For better visibility the profiles are scaled to a common amplitude and shifted against each other according to their 35 d phase. The profiles were generated using 128 phase bins and the curves are the straight line connection between adjacent data points (which are not shown). |
| Open with DEXTER | |
In Her X-1 the case for free precession is as longstanding (Brecher 1972; Trümper et al. 1986; Shakura et al. 1998) as it is criticized on various grounds (e.g., Bisnovatyi-Kogan et al. 1989). Here we provide new observational clues of a very stable clock that governs the regularly re-appearing pulse profiles. We identify the stable clock with free precession of the neutron star and suggest that the accretion disk with its rather unstable Turn-On clock is a slave to the neutron star on long time scales through a closed loop physical feedback in the binary system.
2 Pulse profile cycle counting
The shape of the pulse profiles of the 1.24 s X-ray pulsations is known to vary in several different ways, e.g., as a function of energy (Gruber et al. 1980) and as a function of 35 d phase (Trümper et al. 1986; Soong et al. 1990; Deeter et al. 1998; Scott et al. 2000). Here, we are concerned with the latter, the systematic variation with 35 d phase. In Fig. 1 we show the result of our analysis for the Main-On state of 2002 November observed by RXTE. Our working hypothesis is that this modulation is due to a precessing neutron star, which forces our viewing angle towards the X-ray emitting polar cap region of the neutron star to vary with the phase of the neutron star precession.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{0743fig2.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg4.gif) |
Figure 2:
Comparison of pulse profiles observed in a number of 35 day
cycles at different 35 day phases to a template profile of cycle No. 257 at
phase 0.12. The match to the template profile is measured by the respective
|
| Open with DEXTER | |
Using observations by RXTE from 1996 until 2005, we verified
that the shape of the pulse profiles is reproduced every ![]() 35 days.
A careful timing analysis was performed of all archived RXTE
data on Her X-1
and pulse profiles were generated by folding with the measured pulse periods.
Figure 1 shows a set
of pulse profiles (PCA, 3-20 keV) from 35 d cycle No. 323
35 days.
A careful timing analysis was performed of all archived RXTE
data on Her X-1
and pulse profiles were generated by folding with the measured pulse periods.
Figure 1 shows a set
of pulse profiles (PCA, 3-20 keV) from 35 d cycle No. 323![]() (Nov. 2002) for eight different 35 d phases. The variation of the pulse shape
is evident. Using a profile from cycle No. 257 at 35 d phase 0.12 as a
template (quite similar to the phase 0.12 profile of cycle No. 323, highlighted in
Fig. 2), we performed a comparison to profiles from other
cycles. For this purpose all profiles were normalized using the amplitude of the
main peak. Then the profiles were aligned in pulse phase. Within one 35 d
main-on this is assured by phase connection, the alignment of profiles from
different 35 d cycles was done using the ``sharp edge'' at the decay of the
shoulder to the right of the main peak, which was found to be the sharpest
and most stable feature of the Her X-1 pulse profile.
Then the difference between the count rates in the 128 phase bins were taken,
squared, and summed. This
(Nov. 2002) for eight different 35 d phases. The variation of the pulse shape
is evident. Using a profile from cycle No. 257 at 35 d phase 0.12 as a
template (quite similar to the phase 0.12 profile of cycle No. 323, highlighted in
Fig. 2), we performed a comparison to profiles from other
cycles. For this purpose all profiles were normalized using the amplitude of the
main peak. Then the profiles were aligned in pulse phase. Within one 35 d
main-on this is assured by phase connection, the alignment of profiles from
different 35 d cycles was done using the ``sharp edge'' at the decay of the
shoulder to the right of the main peak, which was found to be the sharpest
and most stable feature of the Her X-1 pulse profile.
Then the difference between the count rates in the 128 phase bins were taken,
squared, and summed. This ![]() -sum is taken as a quantitative measure
for the ``matching'' of the individual profiles to the template.
There are profiles from 16 different 35 d cycles taken by RXTE over 8.8 years.
However, only in 7 cycles are pulse profiles for 4 or more different 35 d phases available.
In Fig. 2 the
-sum is taken as a quantitative measure
for the ``matching'' of the individual profiles to the template.
There are profiles from 16 different 35 d cycles taken by RXTE over 8.8 years.
However, only in 7 cycles are pulse profiles for 4 or more different 35 d phases available.
In Fig. 2 the ![]() -values are plotted for those 5 cycles for which
profiles at 7 or more different phases are available.
Each data point corresponds to a pulse profile generated from data of one
complete day of RXTE observations. The center time of the observing
interval is translated into a 35 d phase (using a constant period of 34.85 days).
The minimum in
-values are plotted for those 5 cycles for which
profiles at 7 or more different phases are available.
Each data point corresponds to a pulse profile generated from data of one
complete day of RXTE observations. The center time of the observing
interval is translated into a 35 d phase (using a constant period of 34.85 days).
The minimum in ![]() for the different cycles is generally found
around 35 d phase 0.12
(the phase of the template), demonstrating that the profiles are repeating
regularly. The
for the different cycles is generally found
around 35 d phase 0.12
(the phase of the template), demonstrating that the profiles are repeating
regularly. The ![]() comparison was repeated with three other templates
(from different 35 d cycles and different phases), yielding the same result.
This establishes a method of cycle counting that is based solely on the
shape of the pulse profile.
comparison was repeated with three other templates
(from different 35 d cycles and different phases), yielding the same result.
This establishes a method of cycle counting that is based solely on the
shape of the pulse profile.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig3.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg5.gif) |
Figure 3: Pulse period and Turn-On histories of Her X-1 (an update of Fig. 1 of Staubert et al. 2006). |
| Open with DEXTER | |
3 Turn-On cycle counting
The second method of cycle counting uses the well-established
35 d modulation of the X-ray flux (Giacconi et al. 1973): the X-ray flux
increases sharply at Turn-On, reaching a maximum of the
Main-On which lasts for a few days, before fading slowly into the first
minimum. After that, a second, substantially lower maximum, the
Short-On, emerges for a few days, after which a second minimum
concludes the cycle (see Klochkov et al. 2006). It is generally assumed that
the modulation is due to shading by the precessing accretion disk
(Gerend & Boynton 1976). There is a Turn-On roughly every 35 days. However,
this clock is not very accurate: the length of a particular cycle may be longer
or shorter than the previous one by ![]() 0.85 days (=
0.85 days (=
![]() ).
).
The irregularity of the Turn-On clock is demonstrated by the (O-C)
diagram (Fig. 3, lower panel). Here the difference between the
observed turn-on time (O) and the calculated turn-on time (C) is
plotted against time (Staubert et al. 1983; Staubert et al. 2000; Still & Boyd 2004; Staubert et al. 2006).
To calculate the turn-on time, a constant period of 34.85 d was
used (equal to
![]() ,
with
,
with
![]() d).
Figure 3 is our latest update of this diagram. If (O-C) is measured
in units of
d).
Figure 3 is our latest update of this diagram. If (O-C) is measured
in units of
![]() ,
all data points fall more or less on horizontal lines
(spaced by
,
all data points fall more or less on horizontal lines
(spaced by
![]() ), due to the observed fact that the
Turn-Ons occur close
to binary phases 0.25 or 0.75. Staubert et al. (1983) (at a time when only data just
beyond the first Anomalous Low - AL1 - were available) had postulated that
the change in (O-C) from one cycle to the next should be either 0 or +1 or -1 in
units of
), due to the observed fact that the
Turn-Ons occur close
to binary phases 0.25 or 0.75. Staubert et al. (1983) (at a time when only data just
beyond the first Anomalous Low - AL1 - were available) had postulated that
the change in (O-C) from one cycle to the next should be either 0 or +1 or -1 in
units of
![]() /2 (corresponding to a cycle length of 20.5 or 21 or 20 binary
periods). Even though the short-term development was successfully modeled by
a random-walk process, they argued for the possibility that the global long-term
development of the diagram might be nearly flat, indicating some sort of a
``back-driving force'' that would prevent the wandering off to one or the other
side. These assumptions have been found to hold until the
dramatic event of the Anomalous Low of 1999/2000 (AL3).
/2 (corresponding to a cycle length of 20.5 or 21 or 20 binary
periods). Even though the short-term development was successfully modeled by
a random-walk process, they argued for the possibility that the global long-term
development of the diagram might be nearly flat, indicating some sort of a
``back-driving force'' that would prevent the wandering off to one or the other
side. These assumptions have been found to hold until the
dramatic event of the Anomalous Low of 1999/2000 (AL3).
Figure 3 demonstrates that the Turn-On clock is quite noisy, with additional quasi-periodic variations on a 5 year time scale. (O-C) correlates with the appearance of the Anomalous Lows (AL), and it also strongly correlates with the neutron star's spin period (Staubert et al. 2006, 2008b).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg11.gif) |
Figure 4: The Anomalous Low AL3 must be bridged by 18 (not 17) Turn-On cycles: from cycle No. 284 to cycle No. 302. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg12.gif) |
Figure 5:
Cycle counting by pulse-profile fitting. Upper panel: absolute times
of |
| Open with DEXTER | |
4 Difference between pulse profile counting and Turn-On counting
The two ways of cycle counting are normally consistent with one another. However, during the long Anomalous Low in 1999/2000 (AL3 in Fig. 3) the synchronization was apparently lost.
In Fig. 5 we plot the absolute times of the ![]() -minima
(see Figs. 1 and 2) found when the pulse profiles
observed in the respective Main-Ons were compared to the template profile
of cycle No. 257, against the cycle number (from pulse profile counting). The last
Main-On before AL3 in which good pulse profiles were obtained belongs to
cycle No. 269, and the first Main-On after AL3 is cycle No. 303.
The straight line in Fig. 5 (upper panel) is the connection
between the data points of cycle No. 269 and cycle No. 303. Dividing the difference
in the corresponding absolute times for the
-minima
(see Figs. 1 and 2) found when the pulse profiles
observed in the respective Main-Ons were compared to the template profile
of cycle No. 257, against the cycle number (from pulse profile counting). The last
Main-On before AL3 in which good pulse profiles were obtained belongs to
cycle No. 269, and the first Main-On after AL3 is cycle No. 303.
The straight line in Fig. 5 (upper panel) is the connection
between the data points of cycle No. 269 and cycle No. 303. Dividing the difference
in the corresponding absolute times for the ![]() -minima by 34 (=303-269)
leads to a cycle length of
-minima by 34 (=303-269)
leads to a cycle length of
![]() d. The lower panel in
Fig. 5 shows the residuals of the data points to the straight
line: the center curve is for the proposed cycle counting (269/303). Any different
counting to bridge the gap (e.g., 269/302 or 269/304) can be ruled out,
Fig. 5 establishes that the reference pulse shape (our
template at 35 d phase 0.12) does regularly repeat and that the corresponding
observing times can be associated with unique cycle numbers.
A linear fit to the data point in the upper panel of Fig. 5
yields a mean period of
d. The lower panel in
Fig. 5 shows the residuals of the data points to the straight
line: the center curve is for the proposed cycle counting (269/303). Any different
counting to bridge the gap (e.g., 269/302 or 269/304) can be ruled out,
Fig. 5 establishes that the reference pulse shape (our
template at 35 d phase 0.12) does regularly repeat and that the corresponding
observing times can be associated with unique cycle numbers.
A linear fit to the data point in the upper panel of Fig. 5
yields a mean period of
![]() d (=
d (=
![]() )
from pulse profile counting. (Repeating the exercise with three other template
profiles yields the same result within uncertainties.)
)
from pulse profile counting. (Repeating the exercise with three other template
profiles yields the same result within uncertainties.)
Figure 4 shows the (O-C) diagram around AL3. Turn-Ons
are not observed during the AL, since the source is strongly obscured
for a total of 602 days. Assuming that the physics behind this counting, that is
the precession of the accretion disk, is continuing during the AL, one can
estimate the number of cycles during AL3. There are two possible solutions:
17 cycles with a mean period
![]() or 18 cycles with
a mean period of
or 18 cycles with
a mean period of
![]() .
We conclude that there
must have been 18 cycles, not 17, because of the following arguments.
.
We conclude that there
must have been 18 cycles, not 17, because of the following arguments.
- 1.
- Before AL3 the mean period was low
(
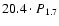 ), as it is always the case when going into an AL
(Coburn et al. 2002). Coming out of AL3, the mean period of the next 6 cycles is
even lower (
), as it is always the case when going into an AL
(Coburn et al. 2002). Coming out of AL3, the mean period of the next 6 cycles is
even lower (
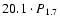 ). It is unreasonable to assume
that the period was longer in between.
). It is unreasonable to assume
that the period was longer in between.
- 2.
- The strong long-term anti-correlation between (O-C) and the neutron star's spin and the observed dramatic spin-down during AL3 requires that (O-C) needs to drop during AL3 (Staubert et al. 2006), equivalent to a short period.
- 3.
- It is believed that the Anomalous Low is caused by the blocking of the line of sight to the X-ray emitting region by the accretion disk due to a decreased tilt of the disk with respect to the orbital plane.
We conclude that during AL3 the accretion disk did one extra cycle in comparison to the regular cycle counting using the pulse profiles.
5 Summary of observational facts
Before entering the discussion, we summarize the observational facts relevant to our conclusion about the reality of free precession of the neutron star in Her X-1.
- 1.
- The pulse profile shape varies with 35 d phase and repeats regularly.
The observations by RXTE over
 9 yrs establish a stable
clock with a period of
9 yrs establish a stable
clock with a period of
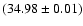 d.
d.
- 2.
- The Turn-On clock is rather unstable: it shows a quasi-periodic
variation in (O-C) with a
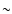 5 yr period and an amplitude of
5 yr period and an amplitude of
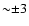
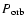 ,
with ``substructure'' and additional noise, and
a large step in (O-C) during the 1999/2000 Anomalous Low
(AL3), in correlation with a dramatic spin-down (Fig. 3).
,
with ``substructure'' and additional noise, and
a large step in (O-C) during the 1999/2000 Anomalous Low
(AL3), in correlation with a dramatic spin-down (Fig. 3).
- 3.
- Anomalous Lows (ALs) appear quasi-periodically every
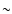 5 yrs, in correlation with minima in (O-C).
5 yrs, in correlation with minima in (O-C).
- 4.
- The Turn-On history (O-C) is strongly correlated to the
pulse period evolution (Fig. 3, and Staubert et al. 2006).
- 5.
- The counting of 35 d cycles by Turn-Ons, the (O-C) diagram,
is generally synchronized (with deviations of up to
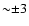
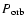 )
to the counting of 35 d cycles using pulse profiles.
)
to the counting of 35 d cycles using pulse profiles.
- 6.
- During the long AL of 1999/2000 (AL3), the Turn-On period was so low such that one extra cycle was done compared to the pulse profile counting.
6 Discussion and conclusions
We conclude that there are two clocks in Her X-1, both with a period of about 35 d: precession of the accretion disk and free precession of the neutron star. The precessing outer rim of the accretion disk regularly blocks the line of sight to the X-ray emitting polar caps of the neutron star, thereby producing the Turn-On cycle. The free precession of the neutron star is responsible for the orientation of the beamed X-ray emission, thereby producing the periodic modulation of the shape of the observed pulse profiles.
The two clocks are so similar in period because of synchronization due to strong feedback in the system. (It would seem unreasonable to assume that the two clocks have nearly the same frequency purely by chance.) We propose that free precession of the neutron star is the master clock which is rather stable. (It could however change rapidly due to a change in the shape of the neutron star, e.g., as a result of a star quake.) The accretion disk precession is observed to be a noisy clock with some systematic variations. There are quite a number of torques acting on the accretion disk: the tidal force from the optical star, the internal viscous force, dynamical forces due to the impact of the accretion stream and the illumination by the X-ray beam, and, finally, the neutron star magnetosphere interacting with the inner edge of the disk. These forces collectively produce the precession (as well as the tilt and the warp) of the disk (Shakura et al. 1998; Klochkov et al. 2006). We consider the tidal force and the dynamical forces to be the dominating ones. In the absence of dynamical forces, the precession would be much faster, with a period around 15 d (Shakura et al. 1999).
So the question is: how does the neutron star with its inherent period of free precession of 35 d manage to ``enslave'' the accretion disk? We believe that the critical parameter for the closed loop feedback in the system is the rate of mass transfer from the optical star. The surface of HZ Her facing the neutron star is illuminated and heated by the neutron star's X-ray emission, enhancing the mass transfer. However, the heating is not constant and uniform because the accretion disk blocks part of the X-ray beam and modulates (spatially and temporally) the heating of the optical star's surface according to its precessional motion. A first loop may be the following. The inner part of the accretion disk follows the free precession of the neutron star (because of the magnetospheric interaction), and the shadowing of the optical star from the X-ray beam follows the movement of the inner disk, modulating the mass transfer rate with the period of the neutron star free precession. The accretion stream hits the accretion disk applying a force to slow down the disk's precession and to influence its tilt, as shown by numerical simulations (Shakura et al. 1999; Klochkov et al. 2006). A variable tilt of the outer disk results again in a variable shading of the optical star. Finally, the variable mass transfer rate will eventually (after a viscous time scale) show up in a variable mass accretion rate that governs the X-ray luminosity. The X-ray luminosity, on the other hand, is crucial for the heating of the optical star as well as for the illumination of the outer parts of the accretion disk where coronal winds and torques may be produced (Schandl et al. 1994). With the variable heating of the optical star by the X-ray beam, both through variable shading and through variable X-ray flux, the loop is closed.
Also, the strong correlation between the (O-C) diagram and the pulse period evolution (Fig. 3 and Staubert et al. 2006) can be understood within this model. Any enhanced mass accretion rate (because of an enhanced mass transfer rate) will result in an enhanced angular momentum transfer, hence in a spin-up.
We propose that the described physical couplings provide
strong feedback mechanisms in the Her X-1/HZ Her binary system that
establish a delicate equilibrium in the whole system.
We assume that the physical coupling described above is strong enough
to lock the precession of the outer accretion disk to that of the neutron star.
(This may not be possible if the natural frequencies of the precession
of the neutron star and that of the accretion disk were different by much more
than the estimated factor of about 2.) Due to the large number of forces acting on
the accretion disk (probably all of them being subject to noise) one may
understand that the synchronization between the two clocks is not perfect:
First, there is the modulation of the Turn-On times. We know now that
a random walk is not the right model for this modulation. There seems to be just
random noise superimposed onto the quasi-periodic up and down in (O-C).
Over long times the deviations are limited to
![]()
![]() .
In our
current model we would now interpret the ``back-driving force'' postulated by
Staubert et al. (1983) as being due to the coupling of the accretion disk to
the neutron star. Second, the dramatic event observed during AL3, in which
the accretion disk showed a low tilt and a fast precession, could then
be viewed as extreme behavior, demonstrating that the accretion
disk has a ``life of its own'', and it is able to temporarily escape the slaving
by the neutron star. It seems, however, that the equilibrium is
re-established rather quickly. In quoting a 35 d
cycle no. for the time after AL3, one has to clearly state what method of cycle
counting it refers to: pulse profile counting or Turn-On counting,
the latter is advanced by one cycle.
.
In our
current model we would now interpret the ``back-driving force'' postulated by
Staubert et al. (1983) as being due to the coupling of the accretion disk to
the neutron star. Second, the dramatic event observed during AL3, in which
the accretion disk showed a low tilt and a fast precession, could then
be viewed as extreme behavior, demonstrating that the accretion
disk has a ``life of its own'', and it is able to temporarily escape the slaving
by the neutron star. It seems, however, that the equilibrium is
re-established rather quickly. In quoting a 35 d
cycle no. for the time after AL3, one has to clearly state what method of cycle
counting it refers to: pulse profile counting or Turn-On counting,
the latter is advanced by one cycle.
We would also like to draw attention to the fact that the (O-C) diagram
(Figs. 3 and 4) has - averaged over time
scales >15 yrs - a positive slope from the time of discovery of the
source until today, if pulse profile counting is used.
In this case the diagram continues after AL3 with the upper right hand
curve in Fig. 4, corresponding to the solution with 17
neutron star cycles inside AL3. A linear fit to all data of the (O-C)
diagram in pulse profile counting yields a mean cycle duration of
(
![]() ) d, which we associate with the long-term average
period of the neutron star precession. Using only data after AL2, we find
an average period of (
) d, which we associate with the long-term average
period of the neutron star precession. Using only data after AL2, we find
an average period of (
![]() ) d, quite close to the period
of (
) d, quite close to the period
of (
![]() ) d, found from pulse-profile fitting (over a similar
observational period). The quoted uncertainties, however, are only statistical
uncertainties; for the true physical uncertainties, one would have to
add systematic uncertainties due to the irregular modulation over the
limited time base and the non-uniform sampling of (O-C). We thus
refrain from speculating about variation in the period over time.
We take the above finding as independent support for the already reached
conclusion that the precession of the accretion disk follows that of the
neutron star on long time scales. We predict that the mean upward trend
in (O-C) will continue in the future.
) d, found from pulse-profile fitting (over a similar
observational period). The quoted uncertainties, however, are only statistical
uncertainties; for the true physical uncertainties, one would have to
add systematic uncertainties due to the irregular modulation over the
limited time base and the non-uniform sampling of (O-C). We thus
refrain from speculating about variation in the period over time.
We take the above finding as independent support for the already reached
conclusion that the precession of the accretion disk follows that of the
neutron star on long time scales. We predict that the mean upward trend
in (O-C) will continue in the future.
The key feature of our model is that free precession of the neutron star is responsible for the observed long-term stability of the 35 d cycle (both, the regular re-appearance of pulse profiles as well as the long-term turn-on history). Unlike in isolated neutron stars, where free precession is damped by dissipative processes, the free precession of the old neutron star in Her X-1 can be sustained for long times by the accretion feedback loop described above, which may lead to quite different properties. We also note that Lamb et al. (1975) have already concluded that phase dependent torques are capable of exciting (or damping) large amplitude neutron star wobble.
With regard to the apparent quasi-periodic 5 yr (10 yr) modulation in
(O-C), seen in correlation with the pulse period evolution and the
appearance of the Anomalows Lows, we have no definite answer.
We see two possibilities (Staubert et al. 2006): either the
modulation is due to an ``activity cycle'' of HZ Her changing the mass
transfer rate (see also Still & Jurua 2006), or the ![]() 5 yr
may represent a natural ringing frequency of a system of several coupled
physical components.
5 yr
may represent a natural ringing frequency of a system of several coupled
physical components.
We would like to address a final question: are shifts in pulse arrival time
observed, which are expected to occur for a precessing pulsar?
A decomposition analysis of high-quality pulse profiles observed
with RXTE using eight Gaussian components shows that the main
peak (as well as other peaks) is (are) systematically varying in amplitude and in
relative phase (e.g., with respect to the well-defined minimum). A quantitative
description is in preparation. In addition, we are making progress in
modeling the changing shape of the pulse profiles. First results, assuming a
spot-like emission region at each of the two magnetic poles and additional arc-like
emission structures around the poles, were published by Wilms et al. (2003)
and again reported by Postnov (2004). In the case of a freely precessing
neutron star radiating like a pulsar, systematic variations in the observed
period and pulse phase with 35 d phase are expected
(Ruderman 1970; Shakura 1988; Postnov et al. 1991; Bisnovatyi-Kogan & Kahabka 1993),
with a maximum relative change in period
on the order 10-6. Any change in pulse period will result in a shift in the
pulse arrival time. Unfortunately, such shifts are observationally
indistinguishable from shifts resulting from period variations
due to accretion torque changes. The pulse period history shown in
Fig. 3 (upper panel) shows strong and frequent period variations on
time scales ranging from 18 d to beyond 1000 d. The strongest variations reach
dP/dt-values of nearly
![]() s s-1 (observed on the smallest
time scales), corresponding to a relative change of 10-6 over a few days.
In addition, detailed pulse arrival time analysis of RXTE data has shown
that similar changes (of both signs) are found on time scales of a few days
(see also Klochkov et al. 2008).
Our six measured values do not show any correlation with
35 d phase. We attribute these to changes in mass accretion rate.
s s-1 (observed on the smallest
time scales), corresponding to a relative change of 10-6 over a few days.
In addition, detailed pulse arrival time analysis of RXTE data has shown
that similar changes (of both signs) are found on time scales of a few days
(see also Klochkov et al. 2008).
Our six measured values do not show any correlation with
35 d phase. We attribute these to changes in mass accretion rate.
In summary, we conclude that our analysis does support the idea of free precession to be present in the neutron star of Her X-1. Our main line of arguments rest on the identification of two different 35 d clocks in this system: free precession of the neutron star (as the master clock) and precession of the accretion disk (which is quasi-synchronized to the neutron star for most of the time). Long-term shifts in pulse arrival time, as seen in radio pulsars, are principally non-observable because of the always present accretion torque noise and resulting pulse-frequency variations. However, the observed systematic relative shifts of structures in the pulse profile with corresponding changes in pulse width and amplitude as a function of precessional phase are reminiscent of precessing radio pulsars. Link (2007) has concluded that the standard picture of an outer core of a neutron star consisting of coexisting superfluid neutrons and type II superconducting protons is inconsistent with the existence of long-period precession. Free precession then means that the neutron vortices at the inner crust must not be pinned, in agreement with similar conclusions reached by Shaham (1977) and Jones & Anderson (2001).
Acknowledgements
We acknowledge the support through DFG grant St 173/31 and the corresponding RFBR grant 06-02-16025, as well as significant contributions to the data analysis by L. Rodina. We thank the anonymous referee for pointing to the question of shifts in pulse arrival time. We are thankful to J. Trümper for suggesting that we emphasize the general importance of free precession to the physics of the neutron star interior.
References
- Alpar, A., & Ögelman, H. 1987, A&A, 185, 196 [NASA ADS] (In the text)
- Anderson, P. W., & Itoh, N. 1975, Nature, 256, 25 [CrossRef] (In the text)
- Brecher, K. 1972, Nature, 239, 325 [NASA ADS] [CrossRef] (In the text)
- Bisnovatyi-Kogan, G. S., & Kahabka, P. 1993, A&A, 267, L43 [NASA ADS] (In the text)
- Bisnovatyi-Kogan, G. S., Mersov, G. A., & Scheffer, E. K. 1989, A&A, 221, L7 [NASA ADS] (In the text)
- Coburn, W., Heindl, W. A., Rothschild, R. E., et al. 2002, ApJ, 580, 394 [NASA ADS] [CrossRef] (In the text)
- Cutler, C., Ushomirsky, G., & Link, B. 2003, ApJ, 588, 975 [NASA ADS] [CrossRef] (In the text)
- Deeter, J. E., Scott, D. M., Boynton, P. E., et al. 1998, ApJ, 502, 802 [NASA ADS] [CrossRef] (In the text)
- Gerend, D., & Boynton, P. E. 1976, ApJ, 209, 562 [NASA ADS] [CrossRef] (In the text)
- Giacconi, R., Gursky, H., Kellog, E., et al. 1973, ApJ, 184, 227 [NASA ADS] [CrossRef] (In the text)
- Gruber, D. E., Matteson, J. L., Nolan, P. L., et al. 1980, ApJ, 240, L127 [NASA ADS] [CrossRef] (In the text)
- Haberl, F., Turolla, R., de Vries, C. P., et al. 2006, A&A, 451, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jones, D. I., & Anderson, N. 2001, MNRAS, 324, 811 [NASA ADS] [CrossRef] (In the text)
- Ketsaris, N. A., Kuster, M., Postnov, K. A., et al. 2000, in Proc. Hot points in Astrophysics, Joint Inst. for Nucl. Res., Dubna, 192
- Klein, F., & Sommerfeld, A. 1910, Theorie des Kreisels (Leibzig: Teubner) (In the text)
- Klochkov, D., Shakura, N., Postnov, K., et al. 2006, Astron. Lett., 32, 804 [NASA ADS] [CrossRef] (In the text)
- Klochkov, D., Staubert, R., Postnov, K., et al. 2008, A&A, 482, 907 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lamb, D. Q., Lamb, F. K., Pines, D., & Shaham, J. 1975, ApJ, 198, L21 [CrossRef]
- Levin, Y., & D'Angelo 2004, ApJ, 613, 1157 [NASA ADS] [CrossRef] (In the text)
- Link, B. 2007, Ap&SS, 308, 435 [NASA ADS] [CrossRef] (In the text)
- Link, B., & Epstein, R. I. 2001, ApJ, 556, 392 [NASA ADS] [CrossRef] (In the text)
- Postnov, K. A., Prokhorov, M. E., & Shakura, N. I. 1991, in NAS-NRC, High Energy Astrophysics, American and Soviet Perspectives, 307 (In the text)
- Postnov, K. 2004, Topics in X-ray Astronomy (Tübingen), see http:astro.uni-tuebingen.de/staubert65/talks/postnov.pdf
- Ruderman, M. A. 1970, Nature, 225, 838 [NASA ADS] [CrossRef] (In the text)
- Schandl, S., & Meyer, F. 1994, A&A, 289, 149 [NASA ADS] (In the text)
- Scott, D. M., Leahy, D. A., & Wilson, R. B. 2003, ApJ, 539, 392 [NASA ADS] (In the text)
- Sedrakian, A., Wasserman, I., & Cordes, J. M., ApJ, 524, 341 (In the text)
- Shaham, J. 1977, ApJ, 214, 251 [NASA ADS] [CrossRef] (In the text)
- Shakura, N. I. 1988, in Physics of Neutron Stars, Liningrad, 34 (in Russian), and in Physics of Neutron Stars, ed. A. M. Kaminker (Commack, N.Y.: Nova Science Publisher), 1995, 55 (English translation) (In the text)
- Shakura, N. I., Postnov, K., & Prokhorov, M. 1998, A&A, 331, L37 [NASA ADS] (In the text)
- Shakura, N. I., Prokhorov, M. E., Postnov, K. A., & Ketsaris, N. A. 1999, A&A, 348, 917 (In the text)
- Soong, Y., Gruber, D. E., Peterson, L. E., & Rothschild, R. E. 1990, ApJ, 348, 634 [NASA ADS] [CrossRef] (In the text)
- Staubert, R., Bezler, M., & Kendziorra, E. 1983, A&A, 117, 215 [NASA ADS] (In the text)
- Staubert, R., Schandl, S., & Wilms, J. 2000, in Proc. 4th COMPTON Symp., AIP Conf. Proc., 510, 153 (In the text)
- Staubert, R., Schandl, S., Klochkov, D., et al. 2006, in Proc. The transparent Milky Way: a perspective for MIRAX, AIP Conf. Proc., 840, 65 (In the text)
- Still, M., & Boyd, P. 2004, ApJ, 606, L135 [NASA ADS] [CrossRef] (In the text)
- Still, M., & Jurua, E. 2006, BAAS, 38, 339 [NASA ADS] (In the text)
- Trümper, J., Kahabka, P., Ögelmann, H., Pietsch, W., & Voges, W. 1986, ApJ, 300, L63 [NASA ADS] [CrossRef] (In the text)
- Tananbaum, H., Gursky, H., Kellog, E. M., et al. 1972, ApJ, 174, L143 [NASA ADS] [CrossRef] (In the text)
- Wasserman, I. 2003, MNRAS, 341, 1020 [NASA ADS] [CrossRef] (In the text)
- Wilms, J., Ketsaris, N. A., Postnov, K. A., et al. 2003, Isvestiya Akademii Nauk, Ser. Fizicheskaya, 67, 310 (in Russian)
Footnotes
- ... No. 323
![[*]](/icons/foot_motif.gif)
- The counting of 35 d cycles follows the convention used by Staubert et al. (1983): (O-C) = 0 for cycle No. 31 with turn-on near JD 2 442 410.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig1.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg3.gif) |
Figure 1: Pulse profiles of Her X-1 as observed by RXTE/PCA (3-20 keV) during the Main-On of November 2002 (35 d cycle No. 3231, according to the pulse profile counting) as a function of 35 d phase. For better visibility the profiles are scaled to a common amplitude and shifted against each other according to their 35 d phase. The profiles were generated using 128 phase bins and the curves are the straight line connection between adjacent data points (which are not shown). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm]{0743fig2.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg4.gif) |
Figure 2:
Comparison of pulse profiles observed in a number of 35 day
cycles at different 35 day phases to a template profile of cycle No. 257 at
phase 0.12. The match to the template profile is measured by the respective
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig3.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg5.gif) |
Figure 3: Pulse period and Turn-On histories of Her X-1 (an update of Fig. 1 of Staubert et al. 2006). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg11.gif) |
Figure 4: The Anomalous Low AL3 must be bridged by 18 (not 17) Turn-On cycles: from cycle No. 284 to cycle No. 302. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0743fig5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10743-08/Timg12.gif) |
Figure 5:
Cycle counting by pulse-profile fitting. Upper panel: absolute times
of |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


