| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 933 - 948 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361:200810725 | |
| Published online | 22 December 2008 | |
An HST/WFPC2 survey of bright young clusters in M31
I. VdB0, a massive star cluster seen at
t  25 Myr
25 Myr![[*]](/icons/foot_motif.gif)
S. Perina1,2 - P. Barmby3 - M. A. Beasley4,5 -
M. Bellazzini1 - J. P. Brodie4 - D. Burstein6 -
J. G. Cohen7 - L. Federici1 - F. Fusi Pecci1 - S. Galleti1 - P. W. Hodge8 - J. P. Huchra9 -
M. Kissler-Patig10 - T. H. Puzia11,![]() - J. Strader9,
- J. Strader9,![]()
1 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
2 -
Università di Bologna, Dipartimento di Astronomia, via Ranzani 1, 40127 Bologna, Italy
3 -
Department of Physics and Astronomy, University of Western Ontario, London, ON, N6A 3K7, Canada
4 -
UCO/Lick Observatory, University of California, Santa Cruz, CA 95064, USA
5 -
Instituto de Astrofísica de Canarias, La Laguna 38200, Canary Islands, Spain
6 -
Department of Physics and Astronomy, Arizona State University, Tempe, AZ, USA
7 -
Palomar Observatory, Mail Stop 105-24, California Institute of Technology, Pasadena, CA 91125, USA
8 -
Department of Astronomy, University of Washington, Seattle, WA 98195, USA
9 -
Harvard-Smithsonian Center for Astrophysics, Cambridge, MA, USA
10 -
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
11 -
Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
Received 31 July 2008 / Accepted 28 November 2008
Abstract
Aims. We introduce our imaging survey of possible young massive globular clusters in M31 performed with the Wide Field and Planetary Camera 2 (WFPC2) on the Hubble Space Telescope (HST). We obtained shallow (to ![]() )
photometry of individual stars in 20 candidate clusters. We present here details of the data reduction pipeline that is being applied to all the survey data and describe its application to the brightest among our targets, van den Bergh 0 (VdB0), taken as a test case.
)
photometry of individual stars in 20 candidate clusters. We present here details of the data reduction pipeline that is being applied to all the survey data and describe its application to the brightest among our targets, van den Bergh 0 (VdB0), taken as a test case.
Methods. Point spread function fitting photometry of individual stars was obtained for all the WFPC2 images of VdB0 and the completeness of the final samples was estimated using an extensive set of artificial stars experiments. The reddening, the age and the metallicity of the cluster were estimated by comparing the observed color magnitude diagram (CMD) with theoretical isochrones. Structural parameters were obtained from model-fitting to the intensity profiles measured within circular apertures on the WFPC2 images.
Results. Under the most conservative assumptions, the stellar mass of VdB0 is M> 2.4 ![]()
![]() ,
but our best estimates lie in the range
,
but our best estimates lie in the range ![]() 4-9
4-9 ![]()
![]() .
The CMD of VdB0 is best reproduced by models having solar metallicity and age
.
The CMD of VdB0 is best reproduced by models having solar metallicity and age ![]() 25 Myr. Ages less than
25 Myr. Ages less than ![]() 12 Myr and greater than
12 Myr and greater than ![]() 60 Myr are clearly ruled out by the available data. The cluster has a remarkable number of red super giants (
60 Myr are clearly ruled out by the available data. The cluster has a remarkable number of red super giants (![]() 18) and a CMD very similar to Large Magellanic Cloud clusters usually classified as young globulars such as NGC 1850, for example.
18) and a CMD very similar to Large Magellanic Cloud clusters usually classified as young globulars such as NGC 1850, for example.
Conclusions. VdB0 is significantly brighter (![]() 1 mag) than Galactic open clusters of similar age. Its present-day mass and half-light radius (
1 mag) than Galactic open clusters of similar age. Its present-day mass and half-light radius (
![]() pc) are more typical of faint globular clusters than of open clusters. However, given its position within the disk of M31, it is expected to be destroyed by dynamical effects, in particular by encounters with giant molecular clouds, within the next
pc) are more typical of faint globular clusters than of open clusters. However, given its position within the disk of M31, it is expected to be destroyed by dynamical effects, in particular by encounters with giant molecular clouds, within the next ![]() 4 Gyr.
4 Gyr.
Key words: galaxies: star clusters - galaxies: individual: M31 - stars: supergiants - stars: evolution
1 Introduction
Much of the star formation in the Milky Way is thought to have occurred within star clusters (Lada et al. 1991; Carpenter et al. 2000). Therefore, understanding the formation and evolution of star clusters is an important piece of the galaxy formation puzzle. Our understanding of the star cluster systems of spiral galaxies has largely come from studies of the Milky Way. Star clusters in our Galaxy have traditionally been separated into two varieties, open and globular clusters (OCs and GCs hereafter). OCs are conventionally regarded as young (<2 Gyr),
low-mass (<
![]() )
and metal-rich systems that reside in the Galactic disk. In contrast, GCs are characterized as old, massive systems. In the Milky Way, GCs can be broadly separated into two components: a metal-rich disk/bulge subpopulation, and a spatially extended, metal-poor halo subsystem (Kinman 1959; Zinn 1985; see also Brodie & Strader
2006; Harris 2001, for general reviews of GCs).
)
and metal-rich systems that reside in the Galactic disk. In contrast, GCs are characterized as old, massive systems. In the Milky Way, GCs can be broadly separated into two components: a metal-rich disk/bulge subpopulation, and a spatially extended, metal-poor halo subsystem (Kinman 1959; Zinn 1985; see also Brodie & Strader
2006; Harris 2001, for general reviews of GCs).
However, the distinction between OCs and GCs has become increasingly blurred. For example, some OCs are sufficiently luminous and old to be confused with GCs (e.g., Phelps & Schick 2003). Similarly, some GCs are very low-luminosity systems (e.g., Koposov et al. 2007) and at least one has an age that is consistent with the OC age distribution (Palomar 1; Sarajedini et al. 2007). Moreover, a third category of star cluster, ``young massive clusters'' (YMCs) are observed to exist in both merging (e.g., Whitmore & Schweizer 1995) and quiescent galaxies (Larsen & Richtler 1999), Indeed, YMCs have been known to exist in the Large Magellanic Cloud for over half a century (Hodge 1961). These objects are significantly more luminous than OCs (![]() up to
up to
![]() ), making them promising candidate young GCs. Once thought to be absent in the Milky Way, recent observations suggest that their census may be quite incomplete, as some prominent cases have been found recently in the Galaxy as well
(Clark et al. 2005; Figer 2008).
), making them promising candidate young GCs. Once thought to be absent in the Milky Way, recent observations suggest that their census may be quite incomplete, as some prominent cases have been found recently in the Galaxy as well
(Clark et al. 2005; Figer 2008).
Thus, a picture has emerged that, rather than representing distinct entities, OCs, YMCs and GCs may represent regions within a continuum of cluster properties dependent upon local galaxy conditions (Larsen 2003). The lifetime of a star cluster is dependent upon its mass and environment. Most low-mass star clusters in disks are rapidly disrupted via interactions with giant molecular clouds (Lamers & Gieles 2006; Gieles et al. 2007). These disrupted star clusters are thought to be the origin of much of the present field star populations (Lada & Lada 2003). Surviving disk clusters may then be regarded as OCs or YMCs, depending upon their mass. Star clusters in the halo may survive longer since they are subjected to the more gradual dynamical processes of two-body relaxation and evaporation. The clusters which survive for an Hubble time - more likely to occur away from the disk - are termed GCs (see also Krienke & Hodge 2007). To date, no known thin disk GCs have been identified in the Milky Way.
After the Milky Way, M31 is the prime target for expanding our knowledge of cluster systems in spirals. However, our present state of knowledge about the M31 cluster system is far from complete. Similar to the Milky Way, M31 appears to have at least two GC subpopulations; a metal-rich, spatially concentrated subpopulation of GCs and a more metal-poor, spatially extended GC subpopulation (Huchra et al. 1991; Barmby et al. 2000). Also, again similar to
the Milky Way GCs, the metal-rich GCs in M31 rotate and show ``bulge-like'' kinematics (Perrett et al. 2002). However, unlike the case in the Milky Way, the metal-poor GCs also show significant rotation (Huchra et al. 1991; Perrett et al. 2002; Lee et al. 2008). Using the Perrett et al. (2002) data, Morrison et al. (2004)
identified what appeared to be a thin disk population of GCs, constituting some 27% of the Perrett et al. (2002) sample. Subsequently, it has been shown that at least a subset of these objects are in fact young (![]() 1 Gyr), metal-rich star clusters rather than old ``classical'' GCs (Beasley et al. 2004; Burstein et al. 2004; Fusi Pecci et al. 2005; Puzia et al. 2005).
1 Gyr), metal-rich star clusters rather than old ``classical'' GCs (Beasley et al. 2004; Burstein et al. 2004; Fusi Pecci et al. 2005; Puzia et al. 2005).
Fusi Pecci et al. (2005; hereafter F05) presented a comprehensive study of bright young disk clusters in M31, selected from the Revised Bologna Catalogue![]() (RBC, Galleti et al. 2004) by color [
(RBC, Galleti et al. 2004) by color [
![]() ]
or by the strength of the H
]
or by the strength of the H![]() line in their spectra (H
line in their spectra (H
![]() ). While these clusters have been noted since Vetesnik (1962) and have been studied by various authors, a systematic study was lacking.
F05 found that these clusters, that they termed - to add to the growing menagerie of star cluster species - ``Blue Luminous Compact Clusters'' (BLCCs), are fairly numerous in M31 (15% of the whole GC sample), they have positions and kinematics typical of thin disk objects, and
their colors and spectra strongly suggest that they have ages (significantly) less than 2 Gyr.
). While these clusters have been noted since Vetesnik (1962) and have been studied by various authors, a systematic study was lacking.
F05 found that these clusters, that they termed - to add to the growing menagerie of star cluster species - ``Blue Luminous Compact Clusters'' (BLCCs), are fairly numerous in M31 (15% of the whole GC sample), they have positions and kinematics typical of thin disk objects, and
their colors and spectra strongly suggest that they have ages (significantly) less than 2 Gyr.
Since they are quite bright (
![]() )
and - at least in some cases - morphologically similar to old GCs (see Williams & Hodge 2001, hereafter WH01), BLCCs could be regarded as YMCs, that is to say, candidate young globular clusters. In particular, F05 concluded that if most of the BLCCs have an age
)
and - at least in some cases - morphologically similar to old GCs (see Williams & Hodge 2001, hereafter WH01), BLCCs could be regarded as YMCs, that is to say, candidate young globular clusters. In particular, F05 concluded that if most of the BLCCs have an age ![]() 50-100 Myr they are likely brighter than Galactic Open Clusters (OC) of similar ages, thus they should belong to a class of objects that is not present, in large numbers, in our own Galaxy. Unfortunately, the accuracy in the age estimates obtained from the integrated properties of the clusters is not sufficient to determine their
actual nature on an individual basis, i.e., to compare their total luminosity with the luminosity distribution of OCs of similar age (see Bellazzini et al. 2008, and references therein).
50-100 Myr they are likely brighter than Galactic Open Clusters (OC) of similar ages, thus they should belong to a class of objects that is not present, in large numbers, in our own Galaxy. Unfortunately, the accuracy in the age estimates obtained from the integrated properties of the clusters is not sufficient to determine their
actual nature on an individual basis, i.e., to compare their total luminosity with the luminosity distribution of OCs of similar age (see Bellazzini et al. 2008, and references therein).
In addition to the question of the masses and ages of these BLCCs, it has become clear that the BLCC photometric and spectroscopic samples in M31 may suffer from significant contamination.
Cohen et al. (2006, hereafter C06) presented NIRC2@KeckII Laser Guide Star Adaptive Optics (LGSAO) images of six candidate BLCCs. Their
![]() very-high spatial resolution images revealed that in the fields of four of the candidates there was no apparent cluster. This lead C06 to the conclusion that some/many of the claimed BLCC may in fact be just asterisms, i.e. chance groupings of stars in the dense disk of M31. While the use of the near infrared
very-high spatial resolution images revealed that in the fields of four of the candidates there was no apparent cluster. This lead C06 to the conclusion that some/many of the claimed BLCC may in fact be just asterisms, i.e. chance groupings of stars in the dense disk of M31. While the use of the near infrared
![]() band (required by the LGSAO technique) may be largely insensitive to very young clusters that are dominated by relatively few hot stars, which emit most of the light in the blue region of the spectrum, the inference is that the true number of massive young clusters of M31 may
have been severely overestimated.
band (required by the LGSAO technique) may be largely insensitive to very young clusters that are dominated by relatively few hot stars, which emit most of the light in the blue region of the spectrum, the inference is that the true number of massive young clusters of M31 may
have been severely overestimated.
Therefore, in order to ascertain the real nature of these BLCCs we have performed an HST survey to image 20 BLCCs in the disk of M31 (program GO-10818, P.I.: J. G. Cohen). The key aims of the survey are:
- 1.
- to check if the imaged targets are real clusters or asterisms, and to determine the fraction of contamination of BLCCs by asterisms;
- 2.
- to obtain an estimate of the age of each cluster in order to verify whether it is brighter than Galactic OCs of similar age. Ultimately the survey aims to provide firm conclusions on the existence of BLCCs (YMCs) in M31 as a distinct class of object with respect to OCs (see Krienke & Hodge 2007,2008, and references therein).
The present paper is organized as follows. The observations and the data reduction procedure are described in detail in Sect. 2; the principal assumptions that will be adopted in the whole survey are also reported in this section. Section 3 is devoted to the analysis of the surface brightness profile and of the Color Magnitude Diagram of VdB0, including total luminosity, age and metallicity estimates. In Sect. 4 our main results are briefly summarized and discussed.
Table 1: Positional and photometric parameters for VdB0 from the RBCa.
1.1 The cluster van den Bergh 0 (VdB0)
VdB0 was indicated as an open cluster by Hubble (1936) in the image on the frontispiece of his book The Realm of the Nebulae![]() . van den Bergh (1969) presents VdB0 as the brightest open cluster of M31, reporting an integrated spectral type A0. He also notes that the cluster contains the Cepheid variable V40 (Hubble 1929). A check of Hubble's (1929) finding charts revealed that two sources are labeled # 40 in his plate VII: one of them seems indeed
associated with the cluster, while the other is
. van den Bergh (1969) presents VdB0 as the brightest open cluster of M31, reporting an integrated spectral type A0. He also notes that the cluster contains the Cepheid variable V40 (Hubble 1929). A check of Hubble's (1929) finding charts revealed that two sources are labeled # 40 in his plate VII: one of them seems indeed
associated with the cluster, while the other is ![]()
![]() away from VdB0, near the association OB78 = NGC 206 (van den Bergh 1964; see also Hodge 1979).
The cluster was re-discovered by Hodge (1979), who classified it as an open cluster (C107, see also Hodge 1981). Finally, Battistini et al. (1987) listed the cluster as their class D candidate globular cluster number 195 (B195D in the RBC). The failure to identify
B195D with VdB0 was due to the fact that the coordinates provided by van den Bergh (1969) were in error by
away from VdB0, near the association OB78 = NGC 206 (van den Bergh 1964; see also Hodge 1979).
The cluster was re-discovered by Hodge (1979), who classified it as an open cluster (C107, see also Hodge 1981). Finally, Battistini et al. (1987) listed the cluster as their class D candidate globular cluster number 195 (B195D in the RBC). The failure to identify
B195D with VdB0 was due to the fact that the coordinates provided by van den Bergh (1969) were in error by ![]()
![]() .
For this reason VdB0 and B195D survived as independent entries in M31 GC catalogues until the present day. In our survey we imaged both the clusters and the WFPC2 images revealed unequivocally that the two targets are in fact the same
cluster. In particular the images intended to observe B195D have the cluster in the center of the PC camera while in the VdB0 images the cluster lie in the corner of the PC opposite to the WF cameras, such that part of the cluster is out of the image. In the following (and in the future) we will refer to the cluster as VdB0. The dataset analysed here is the one with the cluster
centered on the PC images, hence the actual label in the header of the fits files is B195D.
.
For this reason VdB0 and B195D survived as independent entries in M31 GC catalogues until the present day. In our survey we imaged both the clusters and the WFPC2 images revealed unequivocally that the two targets are in fact the same
cluster. In particular the images intended to observe B195D have the cluster in the center of the PC camera while in the VdB0 images the cluster lie in the corner of the PC opposite to the WF cameras, such that part of the cluster is out of the image. In the following (and in the future) we will refer to the cluster as VdB0. The dataset analysed here is the one with the cluster
centered on the PC images, hence the actual label in the header of the fits files is B195D.
VdB0 is located at a projected distance of
![]() kpc from the center of M31 to the South-West, just
kpc from the center of M31 to the South-West, just ![]()
![]() from the major axis of the galaxy (see Table 1), near the edge of one of the most prominent substructures of the M31 disk, the so called 10 kpc ring
(see Hodge 1992; Barmby et al. 2006, and references therein) and within the large OB association OB80 (van den Bergh 1964; A80 in Hodge 1981 atlas). Its radial velocity (
from the major axis of the galaxy (see Table 1), near the edge of one of the most prominent substructures of the M31 disk, the so called 10 kpc ring
(see Hodge 1992; Barmby et al. 2006, and references therein) and within the large OB association OB80 (van den Bergh 1964; A80 in Hodge 1981 atlas). Its radial velocity (
![]() km s-1, Perrett et al. 2002) is in full agreement with the rotation curve of the HI disk of M31 (Carignan et al. 2006), thus confirming the physical association with the thin disk of the parent galaxy (F05). The strong value of the H
km s-1, Perrett et al. 2002) is in full agreement with the rotation curve of the HI disk of M31 (Carignan et al. 2006), thus confirming the physical association with the thin disk of the parent galaxy (F05). The strong value of the H![]() index supports the idea that the cluster is younger than 1 Gyr (
index supports the idea that the cluster is younger than 1 Gyr (
![]() Å, Perrett et al. 2002
Å, Perrett et al. 2002![]() ). The existing estimates of both
). The existing estimates of both ![]() and H
and H![]() are nicely confirmed by recent high signal-to-noise spectra acquired at the Italian Telescopio Nazionale Galileo (Galleti, private communication).
are nicely confirmed by recent high signal-to-noise spectra acquired at the Italian Telescopio Nazionale Galileo (Galleti, private communication).
With the assumed reddening and distance, the integrated V magnitude reported in the RBC (see Table 1) gives an absolute magnitude MV=-10.03, much brighter than any Galactic open cluster older than 10 Myr (see Bellazzini et al. 2008, and below); it appears quite extended and irregular in shape even in ground based images. In these ways VdB0 stands out among the members of our candidate BLCC sample that are, in general, fainter and more compact than it.
2 Observations and data reduction
Our survey was originally planned for the Advanced Camera for Surveys (ACS) but it was performed with the Wide Field and Planetary Camera 2 (WFPC2) during cycle 16 because of the failure of ACS.
For each target of our survey we acquired two F450W and two F814W images, all with 400 s exposure time and gain =
![]() .
The pointings were chosen to place the main target at the center of the PC (800
.
The pointings were chosen to place the main target at the center of the PC (800 ![]()
![]() ,
with pixel scale 0.045 arcsec/px), while the three WF cameras (800
,
with pixel scale 0.045 arcsec/px), while the three WF cameras (800 ![]()
![]() ,
with 0.099 arcsec/px) are supposed to sample the surrounding fields. The images of VdB0 discussed here were acquired on July 2, 2007. The image of the whole WFPC2 mosaic image is shown in Fig. 1. It is clear that there are substructures and density gradients on the scale of the whole mosaic image, mainly due to the inclusion of the edges of the large stellar association embedding the cluster (A80, Hodge 1981). As the overall stellar density on the WF2 field is larger than in WF3 and WF4, we make the conservative choice to adopt the WF2 as our preferred sample of the background population that is expected to contaminate the Color Magnitude Diagram of the cluster, while we will consider the average density over all the WF fields when we will compute stellar density profiles based on star counts (Sect. 3). In the present context, when we speak of ``background population'' we refer to all the stars belonging to the field of M31 but unrelated to the cluster we are studying. Zoomed views of the PC field in both F450W and F814W passbands are shown in Fig. 2.
,
with 0.099 arcsec/px) are supposed to sample the surrounding fields. The images of VdB0 discussed here were acquired on July 2, 2007. The image of the whole WFPC2 mosaic image is shown in Fig. 1. It is clear that there are substructures and density gradients on the scale of the whole mosaic image, mainly due to the inclusion of the edges of the large stellar association embedding the cluster (A80, Hodge 1981). As the overall stellar density on the WF2 field is larger than in WF3 and WF4, we make the conservative choice to adopt the WF2 as our preferred sample of the background population that is expected to contaminate the Color Magnitude Diagram of the cluster, while we will consider the average density over all the WF fields when we will compute stellar density profiles based on star counts (Sect. 3). In the present context, when we speak of ``background population'' we refer to all the stars belonging to the field of M31 but unrelated to the cluster we are studying. Zoomed views of the PC field in both F450W and F814W passbands are shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm]{0725mosa.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg48.gif) |
Figure 1: F450W mosaic of the whole field sampled by our WFPC2 observations. The cluster VdB0 is at the center of the PC camera. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0725imaB.ps}\par\includegraphics[width=8.8cm,clip]{0725imaI.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg49.gif) |
Figure 2: F450W ( upper panel) and F814W ( lower panel) images of the whole PC camera, with VdB0 at the center. The superposed circles have radius r=160, 205, 260, 288 and 330 pixels, from inside out, and mark the edges of the annuli whose CMDs are shown in Fig. 9, below. The light stripes associated with stars in the F450W image are due to the effect of CTE that is particularly strong in this shallow low-background image. |
| Open with DEXTER | |
As the observational material and the degree of crowding are essentially the same for all the surveyed fields, we tuned our data-reduction strategy to be exactly the same in all cases, to
maintain the highest degree of homogeneity in the final products of the survey. Data reduction has been performed on the pre-reduced images provided by STScI, using HSTPHOT![]() (Dolphin 2000a), a Point Spread Function-fitting package specifically devoted to the photometry of WFPC2 data. The package identifies the sources above a fixed flux threshold on a stacked image and performs photometry on individual frames, and automatically applies the correction for the Charge Transfer Efficiency
(CTE, Dolphin 2000b). It then transforms instrumental magnitude to the VEGAMAG system (see Holtzman et al. 1995; Dolphin 2000b), deals with cosmic-ray hits, and takes also into account all the information about image defects that is attached to the observational material. We fixed the threshold for the search of sources on the images at 3
(Dolphin 2000a), a Point Spread Function-fitting package specifically devoted to the photometry of WFPC2 data. The package identifies the sources above a fixed flux threshold on a stacked image and performs photometry on individual frames, and automatically applies the correction for the Charge Transfer Efficiency
(CTE, Dolphin 2000b). It then transforms instrumental magnitude to the VEGAMAG system (see Holtzman et al. 1995; Dolphin 2000b), deals with cosmic-ray hits, and takes also into account all the information about image defects that is attached to the observational material. We fixed the threshold for the search of sources on the images at 3![]() above the background.
HSTPHOT provides as output the magnitudes and positions of the detected sources, as well as a number of quality parameters for a suitable sample selection, in view of the actual scientific objective one has in mind. Here we selected all the sources having valid magnitude measurements in both passbands, global quality flag = 1 (i.e., best measured stars), crowding parameter <0.3,
above the background.
HSTPHOT provides as output the magnitudes and positions of the detected sources, as well as a number of quality parameters for a suitable sample selection, in view of the actual scientific objective one has in mind. Here we selected all the sources having valid magnitude measurements in both passbands, global quality flag = 1 (i.e., best measured stars), crowding parameter <0.3,
![]() and
and
![]() ,
in both passbands, (see Dolphin 2000a, for details on the parameters). This selection cleans the sample from the vast majority of spurious and/or badly measured sources without significant loss of information, and it has been found
to be appropriate for the whole survey.
,
in both passbands, (see Dolphin 2000a, for details on the parameters). This selection cleans the sample from the vast majority of spurious and/or badly measured sources without significant loss of information, and it has been found
to be appropriate for the whole survey.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0725cmd.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg52.gif) |
Figure 3: CMD of the fields sampled by the four chips of the WFPC2. The number of stars plotted is reported in the upper right corner of each panel. The upper line marks the threshold above which stars saturate the intensity scale of the images. The lower lines are CMD loci at the same level of completeness, 90%, 70% and 50% from top to bottom, respectively (see labels in the WF2 panel). |
| Open with DEXTER | |
In Fig. 3 the Color Magnitude Diagrams (CMD) of the fields imaged by the four chips of WFPC2 are shown. The threshold for the saturation of bright stars and the boundaries at which the
completeness of the sample reaches 90%, 70% and 50% are also shown, as derived from the artificial stars experiments described below. As the CMD is quite typical of our survey, it is worthy of some general comments while a detailed analysis is deferred to Sect. 3 below. First, our photometry is relatively shallow, due the short exposure times of our images; the 50% completeness
level is reached at
![]()
![]() . For the same reason our images, and particularly the F450W ones in which the background
light is very low, are badly affected by CTE (see Fig. 2). Therefore the accuracy of the absolute and relative photometry is not particularly good (see, for example, Fig. 4 and Table 2, below). In spite of that, the very wide wavelength baseline provided
by the F450W and F814W filters produces relatively well defined sequences in the CMD (compare, for example, with the CMD of similar fields obtained by WH01 with the same camera
and longer exposure times but using F439W and F555W filters).
. For the same reason our images, and particularly the F450W ones in which the background
light is very low, are badly affected by CTE (see Fig. 2). Therefore the accuracy of the absolute and relative photometry is not particularly good (see, for example, Fig. 4 and Table 2, below). In spite of that, the very wide wavelength baseline provided
by the F450W and F814W filters produces relatively well defined sequences in the CMD (compare, for example, with the CMD of similar fields obtained by WH01 with the same camera
and longer exposure times but using F439W and F555W filters).
All the fields targeted by our survey cross the outer regions of the star-forming thin disk of M31 (see F05), and as a consequence, in most cases, the most prominent feature of the CMD is the
nearly vertical plume of young Main Sequence stars that is seen in Fig. 3 around
![]() .
The wide blob of stars at
F450W>24.0 and
.
The wide blob of stars at
F450W>24.0 and
![]() is consistent with being due to the brightest Red Giants near the tip of the Red Giant Branch (RGB) of the old-intermediate population that seems to be pervasive in the M31 disk (see Bellazzini et al.
2003, and references therein). Red and blue supergiants as well as other less-massive evolved stars are likely present at bright magnitudes over the whole color range covered by our CMD
(see Massey 2006).
is consistent with being due to the brightest Red Giants near the tip of the Red Giant Branch (RGB) of the old-intermediate population that seems to be pervasive in the M31 disk (see Bellazzini et al.
2003, and references therein). Red and blue supergiants as well as other less-massive evolved stars are likely present at bright magnitudes over the whole color range covered by our CMD
(see Massey 2006).
2.1 Artificial stars experiments
The completeness of the samples and the accuracy in the relative photometry are best estimated with extensive sets of artificial stars experiments (see Bellazzini et al. 2002a,b; and Tosi et al. 2001, for detailed discussions and references).
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{0725err.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg57.gif) |
Figure 4:
Distributions of the differences between the output and input magnitudes of artificial stars as a function of F450W ( left panels) and F814W ( right panels) magnitudes, for the PC and WF fields. The top panel displays the distributions for the most crowded region of the PC camera, i.e. the one containing the cluster.
|
| Open with DEXTER | |
HSTPHOT allows easy, fast and fully automated runs of artificial stars experiments. Fake stars in a user-selected color range, extracted at random from a Luminosity Function (LF) similar to the observed one, are added to the original frames one at a time to avoid self-crowding (Dolphin, private communication) and the photometric reduction is repeated. With the final catalogue of input and output magnitudes of artificial stars the distribution of photometric errors and the completeness of the samples can be studied as a function of color and as a function of the distance from the center of the cluster under consideration (i.e. as a function of crowding). We simulated a total of 728 398 artificial stars, roughly equally distributed on the four WFPC2 chips.
Table 2:
Uncertainties in the relative photometry from artificial stars experiments, for 10 px < r ![]() 160 px, PC field.
160 px, PC field.
Figure 4 shows the distributions of the differences between the output and input magnitudes of artificial stars as a function of F450W (left panels) and F814W (right panels) magnitudes, providing a direct estimate of the typical uncertainties of our relative photometry. The small excess of stars at negative
![]() ,
increasing in number and amplitude of the difference for fainter magnitudes, is due to artificial sources that are erroneously recovered with a brighter magnitude because they are blended with real sources present on the image (see Tosi et al. 2001). Even in the most crowded region of the PC that includes the cluster (top panels of Fig. 4) the effects of blending are not particularly severe, at least for relatively bright stars. The probability of a star with
,
increasing in number and amplitude of the difference for fainter magnitudes, is due to artificial sources that are erroneously recovered with a brighter magnitude because they are blended with real sources present on the image (see Tosi et al. 2001). Even in the most crowded region of the PC that includes the cluster (top panels of Fig. 4) the effects of blending are not particularly severe, at least for relatively bright stars. The probability of a star with
![]() to have its magnitude decreased by more than 0.1(0.2) mag by the combination of blending and photometric error is 2.8%(1.4%) if its color lies in the range
to have its magnitude decreased by more than 0.1(0.2) mag by the combination of blending and photometric error is 2.8%(1.4%) if its color lies in the range
![]() and 3.5%(1.6%) for
and 3.5%(1.6%) for
![]() .
Typical photometric uncertainties as a function of magnitude are reported in Table 2 for the innermost region of the PC field, covering most of the cluster that is the main subject of the present study.
.
Typical photometric uncertainties as a function of magnitude are reported in Table 2 for the innermost region of the PC field, covering most of the cluster that is the main subject of the present study.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725comp.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg64.gif) |
Figure 5:
Completeness factor ( |
| Open with DEXTER | |
Finally the completeness factors (![]() )
as a function of magnitude for different regions of the PC and for the WF fields are shown in Fig. 5, for stars in the wide color range
)
as a function of magnitude for different regions of the PC and for the WF fields are shown in Fig. 5, for stars in the wide color range
![]() .
Outside of the innermost region of the PC including the cluster, the
.
Outside of the innermost region of the PC including the cluster, the ![]() functions are nearly indistinguishable. For r > 50 px the completeness is larger than 80% for
functions are nearly indistinguishable. For r > 50 px the completeness is larger than 80% for
![]() and in any case
and in any case
![]() (i.e. completeness
(i.e. completeness ![]() 100%) for
100%) for
![]() .
.
2.2 Theoretical stellar models
Most of our inferences about the physical parameters of the stellar populations (clusters or field) considered in our survey will be obtained from the comparison between the observed CMDs and theoretical stellar models, in the form of isochrones or synthetic CMDs. The need to have models in the natural photometric system in which the observations were obtained (HST/WFPC2 VEGAMAG) and to have a set of isochrones reaching ages as young as 10 Myr led us to chose the set by Girardi et al. (2002, hereafter G02), as our reference grid of stellar models. In particular we took their HST-color version of the solar-scaled models by Salasnich et al. (2000), with overshooting and a simplified TP-AGB evolution, as this set includes 10 Myr old isochrones up to super-solar metallicities![]() . In some cases, when a particular model is needed, we use the CMD web tool
. In some cases, when a particular model is needed, we use the CMD web tool![]() (Marigo et al. 2008), that allows the on-line computation of models from user specified inputs, using the G02 set.
(Marigo et al. 2008), that allows the on-line computation of models from user specified inputs, using the G02 set.
In some cases, for comparison and/or for special applications, we use the BASTI![]() database, collecting the theoretical models by Pietrinferni et al. (2004), and updates. In particular BASTI provides a very practical Web Tool to produce synthetic CMDs of populations with ages, chemical composition,
initial mass function, binary fraction (
database, collecting the theoretical models by Pietrinferni et al. (2004), and updates. In particular BASTI provides a very practical Web Tool to produce synthetic CMDs of populations with ages, chemical composition,
initial mass function, binary fraction (![]() )
etc. selected by the user (Cordier et al. 2007), that can be used to compare models and observations in term of star counts in different color and magnitude ranges (see Fig. 6, for an example of application). Unfortunately, the models are not provided in the WFPC2 photometric system - so theoretical magnitudes have to be transformed - and isochrones/synthetic CMDs for ages < 30 Myr are not provided; for these reasons we didn't adopt the BASTI set as the reference for our survey. In the considered range of ages G02 and BASTI isochrones (with overshooting) provide very similar
predictions of color and magnitudes, while evolving masses may differ by
)
etc. selected by the user (Cordier et al. 2007), that can be used to compare models and observations in term of star counts in different color and magnitude ranges (see Fig. 6, for an example of application). Unfortunately, the models are not provided in the WFPC2 photometric system - so theoretical magnitudes have to be transformed - and isochrones/synthetic CMDs for ages < 30 Myr are not provided; for these reasons we didn't adopt the BASTI set as the reference for our survey. In the considered range of ages G02 and BASTI isochrones (with overshooting) provide very similar
predictions of color and magnitudes, while evolving masses may differ by ![]() 20% (see also Gallart et al. 2005).
20% (see also Gallart et al. 2005).
2.3 Reddening and distance
To correct for the effects of interstellar extinction and reddening we will always adopt the relations
AF450W=4.015E(B-V) and
AF814=1.948E(B-V), as reported by Schlegel et al. (1998). As our clusters are embedded in the structured dusty disk of M31 it does not seem appropriate to assume a unique value of reddening for all of them; the typical reddening value attributed to Galactic dust toward M31 ranges from
E(B-V)=0.06 (Schlegel et al. 1998) to
![]() (see Galleti 2004, and references therein), but it is likely that our clusters are more reddened than this (Barmby et al. 2000; Fan et al. 2008). To get an estimate of the reddening affecting the clusters in our survey we compare theoretical models (isochrones and synthetic CMDs) to the observed MS in the range
(see Galleti 2004, and references therein), but it is likely that our clusters are more reddened than this (Barmby et al. 2000; Fan et al. 2008). To get an estimate of the reddening affecting the clusters in our survey we compare theoretical models (isochrones and synthetic CMDs) to the observed MS in the range
![]() .
In this range, corresponding to absolute magnitudes
.
In this range, corresponding to absolute magnitudes
![]() ,
the color of the MS is only weakly sensitive to metallicity and various sets of theoretical models provide very consistent
predictions. An example of our analysis is presented in Fig. 6, where we compare the color distribution at the blue edge of the MS of the observed sample and of synthetic samples (from the BASTI webtool) of different metallicities, adopting different reddening values. The comparisons confirm that the sensitivity to metallicity of the reddening estimate is very weak, as expected.
In the case of VdB0 we obtain
E(B-V)=0.2
,
the color of the MS is only weakly sensitive to metallicity and various sets of theoretical models provide very consistent
predictions. An example of our analysis is presented in Fig. 6, where we compare the color distribution at the blue edge of the MS of the observed sample and of synthetic samples (from the BASTI webtool) of different metallicities, adopting different reddening values. The comparisons confirm that the sensitivity to metallicity of the reddening estimate is very weak, as expected.
In the case of VdB0 we obtain
E(B-V)=0.2 ![]() 0.03 with this method, and we will always adopt this value below.
0.03 with this method, and we will always adopt this value below.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725ebv.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg73.gif) |
Figure 6:
The observed CMD of VdB0 (black dots, only stars with |
| Open with DEXTER | |
In the following and for the whole survey we adopt (m-M)0 = 24.47 ![]() 0.07 as the distance modulus of all the considered populations, from McConnachie et al. (2005), corresponding to an heliocentric distance D = 783 kpc. At this distance
0.07 as the distance modulus of all the considered populations, from McConnachie et al. (2005), corresponding to an heliocentric distance D = 783 kpc. At this distance
![]() corresponds to 3.8 pc,
corresponds to 3.8 pc,
![]() to 228 pc.
to 228 pc.
2.4 Accessible age range
As the degree of crowding of all the surveyed fields is quite similar and the observational set-up is identical in all cases, the saturation limit and the
![]() limit reported in the CMDs of Fig. 3 can be considered representative of the typical CMD window that is accessible with the survey data. In Fig. 7 we compare isochrones of different ages and metallicities with this window to have an idea of the age range in which we can obtain reasonable age estimates for the considered clusters from the luminosity of their Turn Off (TO) points and/or from the distribution of their Super Giant populations.
limit reported in the CMDs of Fig. 3 can be considered representative of the typical CMD window that is accessible with the survey data. In Fig. 7 we compare isochrones of different ages and metallicities with this window to have an idea of the age range in which we can obtain reasonable age estimates for the considered clusters from the luminosity of their Turn Off (TO) points and/or from the distribution of their Super Giant populations.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725eta.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg77.gif) |
Figure 7:
Isochrones of different ages and metal content are plotted on the ``visibility window'' of our CMDs, enclosed on the bright side by the saturation limits and on the faint side by the
|
| Open with DEXTER | |
In the metallicity range that is most likely to enclose the disk populations (we are considering
![]() )
we can detect the TO point of clusters roughly ranging from 10 to 500 Myr old. As the only BLCCs for which a direct CMD-based age estimate has been obtained are 60-160 Myr old (WH01), the age sensitivity of the survey seems rather appropriate; however clusters in the age range 0.5-2 Gyr may prove very difficult to age date with our data. For the oldest populations (age
)
we can detect the TO point of clusters roughly ranging from 10 to 500 Myr old. As the only BLCCs for which a direct CMD-based age estimate has been obtained are 60-160 Myr old (WH01), the age sensitivity of the survey seems rather appropriate; however clusters in the age range 0.5-2 Gyr may prove very difficult to age date with our data. For the oldest populations (age ![]() 2 Gyr) we can hope to detect just the tip of the RGB, as shown by the age = 12 Gyr isochrones plotted as thick lines in Fig. 9, below.
2 Gyr) we can hope to detect just the tip of the RGB, as shown by the age = 12 Gyr isochrones plotted as thick lines in Fig. 9, below.
3 The CMD and structure of the cluster VdB0
3.1 Distribution of resolved stars
To identify the stellar population of the cluster as securely as possible, it is useful to have an idea of the surface density distribution of its resolved stars. In the present context we are interested only in defining the characteristic size of the region dominated by cluster stars, in order to select samples of likely cluster members by radius (see Sect. 3.4 for a detailed analysis of the light profiles).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725prof.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg79.gif) |
Figure 8:
Upper panel: background-subtracted surface density profile of
VdB0 computed by counting stars on circular concentric annuli around the center of the cluster. The arrow marks the radius where a sudden change of slope in the profile appears, at
|
| Open with DEXTER | |
Stars were selected on the CMD from the box shown in the diagram enclosed in the lower panel of Fig. 8. The box is expected to pick up the best-measured MS and SG stars typical of the
cluster population, while excluding populations that are clearly not associated with the cluster, such as the much older stars around the tip of the RGB. For
![]() star counts are significantly affected by radially varying incompleteness in the range of magnitudes considered.
Beyond this limit the degree of completeness is fairly high and essentially constant with radius
(see Fig. 5, above), hence the derived profile should be reliable.
star counts are significantly affected by radially varying incompleteness in the range of magnitudes considered.
Beyond this limit the degree of completeness is fairly high and essentially constant with radius
(see Fig. 5, above), hence the derived profile should be reliable.
In the upper panel of Fig. 8 we show the surface density profile obtained by counting stars on circular annuli centered on the cluster center. The observed profile displays an obvious break at
![]() ,
where it begins to decline with a gentler slope out to
,
where it begins to decline with a gentler slope out to
![]() .
The break in the profile may reflect an inner core + outer corona structure of VdB0, which is typical of Galactic Open Clusters (see Kubiak et al. 1992; Kharchenko et al. 2005; Mackey & Gilmore 2003; Elson et al. 1987, and references therein), or it may be - at least partially - due to the elongated distribution of the cluster stars unaccounted for by our adoption of circular annuli. To investigate this possibility we transformed the radial coordinate of each star (r) into a major-axis radius (
.
The break in the profile may reflect an inner core + outer corona structure of VdB0, which is typical of Galactic Open Clusters (see Kubiak et al. 1992; Kharchenko et al. 2005; Mackey & Gilmore 2003; Elson et al. 1987, and references therein), or it may be - at least partially - due to the elongated distribution of the cluster stars unaccounted for by our adoption of circular annuli. To investigate this possibility we transformed the radial coordinate of each star (r) into a major-axis radius (
![]() )
defined as
)
defined as
where
| (2) |
| (3) |
and (X0,Y0) are the coordinate of the center of the cluster,
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{0725clus.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg88.gif) |
Figure 9:
CMDs of different circular annuli around the center of VdB0 in the PC field (see Fig. 2, above), all having the same area ( upper panels and lower left panel),
and of the whole WF2 field, whose area is 32 times that of the PC annuli ( lower right panel).
The thin line is a
|
| Open with DEXTER | |
The ellipticity-corrected major axis profile is plotted in the lower panel of Fig. 8, and it clearly shows that the change of slope in the original profile was an artifact due to the inadequacy of the assumption of circular symmetry. The result is supported by the good match between the star-counts profile and the light profiles (from Sect. 3.4) over the large radial range where they can be compared (
![]() ).
).
It is interesting to note that the cluster profile appears to extend to remarkably large distances from the center, out to ![]()
![]() pc. As the process of profile analysis described in Sect. 3.4 includes also the fitting of King (1966, hereafter K66) models,
it is interesting to note that the limiting radius of the K66 models that best fits the surface brightness profiles is also
pc. As the process of profile analysis described in Sect. 3.4 includes also the fitting of King (1966, hereafter K66) models,
it is interesting to note that the limiting radius of the K66 models that best fits the surface brightness profiles is also
![]() ,
thus supporting the conclusion that the cluster is very extended.
,
thus supporting the conclusion that the cluster is very extended.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0725rsg.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg92.gif) |
Figure 10:
CMDs of different annuli around the center of VdB0 in the PC field ( upper panels) and of a large area in the WF2 field ( lower left panel), expected to sample the surrounding ``field'' population. An isochrone of
|
| Open with DEXTER | |
The elongated shape of the cluster will be taken into account in the detailed analysis of the profiles of Sect. 3.4. For present purposes it is sufficient to conclude that most of the cluster
stars are enclosed within a (circular) radius of
![]() (160 px) from the center. We take this as a reference radius for the following analysis of the CMD, as it allows a very simple radial selection, remembering that some cluster members are also present at larger radii.
(160 px) from the center. We take this as a reference radius for the following analysis of the CMD, as it allows a very simple radial selection, remembering that some cluster members are also present at larger radii.
The upper left panel of Fig. 9 shows the CMD of stars within
10 < r< 160 px, an annulus that, as stated earlier, should be dominated by cluster stars. The innermost ![]() px region has been excluded because of severe incompleteness. A main sequence with a TO around
px region has been excluded because of severe incompleteness. A main sequence with a TO around
![]() is the most populated branch of the diagram, with a blue edge at
is the most populated branch of the diagram, with a blue edge at
![]() .
Blue and red supergiants (BSGs, RSGs) are clearly identified, spanning a large color
range (
.
Blue and red supergiants (BSGs, RSGs) are clearly identified, spanning a large color
range (
![]() mag). A 25 Myr isochrone of solar metallicity (from the G02 set) seems to provide a satisfactory fit to the MS and to the sizable luminosity range spanned by supergiants, suggesting an extended Blue Loop phase (see Williams & Hodge 2001). The color of the reddest supergiants is not fully reproduced (a long standing and not-so-critical problem of theoretical models, see Massey 2003). An handful of field RGB stars (at
mag). A 25 Myr isochrone of solar metallicity (from the G02 set) seems to provide a satisfactory fit to the MS and to the sizable luminosity range spanned by supergiants, suggesting an extended Blue Loop phase (see Williams & Hodge 2001). The color of the reddest supergiants is not fully reproduced (a long standing and not-so-critical problem of theoretical models, see Massey 2003). An handful of field RGB stars (at
![]() and
and
![]() )
is the only population identified in this inner annulus which is clearly not associated with the cluster.
)
is the only population identified in this inner annulus which is clearly not associated with the cluster.
The upper right and lower left panels of Fig. 9 shows the CMD of outer annuli of the PC field with the same area as the 10 px < r < 160 px annulus. Even if these fields still contain some cluster members, their stellar mix should be fairly representative of the surrounding field population (compare with the WF2 CMD shown in the lower right panel). The comparison of the innermost annulus with the outer two of the same area shows that the supergiant population is
characteristic of the cluster and is much less frequent in the field, suggesting an older average age of the field population with respect to the cluster. The comparison between the morphologies of the MS is consistent with this view. The lower right panel of the figure shows the CMD of a WF2 field whose area is 32 times that of the annuli described above. The larger sampled area provides
a clearer picture of the population mix of the M31 disk in the surroundings of VdB0. While MS and evolved stars of age (mass) similar to that encountered in the cluster are present, the majority of the stars seem to have ages greater than 100 Myr. In particular the evolved stars at
![]() and
and
![]() that are well fitted by the over-plotted 125 Myr, Z=0.008isochrone are not seen in the 10 px < r < 160 px annulus.
that are well fitted by the over-plotted 125 Myr, Z=0.008isochrone are not seen in the 10 px < r < 160 px annulus.
The CMD of the cluster (innermost annulus) is very similar to that of rich Large Magellanic Cloud clusters of age ![]() 30-50 Myr, such as NGC 1711 (Sagar et al. 1991) and, in particular, NGC 1850 (Vallenari et al. 1994; Gilmozzi et al. 1994).
30-50 Myr, such as NGC 1711 (Sagar et al. 1991) and, in particular, NGC 1850 (Vallenari et al. 1994; Gilmozzi et al. 1994).
3.2 Supergiant stars
The analysis illustrated in Fig. 10 and reported in Table 3 quantitatively demonstrates the presence of a significant overabundance of supergiants in the cluster with respect to the surrounding field. We counted stars in the different boxes on the CMDs shown in Fig. 10, sampling the upper MS (box A) and supergiants of blue (B), intermediate (C) and red (D) colors. The counts obtained in the ![]() px and 160 px < r < 330 px annuli
are compared with those expected from the field population, computed by rescaling the observed counts in the WF2 field by the ratio of the sampled areas. The lower right panel shows that in the
px and 160 px < r < 330 px annuli
are compared with those expected from the field population, computed by rescaling the observed counts in the WF2 field by the ratio of the sampled areas. The lower right panel shows that in the ![]() px annulus a clear excess of stars is present in all of the boxes considered.
The excess of bright MS stars is very significant and the excess of RSGs is above the 3
px annulus a clear excess of stars is present in all of the boxes considered.
The excess of bright MS stars is very significant and the excess of RSGs is above the 3![]() level. Even if the low number of stars prevents the detection of significant excesses, the 160 px < r < 330 px annulus shows some excess with respect to the field in all of the considered boxes, in agreement with the results of Fig. 8.
level. Even if the low number of stars prevents the detection of significant excesses, the 160 px < r < 330 px annulus shows some excess with respect to the field in all of the considered boxes, in agreement with the results of Fig. 8.
Table 3:
Star counts in the CMD boxes defined in Fig. 10. Box A samples the upper MS, boxes B, C, and D samples SG stars of blue, intermediate and red colors, respectively.
![]() is the number of stars expected in a given box from the field population, computed by
rescaling the observed counts in the WF2 field by the ratio of the sampled areas. The ratio between the area of the considered field (annulus) and the area of the WF2 field (used as representative of the field population) is reported in the last column.
is the number of stars expected in a given box from the field population, computed by
rescaling the observed counts in the WF2 field by the ratio of the sampled areas. The ratio between the area of the considered field (annulus) and the area of the WF2 field (used as representative of the field population) is reported in the last column.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{0725agei.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg114.gif) |
Figure 11: Age estimates for VdB0 for different assumptions about the total metallicity (Z). Isochrones from the G02 set are compared to the CMD of the cluster (10 px < r < 160 px). The best-fit isochrone is plotted as a thick continuous line while the dashed isochrones bracket the upper and lower limits on age. The ages and metallicities of the adopted isochrones are reported in each panel. The dotted lines mark the limiting magnitude as a function of color: the diagonal plume of stars just above the lines (with F450W-F814W > 1.5) is populated by likely RGB and AGB field stars, not associated with the cluster. |
| Open with DEXTER | |
The total background-subtracted number of RSGs attributable to VdB0 is ![]() 18. The true number is likely larger than this, as some RSGs are likely to reside in the innermost
18. The true number is likely larger than this, as some RSGs are likely to reside in the innermost ![]() px, which are not included in the present analysis as they are not well resolved in our images. According to Figer (2008) a richer harvest of RSGs is observed in only one known YMC of the Milky Way,
RSGC2, with twenty-six RSG stars. RSGC1 has fourteen, while other young clusters listed by Figer have less than five. RSGC2 is reported to have an age
px, which are not included in the present analysis as they are not well resolved in our images. According to Figer (2008) a richer harvest of RSGs is observed in only one known YMC of the Milky Way,
RSGC2, with twenty-six RSG stars. RSGC1 has fourteen, while other young clusters listed by Figer have less than five. RSGC2 is reported to have an age ![]() 21 Myr, RSGC1 has age
21 Myr, RSGC1 has age ![]() 14 Myr, and all the other clusters listed by Figer have ages
14 Myr, and all the other clusters listed by Figer have ages ![]() 7 Myr, i.e. younger than VdB0 (see below). As noted above, some rich clusters of similar age are known in the LMC (Vallenari
et al. 1994; Brocato et al. 2001), but even there RSGs are not present in large numbers.
7 Myr, i.e. younger than VdB0 (see below). As noted above, some rich clusters of similar age are known in the LMC (Vallenari
et al. 1994; Brocato et al. 2001), but even there RSGs are not present in large numbers.
3.3 Age and metallicity
Having fixed the amount of reddening and the distance modulus to the cluster, we obtain an age estimate and an indication of the metallicity by comparison with isochrones from the G02 set, following the approach used by WH01. In Fig. 11 we present a comparison with isochrones of various metallicities in the range
![]() .
In all the panels, the isochrone that is judged (by eye) to provide the best-fit to the observed CMD is plotted
as a continuous line. Dashed lines correspond to isochrones providing strong upper and lower limits to the age estimates, which serve as conservative estimates of the associated uncertainties.
.
In all the panels, the isochrone that is judged (by eye) to provide the best-fit to the observed CMD is plotted
as a continuous line. Dashed lines correspond to isochrones providing strong upper and lower limits to the age estimates, which serve as conservative estimates of the associated uncertainties.
The first very basic conclusion to be drawn from the reported upper/lower limits, is that, independent of the adopted metallicity, the age of VdB0 must be within the relatively narrow range from 12 to 63 Myr.
The wide range in magnitude covered by supergiant stars strongly indicates the presence of a wide blue loop (Massey 2003). The super-solar isochrones clearly lack this feature, hence can likely be excluded as a possible solution. The larger range of color and magnitude covered by the
![]() isochrone in the blue loop phase seems to provide a slightly better description of the CMD, compared to the Z=0.008 case. We produced a set of synthetic CMDs for populations having
Z=0.008,0.019,0.04, age 30 Myr and 50 Myr, Kroupa (2001), Salpeter (1955) and
isochrone in the blue loop phase seems to provide a slightly better description of the CMD, compared to the Z=0.008 case. We produced a set of synthetic CMDs for populations having
Z=0.008,0.019,0.04, age 30 Myr and 50 Myr, Kroupa (2001), Salpeter (1955) and
![]() Initial Mass Functions
Initial Mass Functions![]() (IMF), using the dedicated Web Tool provided by the BASTI team. After applying the appropriate distance modulus and reddening correction and transforming to the HST VEGAMAG system using the transformations by Dolphin (2000b), we computed a Blue to Red Supergiant
ratio defined as the ratio of stars having
F814W<20.0 and
F450W-F814W<2.0 (B) or
F450W-F814W>2.0 (R). Independent of age and IMF, all the Z=0.008 models have
(IMF), using the dedicated Web Tool provided by the BASTI team. After applying the appropriate distance modulus and reddening correction and transforming to the HST VEGAMAG system using the transformations by Dolphin (2000b), we computed a Blue to Red Supergiant
ratio defined as the ratio of stars having
F814W<20.0 and
F450W-F814W<2.0 (B) or
F450W-F814W>2.0 (R). Independent of age and IMF, all the Z=0.008 models have
![]() (
(
![]() mag for age = 30 Myr), while the observed number is B/R=0.60
mag for age = 30 Myr), while the observed number is B/R=0.60 ![]() 0.27. The Z=0.04 models have
0.27. The Z=0.04 models have
![]() ,
while the solar models have
,
while the solar models have
![]() .
Therefore, the color distribution of SGs provides further quantitative support to the conclusion that the metallicity of VdB0 is nearly solar. Adopting
.
Therefore, the color distribution of SGs provides further quantitative support to the conclusion that the metallicity of VdB0 is nearly solar. Adopting
![]() as our best estimate for the cluster metallicity, the age may be more quantitatively constrained by the comparison of the observed MS Luminosity Function with those predicted by models of various ages. Figure 12
clearly shows that an age = 25 Myr model provides the best-fit to the observed drop in the star counts at
as our best estimate for the cluster metallicity, the age may be more quantitatively constrained by the comparison of the observed MS Luminosity Function with those predicted by models of various ages. Figure 12
clearly shows that an age = 25 Myr model provides the best-fit to the observed drop in the star counts at
![]() .
The result is well reproduced also if a Kroupa IMF is adopted.
.
The result is well reproduced also if a Kroupa IMF is adopted.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0725lf2.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg125.gif) |
Figure 12:
Comparison of the observed LF with theoretical models from the G02 suite. Upper left panel: CMD of VDB0 with overplotted the box adopted to select the sample of stars to be included in the LF. The considered radial range avoids the innermost region where the completeness displays significant radial variations in the range of magnitudes considered. Upper right panel: completeness as a function of magnitude for the color and radial range considered.
Lower panel: the observed LF (before completeness correction = histogram; corrected for completeness = filled circles with error bars) is compared with models of different ages. Note the good fit of the drop at
|
| Open with DEXTER | |
Our age estimate is not expected to depend critically on the set of theoretical models adopted. In their thorough comparison, Gallart et al. (2005) showed that there is reasonably good agreement between all the theoretical isochrones they considered in this range of ages (i.e. ![]() 100 Myr), if stellar models with core overshooting are assumed. Our own (limited) set of experiments with Pietrinferni et al. (2004) models also supports this conclusion. A few tests with a set of isochrones adopting the canonical treatment of convection (from Pietrinferni et al. 2004) has shown that the adoption of such models would lead to younger age estimates, by a factor of
100 Myr), if stellar models with core overshooting are assumed. Our own (limited) set of experiments with Pietrinferni et al. (2004) models also supports this conclusion. A few tests with a set of isochrones adopting the canonical treatment of convection (from Pietrinferni et al. 2004) has shown that the adoption of such models would lead to younger age estimates, by a factor of ![]()
![]() ,
compared to models including overshooting.
,
compared to models including overshooting.
Table 4: Newly derived coordinates, half-light radius, integrated magnitudes, reddening, age and metallicity for the cluster VdB0. The origin of each parameter is described in the last column.
Given all the above, we adopt
![]() as our best guess for the cluster metallicity, and
25 Myr as our best estimate of its age (see Table 4). The mass of the stars at the TO of the best-fit isochrone is
as our best guess for the cluster metallicity, and
25 Myr as our best estimate of its age (see Table 4). The mass of the stars at the TO of the best-fit isochrone is
![]() .
.
This relatively rough age estimate is sufficient for our purposes. Our final aim is to place the cluster into a log(Age) versus absolute integrated magnitude diagram such as that shown in Fig. 14, below (see also Bellazzini et al. 2008, hereafter B08, and references therein), to compare its stellar mass with that of Galactic open clusters of similar ages.
The uncertainties reported here as the adopted upper and lower limits to the age estimates correspond to ![]()
![]() 0.3 dex in log(Age). These imply relatively small changes in the final estimate of the total stellar mass (a factor of
0.3 dex in log(Age). These imply relatively small changes in the final estimate of the total stellar mass (a factor of ![]() 2); the mass estimate also depends relatively weakly on the assumed IMF - see below - and very weakly on the metallicity, at least in the range
considered here, see B08).
2); the mass estimate also depends relatively weakly on the assumed IMF - see below - and very weakly on the metallicity, at least in the range
considered here, see B08).
3.4 Integrated photometry, surface brightness profile and structural parameters
Surface-brightness profile-fitting was carried out using methods similar to those of Barmby et al. (2007). A more detailed description and the results of profile-fitting for the full cluster sample will be presented in Barmby et al. (2009, in prep.). Briefly, the two PC images in each filter were combined with the STScI Multidrizzle software. Intensity profiles were measured using the ellipse fitting routine in IRAF, on logarithmically-spaced isophotes centered on the intensity peaks of the clusters. The isophotal profiles were ``circularized'' by converting the semi-major
axes a of the ellipses to effective radii
![]() ,
converted to electrons s-1 arcsec-2 by multiplying by
,
converted to electrons s-1 arcsec-2 by multiplying by
![]() and then to intensity in
and then to intensity in ![]() pc-2 by multiplying by 14.276 and 6.746 for F450W and F814W, respectively
pc-2 by multiplying by 14.276 and 6.746 for F450W and F814W, respectively![]() . The mean ellipticity and position angle obtained from the analysis of F450W and F814W images are very similar. For this reason we take their average as our best values,
. The mean ellipticity and position angle obtained from the analysis of F450W and F814W images are very similar. For this reason we take their average as our best values,
![]() and PA =
and PA =
![]() ,
measured from North toward East. The available prescription for correcting WFPC2 photometry for CTE effects deals only with photometry of point sources, not semi-resolved objects such as extragalactic star clusters; accordingly, no CTE corrections were made to the profiles.
,
measured from North toward East. The available prescription for correcting WFPC2 photometry for CTE effects deals only with photometry of point sources, not semi-resolved objects such as extragalactic star clusters; accordingly, no CTE corrections were made to the profiles.
Cluster structural models were fit to the profile using the methods described in McLaughlin et al. (2008). Before fitting to the data, the models were convolved with a PSF profile derived from ellipse measurements of TinyTim model Point Spread Functions (PSFs) for the center of the PC camera. We considered the same three models used in Barmby et al. (2007): King (1966), Wilson (1975), and Sérsic (1968). The background level (i.e.,
the intensity of the largest isophotes) was allowed to vary in the fitting. Figure 13 shows the profile data and the best-fit models in the two filters. Small scale bumps in the observed profile are likely due to individual bright stars (SGs). For the F450W filter the Sérsic model with index n=4.0 was the best fit. This model has central intensity I0 = 7.9 ![]()
![]() pc-2 and scale radius r0 = 6.1
pc-2 and scale radius r0 = 6.1 ![]() 10-4 pc. The projected
half-light radius is
10-4 pc. The projected
half-light radius is
![]() pc (2
pc (2
![]() 40) and total luminosity (corrected for extinction) 1.5
40) and total luminosity (corrected for extinction) 1.5 ![]()
![]() .
For the F814W image, the best-fit model was a Wilson (1975) model with W0=11.2, central intensity I0 = 5.0
.
For the F814W image, the best-fit model was a Wilson (1975) model with W0=11.2, central intensity I0 = 5.0 ![]()
![]() pc-2 and scale radius
r0 = 0.072 pc. The projected half-light radius is
pc-2 and scale radius
r0 = 0.072 pc. The projected half-light radius is
![]() pc (1
pc (1
![]() 47) and total luminosity 5.7
47) and total luminosity 5.7 ![]()
![]() .
In the following analysis, we adopt the average of the two half-light radii,
.
In the following analysis, we adopt the average of the two half-light radii,
![]()
![]() 2.5 pc (1
2.5 pc (1
![]() 94
94 ![]() 0
0
![]() 66; the reported uncertainty is the standard deviation of the two
values). It is also interesting to note that the half-light radius we have derived for VdB0 is larger than those for the clusters listed by Figer (see Davies et al. 2008,
66; the reported uncertainty is the standard deviation of the two
values). It is also interesting to note that the half-light radius we have derived for VdB0 is larger than those for the clusters listed by Figer (see Davies et al. 2008,
![]() pc), but smaller than NGC 1850 (
pc), but smaller than NGC 1850 (
![]() pc) and very similar to NGC 1711 (
pc) and very similar to NGC 1711 (
![]() pc), for example
pc), for example![]() . A summary of the adopted structural parameters of VdB0 is reported in Table 4.
. A summary of the adopted structural parameters of VdB0 is reported in Table 4.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725sbpr.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg152.gif) |
Figure 13: Intensity profiles from surface photometry in circular annuli from the F814W image ( upper panel) and for the F450W image ( lower panel). The continuous lines are the respective best-fit models, convolved with the instrumental PSF and with a constant background level added. For the parameters of the best-fit models see text. |
| Open with DEXTER | |
The derived values of the total luminosity correspond to
M450W=-10.13 and
M814W=-10.25, respectively. Using Eq. (12) of Dolphin (2000b) these VEGAMAG magnitudes can be
transformed to standard B and I using the appropriate coefficients from his Table 7. The integrated (B-V)0 color required for the transformation has been taken from the RBC (
(B-V)0=0.05, Table 1, above), while we adopted
(V-I)0=0.40 from Maraston's (2005) model for a solar metallicity Simple Stellar Population (SSP![]() ) with age of 25 Myr, as an observational estimate of the I magnitude of VdB0 was not available (but see below). MV=-9.9 is obtained from M814W and MV=-10.2 from M450W; we adopt the average (in flux) of the two,
MV=-10.06. This value is in excellent agreement with the value of
MV=-10.03 listed in the RBC, and coming, in turn, from the photometry by Sharov et al. (1995).
) with age of 25 Myr, as an observational estimate of the I magnitude of VdB0 was not available (but see below). MV=-9.9 is obtained from M814W and MV=-10.2 from M450W; we adopt the average (in flux) of the two,
MV=-10.06. This value is in excellent agreement with the value of
MV=-10.03 listed in the RBC, and coming, in turn, from the photometry by Sharov et al. (1995).
There are, however, compelling reasons to consider the estimate of MV obtained from our HST images as significantly uncertain because of the unfortunate combination of a very extended cluster and of a very low intrinsic background level (just 1 to 2 DN in the background sky in the original raw WFPC2 images, particularly for the F450W filter). This guarantees that photometry within very large apertures will have a large uncertainty, and the resulting integrated brightness may depend on the details of how the code handles the background estimate in this photon-starved regime.
For this reason we prefer to rely on the excellent ground-based material that is publicly available to obtain a reliable estimate of the total luminosity of the cluster. Existing ground-based photometry of VdB0 taken from Sharov et al. (1995) is compiled in the RBC. However, it is possible that it was obtained adopting apertures that were not large enough to include the whole light distribution of this particularly extended cluster (see Figs. 8 and 13). We have therefore used two independent and well calibrated publicly available imaging surveys covering M31 to determine the integrated brightness of the cluster VdB0, that of Massey et al. (2006, hereafter M06) and the Sloan Digital Sky Survey (SDSS). In both cases we
use an aperture with
![]() .
From the BVRI images of the former we obtained B=14.94
.
From the BVRI images of the former we obtained B=14.94 ![]() 0.09, V=14.67
0.09, V=14.67 ![]() 0.05, R=14.45
0.05, R=14.45 ![]() 0.11 and I=14.01
0.11 and I=14.01 ![]() 0.11
0.11![]() . The SDSS - Data Release 6 (DR6, Adelman-McCarthy et al. 2008) g, r, and i images yielded B=14.92, V=14.63, R=14.45, and I=14.03 using the color transformations of Lupton (2005), in excellent agreement with those inferred from the M06 images. This is
. The SDSS - Data Release 6 (DR6, Adelman-McCarthy et al. 2008) g, r, and i images yielded B=14.92, V=14.63, R=14.45, and I=14.03 using the color transformations of Lupton (2005), in excellent agreement with those inferred from the M06 images. This is ![]() 0.4-0.6 mag brighter
than those reported in the RBC. In Sect. 4 we will show that the J, H, K magnitudes of VdB0 also become brighter by
0.4-0.6 mag brighter
than those reported in the RBC. In Sect. 4 we will show that the J, H, K magnitudes of VdB0 also become brighter by ![]() 0.2-0.5 mag after increasing the adopted aperture from
r= 5
0.2-0.5 mag after increasing the adopted aperture from
r= 5
![]() 0 to 15
0 to 15
![]() 0.
0.
Given all the above, we adopt the r= 14
![]() 4 aperture photometry measured on M06 images as our preferred values, reported in Table 4, below. In particular V=14.67
4 aperture photometry measured on M06 images as our preferred values, reported in Table 4, below. In particular V=14.67 ![]() 0.05 is our final best estimate of the integrated V magnitude of VdB0, corresponding to
MV=-10.42
0.05 is our final best estimate of the integrated V magnitude of VdB0, corresponding to
MV=-10.42 ![]() 0.20; these values will be adopted in the following analysis.
0.20; these values will be adopted in the following analysis.
4 Summary and discussion
We have outlined the data reduction and scientific analysis strategy that we adopt for our HST-WFPC2 survey of M31 candidate YMCs, whose complete results will be presented in future contributions.
As an exemplary case, we have described the study of the cluster VdB0. We have found that VdB0 is a very bright and extended cluster of approximately solar metallicity and of age ![]() 25 Myr,
with a rich population of blue and red supergiants.
25 Myr,
with a rich population of blue and red supergiants.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725vdb0.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg154.gif) |
Figure 14:
Integrated V mag and total mass as a function of age for various clusters. Galactic Open Clusters (OC, from the WEBDA database) are plotted filled circles, Galactic Globular Clusters (GC, MV from the most recent version of the Harris (1996) catalogue, i.e. that of February 2003; the ages have been arbitrarily assumed to be 12.0 Gyr for all the clusters) are plotted as |
| Open with DEXTER | |
Having clearly ascertained that VdB0 is a real cluster, it remains to be established if it is more similar to ordinary open clusters of the Milky Way than to to the Young Massive Clusters that may be considered as possible precursors of ``disk globulars''. The similarity with LMC objects typically classified as ``Young Globular Clusters'' such as NGC 1850 (see Sect. 3., above) is quite remarkable and it suggests that VdB0 is not an ordinary OC (but see also point 1, below).
A more general way to compare clusters of different ages, taking into account the fading of the luminosity of SSPs as they age, it is to plot them into a diagram comparing age to some indicator of the stellar mass of the cluster (see, for example, Whitmore et al. 2007; Gieles et al. 2007; and de Grijs et al. 2008, for recent applications and references). Here we adopt log(Age) vs. absolute integrated magnitude as in B08.
In Fig. 14 VdB0 is compared with Galactic Open Clusters (data taken from the WEBDA database![]() ), with Galactic Globular Clusters (from the latest version of Harris 1996 assuming a uniform age of 12 Gyr, a reasonable approximation for our purpose), and with a grid of SSP models with solar metallicity and Salpeter's IMF from the set by Maraston
), with Galactic Globular Clusters (from the latest version of Harris 1996 assuming a uniform age of 12 Gyr, a reasonable approximation for our purpose), and with a grid of SSP models with solar metallicity and Salpeter's IMF from the set by Maraston![]() (1998,2005). As a SSP ages massive stars die while the mass of the most luminous stars
decreases (passive evolution). Keeping the total mass fixed, the luminosity of the population fades and, as a consequence, the stellar mass-to-light (M/L) ratio increases. The continuous lines plotted in Fig. 14 describe the passive evolution of SSPs of various (stellar) masses: under the adopted assumptions the mass of a cluster of given age and MV can be read from the grid of iso-mass tracks.
(1998,2005). As a SSP ages massive stars die while the mass of the most luminous stars
decreases (passive evolution). Keeping the total mass fixed, the luminosity of the population fades and, as a consequence, the stellar mass-to-light (M/L) ratio increases. The continuous lines plotted in Fig. 14 describe the passive evolution of SSPs of various (stellar) masses: under the adopted assumptions the mass of a cluster of given age and MV can be read from the grid of iso-mass tracks.
The path of the track passing through the cluster shows what its luminosity will be in the future if the cluster did not lose stars through dynamical processes (evaporation, tides, ecc.). The latter is clearly not the case in general, and in particular for VdB0. In addition to the relatively mild evaporation driven by two body encounters, it will suffer from the strain of the M31 tidal field and from encounters with Giant Molecular Clouds (GMC), as the cluster is embedded in the dense thin disk of M31 (Lamers & Gieles 2006, hereafter LG06, and references therein). To take these effects into account we used the analytical approach presented by LG06 to produce an evolutionary track including the cluster mass loss by stellar evolution, galactic tidal field, spiral arm shocking, and encounters with giant molecular clouds, plotted in Fig. 14 as a long-dashed curve. The LG06 formulas describe the evolution of a cluster located within the Milky Way (thin) disk at the Solar circle. They should provide a reasonable approximation for VdB0 which lies in the disk of M31, at a similar distance from the center of a similarly massive spiral galaxy (van den Bergh 2000). The required inputs are the cluster mass, for which we adopted the value that can be read from the SSP grid of Fig. 14 (see below), and the half-light radius, which we obtained in Sect. 3.3, above (see Table 4). The initial expulsion of gas not used in star formation may lead young clusters (age < 50 Myr) to lose their virial equilibrium and it may represent an additional relevant factor driving toward the destruction of clusters like VdB0 that is not included in the LG06 approach (Bastian & Goodwin 2006; Goodwin & Bastian 2006; Bastian et al. 2008).
Figure 14 is worth of some detailed considerations:
- 1.
- Independently of the exact value of MV adopted, VdB0 is significantly brighter (
 1 mag) than Galactic OCs of similar ages, actually it is brighter than Galactic OCs of any age. The same is true also if all other known M31 OCs are considered (Hodge 1979; Krienke & Hodge 2007,2008). However it should be noted that the population of disk clusters in M31 may be so huge (
1 mag) than Galactic OCs of similar ages, actually it is brighter than Galactic OCs of any age. The same is true also if all other known M31 OCs are considered (Hodge 1979; Krienke & Hodge 2007,2008). However it should be noted that the population of disk clusters in M31 may be so huge ( 80 000 clusters, according to Krienke & Hodge 2007) that even the extreme tails of the luminosity distribution may be populated. (This
should not be the case for the LMC, for example, as it is orders of magnitude less massive than M31). Hence it is premature to draw a conclusion from an individual cluster; when the whole sample is analyzed we will get a deeper insight on the actual nature of VdB0.
80 000 clusters, according to Krienke & Hodge 2007) that even the extreme tails of the luminosity distribution may be populated. (This
should not be the case for the LMC, for example, as it is orders of magnitude less massive than M31). Hence it is premature to draw a conclusion from an individual cluster; when the whole sample is analyzed we will get a deeper insight on the actual nature of VdB0.
- 2.
- Assuming the RBC value for the integrated V magnitude,
E(B-V)=0.0 instead of
E(B-V)=0.2 and a grid of iso-mass tracks adopting a Kroupa IMF, we can obtain an extremely conservative strong lower limit to the stellar mass of VdB0, M=2.4

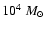 .
Under the same assumptions but adopting the best-fit value
E(B-V)=0.2 we
obtain M=6.5
.
Under the same assumptions but adopting the best-fit value
E(B-V)=0.2 we
obtain M=6.5 
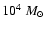 with a Salpeter IMF and M=4.2
with a Salpeter IMF and M=4.2 
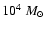 with a Kroupa IMF. These are at the threshold between the OC and GC mass distributions (see van den Bergh & Lafontaine 1984 and B08) and also at the upper end of the mass distribution of Galactic YMC (see Figer 2008 and Fig. 16, below). The conclusion that VdB0 is much more massive than MW clusters of similar ages seems inescapable, unless extreme IMFs are considered (i.e. IMF truncated at low masses, see Sternberg 1998).
with a Kroupa IMF. These are at the threshold between the OC and GC mass distributions (see van den Bergh & Lafontaine 1984 and B08) and also at the upper end of the mass distribution of Galactic YMC (see Figer 2008 and Fig. 16, below). The conclusion that VdB0 is much more massive than MW clusters of similar ages seems inescapable, unless extreme IMFs are considered (i.e. IMF truncated at low masses, see Sternberg 1998).
- 3.
- If
MV=-10.42 is adopted, as obtained from large aperture ground-based V photometry in Sect. 3.4, the total stellar mass is M=9.5

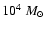 with a Salpeter IMF and
M=6.0
with a Salpeter IMF and
M=6.0 
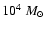 with a Kroupa IMF.
with a Kroupa IMF.
- 4.
- The evolutionary tracks including the LG06 treatment of mass-loss by dynamical effects show that, independent of the actual mass (within the range outlined above), it is unlikely that the cluster VdB0 would survive for an Hubble time. Hence it is very probable that it will never have the opportunity to evolve into a classical (faint) GC. The disruption timescale is dominated by encounters with GMCs; considering this effect alone (Eq. (7) of LG06) the cluster is predicted to dissolve within
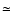 3.6 Gyr if its mass is M=9.5
3.6 Gyr if its mass is M=9.5 
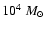 ,
as obtained from our best estimate of the integrated V magnitude and assuming a Salpeter's IMF.
,
as obtained from our best estimate of the integrated V magnitude and assuming a Salpeter's IMF.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725mir.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg157.gif)
Figure 15: The same as Fig. 14 but for near infrared colors. Integrated magnitudes of GCs are taken from Cohen et al. (2007); the IR magnitudes for VdB0 are taken from Table 4. The dotted lines are
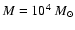 and
and
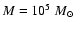 iso-mass models assuming a Kroupa (2001) IMF instead of a Salpeter (1955) IMF, plotted here to illustrate the weak effect of assumptions on IMFs.
iso-mass models assuming a Kroupa (2001) IMF instead of a Salpeter (1955) IMF, plotted here to illustrate the weak effect of assumptions on IMFs.Open with DEXTER - 5.
- In the same grid of Fig. 14 and under the same assumptions the masses of the BLCCs observed by WH01 - adopting their age estimates - range from 8.0

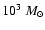 ,
(G293) in the realm of OCs, to
,
(G293) in the realm of OCs, to  2
2 
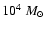 (G44 and G94) and
(G44 and G94) and
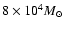 (G38), very similar to that of VdB0
and significantly larger than OCs of similar ages.
(G38), very similar to that of VdB0
and significantly larger than OCs of similar ages.
NIR magnitudes are more reliable mass tracers than visual magnitudes as NIR M/L ratios are smaller and have smaller variations with age, compared to optical M/L ratios. For example, according to Maraston (1998,2005) models, a solar metallicity Salpeter-IMF SSP at Age = 10 Gyr has (M/L)V = 5.5, while (M/L)K = 1.4; the same SSP has
![]() while
while
![]() .
The independent estimates of the stellar mass from J, H, and K magnitudes are essentially identical, ranging from 6 to 9
.
The independent estimates of the stellar mass from J, H, and K magnitudes are essentially identical, ranging from 6 to 9 ![]()
![]() ,
assuming a Salpeter IMF, and from 4 to 5.5
,
assuming a Salpeter IMF, and from 4 to 5.5 ![]()
![]() ,
assuming a Kroupa IMF. These estimates are in fair agreement with those obtained from the integrated V photometry.
,
assuming a Kroupa IMF. These estimates are in fair agreement with those obtained from the integrated V photometry.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725m_rh.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg164.gif) |
Figure 16:
VdB0 (crossed square) is compared to other clusters in the logarithm of
the mass vs. logarithm of the half-light-radius plane. Filled circles are Galactic GCs from Mackey & van den Bergh (2005). Arrows are Galactic OCs: we plot the radii where a break in the surface brightness profile occurs, taken from Kharchenko et al. (2005, their ``core radii''). These should be considered as upper limits for actual |
| Open with DEXTER | |
Finally, in Fig. 16 we compare VdB0 with Galactic OCs, GCs and YMC, plus the BLCCs studied by WH01, in the log of the stellar mass versus log of the half-light radius plane (similar to Mackey & van den Bergh 2005; Federici et al. 2007). The radii at which the break in the profile (core/corona transition) of Galactic OCs (from Kharchenko et al.
2005) occurs is taken as a strong upper limit for their ![]() .
VdB0 has a typical size that is larger than both OCs and YMCs, and is similar to that of several MW GCs of comparable mass.
.
VdB0 has a typical size that is larger than both OCs and YMCs, and is similar to that of several MW GCs of comparable mass.
In conclusion, we can say that VdB0 seems a remarkable cluster in several of its properties when compared to the other known disk clusters of the Milky Way and M31. In this paper we have presented the data reduction, data analysis and diagnostics that will be applied to the whole survey sample and that will allow us to put VdB0 and the other clusters in the more general context of the star cluster populations in the disk of spiral galaxies.
Acknowledgements
S.P. and M.B. acknowledge the financial support of INAF through the PRIN 2007 grant CRA 1.06.10.04 ``The local route to galaxy formation ...''. P.B. acknowledges research support through a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada. J.G.C. is grateful for partial support through grant HST-GO-10818.01-A from the STcI. T.H.P. gratefully acknowledges support in form of a Plaskett Fellowship at the Herzberg institute of Astrophysics in Victoria, BC. J.S. was supported by NASA through an Hubble Fellowship, administered by STScI. We are grateful to S. van den Bergh for having pointed out some errors in the historical reconstruction of the discovery of VdB0 that were reported in a previous version of the paper.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] (In the text)
- Barmby, P., Huchra, J. P., Brodie, J. P., et al. 2000, AJ, 119, 727 [NASA ADS] [CrossRef] (In the text)
- Barmby, P., Huchra, J. P., & Brodie, J. P. 2001, AJ, 121, 1482 [NASA ADS] [CrossRef]
- Barmby, P., Ashby, M. L. N., Bianchi, L., et al. 2006, ApJ, 650, L45 [NASA ADS] [CrossRef] (In the text)
- Barmby, P., McLaughlin, D. E., Harris, W. E., Harris, G. L. H., & Forbes, D. 2007, AJ, 133, 2764 [NASA ADS] [CrossRef] (In the text)
- Bastian, N., & Goodwin, S. P. 2006, MNRAS, 369, L9 [NASA ADS] (In the text)
- Bastian, N., Gieles, M., Goodwin, S. P., et al. 2008, MNRAS, 389, 223 [NASA ADS] [CrossRef] (In the text)
- Battistini, P. L., Bonoli, F., Braccesi, A., et al. 1987, A&AS, 47, 847 (In the text)
- Beasley, M. A., Brodie, J. P., Strader, J., et al. 2004, AJ, 128, 1623 [NASA ADS] [CrossRef] (In the text)
- Bellazzini, M., Fusi Pecci, F., Messineo, M., Monaco, L., & Rood, R. T. 2002a, AJ, 123, 1509 [NASA ADS] [CrossRef] (In the text)
- Bellazzini, M., Fusi Pecci, F., Montegriffo, P., et al. 2002b, AJ, 123, 2541 [NASA ADS] [CrossRef]
- Bellazzini, M., Cacciari, C., Federici, L., Fusi Pecci, F., & Rich, M. 2003, A&A, 405, 867 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bellazzini, M., Perina, S., Galleti, S., et al. 2008, Mem. S.A.It., 79, 663 [NASA ADS] (B08) (In the text)
- Brocato, E., Di Carlo, E., & Menna, G. 2001, A&A, 374, 523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [NASA ADS] [CrossRef] (In the text)
- Burstein, D., Li, Y., Freeman, K. C., et al. 2004, ApJ, 614, 158 [NASA ADS] [CrossRef] (In the text)
- Carignan, C., Chemin, L., Hutchmeier, W. K., & Lockman, F. J. 2006, ApJ, 641, L109 [NASA ADS] [CrossRef] (In the text)
- Carpenter, J. M., Heyer, M. H., & Snell, R. L. 2000, ApJS, 130, 381 [NASA ADS] [CrossRef] (In the text)
- Clark, J. S., Negueruela, I., Crowther, P. A., & Goodwin, S. P. 2005, A&A, 434, 949 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cohen, J. G., Matthews, K., & Cameron, P. B. 2006, ApJ, 634, L45 [NASA ADS] (In the text)
- Cohen, J. G., Hsieh, S., Metchev, S., Djorgovski, S. G., & Malkan, M. 2007, AJ, 133, 99 [NASA ADS] [CrossRef] (In the text)
- Cordier, D., Pietrinferni, A., Cassisi, S., & Salaris, M. 2007, AJ, 133, 468 [NASA ADS] [CrossRef] (In the text)
- Davies, B., Figer, D. F., Law, C. J., et al. 2008, ApJ, 676, 1016 [NASA ADS] [CrossRef] (In the text)
- Dean, J. F., Warren, P. R., & Cousins, A. W. J. 1978, MNRAS, 183, 569 [NASA ADS]
- de Grijs, R., Goodwin, S. P., Kouwenhoven, M. B. N., & Kroupa, P. 2008, MNRAS, in press [arXiv:0803.1991] (In the text)
- Dolphin, A. E. 2000a, PASP, 112, 1383 [NASA ADS] [CrossRef] (In the text)
- Dolphin, A. E. 2000b, PASP, 112, 1397 [NASA ADS] [CrossRef] (In the text)
- Elson, R. A. W., Fall, S. M., & Freeman, K. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] (EFF87) (In the text)
- Fan, Z., Ma, J., de Grijs, R., & Zhou, X. 2008, MNRAS, 385, 1973 [NASA ADS] [CrossRef] (In the text)
- Federici, L., Bellazzini, M., Galleti, S., et al. 2007, A&A, 473, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Figer, D. F. 2008, in Massive Stars as Cosmic Engines, ed. F. Bresolin, P. A. Crowther, & J. Puls (Cambridge: Cambridge Univ. Press), IAU Symp., 250, 247 (In the text)
- Fusi Pecci, F., Bellazzini, M., Buzzoni, A., et al. 2005, AJ, 130, 554 [NASA ADS] [CrossRef] (F05) (In the text)
- Gallart, C., Zoccali, M., & Aparicio, A. 2005, ARA&A, 43, 387 [NASA ADS] [CrossRef] (In the text)
- Galleti, S., Federici, L., Bellazzini, M., et al. 2004, A&A, 416, 917 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gieles, M., Lamers, H. G. L. M., & Portegies-Zwart, S. F. 2007, ApJ, 668, 268 [NASA ADS] [CrossRef] (In the text)
- Gilmozzi, R., Kinney, E. K., Ewald, S. P., Panagia, N., & Romaniello, M. 1994, ApJ, 435, L43 [NASA ADS] [CrossRef] (In the text)
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] (G02) (In the text)
- Goodwin, S. P., & Bastian, N. 2006, MNRAS, 373, 752 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E. 2001, in Star clusters, Saas-Fee Advanced Course 28, Lecture Notes 1998, ed. L. Labhardt, & B. Binggeli (Berlin: Springer), 223 (In the text)
- Hodge, P. W. 1961, ApJ, 133, 413 [NASA ADS] [CrossRef] (In the text)
- Hodge, P. 1979, AJ, 84, 744 [NASA ADS] [CrossRef] (In the text)
- Hodge, P. 1981, Atlas of the Andromeda Galaxy (Seattle and London: University of Washington Press) (In the text)
- Hodge, P. 1992, The Andromeda Galaxy (Dordrecht: Kluwer) (In the text)
- Holmberg, J., Flynn, C., & Portinari, L. 2006, MNRAS, 367, 449 [NASA ADS] [CrossRef]
- Holtzman, J., Burrows, C. J., Casertano, S., et al. 1995, PASP, 107, 1065 [NASA ADS] [CrossRef] (In the text)
- Hubble, E. 1929, ApJ, 69, 103 [NASA ADS] [CrossRef] (In the text)
- Hubble, E. 1936, The Realm of the Nebulae (London: Oxford University Press) (In the text)
- Huchra, J. P., Brodie, J. P., & Kent, S. M. 1991, ApJ, 370, 495 [NASA ADS] [CrossRef] (In the text)
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- King, I. R. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] (K62)
- King, I. R. 1966, AJ, 71, 64 [NASA ADS] [CrossRef] (K66) (In the text)
- Kinman, T. 1959, MNRAS, 119, 538 [NASA ADS] (In the text)
- Koposov, S., de Jong, J. T. A., Belokurov, V., et al. 2007, ApJ, 669, 337 [NASA ADS] [CrossRef] (In the text)
- Krienke, O. K., & Hodge, P. W. 2007, PASP, 119, 7 [NASA ADS] [CrossRef] (In the text)
- Krienke, O. K., & Hodge, P. W. 2008, PASP, 120, 1 [NASA ADS] [CrossRef]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] (In the text)
- Kubiak, M., Kaluzny, J., Krzeminski, W., & Mateo, M. 1992, AcA, 42, 155 [NASA ADS] (In the text)
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] (In the text)
- Lada, E. A., Depoy, D. L., Evans, N. J., II, & Gatley, I. 1991, ApJ, 371, 171 [NASA ADS] [CrossRef] (In the text)
- Lamers, H. J. G. L. M., & Gieles, M. 2006, A&A, 455, L17 [NASA ADS] [CrossRef] [EDP Sciences] (LG06) (In the text)
- Larsen, S. S. 2003, Extragalactic Globular Cluster Systems, 54 [NASA ADS] [CrossRef] (In the text)
- Larsen, S. S., & Richtler, T. 1999, A&A, 345, 59 (In the text)
- Lee, M.-G., Hwang, H.-S., Kim, S.-C., et al. 2008, ApJ, 674, 886 [NASA ADS] [CrossRef] (In the text)
- Lupton, R. 2005, www.sdss.org/dr4/algorithms/sdssUBVRITransform.html#Lupton2005 (In the text)
- Mackey, A. D., & Gilmore, G. F. 2003, MNRAS, 338, 85 [NASA ADS] [CrossRef] (In the text)
- Mackey, A. D., & van den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef] (In the text)
- Maraston, C. 1998, MNRAS, 300, 872 [CrossRef] (In the text)
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] (In the text)
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] (M08) (In the text)
- Martin, N., de Jong, J. T. A., & Rix, H.-W. 2008, ApJ, 684, 1075 [NASA ADS] [CrossRef] (In the text)
- Massey, P. 2003, ARA&A, 41, 15 [NASA ADS] [CrossRef] (In the text)
- Massey, P., Olsen, K. A. G., Hodge, P. W., et al. 2006, AJ, 131, 2478 [NASA ADS] [CrossRef] (M06) (In the text)
- McLaughlin, D. E., Barmby, P., Harris, W. E., Harris, G. L. H., & Forbes, D. 2008, MNRAS, 384, 564 [NASA ADS] (In the text)
- McConnachie, A. W., Irwin, M. J., & Ferguson, A. M. N. 2005, MNRAS, 356, 979 [NASA ADS] [CrossRef] (In the text)
- Morrison, H., Harding, P., Perrett, K. M., & Hurley-Keller, D. 2004, ApJ, 603, 87 [NASA ADS] [CrossRef] (In the text)
- Perrett, K. M., Bridges, T. J., Hanes, D. A., et al. 2002, AJ, 123, 2490 [NASA ADS] [CrossRef] (In the text)
- Phelps, R. L., & Schick, M. 2003, AJ, 126, 265 [NASA ADS] [CrossRef] (In the text)
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] (In the text)
- Puzia, T. H., Perrett, K. M., & Bridges, T. J. 2005, A&A, 434, 909 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Renzini, A., & Fusi Pecci, F. 1988, ARA&A, 26, 199 [NASA ADS] [CrossRef]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef]
- Sagar, R., Richtler, T., & de Boer, K. S. 1991, A&AS, 90, 387 [NASA ADS] (In the text)
- Salasnich, B., Girardi, L., Weiss, A., & Chiosi, C. 2000, A&A, 361, 1023 [NASA ADS] (In the text)
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] (In the text)
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
- Sérsic, J.-L. 1968, Atlas de Galaxias Australes, Cordoba, Obs. Astronomico (In the text)
- Sharov, A. S., Lyutyi, V. M., & Esipov, V. F. 1995, Astr. Lett., 21, 275 [CrossRef] (In the text)
- Sternberg, A. 1998, ApJ, 506, 721 [NASA ADS] [CrossRef] (In the text)
- Tosi, M., Sabbi, E., Bellazzini, M., et al. 2001, AJ, 122, 1271 [NASA ADS] [CrossRef] (In the text)
- Vallenari, A., Aparicio, A., Fagotto, F., et al. 1994, A&A, 284, 447 [NASA ADS] (In the text)
- van den Bergh, S. 1964, ApJS, 9, 65 [NASA ADS] [CrossRef] (In the text)
- van den Bergh, S. 1969, ApJS, 171, 19 (In the text)
- van den Bergh, S. 2000, The Galaxies of the Local Group (Cambridge: Cambridge University Press) (In the text)
- van den Bergh, S., & Lafontaine, A. 1984, AJ, 89, 1822 [NASA ADS] [CrossRef] (In the text)
- Vetesnik, M. 1962, Bull. Astron. Inst. Czechoslovakia, 13, 180 (In the text)
- Williams, B. F., & Hodge, P. W. 2001, ApJ, 548, 190 [NASA ADS] [CrossRef] (In the text)
- Wilson, C. P. 1975, AJ, 80, 175 [CrossRef] (In the text)
- Whitmore, B. C., & Schweizer, F. 1995, AJ, 109, 960 [NASA ADS] [CrossRef] (In the text)
- Whitmore, B. C., Chandar, R., & Fall, S. M. 2007, AJ, 133, 1067 [NASA ADS] [CrossRef] (In the text)
- Zinn, R. 1985, ApJ, 293, 424 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... Myr
![[*]](/icons/foot_motif.gif)
- Based on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with program GO-10818 [P.I.: J. G. Cohen].
- ...
![[*]](/icons/foot_motif.gif)
- Plaskett Fellow.
- ...
![[*]](/icons/foot_motif.gif)
- Hubble Fellow.
- ... Catalogue
![[*]](/icons/foot_motif.gif)
- www.bo.astro.it/M31
- ... Nebulae
![[*]](/icons/foot_motif.gif)
- van den Bergh kindly drove our attention to this curious occurrence.
- ...2002
![[*]](/icons/foot_motif.gif)
- Note that Perret's et al. measures refers to B195D, i.e. the ``alter ego'' of VdB0 whose available coordinates were the most appropriate for the cluster. In this context, it is interesting to note that, adopting a calibration based on old GCs, Perrett et al. found [Fe/H] = -1.64 for VdB0, from integrated spectral indices (see F05).
- ... HSTPHOT
![[*]](/icons/foot_motif.gif)
- See http://purcell.as.arizona.edu/hstphot/
- ...
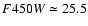
![[*]](/icons/foot_motif.gif)
- Except for the very crowded region at the center of the cluster. For 10 px < r
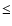 50 px, the 50% completeness level is reached at
50 px, the 50% completeness level is reached at
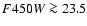 .
.
- ... metallicities
![[*]](/icons/foot_motif.gif)
- http://pleiadi.oapd.inaf.it
- ... tool
![[*]](/icons/foot_motif.gif)
- http://stev.oapd.inaf.it/lgirardi/cgi-bin/cmd
- ... BASTI
![[*]](/icons/foot_motif.gif)
- http://www.oa-teramo.inaf.it/BASTI/index.php
- ... Functions
![[*]](/icons/foot_motif.gif)
- Salpeter's IMF has
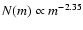 ;
Kroupa's IMF has
;
Kroupa's IMF has
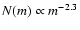 for
for
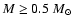 ,
and
,
and
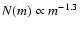 for
for
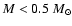 .
.
- ... respectively
![[*]](/icons/foot_motif.gif)
- This conversion assumes DN zeropoints of
Z450=21.884, Z814=21.528, a gain of 7 electrons DN-1, and
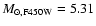 and
and
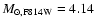 .
.
- ... example
![[*]](/icons/foot_motif.gif)
- The surface brightness profiles of these and other LMC clusters have been studied by Mackey & Gilmore (2003) who provide the parameters of the EFF87 models that best fit the observed profiles. To derive the reported half-light radii we searched for the King 1962 model providing the best match to the EFF87 best-fit profile found by Mackey & Gilmore (2003), and adopted the corresponding
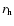 .
.
- ... (SSP
![[*]](/icons/foot_motif.gif)
- A Simple Stellar Population is a population of stars all having the same age and chemical composition and having individual masses extracted from a given Initial Mass Function (IMF); this is a practical idealized model that is generally believed to be a reasonable approximation of a star cluster, see Renzini & Fusi Pecci (1988).
- ... 0.11
![[*]](/icons/foot_motif.gif)
- We note that these values imply (V-I)0=0.41, adopting the reddening law by Dean et al. (1978), in excellent agreement with the prediction, used above, of (V-I)0 from Maraston's (2005) model for a solar metallicity SSP of age 25 Myr.
- ... database
![[*]](/icons/foot_motif.gif)
- http://www.univie.ac.at/webda/integre.html
- ... Maraston
![[*]](/icons/foot_motif.gif)
- http://www-astro.physics.ox.ac.uk/maraston/
- ... above)
![[*]](/icons/foot_motif.gif)
- For J, H, K colors we adopt AJ=0.871E(B-V), AH = 0.540E(B-V), and AK=0.346E(B-V), from Rieke & Lebofsky (1985). The J, H, K absolute magnitudes of the Sun are taken from Holmberg et al. (2006).
All Tables
Table 1: Positional and photometric parameters for VdB0 from the RBCa.
Table 2:
Uncertainties in the relative photometry from artificial stars experiments, for 10 px < r ![]() 160 px, PC field.
160 px, PC field.
Table 3:
Star counts in the CMD boxes defined in Fig. 10. Box A samples the upper MS, boxes B, C, and D samples SG stars of blue, intermediate and red colors, respectively.
![]() is the number of stars expected in a given box from the field population, computed by
rescaling the observed counts in the WF2 field by the ratio of the sampled areas. The ratio between the area of the considered field (annulus) and the area of the WF2 field (used as representative of the field population) is reported in the last column.
is the number of stars expected in a given box from the field population, computed by
rescaling the observed counts in the WF2 field by the ratio of the sampled areas. The ratio between the area of the considered field (annulus) and the area of the WF2 field (used as representative of the field population) is reported in the last column.
Table 4: Newly derived coordinates, half-light radius, integrated magnitudes, reddening, age and metallicity for the cluster VdB0. The origin of each parameter is described in the last column.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm]{0725mosa.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg48.gif) |
Figure 1: F450W mosaic of the whole field sampled by our WFPC2 observations. The cluster VdB0 is at the center of the PC camera. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0725imaB.ps}\par\includegraphics[width=8.8cm,clip]{0725imaI.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg49.gif) |
Figure 2: F450W ( upper panel) and F814W ( lower panel) images of the whole PC camera, with VdB0 at the center. The superposed circles have radius r=160, 205, 260, 288 and 330 pixels, from inside out, and mark the edges of the annuli whose CMDs are shown in Fig. 9, below. The light stripes associated with stars in the F450W image are due to the effect of CTE that is particularly strong in this shallow low-background image. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0725cmd.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg52.gif) |
Figure 3: CMD of the fields sampled by the four chips of the WFPC2. The number of stars plotted is reported in the upper right corner of each panel. The upper line marks the threshold above which stars saturate the intensity scale of the images. The lower lines are CMD loci at the same level of completeness, 90%, 70% and 50% from top to bottom, respectively (see labels in the WF2 panel). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{0725err.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg57.gif) |
Figure 4:
Distributions of the differences between the output and input magnitudes of artificial stars as a function of F450W ( left panels) and F814W ( right panels) magnitudes, for the PC and WF fields. The top panel displays the distributions for the most crowded region of the PC camera, i.e. the one containing the cluster.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725comp.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg64.gif) |
Figure 5:
Completeness factor ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725ebv.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg73.gif) |
Figure 6:
The observed CMD of VdB0 (black dots, only stars with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725eta.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg77.gif) |
Figure 7:
Isochrones of different ages and metal content are plotted on the ``visibility window'' of our CMDs, enclosed on the bright side by the saturation limits and on the faint side by the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0725prof.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg79.gif) |
Figure 8:
Upper panel: background-subtracted surface density profile of
VdB0 computed by counting stars on circular concentric annuli around the center of the cluster. The arrow marks the radius where a sudden change of slope in the profile appears, at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{0725clus.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg88.gif) |
Figure 9:
CMDs of different circular annuli around the center of VdB0 in the PC field (see Fig. 2, above), all having the same area ( upper panels and lower left panel),
and of the whole WF2 field, whose area is 32 times that of the PC annuli ( lower right panel).
The thin line is a
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0725rsg.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg92.gif) |
Figure 10:
CMDs of different annuli around the center of VdB0 in the PC field ( upper panels) and of a large area in the WF2 field ( lower left panel), expected to sample the surrounding ``field'' population. An isochrone of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{0725agei.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg114.gif) |
Figure 11: Age estimates for VdB0 for different assumptions about the total metallicity (Z). Isochrones from the G02 set are compared to the CMD of the cluster (10 px < r < 160 px). The best-fit isochrone is plotted as a thick continuous line while the dashed isochrones bracket the upper and lower limits on age. The ages and metallicities of the adopted isochrones are reported in each panel. The dotted lines mark the limiting magnitude as a function of color: the diagonal plume of stars just above the lines (with F450W-F814W > 1.5) is populated by likely RGB and AGB field stars, not associated with the cluster. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0725lf2.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg125.gif) |
Figure 12:
Comparison of the observed LF with theoretical models from the G02 suite. Upper left panel: CMD of VDB0 with overplotted the box adopted to select the sample of stars to be included in the LF. The considered radial range avoids the innermost region where the completeness displays significant radial variations in the range of magnitudes considered. Upper right panel: completeness as a function of magnitude for the color and radial range considered.
Lower panel: the observed LF (before completeness correction = histogram; corrected for completeness = filled circles with error bars) is compared with models of different ages. Note the good fit of the drop at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725sbpr.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg152.gif) |
Figure 13: Intensity profiles from surface photometry in circular annuli from the F814W image ( upper panel) and for the F450W image ( lower panel). The continuous lines are the respective best-fit models, convolved with the instrumental PSF and with a constant background level added. For the parameters of the best-fit models see text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725vdb0.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg154.gif) |
Figure 14:
Integrated V mag and total mass as a function of age for various clusters. Galactic Open Clusters (OC, from the WEBDA database) are plotted filled circles, Galactic Globular Clusters (GC, MV from the most recent version of the Harris (1996) catalogue, i.e. that of February 2003; the ages have been arbitrarily assumed to be 12.0 Gyr for all the clusters) are plotted as |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725mir.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg157.gif) |
Figure 15:
The same as Fig. 14 but for near infrared colors. Integrated magnitudes of GCs are taken from Cohen et al. (2007); the IR magnitudes for VdB0 are taken from Table 4. The dotted lines are
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0725m_rh.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10725-08/Timg164.gif) |
Figure 16:
VdB0 (crossed square) is compared to other clusters in the logarithm of
the mass vs. logarithm of the half-light-radius plane. Filled circles are Galactic GCs from Mackey & van den Bergh (2005). Arrows are Galactic OCs: we plot the radii where a break in the surface brightness profile occurs, taken from Kharchenko et al. (2005, their ``core radii''). These should be considered as upper limits for actual |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.