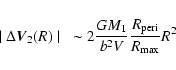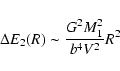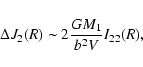| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 891 - 904 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361:200810339 | |
| Published online | 11 December 2008 | |
On the origin of dwarf elliptical galaxies: the fundamental plane
J. A. L. Aguerri1 - A. C. González-García2
1 - Instituto de Astrofísica de Canarias, Calle via Lactea
s/n, 38200 La Laguna, Spain
2 -
Dept. Física Teórica, Universidad Autónoma de Madrid, 28049 Madrid, Spain
Received 6 June 2008 / Accepted 7 November 2008
Abstract
Context. Early-type dwarf (dE) galaxies are the most common type of galaxies observed in the Universe. Their study has important cosmological implications because according to hierarchical galaxy evolution theories they are the progenitors of brighter galaxies. Nevertheless, the origin of this kind of system is still not well understood.
Aims. The aim of the present work is to investigate whether the different locations of dwarf galaxies with respect to ellipticals in the face-on view of the fundamental plane could be due to the transformation of bright disc galaxies in low-mass systems by harassment.
Methods. We have run high-resolution N-body numerical simulations to test the tidal stripping scenario of dE galaxies. The present simulations modelled several individual tidal stripping events in initial disc-like galaxy models with different bulge-to-disc mass ratios.
Results. The models have shown that tidal stripping is a very efficient mechanism for removing stars and dark matter particles from galaxies, specially from their outer parts. The particles of the disc and halo components were easily stripped, while the bulge particles were not. Thus, the scale length of the discs were 40-50![]() shorter than the initial ones. Prograde tidal interactions create tidal features like stable bars in the discs of the galaxies. In contrast, bars are inhibited in retrograde encounters. After several tidal interactions the galaxy remnants looks like a dwarf spheroidal system. The final position of the low-mass systems in the face-on view of the fundamental plane (FP) depends on the initial conditions of the simulations. Thus, simulated galaxies with initial large B/D ratios are closer to the face-on view of the fundamental plane defined by bright E and bulges of early-type galaxies. Nevertheless, galaxies with initially small B/D ratio are located, after four fast tidal encounters, at the position of dE galaxies in the face-on view of the fundamental plane.The final position of the remnants in the FP do not depend on the orbital configuration of the encounters.
shorter than the initial ones. Prograde tidal interactions create tidal features like stable bars in the discs of the galaxies. In contrast, bars are inhibited in retrograde encounters. After several tidal interactions the galaxy remnants looks like a dwarf spheroidal system. The final position of the low-mass systems in the face-on view of the fundamental plane (FP) depends on the initial conditions of the simulations. Thus, simulated galaxies with initial large B/D ratios are closer to the face-on view of the fundamental plane defined by bright E and bulges of early-type galaxies. Nevertheless, galaxies with initially small B/D ratio are located, after four fast tidal encounters, at the position of dE galaxies in the face-on view of the fundamental plane.The final position of the remnants in the FP do not depend on the orbital configuration of the encounters.
Conclusions. We conclude that fast galaxy-galaxy interactions are efficient mechanisms of transforming bright galaxies into dwarf ones. Indeed, the different location observed between Es and dEs in the face-on view of the fundamental plane can be explained by the formation of dwarf galaxies by harassment of late-type bright ones.
Key words: galaxies: evolution - galaxies: clusters: general - galaxies: interactions
1 Introduction
Early-type dwarf (dE) galaxies are low luminosity ( MB > -18) red systems mostly located in galaxy clusters (Phillipps et al. 1998; Pracy et al. 2004). The study of these objects has cosmological interest because, according to the hierarchical theory of galaxy evolution, dwarfs are the building blocks of the brightest galaxies (Kauffmann & White 1993). Nevertheless, their origin is still a matter of debate. There are three formation scenarios of early-type dwarf galaxies: gravitational collapse similar to bright elliptical (E) galaxies, ram-pressure stripping from gas-rich low mass irregular galaxies, and tidal debris left from interactions between galaxies or with the gravitational potential in galaxy clusters.
In the standard picture, early-type dwarf galaxies are formed from the gravitational collapse of primordial density fluctuations, similar to bright E galaxies. Once the first stars are formed, mechanisms of energy feedback into the interstellar medium have been proposed in order to regulate the subsequent star formation or even change the structure of the galaxies (Dekel & Silk 1986). This standard picture is mainly supported by several tight correlations between the structural parameters of bright and dwarf early-type galaxies. Those relations, discovered in Virgo, Fornax and Coma clusters, include those between colour and magnitude (Sandage & Visvanathan 1978), radius and luminosity (Graham & Guzmán 2003; Gutiérrez et al. 2004; Aguerri et al. 2004), surface brightness and luminosity (Kormendy 1977; Binggeli & Cameron 1991; Aguerri et al. 2005a; Graham & Guzmán 2003), or Sèrsic shape parameter and luminosity (Graham & Guzmán 2003; Aguerri et al. 2005a). These tight correlations could indicate a common origin between bright E and early-type dwarf galaxies. However, those common relations have also been explained by some authors as being more due to the uniformity of their dark matter halos than to a common formation mechanism (Navarro et al. 1997).
The second formation scenario is based on the presence of common stellar distributions of early-type dwarf and dwarf irregular (dIrr) galaxies (Lin & Faber 1983; Kormendy 1985; Caldwell & Bothun 1987; Binggeli & Cameron 1991; van Zee et al. 2004a). The role played by the environment in this formation scenario is crucial. Thus, ram pressure stripping can disrupt the gas from gas rich low-mass galaxies and transform them into early-type dwarf galaxies (Boselli et al. 2008; Sánchez-Janssen et al. 2008). Repeated tidal shocks suffered by a dwarf satellite galaxy can also convert the kinematic signature of a dIrr galaxy into an early-type dwarf (Mayer et al. 2001a,b). This formation mechanism has been supported by kinematic studies of early-type dwarf galaxies in the Virgo cluster (Pedraz et al. 2002; Geha et al. 2002; Geha et al. 2003; van Zee et al. 2004b; Corsini et al. 2007). It was found that most of the early-type dwarf galaxies are rotationally supported, similarly to dIrrs. However, a scenario where all early-type dwarf galaxies evolve from dIrr via disc fading does not seem possible, because many early-type dwarfs in the Virgo and Fornax clusters are brighter than the dIrr (Conselice et al. 2001). Another important point against this scenario is the increase in metallicity measured in the old stellar populations in early-type dwarf galaxies with respect to dwarf irregulars of similar luminosity (Grebel et al. 2003). This issue was explained by Boselli et al. (2008).
In the harassment scenario the cumulative effects of tidal fast encounters between galaxies and with the gravitational potential of the galaxy cluster can produce a dramatic morphological transformation from bright spiral galaxies to dwarfs (Moore et al. 1996; Mastropietro et al. 2005). The effects of harassment can be seen in the scale length of the discs of bright spiral galaxies. Thus, Aguerri et al. (2004) and Gutierrez et al. (2004) found that the scale length of the discs of bright spiral galaxies of the Coma cluster was shorter than similar galaxies in the field. The disrupted stars could form part of the so-called diffuse light observed in some nearby clusters such as Virgo (Arnaboldi et al. 2002; Feldmeier et al. 2004; Aguerri et al. 2005b; Williams et al. 2007), Coma (Gerhard et al. 2005, 2007) and Fornax (Theuns & Warren 1997). However, the major part of this diffuse cluster component seems to be associated with the merger history of the brightest cluster galaxies rather than with disrupted dwarf galaxies (Murante et al. 2007). Nevertheless, some bright spiral galaxies can lose part of their stars by fast interactions with the cluster potential and transform into a hot dwarf-like object similar to the observed early-type dwarf galaxies (Mastropietro et al. 2005). Previous dwarf formation scenarios have also some contradictions. In particular, one prediction of the harassment model is that dwarf galaxies should lie in low surface brightness tidal streams or arcs. However, Davies et al. (2008) have found no evidence for any such features in a sample of dwarf galaxies in the Virgo cluster.
In a series of papers, Lisker et al. (2006a,b, 2007) have proposed that the cluster dwarf galaxy population is composed of different sub-categories of objects, not all of which have been formed in the same way. The different formation mechanisms among the population of early-type dwarf galaxies could be seen in different positions on the fundamental plane (FP). The analysis of the location in the FP of harassed bright spiral galaxies is one piece of information lost in this puzzle, and will be analysed in the present paper.
The FP is a tight relation between the surface brightness, effective radius and central velocity dispersion followed by hot systems such as elliptical galaxies and bulges of spirals. One of the projections of this plane is the so-called Faber-Jackson (Faber & Jackson 1976; FJ) relation. It has been observed that dE and bright E galaxies have different FP (Bender et al. 1992; Peterson & Caldwell 1993) and Faber-Jackson relations (Held et al. 1992; Tonry 1981; Davies et al. 1983; Matkovic & Guzmán 2005). In particular, the face-on view of the FP shows that dE are located in an area disconnected from bright E galaxies. It was also observed that bright E galaxies follow the FJ relation which can be expressed as
![]() ,
where
,
where ![]() (Faber & Jackson 1976; Sargent et al. 1977; Schechter & Gunn 1979; Schechter 1980; Tonry 1981; Terlevich et al. 1981; Forbes & Ponman 1999), while dE galaxies show
(Faber & Jackson 1976; Sargent et al. 1977; Schechter & Gunn 1979; Schechter 1980; Tonry 1981; Terlevich et al. 1981; Forbes & Ponman 1999), while dE galaxies show
![]() (Tonry 1981; Davies et al. 1983; Held et al. 1992; Matkovic & Guzmán 2005). These observational evidences suggest a different origin and/or evolution of these two kinds of systems. Thus, Matkovic & Guzmán (2005) demonstrated that the different FJ relation observed between bright E and dE cannot be explained by the presence of rotation in the dE sample. They conclude that faint early-type galaxies in Coma had to be formed at least 6 Gyr ago and over a short 1 Gyr period. The different FPs displayed by bright E and dE was also investigated by de Rijcke et al. (2005). They pointed out that internal processes could produce such differences. They concluded that semi-analytical models that incorporate quiescent star formation combined with post-merger starbursts and the dynamical response after supernova-driven gas-loss were able to reproduce the position of dE in the FP. These two previous works indicate that the differences in the FP and FJ relation could be explained by different internal evolution between bright E and dE galaxies. Nevertheless, little attention has been paid to the analysis of these differences due to other origins.
(Tonry 1981; Davies et al. 1983; Held et al. 1992; Matkovic & Guzmán 2005). These observational evidences suggest a different origin and/or evolution of these two kinds of systems. Thus, Matkovic & Guzmán (2005) demonstrated that the different FJ relation observed between bright E and dE cannot be explained by the presence of rotation in the dE sample. They conclude that faint early-type galaxies in Coma had to be formed at least 6 Gyr ago and over a short 1 Gyr period. The different FPs displayed by bright E and dE was also investigated by de Rijcke et al. (2005). They pointed out that internal processes could produce such differences. They concluded that semi-analytical models that incorporate quiescent star formation combined with post-merger starbursts and the dynamical response after supernova-driven gas-loss were able to reproduce the position of dE in the FP. These two previous works indicate that the differences in the FP and FJ relation could be explained by different internal evolution between bright E and dE galaxies. Nevertheless, little attention has been paid to the analysis of these differences due to other origins.
The origin and evolution of the FP of elliptical galaxies has received considerable attention from N-body modellers (Bekki 1998; Aceves & Velázquez 2005; Capelato et al. 1995). González-García & van Albada (2003) and Nipoti et al. (2003) showed that the FP is not severely affected by a few merging events. This results have been confirmed by several later studies (e.g. Boylan-Kolchin et al. 2006) including self-consistent cosmological simulations (Oñorbe et al. 2006, 2007). However the location of the different galaxy types, like dEs, in the FP has received much less interest.
The aim of the present work is to investigate whether the position of the dE in the FP can be explained by the harassment scenario, which posits that dEs stem from perturbed and stripped late-type disc galaxies that entered in clusters and groups of galaxies some Gyr ago. The structure of the paper is as follow: the sample of galaxies used and the FP of bright and low-luminous galaxies are shown in Sect. 2; N-body numerical simulations of harassed bright galaxies are presented in Sect. 3; our discussion and conclusions are given in Sects. 4 and 5, respectively.
2 The fundamental plane
It is well known that dynamically hot systems (elliptical galaxies and bulges of spiral galaxies) are not scattered randomly in the three-dimensional space spanned by the luminosity, half-light radius, and velocity dispersion (Dressler et al. 1987; Djorgovski & Davis 1987; Bender et al. 1992; Falcón-Barroso et al. 2002; Bernardi et al. 2003). Those objects are located in a plane called the Fundamental Plane given by:
| (1) |
where
The FP can be directly derived from the virial theorem:
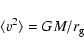 |
(2) |
where M is the total mass of the system,
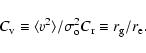 |
(3) |
Introducing these parameters in Eq. (1), and using
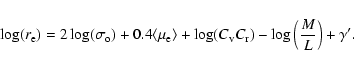 |
(4) |
Thus, the virial theorem predicts that
Another formulation of the FP is the so-called ![]() -space (Bender et al. 1992) expressed by:
-space (Bender et al. 1992) expressed by:
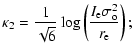 |
|||
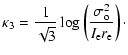 |
(5) |
Using these definitions and the virial theorem,
Most of the studies about the FP have been centred on bright early-type galaxies in nearby galaxy clusters (see D'onofrio et al. 2006, and references therein). Notwithstanding, the location of dwarf galaxies in the fundamental plane has not been extensively analysed since the early works by Nieto et al. (1990), Bender et al. (1992), and Guzman et al. (1993). However, Bender et al. (1992) and Guzman et al. (1993), based on a small sample of dwarf galaxies, found that dwarf galaxies were located in a different position in the face-on view of the FP defined in the ![]() -space. The distribution of the dwarf galaxies were perpendicular to the relationship defined by luminous elliptical galaxies in the
-space. The distribution of the dwarf galaxies were perpendicular to the relationship defined by luminous elliptical galaxies in the
![]() plane. This trend was confirmed on a larger sample by De Rijcke et al. (2005).
plane. This trend was confirmed on a larger sample by De Rijcke et al. (2005).
In the present work we have analysed the fundamental plane of a large sample of bright and dwarf galaxies located in the Coma cluster. The sample is formed by 215 galaxies of different types: 35 bright E, 113 dE, 12 dS0, 23 bulges of early-type spirals, and 11 bulges of late-type galaxies![]() . The photometric parameters of the galaxies (
. The photometric parameters of the galaxies (![]() and
and
![]() )
were obtained from the surface brightness decompositions on these objects carried out by Aguerri et al. (2004, 2005a), and the central velocity dispersion of the galaxies (
)
were obtained from the surface brightness decompositions on these objects carried out by Aguerri et al. (2004, 2005a), and the central velocity dispersion of the galaxies (
![]() )
was taken from Matkovic & Guzmán (2005) and Smith et al. (2004).
)
was taken from Matkovic & Guzmán (2005) and Smith et al. (2004).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0339fig1.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg36.gif) |
Figure 1:
Fundamental plane in the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0339fig2.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg37.gif) |
Figure 2:
Residuals of the face-on fundamental plane in the |
| Open with DEXTER | |
The aim of the present work is to understand whether the segregation between bright and dwarf galaxies in the face-on view of the FP could be explained by the transformation of bright disc galaxies in low-mass systems by fast galaxy-galaxy encounters.
3 Numerical simulations
We have performed several N-body simulations to test the tidal stripping formation scenario for dEs. The present simulations are not cosmological ones. They model several individual tidal stripping events happening on different initial disc-like galaxy models. The simulations are pure N-body models with no gas content. Nevertheless, we have also simulated the effect of gas stripping on two models by removing 10![]() of the luminous particles at the beginning of the simulations. After each tidal interaction or gas stripping event we allow the system to reach virial equilibrium and then we investigate its position in the
of the luminous particles at the beginning of the simulations. After each tidal interaction or gas stripping event we allow the system to reach virial equilibrium and then we investigate its position in the ![]() -space.
-space.
3.1 Initial conditions and units of the simulations
Table 1:
Input number of particles and mass fraction of each component of the different models. Particle number is given in K-particles (
![]() ).
).
The initial galaxies of our simulations consisted of disc galaxies generated by the Kuijken & Dubinsky (1995) disc-bulge-halo algorithm. The galaxy has a King (1966) model for the bulge (if present), a Shu (1969) for the disc and an Evans (Kuijken & Dubinsky 1994) model for the halo, all components being modelled live. Table 1 gives the details of the different initial models of the simulations.
We have simulated galaxies with different bulge-to-disc (B/D) mass ratios in order to test different starting points for the simulations. Thus, the initial B/D mass ratios were 1:12 (TID1 and GST1 models), 1:5 (TID2 and GST2 models), and 1:2 (TID3 and TID4 models). In addition, four more models (TID5, TID6, TID7 and TID8) were pure disc galaxies, where no bulge was considered in the initial conditions. Assuming the well-known observational correlation between morphological type and B/D (e.g. Méndez-Abreu et al. 2008; Aguerri et al. 2004; Simien & de Vaucouleurs 1986) we can say that TID3 and TID4 could represent an early-type Sa galaxy; TID2 and GST2 show an Sb galaxy; TID1 and GST1 are similar to Sc galaxies; TID5-TID8 can be compared with an Sd/Sm galaxy.
We used model units to run the simulations. These units take the total mass of the initial galaxy as unity, the disc scale length as 0.2, and the constant of gravity G=1. However, in order to compare with real galaxies we need to convert the model units to physical ones. This was made by defining a set of conversion units to compare our simulations with observations. For bright galaxies, the scale length of the disc is independent of the morphological type, with ![]() kpc (see e.g. Aguerri et al. 2004, and references therein). This means that we can take a conversion factor of [L]=15 kpc for all simulations as the unit of length. In contrast, different galaxy types show different rotation curves. Thus, the maximum velocity (
kpc (see e.g. Aguerri et al. 2004, and references therein). This means that we can take a conversion factor of [L]=15 kpc for all simulations as the unit of length. In contrast, different galaxy types show different rotation curves. Thus, the maximum velocity (
![]() )
of Sa, Sb, Sc, and Sd galaxies are
)
of Sa, Sb, Sc, and Sd galaxies are ![]() 300,
300, ![]() 250,
250, ![]() 180 and
180 and ![]() 150 km s-1, respectively (Roberts 1978; Rubin et al. 1985). This means that the velocity conversion factor for our simulations were [V]= 496 km s-1 for TID3 and TID4; [V]=345 km s-1 for TID2 and GST2; [V]=230 km s-1 for TID1 and GST1; and [V]=175 km s-1 for TID5-TID8. Figure 3 shows the initial rotation curves of the different simulations. Notice the different
150 km s-1, respectively (Roberts 1978; Rubin et al. 1985). This means that the velocity conversion factor for our simulations were [V]= 496 km s-1 for TID3 and TID4; [V]=345 km s-1 for TID2 and GST2; [V]=230 km s-1 for TID1 and GST1; and [V]=175 km s-1 for TID5-TID8. Figure 3 shows the initial rotation curves of the different simulations. Notice the different
![]() and rotation curve central gradients of the simulations. Thus, TID5-TID8 models show smaller
and rotation curve central gradients of the simulations. Thus, TID5-TID8 models show smaller
![]() and less steep central gradient in the rotation curve than is observed in late-type galaxies. In contrast, TID3 and TID4 models show the largest
and less steep central gradient in the rotation curve than is observed in late-type galaxies. In contrast, TID3 and TID4 models show the largest
![]() and a steeper rotation curve corresponding to Sa galaxies with a large central mass concentration (large bulges). Assuming a time unit
and a steeper rotation curve corresponding to Sa galaxies with a large central mass concentration (large bulges). Assuming a time unit
![]() yr, the total mass of the galaxies is:
yr, the total mass of the galaxies is:
![]() for TID3 and TID4;
for TID3 and TID4;
![]() for TID2 and GST2;
for TID2 and GST2;
![]() for TID1 and GST1; and
for TID1 and GST1; and
![]() for TID5-TID8. Thus, in agreement with observations, the more massive galaxies correspond to those models simulating early-type galaxies.
for TID5-TID8. Thus, in agreement with observations, the more massive galaxies correspond to those models simulating early-type galaxies.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0339fig3.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg51.gif) |
Figure 3: Circular velocity curves for the initial conditions of the different simulations. |
| Open with DEXTER | |
3.2 Galaxy-galaxy encounters
The aim of the present simulations is to model fast encounters of our initial disc galaxy with another system of similar mass. The galactic interactions would be similar to the fast galaxy-galaxy encounters predicted in high density environments such as galaxy clusters (Moore et al. 1996). This kind of encounter has the peculiarity that the effective duration of the encounter is shorter than the characteristic crossing time of the majority of their stars. Moreover, the impact parameter of our fast encounters will be much larger than the typical galaxy scales. Therefore, this kind of galaxy encounter can be modelled using the impulse tidal approximation (see Binney & Tremaine 1987, Sect. 7.2(d)). Thus, we can assume that the galaxies have no time to reorganise during the encounter, hence the energy injection is all kinetic; reorganisation occurs after the encounter has finished.
The commonly used formula for the tidal impulse approximation does not take into account the extended nature of both bodies. Nevertheless, our encounters could not be considered between point-like galaxies. To take this into account, we have applied the formalism proposed by Gnedin et al. (1999) giving that the variation in the velocity (
![]() ), angular momentum (
), angular momentum (
![]() )
and energy (
)
and energy (
![]() )
of the particles in the models are:
)
of the particles in the models are:
where M1 is the total mass of the perturber, b is the impact parameter of the orbit,
The fast encounters were simulated by injecting energy, according to the previous expressions, into each particle of the modelled galaxy. Stars and dark matter particles in the modelled galaxy absorb energy (
![]() )
as well as angular momentum and may become unbound after the interaction. Since the velocity and energy change depend on the distance to the central parts, the particles with higher binding energy (
)
as well as angular momentum and may become unbound after the interaction. Since the velocity and energy change depend on the distance to the central parts, the particles with higher binding energy (
![]() )
are the ones that are most easily stripped away. After each tidal interaction we allow the system to reach virialization in the innermost regions by evolving the galaxy in isolation for more than 25 time units. This amounts to more than 50 half-mass radius crossing times of the bulge. For the different runs we have taken
)
are the ones that are most easily stripped away. After each tidal interaction we allow the system to reach virialization in the innermost regions by evolving the galaxy in isolation for more than 25 time units. This amounts to more than 50 half-mass radius crossing times of the bulge. For the different runs we have taken
![]() ,
V=2,
,
V=2,
![]() and M1 equal to the total mass of the initial galaxy at each tidal interaction, so we model equal-mass encounters. A total number of 4 tidal interactions were simulated for each model.
and M1 equal to the total mass of the initial galaxy at each tidal interaction, so we model equal-mass encounters. A total number of 4 tidal interactions were simulated for each model.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0339fig4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg64.gif) |
Figure 4: Evolution of the tidal events in TID1. Rows give the three views of the system after the different tidal harassment events. Colours indicate the different constituents of the initial galaxy: black-dark halo, green-disc and red-bulge |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0339fig5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg65.gif) |
Figure 5: Evolution of the tidal events in TID3. Rows give the three views of the system after the different tidal harassment events. Colours indicate the different constituents of the initial galaxy: black-dark halo, green-disc and red-bulge |
| Open with DEXTER | |
We have run 10 different simulations (see Table 1). The models TID1, TID2, TID3 and TID5 differ in the bulge-to-disc ratio (B/D), with
B/D=1/12, 1/5, 1/2, and 0 respectively. The relative orientation of the initial disc with respect to the orbital angular momentum was
![]() .
Models TID4 and TID6 are replicas of TID3 and TID5, changing the orientation of the initial discs with respect to the assumed orbit, now being (60,30). Models TID7 and TID8 are also identical to model TID5 but with retrograde orbits with respect to the disc spin; TID7 has
.
Models TID4 and TID6 are replicas of TID3 and TID5, changing the orientation of the initial discs with respect to the assumed orbit, now being (60,30). Models TID7 and TID8 are also identical to model TID5 but with retrograde orbits with respect to the disc spin; TID7 has
![]() ,
while TID8 has a less symmetric configuration
,
while TID8 has a less symmetric configuration
![]() .
The tidal features of these systems were somewhat different from TID3 and TID5, but the amount of material stripped and the general structure of the remnants are similar. We have also run two more models (GST1 and GST2) simulating an initial gas stripping. These simulations have identical initial conditions to TID1 and TID2, respectively. The initial gas stripping was simulated by randomly removing 10
.
The tidal features of these systems were somewhat different from TID3 and TID5, but the amount of material stripped and the general structure of the remnants are similar. We have also run two more models (GST1 and GST2) simulating an initial gas stripping. These simulations have identical initial conditions to TID1 and TID2, respectively. The initial gas stripping was simulated by randomly removing 10![]() of the disc particles of the models. Gas-stripping depends also on the distance from the centre of the galaxy (see the hydrodynamical simulations by Quilis et al. 2000), but here we adopt an extreme situation where at one time all the gas in the galaxy is stripped away. After they reach virialization we applied the first tidal encounter.
of the disc particles of the models. Gas-stripping depends also on the distance from the centre of the galaxy (see the hydrodynamical simulations by Quilis et al. 2000), but here we adopt an extreme situation where at one time all the gas in the galaxy is stripped away. After they reach virialization we applied the first tidal encounter.
Simulations were run using the GADGET2 (Springel 2005) hydrodynamical code, in the tree-code configuration, on the Beowulf cluster of the Instituto de Astrofísica de Canarias (IAC), the Mare Nostrum supercomputer and the La Palma node of the National Supercomputing Center (BSC). A typical run with
![]() particles took of the order of
particles took of the order of
![]() s in 16 CPUs. We used different softening parameters for the different particles, typically
s in 16 CPUs. We used different softening parameters for the different particles, typically
![]() of the half-mass radius of each system. An opening parameter of
of the half-mass radius of each system. An opening parameter of
![]() and quadrupole terms were included in the force calculation.
and quadrupole terms were included in the force calculation.
3.3 Results
Figures 4 and 5 present the initial and evolved states after each tidal interaction for the TID1 and TID3 simulations, respectively. These two models represent two extreme cases because they have the largest (TID3) and smallest (TID1) initial bulges. In both cases, tidal stripping removes first the outer parts of the halo, and after two tidal interactions a fair number of disc particles are also expelled. Models with large bulges (TID2, TID3) show that almost the whole disc was removed after 4 tidal interactions. These models have at the end a disc-to-bulge ratio close to 1:1, leaving the small number of still bounded disc particles in an almost round shape (see Fig. 5). In contrast, the model with the smallest initial bulge (TID1) still presents a short and thick disc after 4 tidal encounters (see Fig. 4). These truncations have been quantified measuring the half mass radius of the bulge (
![]() ), disc (
), disc (
![]() )
and halo (
)
and halo (
![]() )
as showed in Table 2. Notice that while the disc and halo are strongly truncated in all simulations, the bulge enlarges its half mass radius, especially for the models with the largest B/D ratio (TID3 and TID4).
)
as showed in Table 2. Notice that while the disc and halo are strongly truncated in all simulations, the bulge enlarges its half mass radius, especially for the models with the largest B/D ratio (TID3 and TID4).
3.3.1 Disc and halo truncations
The truncation of the disc and halo component results in an important mass loss of the galaxies. Figure 6 presents the evolution of the total content of bound mass in these systems. We find that harassment is highly efficient in removing a large amount of the initial mass in all our simulations. The different encounters remove betweenFigure 7 shows the binding energy vs. the radial distance to the galaxy centre after each tidal encounter for TID1 and TID3 models. It is clear that the outermost particles are stripped first after each tidal interaction because they have higher binding energies. Thus, disc and halo particles were easily stripped away, unlike bulge particles. In both models shown in Fig. 7 the simulated galaxy-galaxy encounters do not provide enough energy to extract the bulge particles. But, some bulge particles occupy higher binding energies previously occupied by the striped disc and halo particles, producing an inflation of the bulge. This behaviour is common to all the simulations, being more prominent in those with high B/D-ratio. The bulge survives in those simulations with an initial bulge. Moreover, at the end of the simulations, the hot component of galaxies with initial bulges is formed by the initial bulge of the galaxies.
3.3.2 Tidally induced bars
The stripping remnants show a number of tidal features, such as extended tidal tails, rings, etc., that indicate that the system has suffered such interactions.
Some systems appear to present a bar-like structure in the disc (see Fig. 8). These bar-like structures induced by tidal interactions are formed in the first tidal encounter and are stable until the end of the simulation. The bars are more prominent in those models with lower central mass concentration, i.e. a smaller bulge component, and a prograde rotation. The bar formation depends on the orbital configuration of the encounters. Thus, retrograde orbits seem to inhibit bar formation. Only the models with the largest bulge component (TID3 and TID4) do not show any bar feature in the disc. This is in agreement with numerical simulations about bar formation and evolution which find that central mass concentrations inhibits bar formation in discs (Pfenniger & Norman 1990; Shen & Sellwood 2004; Athanassoula et al. 2005).
Table 2: Half mass radius for each of the components for the initial and final models of our simulations.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0339fig6.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg77.gif) |
Figure 6: Change of mass in each tidal harassment event. Upper panel: total mass, lower panel: luminous mass. |
| Open with DEXTER | |
3.3.3 Kinematic features of the remnants
Figure 9 shows the rotation curve and the velocity dispersion profile of the initial and final remnants of all simulations. Table 3 gives the maximum rotation and velocity dispersion of the initial and final models. Notice that the rotation velocity of all models is significantly lower in the external regions at the end of the simulations than in the initial conditions. In contrast, the external region of the galaxies show in all simulations higher velocity dispersion than at the beginning. This is because tidal interactions are an efficient mechanism for heating the thin disc of spiral galaxies (see e.g. Aguerri et al. 2001; Eliche-Moral et al. 2006). The central velocity dispersion at the end of the simulations depends on the models. Those models with an initial small bulge show very similar central velocity dispersions at the beginning and at the end of the simulations (TID1, TID2). Models with large bulge in the initial conditions (TID3 and TID4) show a lower central velocity dispersion at the end. This is due to the final bulges of these models suffered an expansion. On the other hand, the models without an initial bulge (TID5-TID8) show larger central velocity dispersion at the end, again due to the tidal heating of the disc and the absence of a stabilising central concentration like a bulge. Retrograde models seem to present slightly higher values of the central velocity dispersion. Table 3 also shows the ![]() ratio measured within an aperture equal to
ratio measured within an aperture equal to ![]() .
Notice that the final remnants are in all cases dominated by random motion. Similar kinematic features have been seen in other simulations of fast galaxy encounters in the literature (see Kronberger et al. 2006).
.
Notice that the final remnants are in all cases dominated by random motion. Similar kinematic features have been seen in other simulations of fast galaxy encounters in the literature (see Kronberger et al. 2006).
The kinematical characteristics of the models with simulated tidal stripping (GST1 and GST2) do not differ much from similar simulations without tidal stripping (TID1 and TID2). This is because the gas particles only account for a few percent (10![]() in our simulations) of the total mass of the disc in the galaxies.
in our simulations) of the total mass of the disc in the galaxies.
3.4 The fundamental plane of the tidal remnants
We analysed the location of the simulated galaxies in the FP after each tidal encounter. We measure the required quantities
![]() ,
,
![]() and
and
![]() ,
in the simulations.
,
in the simulations.
3.4.1 Decomposition of the surface mass density profiles
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{0339fig7.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg78.gif) |
Figure 7: Binding energy vs. distance from the centre for the final snapshots of the simulations TID1 ( up) and TID3 ( bottom). The first panel in each case presents the state of the initial galaxy model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{0339fig8.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg79.gif) |
Figure 8: Snapshot after the evolution of the second tidal harassment event in simulation TID2. Left and central panel show the luminous particles (bulge+disc). We observe the formation of tidal tails ( left) and a prominent bar ( centre). This bar can be seen clearly in the contour plot ( right). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0339fig9.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg80.gif) |
Figure 9: Rotation curves ( left panels) and dispersion velocity profiles ( right panels) for the initial form (full lines) and remnants (dashed lines) of the simulations. |
| Open with DEXTER | |
In a manner similar to real galaxies, we have performed the decomposition of the surface mass density profiles in the different galactic components of the initial modelled galaxy and the remnants after each interaction. This decomposition was done using one or two components depending on whether the systems are dominated by rotation or pressure in their most external regions. Systems with
![]() at all radial distances were considered as hot systems. In contrast, those systems with
at all radial distances were considered as hot systems. In contrast, those systems with
![]() at large radial distances were considered as rotation supported systems in their outer most regions. Thus, the surface mass density profiles of the galaxies with a rotating component in their outermost region were fitted with two components: bulge and disc. The bulge component dominates the surface mass density profiles in the innermost regions of the models, and was represented by a Sèrsic law (Sèrsic 1968). This component represents the hottest part of the galaxy dominated by random motion, and it will be called a ``bulge'', similar to real galaxies. The disc component dominates the outermost regions of the mass density profiles of the galaxies, and was modelled by a Freeman exponential law (Freeman et al. 1970). The surface mass density profiles of those models dominated by random motion at all radial distances were fitted by a one-component model described by a Sèrsic law.
at large radial distances were considered as rotation supported systems in their outer most regions. Thus, the surface mass density profiles of the galaxies with a rotating component in their outermost region were fitted with two components: bulge and disc. The bulge component dominates the surface mass density profiles in the innermost regions of the models, and was represented by a Sèrsic law (Sèrsic 1968). This component represents the hottest part of the galaxy dominated by random motion, and it will be called a ``bulge'', similar to real galaxies. The disc component dominates the outermost regions of the mass density profiles of the galaxies, and was modelled by a Freeman exponential law (Freeman et al. 1970). The surface mass density profiles of those models dominated by random motion at all radial distances were fitted by a one-component model described by a Sèrsic law.
The free parameters of the models were fitted using a Levenberg-Marquard nonlinear fitting routine and were determined by minimising the ![]() of the fit, similarly to real galaxies (Trujillo et al. 2001, 2002; Aguerri & Trujillo 2002; Aguerri et al. 2004, 2005a).
of the fit, similarly to real galaxies (Trujillo et al. 2001, 2002; Aguerri & Trujillo 2002; Aguerri et al. 2004, 2005a).
The decompositions of the surface mass density profiles provided two of the parameters of the hot component of the galaxy needed for the FP, the effective radius (r![]() )
and the effective surface mass density (
)
and the effective surface mass density (
![]() ). The third parameter (central velocity dispersion) was measured from the velocity dispersion profiles of the galaxies in an aperture of radius equal to
). The third parameter (central velocity dispersion) was measured from the velocity dispersion profiles of the galaxies in an aperture of radius equal to
![]() of the hot galaxy component. All these FP parameters were obtained for 9 different points of view in each system.
of the hot galaxy component. All these FP parameters were obtained for 9 different points of view in each system.
As pointed out before, the discs of the galaxies are strongly truncated. This is reflected in the scale-length of the discs which is reduced in all cases by up to 40-50![]() .
In contrast, the variation in the effective radius of the bulges depends on the prominence of this structure in the initial model. Thus, the scale of bulges in models with small B/D ratio (TID1 and GST1) was very small. In contrast, galaxies with large B/D ratio (TID3 and TID4) have larger scales of the bulge at the end of the interactions. This behaviour of the bulge and disc structural parameters result in that the B/D ratio of the tidally truncated galaxies is larger than the initial one.
.
In contrast, the variation in the effective radius of the bulges depends on the prominence of this structure in the initial model. Thus, the scale of bulges in models with small B/D ratio (TID1 and GST1) was very small. In contrast, galaxies with large B/D ratio (TID3 and TID4) have larger scales of the bulge at the end of the interactions. This behaviour of the bulge and disc structural parameters result in that the B/D ratio of the tidally truncated galaxies is larger than the initial one.
3.4.2 Location of tidal remnants in the FP
To locate the modelled galaxies in the observed FP we need to scale them using an appropriate mass-to-light ratio. This M/L was obtained by imposing that the hot systems of the simulated initial galaxy and remnants lie on the edge-on view of the FP described by bright E galaxies. With this M/L we have compared the location of those systems in the face-on view of the FP. We have varied the imposed M/L according to the rms shown in the edge-on view of the FP of early-type bulges (TID2, TID3, TID4 and GST2) and late-type bulges (TID1 and GST1). The result of this variation in the face on view of the FP is given as an error bar in the following FP figures. Figure 10 shows the location in the ![]() -space of the observed galaxies in the Coma cluster presented in Sect. 2, together with the hot components corresponding to the TID1, TID2 and TID3 models. We find that those simulations with initial conditions similar to an early-type spiral (TID3 model) are located close to the face-on view of the FP described by bulges of early-type and E galaxies. In contrast, the remnants of the models with a small B/D ratio at the beginning (TID1 model) are located in a different position in the face-on view of the FP defined by E galaxies, similar to dE ones. The remnants from TID2 are between the TID1 and TID3 models.
-space of the observed galaxies in the Coma cluster presented in Sect. 2, together with the hot components corresponding to the TID1, TID2 and TID3 models. We find that those simulations with initial conditions similar to an early-type spiral (TID3 model) are located close to the face-on view of the FP described by bulges of early-type and E galaxies. In contrast, the remnants of the models with a small B/D ratio at the beginning (TID1 model) are located in a different position in the face-on view of the FP defined by E galaxies, similar to dE ones. The remnants from TID2 are between the TID1 and TID3 models.
Models GST1 and GST2 have a gas-stripping event at the beginning of the simulations. This event is supposed to erase all gas from the galaxy in a rather short amount of time. This modifies the profile of our initial conditions, producing initial bulges with larger scales than in similar models without gas-stripping (TID1 and TID2 models). The final remnants for these models are located at different positions in the face-on view of the FP than those from TID1 and TID2 simulations (see Fig. 11). In fact, we find a marginally better agreement with the locus of dEs in the model GST1.
All these models with galaxies with an initial bulge can explain the location in the face-on view of the FP of dwarf galaxies with a central velocity dispersion larger than ![]() 50 km s-1. Dwarf galaxies with smaller central velocity dispersions are yet not well reproduced.
50 km s-1. Dwarf galaxies with smaller central velocity dispersions are yet not well reproduced.
The M/L ratio for the four models without an initial bulge component (TID5-TID8) were obtained in a different way. In this case the initial models represent pure disc galaxies, and it makes no sense to locate these discs in the FP. We obtained the M/L ratio by locating the initial discs of these models in the Tully-Fisher (Tully & Fisher (1977); TF) relation followed by spiral galaxies. We have the maximum rotational velocity for these discs, and following the Tully-Fisher calibration of Sakai et al. (2000) in the I band we obtained the M/L.
Figure 12 shows the location of the remnants from TID5 and TID6 models in the edge-on (upper panel) and face-on (lower panel) view for the FP. The final remnants from these models show smaller central velocity dispersions than the other simulations, and are located in the region occupied by dE with the smallest central velocity dispersions. These results do not depend on the orbit of the interactions. Thus, the models TID7 and TID8, following retrograde orbits, show similar results.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f10.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg88.gif) |
Figure 10:
Results for the models TID1 ( top), TID2 ( middle) and TID3 ( bottom) presented in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f11a.ps}\par\includegraphics[width=7.5cm,clip]{0339f11b.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg89.gif) |
Figure 11:
Results for the models GST1 and GST2 presented in |
| Open with DEXTER | |
Table 3:
Maximun rotation velocity and velocity dispersion of the initial and final models and mean ![]() inside the effective radius for the final model.
inside the effective radius for the final model.
4 Discussion
The simulations presented here indicate that fast tidal interactions are very efficient in transforming spiral disc galaxies into dwarf like systems. This mechanism produces a large mass loss, especially from the outer parts of the galaxies, and locates the tidal remnants out of the face-on view of the FP described by bright E galaxies. Figure 13 shows the residuals of the observed galaxies and the remnants of the present models with respect to the face-on view of the FP described by E bright galaxies. Notice that the tidal remnants from the present simulations are located in the same position of the FP as dE galaxies. Galaxies with large B/D ratios at the beginning are located after four tidal fast interaction near the loci occupied by bulges of early-type galaxies. In contrast, galaxies with small B/D ratio or without an initial bulge are located at the end of the simulation at the position of the dE galaxies with small central velocity dispersion. This indicates that dE galaxies can be formed by the tidal disruption of late-type disc galaxies. In contrast, the tidal disruption of early-type spirals would produce a final galaxy similar to elliptical or S0 galaxies.
This is not the only mechanism that can explain the location of dwarf galaxies in the face-on view of the fundamental plane. Semi-analytical models of dwarf galaxy evolution by supernova-driven-gas-loss can also explain the position of dwarf galaxies in the face-on view of the FP (see de Rijcke et al. 2005). This could indicate that the origin of the dwarf population could be diverse. Thus, several past studies have shown that dwarf galaxies are not a homogeneous population of objects. Lisker et al. (2007) analysed a large sample of dwarf elliptical galaxies in the Virgo cluster, concluding that they can be grouped in three main families with different dynamical and morphological properties. They found that non-nucleated dE show shapes like thick discs and are not centrally clustered. This indicates that they constitute a non-relaxed galaxy population, and could be formed by tidal interactions as our simulations show. But, how can we know the progenitors of dwarf galaxies? Are there any observational measurements to determine the tidal origin of dwarf galaxies?
4.1 Bar parameters in dwarf galaxies
As we mentioned in the previous sections, one of the most prominent features that tidal interactions induce in the discs of the galaxies is the presence of stable and prominent bars. Those bar features appearded only in those models with a small bulge component and in interactions following prograde orbits. Retrograde orbits inhibits bar formation even in galaxies with a small bulge. We can analyse the properties of these bars and compare them to similar properties of bars observed in bright galaxies without signs of interaction. Numerical simulations of bar formation find that the mean ratio between the bar length and the scale length of the galaxy discs (
![]() )
is well constrained, being 1.0-1.2 (O'Neill & Dubinski 2003; Valenzuela & Klypin 2003). This is in agreement with observational measurements of this quantity in bright unperturbed barred galaxies (
)
is well constrained, being 1.0-1.2 (O'Neill & Dubinski 2003; Valenzuela & Klypin 2003). This is in agreement with observational measurements of this quantity in bright unperturbed barred galaxies (
![]() ;
Aguerri et al. 2005c). We have measured this ratio in the bars induced in our models by tidal interactions. Figure 14 shows the
;
Aguerri et al. 2005c). We have measured this ratio in the bars induced in our models by tidal interactions. Figure 14 shows the
![]() distribution in a sample of 14 bright barred galaxies (Aguerri et al. 2005c) and the values of this ratio for the bars formed in our simulations. It is clear than the tidally induced bars have larger
distribution in a sample of 14 bright barred galaxies (Aguerri et al. 2005c) and the values of this ratio for the bars formed in our simulations. It is clear than the tidally induced bars have larger
![]() values than observed bars. This could be an observational parameter that could be measured in dwarf barred galaxies in order to distinguish between tidally induced bars and those formed by internal discs instabilities.
values than observed bars. This could be an observational parameter that could be measured in dwarf barred galaxies in order to distinguish between tidally induced bars and those formed by internal discs instabilities.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f12a.ps}\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{0339f12b.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg97.gif) |
Figure 12:
Results for the models TID5 and TID6 presented in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f13.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg98.gif) |
Figure 13:
Residuals of the face-on FP in the |
| Open with DEXTER | |
There are few measurements of the ratio
![]() in the literature for dwarf galaxies. Nevertheless, NGC 4431 is one exception. This is a barred dwarf galaxy located in the Virgo cluster and analysed by Corsini et al. (2007). The surface brightness profile of this galaxy was decomposed into three components (bulge, disc and bar) resulting
in the literature for dwarf galaxies. Nevertheless, NGC 4431 is one exception. This is a barred dwarf galaxy located in the Virgo cluster and analysed by Corsini et al. (2007). The surface brightness profile of this galaxy was decomposed into three components (bulge, disc and bar) resulting
![]() ,
similar to the values obtained in our simulations. Therefore, the bar of this galaxy could have been formed in a past tidal interaction.
,
similar to the values obtained in our simulations. Therefore, the bar of this galaxy could have been formed in a past tidal interaction.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0339f14.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg100.gif) |
Figure 14:
Ratio between the length of the bars ( |
| Open with DEXTER | |
4.2 Structural parameters of tidal dwarf galaxies
The analysis of the structural parameters of the dwarf galaxies can also give clues about their tidal origin. Photometric decomposition of bright and unperturbed galaxies have shown several correlations between bulge and disc structural parameters (e.g. de Jong 1996; Khosroshahi et al. 2000; MacArthur et al. 2003; Möllenhoff 2004; Hunt et al. 2004; Méndez-Abreu et al. 2008). In particular, the ratio between the disc and bulge scales (
![]() )
is correlated with the Sèrsic n parameter in real disc galaxies (e.g. MacArthur et al. 2003; Méndez-Abreu et al. 2008). Thus, those bulges with large n values also show large
)
is correlated with the Sèrsic n parameter in real disc galaxies (e.g. MacArthur et al. 2003; Méndez-Abreu et al. 2008). Thus, those bulges with large n values also show large
![]() ratios. We have compared the correlation observed in real galaxies with our simulations. Figure 15 shows the correlation between
ratios. We have compared the correlation observed in real galaxies with our simulations. Figure 15 shows the correlation between
![]() and n for a large sample of bright disc galaxies from the surveys of MacArthur et al. (2003) and Méndez-Abreu et al. (2008). We overplot in this figure the same quantities for our simulated dwarf-like objects. Notice that most dwarf galaxies formed by fast tidal interactions do not follow the trend described by real galaxies. Thus, for a fixed value of n, tidally formed dwarf galaxies have, in general, larger
and n for a large sample of bright disc galaxies from the surveys of MacArthur et al. (2003) and Méndez-Abreu et al. (2008). We overplot in this figure the same quantities for our simulated dwarf-like objects. Notice that most dwarf galaxies formed by fast tidal interactions do not follow the trend described by real galaxies. Thus, for a fixed value of n, tidally formed dwarf galaxies have, in general, larger
![]() ratios than bright disc spirals. This is because, as we discussed in the previous section, the scales of the discs were strongly truncated due to tidal encounters. The search for outliers in the
ratios than bright disc spirals. This is because, as we discussed in the previous section, the scales of the discs were strongly truncated due to tidal encounters. The search for outliers in the
![]() vs. n relation could provide dwarf systems formed by transformed bright disc galaxies by fast tidal encounters.
vs. n relation could provide dwarf systems formed by transformed bright disc galaxies by fast tidal encounters.
We have determined the bulge and disc structural parameters of the dwarf barred galaxy NGC 4431. This galaxy shows a Sèrsic index n=1.5 and
![]() (Corsini et al. 2007). According to Fig. 15 this galaxy would be in the limit of the region described by the observed bright disc galaxies. This would be another indication that NGC 4431 could be a dwarf galaxy formed by stripped bright disc galaxies.
(Corsini et al. 2007). According to Fig. 15 this galaxy would be in the limit of the region described by the observed bright disc galaxies. This would be another indication that NGC 4431 could be a dwarf galaxy formed by stripped bright disc galaxies.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f15.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg102.gif) |
Figure 15:
|
| Open with DEXTER | |
4.3 Metallicity relations
Early-type galaxies follow the well known luminosity-metallicity and velocity dispersion-metallicity relations (see e.g. Tremonti et al. 2004, and references therein). Thus, more metallic galaxies have larger central velocity dispersions and are more luminous. Tidal stripping interactions should not change the metallicity of the galaxies. Indeed, we have also seen that the central velocity dispersion of tidal remnants is not very different from the initial conditions. In contrast, due to the large mass lost, tidally formed dwarf galaxies have lower luminosities than their progenitors. This would imply that low-mass systems formed by harassment of bright disc galaxies could be out of the luminosity-metallicity relation displayed by bright galaxies. In contrast, those dwarf galaxies could lie inside the relation between the metallicity and their central velocity dispersion.
4.4 Group and cluster fast tidal interactions
We have made some attempts to apply the tidal impulse approximation to model encounters with group and cluster potentials. Mastropietro et al. (2005) simulate the harassment of disc galaxies falling onto a cluster environment by re-simulating a cluster formed in a cosmological simulation. We have tried to model the harassment of one of our bulgeless galaxies through the tidal impulse approximation. However, two important problems arise: The most typical orbital configuration from the cosmological simulations (Tormen 1997) are such that the injection of energy is too low to produce significant effects in the discs. This is so because the typical orbits imply wide impact parameters on non-parabolic orbits. The second problem is that under these circumstances the impulse approximation no longer applies (i.e., the interaction is not fast compared to the dynamic time of the galaxy), and the approach followed in this paper is no longer applicable.
Nevertheless we have modelled one encounter with higher mass ratio (1:10). This model (called TID10) simulates the interaction of a bulgeless galaxy with the potential of a group. The orbital parameters chosen for this encounter were: b = 6, V = 4.6 and
![]() .
This orbit is not a typical orbit (Tormen 1997) but the parameters are such that the increment of energy of each particle is comparable to the ones in galaxy-galaxy interactions. In fact, the results are quite similar to the simulations TID5-TID8 (see Fig. 6 for the mass change). The final half mass radii of the halo and disc components were
.
This orbit is not a typical orbit (Tormen 1997) but the parameters are such that the increment of energy of each particle is comparable to the ones in galaxy-galaxy interactions. In fact, the results are quite similar to the simulations TID5-TID8 (see Fig. 6 for the mass change). The final half mass radii of the halo and disc components were
![]() and
and
![]() .
The final maximum rotational velocity and central velocity dispersion were 37 km s-1, and 55.6 km s-1. All these values are similar to the ones shown in Table 2 for the models without a bulge in the initial conditions (TID5-TID8). Indeed, the final position of these remnants in the FP was similar to similar models (TID5-TID8) shown here. However, we must stress that the orbital configuration is not typical at all, compared to those obtained from cosmological simulations (Tormen 1997).
.
The final maximum rotational velocity and central velocity dispersion were 37 km s-1, and 55.6 km s-1. All these values are similar to the ones shown in Table 2 for the models without a bulge in the initial conditions (TID5-TID8). Indeed, the final position of these remnants in the FP was similar to similar models (TID5-TID8) shown here. However, we must stress that the orbital configuration is not typical at all, compared to those obtained from cosmological simulations (Tormen 1997).
The models shown in this subsection are very simple. The interaction of a galaxy with the global cluster or group potentials should take into account NFW-type tidal fields from the potential. This kind of interaction is out of the main scope of the present paper where galaxy-galaxy interactions are shown. We are planning new cosmological simulations considering both the galaxy-galaxy and galaxy-cluster potential interactions.
5 Conclusions
In the present paper we have described the FP of 215 hot systems (ellipcicals and bulges) located in the Coma clusters. The edge-on view of the FP shows that bright E galaxies and early-type bulges are located in the same plane showing similar scatter. In contrast, dwarf galaxies and late-type bulges have more scatter. The differences are more pronounced in the face-on view of the FP. Thus, dwarf galaxies and bulges of late-type galaxies are located perpendicular to the relationship defined by E and early-type bulges.
We have run high-resolution numerical simulations in order to explain the different location of dwarf galaxies in the face-on view of the FP. We have tested if fast galaxy-galaxy tidal interactions can transform bright spiral galaxies in early-type dwarf systems and can explain their different location in the FP. The simulations have disc-like galaxies with different bulge-to-disc mass rations as initial conditions. Thus, these initial disc galaxies represent the full family of Hubble type galaxies, from early- to late-type ones.
Tidal interactions turned out to be very efficient for removing stars from the galaxies, especially from the outermost regions (disc and dark matter halo) where the stars are less bounded. In contrast, particles from bulges were not removed. After several tidal interactions the galaxies lost 50-80![]() of their total mass and 30-60
of their total mass and 30-60![]() of their luminous matter. The discs and haloes were strongly truncated. In particular, the structure of the disc were largely affected. Their scale parameters were 40-50
of their luminous matter. The discs and haloes were strongly truncated. In particular, the structure of the disc were largely affected. Their scale parameters were 40-50![]() shorter than the initial ones. Those models with the smallest B/D ratio retain a short and thick disc. In contrast, the model with the largest B/D ratio have no disc at the end, being a roundish dwarf system. The tidal interactions produce bar-like structures in the galaxy which are stable until the end of the models. The bars were more prominent in those models with smaller bulges at the beginning of the simulations. The formation of bar-like structures depends on the orbital configuration of the encounters. Thus, bars are easily formed in prograde interactions. In contrast, retrograde orbits seem to inhibit the formation of bars even in those simulations without an initial bulge component. Similar results have been obtained for two models in which we have simulated a gas stripping interaction before tidal encounters.
shorter than the initial ones. Those models with the smallest B/D ratio retain a short and thick disc. In contrast, the model with the largest B/D ratio have no disc at the end, being a roundish dwarf system. The tidal interactions produce bar-like structures in the galaxy which are stable until the end of the models. The bars were more prominent in those models with smaller bulges at the beginning of the simulations. The formation of bar-like structures depends on the orbital configuration of the encounters. Thus, bars are easily formed in prograde interactions. In contrast, retrograde orbits seem to inhibit the formation of bars even in those simulations without an initial bulge component. Similar results have been obtained for two models in which we have simulated a gas stripping interaction before tidal encounters.
We have analysed the location of the dwarf-like galaxy remnants in the face-on view of the FP. Their final positions depend on the initial conditions of the simulations. Thus, those dwarf galaxies with progenitors with a large B/D ratio are closer to the location of early-type bulges and Es in the face-on view of the FP. In contrast, the remnants of late-type galaxies are located in the region occupied by dE in the face-on view of the FP. The final location of the remmants in the FP does not depend on the orbital orientation of the encounters.
We have analysed several observational parameters in order to identify tidal dwarf galaxies. The measurement of the
![]() ratio, the relation between
ratio, the relation between
![]() and n, and the mass-metallicity and velocity dispersion-metallicity relations could provide information about the possible tidal origin of observed dwarf galaxies. Therefore, tidal dwarf systems would have larger
and n, and the mass-metallicity and velocity dispersion-metallicity relations could provide information about the possible tidal origin of observed dwarf galaxies. Therefore, tidal dwarf systems would have larger
![]() ratios than observed ones in bright barred galaxies. They would also be outliers in the
ratios than observed ones in bright barred galaxies. They would also be outliers in the
![]() -n and luminosity-metallicity relations. In contrast, they would follow the velocity dispersion-metallicity relation.
-n and luminosity-metallicity relations. In contrast, they would follow the velocity dispersion-metallicity relation.
Acknowledgements
We would like to thank L. Mayer and B. Moore for useful comments during the writing process of the present manuscript. We would also like to thank the anonymous referee. We thank the BSC in Barcelona for computing facilities at the Mare Nostrum supercomputer and at the La Palma node. A.C.G.G. acknowledges financial support from the regional government of Madrid through the ASTROCAM Astrophysics network (S0505/ESP0237). J.A.L.A. also acknowledges financial support from the project AYA2007-67965-C03-01.
References
- Aceves, H., & Velázquez, H. 2005, MNRAS, 360, L50 [NASA ADS]
- Aguerri, J. A. L., & Trujillo, I. 2002, MNRAS, 333, 633 [NASA ADS] [CrossRef]
- Aguerri, J. A. L., Balcells, M., & Peletier, R. F. 2001, A&A, 367, 428 [NASA ADS] [CrossRef] [EDP Sciences]
- Aguerri, J. A. L., Iglesias-Paramo, J., Vilchez, J. M., & Muñoz-Tuñón, C. 2004, AJ, 127, 1344 [NASA ADS] [CrossRef] (In the text)
- Aguerri, J. A. L., Iglesias-Páramo, J., Vílchez, J. M., Muñoz-Tuñón, C., & Sánchez-Janssen, R. 2005a, AJ, 130, 475 [NASA ADS] [CrossRef] (In the text)
- Aguerri, J. A. L., Gerhard, O. E., Arnaboldi, M., et al. 2005b, AJ, 129, 2585 [NASA ADS] [CrossRef] (In the text)
- Aguerri, J. A. L., Elias-Rosa, N., Corsini, E. M., & Muñoz-Tuñón, C. 2005c, A&A, 434, 109 [NASA ADS] [CrossRef] [EDP Sciences]
- Arnaboldi, M., Aguerri, J. A. L., Napolitano, N. R., et al. 2002, AJ, 123, 760 [NASA ADS] [CrossRef] (In the text)
- Athanassoula, E., Lambert, J. C., & Dehnen, W. 2005, MNRAS, 363, 496 [NASA ADS]
- Bekki, K. 1998, ApJ, 496, 713 [NASA ADS] [CrossRef]
- Bender, R., Burstein, D., & Faber, S. M. 1992, ApJ, 399, 462 [NASA ADS] [CrossRef] (In the text)
- Bernardi, M., Sheth, R. K., Annis, J., et al. 2003, AJ, 125, 1866 [NASA ADS] [CrossRef]
- Binggeli, B., & Cameron, L. M. 1991, A&A, 252, 27 [NASA ADS] (In the text)
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton University Press)
- Boselli, A., Boissier, S., Cortese, L., & Gavazzi, G. 2008, ApJ, 674, 742 [NASA ADS] [CrossRef] (In the text)
- Boylan-Kolchin, M., Ma, C. P., & Quataert, E. 2006, MNRAS, 369, 1081 [NASA ADS] [CrossRef]
- Caldwell, N., & Bothun, G. D. 1987, AJ, 94, 1126 [NASA ADS] [CrossRef] (In the text)
- Capelato, H. V., de Carvalho, R. R., & Carlberg, R. G. 1995, ApJ, 451, 525 [NASA ADS] [CrossRef]
- Conselice, C. J., Gallagher, J. S., III, & Wyse, R. F. G. 2001, ApJ, 559, 791 [NASA ADS] [CrossRef] (In the text)
- Corsini, E. M., Aguerri, J. A. L., Debattista, V. P., et al. 2007, ApJ, 659, L121 [NASA ADS] [CrossRef] (In the text)
- Davies, K. I., Roberts, S., & Sabatini, S. 2008, MNRAS, in press
- Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41 [NASA ADS] [CrossRef] (In the text)
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] (In the text)
- de Jong, R. S. 1996, A&A, 313, 45 [NASA ADS] (In the text)
- de Rijcke, S., Michielsen, D., Dejonghe, H., Zeilinger, W. W., & Hau, G. K. T. 2005, A&A, 438, 491 [NASA ADS] [CrossRef] [EDP Sciences]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef]
- D'Onofrio, M., Valentinuzzi, T., Secco, L., Caimmi, R., & Bindoni, D. 2006, New Astron. Rev., 50, 447 [NASA ADS] [CrossRef]
- Dressler, A. 1987, ApJ, 317, 1 [NASA ADS] [CrossRef]
- Eliche-Moral, M. C., Balcells, M., Aguerri, J. A. L., & González-García, C. 2006, A&A, 457, 91 [NASA ADS] [CrossRef] [EDP Sciences].
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] (In the text)
- Falcón-Barroso, J., Peletier, R. F., & Balcells, M. 2002, MNRAS, 335, 741 [NASA ADS] [CrossRef]
- Feldmeier, J. J., Ciardullo, R., Jacoby, G. H., & Durrell, P. R. 2004, ApJ, 615, 196 [NASA ADS] [CrossRef] (In the text)
- Forbes, D. A., & Ponman, T. J. 1999, MNRAS, 309, 623 [NASA ADS] [CrossRef] (In the text)
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef]
- Geha, M., Guhathakurta, P., & van der Marel, R. P. 2002, AJ, 124, 3073 [NASA ADS] [CrossRef] (In the text)
- Geha, M., Guhathakurta, P., & van der Marel, R. P. 2003, AJ, 126, 1794 [NASA ADS] [CrossRef] (In the text)
- Gerhard, O., Arnaboldi, M., Freeman, K. C., Kashikawa, N., Okamura, S., & Yasuda, N. 2005, ApJ, 621, L93 [NASA ADS] [CrossRef]
- Gerhard, O., Arnaboldi, M., Freeman, K. C., et al. 2007, A&A, 468, 815 [NASA ADS] [CrossRef] [EDP Sciences]
- Gnedin, O. Y., Hernquist, L., & Ostriker, J. H. 1999, ApJ, 514, 109 [CrossRef]
- González-García, A. C., & van Albada, T. S. 2003, MNRAS, 342, L36 [NASA ADS] [CrossRef]
- González-García, A. C., Aguerri, J. A. L., & Balcells, M. 2005, A&A, 444, 803 [NASA ADS] [CrossRef] [EDP Sciences]
- Graham, A. W., & Guzmán, R. 2003, AJ, 125, 2936 [NASA ADS] [CrossRef] (In the text)
- Grebel, E. K., Gallagher, J. S., III, & Harbeck, D. 2003, AJ, 125, 1926 [NASA ADS] [CrossRef] (In the text)
- Gutiérrez, C. M., Trujillo, I., Aguerri, J. A. L., Graham, A. W., & Caon, N. 2004, ApJ, 602, 664 [NASA ADS] [CrossRef] (In the text)
- Guzman, R., Lucey, J. R., & Bower, R. G. 1993, MNRAS, 265, 731 [NASA ADS]
- Held, E. V., de Zeeuw, T., Mould, J., & Picard, A. 1992, AJ, 103, 851 [NASA ADS] [CrossRef] (In the text)
- Hunt, L. K., Pierini, D., & Giovanardi, C. 2004, A&A, 414, 905 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jorgensen, I., Franx, M., & Kjaergaard, P. 1996, MNRAS, 280, 167 [NASA ADS]
- Kauffmann, G., & White, S. D. M. 1993, MNRAS, 261, 921 [NASA ADS] (In the text)
- Khosroshahi, H. G., Wadadekar, Y., & Kembhavi, A. 2000, ApJ, 533, 162 [NASA ADS] [CrossRef] (In the text)
- King, I. R. 1966, AJ, 71, 64 [NASA ADS] [CrossRef]
- Kormendy, J. 1985, ApJ, 295, 73 [NASA ADS] [CrossRef] (In the text)
- Kormendy, J. 1977, ApJ, 218, 333 [NASA ADS] [CrossRef] (In the text)
- Kronberger, T., Kapferer, W., Schindler, S., et al. 2006, A&A, 458, 69 [NASA ADS] [CrossRef] [EDP Sciences]
- Kuijken, K., & Dubinski, J. 1994, MNRAS, 269, 13
- Kuijken, K., & Dubinski, J. 1995, MNRAS, 277, 1341 [NASA ADS]
- Lin, D. N. C., & Faber, S. M. 1983, ApJ, 266, L21 [NASA ADS] [CrossRef] (In the text)
- Lisker, T., Glatt, K., Westera, P., & Grebel, E. K. 2006a, AJ, 132, 2432 [NASA ADS] [CrossRef]
- Lisker, T., Grebel, E. K., & Binggeli, B. 2006b, AJ, 132, 497 [NASA ADS] [CrossRef]
- Lisker, T., Grebel, E. K., Binggeli, B., & Glatt, K. 2007, ApJ, 660, 1186 [NASA ADS] [CrossRef]
- Mayer, L., Governato, F., Colpi, M., et al. 2001a, ApJ, 559, 754 [NASA ADS] [CrossRef] (In the text)
- Mayer, L., Governato, F., Colpi, M., et al. 2001b, ApJ, 547, L123 [NASA ADS] [CrossRef]
- Mastropietro, C., Moore, B., Mayer, L., et al. 2005, MNRAS, 364, 607 [NASA ADS] (In the text)
- Matkovic, A., & Guzmán, R. 2005, MNRAS, 362, 289 [NASA ADS] [CrossRef] (In the text)
- MacArthur, L. A., Courteau, S., & Holtzman, J. A. 2003, ApJ, 582, 689 [NASA ADS] [CrossRef] (In the text)
- Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008, A&A, 478, 353 [NASA ADS] [CrossRef] [EDP Sciences]
- Möllenhoff, C. 2004, A&A, 415, 63 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] (In the text)
- Murante, G., Giovalli, M., Gerhard, O., et al. 2007, MNRAS, 377, 2 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] (In the text)
- Nieto, J.-L., Davoust, E., Bender, R., & Prugniel, P. 1990, A&A, 230, L17 [NASA ADS]
- Nipoti, C., Londrillo, P., & Ciotti, L. 2003, MNRAS, 344, 748 [NASA ADS] [CrossRef]
- O'Neill, J. K., & Dubinski, J. 2003, MNRAS, 346, 251 [NASA ADS] [CrossRef]
- Oñorbe, J., Domínguez-Tenreiro, R., Sáiz, A., Artal, H., & Serna, A. 2006, MNRAS, 373, 503 [NASA ADS] [CrossRef]
- Oñorbe, J., Domínguez-Tenreiro, R., Sáiz, A., & Serna, A. 2007, MNRAS, 376, 39 [NASA ADS] [CrossRef]
- Pedraz, S., Gorgas, J., Cardiel, N., Sánchez-Blázquez, P., & Guzmán, R. 2002, MNRAS, 332, L59 [NASA ADS] [CrossRef] (In the text)
- Peterson, R. C., & Caldwell, N. 1993, AJ, 105, 1411 [NASA ADS] [CrossRef] (In the text)
- Pfenniger, D., & Norman, C. 1990, ApJ, 363, 391 [NASA ADS] [CrossRef]
- Phillipps, S., Driver, S. P., Couch, W. J., & Smith, R. M. 1998, ApJ, 498, L119 [NASA ADS] [CrossRef] (In the text)
- Pracy, M. B., De Propris, R., Driver, S. P., Couch, W. J., & Nulsen, P. E. J. 2004, MNRAS, 352, 1135 [NASA ADS] [CrossRef] (In the text)
- Quilis, V., Moore, B., & Bower, R. 2000, Science, 288, 1617 [NASA ADS] [CrossRef]
- Roberts, M. S. 1978, AJ, 83, 1026 [NASA ADS] [CrossRef]
- Rubin, V. C., Burstein, D., Ford, W. K., Jr., & Thonnard, N. 1985, ApJ, 289, 81 [NASA ADS] [CrossRef]
- Sakai, S., Mould, J. R., Hughes, S. M. G., et al. 2000, ApJ, 529, 698 [NASA ADS] [CrossRef]
- Sánchez-Janssen, R., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2008, ApJ, 679, L77 [NASA ADS] [CrossRef] (In the text)
- Sandage, A., & Visvanathan, N. 1978, ApJ, 225, 742 [NASA ADS] [CrossRef] (In the text)
- Sargent, W. L. W., Schechter, P. L., Boksenberg, A., & Shortridge, K. 1977, ApJ, 212, 326 [NASA ADS] [CrossRef] (In the text)
- Schechter, P. L. 1980, AJ, 85, 801 [NASA ADS] [CrossRef] (In the text)
- Schechter, P. L., & Gunn, J. E. 1979, ApJ, 229, 472 [NASA ADS] [CrossRef] (In the text)
- Sèrsic, J. L. 1968, Atlas de galaxias australes (Cordoba, Argentina: Observatorio Astronomico) (In the text)
- Shen, J., & Sellwood, J. A. 2004, ApJ, 604, 614 [NASA ADS] [CrossRef]
- Shu, F. H. 1969, ApJ, 158, 505 [NASA ADS] [CrossRef]
- Simien, F., & de Vaucouleurs, G. 1986, ApJ, 302, 564 [NASA ADS] [CrossRef]
- Smith, R. J., Hudson, M. J., Nelan, J. E., et al. 2004, AJ, 128, 1558 [NASA ADS] [CrossRef]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef]
- Terlevich, R., Davies, R. L., Faber, S. M., & Burstein, D. 1981, MNRAS, 196, 381 [NASA ADS] (In the text)
- Theuns, T., & Warren, S. J. 1997, MNRAS, 284, L11 [NASA ADS] (In the text)
- Tonry, J. L. 1981, ApJ, 251, L1 [NASA ADS] [CrossRef] (In the text)
- Tormen, G. 1997, MNRAS, 290, 411 [NASA ADS]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS]
- Trujillo, I., Aguerri, J. A. L., Gutiérrez, C. M., & Cepa, J. 2001, AJ, 122, 38 [NASA ADS] [CrossRef]
- Trujillo, I., Asensio Ramos, A., Rubiño-Martín, J. A., et al. 2002, MNRAS, 333, 510 [NASA ADS] [CrossRef]
- Valenzuela, O., & Klypin, A. 2003, MNRAS, 345, 406 [NASA ADS] [CrossRef]
- van Zee, L., Barton, E. J., & Skillman, E. D. 2004a, AJ, 128, 2797 [NASA ADS] [CrossRef] (In the text)
- van Zee, L., Skillman, E. D., & Haynes, M. P. 2004b, AJ, 128, 121 [NASA ADS] [CrossRef] (In the text)
- Williams, B. F., Ciardullo, R., Durrell, P. R., et al. 2007, ApJ, 656, 756 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... galaxies
![[*]](/icons/foot_motif.gif)
- See Aguerri et al. (2004, 2005a) for details on the galaxy classification.
All Tables
Table 1:
Input number of particles and mass fraction of each component of the different models. Particle number is given in K-particles (
![]() ).
).
Table 2: Half mass radius for each of the components for the initial and final models of our simulations.
Table 3:
Maximun rotation velocity and velocity dispersion of the initial and final models and mean ![]() inside the effective radius for the final model.
inside the effective radius for the final model.
All Figures
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0339fig1.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg36.gif) |
Figure 1:
Fundamental plane in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0339fig2.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg37.gif) |
Figure 2:
Residuals of the face-on fundamental plane in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0339fig3.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg51.gif) |
Figure 3: Circular velocity curves for the initial conditions of the different simulations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0339fig4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg64.gif) |
Figure 4: Evolution of the tidal events in TID1. Rows give the three views of the system after the different tidal harassment events. Colours indicate the different constituents of the initial galaxy: black-dark halo, green-disc and red-bulge |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0339fig5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg65.gif) |
Figure 5: Evolution of the tidal events in TID3. Rows give the three views of the system after the different tidal harassment events. Colours indicate the different constituents of the initial galaxy: black-dark halo, green-disc and red-bulge |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0339fig6.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg77.gif) |
Figure 6: Change of mass in each tidal harassment event. Upper panel: total mass, lower panel: luminous mass. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{0339fig7.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg78.gif) |
Figure 7: Binding energy vs. distance from the centre for the final snapshots of the simulations TID1 ( up) and TID3 ( bottom). The first panel in each case presents the state of the initial galaxy model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{0339fig8.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg79.gif) |
Figure 8: Snapshot after the evolution of the second tidal harassment event in simulation TID2. Left and central panel show the luminous particles (bulge+disc). We observe the formation of tidal tails ( left) and a prominent bar ( centre). This bar can be seen clearly in the contour plot ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{0339fig9.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg80.gif) |
Figure 9: Rotation curves ( left panels) and dispersion velocity profiles ( right panels) for the initial form (full lines) and remnants (dashed lines) of the simulations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f10.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg88.gif) |
Figure 10:
Results for the models TID1 ( top), TID2 ( middle) and TID3 ( bottom) presented in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f11a.ps}\par\includegraphics[width=7.5cm,clip]{0339f11b.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg89.gif) |
Figure 11:
Results for the models GST1 and GST2 presented in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f12a.ps}\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{0339f12b.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg97.gif) |
Figure 12:
Results for the models TID5 and TID6 presented in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f13.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg98.gif) |
Figure 13:
Residuals of the face-on FP in the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0339f14.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg100.gif) |
Figure 14:
Ratio between the length of the bars ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0339f15.ps}
\end{figure}](/articles/aa/full_html/2009/06/aa10339-08/Timg102.gif) |
Figure 15:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.