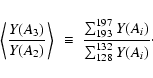| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 829 - 844 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361:200810292 | |
| Published online | 22 December 2008 | |
On the dynamics of proto-neutron star winds and r-process nucleosynthesis
I. V. Panov1,2 - H.-Th. Janka1
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching, Germany
2 - Institute for Theoretical and Experimental Physics, B. Cheremushkinskaya 25, Moscow 117218, Russia
Received 30 May 2008 / Accepted 26 November 2008
Abstract
We study here the formation of heavy r-process nuclei in
the high-entropy environment of rapidly expanding neutrino-driven
winds from compact objects. In particular, we explore the
sensitivity of the element creation in the ![]() region to the
low-temperature behavior of the outflows. For this purpose we employ
a simplified model of the dynamics and of the thermodynamical
evolution for radiation dominated, adiabatic outflows. It consists
of a first stage of fast, exponential cooling with timescale
region to the
low-temperature behavior of the outflows. For this purpose we employ
a simplified model of the dynamics and of the thermodynamical
evolution for radiation dominated, adiabatic outflows. It consists
of a first stage of fast, exponential cooling with timescale
![]() ,
followed by a second phase of slower evolution,
assuming either constant density and temperature or a power-law
decay of these quantities. These cases describe a strong
deceleration or decreasing acceleration of the transsonic outflows,
respectively, and thus are supposed to capture the most relevant
effects associated with a change in the wind expansion behavior at
large radii, for example because of the collision with the slower,
preceding supernova ejecta and the possible presence of a wind
termination shock. We find that for given entropy, expansion
timescale, and proton-to-baryon ratio not only the transition
temperature between the two expansion phases can make a big
difference in the formation of the platinum peak, but also the
detailed cooling law during the later phase. Because the nuclear
photodisintegration rates between about
,
followed by a second phase of slower evolution,
assuming either constant density and temperature or a power-law
decay of these quantities. These cases describe a strong
deceleration or decreasing acceleration of the transsonic outflows,
respectively, and thus are supposed to capture the most relevant
effects associated with a change in the wind expansion behavior at
large radii, for example because of the collision with the slower,
preceding supernova ejecta and the possible presence of a wind
termination shock. We find that for given entropy, expansion
timescale, and proton-to-baryon ratio not only the transition
temperature between the two expansion phases can make a big
difference in the formation of the platinum peak, but also the
detailed cooling law during the later phase. Because the nuclear
photodisintegration rates between about
![]() K and
roughly 109 K are more sensitive to the temperature than the
neutron-capture rates are to the free neutron density, a faster
cooling but continuing high neutron density in this temperature
regime allow the r-process path to move closer to the neutron-drip
line. With low (
K and
roughly 109 K are more sensitive to the temperature than the
neutron-capture rates are to the free neutron density, a faster
cooling but continuing high neutron density in this temperature
regime allow the r-process path to move closer to the neutron-drip
line. With low (![]() ,n)- but high
,n)- but high ![]() -decay rates, the
r-processing does then not proceed through a
(
-decay rates, the
r-processing does then not proceed through a
(![]() ,
n)-(n,
,
n)-(n, ![]() )
equilibrium but through a
quasi-equilibrium of (n,
)
equilibrium but through a
quasi-equilibrium of (n, ![]() )-reactions and
)-reactions and ![]() -decays, as
recently also pointed out by Wanajo. Unless the transition
temperature and corresponding (free neutron) density become too low
(
-decays, as
recently also pointed out by Wanajo. Unless the transition
temperature and corresponding (free neutron) density become too low
(
![]() K), a lower temperature or faster temperature
decline during the slow, late evolution phase therefore allow for a
stronger appearance of the third abundance peak.
K), a lower temperature or faster temperature
decline during the slow, late evolution phase therefore allow for a
stronger appearance of the third abundance peak.
Key words: nuclear reactions, nucleosynthesis, abundances - stars: supernovae: general - stars: winds, outflows - stars: neutron
1 Introduction
Heavy nuclei beyond the iron peak are known to be produced in nature
mainly through neutron capture reactions (Burbidge et al. 1957).
Rapid neutron capture and the reverse photodisintegration processes
achieve an equilibrium among the isotopes of each heavy element. Then
beta-decay occurs that leads to the increase in the nuclear charge and
formation of a new element. When the neutron capture rate is much higher than
the beta-decay rate (
![]() )
and
)
and
![]() (T9 is defined as the temperature normalized to 109 K),
the r-process can start and, for a sufficiently high
neutron-to-seed ratio, the wave of nucleosynthesis drives the process to
heavier nuclei, forming, in part, the abundance r-process peaks at
(T9 is defined as the temperature normalized to 109 K),
the r-process can start and, for a sufficiently high
neutron-to-seed ratio, the wave of nucleosynthesis drives the process to
heavier nuclei, forming, in part, the abundance r-process peaks at
![]() 80, 130 and 196.
80, 130 and 196.
Although the r-process sites remain unknown, many astrophysical models and sources for r-process elements have been proposed during the past 50 years, including, in particular, scenarios such as that of an explosion on a neutron-star surface (Bisnovatyi-Kogan & Chechetkin 1979), a collision of a neutron star with a black hole (Lattimer & Schramm 1976), an explosion of a low-mass neutron star (Imshennik 1992), and the hypothetical escape of nucleon bubbles in case of a soundless stellar collapse (Imshennik & Litvinova 2006). The last scenario was suggested as the origin of gamma-ray bursts but could also be an interesting site for the nucleosynthesis of heavy elements.
Presently, however, it seems most likely that rapid n-capture nucleosynthesis can take place during different stages of supernova explosions (e.g. Hillebrandt 1978; Woosley & Hoffman 1992), or in neutron star mergers (e.g. Lattimer & Schramm 1974; Symbalisty & Schramm 1982; Freiburghaus et al. 1999). An overview of the currently discussed possible sites is given in a recent review paper by Arnould et al. (2007).
Supernovae and neutron star mergers have different advantages and weak points, but the main difference lies probably in the initial neutron-to-proton ratio, which is necessary for supporting a sufficiently high free neutron density during several hundreds of milliseconds. With respect to this parameter, all astrophysical scenarios can be separated into two distinct groups, in which nucleosynthesis can be carried out over short or long timescales (so-called short-time or long-time solutions, respectively), as introduced by Seeger et al. (1965). In nature, the r-process might be realized in both these types of sources and also other ones might contribute (see for example Cameron 2002; Arnould et al. 2007). It is only future modeling and observations that will be able clarify the multiplicity of the r-process models and types, as well as the contributions from different production sites to the r-process element abundances observed in the Solar System.
Among the astrophysical events proposed as sites for the r-process, supernova explosions still remain the preferable ones (see, e.g. Wanajo & Ishimaru 2006, and references therein). In particular, supernova explosions can distribute r-process material all over the Galaxy, and estimated amounts of heavy elements produced in SN explosions are in accordance with the observations.
The neutrino-driven wind from a hot neutron star produced in a supernova explosion has been considered as a probable site for the r-process by many authors (see e.g. Meyer et al. 1992; Woosley et al. 1994; Witti et al. 1993; Otsuki et al. 2000; Sumiyoshi et al. 2000; Terasawa et al. 2001; Wanajo et al. 2001). A part of the surface material of a neutron star is heated by the supernova neutrinos and gets ejected. It can be described as a hot outflow with a fairly high entropy and a moderate density.
Various studies of the r-process element formation in proto-neutron
star winds have been conducted during the past years. Hoffman et al. (1997), employing the analytic wind model of Qian & Woosley
(1996), explored the possibility of third peak creation for different
combinations of the determining parameters of
![]() (the
electron-to-baryon ratio), entropy, and expansion timescale.
Altogether, they showed (see their Fig. 10) that for typical values of
(the
electron-to-baryon ratio), entropy, and expansion timescale.
Altogether, they showed (see their Fig. 10) that for typical values of
![]() in the wind the third r-process peak can be produced for combinations ranging from moderate entropy (
in the wind the third r-process peak can be produced for combinations ranging from moderate entropy (
![]() in units of Boltzmann's
constant per baryon) and very short timescales (
in units of Boltzmann's
constant per baryon) and very short timescales (
![]() a few
milliseconds) to high entropies (
a few
milliseconds) to high entropies (![]() )
and long expansion timescales
(a few 100 ms). The wind models existing at that time failed to provide the necessary conditions (Witti et al. 1994; Qian & Woosley 1996).
)
and long expansion timescales
(a few 100 ms). The wind models existing at that time failed to provide the necessary conditions (Witti et al. 1994; Qian & Woosley 1996).
Subsequently, several other studies of neutrino-driven winds in the
framework of general relativistic gravity (Otsuki et al. 2000;
Sumiyoshi et al. 2000; Thompson et al. 2001; Wanajo et al. 2001, 2002) confirmed the need of fairly extreme conditions concerning
expansion timescale or entropy for strong r-processing up to
![]() .
Since very high entropies could not be obtained in the wind scenario or were found to be associated with too low mass loss rates for any significant production of r-nuclei, these studies also demonstrated a preference for the case of moderate entropies,
.
Since very high entropies could not be obtained in the wind scenario or were found to be associated with too low mass loss rates for any significant production of r-nuclei, these studies also demonstrated a preference for the case of moderate entropies,
![]() -200, and very short timescales. This seemed to give a bias for
winds from compact neutron stars with a large mass,
-200, and very short timescales. This seemed to give a bias for
winds from compact neutron stars with a large mass,
![]() ,
and a small radius
,
and a small radius ![]() km as the most likely site for r-process
element formation up to the platinum peak.
km as the most likely site for r-process
element formation up to the platinum peak.
This conclusion was found to hold independent of whether
freely expanding, transsonic ``wind'' outflows were considered
(Hoffman et al. 1997; Thompson et al. 2001) or subsonic
``breeze'' solutions (Otsuki et al. 2000;
Sumiyoshi et al. 2000; Wanajo et al. 2001;
Terasawa et al. 2001, 2002) or supersonic winds with some
fixed freeze-out temperature ![]() (Wanajo et al. 2002,
Wanajo 2007). Winds are characterized by a monotonically increasing velocity and a continuous temperature decrease when the radius goes to infinity,
whereas breezes are obtained when a prescribed, non-vanishing value of the
pressure and temperature is required to be reached at the outer
boundary at some large radius (this is supposed to mimic the fact that the fast neutrino-driven wind is decelerated again as it collides and merges with the
preceding, more slowly expanding material ejected in the early phase
of the supernova blast). The approach taken by Wanajo et al. (2002)
allowed them to causally disconnect the conditions at large radii from
those at the neutron star and thus to choose the asymptotic temperature
independent of the mass-loss rate (in contrast to the situation for
breezes and winds). The results from these different types of outflow scenarios concerning combinations of entropy,
(Wanajo et al. 2002,
Wanajo 2007). Winds are characterized by a monotonically increasing velocity and a continuous temperature decrease when the radius goes to infinity,
whereas breezes are obtained when a prescribed, non-vanishing value of the
pressure and temperature is required to be reached at the outer
boundary at some large radius (this is supposed to mimic the fact that the fast neutrino-driven wind is decelerated again as it collides and merges with the
preceding, more slowly expanding material ejected in the early phase
of the supernova blast). The approach taken by Wanajo et al. (2002)
allowed them to causally disconnect the conditions at large radii from
those at the neutron star and thus to choose the asymptotic temperature
independent of the mass-loss rate (in contrast to the situation for
breezes and winds). The results from these different types of outflow scenarios concerning combinations of entropy, ![]() ,
and expansion timescale necessary for strong r-processing in the ejecta turned out to be in qualitative
agreement (compare, e.g., Fig. 1 in Thompson et al. 2001 with
Fig. 8 in Otsuki et al. 2000 and with Table 2 and Fig. 6 in
Sumiyoshi et al. 2000).
,
and expansion timescale necessary for strong r-processing in the ejecta turned out to be in qualitative
agreement (compare, e.g., Fig. 1 in Thompson et al. 2001 with
Fig. 8 in Otsuki et al. 2000 and with Table 2 and Fig. 6 in
Sumiyoshi et al. 2000).
Later Terasawa et al. (2002) announced to have found successful
conditions even for proto-neutron stars with a more typical mass
around 1.4![]() and a radius of 10 km. Like previous studies (in particular Sumiyoshi et al. 2000, but also Otsuki et al. 2000) they considered breeze outflows, but different from the earlier investigations they chose a lower value for the outer boundary pressure, which implied a lower asymptotic temperature. They argued that this is favorable for a strong r-processing up to
the third peak because the lower final temperature is associated with a faster expansion and more rapid cooling. The more quickly decreasing temperature leads to a slowing down of charged-particle reactions and reduces the efficiency of
and a radius of 10 km. Like previous studies (in particular Sumiyoshi et al. 2000, but also Otsuki et al. 2000) they considered breeze outflows, but different from the earlier investigations they chose a lower value for the outer boundary pressure, which implied a lower asymptotic temperature. They argued that this is favorable for a strong r-processing up to
the third peak because the lower final temperature is associated with a faster expansion and more rapid cooling. The more quickly decreasing temperature leads to a slowing down of charged-particle reactions and reduces the efficiency of ![]() -particle recombination. Therefore it leads to less production of seed nuclei
and a higher neutron-to-seed ratio. Such a sensitivity to the
expansion timescale was also seen by Arnould et al. (2007), who
performed systematic variations of the parameters in analytic wind
and breeze solutions. Arnould et al. (2007) verified that wind
solutions provide the more favorable conditions for strong
r-processing than the slower breezes, because for given values of
the entropy and mass loss rate the expansion timescale is directly
correlated with the asymptotic value of the temperature and thus of
the total specific energy of the outflowing gas. These values are
lowest in case of freely expanding winds. Arnould et al. (2007),
however, also saw that the mass loss rate has a much more sensitive
influence: breeze solutions with higher mass loss rates (and
otherwise the same characterising parameter values) make a faster
expansion and allow for a stronger r-process despite having higher
asymptotic values of the temperature.
-particle recombination. Therefore it leads to less production of seed nuclei
and a higher neutron-to-seed ratio. Such a sensitivity to the
expansion timescale was also seen by Arnould et al. (2007), who
performed systematic variations of the parameters in analytic wind
and breeze solutions. Arnould et al. (2007) verified that wind
solutions provide the more favorable conditions for strong
r-processing than the slower breezes, because for given values of
the entropy and mass loss rate the expansion timescale is directly
correlated with the asymptotic value of the temperature and thus of
the total specific energy of the outflowing gas. These values are
lowest in case of freely expanding winds. Arnould et al. (2007),
however, also saw that the mass loss rate has a much more sensitive
influence: breeze solutions with higher mass loss rates (and
otherwise the same characterising parameter values) make a faster
expansion and allow for a stronger r-process despite having higher
asymptotic values of the temperature.
Although Arnould et al. (2007) confirmed the formation of the third
r-process peak for combinations of entropy, expansion timescale,
![]() ,
neutron star mass, and asymptotic temperature
in the ballpark of those considered by Terasawa et al. (2002),
the results of the latter paper are nevertheless in contradiction to
the earlier studies by Otsuki et al. (2000), Sumiyoshi et al. (2000), and Thompson et al. (2001):
Terasawa et al. (2002) obtained a significantly higher entropy and
shorter expansion timescale than Sumiyoshi et al. (2000) even for
the same choice of outflow determining conditions, i.e., for
the same individual neutrino luminosity
(
,
neutron star mass, and asymptotic temperature
in the ballpark of those considered by Terasawa et al. (2002),
the results of the latter paper are nevertheless in contradiction to
the earlier studies by Otsuki et al. (2000), Sumiyoshi et al. (2000), and Thompson et al. (2001):
Terasawa et al. (2002) obtained a significantly higher entropy and
shorter expansion timescale than Sumiyoshi et al. (2000) even for
the same choice of outflow determining conditions, i.e., for
the same individual neutrino luminosity
(
![]() erg s-1), the same mean neutrino energies,
and in particular the same outer boundary pressure (compare Table 1 in
the Terasawa et al. work and Sect. 3.2 in Sumiyoshi et al.).
Moreover, for all tested values of the boundary
pressure, Terasawa et al. (2002) found outflow properties
for their 1.4
erg s-1), the same mean neutrino energies,
and in particular the same outer boundary pressure (compare Table 1 in
the Terasawa et al. work and Sect. 3.2 in Sumiyoshi et al.).
Moreover, for all tested values of the boundary
pressure, Terasawa et al. (2002) found outflow properties
for their 1.4![]() neutron star that were
largely different from those plotted for breezes
in Fig. 8 of Otsuki et al. (2000)
and for freely expanding winds in Fig. 11 of Thompson et al. (2001).
These differences seem to have been causal for the successful solar system
like r-process reported by Terasawa et al. (2002), but the actual
reason why the more favorable outflow behavior was obtained, remains
unexplained
neutron star that were
largely different from those plotted for breezes
in Fig. 8 of Otsuki et al. (2000)
and for freely expanding winds in Fig. 11 of Thompson et al. (2001).
These differences seem to have been causal for the successful solar system
like r-process reported by Terasawa et al. (2002), but the actual
reason why the more favorable outflow behavior was obtained, remains
unexplained![]() .
.
Recently, Arcones et al. (2007) performed new hydrodynamic simulations
of neutrino-driven winds, systematically exploring the effects of the
wind termination shock that forms when the supersonic wind collides
with the slower earlier supernova ejecta (Janka & Müller 1995a,b;
Burrows et al. 2005; Buras et al. 2006, see also Tomàs et al.
2004) and that decelerates the outflow abruptly. They found that the
position of the reverse shock is strongly dependent on the evolution
phase, progenitor structure, and explosion energy of the supernova.
Motivated by these studies, interest has recently turned to a closer
exploration of the relevance of the late-time wind dynamics for
r-process nucleosynthesis. On the one hand, Wanajo (2007) showed
numerically that a solar-like r-process can also be produced in
supersonically expanding outflows whose temperature drops quickly to a
few 108 K instead of asymptoting to a value around 109 K as
previously mostly assumed (Otsuki et al. 2000; Sumiyoshi et al. 2000; Wanajo et al. 2001, 2002). In such a low-temperature environment an
![]() -
-
![]() equilibrium is never achieved during the nucleosynthesis of heavy r-process material, but
neutron captures compete with
equilibrium is never achieved during the nucleosynthesis of heavy r-process material, but
neutron captures compete with ![]() -decays in the low-density matter,
similar to what was discussed by Blake & Schramm (1976).
-decays in the low-density matter,
similar to what was discussed by Blake & Schramm (1976).
On the other hand, Kuroda et al. (2008) started to explore for the
first time systematically the consequences of the wind termination
shock for the r-processing in the wind. Decelerating the outflow
abruptly, the reverse shock does not only raise the entropy of the
matter, but in particular it slows down the temperature and density
decline that takes place in the subsequent expansion. Kuroda et al. (2008) pointed out that the change in the temperature behavior
plays a decisive role in determining the r-process abundances,
because the nucleosynthesis path depends strongly on the temperature
during the r-process freeze-out phase. In contrast, the entropy jump
does not seem to be important because high entropies in the shocked
outflows are reached only when the temperature is already well below
![]() K, i.e. not in the regime where the
neutron-to-seed ratio is established before the onset of
r-processing.
K, i.e. not in the regime where the
neutron-to-seed ratio is established before the onset of
r-processing.
In the present paper we also investigate the influence of the late-time outflow dynamics on the r-process nucleosynthesis. To this end we consider outflow trajectories that consist of an initial homologous phase and a second, slower expansion stage. This describes the wind dynamics only schematically but at least some basic features that are found in detailed solutions of unshocked as well as shocked outflows can be reproduced. In contrast to the outflow solutions studied by Arnould et al. (2007), for example, our simple parametric ansatz for the temperature and density decrease in the ejected matter allows us to modify the early expansion behavior and that at late times independently, i.e. in an uncoupled way. This is similar to the approach taken by Wanajo et al. (2002) and closer to how, for example, the presence of a wind termination shock acts on the matter. Motivated by the insensitivity to the entropy jump seen by Kuroda et al. (2008), we ignore the discontinuity of the fluid variables at the location where their time dependence is assumed to change.
In order to obtain r-processing with reasonable instead of
extreme values of the
wind entropy s and electron fraction ![]() ,
we consider
sufficiently short exponential timescales for the first expansion
stage, i.e., we consider timescales in the ballpark of those given
for example by Otsuki et al. (2000) for outflows from
a neutron star with a gravitational mass of 2
,
we consider
sufficiently short exponential timescales for the first expansion
stage, i.e., we consider timescales in the ballpark of those given
for example by Otsuki et al. (2000) for outflows from
a neutron star with a gravitational mass of 2![]() ,
a
radius of 10 km, and a neutrino luminosity of 1052 erg s-1(see their Table 1). We will vary the prescribed
expansion behavior during the second phase in order to discuss the
effects of the late-time temperature evolution on the r-processing
from a more general point of view than done in previous works.
The role of a strong
or weak deceleration of the very fast, transsonic winds will be
investigated by a constant or power-law behavior, respectively, of
the temperature and density during the second stage. The former
may be interpreted as the limiting case of a strong deceleration
by a wind termination shock. The latter may be considered as an
approximation to the reduced acceleration that a freely expanding
wind experiences at larger radii after its roughly homologous
initial phase.
,
a
radius of 10 km, and a neutrino luminosity of 1052 erg s-1(see their Table 1). We will vary the prescribed
expansion behavior during the second phase in order to discuss the
effects of the late-time temperature evolution on the r-processing
from a more general point of view than done in previous works.
The role of a strong
or weak deceleration of the very fast, transsonic winds will be
investigated by a constant or power-law behavior, respectively, of
the temperature and density during the second stage. The former
may be interpreted as the limiting case of a strong deceleration
by a wind termination shock. The latter may be considered as an
approximation to the reduced acceleration that a freely expanding
wind experiences at larger radii after its roughly homologous
initial phase.
Our paper is structured as follows. In Sect. 2 we will describe the dynamical model and the network used in our study, and will present some numerical tests we performed. In Sect. 3 we will describe our results and in Sect. 4 we finish with conclusions.
2 Network, input data, and numerical modeling
of the ( +r)-process
+r)-process
We consider here the conditions for r-process nucleosynthesis
in neutrino-driven outflows from the surface layers of hot nascent
neutron stars, which have been the subject of many previous studies,
where different aspects of the problem were discussed
(see, e.g. Qian & Woosley 1996; Hoffman et al. 1997; Woosley et al. 1994; Cardall & Fuller 1997; Qian & Wasserburg 2000; Takahashi et al. 1994; Otsuki et al. 2000; Sumiyoshi et al. 2000; Thompson et al. 2001; Kuroda et al. 2008; Arnould et al. 2007, and references
therein). Our main goal here is to evaluate numerically the possibility
of producing r-process elements in this environment in dependence of
the late-time behavior of the outflowing gas. Within the framework of a
very simple, purely analytic model of the wind we want to
determine the favorable combinations of entropy,
![]() and
dynamical timescale, and how sensitively these parameters influence the
outcome. Though, of course, our results will not allow us to make a
judgement about whether neutrino-driven winds are the long-sought site
of r-process material or not, our parametric approach has the
advantage of reducing the dynamical aspects of the problem to an
absolute minimum of ingredients, giving one much freedom in the choice
of the involved parameter values.
and
dynamical timescale, and how sensitively these parameters influence the
outcome. Though, of course, our results will not allow us to make a
judgement about whether neutrino-driven winds are the long-sought site
of r-process material or not, our parametric approach has the
advantage of reducing the dynamical aspects of the problem to an
absolute minimum of ingredients, giving one much freedom in the choice
of the involved parameter values.
2.1 Outflow behavior
We represent the outflow behavior during the early and late expansion phases by different analytic functions. These describe qualitatively (but certainly not to very high accuracy) on the one hand the wind acceleration through the sonic point, and on the other hand the evolution of the outflow during a second phase of either deceleration by a reverse shock or reduced acceleration.
In the first stage of the expansion of a spherical mass shell we
assume a homologous velocity-radius dependence,
![]() ,
corresponding to an exponential growth of the radius,
,
corresponding to an exponential growth of the radius,
![]() .
Therefore,
steady-state conditions (which imply
.
Therefore,
steady-state conditions (which imply
![]() const) yield an
exponential decline of the density and for an adiabatically
expanding, radiation-dominated wind (i.e.,
const) yield an
exponential decline of the density and for an adiabatically
expanding, radiation-dominated wind (i.e.,
![]() )
also
an exponential decrease in the temperature:
)
also
an exponential decrease in the temperature:
Here T9 is the temperature normalized to 109 K and
For reasons of simplicity, we will always assume that ![]() is
proportional to T3 and that the gas entropy per nucleon
(in units of Boltzmann's constant
is
proportional to T3 and that the gas entropy per nucleon
(in units of Boltzmann's constant
![]() )
is given by
the relation
)
is given by
the relation
![]() with
with
![]() g cm-3). One should, however,
keep in mind that this is only a simplifying approximation,
which is accurate only when the entropy of the gas is large
enough (
g cm-3). One should, however,
keep in mind that this is only a simplifying approximation,
which is accurate only when the entropy of the gas is large
enough (
![]() per nucleon) and the temperature
sufficiently high (
per nucleon) and the temperature
sufficiently high (![]() ). In this case radiation-dominated
conditions prevail, electrons are relativistic, electron-positron
pairs are abundant, and baryons contribute to the total entropy
only at the level of a few percent. In reality, however, the pairs
begin to disappear below
). In this case radiation-dominated
conditions prevail, electrons are relativistic, electron-positron
pairs are abundant, and baryons contribute to the total entropy
only at the level of a few percent. In reality, however, the pairs
begin to disappear below
![]() and the ratio
and the ratio ![]() increases. Assuming it to be constant also at low temperatures
therefore leads to an overestimation of the density in the
outflowing matter compared to a truely adiabatic evolution
(see Witti et al. 1994, for a detailed discussion).
increases. Assuming it to be constant also at low temperatures
therefore leads to an overestimation of the density in the
outflowing matter compared to a truely adiabatic evolution
(see Witti et al. 1994, for a detailed discussion).
The deceleration by the reverse shock or changing
acceleration behavior are supposed to happen at a
radius r0 and time t0 when the velocity, density, and
temperature reach the values v0, ![]() ,
and T0, respectively.
As discussed in the introduction, we ignore here the discontinuous
behavior of the dynamical and thermodynamical variables at the
shock and connect the early-time behavior continuously with the
late-time behavior. This means that also the ratio
,
and T0, respectively.
As discussed in the introduction, we ignore here the discontinuous
behavior of the dynamical and thermodynamical variables at the
shock and connect the early-time behavior continuously with the
late-time behavior. This means that also the ratio ![]() (and therefore the quantity s that we consider as gas entropy)
remains unchanged at the transition point and
is taken to be constant during the following second stage of the
expansion. For the latter we consider two
cases with different limiting behavior for
(and therefore the quantity s that we consider as gas entropy)
remains unchanged at the transition point and
is taken to be constant during the following second stage of the
expansion. For the latter we consider two
cases with different limiting behavior for ![]() .
In the first
case we assume that the density and temperature asymptote to
constant values,
.
In the first
case we assume that the density and temperature asymptote to
constant values,
For steady-state conditions this implies that the radius and the velocity of a Lagrangian mass shell evolve at
and therefore
In the second investigated case the density and temperature are still assumed
to decline at late times, but much less steeply than during
the exponential first expansion phase:
For steady-state conditions this corresponds to
which yields
Table 1: Parameter values for some of our considered outflows and of relevance for third peak formation.
The slower decline of the density and temperature during the
power-law phase may be considered as a simplified representation of
a reduced wind acceleration occurring after an approximately
homologous (i.e.,
![]() )
early expansion. Neutrino-driven
winds exhibit such a nearly homologous evolution and thus nearly
exponential increase in the radius and velocity with time only up to
some distance, but then the velocity continues to grow less rapidly
even in the absence (or before) a possible strong deceleration by a
termination shock. The basic properties of this behavior are
captured by our approach.
)
early expansion. Neutrino-driven
winds exhibit such a nearly homologous evolution and thus nearly
exponential increase in the radius and velocity with time only up to
some distance, but then the velocity continues to grow less rapidly
even in the absence (or before) a possible strong deceleration by a
termination shock. The basic properties of this behavior are
captured by our approach.
2.2 Calculating the nucleosynthesis
At the onset of its expansion, the ejected matter in the
neutrino-driven wind is very hot and composed of free neutrons and
protons. With ongoing cooling the nuclear statistical equilibrium (NSE)
shifts towards an increasing mass fraction of alpha particles until
finally the recombination to heavy nuclei sets in. Provided the
conditions of entropy, electron fraction, and expansion timescale are
suitable, the production of elements between the first and second peaks
of the abundance curve through charged particle reactions and neutron
captures may occur. For sufficiently extreme conditions even third-peak
elements and (
![]() )
may be assembled. Typically starting our
nucleosynthesis calculations at temperatures
)
may be assembled. Typically starting our
nucleosynthesis calculations at temperatures
![]() and densities
and densities
![]() -106 g cm-3 (the initial density is chosen
according to a specified value for the conserved gas entropy), the
element formation in our model runs first proceeds mainly through
charged-particle reactions. As the temperature and density decrease,
the importance of (
-106 g cm-3 (the initial density is chosen
according to a specified value for the conserved gas entropy), the
element formation in our model runs first proceeds mainly through
charged-particle reactions. As the temperature and density decrease,
the importance of (![]() ,X)- and inverse reactions diminishes and
the nuclear flow begins to be driven by a dynamical r-process, provided
a sufficient number of free neutrons is still present. The production
of a small mass fraction of heavy nuclei with
,X)- and inverse reactions diminishes and
the nuclear flow begins to be driven by a dynamical r-process, provided
a sufficient number of free neutrons is still present. The production
of a small mass fraction of heavy nuclei with ![]() before the
onset of rapid neutron captures significantly reduces the requirements
for the neutron source (a smaller number of free neutrons is required).
before the
onset of rapid neutron captures significantly reduces the requirements
for the neutron source (a smaller number of free neutrons is required).
The time-dependent concentrations of nuclear species, Y(A,Z), during
the r-processing as determined by reactions with neutrons,
beta-decays, and fission processes are described by the nucleosynthesis
network developed by Blinnikov & Panov (1996) and Nadyozhin et al. (1998). This network was here extended by charged-particle reactions
and a larger number of nuclear reactions and fission processes so that
it is possible to handle both the initial ![]() -process and the
subsequent r-process with the same code.
-process and the
subsequent r-process with the same code.
The number of nuclei and reaction equations included in calculations depends on boundary conditions and the employed nuclear mass model and can be as large as about 4300. We considered the region of nuclei with Z ranging from 3 to 100. The minimum and maximum atomic mass values for each chemical element were determined by the proton and neutron drip lines.
The reaction rates entering the system of differential equations differ by tens of orders of magnitude. Thus, the system of equations for nuclear kinetics to be solved is a classical example of a stiff system of ordinary differential equations. We used one of the most effective methods to integrate such a stiff system of equations, Gear's method (Gear 1971). The description of the complete package of solver routines and its applications to the r-process calculations can be found in Nadyozhin et al. (1998).
Nuclear mass values as predicted by FRDM (Möller et al. 1995) were used, the beta-decay rates were calculated in the framework of the QRPA-model (Kratz et al. 1993), and the reaction rates with neutrons were described according to the calculations of Cowan et al. (1991) and of Rauscher & Thielemann (2000).
In the nucleosynthesis studies presented here, the triple ![]() and
and
![]() reactions of helium burning,
reactions of helium burning,
![]() C and
C and
![]() Be, respectively, along with their inverse reactions, were included.
The rates for both processes were taken from the REACLIB library
of Thielemann et al. (1987) and those for the reactions of heavier
nuclei with protons and
Be, respectively, along with their inverse reactions, were included.
The rates for both processes were taken from the REACLIB library
of Thielemann et al. (1987) and those for the reactions of heavier
nuclei with protons and ![]() -particles from Rauscher & Thielemann (2000).
-particles from Rauscher & Thielemann (2000).
2.3 Code tests and comparisons
Code tests for a number of different cases were performed by
Panov et al. (2001a), and for a number of explored cases r-process
calculations with the same rates gave
practically the same isotopic yields as in the paper of Freiburghaus et al. (1999)
Network calculations of the ![]() -process with the present code were
compared with the results shown by Witti et al. (1994)
and yield rather compatible abundance distributions at the
beginning of the r-process, in spite of differences in the employed nuclear reaction rates and the nuclear mass model.
-process with the present code were
compared with the results shown by Witti et al. (1994)
and yield rather compatible abundance distributions at the
beginning of the r-process, in spite of differences in the employed nuclear reaction rates and the nuclear mass model.
In this context we would like to note that the transition from the
![]() -process to the r-process can only be done correctly on the
basis of the same mathematical model. In our calculations we use the
same code for both parts of the nucleosynthetic reaction sequence,
without artificial devision into
-process to the r-process can only be done correctly on the
basis of the same mathematical model. In our calculations we use the
same code for both parts of the nucleosynthetic reaction sequence,
without artificial devision into ![]() - and r-process steps.
- and r-process steps.
![\begin{figure}
\par\includegraphics*[width=8.0cm,clip]{0292fig1.eps}\hspace*{4mm}
\includegraphics*[width=8.0cm,clip]{0292fig2.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg102.gif) |
Figure 1:
T9-dependence of the free neutron density
|
| Open with DEXTER | |
We compared the seed production as calculated with our full
network to results from nuclear statistical equilibrium (NSE) as obtained by
Nadyozhin & Yudin (2004), Blinnikov et al. (to be published), and with the
NSE-code used by Witti et al. (1994). We observed rather
good agreement at temperatures
![]() -6 and a density
around
-6 and a density
around
![]() g cm-3. At such temperatures the
g cm-3. At such temperatures the ![]() -peak is already formed and the mass fraction of seed nuclei (i.e., heavy elements) is still small,
the most abundant nuclei in both cases being 50Ti and 54Cr.
Small discrepancies between the different calculations emerge
mostly from the use of different mass formulas and can lead to
smaller differences in the subsequent
-peak is already formed and the mass fraction of seed nuclei (i.e., heavy elements) is still small,
the most abundant nuclei in both cases being 50Ti and 54Cr.
Small discrepancies between the different calculations emerge
mostly from the use of different mass formulas and can lead to
smaller differences in the subsequent ![]() - and r-process. They
may be important for exact predictions of the abundance flow during
the r-processing, but they should not affect the basic results of our
investigation.
- and r-process. They
may be important for exact predictions of the abundance flow during
the r-processing, but they should not affect the basic results of our
investigation.
We also compared our results for the ![]() -process with the
calculations made by Witti et al. (1994), using conditions
similar to those of the HT-model of Witti et al. (1993),
i.e., s=390,
-process with the
calculations made by Witti et al. (1994), using conditions
similar to those of the HT-model of Witti et al. (1993),
i.e., s=390,
![]() .
For an exponential expansion
with a timescale of
.
For an exponential expansion
with a timescale of
![]() ms, which is the
same as in the HT-model, the number density
ms, which is the
same as in the HT-model, the number density
![]() as a
function of temperature (Fig. 1, left) is clearly
different from what was obtained by Takahashi et al. (1994)
(see Fig. 2 therein and the dashed line in the left panel of
Fig. 1). When we increase the expansion timescale to
as a
function of temperature (Fig. 1, left) is clearly
different from what was obtained by Takahashi et al. (1994)
(see Fig. 2 therein and the dashed line in the left panel of
Fig. 1). When we increase the expansion timescale to
![]() ms, our result becomes close to that of
Takahashi et al. (1994). The reason for this discrepancy is
the fact that our calculations assume homologous expansion with an
exponential decrease in density and temperature, whereas the
temperature and density in the hydrodynamic model considered by
Takahashi et al. asymptote to nonvanishing values, i.e., the
temperature approaches T9 = 1.5 during the later expansion.
Although r-process elements are formed, neither of our exponential
runs leads to the build-up of a strong third r-process peak, despite
the high entropy. While in the case with the short expansion
timescale (
ms, our result becomes close to that of
Takahashi et al. (1994). The reason for this discrepancy is
the fact that our calculations assume homologous expansion with an
exponential decrease in density and temperature, whereas the
temperature and density in the hydrodynamic model considered by
Takahashi et al. asymptote to nonvanishing values, i.e., the
temperature approaches T9 = 1.5 during the later expansion.
Although r-process elements are formed, neither of our exponential
runs leads to the build-up of a strong third r-process peak, despite
the high entropy. While in the case with the short expansion
timescale (
![]() ms) the rapid dilution of the
matter prohibits the efficient formation of seed nuclei, the larger
expansion timescale (
ms) the rapid dilution of the
matter prohibits the efficient formation of seed nuclei, the larger
expansion timescale (
![]() ms) leads to a
strong
ms) leads to a
strong ![]() -process with a lot of seed production and therefore
a neutron-to-seed ratio that is too low for the generation of very
heavy r-process nuclei. In contrast, Takahashi et al. (1994) obtained a prominant third abundance peak. In their
calculation a sufficiently fast initial expansion prevents the
formation of too much seed material before the r-process starts, and
therefore the neutron-to-seed ratio remains high. The asymptoting
temperature and density on the other hand support a high neutron
number density for such a long time that neutron capture reactions
can assemble nuclei also in the third peak.
-process with a lot of seed production and therefore
a neutron-to-seed ratio that is too low for the generation of very
heavy r-process nuclei. In contrast, Takahashi et al. (1994) obtained a prominant third abundance peak. In their
calculation a sufficiently fast initial expansion prevents the
formation of too much seed material before the r-process starts, and
therefore the neutron-to-seed ratio remains high. The asymptoting
temperature and density on the other hand support a high neutron
number density for such a long time that neutron capture reactions
can assemble nuclei also in the third peak.
For lower entropy, s=145, and higher neutron excess,
![]() ,
(Fig. 1, right) the number of free
neutrons can also remain large enough to allow for the onset of
r-processing when the
,
(Fig. 1, right) the number of free
neutrons can also remain large enough to allow for the onset of
r-processing when the ![]() -process freezes out at a temperature of
-process freezes out at a temperature of
![]() .
In this case, however,
much shorter dynamical timescales are needed. Figure 2
displays the decreasing seed formation and increasing neutron-to-seed
ratio for smaller expansion timescales
.
In this case, however,
much shorter dynamical timescales are needed. Figure 2
displays the decreasing seed formation and increasing neutron-to-seed
ratio for smaller expansion timescales
![]() .
.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig3.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fig4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg112.gif) |
Figure 2:
T9-dependence of the neutron-to-seed ratio
|
| Open with DEXTER | |
How many neutrons per seed nucleus are needed to form the third abundance
peak (![]() )? Usually the number mentioned in this context is
not less than 150. But this estimate is based on the simple calculation
how many neutrons a single 56Fe nucleus must capture to finally,
after a chain of beta-decays, end as nucleus in the platinum peak.
In the actual r-process, only a fraction of the nuclei that are
initially formed by the alpha-process - we call these nuclei the ``seed''
- will be ultimately transformed to elements and isotopes with the highest mass numbers.
)? Usually the number mentioned in this context is
not less than 150. But this estimate is based on the simple calculation
how many neutrons a single 56Fe nucleus must capture to finally,
after a chain of beta-decays, end as nucleus in the platinum peak.
In the actual r-process, only a fraction of the nuclei that are
initially formed by the alpha-process - we call these nuclei the ``seed''
- will be ultimately transformed to elements and isotopes with the highest mass numbers.
Taking into account that the observed ratio of the third to second
abundance peak is
![]() ,
we estimate that the
neutron number needed to obtain a strong third peak is of the order of
(196-
,
we estimate that the
neutron number needed to obtain a strong third peak is of the order of
(196-
![]() .
The actual value might even be a bit
lower, because the mean atomic number at the freeze-out time of the
.
The actual value might even be a bit
lower, because the mean atomic number at the freeze-out time of the
![]() -process can be about 80 or more instead of 60 (an exact
estimate, however, also depends on the conditions in which the
r-processing takes place and the corresponding speed of the abundance
flow). Therefore a solar-like formation of the platinum peak can be
expected if one has a neutron-to-seed ratio of around 30 after the
freeze-out of charged-particle reactions.
-process can be about 80 or more instead of 60 (an exact
estimate, however, also depends on the conditions in which the
r-processing takes place and the corresponding speed of the abundance
flow). Therefore a solar-like formation of the platinum peak can be
expected if one has a neutron-to-seed ratio of around 30 after the
freeze-out of charged-particle reactions.
We point out, however, that this value does not ensure that the solar abundance distribution in the whole mass-number region between the second and third abundance peaks is reproduced well. This goal is not attempted in our study here, and it is well known that a superposition of at least two components with different physical conditions instead of a single ejecta trajectory (as considered by us) is needed for matching the solar r-process pattern (see, e.g. Kratz et al. 1993; Goriely & Arnould 1996; Wanajo et al. 2004; Kuroda et al. 2008). In our fast-expansion cases we regard the described criterion as a reasonably good indicator for outflow conditions that allow for the appearance of a strong third peak during the r-processing that follows after the freeze-out of charged-particle reactions.
To judge about the possibility of an r-process for different choices
of the parameters of our dynamical model (s, ![]() ,
,
![]() ), we first consider the seed formation and the
corresponding time evolution of the neutron-to-seed ratio in
the homologous expansion phase. In Fig. 1 we have seen
agreement of the free neutron density as a function of time between
our calculations and the prior ones by Takahashi et al. (1994) for
a suitable choice of the expansion timescale
), we first consider the seed formation and the
corresponding time evolution of the neutron-to-seed ratio in
the homologous expansion phase. In Fig. 1 we have seen
agreement of the free neutron density as a function of time between
our calculations and the prior ones by Takahashi et al. (1994) for
a suitable choice of the expansion timescale
![]() (although the heavy-element nucleosynthesis was considerably
different as discussed above).
Figure 2 shows the neutron-to-seed ratios and the seed
abundances,
(although the heavy-element nucleosynthesis was considerably
different as discussed above).
Figure 2 shows the neutron-to-seed ratios and the seed
abundances,
![]() ,
versus
temperature for the same cases as displayed in the
right panel of Fig. 1. Note that we consider all nuclei
with Z>2 as seeds, which is a different definition than used by
Terasawa et al. (2001), who restriced seed nuclei to the
more narrow range of
,
versus
temperature for the same cases as displayed in the
right panel of Fig. 1. Note that we consider all nuclei
with Z>2 as seeds, which is a different definition than used by
Terasawa et al. (2001), who restriced seed nuclei to the
more narrow range of
![]() and Z>26. The latter mass range
is appropriate when the formation of the second abundance peak in an
incomplete r-process is discussed. Here, however, we explore the
possibility of third-peak production and consider a combined
and Z>26. The latter mass range
is appropriate when the formation of the second abundance peak in an
incomplete r-process is discussed. Here, however, we explore the
possibility of third-peak production and consider a combined
![]() - and r-process. In this case the atomic mass number range
should not be constrained. Because of the very short expansion timescale
and the treatment of both the
- and r-process. In this case the atomic mass number range
should not be constrained. Because of the very short expansion timescale
and the treatment of both the ![]() -process and the r-process
within the framework of the same mathematical model and computer code,
a distinction of seed nuclei and r-processed material becomes
artificial and one has to carefully judge when this information is
measured and what it means for the evolution of the mass number
with time. Often it refers to older calculations in which
the
-process and the r-process
within the framework of the same mathematical model and computer code,
a distinction of seed nuclei and r-processed material becomes
artificial and one has to carefully judge when this information is
measured and what it means for the evolution of the mass number
with time. Often it refers to older calculations in which
the ![]() - and r-process were computed in two independent steps
and with different codes. In this context we note that the amount
of heavy nuclei in our calculations is approximately twice as big
as found by Terasawa et al. (2002). This difference is mostly explained
by the different model parameters (in particular, Terasawa et al.
investigated outflows with higher entropies), but to some extent may
also be a consequence of different nuclear rates and included reactions.
- and r-process were computed in two independent steps
and with different codes. In this context we note that the amount
of heavy nuclei in our calculations is approximately twice as big
as found by Terasawa et al. (2002). This difference is mostly explained
by the different model parameters (in particular, Terasawa et al.
investigated outflows with higher entropies), but to some extent may
also be a consequence of different nuclear rates and included reactions.
With the definition of seed nuclei adopted by us, the seed abundance becomes constant after the freeze-out of the alpha-process and will also be unaffected by the transition to a second stage with modified expansion behavior for the cases considered by us. In contrast, replacing the free (homologous) expansion by a slower second stage of outflow behavior will have an impact on the density of free neutrons as a function of time. The free neutron density determines the r-process path and thus the formation of the heaviest elements in the third abundance peak.
From Fig. 2 (left panel) we see that the expansion
timescale for third peak formation to happen should be less than
about 10 ms. In this case the neutron-to seed ratio
![]() as the decisive macroscopic factor for the
platinum peak formation reaches the interesting values mentioned above.
Naturally, this ratio depends not only on the number of free neutrons,
but also on the seed abundance. Figure 2 (right panel)
shows that the seed production varies strongly with the expansion
timescale: if the dynamical time is large, a lot of seed is assembled
and all neutrons will be captured faster than the platinum peak begins
to appear. With shorter expansion timescale the seed production drops
and at the same time the density of free neutrons increases (see right
panel of Fig. 1). The consequence of both trends with
reduced
as the decisive macroscopic factor for the
platinum peak formation reaches the interesting values mentioned above.
Naturally, this ratio depends not only on the number of free neutrons,
but also on the seed abundance. Figure 2 (right panel)
shows that the seed production varies strongly with the expansion
timescale: if the dynamical time is large, a lot of seed is assembled
and all neutrons will be captured faster than the platinum peak begins
to appear. With shorter expansion timescale the seed production drops
and at the same time the density of free neutrons increases (see right
panel of Fig. 1). The consequence of both trends with
reduced
![]() is a strong growth of the
is a strong growth of the
![]() ratio that is present at the beginning of the
r-process.
ratio that is present at the beginning of the
r-process.
However, as already discussed above in the context of
Fig. 1, too rapid expansion can also be disadvantageous for
a strong r-process. When the dynamical timescale becomes very short,
the expansion and gas dilution proceed faster than the rate of
recombination of alpha particles to seed nuclei and subsequently the
rate of neutron captures. For the conditions considered in
Fig. 2 this happens when the homologous expansion and
density decrease are too rapid to allow for the neutrons to be
assembled into a strong 3rd peak, despite a high neutron-to-seed ratio
and a sufficiently small seed concentration
![]() below a
critical upper value of
below a
critical upper value of
![]() after the freeze-out of charged-particle processes.
after the freeze-out of charged-particle processes.
Of course, as discussed in detail in many previous works, besides
the expansion timescale, the entropy and the neutron excess (or
![]() ), have a sensitive influence on the strength of
the r-processing, i.e., on the question how many nuclei with mass
numbers above the second abundance peak and in particular near the
third peak can be formed. In any case, for rapid expansion (small
), have a sensitive influence on the strength of
the r-processing, i.e., on the question how many nuclei with mass
numbers above the second abundance peak and in particular near the
third peak can be formed. In any case, for rapid expansion (small
![]() )
the seed production is reduced and the neutron-to-seed ratio becomes more favorable for a strong r-process. The heavier the seed nuclei at the end of the
)
the seed production is reduced and the neutron-to-seed ratio becomes more favorable for a strong r-process. The heavier the seed nuclei at the end of the ![]() -process are, the lower can the required number of free neutrons be. This was already discussed by, e.g. Panov & Chechetkin (2002), who showed that fairly low neutron/seed ratios are already sufficient when the seed material at the freeze-out time of charged-particle reactions consists mostly of nuclei in the second abundance peak.
-process are, the lower can the required number of free neutrons be. This was already discussed by, e.g. Panov & Chechetkin (2002), who showed that fairly low neutron/seed ratios are already sufficient when the seed material at the freeze-out time of charged-particle reactions consists mostly of nuclei in the second abundance peak.
3 Asymptotic behavior of temperature and density and formation of the platinum peak
Our combined (![]() +r)-code was applied to
nucleosynthesis calculations assuming the two-stage expansion
behavior described above, with a second phase of either constant
or slowly decreasing temperature and density following a first
phase of rapid, exponential expansion. Our calculations were
started at a temperature of T9= 6, assuming NSE at this point.
For conditions similar to those given in Fig. 2
of Terasawa et al. (2001) with a short expansion timescale
of
+r)-code was applied to
nucleosynthesis calculations assuming the two-stage expansion
behavior described above, with a second phase of either constant
or slowly decreasing temperature and density following a first
phase of rapid, exponential expansion. Our calculations were
started at a temperature of T9= 6, assuming NSE at this point.
For conditions similar to those given in Fig. 2
of Terasawa et al. (2001) with a short expansion timescale
of
![]() ms,
we obtained basically the same results for the development of
the neutron number density and average neutron separation energy
until about half a second, and found gross agreement of the structure of the abundance distribution. Smaller discrepancies might be attributed
to differences in the initial composition and nuclear reaction
rates. The number fraction of seed nuclei reported by Terasawa et al. (2001),
ms,
we obtained basically the same results for the development of
the neutron number density and average neutron separation energy
until about half a second, and found gross agreement of the structure of the abundance distribution. Smaller discrepancies might be attributed
to differences in the initial composition and nuclear reaction
rates. The number fraction of seed nuclei reported by Terasawa et al. (2001),
![]() ,
is a bit low compared to our results, but this is probably mainly caused by a different definition of ``seeds''.
,
is a bit low compared to our results, but this is probably mainly caused by a different definition of ``seeds''.
In contrast, we were not able to confirm the formation of the
third abundance peak for conditions similar to those considered
by Terasawa et al. (2002) with an assumed expansion timescale of
![]() ms. Besides not providing exact
information about the initial density and the kind of network
used for the alpha- and r-process calculations (a full network
or off-line calculations for the r-processing?), some of the
results and explanations are hard to reproduce in detail.
For example, the calculations done by us with different NSE
codes (including that of Nadyozhin & Yudin 2004) and also
the simulations by Witti et al. (1994) show that
ms. Besides not providing exact
information about the initial density and the kind of network
used for the alpha- and r-process calculations (a full network
or off-line calculations for the r-processing?), some of the
results and explanations are hard to reproduce in detail.
For example, the calculations done by us with different NSE
codes (including that of Nadyozhin & Yudin 2004) and also
the simulations by Witti et al. (1994) show that
![]() -particles reassemble mainly down to temperatures around
T9 = 5-6, somewhat dependent on the density, but not at
temperatures as low as T9 = 4 (see Fig. 1 in Terasawa et al. 2002). Moreover, they argued that a lower value of the asymptotic
temperature is favorable for a successful r-processing by allowing
for a higher neutron-to-seed ratio, because such a lower ``outer
boundary'' temperature reduces charged-particle
reactions and thus the production of seed nuclei. This suggested
influence of the chosen asymptotic temperatures in the range between
T9 = 0.4 and T9 = 1.3, however, is implausible, because
charged-particle reactions become inefficient already at temperatures
of
-particles reassemble mainly down to temperatures around
T9 = 5-6, somewhat dependent on the density, but not at
temperatures as low as T9 = 4 (see Fig. 1 in Terasawa et al. 2002). Moreover, they argued that a lower value of the asymptotic
temperature is favorable for a successful r-processing by allowing
for a higher neutron-to-seed ratio, because such a lower ``outer
boundary'' temperature reduces charged-particle
reactions and thus the production of seed nuclei. This suggested
influence of the chosen asymptotic temperatures in the range between
T9 = 0.4 and T9 = 1.3, however, is implausible, because
charged-particle reactions become inefficient already at temperatures
of
![]() ,
when the thermal energies of protons and
,
when the thermal energies of protons and
![]() -particles become too low for enabling these particles
to overcome the nuclear Coulomb barriers.
-particles become too low for enabling these particles
to overcome the nuclear Coulomb barriers.
We will therefore not further attempt to compare our calculations with those done by Terasawa et al. (2002). Instead, we will in the following present our results for the formation of the third abundance peak in dependence of entropy, electron fraction, and dynamical timescale during the first, exponential expansion phase. In particular we will also study variations with the asymptotic values of temperature and density during the second, slower phase of expansion. This will help us in the analysis of the physical effects that can explain our results. Our goal is to develop a deeper understanding of the influence of the late-time behavior of neutrino-driven winds on the possibility of strong r-processing in such an environment.
To this end we carried out a set of calculations for exponential
timescales in the range from 1.0 to 25 ms and for four values of
the wind entropy (in units of Boltzmann's constant per nucleon),
s=105, 145, 170, and 200. The initial neutron to proton ratio was determined by an electron fraction of usually
![]() ;
some runs were performed with a value of
;
some runs were performed with a value of
![]() .
.
Our special attention was on the second stage of slower expansion,
which was chosen to either proceed with constant temperature and
density (Eqs. (3)-(6)) or gradually decreasing
temperature and density (Eqs. (7)-(10)).
In the former case we defined the asymptotic
temperature as
![]() (Sect. 3.1),
in the latter case the temperature was assumed to follow a
power-law time-dependence according to
(Sect. 3.1),
in the latter case the temperature was assumed to follow a
power-law time-dependence according to
![]() for
for
![]() (Sect. 3.2).
The range of temperatures
(Sect. 3.2).
The range of temperatures
![]() ,
where
the second expansion phase began, had a broad overlap with
the ``boundary temperatures'' considered by Terasawa et al. (2001,
2002) and Wanajo et al. (2002).
,
where
the second expansion phase began, had a broad overlap with
the ``boundary temperatures'' considered by Terasawa et al. (2001,
2002) and Wanajo et al. (2002).
Our standard calculations were performed with an entropy of s = 145.
Values of less than
![]() turned out to lead only to the
production of the second abundance peak around
turned out to lead only to the
production of the second abundance peak around ![]() ,
but r-processing up to the platinum peak was not possible when the other characteristic wind parameters
were varied within the limits mentioned above.
,
but r-processing up to the platinum peak was not possible when the other characteristic wind parameters
were varied within the limits mentioned above.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg124.gif) |
Figure 3:
Time evolution of the temperature for the different considered cases with exponential first expansion phase (starting at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig6}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fig7}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg127.gif) |
Figure 4:
Time dependence of the neutron number density,
|
| Open with DEXTER | |
3.1 Constant asymptotic temperature and density
In this section we consider an exponential first expansion phase
that is superseded at evolution time t0 by a second, slow
expansion phase whose asymptotic velocity at large radii goes to
zero. In this case the density and temperature during the second
phase adopt constant values (Eqs. (3)-(6)).
We explore various choices of the asymptotic temperature
![]() between 0.1 and 1.4 (see Fig. 3).
For an entropy of s= 145, for which results are
displayed in Figs. 4-6, these temperatures
correspond to constant densities
between 0.1 and 1.4 (see Fig. 3).
For an entropy of s= 145, for which results are
displayed in Figs. 4-6, these temperatures
correspond to constant densities ![]() between about
1 g cm-3 and 104 g cm-3. For these values the
neutron number density at time t0 shows differences by more than
three orders of magnitude (see Fig. 4). Although the
lowest assumed value of T9=0.1 might appear extreme, because it
requires very rapid exponential expansion for a longer time with
fairly high velocities at the end of this phase
(see Table 1),
the wide range of asymptotic temperatures allows us to
better understand the dependence of the nucleosynthesis on the
late-time expansion behavior of the outflowing matter.
between about
1 g cm-3 and 104 g cm-3. For these values the
neutron number density at time t0 shows differences by more than
three orders of magnitude (see Fig. 4). Although the
lowest assumed value of T9=0.1 might appear extreme, because it
requires very rapid exponential expansion for a longer time with
fairly high velocities at the end of this phase
(see Table 1),
the wide range of asymptotic temperatures allows us to
better understand the dependence of the nucleosynthesis on the
late-time expansion behavior of the outflowing matter.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig8.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fig9.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg129.gif) |
Figure 5:
Time dependence of the neutron-to-seed ratios,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi10.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi11}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg130.gif) |
Figure 6:
Left: the changing strength of the third abundance peak,
measured in terms of the ratio
|
| Open with DEXTER | |
When the asymptotic temperature is as high as
![]() ,
the
third peak hardly develops (see the abundance distribution at the
end of our calculations in the right panel of Fig. 4).
Only when the asymptotic temperature is reduced from this value to
smaller numbers, the platinum peak grows in strength, because the
free neutrons are exhausted more rapidly and the r-processing
proceeds faster towards the high mass-number region. The latter fact
can be seen by comparing the decrease in the neutron density with
time for
T90 = 1.4, 1, and 0.4 in the left panel of
Fig. 4, and it is also visible from the neutron-to-seed
ratios
,
the
third peak hardly develops (see the abundance distribution at the
end of our calculations in the right panel of Fig. 4).
Only when the asymptotic temperature is reduced from this value to
smaller numbers, the platinum peak grows in strength, because the
free neutrons are exhausted more rapidly and the r-processing
proceeds faster towards the high mass-number region. The latter fact
can be seen by comparing the decrease in the neutron density with
time for
T90 = 1.4, 1, and 0.4 in the left panel of
Fig. 4, and it is also visible from the neutron-to-seed
ratios
![]() as functions of time in the
left panel of Fig. 5. When the asymptotic temperature is
lowered to less than
as functions of time in the
left panel of Fig. 5. When the asymptotic temperature is
lowered to less than
![]() ,
the free neutron density
,
the free neutron density
![]() during the slow-expansion phase becomes so low that
the formation of the third abundance peak under such conditions
slows down considerably. Correspondingly,
during the slow-expansion phase becomes so low that
the formation of the third abundance peak under such conditions
slows down considerably. Correspondingly, ![]() as well as
as well as
![]() decrease less quickly (see again the
left panels of Figs. 4 and 5) and the height
of the third peak at the time of neutron exhaustion becomes clearly
lower (Fig. 4, right panel).
decrease less quickly (see again the
left panels of Figs. 4 and 5) and the height
of the third peak at the time of neutron exhaustion becomes clearly
lower (Fig. 4, right panel).
This inversion of the third peak formation with decreasing
value of the asymptotic temperature T90 can be clearly seen from the
time evolution of the average of the yields in the platinum peak
relative to those in the N=82 peak,
![]() ,
in the right panel of Fig. 5. The displayed quantity is defined by summing up the produced yields for five mass numbers around A=130 and A=196 and then computing the ratio
,
in the right panel of Fig. 5. The displayed quantity is defined by summing up the produced yields for five mass numbers around A=130 and A=196 and then computing the ratio![]()
The left panel of Fig. 6 shows the sensitivity of the final value of this ratio to the chosen temperature
We note here that often the change in the average atomic number is
used for following the assembling of heavy elements beyond the
![]() abundance peak. We found this quantity to be less
suitable for this purpose than our height ratio
abundance peak. We found this quantity to be less
suitable for this purpose than our height ratio
![]() ,
in particular when the second peak is
much stronger than the third. A growth of the latter by one order of
magnitude can mean a change in
,
in particular when the second peak is
much stronger than the third. A growth of the latter by one order of
magnitude can mean a change in
![]() by just
one or a few units, whereas
by just
one or a few units, whereas
![]() varies sensitively and thus serves well
as a tracer of changes in the abundance distribution in the
high-mass number region. The numbers listed in
Table 1, for example, confirm the usefulness, in
fact the superiority, of the ratio
varies sensitively and thus serves well
as a tracer of changes in the abundance distribution in the
high-mass number region. The numbers listed in
Table 1, for example, confirm the usefulness, in
fact the superiority, of the ratio
![]() instead of the mean mass number,
instead of the mean mass number,
![]() ,
as an indicator of the third peak
formation at least in the cases with very fast outflow expansion
considered here (of course, again we do not claim that a single
parameter value or a single outflow trajectory is sufficient for
getting a good match of the whole r-process abundance distribution
between the second and third peaks). While
,
as an indicator of the third peak
formation at least in the cases with very fast outflow expansion
considered here (of course, again we do not claim that a single
parameter value or a single outflow trajectory is sufficient for
getting a good match of the whole r-process abundance distribution
between the second and third peaks). While
![]() exhibits a rapid growth during the
build-up of the third abundance peak and changes by many orders of
magnitude between cases with weak or strong third peak, the average
mass number remains within the relatively narrow interval of
exhibits a rapid growth during the
build-up of the third abundance peak and changes by many orders of
magnitude between cases with weak or strong third peak, the average
mass number remains within the relatively narrow interval of
![]() (see
Table 1).
(see
Table 1).
The variation of the strength of the third peak with different
asymptotic temperatures can be understood from the sensitivity of the
neutron capture rates and nuclear photodisintegration rates to the
neutron number density and temperature, respectively, and by the
competition of these rates. This competition determines the location of
the r-process path and thus the speed of the nucleosynthesis, which is
defined by the ![]() -decay rates. When the temperature during the
second, slow expansion phase is large (
-decay rates. When the temperature during the
second, slow expansion phase is large (
![]() ), the
(
), the
(![]() ,n)-reactions are very fast and the r-process path lies
closer to the stability region than in case of smaller T90. The
r-process flow beyond the second peak is then rather weak because of
the low beta-decay rates and a correspondingly slow progression of the
nuclear flow. When the asymptotic temperature is reduced to
,n)-reactions are very fast and the r-process path lies
closer to the stability region than in case of smaller T90. The
r-process flow beyond the second peak is then rather weak because of
the low beta-decay rates and a correspondingly slow progression of the
nuclear flow. When the asymptotic temperature is reduced to
![]() -0.7, the (
-0.7, the (![]() ,n)-rates decrease and the r-process
path moves towards the neutron-drip line where the
,n)-rates decrease and the r-process
path moves towards the neutron-drip line where the ![]() -decay rates
are higher. Therefore the r-processing proceeds faster beyond the
second peak, leading to a more rapid drop of the free neutron density
and a more efficient third peak production. When the asymptotic
temperature is lowered to less than
-decay rates
are higher. Therefore the r-processing proceeds faster beyond the
second peak, leading to a more rapid drop of the free neutron density
and a more efficient third peak production. When the asymptotic
temperature is lowered to less than
![]() during the late
expansion phase, the neutron densities are very low so that the
r-process path returns to a location closer to the
during the late
expansion phase, the neutron densities are very low so that the
r-process path returns to a location closer to the ![]() -stable
region. In this case the
-stable
region. In this case the ![]() -decays again become slower and
therefore the r-process nucleosynthesis decelerates and the third peak
builds up to a smaller height.
-decays again become slower and
therefore the r-process nucleosynthesis decelerates and the third peak
builds up to a smaller height.
These movements of the r-process path are a consequence of the
different influence of a change in the asymptotic temperature on the
(![]() ,n)- and the neutron captures rates. For asymptotic
temperatures in the interval
,n)- and the neutron captures rates. For asymptotic
temperatures in the interval
![]() the
(
the
(![]() ,n)-rates are very sensitive to temperature variations. In
contrast, the neutron capture rates change with the corresponding
variations of the density and free neutron density less strongly. A
reduced temperature therefore decreases the photodisintegration
rates significantly, whereas the neutron captures remain fast
despite the lower neutron density. When
,n)-rates are very sensitive to temperature variations. In
contrast, the neutron capture rates change with the corresponding
variations of the density and free neutron density less strongly. A
reduced temperature therefore decreases the photodisintegration
rates significantly, whereas the neutron captures remain fast
despite the lower neutron density. When
![]() ,
the
(
,
the
(![]() ,n)-rates become less relevant, but neutron captures still
compete with
,n)-rates become less relevant, but neutron captures still
compete with ![]() -decays. For such low temperatures and thus low
neutron densities, the neutron capture rates are too low to drive
the r-process path far away from the valley of stability.
-decays. For such low temperatures and thus low
neutron densities, the neutron capture rates are too low to drive
the r-process path far away from the valley of stability.
The shift of the r-process path that is caused by different asymptotic temperatures (and connected parameters) manifests itself in different isotopic profiles of the elements formed by the r-processing (i.e. in different yield of the isotopes of an element). This can be seen for the case of cadmium in the right panel of Fig. 6.
3.2 Power-law time-dependence of the asymptotic temperature and density
In this section we consider the case that the
initial exponential phase is superseded at time t = t0 by a
slow expansion phase in which the temperature and density decay
according to power laws, i.e.,
![]() and
and
![]() for
for
![]() (Eqs. (7)-(10)).
The temperature evolution as function of time for the considered
cases is displayed in Fig. 7.
(Eqs. (7)-(10)).
The temperature evolution as function of time for the considered
cases is displayed in Fig. 7.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi12.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg144.gif) |
Figure 7:
Time evolution of the temperature for the different
considered cases with exponential first expansion phase (starting at
|
| Open with DEXTER | |
For our standard set of wind parameters, s = 145 (in units of
Boltzmann's constant per nucleon),
![]() ,
and
,
and
![]() ms already used in Sect. 3.1,
Fig. 8 shows the time evolution of the free neutron density
(left panel) and the final abundance distributions for four different
values of the transition temperature
ms already used in Sect. 3.1,
Fig. 8 shows the time evolution of the free neutron density
(left panel) and the final abundance distributions for four different
values of the transition temperature
![]() (right panel).
The formation of the third abundance peak turns out to be fairly
insensitive to variations of
(right panel).
The formation of the third abundance peak turns out to be fairly
insensitive to variations of
![]() between about 0.4
and 1.4. For all transition temperatures in this interval
the temperature evolution is very similar (Fig. 7) and a prominent
third peak appears.
between about 0.4
and 1.4. For all transition temperatures in this interval
the temperature evolution is very similar (Fig. 7) and a prominent
third peak appears.
Since the temperature in the post-exponential phase drops rapidly,
the strongly temperature-dependent (![]() ,n)-reactions become
unimportant very soon, while the considered entropy allows
a high free neutron density (
,n)-reactions become
unimportant very soon, while the considered entropy allows
a high free neutron density (
![]() cm-3)
to be present still for a long time. At such conditions the
r-process path moves very close to the neutron-drip line and
returns to the classical r-process path during free neutron
exhaustion (Panov 2003). For the considered conditions its location
shifts significantly only when the free neutron density changes
by 2-3 orders of magnitude. This explains the relative robustness
of the abundance yields to variations of
cm-3)
to be present still for a long time. At such conditions the
r-process path moves very close to the neutron-drip line and
returns to the classical r-process path during free neutron
exhaustion (Panov 2003). For the considered conditions its location
shifts significantly only when the free neutron density changes
by 2-3 orders of magnitude. This explains the relative robustness
of the abundance yields to variations of
![]() around 1.0.
around 1.0.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi13.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi14.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg147.gif) |
Figure 8:
Same as Fig. 4 (with s = 145,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi15.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi16.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg148.gif) |
Figure 9:
Same as Fig. 5 (with s = 145,
|
| Open with DEXTER | |
The left panel of Fig. 9 displays the evolution of the
neutron-to-seed ratios
![]() that
correspond to the neutron number densities of Fig. 8.
With an entropy of s = 145 and an exponential timescale
that
correspond to the neutron number densities of Fig. 8.
With an entropy of s = 145 and an exponential timescale
![]() ms the values of
ms the values of
![]() at the time when the r-process has
made the second abundance peak (at
at the time when the r-process has
made the second abundance peak (at
![]() )
are around 20
for
)
are around 20
for
![]() -1.4. As discussed in
Sect. 2, this is a slightly insufficient number of
neutrons per seed nucleus to create a third peak with exactly the
observed yields. The small underabundance of the third peak can also
be seen in the right panel of Fig. 9, where the height
of the platinum peak relative to the tellurium peak is given as
function of time. Different from the case of constant asymptotic
temperature (see Fig. 5),
-1.4. As discussed in
Sect. 2, this is a slightly insufficient number of
neutrons per seed nucleus to create a third peak with exactly the
observed yields. The small underabundance of the third peak can also
be seen in the right panel of Fig. 9, where the height
of the platinum peak relative to the tellurium peak is given as
function of time. Different from the case of constant asymptotic
temperature (see Fig. 5),
![]() is nearly the same for
is nearly the same for
![]() and 1.4, and is only slightly reduced
for
and 1.4, and is only slightly reduced
for
![]() .
For even lower transition
temperatures the height of the third peak drops steeply. This is
evident from the blue line in the left panel of Fig. 10
and is a consequence of a faster decrease in the free neutron
density (compare the left panels in Figs. 4 and 8), which for
.
For even lower transition
temperatures the height of the third peak drops steeply. This is
evident from the blue line in the left panel of Fig. 10
and is a consequence of a faster decrease in the free neutron
density (compare the left panels in Figs. 4 and 8), which for
![]() falls quickly to a value of
falls quickly to a value of
![]() cm-3, below which the equilibrium of n-captures and
cm-3, below which the equilibrium of n-captures and ![]() -decays is shifted to a region of slow beta-decay rates, leading to reduction of the third peak.
-decays is shifted to a region of slow beta-decay rates, leading to reduction of the third peak.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi17.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi18.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg156.gif) |
Figure 10:
Left: height of the third abundance peak relative to the
second, measured in terms of the ratio
|
| Open with DEXTER | |
The left panel of Fig. 10 provides a direct comparison
of the variation of
![]() with
the transition temperature between the exponential first expansion
phase to the second phase of either constant temperature or
power-law temperature decrease. Above a transition temperature
with
the transition temperature between the exponential first expansion
phase to the second phase of either constant temperature or
power-law temperature decrease. Above a transition temperature
![]() the behavior in both cases is
dramatically different. While in the case of constant asymptotic
temperature the relative height of the third peak decreases with
higher values of T90 (see Fig. 6 and
Sect. 3.1), a power-law decay of the temperature in the
second expansion phase leads to a prominent platinum peak for all
values of
the behavior in both cases is
dramatically different. While in the case of constant asymptotic
temperature the relative height of the third peak decreases with
higher values of T90 (see Fig. 6 and
Sect. 3.1), a power-law decay of the temperature in the
second expansion phase leads to a prominent platinum peak for all
values of
![]() between 0.5 and 1.4. The reason is
again the large sensitivity of the photodisintegration reactions to
the late-time behavior of the temperature. Because of the power-law
decline the temperature drops within milliseconds to values where a
(n,
between 0.5 and 1.4. The reason is
again the large sensitivity of the photodisintegration reactions to
the late-time behavior of the temperature. Because of the power-law
decline the temperature drops within milliseconds to values where a
(n,![]() )-(
)-(![]() ,n) equilibrium is no longer possible but is
replaced by a quasi-equilibrium between (n,
,n) equilibrium is no longer possible but is
replaced by a quasi-equilibrium between (n,![]() )-reactions and
)-reactions and
![]() -decays. The nucleosynthesis at these conditions resembles
the n-process of Blake & Schramm (1976), but there it was discussed
to occur because of a decrease in the neutron density below
-decays. The nucleosynthesis at these conditions resembles
the n-process of Blake & Schramm (1976), but there it was discussed
to occur because of a decrease in the neutron density below
![]() ,
while here it happens because of a decrease in the
temperature and an associated strong reduction of the (
,
while here it happens because of a decrease in the
temperature and an associated strong reduction of the (![]() ,n)-rates. It should be noted that the prominent odd-even effect in the isotope distributions in the right panel of Fig. 6 for
T90 = 1.4 and 0.4 has practically disappeared in Fig. 10, where the isotope distributions for the same values of the transition temperature are much smoother.
,n)-rates. It should be noted that the prominent odd-even effect in the isotope distributions in the right panel of Fig. 6 for
T90 = 1.4 and 0.4 has practically disappeared in Fig. 10, where the isotope distributions for the same values of the transition temperature are much smoother.
We point out here that the r-processing of heavy nuclei
through a quasi-equilibrium of (n,![]() )-reactions and
)-reactions and
![]() -decays at conditions where photodisintegrations are
practically unimportant was recently also discussed by Wanajo
(2007), who coined the term ``cold r-process''
-decays at conditions where photodisintegrations are
practically unimportant was recently also discussed by Wanajo
(2007), who coined the term ``cold r-process''![]() .
We prefer to call it ``r
.
We prefer to call it ``r![]() -process'', because this name is conform with the denotation of other processes (r-process, rp-process,
-process'', because this name is conform with the denotation of other processes (r-process, rp-process, ![]() p-process,...) and reflects the essential aspect that characterizes this variant of the rapid neutron-capture process.
p-process,...) and reflects the essential aspect that characterizes this variant of the rapid neutron-capture process.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi19.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg160.gif) |
Figure 11:
Time evolution of the temperature for the different
expansion histories considered in Fig. 12. All have
an exponential first expansion phase and second stage of power-law decline. Note
that the lines coincide for cases with different entropies s but
the same expansion timescale
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi20.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi21.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg161.gif) |
Figure 12:
Time evolution of the free neutron density ( left) and
final abundance distributions of r-process nuclei ( right) for
outflows with different assumed entropies s and exponential
expansion timescales
|
| Open with DEXTER | |
3.3 Variations of wind parameters in the exponential phase
In this section we will discuss the sensitivity of our nucleosynthesis
results to variations of the characteristic outflow conditions like
exponential expansion timescale, entropy, and electron fraction.
Table 1 lists corresponding parameter values for
some of the considered outflows:
![]() is the exponential
expansion timescale
is the exponential
expansion timescale![]() ,
,
![]() and t0 the temperature and
time at which the transition occurs from the exponential first expansion
phase to the second phase with power-law decline of temperature and
density (the temperature evolution for different considered cases
is displayed in Fig. 11),
and t0 the temperature and
time at which the transition occurs from the exponential first expansion
phase to the second phase with power-law decline of temperature and
density (the temperature evolution for different considered cases
is displayed in Fig. 11),
![]() is the initial outflow velocity at an assumed initial radius
is the initial outflow velocity at an assumed initial radius
![]() km,
km,
![]() is the outflow
velocity at transition time t0,
is the outflow
velocity at transition time t0,
![]() is
the average mass number of nucleosynthesis yields, and
is
the average mass number of nucleosynthesis yields, and
![]() the ratio of the height
of the third abundance peak relative to the second as defined in
Sect. 3.1.
the ratio of the height
of the third abundance peak relative to the second as defined in
Sect. 3.1.
As discussed in Sect. 2, the strength of the r-process
is determined by the abundance of seed nuclei that is able to form,
and by the number of remaining free neutrons when the r-processing
sets in at
![]() -3. For the homologous outflows
considered there we saw that a larger dynamical timescale increases
the efficiency of seed formation at the expense of free neutrons,
and for a very short dynamical timescale the expansion can be so
rapid that
-3. For the homologous outflows
considered there we saw that a larger dynamical timescale increases
the efficiency of seed formation at the expense of free neutrons,
and for a very short dynamical timescale the expansion can be so
rapid that ![]() particles and neutrons do not have any time to
assemble to very heavy elements. In both cases a strong third
abundance peak cannot develop. A lower value of the outflow entropy
also allows neutrons, protons, and
particles and neutrons do not have any time to
assemble to very heavy elements. In both cases a strong third
abundance peak cannot develop. A lower value of the outflow entropy
also allows neutrons, protons, and ![]() -particles to recombine
to nuclei more efficiently and therefore lower entropies have a
similar effect as a slow expansion.
-particles to recombine
to nuclei more efficiently and therefore lower entropies have a
similar effect as a slow expansion.
For a given value of the entropy, significant production of high-mass
elements therefore on the one hand requires that the expansion timescale
is sufficiently long, corresponding to a critical lower limit
![]() of the seed abundance
at the start of the r-processing.
On the other hand, the expansion must be enough
fast because otherwise the seed production
exceeds
of the seed abundance
at the start of the r-processing.
On the other hand, the expansion must be enough
fast because otherwise the seed production
exceeds
![]() too much, and the platinum
peak cannot be formed because of a disfavorably low neutron-to-seed
ratio. Our systematic runs for homologous outflows
showed (see Fig. 2) that with an
entropy of s = 145 and an electron fraction of
too much, and the platinum
peak cannot be formed because of a disfavorably low neutron-to-seed
ratio. Our systematic runs for homologous outflows
showed (see Fig. 2) that with an
entropy of s = 145 and an electron fraction of
![]() only exponential timescales
only exponential timescales
![]() of less than about 10 ms
lead to a neutron number fraction of
of less than about 10 ms
lead to a neutron number fraction of
![]() and thus
to neutron-to-seed ratios around 20 at the beginning of the r-process.
Only then the nuclear flow has a chance to go beyond a mass number of
130 and to reach the range of
and thus
to neutron-to-seed ratios around 20 at the beginning of the r-process.
Only then the nuclear flow has a chance to go beyond a mass number of
130 and to reach the range of
![]() ,
although the third peak may still be significantly
underabundant compared to solar values (see below).
The critical limit for the seed abundance turned out to be
,
although the third peak may still be significantly
underabundant compared to solar values (see below).
The critical limit for the seed abundance turned out to be
![]() (cf. Sect. 2).
Of course, this number depends on s and
(cf. Sect. 2).
Of course, this number depends on s and ![]() ,
and the
homologous expansion timescale that enables third peak
formation is shorter for lower entropy values.
,
and the
homologous expansion timescale that enables third peak
formation is shorter for lower entropy values.
Let us now discuss the case in which
the homologous outflow with its exponential density and
temperature decline is replaced by a slower power-law temperature decay during the late expansion stage, i.e. after the freeze-out of charged-particle reactions. This makes strong r-processing up to the platinum peak possible for a much wider
range of dynamical timescales
![]() than in the case
of purely homologous evolution, practically for all values below
some upper limit. This can be seen in Fig. 12, which displays the time-evolution of the neutron number density and the final abundance distribution
for different choices of entropies and dynamical timescales.
The second stage of power-law temperature decline is assumed to
set in at t = t0 with a transition temperature of
than in the case
of purely homologous evolution, practically for all values below
some upper limit. This can be seen in Fig. 12, which displays the time-evolution of the neutron number density and the final abundance distribution
for different choices of entropies and dynamical timescales.
The second stage of power-law temperature decline is assumed to
set in at t = t0 with a transition temperature of
![]() .
A pronounced platinum peak develops
for s = 105 if
.
A pronounced platinum peak develops
for s = 105 if
![]() ms,
for s = 145 this needs
ms,
for s = 145 this needs
![]() ms, and for
ms, and for
![]() -200 it requires
-200 it requires
![]() ms.
An extreme case with s = 200 and
ms.
An extreme case with s = 200 and
![]() ms
leads to fission cycling and demonstrates that even for very
fast homologous expansion during the first stage the slower evolution in the second phase allows all neutrons to be captured into heavy nuclei. The dashed lines belong to cases where the expansion in the homologous phase is too slow for third peak formation.
ms
leads to fission cycling and demonstrates that even for very
fast homologous expansion during the first stage the slower evolution in the second phase allows all neutrons to be captured into heavy nuclei. The dashed lines belong to cases where the expansion in the homologous phase is too slow for third peak formation.
Figure 12 demonstrates that for a wide range of
timescale-entropy combinations in the considered intervals,
![]() ms and
ms and
![]() ,
heavy r-process elements up to the third abundance peak
and beyond can be produced. Inspecting our results we find that a
very strong platinum peak appears for conditions that roughly
fulfill the relation
,
heavy r-process elements up to the third abundance peak
and beyond can be produced. Inspecting our results we find that a
very strong platinum peak appears for conditions that roughly
fulfill the relation
![]() .
.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi22.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi23.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg175.gif) |
Figure 13:
Time-evolution of the free neutron number
density ( left) and final abundance distribution of r-process nuclei
( right) for
|
| Open with DEXTER | |
In Fig. 13 the sensitivity of the r-processing to
variations of
![]() is shown in the case with s = 170 and
is shown in the case with s = 170 and
![]() ms. In the left panel one can see that a
change in
ms. In the left panel one can see that a
change in
![]() from 0.42 to 0.46 leads to a reduction of
from 0.42 to 0.46 leads to a reduction of
![]() at the beginning of the r-process and a more rapid
exhaustion of free neutrons. The yields beyond the second peak are
correspondingly lower, with a growing discrepancy at higher mass
numbers A (right panel of Fig. 13. While for
at the beginning of the r-process and a more rapid
exhaustion of free neutrons. The yields beyond the second peak are
correspondingly lower, with a growing discrepancy at higher mass
numbers A (right panel of Fig. 13. While for
![]() the platinum peak is slighly overabundant
compared to observations (see below), increasing
the platinum peak is slighly overabundant
compared to observations (see below), increasing
![]() by
about 10% to 0.46 is enough to lead to a significant
underproduction. For the considered short dynamical timescale this
can be compensated by a roughly 30% higher value of the outflow
entropy.
by
about 10% to 0.46 is enough to lead to a significant
underproduction. For the considered short dynamical timescale this
can be compensated by a roughly 30% higher value of the outflow
entropy.
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi24.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi25.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg176.gif) |
Figure 14:
Left: height of the third abundance peak relative to the
second as function of the exponential expansion timescale
|
| Open with DEXTER | |
In Fig. 14 we provide an overview of the platinum peak
formation in dependence of the entropy and dynamical timescale of
the model outflows, using
![]() and assuming a
transition temperature of
and assuming a
transition temperature of
![]() between the
exponential first cooling phase and the second phase with power-law
decrease in temperature and density. The left panel confirms what we
described above: for higher values of the entropy the
between the
exponential first cooling phase and the second phase with power-law
decrease in temperature and density. The left panel confirms what we
described above: for higher values of the entropy the
![]() peak can be assembled for an increasingly wider range of expansion
timescales. The bold horizontal lines in the left panel mark the
observational band for the abundance ratio
peak can be assembled for an increasingly wider range of expansion
timescales. The bold horizontal lines in the left panel mark the
observational band for the abundance ratio
![]() .
The third peak relative to the second
tends to become overabundant compared to the observations when the
expansion timescale is low, whereas it remains too weak for long
expansion timescales.
.
The third peak relative to the second
tends to become overabundant compared to the observations when the
expansion timescale is low, whereas it remains too weak for long
expansion timescales.
The dashed line in the left panel of Fig. 14
corresponds to runs with s = 145where a constant density and temperature
were adopted during the second phase instead of the power-law
behavior. The differences between the dashed and solid lines
for the same entropy are large, in particular for
longer dynamical timescales. This demonstrates again the
importance of the late-time behavior of the outflow. This
importance, however, is significantly reduced when the
transition temperature
![]() is chosen to be
near 0.4 (see the left panel of Fig. 10).
is chosen to be
near 0.4 (see the left panel of Fig. 10).
For entropies near 200 or higher fission cycling can occur. The
right panel of Fig. 14 shows the time evolution of the
second and third abundance peaks and of the ratio between both for a
case with s = 200,
![]() ms, and
ms, and
![]() .
The periodic changes in the abundances and of
.
The periodic changes in the abundances and of
![]() reflect the repeated propagation of
nucleosynthesis wave through the transuranium region via fission
cycling (the number of nuclear species is increased roughly by a
factor of three due to fission), similar to what was observed by
Panov et al. (2003), Goriely et al. (2005), and Beun et al.
(2008). The overabundance of the platinum peak in this case depends
significantly on the nuclear data Panov et al. (2001b) and should be
explored separately on the basis of new fission data calculations
(Panov et al. 2005).
reflect the repeated propagation of
nucleosynthesis wave through the transuranium region via fission
cycling (the number of nuclear species is increased roughly by a
factor of three due to fission), similar to what was observed by
Panov et al. (2003), Goriely et al. (2005), and Beun et al.
(2008). The overabundance of the platinum peak in this case depends
significantly on the nuclear data Panov et al. (2001b) and should be
explored separately on the basis of new fission data calculations
(Panov et al. 2005).
4 Discussion and conclusions
Focussing on the high-entropy neutrino-driven wind environment, we investigated the sensitivity of r-process nucleosynthesis to the asymptotic low-temperature behavior that is assumed to follow an approximately homologous early expansion of very rapidly accelerated outflows. On the one hand we compared the continuously homologously evolving case to a situation where the temperature and density reach a lower limit and remain constant later on. The latter setting is equivalent to the choice of a freeze-out temperature for supersonic wind solutions by Wanajo et al. (2002) and Wanajo (2007), and it is similar to the use of a constant value for the outer boundary pressure of subsonic breeze solutions as adopted by Sumiyoshi et al. (2000), Terasawa et al. (2002), and Wanajo et al. (2001). Breeze solutions, however, are characterized by the very important feature that they imply a causal connection between the physical conditions at the neutron star and at the outer boundary, i.e. the mass-loss rate and asymptotic temperature are not independent, whereas supersonic outflows with a limiting temperature are not subject to such a constraint. The constant conditions at late times correspond to a situation where the homologous outflow is asymptotically decelerated to very small (zero) velocity. This can be considered as a reasonably good representation of the situation when a supersonic wind is slowed down in a termination shock at colliding with the preceding supernova ejecta. On the other hand we investigated a case where the velocity was assumed to make a transition from the linear radial growth of the homologous phase to an asymptotically constant, nonvanishing value. In this case the density was assumed to decrease with time like t-2and the temperature (for constant radiation entropy) like t-2/3. This is supposed to be a model for the situation when a supersonic wind reaches a second stage of slower acceleration at late times.
We have found that for given and constant wind radiation entropy (we
explored ![]() -200
-200
![]() per nucleon),
electron-to-baryon ratio (
per nucleon),
electron-to-baryon ratio (
![]() -0.46), and
(sufficiently small) wind expansion timescale (
-0.46), and
(sufficiently small) wind expansion timescale (
![]() -10 ms), a strong r-process with production of the third
abundance peak depends not only on the value of the transition
temperature between the two expansion phases, but also on the evolution
of temperature and density during the second, slower stage. In the case
of a constant asymptotic temperature and density, the formation of the
platinum peak is enabled when the asymptotic temperature value is
moderately high (
-10 ms), a strong r-process with production of the third
abundance peak depends not only on the value of the transition
temperature between the two expansion phases, but also on the evolution
of temperature and density during the second, slower stage. In the case
of a constant asymptotic temperature and density, the formation of the
platinum peak is enabled when the asymptotic temperature value is
moderately high (
![]() -0.8). When leaving this range towards
lower or higher asymptotic temperatures, the possibility of third-peak
formation strongly decreases. This behavior was also seen by Wanajo et al. (2002) and Terasawa et al. (2002) for, as they called them, ``freeze-out temperatures'' or ``boundary temperatures'' above
-0.8). When leaving this range towards
lower or higher asymptotic temperatures, the possibility of third-peak
formation strongly decreases. This behavior was also seen by Wanajo et al. (2002) and Terasawa et al. (2002) for, as they called them, ``freeze-out temperatures'' or ``boundary temperatures'' above
![]() ,
but the variation with even lower temperatures remained unexplored in both works.
,
but the variation with even lower temperatures remained unexplored in both works.
In our second considered case with power-law decline of T(t) and
![]() ,
the strength of the
,
the strength of the ![]() abundance peak compared
to the
abundance peak compared
to the ![]() peak turned out to be relatively independent of
the transition temperature
peak turned out to be relatively independent of
the transition temperature
![]() in the interval
between about
in the interval
between about
![]() K and
K and
![]() K. For
lower transition temperatures the third-peak formation decreases
steeply and behaves
similar to the case with constant asymptotic temperature and density.
This means that the appearance and disappearance of a prominent
platinum peak when the constant asymptotic temperature
is lowered from
K. For
lower transition temperatures the third-peak formation decreases
steeply and behaves
similar to the case with constant asymptotic temperature and density.
This means that the appearance and disappearance of a prominent
platinum peak when the constant asymptotic temperature
is lowered from
![]() to
to
![]() ,
is not observed in
the case of a power-law decline of temperature and density during
the late wind evolution. Interestingly, both considered cases of
late-time expansion behavior also lead to distinctive differences
in the abundances of neighboring isotopes of r-process elements.
For the power-law time-dependence not only more neutron-rich
isotopes are formed but the isotopic distribution is also smoother.
,
is not observed in
the case of a power-law decline of temperature and density during
the late wind evolution. Interestingly, both considered cases of
late-time expansion behavior also lead to distinctive differences
in the abundances of neighboring isotopes of r-process elements.
For the power-law time-dependence not only more neutron-rich
isotopes are formed but the isotopic distribution is also smoother.
Strong r-processing naturally requires a sufficiently fast expansion
in the homologous phase so that charged-particle reactions freeze
out before excessive seed production occurs and high neutron-to-seed
ratios cannot be reached. Moreover, a relatively rapid temperature
decline during the second, slower expansion phase, and at the same
time a persistence of sufficiently high neutron number densities
(
![]() cm-3) are favorable for driving the
nuclear flow beyond the second abundance peak. For fixed radiation
entropy s as assumed in our models, temperature and density are
coupled by the relation
cm-3) are favorable for driving the
nuclear flow beyond the second abundance peak. For fixed radiation
entropy s as assumed in our models, temperature and density are
coupled by the relation
![]() .
In
this case the asymptotic power-law decrease in both quantities
enables third peak formation for a wider range of transition
temperatures.
.
In
this case the asymptotic power-law decrease in both quantities
enables third peak formation for a wider range of transition
temperatures.
Terasawa et al. (2002) argued that lower asymptotic temperatures
reduce the charged-particle reactions, which leads to less seed production
and a higher neutron-to-seed ratio, thus causing a better agreement
of the r-process yields with the solar abundances. For our calculations,
which are based on the idealized two-stage model of the wind
expansion, this argument cannot be made. Long before the corresponding
asymptotic temperatures (between T9 = 0.1 and T9 = 1.4) are
reached, namely already above
![]() ,
charged-particle
reactions become inefficient because of the impenetrability of the
nuclear Coulomb barrier for low-energy thermal protons. Instead,
the described nucleosynthesis results can be understood by the density
and temperature dependence of neutron-captures and nuclear
photodisintegration reactions.
,
charged-particle
reactions become inefficient because of the impenetrability of the
nuclear Coulomb barrier for low-energy thermal protons. Instead,
the described nucleosynthesis results can be understood by the density
and temperature dependence of neutron-captures and nuclear
photodisintegration reactions.
Since the (![]() ,n)-rates decrease steeply with falling
temperature, their role diminishes with a lower transition
temperature. For sufficiently high neutron densities the still rapid
neutron captures force the r-process path towards the neutron-drip
line, where the
,n)-rates decrease steeply with falling
temperature, their role diminishes with a lower transition
temperature. For sufficiently high neutron densities the still rapid
neutron captures force the r-process path towards the neutron-drip
line, where the ![]() -decay rates are high. Instead of going
through a (
-decay rates are high. Instead of going
through a (![]() ,n)-(n,
,n)-(n,![]() )
equilibrium, the r-processing
proceeds now as a quasi-equilibrium of (n,
)
equilibrium, the r-processing
proceeds now as a quasi-equilibrium of (n,![]() )
reactions and
)
reactions and
![]() -decays, which suggests the term ``r
-decays, which suggests the term ``r![]() -process''. This
sitation in outflows that expand supersonically and cool quickly to
a few 108 K was recently also discussed by Wanajo (2007), who
named it ``cold r-process''. The formation of the third abundance
peak is possible in this situation, provided the neutron-to-seed
ratio is high enough, because the
-process''. This
sitation in outflows that expand supersonically and cool quickly to
a few 108 K was recently also discussed by Wanajo (2007), who
named it ``cold r-process''. The formation of the third abundance
peak is possible in this situation, provided the neutron-to-seed
ratio is high enough, because the ![]() -decays are fast and allow
for a quick assembling of heavy nuclei. In contrast, if the
exponential expansion makes a transition to a constant temperature
that is high, (
-decays are fast and allow
for a quick assembling of heavy nuclei. In contrast, if the
exponential expansion makes a transition to a constant temperature
that is high, (![]() ,n)-reactions drive the r-process path
towards the valley of stability where the
,n)-reactions drive the r-process path
towards the valley of stability where the ![]() -decay rates are
low and the r-processing therefore slows down. In this case the free
neutrons are used up in forming the second abundance peak before any
significant third maximum can build up. On the other hand, the
power-law temperature decline in the slow expansion phase leads to
an efficient r
-decay rates are
low and the r-processing therefore slows down. In this case the free
neutrons are used up in forming the second abundance peak before any
significant third maximum can build up. On the other hand, the
power-law temperature decline in the slow expansion phase leads to
an efficient r![]() -process for a wide range of transition
temperatures
-process for a wide range of transition
temperatures
![]() .
Because the strength of the
third abundance peak then depends only on the neutron density, it
becomes relatively insensitive to the value of
.
Because the strength of the
third abundance peak then depends only on the neutron density, it
becomes relatively insensitive to the value of
![]() between about 0.3 and 1.4. If the transition
temperature is even lower, the free neutron density during the slow
expansion phase of the outflow is not large enough any more to
support a strong r-processing.
between about 0.3 and 1.4. If the transition
temperature is even lower, the free neutron density during the slow
expansion phase of the outflow is not large enough any more to
support a strong r-processing.
In previous investigations (Terasawa et al. 2001, 2002; Wanajo et al. 2002) the complex influence of the late-time outflow behavior
was not explored, but it matters when the robustness of abundance
yields to variations in the neutrino-driven wind models is
discussed, especially in situations where high entropies, low
temperatures, and high neutron densities lead to a change in the
r-process to an r![]() -process.
-process.
In summary, we therefore conclude that the detailed cooling
behavior during the late expansion of supernova outflows can
have important consequences for r-process nucleosynthesis.
In particular, a
slow expansion phase with decreasing temperature and density
following a rapid, supersonic initial outflow expansion, is more
favorable for a strong r-process than the constant boundary
conditions assumed previously (e.g., Wanajo et al. 2001, 2002;
Terasawa et al. 2001, 2002).
Despite differences in the initial neutron
number density by more than two orders of magnitude, such
conditions can lead to a fairly robust production of the platinum
peak for a wider range of transition temperatures (at least
for the cases of very fast early expansion and modest values of
entropy and neutron excess as considered in our study). This is
caused by a kind of self-regulation of the quasi-equilibrium
of (![]() ,n)-reactions and
,n)-reactions and ![]() -decays in the
r
-decays in the
r![]() -process, which leads to roughly the same number of
neutron captures per seed nucleus, independent of whether the
process proceeds quickly for high neutron densities (in which
case the r-process path is closer to the neutron-drip line) or
slower in the case of low neutron densities. This might give a
hint for the outflow dynamics of neutrino-driven wind ejecta that
can enable the uniform production of heavy r-process elements
suggested by the abundance patterns observed in metal-poor
stars (see e.g., Cowan & Sneden 2006).
-process, which leads to roughly the same number of
neutron captures per seed nucleus, independent of whether the
process proceeds quickly for high neutron densities (in which
case the r-process path is closer to the neutron-drip line) or
slower in the case of low neutron densities. This might give a
hint for the outflow dynamics of neutrino-driven wind ejecta that
can enable the uniform production of heavy r-process elements
suggested by the abundance patterns observed in metal-poor
stars (see e.g., Cowan & Sneden 2006).
For the explored range of parameter values, the r-processing
can last 150-200 ms or even longer. This duration
is the lower time limit for the formation of heavy elements
from iron-group seeds up to the platinum peak. For entropies s between 100 and 200
![]() per nucleon,
a solar-like production of the heaviest elements can occur
only in the case that the outflow expansion decelerates
and a transition from the initial homologous phase
to a slower later stage of expansion occurs. In addition, a short
or very short exponential timescale (
per nucleon,
a solar-like production of the heaviest elements can occur
only in the case that the outflow expansion decelerates
and a transition from the initial homologous phase
to a slower later stage of expansion occurs. In addition, a short
or very short exponential timescale (
![]() ms for s = 200 and
ms for s = 200 and
![]() ms for
s = 100) is needed during the homologous expansion, if moderately
neutron-rich conditions (
ms for
s = 100) is needed during the homologous expansion, if moderately
neutron-rich conditions (
![]() )
are considered.
Of course, if the neutron excess decreases, the formation of the
third abundance peak requires a higher entropy. These parameter
constraints are rather similar to those shown in Fig. 1 of Hoffman et al. (1997). This can be understood from the fact that supersonic
solutions of the neutrino-driven wind equations as those employed by
Hoffman et al. (1997) show approximately
homologous expansion (
)
are considered.
Of course, if the neutron excess decreases, the formation of the
third abundance peak requires a higher entropy. These parameter
constraints are rather similar to those shown in Fig. 1 of Hoffman et al. (1997). This can be understood from the fact that supersonic
solutions of the neutrino-driven wind equations as those employed by
Hoffman et al. (1997) show approximately
homologous expansion (
![]() )
only up to some maximum radius,
above which the velocity continues to grow much less
rapidly. Although there is no deceleration as it is caused by a wind
termination shock (see Arcones et al. 2007), the slow-down of the
acceleration of supersonic winds has still some basic similarity to
the transition from a rapid first expansion phase to a slower second
stage as assumed in our simplified outflow models.
)
only up to some maximum radius,
above which the velocity continues to grow much less
rapidly. Although there is no deceleration as it is caused by a wind
termination shock (see Arcones et al. 2007), the slow-down of the
acceleration of supersonic winds has still some basic similarity to
the transition from a rapid first expansion phase to a slower second
stage as assumed in our simplified outflow models.
Acknowledgements
We are grateful to an anonymous referee for very valuable suggestions for improving our presentation. This work was in part supported by the SNF project No. IB7320-110996 and by the Deutsche Forschungsgemeinschaft through the Transregional Collaborative Research Centers SFB/TR 27 ``Neutrinos and Beyond'' and SFB/TR 7 ``Gravitational Wave Astronomy'', and through the Cluster of Excellence EXC 153 ``Origin and Structure of the Universe'' (http://www.universe-cluster.de).
References
- Arcones, A., Janka, H.-Th., & Scheck, L. 2007, A&A, 467, 1227 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Arnould, M., Goriely, S., & Takahashi, K. 2007, Phys. Rep., 450, 97 [NASA ADS] [CrossRef] (In the text)
- Beun, J., McLaughlin, G. C., Surman, R., & Hix, W. R. 2008, Phys. Rev. C, 77, 035804 [NASA ADS] [CrossRef] (In the text)
- Bisnovatyi-Kogan, G. S., & Chechetkin, V. M. 1979, Sov. Uspehi Phys. Nauk, 127, 263 [NASA ADS] (In the text)
- Blake, J. B., & Schramm, D. N. 1976, ApJ, 209, 846 [NASA ADS] [CrossRef]
- Blinnikov, S. I., & Panov, I. V. 1996, Astron. Lett., 22, 39 [NASA ADS] (In the text)
- Buras, R., Janka, H.-Th., Rampp, M., & Kifonidis, K. A&A, 2006, 457, 281 (In the text)
- Burbidge, G. R., Burbidge, E. M., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] (In the text)
- Burrows, A., Hayes, J., & Fryxell, B. A. 1995, ApJ, 450, 830 [NASA ADS] [CrossRef]
- Cameron, A. G. W. 2003, ApJ, 587, 327 [NASA ADS] [CrossRef] (In the text)
- Cameron, A. G. W., Cowan, J. J., & Truran, J. W. 1983, Ap&SS, 91, 235 [NASA ADS] [CrossRef]
- Cardall, C. Y., & Fuller, G. M. 1997, ApJ, 486, L111 [NASA ADS] [CrossRef] (In the text)
- Cowan, J. J., & Sneden, C. 2006, Nature, 440, 1151 [NASA ADS] [CrossRef] (In the text)
- Cowan, J. J., Thielemann, F.-K., & Truran, J. W. 1991, Phys. Rep., 208, 267 [NASA ADS] [CrossRef] (In the text)
- Freiburghaus, C., Rosswog, S., & Thielemann, F.-K. 1999, ApJ, 525, L121 [CrossRef] (In the text)
- Gear, C. W. 1971, Numerical Initial Value Problems in Ordinary Differential Equations (Englewood Cliffs, New Jersey: Prentice-Hall) (In the text)
- Goriely, S., & Arnould, M. 1996, A&A, 312, 327 [NASA ADS] (In the text)
- Goriely, S., Demetriou, P., Janka, H.-Th., Pearson, J. M., & Samyn, M. 2005, Nucl. Phys. A, 758 587c (In the text)
- Hillebrandt, W. 1978, Space Sci. Rev., 21, 639 [NASA ADS] [CrossRef] (In the text)
- Hoffman, R. D., Woosley, S. E., & Qian, Y.-Z. 1997, ApJ, 482, 951 [NASA ADS] [CrossRef] (In the text)
- Imshennik, V. S. 1992, Astron. Lett., 18, 194 (In the text)
- Imshennik, V. S., & Litvinova, I. Yu. 2006. Atomic Nuclei, 69, 660 (In the text)
- Janka, H.-Th., & Müller, E. 1995, Phys. Rep., 256, 135 [NASA ADS] [CrossRef] (In the text)
- Janka, H.-Th., & Müller, E. 1995, ApJ, 448, L109 [NASA ADS]
- Kratz, K.-L., Bitouzet, J.-P., Thielemann, F.-K., Möller, P., & Pfeiffer, B. 1993, ApJ, 403, 216 [NASA ADS] [CrossRef] (In the text)
- Kuroda, T., Wanajo, S., & Nomoto, K. 2008, ApJ, 672, 1068 [NASA ADS] [CrossRef]
- Lattimer, J. M., & Schramm, D. N. 1974, ApJ, 192, L145 [NASA ADS] [CrossRef] (In the text)
- Lattimer, J. M., & Schramm, D. N. 1976, ApJ, 210, 549 [NASA ADS] [CrossRef] (In the text)
- Meyer, B. S., Mathews, G. J., Howard, W. M., Woosley, S. E., & Hoffman, R. D. 1992, ApJ, 399, 656 [NASA ADS] [CrossRef] (In the text)
- Möller, P., Nix, J. R., Myers, W. D., & Swiatecki, W. J. 1995, Atomic Data Nucl. Data Tables, 59, 185 [NASA ADS] [CrossRef] (In the text)
- Nadyozhin, D. K., & Yudin, A. V. 2004, Astron. Lett., 30, 697 (In the text)
- Nadyozhin, D. K., Panov, I. V., & Blinnikov, S. I. 1998, A&A, 335, 207 [NASA ADS]. (In the text)
- Otsuki, K., Tagoshi, H., Kajino, T., & Wanajo, S. 2000, ApJ, 533, 424 [NASA ADS] [CrossRef] (In the text)
- Panov, I. V. 2003, Astron. Lett., 29, 163 [NASA ADS] [CrossRef] (In the text)
- Panov, I. V., & Chechetkin, V. M. 2002, Astron. Lett., 28, 476 [NASA ADS] [CrossRef] (In the text)
- Panov, I. V., & Thielemann F.-K. 2003, Nucl. Phys. A, 718, 647 [NASA ADS] [CrossRef] (In the text)
- Panov, I. V., Blinnikov, S. I., & Thielemann, F.-K. 2001a, Astron. Lett., 27, 1 [CrossRef] (In the text)
- Panov, I. V., Freiburghaus, C., & Thielemann, F.-K. 2001b, Nucl. Phys. A, 688, 587 [NASA ADS] [CrossRef] (In the text)
- Panov, I. V., Kolbe, E., Pfeiffer, B., Rauscher, Th., Kratz, K.-L., & Thielemann, F.-K. 2005, Nucl. Phys. A, 747, 633 [NASA ADS] [CrossRef] (In the text)
- Qian, Y.-Z., & Wasserburg, G. J. 2000, Phys. Rep., 333, 77 [NASA ADS] [CrossRef] (In the text)
- Qian, Y.-Z., & Woosley, S. E. 1996, ApJ, 471, 331 [NASA ADS] [CrossRef] (In the text)
- Rauscher, T., & Thielemann, F.-K. 2000, Atomic Data Nucl. Data Tables, 75, 1 [NASA ADS] [CrossRef] (In the text)
- Rauscher, T., Thielemann, F.-K., & Kratz, K.-L. 1997, Nucl. Phys., A 621, 331c.
- Symbalisty, E. M. D., & Schramm, D. N. 1982, ApL, 22, 143 [NASA ADS] (In the text)
- Seeger, P. A., Fowler, W. A., & Clayton, D. D. 1965, ApJS, 11, 121 [NASA ADS] [CrossRef] (In the text)
- Sumiyoshi, K., Suzuki, H., Otsuki, K., Terasawa, M., & Yamada Sh. 2000, Publ. Astron. Soc. Japan., 52, 601 [NASA ADS] (In the text)
- Takahashi, K., & Janka, H.-T. 1997, Proc. of Int. Conf. Origin of Matter and Evolution of Galaxies in the Universe '96 Atami, Japan, 18-20 January 1996, ed. T. Kajino, Y. Yoshii, & S. Kubono (World Scientific, Singapore), 213
- Takahashi, K., Witti, J., & Janka, H.-T. 1994, A&A, 286, 857 [NASA ADS] (In the text)
- Terasawa, M., Sumiyoshi, K., Kajino, T., Mathews, G. J., & Tanihata, I. 2001, ApJ, 562, 470 [NASA ADS] [CrossRef] (In the text)
- Terasawa, M., Sumiyoshi, K., Yamada, S., Suzuki, H., & Kajino, T. 2002, ApJ, 578, L137 [NASA ADS] [CrossRef] (In the text)
- Thielemann, F.-K., Arnould, M., & Truran, J. W. 1987, in Advances in Nuclear Astrophysics, ed. E. Vangioni-Flam et al. (Gif-sur-Yvette: Éditions frontière) 525 (In the text)
- Thompson, T. A., Burrows, A., & Meyer, B. S. 2001, ApJ, 562, 887 [NASA ADS] [CrossRef] (In the text)
- Tomàs, R., Kachelrieß, M., Raffelt, G., et al. 2004, J. Cos. Astropart. Phys., 09, 015 [NASA ADS] (In the text)
- Wanajo, S. 2007, ApJ, 666, L77 [NASA ADS] [CrossRef] (In the text)
- Wanajo, S., & Ishimaru, Y. 2006, Nucl. Phys. A, 777, 676 [NASA ADS] [CrossRef] (In the text)
- Wanajo, S., Kajino, T., Mathews, G. J., & Otsuki, K. 2001, ApJ, 554, 578 [NASA ADS] [CrossRef] (In the text)
- Wanajo, S., Itoh, N., Ishimaru, Yu., Nozawa, S., & Beers, T. C. 2002, ApJ, 577, 853 [NASA ADS] [CrossRef] (In the text)
- Wanajo, S., Goriely, S., Samyn, M., & Itoh, N. 2004, ApJ, 606, 1057 [NASA ADS] [CrossRef] (In the text)
- Witti, J., Janka, H.-T., & Takahashi, K. 1994, A&A, 286, 841 [NASA ADS] (In the text)
- Witti, J., Janka, H.-Th., Takahashi, K., & Hillebrandt, W. 1993, in Nuclei in the Cosmos-IX, ed. F. Käppeler, & K. Wisshak (Bristol and Philadelphia: Inst. of Phys. Publ.), 601 (In the text)
- Woosley, S. E., & Hoffman, R. D. 1992, ApJ, 395, 202 [NASA ADS] [CrossRef] (In the text)
- Woosley, S. E., Wilson, J. R., Mathews, G. J., Hoffman, R. D., & Meyer, B. S. 1994, ApJ, 433, 229 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
unexplained
![[*]](/icons/foot_motif.gif)
- Note that Thompson et al. (2001) used a sophisticated description of the equation of state and thus explicitly accounted for the nonrelativistic character of electrons and positrons at low temperatures, an effect that Sumiyoshi et al. (2000) pointed out to be important for a reliable determination of the expansion timescale.
- ... ratio
![[*]](/icons/foot_motif.gif)
- A similar peak ratio was considered in a recent paper by Beun et al. (2008).
- ...r-process''
![[*]](/icons/foot_motif.gif)
- Different
from us, Wanajo (2007) used neutrino-driven wind
trajectories obtained as solutions of the steady-state wind
equations, and assumed the transition to a constant freeze-out
temperature
 at some radius. As argued in
Sect. 2.1, such a more realistic description of the
early outflow dynamics in combination with constant conditions at
late times shares some basic features with the simple
two-stage expansion behavior considered in our work.
at some radius. As argued in
Sect. 2.1, such a more realistic description of the
early outflow dynamics in combination with constant conditions at
late times shares some basic features with the simple
two-stage expansion behavior considered in our work.
- ... timescale
![[*]](/icons/foot_motif.gif)
- We stress that comparing our expansion timescale with those given in other papers requires some caution. Otsuki et al. (2000), Sumiyoshi et al. (2000), and Terasawa et al. (2002) defined the expansion timescale as e-folding time at T = 0.5 MeV, which is compatible with our use. In contrast, Wanajo et al. (2001, 2002) defined it as the cooling time from T = 0.5 MeV to T = 0.2 MeV, which is about 10% smaller.
All Tables
Table 1: Parameter values for some of our considered outflows and of relevance for third peak formation.
All Figures
![\begin{figure}
\par\includegraphics*[width=8.0cm,clip]{0292fig1.eps}\hspace*{4mm}
\includegraphics*[width=8.0cm,clip]{0292fig2.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg102.gif) |
Figure 1:
T9-dependence of the free neutron density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig3.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fig4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg112.gif) |
Figure 2:
T9-dependence of the neutron-to-seed ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg124.gif) |
Figure 3:
Time evolution of the temperature for the different considered cases with exponential first expansion phase (starting at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig6}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fig7}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg127.gif) |
Figure 4:
Time dependence of the neutron number density,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fig8.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fig9.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg129.gif) |
Figure 5:
Time dependence of the neutron-to-seed ratios,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi10.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi11}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg130.gif) |
Figure 6:
Left: the changing strength of the third abundance peak,
measured in terms of the ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi12.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg144.gif) |
Figure 7:
Time evolution of the temperature for the different
considered cases with exponential first expansion phase (starting at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi13.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi14.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg147.gif) |
Figure 8:
Same as Fig. 4 (with s = 145,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi15.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi16.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg148.gif) |
Figure 9:
Same as Fig. 5 (with s = 145,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi17.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi18.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg156.gif) |
Figure 10:
Left: height of the third abundance peak relative to the
second, measured in terms of the ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi19.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg160.gif) |
Figure 11:
Time evolution of the temperature for the different
expansion histories considered in Fig. 12. All have
an exponential first expansion phase and second stage of power-law decline. Note
that the lines coincide for cases with different entropies s but
the same expansion timescale
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi20.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi21.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg161.gif) |
Figure 12:
Time evolution of the free neutron density ( left) and
final abundance distributions of r-process nuclei ( right) for
outflows with different assumed entropies s and exponential
expansion timescales
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi22.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi23.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg175.gif) |
Figure 13:
Time-evolution of the free neutron number
density ( left) and final abundance distribution of r-process nuclei
( right) for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics*[width=8cm,clip]{0292fi24.eps}\hspace*{4mm}
\includegraphics*[width=8cm,clip]{0292fi25.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10292-08/Timg176.gif) |
Figure 14:
Left: height of the third abundance peak relative to the
second as function of the exponential expansion timescale
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle r(t) = r_0~\left[ 1+ 3~{v_0\over r_0}~(t-t_0)\right]^{1/3}~,$](/articles/aa/full_html/2009/06/aa10292-08/img76.gif)
![$\displaystyle v(t) = v_0~\left[ 1+ 3~{v_0\over r_0}~(t-t_0)\right]^{-2/3},$](/articles/aa/full_html/2009/06/aa10292-08/img77.gif)
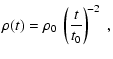
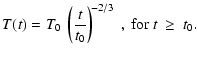
![$\displaystyle r(t) = r_0~\left[ 1 - {v_0t_0\over r_0} + {v_0t_0\over r_0}
\left({t\over t_0}\right)^{\! 3}\right]^{1/3}~,$](/articles/aa/full_html/2009/06/aa10292-08/img82.gif)
![$\displaystyle v(t) = v_0~\left[ 1 - {v_0t_0\over r_0} + {v_0t_0\over r_0}
\left({t\over t_0}\right)^{\! 3}\right]^{-2/3}
\!\! \left({t\over t_0}\right)^{\! 2}~,$](/articles/aa/full_html/2009/06/aa10292-08/img83.gif)