| Issue |
A&A
Volume 494, Number 2, February I 2009
|
|
|---|---|---|
| Page(s) | 637 - 646 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361:200810930 | |
| Published online | 20 November 2008 | |
Water and ammonia abundances in S140 with the Odin![[*]](/icons/foot_motif.gif) satellite
satellite![[*]](/icons/foot_motif.gif)
C. M. Persson1 - M. Olberg1 - Å. Hjalmarson1 - M. Spaans2 - J. H. Black1 - U. Frisk3 - T. Liljeström4 - A. O. H. Olofsson1,5 - D. R. Poelman6 - Aa. Sandqvist7
1 - Onsala Space Observatory, Chalmers University of Technology, 439 92 Onsala, Sweden
2 - Kapteyn Astronomical Institute, Rijksuniversiteit Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
3 - Swedish Space Corporation, PO Box 4207, 171 04 Solna, Sweden
4 - Metsähovi Radio Observatory, Helsinki University of Technology, Otakaari 5A, 02150 Espoo, Finland
5 - GEPI, Observatoire de Paris, CNRS, 5 place Jules Janssen, 92195 Meudon, France
6 - SUPA, School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
7 - Stockholm Observatory, AlbaNova University Center, 10691 Stockholm, Sweden
Received 7 September 2008 / Accepted 14 November 2008
Abstract
Aims. We investigate the effect of the physical environment on water and ammonia abundances across the S140 photodissociation region (PDR) with an embedded outflow.
Methods. We used the Odin satellite to obtain strip maps of the ground-state rotational transitions of ortho-water and ortho-ammonia, as well as CO(5-4) and 13CO(5-4) across the PDR, and H218O in the central position. A physi-chemical inhomogeneous PDR model was used to compute the temperature and abundance distributions for water, ammonia, and CO. A multi-zone escape probability method then calculated the level populations and intensity distributions. These results are compared to a homogeneous model computed with an enhanced version of the RADEX code.
Results. H2O, NH3, and 13CO show emission from an extended PDR with a narrow line width of ![]() 3 km s-1. Like CO, the water line profile is dominated by outflow emission, but mainly in the red wing. Even though CO shows strong self-absorption, no signs of self-absorption are seen in the water line. The H218O molecule is not detected. The PDR model suggests that the water emission arises mainly from the surfaces of optically thick, high-density clumps with
3 km s-1. Like CO, the water line profile is dominated by outflow emission, but mainly in the red wing. Even though CO shows strong self-absorption, no signs of self-absorption are seen in the water line. The H218O molecule is not detected. The PDR model suggests that the water emission arises mainly from the surfaces of optically thick, high-density clumps with
![]() )
) ![]() 106 cm-3 and a clump water abundance, with respect to H2, of 5
106 cm-3 and a clump water abundance, with respect to H2, of 5 ![]() 10-8. The mean water abundance in the PDR is 5
10-8. The mean water abundance in the PDR is 5 ![]() 10-9 and between
10-9 and between ![]() 4
4 ![]() 10
10
![]() in the outflow derived from a simple two-level approximation. The RADEX model points to a somewhat higher average PDR water abundance of 1
in the outflow derived from a simple two-level approximation. The RADEX model points to a somewhat higher average PDR water abundance of 1 ![]() 10-8. At low temperatures deep in the cloud, the water emission is weaker, likely due to adsorption onto dust grains, while ammonia is still abundant. Ammonia is also observed in the extended clumpy PDR, likely from the same high density and warm clumps as water. The average ammonia abundance is about the same as for water: 4
10-8. At low temperatures deep in the cloud, the water emission is weaker, likely due to adsorption onto dust grains, while ammonia is still abundant. Ammonia is also observed in the extended clumpy PDR, likely from the same high density and warm clumps as water. The average ammonia abundance is about the same as for water: 4 ![]() 10-9 and 8
10-9 and 8 ![]() 10-9 given by the PDR model and RADEX, respectively. The differences between the models most likely arise from uncertainties in density, beam-filling, and volume-filling of clumps. The similarity of water and ammonia PDR emission is also seen in the almost identical line profiles observed close to the bright rim. Around the central position, ammonia also shows some outflow emission, although weaker than water in the red wing. Predictions of the H2O
11,0-10,1 and 11, 1 - 00, 0 antenna temperatures across the PDR are estimated with our PDR model for the forthcoming observations with the Herschel Space Observatory.
10-9 given by the PDR model and RADEX, respectively. The differences between the models most likely arise from uncertainties in density, beam-filling, and volume-filling of clumps. The similarity of water and ammonia PDR emission is also seen in the almost identical line profiles observed close to the bright rim. Around the central position, ammonia also shows some outflow emission, although weaker than water in the red wing. Predictions of the H2O
11,0-10,1 and 11, 1 - 00, 0 antenna temperatures across the PDR are estimated with our PDR model for the forthcoming observations with the Herschel Space Observatory.
Key words: ISM: abundances - ISM: individual objects: S140 - ISM: molecules - submillimeter - line: profiles - line: formation
1 Introduction
The chemistry and the evolution of the interstellar medium depend to a high degree on the available amount of carbon and oxygen. The carbon-based chemistry is understood fairly well, but the oxygen chemistry is not. Two molecules vital to understanding the oxygen chemistry are water and molecular oxygen, since some chemical models predict that a large fraction of oxygen could be in the form of these molecules.
Observations of the ground-state rotational water transition with NASA's Submillimeter Wave Astronomy Satellite (SWAS; Melnick et al. 2000b) and the Odin satellite (Nordh et al. 2003) have both shown very low abundances of molecular oxygen, 5 ![]() 10-8 (Larsson et al. 2007), and water, 10-8-10-9 (Olofsson et al. 2003), in the extended cold clouds in contrast to the predictions from chemical models. However, on smaller scales in warm or shocked regions and outflows, where the density is higher than 105-106 cm-3, SWAS (e.g. Melnick et al. 2000a) and Odin (e.g. Persson et al. 2007) have also shown locally increased water abundance by several orders of magnitude, 10-6-10-4 with respect to molecular hydrogen.
The analysis of the data is, however, somewhat difficult and uncertain due to observations of a single line and large beam-widths, but is in agreement with observations of a wealth of highly excited water vapour transitions with ISO (the Infrared Space Observatory, Cernicharo & Crovisier 2005). These locally high abundances support the predictions that water should be an important cooling agent in the star-forming process, especially at high temperatures and densities (e.g. Neufeld et al. 1995; Bergin et al. 2003).
The strong dependence of the water chemistry on the temperature changes seen in star-forming regions also make water an excellent tracer of shocks and outflows from protostars still hidden within their dusty envelopes (e.g. Bergin et al. 1998).
10-8 (Larsson et al. 2007), and water, 10-8-10-9 (Olofsson et al. 2003), in the extended cold clouds in contrast to the predictions from chemical models. However, on smaller scales in warm or shocked regions and outflows, where the density is higher than 105-106 cm-3, SWAS (e.g. Melnick et al. 2000a) and Odin (e.g. Persson et al. 2007) have also shown locally increased water abundance by several orders of magnitude, 10-6-10-4 with respect to molecular hydrogen.
The analysis of the data is, however, somewhat difficult and uncertain due to observations of a single line and large beam-widths, but is in agreement with observations of a wealth of highly excited water vapour transitions with ISO (the Infrared Space Observatory, Cernicharo & Crovisier 2005). These locally high abundances support the predictions that water should be an important cooling agent in the star-forming process, especially at high temperatures and densities (e.g. Neufeld et al. 1995; Bergin et al. 2003).
The strong dependence of the water chemistry on the temperature changes seen in star-forming regions also make water an excellent tracer of shocks and outflows from protostars still hidden within their dusty envelopes (e.g. Bergin et al. 1998).
The intention of this paper is to continue the previous work with ISO, SWAS, and Odin, and also to be a valuable input to future observations with the Heterodyne Instrument for the Far Infrared (HIFI) on board the Herschel![]() satellite to be launched in 2009. Our aim is to investigate how the water abundance depends on the environment in a star-forming region. The high spectral resolution (0.5 km s-1) and the smaller beam-size of Odin compared to SWAS (2
satellite to be launched in 2009. Our aim is to investigate how the water abundance depends on the environment in a star-forming region. The high spectral resolution (0.5 km s-1) and the smaller beam-size of Odin compared to SWAS (2
![]() 1 vs. 3
1 vs. 3
![]() 3
3 ![]() 4
4
![]() 5), which enable higher spatial resolution maps, allow a more detailed analysis of the line profile observed at each map position.
We can also obtain an estimate of the beam-filling by comparing SWAS and Odin line profiles
if the same object has been observed. If not properly taken into account the beam-filling may otherwise influence the results by orders of magnitude.
5), which enable higher spatial resolution maps, allow a more detailed analysis of the line profile observed at each map position.
We can also obtain an estimate of the beam-filling by comparing SWAS and Odin line profiles
if the same object has been observed. If not properly taken into account the beam-filling may otherwise influence the results by orders of magnitude.
In addition to the water observations a second goal of our work is to perform and analyse observations of the important ground-state rotational transition of ammonia. While ammonia has been extensively observed in the inversion transitions at cm-wavelengths (e.g. Zhou et al. 1993; Ungerechts et al. 1986), the 10-00 transition, however, cannot be observed from ground due to the opaque terrestrial atmosphere. The first observation of this transition was performed by the Kuiper Airborne Observatory (Keene et al. 1983), and was later followed up with Odin (Olofsson et al. 2007; Larsson et al. 2003; Liseau et al. 2003).
Our chosen target is the well known molecular cloud and bright nebula Sh 2-140, more commonly known as S140 (Sharpless 1959; Blair et al. 1978). It is located at a distance of 910 pc (Crampton & Fisher 1974) in the large L1202/L1204 dark cloud. This region is illuminated from the south-western side by the nearby B0.5V star HD 211880, creating a bright HII region and an almost edge-on PDR adjacent to the molecular cloud and extending deeply into the cloud. The core in S140 also contains a small cluster of deeply embedded young stellar objects which illuminate the cloud from within. One or more of these early B-stars are undergoing some mass-loss process and molecular outflows are observed from this dense and warm region (e.g. Preibisch & Smith 2002; Hayashi et al. 1987; Minchin et al. 1993; Rouan et al. 1977). The brightest infrared source in S140, called IRS1, is on small scales composed of several sources, two of which might be powering bipolar molecular outflows in almost perpendicular directions (Trinidad et al. 2007). The increased temperature and density in both the PDR and the outflows are likely expected to produce a higher than average water abundance. For these reasons, S140 is a promising target for our purposes.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0930fig1.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg16.gif) |
Figure 1:
A CI map (492 GHz) of S140 observed with JCMT (Minchin et al. 1993).
The Odin 2
|
| Open with DEXTER | |
Both ISO (Boonman & van Dishoeck 2003) and SWAS (Snell et al. 2000a; Ashby et al. 2000a; Franklin et al. 2008; Ashby et al. 2000b) have observed water in S140 and several attempts have been made to model these observations (e.g. Poelman & Spaans 2006; Ashby et al. 2000a; Poelman & Spaans 2005; Boonman et al. 2003; Ashby et al. 2000b). However, they all have had difficulties to explain the unusual, narrow 11,0-10,1 emission line with no or little evidence of self-absorption. In order to obtain more information about the water emission we have conducted strip map observations of S140, starting deep within the molecular cloud and reaching outside the bright rim (see Fig. 1). Strip maps are also simultaneously performed of the previously unobserved NH3(10-00) transition.
To aid the analysis of water and ammonia, we have in addition performed H218O observations in the central position, strip maps of CO(5-4) and 13CO(5-4) with the Odin satellite, and a 13CO(1-0) map with the Onsala 20-m telescope.
2 Observations
All transitions, except 13CO(1-0), were acquired with the Odin satellite from 2003 to 2006 with a total of 561 orbits (see Table 1). The calibration procedure (the chopper wheel method) is described in Olberg et al. (2003). The Odin 1.1 m offset Gregorian telescope has a circular beam at 557 GHz with a Full Width of Half Maximum (FWHM) of 2
![]() 1 (Frisk et al. 2003). Being outside the atmosphere, and with an exceptionally high main beam efficiency,
1 (Frisk et al. 2003). Being outside the atmosphere, and with an exceptionally high main beam efficiency,
![]() = 0.9, our intensity calibration is very accurate. The intensity scale in the figures is expressed in terms of antenna temperature
= 0.9, our intensity calibration is very accurate. The intensity scale in the figures is expressed in terms of antenna temperature
![]() .
In all calculations, however, the main beam efficiency is properly taken into account. The reconstructed pointing offset was <15
.
In all calculations, however, the main beam efficiency is properly taken into account. The reconstructed pointing offset was <15
![]() during most of the time.
The simultaneous observations of H2O and NH3, and of 13CO, CO and H2O guarantee their pointing to be identical.
during most of the time.
The simultaneous observations of H2O and NH3, and of 13CO, CO and H2O guarantee their pointing to be identical.
Three different tunable submm receivers were used, having average single-sideband (SSB) system temperatures of about 3300 K. They were used in combination with a hybrid autocorrelator spectrometer (300-400 MHz working bandwidth) and an acousto-optical spectrometer (1 GHz working bandwidth), both with a channel spacing of ![]() 0.3 km s-1. All observations were performed in the sky-switching mode with reference sky beams at 42
0.3 km s-1. All observations were performed in the sky-switching mode with reference sky beams at 42![]() distance and 4.4
distance and 4.4![]() FWHM. To correct for ripple, observations of a reference off position 30
FWHM. To correct for ripple, observations of a reference off position 30![]() east of S140 were conducted as well.
east of S140 were conducted as well.
Table 1: All molecular transitions are observed with the Odin satellite except the 13CO(1-0) map which is observed with the Onsala 20-m telescope.
The five point strip maps have 60
![]() step size with strip centre coordinates RA 22
step size with strip centre coordinates RA 22
![]() 17
17
![]() 42
42
![]() 0, Dec +63
0, Dec +63
![]() 03
03
![]() 45
45
![]() 0 (B1950) at the cloud core (our position 3, Fig. 1). Position 1 is in NE and position 5 in SW. The frequency scale is set relative to a source LSR velocity of -7.5 km s-1.
0 (B1950) at the cloud core (our position 3, Fig. 1). Position 1 is in NE and position 5 in SW. The frequency scale is set relative to a source LSR velocity of -7.5 km s-1.
In addition, the Onsala 20-m telescope was used in 2006 for a 13CO(1-0) 10 ![]() 11 point map of the S140 molecular cloud with a spacing of 30
11 point map of the S140 molecular cloud with a spacing of 30
![]() .
The SSB system temperature was
.
The SSB system temperature was ![]() 500 K, the main-beam efficiency 0.5, and the FWHM beam at 110.201 GHz is 34
500 K, the main-beam efficiency 0.5, and the FWHM beam at 110.201 GHz is 34
![]() .
.
3 Results
The observed Odin spectra of CO, H2O, and NH3 are shown together with 13CO(5-4) in Figs. 2-4 to allow a comparison of the line profiles of the different molecules at each position. The water and ammonia spectra are also shown together in Fig. 5.
No H218O emission was detected in the central position (Fig. B.1, on-line material) at an rms noise level of 8 mK. Tables with 1![]() rms, integrated intensities, peak antenna temperatures, line widths and amplitudes of Gaussian fits, and centre velocities
for species observed with Odin are found in the on-line Tables B.1-B.4. The on-line material also includes figures of
Gaussian fits to 13CO(1-0) and J = 5-4, H2O and NH3(11-0 0) (Figs. B.4-B.7).
rms, integrated intensities, peak antenna temperatures, line widths and amplitudes of Gaussian fits, and centre velocities
for species observed with Odin are found in the on-line Tables B.1-B.4. The on-line material also includes figures of
Gaussian fits to 13CO(1-0) and J = 5-4, H2O and NH3(11-0 0) (Figs. B.4-B.7).
Below we will discuss the observations and some straight forward results, while the model results for the narrow PDR component are presented in Sects. 4 and 5.
3.1 Carbon monoxide
The CO(5-4) and 13CO(5-4) observations show a narrow line from the PDR in all positions superimposed on a broader outflow feature seen in CO at positions 1-4 and in 13CO
at the centre position (Fig. 2). The emission peaks about 20
![]() from the central position towards position 2 deeper in the cloud. A comparison of the 12CO and 13CO line shapes suggests strong CO(5-4) self-absorption by lower excitation foreground gas. This is also discussed by e.g. Minchin et al. (1993) and Boonman et al. (2003) where the higher J-level CO lines are strongly self-absorbed. No strong self-absorption is visible in 13CO.
from the central position towards position 2 deeper in the cloud. A comparison of the 12CO and 13CO line shapes suggests strong CO(5-4) self-absorption by lower excitation foreground gas. This is also discussed by e.g. Minchin et al. (1993) and Boonman et al. (2003) where the higher J-level CO lines are strongly self-absorbed. No strong self-absorption is visible in 13CO.
The mean opacity of 12CO and 13CO can be determined by comparison of their antenna peak temperatures if the isotopologue abundance ratio R is known. Assuming that the opacity of 12CO is larger than the opacity of 13CO by a factor R, we will have
where the radiation temperature,
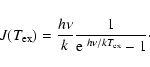 |
(2) |
The beam-filling factor is calculated with
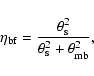 |
(3) |
assuming that both the source brightness distribution and the antenna response are circularly symmetric and Gaussian.
Assuming that the excitation temperatures are the same for both species, co-spatial emissions and using R = 70, the opacities of the narrow component of 12CO and 13CO are estimated to be ![]() 70 and
70 and ![]() 1, while the opacities in the broad outflow component are
1, while the opacities in the broad outflow component are ![]() 7 and
7 and ![]() 0.1, respectively. Due to the self-absorption of 12CO the opacities are upper limits.
0.1, respectively. Due to the self-absorption of 12CO the opacities are upper limits.
The size of the emission region can be estimated by comparing Odin and SWAS antenna temperatures
where
A second approach to estimate the source size is performed by plotting the antenna temperatures in our Odin strip map vs. position, and fitting a Gaussian. After deconvolution with the 126
![]() Odin beam, the resulting one dimensional source size is about 106
Odin beam, the resulting one dimensional source size is about 106
![]() .
Together with the mean source size of
.
Together with the mean source size of ![]() 100
100
![]() ,
this implies a relatively circular source.
,
this implies a relatively circular source.
The excitation temperature can be estimated by plotting a rotation diagram of several transitions.
The level populations are given by the Boltzmann distribution and the excitation temperatures for all the energy levels are assumed to be the same. The beam-filling corrected integrated intensities of all lines are plotted as a function of the upper state energy in a semi-log plot
based upon the relation (Persson et al. 2007)
where k is the Boltzmann constant,
Our rotation diagram of the broad outflow 13CO component in the central position (on-line Fig. B.2), including the Onsala 20-m J = 1-0 transition, the J = 2-1 and 3-2 transitions from Minchin et al. (1993), and the Odin J = 5-4 transition, produces
![]() = 24
= 24 ![]() 2 K and
2 K and
![]() = (2.5
= (2.5 ![]() 0.4)
0.4) ![]() 1016 cm-2. All antenna temperatures are corrected with respective beam-filling and beam-efficiencies. This temperature is in agreement with the previously estimated lower limit of the outflow excitation temperature of about 15-20 K (Minchin et al. 1993). The low temperature of the outflow indicates that the emission arises from gas far behind the shock front where the gas has already cooled (Snell et al. 1984b).
1016 cm-2. All antenna temperatures are corrected with respective beam-filling and beam-efficiencies. This temperature is in agreement with the previously estimated lower limit of the outflow excitation temperature of about 15-20 K (Minchin et al. 1993). The low temperature of the outflow indicates that the emission arises from gas far behind the shock front where the gas has already cooled (Snell et al. 1984b).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig2.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg48.gif) |
Figure 2: Comparison of the CO(5-4) (thick magenta line) and 13CO(5-4) (thin black line) line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig3.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg49.gif) |
Figure 3: Comparison of the H2O 11,0-10,1 (thick magenta line) and 13CO(5-4) (thin black line) line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig4.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg50.gif) |
Figure 4: Comparison of the NH3 10-0 0 (thick magenta line) and 13CO(5-4) (thin black line) line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig5.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg51.gif) |
Figure 5: Comparison of the H2O (thick magenta line) 11,0-10,1 and the NH3 (thin black line) 10-0 0 line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
The excitation temperature of the narrow 13CO PDR emission in the central position is also estimated by means of a rotation diagram (on-line Fig. B.3), including the above mentioned transitions with addition of the J = 6-5 line from Graf et al. (1993), but excluding J = 1-0 which seems to originate only in the colder gas component. This produces
![]() = 69
= 69 ![]() 27 K, in agreement with Minchin et al. (1993) who find a PDR excitation temperature of about 70 K at IRS and a steep rise in temperature to about 250 K at the dissociation front 60
27 K, in agreement with Minchin et al. (1993) who find a PDR excitation temperature of about 70 K at IRS and a steep rise in temperature to about 250 K at the dissociation front 60
![]() -80
-80
![]() SW of IRS1. Our PDR column density,
SW of IRS1. Our PDR column density,
![]() (13CO) = (3.2
(13CO) = (3.2 ![]() 1.8)
1.8) ![]() 1016 cm-2, is relatively uncertain but in agreement with the RADEX result in Sect. 4, N(13CO) = 2.8
1016 cm-2, is relatively uncertain but in agreement with the RADEX result in Sect. 4, N(13CO) = 2.8 ![]() 1016 cm-2, and with Plume et al. (1994), 3.4
1016 cm-2, and with Plume et al. (1994), 3.4 ![]() 1016 cm-2.
1016 cm-2.
3.2 Water
The ortho-water 11,0-10,1 ground-state rotational transition is detected in all positions except outside the bright rim (position 5). Similar to CO and 13CO, a
narrow component (
![]()
![]() 3 km s-1) superimposed on a broader outflow component (
3 km s-1) superimposed on a broader outflow component (
![]()
![]() 8.5 km s-1) is observed with emission originating around the central position. Like CO, the water line profile is dominated by outflow emission, clearly seen in a two Gaussian component fit in the on-line Fig. B.6. This is in contrast to 13CO which is dominated by the narrow component (on-line Fig. B.4). The water outflow emission, in addition, mainly shows a red wing.
8.5 km s-1) is observed with emission originating around the central position. Like CO, the water line profile is dominated by outflow emission, clearly seen in a two Gaussian component fit in the on-line Fig. B.6. This is in contrast to 13CO which is dominated by the narrow component (on-line Fig. B.4). The water outflow emission, in addition, mainly shows a red wing.
The non-detection of H218O can be used to set upper limits on the opacity of the main water line using Eq. (1). However, the calculation is not as straightforward as for CO.
Because of the high critical density (the ratio of the spontaneous de-excitation and collision coefficients) of the H2O 557 GHz line, the emission of this transition is highly sub-thermal and has a high opacity even for rather low abundances. This high optical depth allows the excitation
temperature to be enhanced by radiative trapping. As a result, the corresponding lines of H2O and H218O have quite different values of excitation temperature. Their excitation temperatures will also be much lower than the kinetic temperature. Using the RADEX code in Sect. 4 for a kinetic temperature of 55 K and a molecular hydrogen density
![]() = 4
= 4 ![]() 105 cm-3, we find excitation temperatures of 8.2 and 6.3 K for the
11,0-10,1 transitions of H2O and H218O, respectively. If the abundance ratio
[16O/18O] = 330 in water (Persson et al. 2007) and if the two isotopologues are distributed similarly, then the 5
105 cm-3, we find excitation temperatures of 8.2 and 6.3 K for the
11,0-10,1 transitions of H2O and H218O, respectively. If the abundance ratio
[16O/18O] = 330 in water (Persson et al. 2007) and if the two isotopologues are distributed similarly, then the 5![]() upper limit on the intensity of the H218O line implies that the optical depth of the H2O line is
upper limit on the intensity of the H218O line implies that the optical depth of the H2O line is ![]() 60. If the assumed density is lower by a factor of 10, the difference in excitation temperatures will increase and change the
upper limit to
60. If the assumed density is lower by a factor of 10, the difference in excitation temperatures will increase and change the
upper limit to ![]() 120.
120.
The high H2O opacity, in addition, often produces self-absorbed spectra. Our observations, however, do not show any obvious signs of self-absorption in contrast to our CO observations. When comparing the centre velocities of the narrow components of water and CO to 13CO, we find that the velocities of water and 13CO are well matched (Fig. 3 and Tables B.2, B.3), while CO and 13CO in positions 1-4 are not (Fig. 2). This supports our conclusion that there is no severe self-absorption in H2O in contrast to observations of other sources in which corresponding self-absorptions were seen in CO(7-6) and in ISO measurements of H2O (Boonman et al. 2003).
The lack of self-absorption points to a rather constant excitation across the region (cf. Snell et al. 1984a). It also implies a lower water abundance in the blue than in the red outflow. A higher water abundance in the red wing may be caused by outflowing gas pushing into the ambient high density cloud thereby producing water. The blue outflow, on the other hand, is leaving the molecular cloud, and expands into an ionized region with low density gas with no or very low water production as a result. This is in agreement with the results in Franklin et al. (2008) who investigated water abundance in molecular outflows with SWAS and find about five times higher abundance in the red outflow compared to the blue.
The sizes of the emitting regions are estimated in the same way as for 13CO (Eq. (4)). For the central position the ratio of the Odin and SWAS peak antenna temperatures is
![]() 2.4, equivalent to a mean source size of
2.4, equivalent to a mean source size of ![]() 100
100
![]() .
This confirms previous suggestions that the water emission does not fill the SWAS beam (Boonman et al. 2003). To obtain estimates of the size of each component, we use
the amplitudes of the fitted Gaussians from the Odin and SWAS spectra. The ratios of the PDR and outflow components are
.
This confirms previous suggestions that the water emission does not fill the SWAS beam (Boonman et al. 2003). To obtain estimates of the size of each component, we use
the amplitudes of the fitted Gaussians from the Odin and SWAS spectra. The ratios of the PDR and outflow components are ![]() 2.2 and
2.2 and ![]() 2.6, which corresponds to mean source sizes of 120
2.6, which corresponds to mean source sizes of 120
![]() and 85
and 85
![]() ,
respectively.
,
respectively.
Gaussian fits to the amplitudes in each position in the Odin strip map results in one-dimensional source sizes of ![]() 150
150
![]() and
and ![]() 50
50
![]() for the PDR and outflow, respectively.
Taken together, these two calculations of source sizes suggest that the water emission from the PDR is more extended in the NE-SW direction (same direction as our strip map), while the contrary applies to the outflow, indicating a NW-SE elongation.
for the PDR and outflow, respectively.
Taken together, these two calculations of source sizes suggest that the water emission from the PDR is more extended in the NE-SW direction (same direction as our strip map), while the contrary applies to the outflow, indicating a NW-SE elongation.
A third approach to estimate the beam-filling can be achieved by using the radiative transfer equation. With a constant source function, the solution of the radiative transport equation is
where
For an optically thick line and neglecting the background radiation
If
3.3 Ammonia
A complex energy level diagram with a wealth of transitions covering different temperatures and densities has made ammonia a very valuable diagnostic of physical conditions in the interstellar medium. The 10-0 0 ground-state rotational transition, observed by Odin, has an upper state energy comparable to the extensively observed inversion transitions (e.g. Zhou et al. 1993; Ungerechts et al. 1986), but the critical density is about four orders of magnitude larger. It is therefore likely that these transitions partly probe different gas components. The 10-0 0 transition has a high opacity and is highly sub-thermally excited in most cases like our observed water transition.
The 10-0 0 transition of ortho-NH3 is detected in all positions except outside the bright rim (position 5). The line profiles and centre velocities are very similar to those of 13CO(5-4) with an exception in position 1 (Fig. 4). Our comparison of ammonia and water in Fig. 5 shows an almost identical line profile at the bright rim (position 4), which suggests emission from the same gas and velocity fields at this position originating in the PDR. In the central position, the water line profile is dominated by the outflow in contrast to ammonia. Both species displays, however, very similar emission in the blue outflow, while water has a more pronounced outflow in the red wing. The water emission from the outflow seems to be almost the same in position 2 and 3, while the ammonia emission from the outflow decreases in position 2. This suggests that the outflow production mechanism is more efficient for water than ammonia.
Deepest in the molecular cloud a very weak water line is seen. The ammonia emission is, however, considerably stronger than the water emission at this position. This confirms previous observations of NH3 inversion transitions (Zhou et al. 1993; Ungerechts et al. 1986) who find an NH3 peak further into the cloud at about 1![]() northeast of IRS1. When we plot the peak antenna temperatures vs. position it is obvious that we see additional emission in position 1. A Gaussian fit to positions 2-4 gives a source size of
northeast of IRS1. When we plot the peak antenna temperatures vs. position it is obvious that we see additional emission in position 1. A Gaussian fit to positions 2-4 gives a source size of ![]() 130
130
![]() ,
with a peak about 10
,
with a peak about 10
![]() into the cloud from the centre. This size is relatively uncertain due to a fit to only three positions, but agrees well with the source sizes estimated from 13CO and H2O.
into the cloud from the centre. This size is relatively uncertain due to a fit to only three positions, but agrees well with the source sizes estimated from 13CO and H2O.
The Odin observations indicate that in addition to the warm, dense PDR and a weak outflow around IRS, we also observe NH3 from the same cold and extended gas deep in the cloud (position 1) as 13CO(1-0) at a temperature about 20-30 K. This is also in agreement with
Ungerechts et al. (1986) and Zhou et al. (1993) who find an NH3 rotation temperature of 40 K in between our first and second position. Chemical models predict that NH3 is not depleted in high density regions (![]() 1
1 ![]() 106 cm-3) and is therefore relatively more abundant than other molecules such as water and CO (Bergin & Langer 1997; Bergin 2003).
106 cm-3) and is therefore relatively more abundant than other molecules such as water and CO (Bergin & Langer 1997; Bergin 2003).
The surface filling fraction of the narrow PDR component of ammonia is also estimated using the radiative transfer equation (Eq. (7)). The excitation temperature is approximately the same as for water thereby producing similar surface filling factors. Together with the similarity of the line profiles, source sizes and centre velocities of the H2O, NH3 and 13CO(5-4) narrow components, this points to emission from the same high density PDR clumps with the same temperature of about 70 K for all species (cf. Boonman et al. 2003).
3.4 Outflow abundances
The collisional de-excitation of the ground-state rotational transition of ortho-water is very low in the density ranges considered here due to the high critical density of ![]() 3
3 ![]() 108 cm-3 at a temperature of 40 K. A simple analytic expression for the antenna temperature of a two-level system in the low collision rate limit can therefore be used
since collisional excitation always results in a photon that escapes the cloud. Thus, even though our transition may be optically thick, it is effectively thin (Linke et al. 1977; Snell et al. 2000b). We use this approach to estimate the water abundance in the outflow (Snell et al. 2000b)
108 cm-3 at a temperature of 40 K. A simple analytic expression for the antenna temperature of a two-level system in the low collision rate limit can therefore be used
since collisional excitation always results in a photon that escapes the cloud. Thus, even though our transition may be optically thick, it is effectively thin (Linke et al. 1977; Snell et al. 2000b). We use this approach to estimate the water abundance in the outflow (Snell et al. 2000b)
where C is the collision rate which equals the product of the cross-section and velocity. Dividing Eq. (8) with N(H2) and scaling the calculated factor in Snell et al. (2000b) to our derived rotational outflow temperature of 24 K (with
The H2 column density in the outflow is calculated from
The ammonia abundance in the outflow is estimated using the Local Thermal Equilibrium (LTE) approximation. Assuming LTE and adding corrections for opacity and beam-filling, the total source averaged column density can be calculated as
where
Table 2: Observations and model calculations for the narrow PDR component in the RADEX homogeneous modela.
4 Model results: RADEX - a homogeneous model
In this section we use an enhanced version of the RADEX![]() (van der Tak et al. 2007) code
to compute the intensities of the narrow components of the transitions observed by Odin, and the intensities of several atomic and molecular transitions that previously have been observed in S140. The RADEX codex applies a very simple method of mean escape probabilities to the
radiative transfer and yields results that are similar to those in the large-velocity-gradient approximation, assuming an isothermal and homogeneous medium, but without an implicit
assumption of a gradient in velocity. Although much more sophisticated methods of radiative transfer have been used to construct models of the atomic and molecular line emission from this region, it is useful to examine a simple, internally consistent model of a homogeneous cloud that reproduces the principal observed facts. Such a model can be used in particular to assess the role of radiative coupling of molecular excitation to the intense continuum radiation within the PDR.
In Sect. 5, these results are compared to the results from
a 3D inhomogeneous PDR model that calculates the temperature and abundance distributions, and a multi-zone escape probability method that calculates the level populations and intensity distributions of water and ammonia (Poelman & Spaans 2006,2005).
(van der Tak et al. 2007) code
to compute the intensities of the narrow components of the transitions observed by Odin, and the intensities of several atomic and molecular transitions that previously have been observed in S140. The RADEX codex applies a very simple method of mean escape probabilities to the
radiative transfer and yields results that are similar to those in the large-velocity-gradient approximation, assuming an isothermal and homogeneous medium, but without an implicit
assumption of a gradient in velocity. Although much more sophisticated methods of radiative transfer have been used to construct models of the atomic and molecular line emission from this region, it is useful to examine a simple, internally consistent model of a homogeneous cloud that reproduces the principal observed facts. Such a model can be used in particular to assess the role of radiative coupling of molecular excitation to the intense continuum radiation within the PDR.
In Sect. 5, these results are compared to the results from
a 3D inhomogeneous PDR model that calculates the temperature and abundance distributions, and a multi-zone escape probability method that calculates the level populations and intensity distributions of water and ammonia (Poelman & Spaans 2006,2005).
The molecular data files for H2O and NH3 have been enlarged, compared with those previously available through the Leiden Atomic and Molecular Database (LAMDA)![]() . Data for the ortho and para forms of these molecules have been combined into a single file and infrared transitions have been added. Collision rates published by Faure et al. (2007) for H2 + H2O and by
Faure et al. (2004) for e- + H2O are now used. Two different data files have been used to analyse the excitation of NH3. The smaller includes only the lowest 112 levels of the vibrational ground state and 140 radiative transitions between them. A larger file, derived mainly
from the HITRAN
. Data for the ortho and para forms of these molecules have been combined into a single file and infrared transitions have been added. Collision rates published by Faure et al. (2007) for H2 + H2O and by
Faure et al. (2004) for e- + H2O are now used. Two different data files have been used to analyse the excitation of NH3. The smaller includes only the lowest 112 levels of the vibrational ground state and 140 radiative transitions between them. A larger file, derived mainly
from the HITRAN![]() database, has also been tested: it contains 2392 levels and 15 067 radiative transitions, including lines of several
database, has also been tested: it contains 2392 levels and 15 067 radiative transitions, including lines of several ![]() and
and ![]() vibrational bands in the mid-infrared.
vibrational bands in the mid-infrared.
We include a simple dust model of the broad-band spectrum (Thronson et al. 1983; Minchin et al. 1995; Ney & Merrill 1980) at submm and far-infrared wavelengths in order to characterise the internal radiation sensed by the molecules (a detailed description is found in Appendix A of the on-line material).
The principal parameters needed to specify a model are the kinetic temperature ![]() and the average number density of molecular hydrogen
and the average number density of molecular hydrogen
![]() .
Our adopted dust model implies
.
Our adopted dust model implies
![]() = 4.7
= 4.7 ![]() 1022 cm-2 and an average density
1022 cm-2 and an average density
![]() = 3
= 3 ![]() 104 cm-3 in a homogeneous, spherical cloud with a source size L = 0.5 pc (derivation in Appendix A, on-line material). Unfortunately, this average density is inconsistent with our observations. Although a uniform RADEX model can be constructed based upon this density, this low-density model cannot explain the observed intensities of the pure rotational lines of H2O and NH3 unless the line-centre optical depths are of the order of 200 and 100, respectively. Such large opacities would imply significant line broadening through saturation of the emission, which conflicts with the observed narrow profiles.
104 cm-3 in a homogeneous, spherical cloud with a source size L = 0.5 pc (derivation in Appendix A, on-line material). Unfortunately, this average density is inconsistent with our observations. Although a uniform RADEX model can be constructed based upon this density, this low-density model cannot explain the observed intensities of the pure rotational lines of H2O and NH3 unless the line-centre optical depths are of the order of 200 and 100, respectively. Such large opacities would imply significant line broadening through saturation of the emission, which conflicts with the observed narrow profiles.
High densities of 7 ![]() 105 cm-3 are found by multitransition CS observations (Snell et al. 1984a), and 5
105 cm-3 are found by multitransition CS observations (Snell et al. 1984a), and 5 ![]() 105 cm-3 from NH3 inversion transitions (Ungerechts et al. 1986). We include the CS transitions in our RADEX model in addition to our own observations, and our best fit suggests a mean molecular density of 4
105 cm-3 from NH3 inversion transitions (Ungerechts et al. 1986). We include the CS transitions in our RADEX model in addition to our own observations, and our best fit suggests a mean molecular density of 4 ![]() 105 cm-3 and a temperature of 55 K. This suggests that the strongly emitting molecules occupy only a 7% fraction of the volume. The H2 column density, which is needed to obtain the abundances, X(x) = N(x)/N(H2), is calculated from the N(13CO) obtained with RADEX. This column density is also in agreement with
105 cm-3 and a temperature of 55 K. This suggests that the strongly emitting molecules occupy only a 7% fraction of the volume. The H2 column density, which is needed to obtain the abundances, X(x) = N(x)/N(H2), is calculated from the N(13CO) obtained with RADEX. This column density is also in agreement with
![]() (13CO) found in Sect. 3.1. Using [12C/13C] = 70 and [CO/H2] = 10-4 we obtain
(13CO) found in Sect. 3.1. Using [12C/13C] = 70 and [CO/H2] = 10-4 we obtain
![]() = 2.0
= 2.0 ![]() 1022 cm-2 for the narrow PDR component.
1022 cm-2 for the narrow PDR component.
Table 2 collects the observed intensities and the corresponding values
calculated from the model. A source size of 120
![]() ,
derived in Sect. 2, is used to correct the antenna temperatures
,
derived in Sect. 2, is used to correct the antenna temperatures
![]() to Rayleigh-Jeans brightness temperatures
to Rayleigh-Jeans brightness temperatures ![]() according to the scaling in Eq. (6).
The estimated abundances and column densities are summarized in Table 3. Note that the best-fitting model of the [C II]
according to the scaling in Eq. (6).
The estimated abundances and column densities are summarized in Table 3. Note that the best-fitting model of the [C II]
![]() m line emission implies a density of carbon ions,
m line emission implies a density of carbon ions,
![]() = 7.7 cm-3. This is taken to be equal to the electron density, which implies an average electron fraction of
= 7.7 cm-3. This is taken to be equal to the electron density, which implies an average electron fraction of
![]() = 1.9
= 1.9 ![]() 10-5. This electron fraction is large enough that electron-impact on polar molecules like H2O must be competitive with H2 collisions in exciting rotational states. However, the results presented for NH3 so far neglect electron collisions.
10-5. This electron fraction is large enough that electron-impact on polar molecules like H2O must be competitive with H2 collisions in exciting rotational states. However, the results presented for NH3 so far neglect electron collisions.
The model reproduces nicely all the observations except the ammonia inversion transitions which are predicted to be lower than the observed intensities. The 13CO(2-1) transition is also predicted to be slightly lower than what is observed. These discrepancies may be caused by a co-existing, extended lower excitation gas component, which is not contributing much to the emission of the 13CO(5-4) or NH3(10-0 0) lines. Even so, the column densities of C, 13CO and CS agree well with Plume et al. (1994) and Snell et al. (1984a), and the C abundance is also in agreement with Franklin et al. (2008). The water abundance was previously estimated by Snell et al. (2000a) to be 9 ![]() 10-9, and by Ashby et al. (2000a) to be 2
10-9, and by Ashby et al. (2000a) to be 2 ![]() 10-8, both very similar to the abundance calculated by RADEX.
10-8, both very similar to the abundance calculated by RADEX.
The RADEX model is also tested for higher transitions of H2O and shows that some lines are sensitive to various effects. For example, the intensity ratio of the 1661 and 1670 GHz lines appears to be sensitive to the total column density. When the internal radiation field is switched off in the models, the intensities of the transitions involving the lowest rotational levels increase slightly, while the intensities of lines involving more highly excited states are diminished. In particular, the 1661 GHz line is enhanced by radiative excitation and is very sensitive to the total column density. This line will appear in absorption if the opacity in the 557 GHz transition is small since photon-trapping is ineffective at column densities around 1014 cm-2 or less.
The excitation of NH3 also shows some interesting effects in these models. Due to the rather high density of C+ ions, the reaction of C+ with NH3 will destroy ammonia at a rate exceeding 10-8 s-1, which is rapid enough to affect the excitation of the metastable levels involved in several of the inversion transitions near 23 GHz. Indeed, the calculations indicate that the (J,K) = (3, 3) inversion transition is a weak maser (cf. Walmsley & Ungerechts 1983). In addition, NH3 has strong vibrational transitions in the mid- and near-infrared. When these are included, the intensity of the 572 GHz transition is somewhat suppressed while the lowest inversion transitions are somewhat enhanced.
Table 3: Results of the homogeneous RADEX model for the narrow PDR component: column densities and abundancesa.
5 Model results: clumpy PDR model
A self-consistent physi-chemical 3D inhomogeneous model is used to compute the temperature of the gas and dust, and the abundance distributions inside the clumpy cloud
(detailed descriptions are found in Poelman & Spaans 2005; Spaans & van Dishoeck 1997; Spaans 1996). This clumpy PDR model has three free parameters; the volume filling factor F (fraction of the cloud that is occupied by clumps), a clump size ![]() ,
and the clump-interclump ratio
,
and the clump-interclump ratio ![]() (H)/
(H)/
![]() (H). The total hydrogen density
(H). The total hydrogen density ![]() =
=
![]() + 2
+ 2
![]() .
In the dense clumps, hydrogen is entirely molecular, thus
.
In the dense clumps, hydrogen is entirely molecular, thus
![]() = 2
= 2
![]() .
The PDR model parameters used in this paper are given in Table 4. We use a velocity dispersion of 1.2 km s-1 (Zhou et al. 1994) equivalent to a FWHM line width of 2.0 km s-1 for an optically thin line. With an opacity of about 5-10 the line is broadened by a factor of
.
The PDR model parameters used in this paper are given in Table 4. We use a velocity dispersion of 1.2 km s-1 (Zhou et al. 1994) equivalent to a FWHM line width of 2.0 km s-1 for an optically thin line. With an opacity of about 5-10 the line is broadened by a factor of ![]() 1.5-2 to 3-4 km s-1, consistent with our observations. The incident radiation field is taken to be
1.5-2 to 3-4 km s-1, consistent with our observations. The incident radiation field is taken to be
![]() = 140 with respect to the Draine (1978) field. The clumps are randomly distributed in the interclump medium
and the volume filling fraction is taken to be 8% (Poelman & Spaans 2005; Ashby et al. 2000a; Spaans & van Dishoeck 1997).
The grid size is 81
= 140 with respect to the Draine (1978) field. The clumps are randomly distributed in the interclump medium
and the volume filling fraction is taken to be 8% (Poelman & Spaans 2005; Ashby et al. 2000a; Spaans & van Dishoeck 1997).
The grid size is 81 ![]() 81
81 ![]() 81, corresponding to a resolution of 0.006 pc and a total size of 0.5 pc (about 110
81, corresponding to a resolution of 0.006 pc and a total size of 0.5 pc (about 110
![]() at a distance of 910 pc).
at a distance of 910 pc).
In the PDR computation, each clump is joined smoothly to the inter-clump medium through a power-law ![]() 1/R2 density distribution. This envelope contains very little molecular material and the bulk of the impinging radiation field is always absorbed by the clumps and not the inter-clump medium. The definition of the mean H2 density and the mean molecular abundances X of species x is thus made through
1/R2 density distribution. This envelope contains very little molecular material and the bulk of the impinging radiation field is always absorbed by the clumps and not the inter-clump medium. The definition of the mean H2 density and the mean molecular abundances X of species x is thus made through
![]() =
=
![]() +
+
![]() and
and
![]() (x) =
(x) =
![]() +
+
![]() to allow an unambiguous
comparison with molecular line observations.
to allow an unambiguous
comparison with molecular line observations.
A high molecular hydrogen density of ![]() 1
1 ![]() 106 cm-3 in the clumps is required
to match the intensities observed by Odin and SWAS. Note that this clump density is considerably higher than that used by Poelman & Spaans (2006,2005).
The high density and clumpy medium suggested by our PDR model is, however, also supported by previous density estimates. For example, density variations between 104-106 cm-3 are necessary to explain the apparent coincidence of the C I and CO ridges as well as the distance between the C I ridge and the bright rim (Hayashi & Murata 1992).
Emission from numerous, small, dense (105-2
106 cm-3 in the clumps is required
to match the intensities observed by Odin and SWAS. Note that this clump density is considerably higher than that used by Poelman & Spaans (2006,2005).
The high density and clumpy medium suggested by our PDR model is, however, also supported by previous density estimates. For example, density variations between 104-106 cm-3 are necessary to explain the apparent coincidence of the C I and CO ridges as well as the distance between the C I ridge and the bright rim (Hayashi & Murata 1992).
Emission from numerous, small, dense (105-2 ![]() 106 cm-3) and optically thick clumps of gas, where the number density of clumps decreases with distance from the CS cloud centre close to IRS, is the best explanation of the CS column density variations, as well as the observed opacities and temperatures obtained from multitransition observations of CS (Zhou et al. 1994; Snell et al. 1984a). As molecular hydrogen density in the interclump medium we use 5
106 cm-3) and optically thick clumps of gas, where the number density of clumps decreases with distance from the CS cloud centre close to IRS, is the best explanation of the CS column density variations, as well as the observed opacities and temperatures obtained from multitransition observations of CS (Zhou et al. 1994; Snell et al. 1984a). As molecular hydrogen density in the interclump medium we use 5 ![]() 103 cm-3.
103 cm-3.
Table 4: Clumpy PDR model parameters.
The resulting abundances, with respect to H2, in the clumps and the inter-clump medium, as well as a mean value over the whole region, are found in Table 5. The mean value is about half than found by RADEX. In the clumps, the water abundances vary between 10-7-10-9 with an average of 4.8 ![]() 10-8. The low density in the interclump medium results in low water abundances between 1
10-8. The low density in the interclump medium results in low water abundances between 1 ![]() 10-11-5
10-11-5 ![]() 10-9 with an average of 8.9
10-9 with an average of 8.9 ![]() 10-10. Ammonia is found to have about the same average abundance as water, 4.3
10-10. Ammonia is found to have about the same average abundance as water, 4.3 ![]() 10-8, in the clumps, while lower by almost an order of magnitude in the inter-clump medium, 1.1
10-8, in the clumps, while lower by almost an order of magnitude in the inter-clump medium, 1.1 ![]() 10-10.
10-10.
Table 5:
Resulting abundances with respect to
![]() for the narrow PDR components of water and ammonia from the clumpy PDR model.
for the narrow PDR components of water and ammonia from the clumpy PDR model.
Table 6:
Observed and predicted
![]() in the PDR for o-H2O(
11,0-10,1) with SWAS and Odin at the central position.
in the PDR for o-H2O(
11,0-10,1) with SWAS and Odin at the central position.
The result from our PDR model is used as input to a three-dimensional multi-zone escape probability method which computes the level populations of ortho- and para-H2O (up to ![]() 350 K), CO and NH3, as well as line intensities and opacities (Poelman & Spaans 2006,2005). The excitation due to dust emission is fully included. The dust temperature in the model varies between 18 and 32 K. However, due to geometry the highest
350 K), CO and NH3, as well as line intensities and opacities (Poelman & Spaans 2006,2005). The excitation due to dust emission is fully included. The dust temperature in the model varies between 18 and 32 K. However, due to geometry the highest
![]() is only achieved at the edge of the PDR and the dust component fills only a small part of the region. The bulk of the dust has a temperature of about 25 K and the dust continuum opacity
is only achieved at the edge of the PDR and the dust component fills only a small part of the region. The bulk of the dust has a temperature of about 25 K and the dust continuum opacity ![]() 100
100 ![]() m is 0.02 or smaller. Results from this code differ at most by 10% compared to other Monte Carlo/Accelerated Lambda Iteration codes. Figure 6 shows the predicted water intensities on a logarithmic scale. Note that the ionizing star is located on the left side of the displayed region.
The peak emission is found about 70-80
m is 0.02 or smaller. Results from this code differ at most by 10% compared to other Monte Carlo/Accelerated Lambda Iteration codes. Figure 6 shows the predicted water intensities on a logarithmic scale. Note that the ionizing star is located on the left side of the displayed region.
The peak emission is found about 70-80
![]() from the bright rim, in agreement with our observations of all species.
from the bright rim, in agreement with our observations of all species.
The resulting model intensities are then used to calculate the expected antenna temperature via
where S is the integrated flux density in [erg s-1 cm-2], the intensity b is in [erg s-1 cm-2 sr-1],
The model ortho-water opacities are relatively low with a unweighted mean opacity of 17 over the entire source, with a range between 10-5-800.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0930fig6.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg132.gif) |
Figure 6: Result of the PDR high-density model. The water intensity is shown on a logarithmic scale. The ionizing star is located on the left side of the displayed region. |
| Open with DEXTER | |
The antenna temperatures from the PDR model agree well with our observations, especially considering uncertainties in source and clump size, as well as the volume filling fraction, which is the main uncertainty and can be varied to obtain slightly higher or lower
![]() .
The dust background continuum is also lower than in the RADEX model, which
diminishes the effect of radiative excitation of water. A clumpy medium with high clump densities above 106 cm-3 is, however, necessary to produce model antenna temperatures close to the observed values. This is also supported by the resulting low density of 3
.
The dust background continuum is also lower than in the RADEX model, which
diminishes the effect of radiative excitation of water. A clumpy medium with high clump densities above 106 cm-3 is, however, necessary to produce model antenna temperatures close to the observed values. This is also supported by the resulting low density of 3 ![]() 104 cm-3 obtained by the dust model in Sect. 4 assuming a homogeneous, spherical cloud, which is about 7% of the density in our best fitting model.
104 cm-3 obtained by the dust model in Sect. 4 assuming a homogeneous, spherical cloud, which is about 7% of the density in our best fitting model.
A clump-interclump density ratio of ![]() 100 is in general agreement with observations of dense PDRs. Data in CO, sensitive to
100 is in general agreement with observations of dense PDRs. Data in CO, sensitive to
![]() cm-3, and high density tracers like CS and HCN, probing
cm-3, and high density tracers like CS and HCN, probing
![]() cm-3, often show an extended morphology in CO lines and clump-like features in the CS and HCN gas. Maintaining such a density contrast is a challenge, since the clumps likely evolve on a sound crossing time of
cm-3, often show an extended morphology in CO lines and clump-like features in the CS and HCN gas. Maintaining such a density contrast is a challenge, since the clumps likely evolve on a sound crossing time of ![]() 105 yr (
105 yr (![]() 0.1 pc clumps). If the interclump medium has a much higher temperature or a higher degree of turbulent motion than the
clumps, then a rough pressure equilibrium might hold for times exceeding the sound crossing time, supporting our best-fit density contrast. This would, however, require interclump temperatures of >103 K or turbulent motions of >3 km s-1.
0.1 pc clumps). If the interclump medium has a much higher temperature or a higher degree of turbulent motion than the
clumps, then a rough pressure equilibrium might hold for times exceeding the sound crossing time, supporting our best-fit density contrast. This would, however, require interclump temperatures of >103 K or turbulent motions of >3 km s-1.
6 Summary and conclusions
We have used the Odin satellite to observe water, ammonia, and carbon-monoxide in the well-known molecular cloud S140. We have simultaneously observed five-point strip maps across the bright rim in S140 of the ortho-H2O 11,0-10,1 and the ortho-NH3 10-0 0 transitions, as well as CO(5-4) and 13CO(5-4). The NH3 transition has never previously been observed in S140. Observations of H218O in the central position resulted in a non-detection at an rms level of 8 mK. As support observation we also mapped 13CO(1-0) with the Onsala 20 m telescope.
Like CO, the water line-profile is dominated by emission from a NW-SE outflow, however, mainly in the red wing. Strong self-absorption is seen in the optically thick CO emission, while no obvious signs are seen in the ortho-H2O, ortho-NH3 or the almost optically thin 13CO line profiles. In addition to the outflow, our water line shows emission from a more extended NE-SW elongated PDR. Both these components originate approximately around our central position. No additional emission is detected closer to the bright rim or further into the molecular cloud where the water most likely is adsorbed onto dust grains. Close to the bright rim the temperature is most likely too high for a detection of our transition with an upper state energy of 61 K. Instead, higher-lying transitions, observable with the Herschel Space Observatory, will have their peak intensity shifted towards the bright rim (Poelman & Spaans 2006,2005). Even closer to the bright rim at a few magnitudes of ![]() ,
water is, however, photo-dissociated by the UV field.
,
water is, however, photo-dissociated by the UV field.
| |
Figure 7:
Predicted antenna temperatures of the ortho-H2O(
11,0-10,1) and para-H2O(1
1,1-00,0) transitions for the forthcoming Herschel-HIFI observations along a cut 20-100
|
| Open with DEXTER | |
The ortho-NH3 emission seems to emanate from the same high density clumps in the PDR and the outflow as water, but also shows additional emission further into the cloud where the ambient gas temperature drops to about 30 K. Compared to water in the central position, ammonia has a weaker outflow emission in the red wing although similar in the blue outflow. Close to the bright rim, where the outflow contribution to the emission is very low, the water and ammonia line profiles are almost identical, suggesting an origin in the same gas and velocity fields of the PDR. The 13CO line also shows a very similar line profile as H2O and NH3 in this position with a narrow line width of ![]() 3 km s-1.
3 km s-1.
Abundances, with respect to H2, in the PDR are estimated both with an enhanced version of the homogeneous RADEX code and with a clumpy PDR model. This model points to low mean water and ammonia abundances in the PDR of 5 ![]() 10-9 and 4
10-9 and 4 ![]() 10-9, respectively. In the high-density clumps both the average water and ammonia abundances increase to 5
10-9, respectively. In the high-density clumps both the average water and ammonia abundances increase to 5 ![]() 10-8.
To match the observed PDR antenna temperatures with Odin and SWAS, a clumpy medium is required by the model with a high molecular hydrogen density in the clumps of
10-8.
To match the observed PDR antenna temperatures with Odin and SWAS, a clumpy medium is required by the model with a high molecular hydrogen density in the clumps of ![]() 1
1 ![]() 106 cm-3. The resulting RADEX mean abundances are twice as high: 1.0
106 cm-3. The resulting RADEX mean abundances are twice as high: 1.0 ![]() 10-8 and 8
10-8 and 8 ![]() 10-9 for water and ammonia, respectively, using a molecular hydrogen density of 4
10-9 for water and ammonia, respectively, using a molecular hydrogen density of 4 ![]() 105 cm-3 and a kinetic temperature of 55 K. The differences most likely arise from the uncertainty in density, beam-filling, and volume filling of the clumps. The opacity of the narrow PDR component of the
11,0-10,1 transition is constrained by the narrow line width, and is estimated by RADEX to be
105 cm-3 and a kinetic temperature of 55 K. The differences most likely arise from the uncertainty in density, beam-filling, and volume filling of the clumps. The opacity of the narrow PDR component of the
11,0-10,1 transition is constrained by the narrow line width, and is estimated by RADEX to be ![]() 7. The PDR model also confirm a low water opacity with an unweighted mean opacity of 17 and a model range of
7. The PDR model also confirm a low water opacity with an unweighted mean opacity of 17 and a model range of ![]() 10-5-800. The mean outflow water abundance, derived from a simple two-level approximation, is higher than in the PDR by at least one order of magnitude,
10-5-800. The mean outflow water abundance, derived from a simple two-level approximation, is higher than in the PDR by at least one order of magnitude,
![]() 4
4 ![]() 10-8-4
10-8-4 ![]() 10-7.
10-7.
Predictions of antenna temperatures for observations with HIFI are given by our PDR model
of the ortho- and para-H2O
11,0-10,1 and 1
1,1-00,0 transitions for nine positions across the bright rim, and are found to peak around 70-80
![]() from the dissociation front in agreement with our observations.
from the dissociation front in agreement with our observations.
Acknowledgements
We thank Per Bergman, Per Bjerkeli, Magnus Gustavsson, Matthijs Klomp and also Steve Shore and the organizers of the A&A and EDP sciences school: Scientific Writing for Young Astronomers for helpful discussions. Generous financial support from the Research Councils and Space Agencies in Sweden, Canada, Finland and France is gratefully acknowledged.
References
- Ashby, M. L. N., Bergin, E. A., Plume, R., et al. 2000a, ApJ, 539, L119 [NASA ADS] [CrossRef]
- Ashby, M. L. N., Bergin, E. A., Plume, R., et al. 2000b, ApJ, 539, L115 [NASA ADS] [CrossRef]
- Bergin, E. A. 2003, in SFChem 2002: Chemistry as a Diagnostic of Star Formation, proceedings of a conference held August 21-23, 2002 at University of Waterloo, Waterloo, Ontario, Canada N2L 3G1, ed. C. L. Curry, & M. Fich (Ottawa, Canada: NRC Press), 63
- Bergin, E. A., & Langer, W. D. 1997, ApJ, 486, 316 [NASA ADS] [CrossRef]
- Bergin, E. A., Neufeld, D. A., & Melnick, G. J. 1998, ApJ, 499, 777 [NASA ADS] [CrossRef] (In the text)
- Bergin, E. A., Kaufman, M. J., Melnick, G. J., Snell, R. L., & Howe, J. E. 2003, ApJ, 582, 830 [NASA ADS] [CrossRef]
- Blair, G. N., Evans, II, N. J., Vanden Bout, P. A., & Peters, III, W. L. 1978, ApJ, 219, 896 [NASA ADS] [CrossRef]
- Boonman, A. M. S., & van Dishoeck, E. F. 2003, A&A, 403, 1003 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boonman, A. M. S., Doty, S. D., van Dishoeck, E. F., et al. 2003, A&A, 406, 937 [NASA ADS] [CrossRef] [EDP Sciences]
- Cernicharo, J., & Crovisier, J. 2005, Space Sci. Rev., 119, 29 [NASA ADS] [CrossRef] (In the text)
- Crampton, D., & Fisher, W. A. 1974, Publications of the Dominion Astrophysical Observatory Victoria, 14, 283 [NASA ADS] (In the text)
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] (In the text)
- Emery, R., Aannestad, P., Minchin, N., et al. 1996, A&A, 315, L285 [NASA ADS]
- Faure, A., Gorfinkiel, J. D., & Tennyson, J. 2004, MNRAS, 347, 323 [NASA ADS] [CrossRef] (In the text)
- Faure, A., Crimier, N., Ceccarelli, C., et al. 2007, A&A, 472, 1029 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Franklin, J., Snell, R. L., Kaufman, M. J., et al. 2008, ApJ, 674, 1015 [NASA ADS] [CrossRef]
- Frisk, U., Hagström, M., Ala-Laurinaho, J., et al. 2003, A&A, 402, L27 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Graf, U. U., Eckart, A., Genzel, R., et al. 1993, ApJ, 405, 249 [NASA ADS] [CrossRef] (In the text)
- Hayashi, M., & Murata, Y. 1992, PASJ, 44, 391 [NASA ADS]
- Hayashi, M., Hasegawa, T., Omodaka, T., Hayashi, S. S., & Miyawaki, R. 1987, ApJ, 312, 327 [NASA ADS] [CrossRef]
- Keene, J., Blake, G. A., & Phillips, T. G. 1983, ApJ, 271, L27 [NASA ADS] [CrossRef] (In the text)
- Larsson, B., Liseau, R., Bergman, P., et al. 2003, A&A, 402, L69 [NASA ADS] [CrossRef] [EDP Sciences]
- Larsson, B., Liseau, R., Pagani, L., et al. 2007, A&A, 466, 999 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Linke, R. A., Goldsmith, P. F., Wannier, P. G., Wilson, R. W., & Penzias, A. A. 1977, ApJ, 214, 50 [NASA ADS] [CrossRef]
- Liseau, R., Larsson, B., Brandeker, A., et al. 2003, A&A, 402, L73 [NASA ADS] [CrossRef] [EDP Sciences]
- Melnick, G. J., Ashby, M. L. N., Plume, R., et al. 2000a, ApJ, 539, L87 [NASA ADS] [CrossRef] (In the text)
- Melnick, G. J., Stauffer, J. R., Ashby, M. L. N., et al. 2000b, ApJ, 539, L77 [NASA ADS] [CrossRef] (In the text)
- Minchin, N. R., White, G. J., & Padman, R. 1993, A&A, 277, 595 [NASA ADS]
- Minchin, N. R., Ward-Thompson, D., & White, G. J. 1995, A&A, 298, 894 [NASA ADS]
- Neufeld, D. A., Lepp, S., & Melnick, G. J. 1995, ApJS, 100, 132 [NASA ADS] [CrossRef]
- Ney, E. P., & Merrill, K. M. 1980, AFGL Report, 80, 50
- Nordh, H. L., von Schéele, F., Frisk, U., et al. 2003, A&A, 402, L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Olberg, M., Frisk, U., Lecacheux, A., et al. 2003, A&A, 402, L35 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Olofsson, A. O. H., Olofsson, G., Hjalmarson, Å., et al. 2003, A&A, 402, L47 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Olofsson, A. O. H., Persson, C. M., Koning, N., et al. 2007, A&A, 476, 791 [NASA ADS] [CrossRef] [EDP Sciences]
- Persson, C. M., Olofsson, A. O. H., Koning, N., et al. 2007, A&A, 476, 807 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Plume, R., Jaffe, D. T., & Keene, J. 1994, ApJ, 425, L49 [NASA ADS] [CrossRef] (In the text)
- Poelman, D. R., & Spaans, M. 2005, A&A, 440, 559 [NASA ADS] [CrossRef] [EDP Sciences]
- Poelman, D. R., & Spaans, M. 2006, A&A, 453, 615 [NASA ADS] [CrossRef] [EDP Sciences]
- Preibisch, T., & Smith, M. D. 2002, A&A, 383, 540 [NASA ADS] [CrossRef] [EDP Sciences]
- Rouan, D., Lena, P. J., Puget, J. L., de Boer, K. S., & Wijnbergen, J. J. 1977, ApJ, 213, L35 [NASA ADS] [CrossRef]
- Sharpless, S. 1959, ApJS, 4, 257 [NASA ADS] [CrossRef]
- Snell, R. L., Goldsmith, P. F., Erickson, N. R., Mundy, L. G., & Evans, II, N. J. 1984a, ApJ, 276, 625 [NASA ADS] [CrossRef] (In the text)
- Snell, R. L., Scoville, N. Z., Sanders, D. B., & Erickson, N. R. 1984b, ApJ, 284, 176 [NASA ADS] [CrossRef] (In the text)
- Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000a, ApJ, 539, L101 [NASA ADS] [CrossRef]
- Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000b, ApJ, 539, L93 [NASA ADS] [CrossRef]
- Spaans, M. 1996, A&A, 307, 271 [NASA ADS]
- Spaans, M., & van Dishoeck, E. F. 1997, A&A, 323, 953
- Thronson, Jr., H. A., Lada, C. J., Smith, H. A., et al. 1983, ApJ, 271, 625 [NASA ADS] [CrossRef]
- Trinidad, M. A., Torrelles, J. M., Rodríguez, L. F., & Curiel, S. 2007, AJ, 134, 1870 [NASA ADS] [CrossRef] (In the text)
- Ungerechts, H., Winnewisser, G., & Walmsley, C. M. 1986, A&A, 157, 207 [NASA ADS]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Walmsley, C. M., & Ungerechts, H. 1983, A&A, 122, 164 [NASA ADS] (In the text)
- Zhou, S., Evans, II, N. J., Mundy, L. G., & Kutner, M. L. 1993, ApJ, 417, 613 [NASA ADS] [CrossRef]
- Zhou, S., Butner, H. M., Evans, II, N. J., et al. 1994, ApJ, 428, 219 [NASA ADS] [CrossRef] (In the text)
Online Material
Appendix A: RADEX - construction of a dust model
In order to relate the molecular column densities, N(x) of species x, to fractional abundances, X(x) =
![]() ,
a uniform, homogeneous sphere of diameter L =
,
a uniform, homogeneous sphere of diameter L =
![]() is assumed here. The adopted physical diameter of the PDR corresponding to an angular diameter of 120
is assumed here. The adopted physical diameter of the PDR corresponding to an angular diameter of 120
![]() (Sect. 3) at a distance of 910 pc is 0.53 pc. This is assumed to be equal to the line-of-sight depth.
(Sect. 3) at a distance of 910 pc is 0.53 pc. This is assumed to be equal to the line-of-sight depth.
The observed intensity of the continuum is used to estimate the internal radiation field sensed by
the molecules. We construct a simple model of the broad-band spectrum at submm and far-infrared wavelengths in order both to characterise the internal radiation and to estimate the total
column densities of dust and hydrogen. Thronson et al. (1983) measured the far-infrared emission of S140 and found a peak flux density of the order of 104 Jy slightly shortward of ![]() 100
100 ![]() m in a 49
m in a 49
![]() beam. Minchin et al. (1995) presented total broad-band fluxes in a
beam. Minchin et al. (1995) presented total broad-band fluxes in a
![]()
![]()
![]() box. We represent the latter results with a
two-component model of thermal emission by dust over a solid angle of
box. We represent the latter results with a
two-component model of thermal emission by dust over a solid angle of
![]()
![]() 10-7 sr. The main component has a dust temperature
10-7 sr. The main component has a dust temperature
![]() = 40 K and a long-wavelength (
= 40 K and a long-wavelength (
![]() m) form of the opacity law
m) form of the opacity law
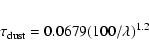
where
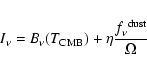
where
For the adopted interstellar extinction law and a standard gas/extinction ratio,
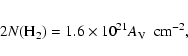
the adopted dust model implies
Appendix B: Figures and tables
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0930fig8.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg151.gif) |
Figure B.1: Odin observations of H218O in the central position. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8cm,clip]{0930fig9.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg152.gif) |
Figure B.2:
Rotation diagram of the broad component of 13CO(1-0) with the Onsala 20-m telescope, J = 2-1 and J = 3-2 from Minchin et al. (1993), and J = 5-4 with Odin, producing
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8cm,clip]{0930fg10.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg153.gif) |
Figure B.3:
Rotation diagram of the narrow component of 13CO(2-1) and J = 3-2 from Minchin et al. (1993), J = 5-4
with Odin, and J = 6-5 from Graf et al. (1993), producing
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{0930fg11.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg154.gif) |
Figure B.4: Gaussian fits to 13CO(5-4) at the central position. The widths, amplitudes and centre velocities are 3.2 km s-1 and 8.2 km s-1; 6.610 K and 0.612 K; -7.3 km s-1 and -6.8 km s-1, respectively. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[width=6.9cm,clip]{0930fg12.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg155.gif) |
Figure B.5:
Gaussian fits to the convolved (to the Odin 126
|
| Open with DEXTER | |
![\begin{figure}\includegraphics[width=6.9cm,clip]{0930fg13.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg156.gif) |
Figure B.6: Gaussian fits to H2O at the central position. The widths, amplitudes and centre velocities are 3.1 km s-1 and 8.8 km s-1; 416 mK and 213 mK; -7.1 km s-1 and -6.1 km s-1, respectively. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[width=6.9cm,clip]{0930fg14.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg157.gif) |
Figure B.7: Gaussian fits to NH3 at the central position. The widths, amplitudes and centre velocities are 3.3 km s-1 and 8.5 km s-1; 487 mK and 100 mK; -7.6 km s-1 and -6.4 km s-1, respectively. |
| Open with DEXTER | |
Table B.1: Observed transitions and their parametersa in S140 with the Odin satellite in a five point NE-SW strip.
Table B.2:
13CO Gaussian fitsa. ![]() uses a source size for the PDR (narrow component) of 120
uses a source size for the PDR (narrow component) of 120
![]()
![]() = 2, and a source size for the broad outflow component of 85
= 2, and a source size for the broad outflow component of 85
![]()
![]() = 3.
= 3.
Table B.3:
H2O Gaussian fitsa. ![]() (PDR) uses a source size of 120
(PDR) uses a source size of 120
![]()
![]() = 2, while
= 2, while ![]() (outflow) uses a source size of 85
(outflow) uses a source size of 85
![]()
![]() = 3.
= 3.
Table B.4:
NH3 Gaussian fitsa. ![]() (PDR) uses a source size of 120
(PDR) uses a source size of 120
![]()
![]() = 2, while
= 2, while ![]() (outflow) uses a source size of 85
(outflow) uses a source size of 85
![]()
![]() = 3.
= 3.
Footnotes
- ... Odin
![[*]](/icons/foot_motif.gif)
- Odin is a Swedish-led satellite project funded jointly by the Swedish National Space Board (SNSB), the Canadian Space Agency (CSA), the National Technology Agency of Finland (Tekes) and Centre National d'Etudes Spatiales (CNES). The Swedish Space Corporation was the prime contractor and also is responsible for the satellite operation.
- ... satellite
![[*]](/icons/foot_motif.gif)
- Appendices A and B are available in electronic form at http://www.aanda.org
- ... Herschel
![[*]](/icons/foot_motif.gif)
- http://herschel.esac.esa.int/
- ... RADEX
![[*]](/icons/foot_motif.gif)
- The published version will soon include these enhancements, see http://www.sron.rug.nl/~vdtak/radex/index.shtml
- ... (LAMDA)
![[*]](/icons/foot_motif.gif)
- http://www.strw.leidenuniv.nl/~moldata
- ... HITRAN
![[*]](/icons/foot_motif.gif)
- http://cfa-www.harvard.edu/hitran
All Tables
Table 1: All molecular transitions are observed with the Odin satellite except the 13CO(1-0) map which is observed with the Onsala 20-m telescope.
Table 2: Observations and model calculations for the narrow PDR component in the RADEX homogeneous modela.
Table 3: Results of the homogeneous RADEX model for the narrow PDR component: column densities and abundancesa.
Table 4: Clumpy PDR model parameters.
Table 5:
Resulting abundances with respect to
![]() for the narrow PDR components of water and ammonia from the clumpy PDR model.
for the narrow PDR components of water and ammonia from the clumpy PDR model.
Table 6:
Observed and predicted
![]() in the PDR for o-H2O(
11,0-10,1) with SWAS and Odin at the central position.
in the PDR for o-H2O(
11,0-10,1) with SWAS and Odin at the central position.
Table B.1: Observed transitions and their parametersa in S140 with the Odin satellite in a five point NE-SW strip.
Table B.2:
13CO Gaussian fitsa. ![]() uses a source size for the PDR (narrow component) of 120
uses a source size for the PDR (narrow component) of 120
![]()
![]() = 2, and a source size for the broad outflow component of 85
= 2, and a source size for the broad outflow component of 85
![]()
![]() = 3.
= 3.
Table B.3:
H2O Gaussian fitsa. ![]() (PDR) uses a source size of 120
(PDR) uses a source size of 120
![]()
![]() = 2, while
= 2, while ![]() (outflow) uses a source size of 85
(outflow) uses a source size of 85
![]()
![]() = 3.
= 3.
Table B.4:
NH3 Gaussian fitsa. ![]() (PDR) uses a source size of 120
(PDR) uses a source size of 120
![]()
![]() = 2, while
= 2, while ![]() (outflow) uses a source size of 85
(outflow) uses a source size of 85
![]()
![]() = 3.
= 3.
All Figures
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0930fig1.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg16.gif) |
Figure 1:
A CI map (492 GHz) of S140 observed with JCMT (Minchin et al. 1993).
The Odin 2
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig2.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg48.gif) |
Figure 2: Comparison of the CO(5-4) (thick magenta line) and 13CO(5-4) (thin black line) line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig3.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg49.gif) |
Figure 3: Comparison of the H2O 11,0-10,1 (thick magenta line) and 13CO(5-4) (thin black line) line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig4.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg50.gif) |
Figure 4: Comparison of the NH3 10-0 0 (thick magenta line) and 13CO(5-4) (thin black line) line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0930fig5.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg51.gif) |
Figure 5: Comparison of the H2O (thick magenta line) 11,0-10,1 and the NH3 (thin black line) 10-0 0 line profiles in a strip map from NE to SW across the PDR. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0930fig6.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg132.gif) |
Figure 6: Result of the PDR high-density model. The water intensity is shown on a logarithmic scale. The ionizing star is located on the left side of the displayed region. |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Predicted antenna temperatures of the ortho-H2O(
11,0-10,1) and para-H2O(1
1,1-00,0) transitions for the forthcoming Herschel-HIFI observations along a cut 20-100
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0930fig8.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg151.gif) |
Figure B.1: Odin observations of H218O in the central position. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8cm,clip]{0930fig9.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg152.gif) |
Figure B.2:
Rotation diagram of the broad component of 13CO(1-0) with the Onsala 20-m telescope, J = 2-1 and J = 3-2 from Minchin et al. (1993), and J = 5-4 with Odin, producing
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8cm,clip]{0930fg10.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg153.gif) |
Figure B.3:
Rotation diagram of the narrow component of 13CO(2-1) and J = 3-2 from Minchin et al. (1993), J = 5-4
with Odin, and J = 6-5 from Graf et al. (1993), producing
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{0930fg11.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg154.gif) |
Figure B.4: Gaussian fits to 13CO(5-4) at the central position. The widths, amplitudes and centre velocities are 3.2 km s-1 and 8.2 km s-1; 6.610 K and 0.612 K; -7.3 km s-1 and -6.8 km s-1, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\includegraphics[width=6.9cm,clip]{0930fg12.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg155.gif) |
Figure B.5:
Gaussian fits to the convolved (to the Odin 126
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\includegraphics[width=6.9cm,clip]{0930fg13.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg156.gif) |
Figure B.6: Gaussian fits to H2O at the central position. The widths, amplitudes and centre velocities are 3.1 km s-1 and 8.8 km s-1; 416 mK and 213 mK; -7.1 km s-1 and -6.1 km s-1, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\includegraphics[width=6.9cm,clip]{0930fg14.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa10930-08/Timg157.gif) |
Figure B.7: Gaussian fits to NH3 at the central position. The widths, amplitudes and centre velocities are 3.3 km s-1 and 8.5 km s-1; 487 mK and 100 mK; -7.6 km s-1 and -6.4 km s-1, respectively. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



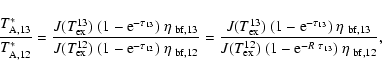
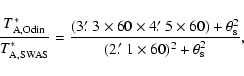
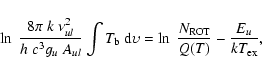
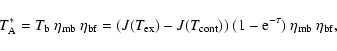
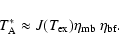
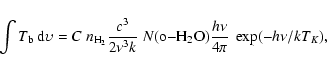
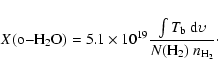
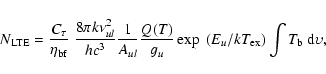
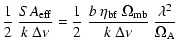
![$\displaystyle \frac{1}{2}~\frac{b~\lambda^2}{k~\Delta\nu}~ \eta_{\rm bf}~\eta_{...
...rac{b~\lambda^3}{2~k~\Delta\upsilon}~\eta_{\rm mb}~\eta_{\rm bf}
~~ ~[{\rm K}],$](/articles/aa/full_html/2009/05/aa10930-08/img126.gif)