Generation of highly energetic electrons at reconnection outflow shocks during solar flares

G. Mann; A. Warmuth; H. Aurass

doi:10.1051/0004-6361:200810099

Free Access

Issue		A&A Volume 494, Number 2, February I 2009


Page(s)		669 - 675
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361:200810099
Published online		30 October 2008

Generation of highly energetic electrons at reconnection outflow shocks during solar flares

G. Mann - A. Warmuth - H. Aurass

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 30 April 2008 / Accepted 17 October 2008

Abstract
Context. During solar flares a large amount of energy is suddenly released and partly transferred into energetic electrons. They are of special interest since a substantial part of the energy released during a flare is deposited into the energetic electrons. RHESSI observations, e.g. of the 2003 October 28 solar event, show that 10³⁶ electrons with energies >20 keV are typically produced per second during large flares. They are related to a power of about 10²² W. It is still an open question in which way so many electrons are accelerated up to high energies during a fraction of a second.
Aims. Within the framework of the magnetic reconnection scenario, jets appear in the outflow region and can establish standing fast-mode shocks if they penetrate the surrounding plasma with super-Alfvénic speed. It is our aim to show that this shock can be the source of the energetic electrons produced during flares.
Methods. The electrons are regarded as energized by shock drift acceleration. The process is necessarily treated in a fully relativistic manner. The resulting distribution function of accelerated electrons is a loss-cone one and it allows to calculate the differential electron flux, which can be compared with RHESSI.
Results. The theoretically obtained fluxes of energetic electrons agree with the observed ones as demonstrated for the 2003 October 28 solar event.

Key words: acceleration of particles - shock waves - Sun: flares - Sun: X-rays, gamma rays - Sun: radio radiation

1 Introduction

During solar flares a large amount of energy is suddenly released and transferred into a local heating of the coronal plasma, mass motions (e.g. jets), enhanced emission of electromagnetic radiation (from the radio up to the $\gamma$ -ray range), and energetic particles (e.g. electrons, protons, and heavy ions). The electrons play an important role, since they carry a substantial part of the energy released during a flare (Lin & Hudson 1971, 1976; Emslie et al. 2004). RHESSI (Lin et al. 2002) observations show that 10³⁶ electrons with energies of >20 keV are typically produced per second during large solar flares (Warmuth et al. 2007). They are related to a power of about 10²² W. It is still an open question as to which way such a huge number of electrons is accelerated up to high energies within a fraction of a second during solar flares.

Figure 1 shows the widely accepted flare scenario based on magnetic reconnection in a schematic manner. A prominence is destabilized by its photospheric footpoint motions. The resulting upward motion stretches the underlying magnetic field lines, leading to the formation of a current sheet. If the current within this sheet exceeds a critical value, the resistivity is suddenly increased by plasma wave excitation due to various instabilities (see e.g. Treumann & Baumjohann 1997). Then, magnetic reconnection can take place in the region of enhanced resistivity (called diffusion region). Because of the strong curvature of the magnetic field lines in the vicinity of the diffusion region, the slowly inflowing plasma is shooting away from the reconnection site as oppositely directed hot jets (see Fig. 1). They are embedded between a pair of slow magnetosonic shocks, which heat the plasma. If the speed of this outflow jet is super-Alfvénic, a fast magnetosonic shock, also called termination shock (TS), can be established due to the deceleration of the jet. Such a deceleration can happen because of either an underlying post flare loop or a spread of the outflow region, e.g. by the increasing distance of the slow mode shocks (see Fig. 1). The appearance of TSs is predicted in the numerical simulations by Forbes (1986) and Shibata et al. (1995). Aurass et al. (2002) and Aurass & Mann (2004) report on the signatures of such shocks in the solar radio burst radiation.

$\begin{figure} \par\includegraphics[width=8.6cm,clip]{0099fig1.eps} \end{figure}$	Figure 1: Sketch of the reconnection process in the solar corona as described in Sect. 1. The termination shock is established by the outflow jet, if it comes from the reconnection site and, subsequently, penetrates into the surrounding plasma of the corona. The grey shaded areas with the black arrows show the reconnection outflow jets.
Open with DEXTER

One possible mechanism of electron acceleration within the flare scenario is the direct acceleration at the large scale DC electric field in the diffusion region (e.g. Holman 1985; Benz 1987; Litvinenko 2000). Since the diffusion region is spatially very small, this process can explain the acceleration of a single electron up to high energies, but it is not able to provide a high production rate of energetic electrons (typically 10³⁶ s^-1) as required by the observations. Therefore, Tsuneta & Naito (1998) proposed that the TS could be the source of energetic electrons, since the TS has a much greater space than the diffusion region. That is the reason, why the electron acceleration at the TS is studied in a quantitative manner in Sect. 2. In Sect. 3, the theoretically obtained results are compared with RHESSI observations of the solar event on October 28, 2003. In the paper by Warmuth et al. (2009) (henceforth called Paper II) the outcome of this model, i.e. the differential electron fluxes, are compared with 1053 electron spectra derived from the RHESSI photon spectra of 18 flares.

2 Relativistic shock drift acceleration

It is well-known that fast magnetsonic shocks are accompanied by a compression of both the density and the magnetic field (see e.g. Priest 1982). Hence, they represent moving magnetic mirrors at which charged particles can be reflected and accelerated. That is usually called shock drift acceleration (Holman & Pesses 1983; Leroy & Mangeney 1984; Wu 1984). During flares nonthermal hard X-ray fluxes above 100 keV are observed e.g. by RHESSI (Lin et al. 2002) indicating the production of electrons with energies >100 keV. Since it is assumed here that the energetic electrons are generated at the TS, the shock drift acceleration must necessarily be treated in a fully relativistic manner as done by Mann et al. (2006). Here, the relativistic shock drift acceleration is used to determine the resulting fluxes of energetic electrons. Note that these fluxes can directly be compared with RHESSI observations.

Following the treatment of shock drift accleration in the non-relativistic approach (Ball & Melrose 2001; Mann & Klassen 2003), the vector of the particle velocity is transformed into the de Hoffmann-Teller frame, which is defined by removing the motional electric field. Note that the shock is also at rest in this frame. Then, the reflection process can be performed under the conservation of energy and magnetic moment of the particle. Note that all these transformations must necessarily be Lorentzian ones. As result, one obtains a relationship between the velocity components parallel (i.e. $\beta_{\parallel}$ ) and perpendicular (i.e. $\beta_{\perp}$ ) to the upstream magnetic field before (i) and after (r) the reflection

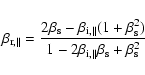$\begin{displaymath}\beta_{{\rm r},\parallel} = \frac{2\beta_{\rm s} - \beta_{{\r... ...- 2\beta_{{\rm i},\parallel}\beta_{\rm s} + \beta_{\rm s}^{2}} \end{displaymath}$

(1)

and

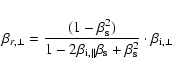$\begin{displaymath}\beta_{r,\perp} = \frac{(1-\beta_{\rm s}^{2})} {1 - 2\beta_{... ...eta_{\rm s} + \beta_{\rm s}^{2}} \cdot \beta_{{\rm i},\perp} \end{displaymath}$

(2)

(Mann et al. 2006), respectively. $\beta_{\rm s} = v_{\rm s} \sec\theta/c$ denotes the shock speed in the de Hoffmann-Teller frame, i.e. the shock speed projected to the magnetic field line. $v_{\rm s}$ is the shock speed in the laboratory frame. Note, that all velocities are normalized to the velocity of light c, here. $\theta$ is the angle between the shock normal and the upstream magnetic field.

Additionally, the reflection conditions

$\begin{displaymath}\beta_{{\rm i},\parallel} \leq \beta_{\rm s} \end{displaymath}$

(3)

and

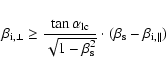$\begin{displaymath}\beta_{{\rm i},\perp} \geq \frac{\tan\alpha_{\rm lc}}{\sqrt{1... ...\rm s}^{2}}} \cdot (\beta_{\rm s}-\beta_{{\rm i},\parallel}) \end{displaymath}$

(4)

must be fulfilled by the initial particles in order to be accelerated. The loss-cone angle $\alpha _{\rm lc}$ is defined by $\alpha_{\rm lc} = \arcsin[(B_{\rm up}/B_{\rm down})^{1/2}]$ . $B_{\rm up}$ and $B_{\rm down}$ denote the magnetic field in the up- and downstream region, respectively.

The acceleration process actually represents a transformation in the $\beta_{\perp}$ - $\beta_{\parallel}$ plane as illustrated in Fig. 2

$\begin{figure} \par\includegraphics[width=5.8cm,clip]{0099fig2.eps} \end{figure}$	Figure 2: Illustration of the shock drift acceleration in the $\beta _{\perp }-\beta _{\parallel }$ plane for a shock wave with $\beta _{\rm s} = 0.8$ and $\alpha _{\rm lc} = 45^{\circ }$ .
Open with DEXTER

for a shock wave with $\beta _{\rm s} = 0.8$ and $B_{\rm down}/B_{\rm up} = 2$ , i.e. $\alpha _{\rm lc} = 45^{\circ }$ . The initial particles located in the grey area left of the dashed line are transformed into the dark one to the right of it due to shock drift acceleration as indicated by the arrow in Fig. 2. This transformation leads to both a gain of energy of each individual particle and an enhancement of the paricle density at high energies in the phase space.

As seen in Fig. 2, the resulting distribution function of the accelerated electrons is a shifted loss-cone distribution (see Leroy & Mangeney 1984; and Wu 1984, for the non-relativisitc case). If f₀ is the distribution function of the initial state in the upstream region, then these particles with the distribution function

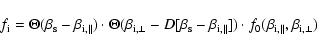$\begin{displaymath}f_{\rm i} = \Theta(\beta_{\rm s}-\beta_{{\rm i},\parallel}) \... ...\cdot f_{0}(\beta_{{\rm i},\parallel}, \beta_{{\rm i},\perp}) \end{displaymath}$

(5)

( $D = (\tan \alpha_{\rm lc})/(1-\beta_{\rm s}^{2})^{1/2}$ ) are finally accelerated. Here, $\Theta(x)$ denotes the usual step-function, i.e. $\Theta = 1$ and $\Theta = 0$ for $x \geq 0$ and $x \leq 0$ , respectively. Now, a Maxwellian distribution

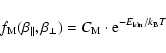$\begin{displaymath}f_{\rm M}(\beta_{\parallel}, \beta_{\perp}) = C_{\rm M} \cdot {\rm e}^{-E_{\rm kin}/k_{\rm B}T} \end{displaymath}$

(6)

( $k_{\rm B}$ , Boltzmann's constant; T, temperature) is assumed to be the initial one. Here, the kinetic energy $E_{\rm kin}$ is defined by

$\begin{displaymath}E_{\rm kin} = m_{\rm e}c^{2} \left [ \frac{1}{\sqrt{1-\beta^{2}}} -1 \right ] \end{displaymath}$

(7)

with the electron mass $m_{\rm e}$ and $\beta^{2} = \beta_{\parallel}^{2} + \beta_{\perp}^{2}$ . If the distribution function is normalized to unity in the velocity space, the constant $C_{\rm M}$ is fixed to

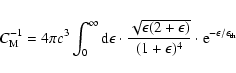$\begin{displaymath}C_{\rm M}^{-1} = 4\pi c^{3} \int_{0}^{\infty} {\rm d}\epsilon... ...1+\epsilon)^{4}} \cdot {\rm e}^{-\epsilon /\epsilon_{\rm th}} \end{displaymath}$

(8)

with $\epsilon = E_{\rm kin}/m_{\rm e}c^{2}$ and $\epsilon_{\rm th} = k_{\rm B}T/m_{\rm e}c^{2}$ . Inserting the distribution function (6) into Eq. (5), the distribution function of accelerated electrons is found to be

$\displaystyle f_{\rm acc}$	=	$\displaystyle C_{\rm M} \cdot \Theta(\beta_{\parallel}-\beta_{\rm s}) \cdot \Theta(\beta_{\perp}-D[\beta_{\rm s}-\beta_{\parallel}])$
		$\displaystyle \times \exp\left [ \frac{(-1)}{\epsilon_{\rm th}} \cdot \left ( \... ..._{\rm s}^{2}} {(1-\beta_{\rm s}^{2})(1-\beta^{2})^{1/2}} - 1 \right ) \right ].$	(9)

Here, Eqs. (1) and (2) were inverted with respect to $\beta_{{\rm i},\parallel}$ and $\beta_{{\rm i},\perp}$ and subsequently inserted into Eqs. (5) and (6).

In the magnetized plasma of the corona, the electrons predominantly move along the magnetic field, since their gyroradius is much smaller than the typical spatial scale length in the corona. Hence, the magnetic field aligned flux of electrons is of special interest. It is defined by

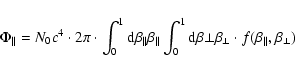$\begin{displaymath}\Phi_{\parallel} = N_{0}c^{4} \cdot 2\pi \cdot \int_{0}^{1}... ...erp} \beta_{\perp} \cdot f(\beta_{\parallel}, \beta_{\perp}) \end{displaymath}$

(10)

with N₀ as the total electron number density. Then, the differential flux is obtained to be

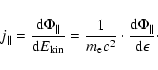$\begin{displaymath}j_{\parallel} = \frac{{\rm d}\Phi_{\parallel}}{{\rm d}E_{\rm ... ...2}} \cdot \frac{{\rm d}\Phi_{\parallel}}{{\rm d}\epsilon}\cdot \end{displaymath}$

(11)

Inserting the distribution function (9) into Eq. (10), introducing polar coordinates according to

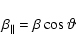$\begin{displaymath}\beta_{\parallel} = \beta \cos \vartheta \end{displaymath}$

(12)

$\begin{displaymath}\beta_{\perp} = \beta \sin \vartheta \end{displaymath}$

(13)

integrating over the pitch angle $\vartheta$ , introducing the substitution $\beta = [\epsilon (2+\epsilon)]^{1/2}/(1+\epsilon)$ (see Eq. (7)) and, finally, performing the derivative with respect to $\epsilon$ (see Eq. (11)), the differential flux of the accelerated electrons is found to be

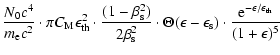$\displaystyle j_{{\rm acc},\parallel} =$	$\displaystyle \frac{N_0 c^{4}}{m_{\rm e} c^{2}} \cdot \pi C_{\rm M} \epsilon_{\... ..._{\rm s}) \cdot \frac{{\rm e}^{-\epsilon /\epsilon_{\rm th}}}{(1+\epsilon)^{5}}$
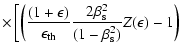	$\displaystyle \times \left[ \left( \frac{(1+\epsilon)}{\epsilon_{\rm th}} \frac{2\beta_{\rm s}^{2}}{(1-\beta_{\rm s}^{2})} Z(\epsilon) - 1 \right) \right.$
	$\displaystyle \cdot \exp{ \left( \frac{(1+\epsilon)}{\epsilon_{\rm th}} \frac{2\beta_{\rm s}^{2}} {(1-\beta_{\rm s}^{2})} [Z(\epsilon) - 1] \right)}$
	$\displaystyle \left. - \frac{(1+\epsilon)}{\epsilon_{\rm th}} \frac{2\beta_{\rm s}^{2}} {(1-\beta_{\rm s}^{2})} + 1 \right]$	(14)

with

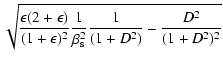$\displaystyle Z(\epsilon)$	=	$\displaystyle \sqrt{\frac{\epsilon (2+\epsilon)}{(1+\epsilon)^{2}} \frac{1}{\beta_{\rm s}^{2}} \frac{1}{(1+D^{2})} - \frac{D^{2}}{(1+D^{2})^{2}}}$
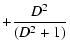		$\displaystyle + \frac{D^{2}}{(D^{2}+1)}$	(15)

and $\epsilon_{\rm s} = (1-\beta_{\rm s}^{2})^{-1/2} - 1$ . $j_{{\rm acc},\parallel}$ is a function of the normalized energy $\epsilon$ and depends on the input parameters, i.e. the shock speed $v_{\rm s}$ , the jump $B_{\rm down}/B_{\rm up}$ of the magnetic field across the shock, and the angle $\theta$ as well as the total electron number density N₀ and temperature T in the upstream region. Note that these parameters are not independent on each other but must agree with the Rankine-Hugoniot relationships (see e.g. Priest 1982). This analytically found expression (Eq. (14)) is numerically illustrated in Fig. 3 for a temperature $T = 10 \times 10^{6}$ K and a shock speed $v_{\rm s} = 1500$ km s^-1(i.e. $\beta_{\rm s} = 0.005$ ) and several angles $\theta$ . The jump of the magnetic field $B_{\rm down}/B_{\rm up}$ is taken to be 2 resulting into $\alpha _{\rm lc} = 45^{\circ }$ .

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{0099fig3.eps} \end{figure}$

Figure 3:

The differential magnetic field aligned flux (Eq. (14)) normalized to N₀ is obtained for electrons accelerated by shock drift acceleration with a shock speed of 1500 km s^-1 for several angles $\theta$ . The loss-cone angle $\alpha _{\rm lc}$ is taken to be 45 $^{\circ }$ . The corresponding normalized flux $j_{{\rm M},\parallel }/N_{0}$ of a pure Maxwellian distribution (Eq. (16)) is presented by the dashed line. A temperature of 10 $\times$ 10⁶ K is adopted in all cases.

Open with DEXTER

Figure 3 shows that the maximum of the differential flux is shifted towards higher energies with increasing $\theta$ . On the other hand, the magnitude of the maximum of the differential flux is decreasing with increasing $\theta$ . For comparison, the differential magnetic field aligned flux of a pure Maxwellian population (see Eq. (6)) is found to be

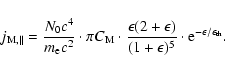$\begin{displaymath}j_{{\rm M},\parallel} = \frac{N_{0}c^{4}}{m_{\rm e}c^{2}} \cd... ...1+\epsilon)^{5}} \cdot {\rm e}^{-\epsilon/\epsilon_{\rm th}}. \end{displaymath}$

(16)

It is plotted for the same temperature, i.e. $T = 10 \times 10^{6}$ K, as the dashed line in Fig. 3.

In-situ spacecraft measurements (Lin et al. 1996) in the quiet solar wind have revealed that electron distribution functions are usually not Maxwellian but show an enhanced supra-thermal tail. Such a distribution can be described in terms of a kappa distribution defined by

$\begin{displaymath}f_{\kappa}(\beta_{\parallel},\beta_{\perp}) = C_{\kappa} \cdo... ... + \frac{E_{\rm kin}}{\kappa E_{\kappa}} \right ]^{-\kappa -1} \end{displaymath}$

(17)

(see e.g. Maksimovich et al. 1997; Pierrard et al. 1999). In the limit $\kappa \rightarrow \infty$ , it transfers into a Maxwellian one. The constant $C_{\kappa}$ is fixed by the normalization of the distribution function to unity in the velocity space.

$\begin{displaymath}C_{\kappa}^{-1} = 4\pi c^{3} \int_{0}^{\infty} {\rm d}\epsilo... ...\epsilon}{\kappa \epsilon_{\kappa}} \right ]^{-\kappa -1}\cdot \end{displaymath}$

(18)

The same procedure as previously described for the Maxwellian distribution is done for the kappa distribution for completeness. Inserting it Eq. (17) into Eq. (5), one gets

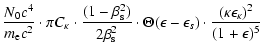$\displaystyle j_{{\rm acc},\parallel}$	=	$\displaystyle \frac{N_0 c^{4}}{m_{\rm e} c^{2}} \cdot \pi C_{\kappa} \cdot \fra... ...silon-\epsilon_s) \cdot \frac{(\kappa \epsilon_{\kappa})^{2}}{(1+\epsilon)^{5}}$
	$\textstyle \times$	$\displaystyle \left[ \frac{-1}{(\kappa -1) \cdot \left[1 + \frac{1}{\kappa \epsilon_{\kappa}} B(\epsilon) \right]^{(\kappa -1)}} \right.$
		$\displaystyle + \frac{A(\epsilon)}{\kappa \cdot \left [1 + \frac{1}{\kappa \epsilon_{\kappa}} B(\epsilon) \right ]^{\kappa}}$
		$\displaystyle \left. + \frac{1}{(\kappa-1) \cdot \left[ 1 + \frac{\epsilon}{\ka... ...t \left[ 1 + \frac{\epsilon}{\kappa \epsilon_{\kappa}}\right]^{\kappa}} \right]$	(19)

with

$\begin{displaymath}A(\epsilon) = 1 + \frac{1}{\kappa \epsilon_{\kappa}} \cdot \... ...{\rm s}^{2})(1+\epsilon)}{(1-\beta_{\rm s}^{2})} - 1 \right ] \end{displaymath}$

(20)

and

$\begin{displaymath}B(\epsilon) = \epsilon-\frac{2\beta_{\rm s}^{2}}{(1-\beta_{\rm s}^{2})} (1+\epsilon) [Z(\epsilon)-1] \end{displaymath}$

(21)

for the differential flux of accelerated electrons in the case of an initial kappa distribution. The comparison of the theoretically obtained fluxes of accelerated electrons with the observed ones in dependence from the parameter $\kappa$ is dicussed in Paper II.

Figure 3 demonstrates that shock drift acceleration at the TS is able to produce highly energetic electrons for circumstances typically found in the flare region. The efficiency of shock drift acceleration is crucially depending on the angle $\theta$ , i.e. the angle between the shock normal to the upstream magnetic field. In the vicinity of the reconnection region, the magnetic field lines are flowing away from the diffusion region toward the TS as sketched in Fig. 4. Thus, the angle $\theta$ is varying across the TS due to the curvature of the magnetic field lines.

$\begin{figure} \par\includegraphics[width=4cm,clip]{0099fig4.eps} \end{figure}$	Figure 4: Sketch of the magnetic field geometry at the TS. The magnetic field lines reconnected in the diffusion region (DR) are propagating away from it through the TS. The magnetic field line takes a local angle $\theta$ with the normal of the TS, if it is crossing the TS at x.
Open with DEXTER

Approximating such a magnetic field line by a circle with the radius R, the angle $\theta$ at the point x is found to be

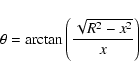$\begin{displaymath}\theta = \arctan \left ( \frac{\sqrt{R^{2}-x^{2}}}{x} \right ) \end{displaymath}$

(22)

x gives the distance of the crossing point of the magnetic field line from the center of the TS. In reality, the angle $\theta$ is varying between a minimum $\theta_{\rm min}$ and a maximum $\theta_{\rm max}$ . Assuming that the angle $\theta$ has the value $\theta_{\rm min}$ at the outer edge of the TS, which has a half width d, the radius of this assumed circle can be calculated by $R = d \cdot \sec (\theta_{\rm min})$ . Then, the variation of the angle $\theta$ on the TS is completely given by Eq. (22). The value of the angle $\theta_{\rm max}$ is determined by the requirement $\beta_{\rm s} < 1$ , i.e. the shock speed in the de Hoffmann-Teller frame may not exceed the velocity of light, resulting in $\theta_{\rm max} = \arccos (v_{\rm s}/c)$ .

3 Discussion

In the previous section, it was demonstrated, that shock drift acceleration is able to accelerate electrons up to high energies for circumstances typically found in the flare region. The electrons are accelerated at the shock and reflected back towards the upstream region. They get a substantial gain in the velocity parallel to the magnetic field, whereas the pitch angle is decreasing. Due to the curvature of the magnetic field lines in the upstream region of the TS, the accelerated electrons encounter the TS once again. But now, a substantial part of them do not fulfill the reflection condition (4) because of their low pitch angle. Hence, they transmit into the downstream region and travel along the magnetic field line towards the denser chromosphere, where they emit hard X-ray radiation via bremsstrahlung (Brown 1971).

In the present section, the theoretically obtained results from Sect. 2 are compared with observations. The solar event on October 28, 2003 is chosen for that, since it is one of the best observed flares.

In October/November 2003 several flares of X-class importance occured. Especially, the event on October 28, 2003 showed a strong enhancement of the hard X- and $\gamma$ -ray radiation (see Fig. 5) as observed by the SPI spectrometer (consisting of the ACS anti-coincidence system and a Ge detector matrix) aboard the INTEGRAL spacecraft (Gros et al. 2004; Kiener et al. 2006).

$\begin{figure} \par\includegraphics[width=8cm,clip]{0099fig5.eps} \end{figure}$

Figure 5:

Hard X- and $\gamma$ -ray radiation ( top) and radio radiation ( bottom) during the impulsive phase 11:00-11:10 UT of the solar event on October 28, 2003. Top panel: Photon count rates (in arbitrary units) of the ACS/SPI (blue: for energies >150 kev) and the Ge matrix of SPI (red: 7.5-10 MeV) aboard INTEGRAL. Bottom panel: dynamic radio spectrum in the range 200-400 MHz as measured by the radio spectralpolarimeter (Mann et al. 1992) of the Astrophysical Institute Potsdam. The radio signatures of the TS are marked by arrows.

Open with DEXTER

During the time interval between 11:02:30 and 11:04:30 UT, the dynamic radio spectrum (see bottom panel of Fig. 5) shows a roughly non-drifting lane of enhanced radio emission at $\approx$ 300 MHz. Evaluating the dynamic radio spectrum in the spectral range 40-800 MHz, it is identified to be the harmonic (H) emission, i.e. the fundamental (F) one appears at about 150 MHz. Since this lane shows the typical components of type II radio bursts, i.e. the (here nearly non-drifting) ``backbone'' and the ``herringbones'' shooting away from the backbone towards both higher and lower frequencies (see e.g. Nelson & Melrose 1985; and Mann 1995, for reviews), it is regarded to be the radio signature of the TS. Note that Aurass et al. (2002) and Aurass & Mann (2004) have already argued that such spectral features can be considered as the radio signature of the TS. Since the enhancement of the hard X- and $\gamma$ -ray fluxes simultaneously appears with the occurrence of the radio signatures of the TS in this special event, Mann et al. (2006) argued that the energetic electrons needed for the hard X- and $\gamma$ -ray radiation are generated at the TS.

Employing the Nançay radio-heliographic (Kerdraon & Delouis 1996) data at 327 MHz, the source of the TS is located $\approx$ 250 Mm away from the hard X-ray sources as seen in Fig. 6.

$\begin{figure} \par\includegraphics[width=8cm,clip]{0099fig6.eps} \end{figure}$

Figure 6:

The nonthermal (blue) and thermal (red) hard X-ray sources as observed by RHESSI and of the TS radio source are overplotted on a composite EUV image from SOHO/EIT and TRACE for the event on Ocotber 28, 2003. All outer contours represent the 50% level. The location of the TS is obtained from the Nançay radio heliographic data at 327 MHz. The black line represents the magnetic field lines connecting the hard X-ray footpoints. The white lines illustrate the magnetic field lines connecting the reconnection site, which is thought to be right outside the figure. Note that the magnetic field lines are drawn for illustration and not the result of any magnetic field extrapolation.

Open with DEXTER

The radio source of the TS (Fig. 6) has an area of $3 \times 10^{16}$ m².

Figure 7 shows the hard X-ray photon spectrum of the event of discussion as obserevd by RHESSI. The spectrum has been corrected for photospheric albedo (see Kontar et al. 2006) and pulse pile-up (see Smith et al. 2002) using the OSPEX software of the standard RHESSI analysis tools. Pile-up was treated with the new PILEUP_MOD function in OSPEX, which should give more accurate results than the old correction method. Note that the spectrum (see Fig. 7) has been accumulated from the front segment of detector 1 of RHESSI only, since PILEUP_MOD works only for single detectors. The photon spectrum reveals a thermal and nonthermal component. The nonthermal component is strongly pronounced above 28 keV. The nonthermal hard X-ray radiation is assumed to be emitted by thick-target bremsstrahlung (Brown 1971). Then, the photon spectrum can be converted into a differential injected nonthermal electron flux, i.e. electrons per second per keV, by means of a forward-fitting method (Holman et al. 2003). Performing this procedure, a total flux of $F_{\rm e} = 1.6 \times 10^{36}$ electrons with energies >28 keV per second is obtained. It is related to a power of $P_{\rm e} = 1.5 \times 10^{22}$ W (Warmuth et al. 2007). Both values are to be compared with the theory.

For comparing the theoretically obtained results with the observations, the basic plasma parameters of the flare region must be given. Since the TS appears at 300 MHz for the harmonic emission at the solar event on October 28, 2003, an electron number density $N_{\rm e} = 2.8 \times 10^{14}$ m^-3 has to be used for this quantity in the upstream region of the TS. According to the twofold Newkirk (1962) density model for the corona, such a density level is located 160 Mm above the photosphere. There, a magnetic field of 4.6 G is expected according to the model by Dulk & McLean (1978) leading to an Alfvén speed of 557 km s^-1. In Paper II, the dependence of the theoretically obtained fluxes of accelerated electrons from the plasma parameters in the upstream region and the shock (TS) parameters are investigated in detail and compared with electron spectra derived from X-ray spectra measured by RHESSI. The study shows that the theoretical fluxes agree with the observed ones only if high temperatures of the upstream plasma of about > $20 \times 10^{6}$ K is assumed. Of course, the coronal plasma inflowing towards the reconnection site with typical temperatures of 1-2 $~\times ~10^{6}$ K is strongly heated at the slow shocks (see e.g. Cargill and Priest 1982), so that the outflow jets are hot. Thus, a temperature of $40 \times 10^{6}$ K seems to be appropriate to assume in the upstream region of the TS (see the discussion in Paper II). That results in a thermal electron speed of 24 600 km s^-1. A jump of the density across the TS of about 2 is deduced from the dynamic radio spectrum of the TS (see Fig. 5 bottom). Here, this jump is assumed to be associated with the bandwidth of the radio signature of the TS in the dynamic radio spectrum (Mann et al. 1995; Vrsnak et al. 2001). Then, a jump of the magnetic field $B_{\rm down}/B_{\rm up} = 2$ and an Alfvén-Mach number $M_{\rm A} = 3.5$ are found by means of the Rankine-Hugoniot relationships (Priest 1982). It corresponds to a real shock speed $v_{\rm s} = 1950$ km s^-1.

$\begin{figure} \par\includegraphics[width=9cm,clip]{0099fig7.eps} \end{figure}$	Figure 7: The hard X-ray photon spectrum as recorded by RHESSI during the time period 11:06:40-11:07:40 UT on October 28, 2003. The dashed and dotted dashed line represent the thermal and nonthermal component of the X-ray radiation, respectively.
Open with DEXTER

The electron number density $N_{\rm e}$ , the temperature T, and the magnetic field $B_{\rm up}$ in the upstream region as well as the shock speed $v_{\rm s}$ , the loss-cone angle $\alpha _{\rm lc}$ , the shock area $A_{\rm s}$ , and the angle $\theta$ are the input parameters for calculating the differential flux according to Eq. (14). Figure 3 reveals that the magnetic field aligned flux of accelerated electrons is crucially depending on the angle $\theta$ . As already discussed in Sect. 2, the value of the angle $\theta$ is varying across the TS. Therefore, the resulted flux is finally averaged over the angles $\theta$ according to Eq. (22), where $\theta$ is varying between 85.3 $^{\circ }$ and 89.6 $^{\circ }$ . The upper value is found as discussed in Sect. 2 i.e. $\theta_{\rm max} = \arccos (v_{\rm s}/c)$ . The lower value is chosen in the following way: the TS is recognized by its radio radiation. That implies the presence of supra-thermal electrons for exciting Langmuir waves (see e.g. Melrose 1985), i.e. their velocity should exceed the thermal speed $v_{\rm the}$ . Such electrons are produced by shock drift acceleration if the angle $\theta$ is greater than $\theta_{\rm min} = \arccos(v_{\rm the}/c) = 85.3^{\circ}$ . In result, the so-obtained flux is drawn in Fig. 8.

$\begin{figure} \par\includegraphics[width=9cm,clip]{0099fig8.eps} \end{figure}$	Figure 8: The magnetic field aligned differential flux of accelerated electrons (full line) according to Eq. (14) with the parameters derived from the solar event on October 28, 2003. The values of these parameters are given in Sect. 3. The dashed line represents the corresponding flux (see Eq. (16)) of a pure Maxwellian population for the same temperature of 40 $\times$ 10⁶ K for comparison.
Open with DEXTER

It shows an enhanced flux of electrons beyond 10 keV in comparison to the pure Maxwellian population. It provides a production rate $F_{\rm e} = 7.4 \times 10^{35}$ s^-1 and a related power $P_{\rm e} = 4.5~ \times ~10^{21}$ W for electrons with energies >28 keV. Both values roughly agree with the observed ones, i.e. $F_{\rm e} = 1.6~ \times~ 10^{36}$ s^-1 and $P_{\rm e} = 1.5 \times 10^{22}$ W (see above and Warmuth et al. 2007). Note that a close match between the modelled and observed values can be achieved by a modest increase of the density compression across the shock from 2 to 2.5. The local power law index derived from the derivative at a given energy is gradually increasing from 1 to 5 in the range 20-100 keV, but it is sharply increasing for energies >100 keV. The spectra of flare electrons derived from the RHESSI photon spectra by means of a forward-fitting method (Holman et al. 2003) show a broken power law. In result, the theoretically obtained flux of energetic electrons provides a production rate of energetic electrons and the related power in them in agreement with the observations. But the shape of this flux (see Fig. 8) doesn't show a broken power law but a steeper decay beyond 100 keV than the observations.

Note, that the dependence of the differential flux of energetic electrons generated by shock drift acceleration and the related production rate $F_{\rm e}$ and power $P_{\rm e}$ on the shock parameter is studied in detail in Paper II.

Since the total flux of the electrons coming towards the TS is calculated to be $F_{\rm in} = N_{\rm e}A_{\rm s}v_{\rm s} = 1.7~\times 10^{37}$ s^-1, 4% of the inflowing electrons are accelerated up to energies >28 keV by the proposed mechanism. Assuming a barometric height scale $l_{\rm sbar} = 70$ Mm, which corresponds to a temperature of $1.4 \times 10^{6}$ K, the volume $A_{\rm s} \cdot l_{\rm bar} = 2.1 \times 10^{24}$ m^-3above the TS would completely be evacuated after 35 s, if the electron number density is $2.8 \times 10^{14}$ m^-3. But, in the framework of the discussed flare scenario (see Fig. 1) plasma is continuously supplied by the lateral inflow through the slow shocks. Since these slow shocks have a great spatial extension, enough electrons are supplied into the outflow region, in order to be finally accelerated at the TS. In the upstream region of the TS, the inflowing energy consists of the kinetic energy of the jet, the thermal energy of the electrons and protons, and the magnetic energy. Adopting the parameters given above, the following values $w_{\rm kin} = N_{\rm e}m_{\rm p}v_{\rm s}^{2}/2 = 1.0$ J m^-3(m_p, proton mass), $w_{\rm th} = 3N_{\rm e}k_{\rm B}T =0.5$ J m^-3, and $w_{\rm mag} = B^{2}/8\pi = 0.01$ J m^-3 are obtained for the densities of the kinetic, thermal, and magnetic energy of the upstream flow, respectively. Note that the kinetic energy of the reconnection outflow jet is the dominant one in comparison to the other ones. Then, the total inflowing power is found to be $P_{\rm in} = w_{\rm tot}A_{\rm s}v_{\rm s} = 8.83~ \times ~10^{22}$ W with $w_{\rm tot} = w_{\rm kin}+w_{\rm therm}+w_{\rm mag}$ . In result, 5% of the total energy inflowing towards the TS is finally transfered into the energetic electrons with energies >28 keV, if the electrons are acclerated at the TS.

4 Summary

During solar flares a large amount of electromagnetic radiation from the radio up to the hard X- and $\gamma$ -ray range is emitted from the corona. In particular, the huge solar event on October 28, 2003 was accompanied by a strongly enhanced emission of hard X- and $\gamma$ -ray radiation (up to $\sim$ 10 MeV) during the impulsive phase. These observational facts indicate the generation of highly energetic electrons during this event. These electrons are not only responsible for the nonthermal radio and X-ray radiation but also carry a substantial part of the energy released during flars (Lin & Hudson 1971; Emslie 2004). That is the reason, why the acceleration of electrons up to high energies within a fraction of seconds is one of the open questions in solar physics.

Magnetic reconnection is one possible process for explaining flares in the solar corona. In the framework of this scenario (see Fig. 1), a jet of hot plasma streams away from the reconnection site into the surrounding plasma. If its speed is super-Alfvénic, a shock wave (TS) can be established in the outflow region. For the solar event on October 28, 2003 radio data revealed signatures of such a shock only during the impulsive phase. The simultaneous appearance of enhanced photon fluxes up to 10 MeV and the radio signatures of the TS (see Sect. 2) suggests that the TS is the source of those electrons, which are needed to generate hard X- and $\gamma$ -ray radiation.

In the present paper, the highly energetic electrons are considered to be generated by shock drift acceleration at the TS. That requires a fully relativistic treatment as done by Mann et al. (2006) and briefly summarized in Sect. 2. The resulting distribution function of accelerated electrons has the form of a shifted loss-cone distribution (see. Eq. (9)). Taking such a distribution function the resulting magnetic field aligned differential flux can analytically be given by Eq. (14). Adopting the parameters of the flare plasma as observed for the event on October 28, 2003, the theoretically obtained flux (see Eq. (14)) provides a production rate $F_{\rm e} = 7.40 \times 10^{35}$ electrons with energies >28 keV per second and is related to a power $P_{\rm e} = 4.5 \times 10^{21}$ W. These values approximately agree with the observations (see Sect. 3). As discussed above (see Sect. 3), a minor, but not negligible, part (i.e. about 5%) of the inflowing energy is tranfered into the energetic electrons by this mechanism. That was originally presumed by Lin & Hudson (1971, 1976) and later on confirmed by Emslie et al. (2004).

Note, that the scenario as illustrated in Fig. 1 was found in the observations of the solar event on October 28, 2003, as demonstrated in Fig. 6. In Paper II, the proposed mechanism was applied and compared with 1053 electron spectra derived from the X-ray spectra as measured by RHESSI during 18 individual flares.

In summary, the proposed model is able to explain the observation at least up to an energy of 100 keV. All these results support the presented mechanism, which was originally proposed by Tsuneta & Naito (1998) and quantitatively treated in the presented paper.

Acknowledgements

The authors thank G. Emslie, G. Holman, H. Hudson, R. P. Lin, and L. Vlahos for stimulating discussions. We gratefully acknowledge the use of the SOHO-MDI, RHESSI, and Nançay Multifrequency Radioheliograph data. Furthermore, we thank J. Kiener for the provision of INTEGRAL data. The work was financially supported by the German space agency Deutsches Zentrum für Luft- und Raumfahrt (DLR), under grant No. 50 QL 0001.

References

Aurass, H., & Mann, G. 2004, ApJ, 615, 526 [NASA ADS] [CrossRef] (In the text)
Aurass, H., Vrsnak, B., & Mann, G. 2002, A&A, 384, 273 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Ball, L., & Melrose, D. B. 2001, Publ. Astron. Soc. Austr., 18, 361 [NASA ADS] [CrossRef] (In the text)
Benz, A. O. 1987, Sol. Phys., 111, 1 [NASA ADS] [CrossRef] (In the text)
Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] (In the text)
Cargill, P. J., & Priest, E. R. 1982, Sol. Phys., 76, 357 [NASA ADS]
Dulk, G. A., & McLean, D. J. 1978, Sol. Phys., 57, 235 (In the text)
Emslie, A. G., Kucharek, H., Dennis, B. R., et al. 2004, J. Geophys. Res., 109, 10104 (In the text)
Forbes, T. G. 1986, ApJ 305, 553 [NASA ADS] [CrossRef] (In the text)
Gros, M., et al. 2004, in Proc. 5th INTEGRAL Workshop, ed. V. Schönfelder, et al., ESA-SP 552, 669 (In the text)
Holman, G. D. 1985, ApJ, 293, 584 [NASA ADS] [CrossRef] (In the text)
Holman, G. D., & Pesses, M. E. 1983, ApJ, 267, 837 [NASA ADS] [CrossRef] (In the text)
Holman, G. D., Sui, L., Schwartz, R. A., & Emslie, A. G. 2003, ApJ, 595, L97 [NASA ADS] [CrossRef] (In the text)
Kerdraon, A., & Delouis, J. 1997, The Nancay radioheliograph, in Coronal Physics from Radio and Space Observations, ed. G. Trottet (Heidelberg: Springer), 192 (In the text)
Kiener, J., Gros, M., Tatischeff, V., & Weidenspointer, G. 2006, A&A, 445, 725 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kontar, E. P., MacKinnon, A. L., Schwartz, R. A., & Brown, J. C. 2006, A&A, 446, 1157 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Leroy, M. M., & Mangeney, A. 1984, Ann. Geophys., 2, 449 [NASA ADS] (In the text)
Lin, R. P., & Hudson, H. S. 1971, Sol. Phys., 17, 412 [NASA ADS] [CrossRef] (In the text)
Lin, R. P., & Hudson, H. S. 1976, Sol. Phys., 50, 153 [NASA ADS] (In the text)
Lin, R. P., Larson, D., McFadden, J., et al. 1996, Geophys. Res. Lett., 23, 1211 [NASA ADS] [CrossRef] (In the text)
Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [NASA ADS] [CrossRef] (In the text)
Litvinenko, Y. E. 2000, in High Energy Solar Physics - Anticipating HESSI, ed. R. Ramaty, & N. Mandzhavidze, ASPC Conf. Ser., 206, 167 (In the text)
Maksimovich, M., Pierrard, V., & Lemaire, J. 1997, A&A, 324, 725 (In the text)
Mann, G. 1995, in Coronal Magnetic Energy Release, ed. A. O. Benz, & A. Krüger, Lecture Notes in Physics (Heidelberg: Springer Verlag), 183 (In the text)
Mann, G., & Klassen, A. 2005, A&A, 441, 319 [NASA ADS] [CrossRef] [EDP Sciences]
Mann, G., Aurass, H., Voigt, W., & Paschke, J. 1992, in Proc. 1st SOHO Workshop, ESA-SP 348, 129 (In the text)
Mann, G., Classen, T., & Aurass, A. 1995, A&A, 295, 775
Mann, G., Aurass, H., & Warmuth, A. 2006, A&A, 454, 969 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Melrose, D. B. 1985, Plasma emission mechanisms, in Solar Radiophysics, ed. D. J. McLean, & N. R. Labrum (Cambridge: Cambridge University Press), 177 (In the text)
Nelson, G. S., & Melrose, D. 1985, Type II Bursts, in Solar Radiophysics, ed. D. J. McLean & N. R. Labrum (Cambridge: Cambridge University Press), 333 (In the text)
Newkirk, G. A., 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] (In the text)
Pierrard, V., Maksimovivh, M., & Lemaire, J. 1999, J. Geophys. Res., 104, 17.021 (In the text)
Priest, E. R. 1982, Solar Magnetohydrodynamics (Dordrecht: Reidel Publ. Comp.) (In the text)
Shibata, K., Masuda, S., Shimojo, M., et al. 1995, ApJ, 451, L83 [NASA ADS] (In the text)
Smith, D. M., Lin, R. P., Turin, P., et al. 2002, Sol. Phys., 210, 33 [NASA ADS] [CrossRef] (In the text)
Treumann, R. A., & Baumjohann, W. 1997, Advances Space Plasma Physics (London Imperial College Press), 143 [NASA ADS] (In the text)
Tsuneta, S., & Naito, T. 1998, ApJ, 495, L67 [NASA ADS] [CrossRef] (In the text)
Vrsnak, B., Aurass, H., Magdalenic, J., & Gopalswamy, N. 2001, A&A, 377, 321 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Warmuth, A., Mann, G., & Aurass, H. 2007, Central European Astrophysical Bulletin, 31, 135 [NASA ADS] (In the text)
Warmuth, A., Mann, G., & Aurass, H. 2009, A&A, 494, 677 [CrossRef] [EDP Sciences] (In the text)
Wu, C. S. 1984, J. Geophys. Res., 89, 8857 [CrossRef] (In the text)

All Figures

$\begin{figure} \par\includegraphics[width=8.6cm,clip]{0099fig1.eps} \end{figure}$	Figure 1: Sketch of the reconnection process in the solar corona as described in Sect. 1. The termination shock is established by the outflow jet, if it comes from the reconnection site and, subsequently, penetrates into the surrounding plasma of the corona. The grey shaded areas with the black arrows show the reconnection outflow jets.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.8cm,clip]{0099fig2.eps} \end{figure}$	Figure 2: Illustration of the shock drift acceleration in the $\beta _{\perp }-\beta _{\parallel }$ plane for a shock wave with $\beta _{\rm s} = 0.8$ and $\alpha _{\rm lc} = 45^{\circ }$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{0099fig3.eps} \end{figure}$	Figure 3: The differential magnetic field aligned flux (Eq. (14)) normalized to N₀ is obtained for electrons accelerated by shock drift acceleration with a shock speed of 1500 km s^-1 for several angles $\theta$ . The loss-cone angle $\alpha _{\rm lc}$ is taken to be 45 $^{\circ }$ . The corresponding normalized flux $j_{{\rm M},\parallel }/N_{0}$ of a pure Maxwellian distribution (Eq. (16)) is presented by the dashed line. A temperature of 10 $\times$ 10⁶ K is adopted in all cases.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4cm,clip]{0099fig4.eps} \end{figure}$	Figure 4: Sketch of the magnetic field geometry at the TS. The magnetic field lines reconnected in the diffusion region (DR) are propagating away from it through the TS. The magnetic field line takes a local angle $\theta$ with the normal of the TS, if it is crossing the TS at x.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0099fig5.eps} \end{figure}$	Figure 5: Hard X- and $\gamma$ -ray radiation ( top) and radio radiation ( bottom) during the impulsive phase 11:00-11:10 UT of the solar event on October 28, 2003. Top panel: Photon count rates (in arbitrary units) of the ACS/SPI (blue: for energies >150 kev) and the Ge matrix of SPI (red: 7.5-10 MeV) aboard INTEGRAL. Bottom panel: dynamic radio spectrum in the range 200-400 MHz as measured by the radio spectralpolarimeter (Mann et al. 1992) of the Astrophysical Institute Potsdam. The radio signatures of the TS are marked by arrows.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0099fig6.eps} \end{figure}$	Figure 6: The nonthermal (blue) and thermal (red) hard X-ray sources as observed by RHESSI and of the TS radio source are overplotted on a composite EUV image from SOHO/EIT and TRACE for the event on Ocotber 28, 2003. All outer contours represent the 50% level. The location of the TS is obtained from the Nançay radio heliographic data at 327 MHz. The black line represents the magnetic field lines connecting the hard X-ray footpoints. The white lines illustrate the magnetic field lines connecting the reconnection site, which is thought to be right outside the figure. Note that the magnetic field lines are drawn for illustration and not the result of any magnetic field extrapolation.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{0099fig7.eps} \end{figure}$	Figure 7: The hard X-ray photon spectrum as recorded by RHESSI during the time period 11:06:40-11:07:40 UT on October 28, 2003. The dashed and dotted dashed line represent the thermal and nonthermal component of the X-ray radiation, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{0099fig8.eps} \end{figure}$	Figure 8: The magnetic field aligned differential flux of accelerated electrons (full line) according to Eq. (14) with the parameters derived from the solar event on October 28, 2003. The values of these parameters are given in Sect. 3. The dashed line represents the corresponding flux (see Eq. (16)) of a pure Maxwellian population for the same temperature of 40 $\times$ 10⁶ K for comparison.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.