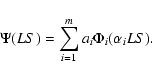| Issue |
A&A
Volume 494, Number 2, February I 2009
|
|
|---|---|---|
| Page(s) | 729 - 737 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361:200809788 | |
| Published online | 11 December 2008 | |
Breit-Pauli R-matrix calculation of fine-structure effective collision strengths for the electron impact excitation of Mg V![[*]](/icons/foot_motif.gif)
C. E. Hudson - C. A. Ramsbottom - P. H. Norrington - M. P. Scott
School of Mathematics and Physics, The Queens University of Belfast, Belfast BT7 1NN, Northern Ireland, UK
Received 17 March 2008 / Accepted 13 November 2008
Abstract
Context. Electron-impact excitation collision strengths are required for the analysis and interpretation of stellar observations.
Aims. This calculation aims to provide effective collision strengths for the Mg V ion for a larger number of transitions and for a greater temperature range than previously available, using collision strength data that include contributions from resonances.
Methods. A 19-state Breit-Pauli R-matrix calculation was performed. The target states are represented by configuration interaction wavefunctions and consist of the 19 lowest LS states, having configurations 2s22p4, 2s2p5, 2p6, 2s22p33s, and 2s22p33p. These target states give rise to 37 fine-structure levels and 666 possible transitions. The effective collision strengths were calculated by averaging the electron collision strengths over a Maxwellian distribution of electron velocities.
Results. The non-zero effective collision strengths for transitions between the fine-structure levels are given for electron temperatures (![]() )
in the range
)
in the range
![]() .
Data for transitions among the 5 fine-structure levels arising from the 2s22p4 ground state configurations, seen in the UV range, are discussed in the paper, along with transitions in the EUV range - transitions from the ground state 3P levels to 2s2p5 3P
.
Data for transitions among the 5 fine-structure levels arising from the 2s22p4 ground state configurations, seen in the UV range, are discussed in the paper, along with transitions in the EUV range - transitions from the ground state 3P levels to 2s2p5 3P![]() levels. The 2s22p4 1D-2s2p5 1P
levels. The 2s22p4 1D-2s2p5 1P![]() transition is also noted. Data for the remaining transitions are available at the CDS.
transition is also noted. Data for the remaining transitions are available at the CDS.
Key words: atomic processes - line: formation - methods: analytical
1 Introduction
Recently, high-ionisation forbidden lines from Mg V were found in Hubble Space Telescope STIS ultraviolet spectra of the symbiotic star AG Draconis (Young et al. 2006). Here, Young et al. use the density and temperature sensitive pair of lines 2s22p4 3P1-2s22p4 1S0 and 2s22p4 3P2-2s22p4 1D2 (occurring at 1324 and 2782 Å in the UV range, respectively) as a diagnostic. In the EUV range, the 2s22p4 1D2-2s2p5 1P
![]() emission line at 276.58 Å has been observed using the EIS instrument onboard Hinode (Young et al. 2007a). Young et al. (2007b) note that this line gives valuable temperature information.
emission line at 276.58 Å has been observed using the EIS instrument onboard Hinode (Young et al. 2007a). Young et al. (2007b) note that this line gives valuable temperature information.
Observational data such as these require atomic data in the form of effective collision strengths for analysis and interpretation. Two previous close-coupling calculations have been carried out but were limited to data for a handful of transitions. The work of Mendoza & Zeippen (1987) was a six-state calculation with LS-coupled collision strengths calculated using the IMPACT (Crees et al. 1978) code. The LS-coupled reactance matrices were adapted to intermediate coupling by algebraic transformations neglecting relativistic effects and fine-structure energy splittings using the JAJOM (Saraph 1972,1978) program. This calculation determined effective collision strengths for the 3 fine-structure transitions within the ground state 2p4 3PJ levels and for the 3 LS transitions between the 2p4 3P, 1D and 1P levels. The R-matrix calculation of Butler & Zeippen (1994) was also a six-state calculation carried out in LS-coupling with the K-matrices being transformed, and here values are given for the 10 fine-structure transitions arising from the 2p4 3PJ, 1D and 1S levels. However, neither of these calculations gives data for the EUV lines, in particular the line at 276 Å observed by Hinode.
The more recent work of Bhatia et al. (2006) calculated collision strengths in the Distorted Wave approximation. In this calculation 44 LS states were employed which gives rise to 86 j-levels and a total of 3655 transitions. However, the Distorted Wave approximation does not take into account contributions from the resonances, and so the collision strengths are less accurate. Therefore, these authors have used the results of Butler & Zeippen (1994) for the transitions within the ground configuration to complement their data. However, Butler & Zeippen (1994) only provide data for temperatures up to 105 K and so in their paper Bhatia et al. (2006) call for a new close-coupling calculation to provide values for the 105-106 K range, since Mg V lines are formed in plasmas at these temperatures.
Therefore to provide accurate collisional data for this ion we have carried out a sophisticated Breit-Pauli R-matrix calculation. Such calculations are carried out in intermediate coupling and hence using a transformation such as JAJOM is no longer required and the collision strengths become more accurate in the resonance region. This calculation was performed with 19 LS target states (including levels up to 2s22p3(2D![]() )3p 3P) which give rise to 37 j-levels, and a total of 666 possible fine-structure transitions. The effective collision strengths have been determined for electron temperatures in the range
)3p 3P) which give rise to 37 j-levels, and a total of 666 possible fine-structure transitions. The effective collision strengths have been determined for electron temperatures in the range
![]() .
We present some of these values in this paper, with the remainder being tabulated at the CDS website.
.
We present some of these values in this paper, with the remainder being tabulated at the CDS website.
2 Calculation details
Configuration interaction wavefunctions for the 19 LS target states used in this calculation were constructed using the CIV3 code of Hibbert (1975). Each target-state wavefunction ![]() is represented by a linear combination of single-configuration functions
is represented by a linear combination of single-configuration functions ![]() ,
each of which has the same total
,
each of which has the same total ![]() symmetry as the target-state
symmetry as the target-state
The
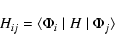 |
(2) |
where H denotes the Hamiltonian operator. The one-electron orbitals used to construct the
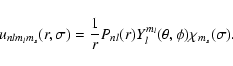 |
(3) |
These orbitals are chosen to be analytic, with the radial part being expressed as a sum of Slater-type orbitals:
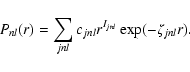 |
(4) |
In this expression, for each orbital, the powers of r (Ijnl) are kept fixed and the coefficients cjnl and exponents
In describing these target states (![]() )
we employed eight one-electron orbitals, including five real orbitals - 1s, 2s, 2p, 3s, 3p and to these we added three pseudo-orbitals - a
)
we employed eight one-electron orbitals, including five real orbitals - 1s, 2s, 2p, 3s, 3p and to these we added three pseudo-orbitals - a
![]() orbital which corrects for the differing
orbital which corrects for the differing ![]() orbital in the 2s2p5 and 2s22p3nl configurations; a
orbital in the 2s2p5 and 2s22p3nl configurations; a
![]() orbital which corrects for the 2p orbital differing from the 2s2p5 configuration; and a
orbital which corrects for the 2p orbital differing from the 2s2p5 configuration; and a
![]() orbital which allows for coupling between 2s2p5-2s22p3nd. The states used in the orbital optimisations are given in Table 1, and the resulting orbital parameters are shown in Table 2.
orbital which allows for coupling between 2s2p5-2s22p3nd. The states used in the orbital optimisations are given in Table 1, and the resulting orbital parameters are shown in Table 2.
Table 1: Orbital optimisations.
Table 2:
Orbital parameters (c, I, ![]() )
of the radial wavefunctions.
)
of the radial wavefunctions.
Table 3: Distribution of configurations for each symmetry in the two versions of the calculation.
The orbitals from Table 2 were used to build a set of single-configuration functions (![]() ), which were generated by a two electron replacement on the 1s22s22p4 basis configuration, with the 1s shell being kept closed, and allowing at most only one of the pseudo-orbitals to be occupied. Using the 14 symmetries involved in the target state set, this generation leads to a total of 1044 configurations. A larger set of configurations was also employed for comparison at this stage, but due to memory constraints within the collision calculation only the smaller set was retained for the remainder of the calculation. This larger set utilised the same orbitals and the configurations were generated in the same manner but the restriction of only allowing one pseudo-orbital to be occupied was removed. This leads to 1350 configurations being produced. The distribution of configurations between the 14 symmetries is shown in Table 3.
), which were generated by a two electron replacement on the 1s22s22p4 basis configuration, with the 1s shell being kept closed, and allowing at most only one of the pseudo-orbitals to be occupied. Using the 14 symmetries involved in the target state set, this generation leads to a total of 1044 configurations. A larger set of configurations was also employed for comparison at this stage, but due to memory constraints within the collision calculation only the smaller set was retained for the remainder of the calculation. This larger set utilised the same orbitals and the configurations were generated in the same manner but the restriction of only allowing one pseudo-orbital to be occupied was removed. This leads to 1350 configurations being produced. The distribution of configurations between the 14 symmetries is shown in Table 3.
Wavefunctions (![]() )
for the 19 Mg V target states are constructed as linear combinations of these single-configuration functions (
)
for the 19 Mg V target states are constructed as linear combinations of these single-configuration functions (![]() )
according to Eq. (1). In Table 4 we show the target state energies calculated from these wavefunctions (noted as ``This work:1044'' in the table). The energies calculated for the target states using the larger set of configurations are also noted in Table 4 as ``This work:1350''.
)
according to Eq. (1). In Table 4 we show the target state energies calculated from these wavefunctions (noted as ``This work:1044'' in the table). The energies calculated for the target states using the larger set of configurations are also noted in Table 4 as ``This work:1350''.
Table 4 compares the calculated LS target state energies in Rydbergs (1 Ryd = 2.17987
![]() J) relative to the 2s22p4 3P ground state with values from NIST. The NIST database is available at http://www.physics.nist.gov/PhysRefData and the data for this ion is attributed to Artru & Kaufman (1979), Edlen (1964), Fawcett et al. (1974), Guennou et al. (1979), Johannesson et al. (1972) and Soderqvist (1934,1946). From Table 4, we find that using our smaller set of configurations (1044, instead of 1350) gives slightly better energy levels, when compared to the values of NIST.
J) relative to the 2s22p4 3P ground state with values from NIST. The NIST database is available at http://www.physics.nist.gov/PhysRefData and the data for this ion is attributed to Artru & Kaufman (1979), Edlen (1964), Fawcett et al. (1974), Guennou et al. (1979), Johannesson et al. (1972) and Soderqvist (1934,1946). From Table 4, we find that using our smaller set of configurations (1044, instead of 1350) gives slightly better energy levels, when compared to the values of NIST.
As an additional check on the quality of the wavefunctions for the target states, we also examine the oscillator strengths produced using the wavefunctions generated. Oscillator strengths for the allowed transitions between the 19 LS target states are given in Table 5. We show values obtained using both our configuration sets - the larger set of 1350 and the smaller set of 1044 which was retained for the scattering calculation. Comparisons are made with Tachiev & Froese Fischer (2002) and we have averaged over the fine-structure oscillator strengths of Tachiev & Froese Fischer (2002) to compare with our LS values.
For the transitions noted in Table 5, on the whole, there is not much difference between the values for the larger calculation (1350 configurations) and the smaller calculation (1044 configurations). In both calculations the agreement between the length and velocity forms of the oscillator strengths is quite reasonable, and it is only for the very small oscillator strengths that larger differences are seen. The values from the current work also compare well with those of Tachiev & Froese Fischer (2002). This analysis of the energy levels and oscillator strengths generated using the constructed target state wavefunctions from the smaller calculation leads us to be confident that we have an accurate representation of the target system.
Table 4: Target state energies for our two configuration sets (1350 and 1044) compared to available NIST data.
Table 5: Oscillator strengths for the allowed transitions, in both length and velocity forms (fl and fv) for our two configuration sets (1350 and 1044), compared to Tachiev & Froese Fischer (2002)[T&F].
Table 6: Fine-structure energy levels for the current calculation compared to the earlier works of Bhatia et al. (2006), Tachiev & Froese Fischer (2002) [T&F] and Butler & Zeippen (1994) [B&Z], along with the observed values from NIST.
Table 7: Effective Collision Strengths for transitions between the first 5 j-levels of Mg V at selected temperaturesa.
Using these wavefunctions for the Mg V target ion, the electron-ion collision problem was investigated using the Breit-Pauli R-matrix method (Scott & Burke 1980), employing the RMATRX1 codes of Berrington et al. (Berrington et al. 1987). The version of the codes used here are the serial version available at http://amdpp.phys.strath.ac.uk/tamoc/code.html.
The R-matrix radius was calculated to be 7.0 atomic units and for each orbital angular momentum, 17 Schmidt-orthogonalised continuum orbitals were included, ensuring that a converged collision strength was obtained up to an incident electron energy of 28 Rydbergs (1 Ryd =
![]() J).
J).
The (N+1)-electron bound configurations, which are included in the expansion of the (N+1)-electron collision wavefunction to describe the situation when the scattering electron comes close into the target ion were obtained by systematically adding one electron to the N-electron configurations used in the description of the target Mg V ion.
The current 19 LS state calculation was carried out for all contributing partial waves with ![]() .
Within the Breit-Pauli framework this gives rise to a
37 fine-structure level problem for partial waves up to 2J=29 (J=L+S), for both even and odd parity. For optically forbidden transitions, this is sufficient to obtain converged results. However, for optically allowed transitions, additional partial waves or a top-up procedure is required. In this case, our calculation was supplemented by a non-exchange calculation for partial waves up to L=40 (in terms of J-value this allows access up to 2J=85). The ICFT method (as discussed by Griffin et al. 1998) was then used to generate the intermediate-coupling results and finally top-up was used to account for contributions from any higher partial waves (i.e. L>40).
.
Within the Breit-Pauli framework this gives rise to a
37 fine-structure level problem for partial waves up to 2J=29 (J=L+S), for both even and odd parity. For optically forbidden transitions, this is sufficient to obtain converged results. However, for optically allowed transitions, additional partial waves or a top-up procedure is required. In this case, our calculation was supplemented by a non-exchange calculation for partial waves up to L=40 (in terms of J-value this allows access up to 2J=85). The ICFT method (as discussed by Griffin et al. 1998) was then used to generate the intermediate-coupling results and finally top-up was used to account for contributions from any higher partial waves (i.e. L>40).
Effective collision strengths
![]() for electron temperatures
for electron temperatures ![]() (in K) were obtained by averaging the electron collision strengths
(in K) were obtained by averaging the electron collision strengths
![]() over a Maxwellian distribution of velocities, so that
over a Maxwellian distribution of velocities, so that
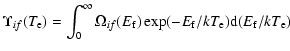 |
(5) |
where
3 Results and discussion
The collision strengths calculated in this work have been evaluated for a fine mesh of incident impact energies, at energy intervals of 0.0008 Rydbergs (0.00005 in z-scaled Rydbergs) across the energy range from threshold up to the energy of the last target state considered. This ensured that the autoionising resonances which converge to the target state thresholds were fully delineated.
Those resonances located at energies lower than the highest target threshold, i.e. 2s22p3(2D![]() )3p 3P at
)3p 3P at ![]() 7.4 Ryd, are physically meaningful; however at higher energies pseudo-resonances appear. These arise from the inclusion of pseudo-orbitals in the wavefunction expansion (Burke et al. 1981). At higher temperatures the high-impact energy region is much more important and so it is necessary to properly average over the pseudo-resonances to prevent distortion of the correct results in the calculation of the effective collision strengths. Thus above the last target state energy, a coarser mesh of energies is used (0.002 in z-scaled Rydbergs). Much of the detail is filtered out and any very large pseudo-resonances are removed, so that in essence a ``background'' level is retained in this region. This is achieved by a scheme which compares each collision strength point in the high energy/pseudo-resonance region with its neighbour on either side, and if it is larger than either neighbour by a certain factor, the collision strength at that point is reset to be the smaller of the two neighbours. In this calculation successively smaller factors were used (e.g. 10% difference, 5%, 1%, 0.1% and 0.01%) until the results converged.
7.4 Ryd, are physically meaningful; however at higher energies pseudo-resonances appear. These arise from the inclusion of pseudo-orbitals in the wavefunction expansion (Burke et al. 1981). At higher temperatures the high-impact energy region is much more important and so it is necessary to properly average over the pseudo-resonances to prevent distortion of the correct results in the calculation of the effective collision strengths. Thus above the last target state energy, a coarser mesh of energies is used (0.002 in z-scaled Rydbergs). Much of the detail is filtered out and any very large pseudo-resonances are removed, so that in essence a ``background'' level is retained in this region. This is achieved by a scheme which compares each collision strength point in the high energy/pseudo-resonance region with its neighbour on either side, and if it is larger than either neighbour by a certain factor, the collision strength at that point is reset to be the smaller of the two neighbours. In this calculation successively smaller factors were used (e.g. 10% difference, 5%, 1%, 0.1% and 0.01%) until the results converged.
The inclusion of the 19 LS target states leads to 37 J-levels (see Table 6) and a total of 666 transitions. The fine-structure energies obtained for these J-levels are also shown in Table 6 and are compared to values from Bhatia et al. (2006), NIST and Butler & Zeippen (1994), as well as values from the extensive MCHF+BP calculation of Tachiev & Froese Fischer (2002). Although the list of levels available from NIST is limited, we find that calculation of Tachiev & Froese Fischer (2002) achieves the best agreement with these observed values, the agreement being to within 1%. Of the three other calculations the current work agrees best with Tachiev & Froese Fischer (2002) - all the values are within 4%, with 35 of the 39 levels being within 1% of the Tachiev & Froese Fischer (2002) values. The Bhatia et al. (2006) values are found to differ by up to 8% from those of Tachiev & Froese Fischer (2002) (with 4 values agreeing to within 1% and 27 values agreeing to within 2%). The Butler & Zeippen (1994) values lie within 6% of both the NIST and Tachiev & Froese Fischer (2002) values. Thus since the Tachiev & Froese Fischer (2002) energy levels are so close to the NIST values and since in turn the current work is in such good agreement with the Tachiev & Froese Fischer (2002) values for the 39 levels considered, we are confident that we have achieved a good representation of the target.
In Table 7 we present the effective collision strengths
for 10 of these transitions, namely those between the first 5 J-levels arising from the first 3 LS targets - the 2p4 ground configurations. The data are given for a range of electron temperatures [
![]() (K) = 3.0-7.0, in steps of 0.2 dex] suitable for application in plasma and astronomical diagnostics. These transitions are also plotted in Fig. 1, for the temperature range
(K) = 3.0-7.0, in steps of 0.2 dex] suitable for application in plasma and astronomical diagnostics. These transitions are also plotted in Fig. 1, for the temperature range
![]() -6.0, and are compared to the values from Bhatia et al. (2006) and Butler & Zeippen (1994).
-6.0, and are compared to the values from Bhatia et al. (2006) and Butler & Zeippen (1994).
We find that our results are generally in good agreement with both the earlier R-matrix work of Butler & Zeippen (1994) and also the Distorted Wave approximation data of Bhatia et al. (2006), although it should be noted that for all the transitions in Fig. 1, Bhatia et al. (2006) merged their Distorted Wave results with the R-matrix results of Butler & Zeippen (1994). For the most part however, our results are slightly higher than the other two calculations. Focusing on the pair of lines used as a diagnostic by Young et al. (2006), i.e. 2s22p4 3P1-2s22p4 1S0 and 2s22p4 3P2-2s22p4 1D2 occurring at 1324 and 2782 Å in the UV range, these are transitions 2-5 and 1-4 respectively using the current system of labelling (see Table 6). For transition 2-5, the current calculation is up to 25% higher than the calculation of Bhatia et al. (2006), while for transition 1-4, we find that for lower temperatures (
![]() )
the current work is up to 10% lower than Bhatia et al. (2006) and for higher temperatures (
)
the current work is up to 10% lower than Bhatia et al. (2006) and for higher temperatures (
![]() )
the current work is up to 12% higher.
)
the current work is up to 12% higher.
The high temperature behaviour for transition 4-5, i.e. 2s22p4 1D2-2s22p4 1S0, differs significantly between Bhatia et al. (2006) and the current work, with the Bhatia et al. (2006) values falling off much more sharply than the current values. Since the Bhatia et al. (2006) values for this transition are their Distorted Wave results merged with the Butler & Zeippen (1994) R-matrix data, it could be that the pure Distorted Wave results give an effective collision strength which is relatively low but when merged with the Butler & Zeippen (1994) R-matrix data (which was produced in the range
![]() )
gives rise to a large enhancement at the upper end of this region near
)
gives rise to a large enhancement at the upper end of this region near
![]() .
Beyond this one assumes the sharp drop is because the values connect back to the possibly low pure Distorted Wave results. Certainly when the collision strength from the current calculation is examined and compared to the values presented in Bhatia et al. (2006), the Distorted Wave values are lower than the background level of the R-matrix results by about 40 per cent at the high energy extremity and so this suggests that the Distorted Wave effective collision strength results should be in the region of about 40 per cent lower than the current work, which does seem to be the case at
.
Beyond this one assumes the sharp drop is because the values connect back to the possibly low pure Distorted Wave results. Certainly when the collision strength from the current calculation is examined and compared to the values presented in Bhatia et al. (2006), the Distorted Wave values are lower than the background level of the R-matrix results by about 40 per cent at the high energy extremity and so this suggests that the Distorted Wave effective collision strength results should be in the region of about 40 per cent lower than the current work, which does seem to be the case at
![]() .
.
In Figure 2, we plot some transitions which appear in the EUV range. These involve initial levels 1, 2 and 3, and final levels 6, 7 and 8, and occur at ![]() 350 Å. Also plotted on the same figure, is transition 4-9, which is the line recently seen by Hinode, i.e. the 2s22p4 1D2-2s2p5 1P
350 Å. Also plotted on the same figure, is transition 4-9, which is the line recently seen by Hinode, i.e. the 2s22p4 1D2-2s2p5 1P
![]() emission line at 276.58 Å. The transitions 1, 2, 3-6, 7, 8 are from the ground 2s22p4 3P0,1,2 levels to the 2s2p5 3P
emission line at 276.58 Å. The transitions 1, 2, 3-6, 7, 8 are from the ground 2s22p4 3P0,1,2 levels to the 2s2p5 3P
![]() levels. We find that in all cases, except one (transition 3-6), the Distorted Wave values are higher than the those of the current R-matrix calculation.
levels. We find that in all cases, except one (transition 3-6), the Distorted Wave values are higher than the those of the current R-matrix calculation.
For the graphs plotted in Fig. 2, where the Distorted wave is larger than the R-matrix values, we see differences of up to almost 40%. For transition 3-6, i.e. 2s22p4 3P0-2s2p5 3P
![]() ,
the R-matrix results are larger by almost a factor of two in the lower temperature region, and the two calculations converge at the upper temperature extremity. For transition 4-9, i.e. 2s22p4 1D2-2s2p5 1P
,
the R-matrix results are larger by almost a factor of two in the lower temperature region, and the two calculations converge at the upper temperature extremity. For transition 4-9, i.e. 2s22p4 1D2-2s2p5 1P
![]() which is seen by Hinode at 276.58 Å, the Distorted Wave values are larger by 13%.
which is seen by Hinode at 276.58 Å, the Distorted Wave values are larger by 13%.
![\begin{figure}
\par\includegraphics[height=23cm,clip]{9788fig1.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09788-08/Timg47.gif) |
Figure 1:
Effective collision strengths as a function of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=23cm,clip]{9788fig2.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09788-08/Timg48.gif) |
Figure 2:
Effective collision strengths as a function of |
| Open with DEXTER | |
As a sample of the detail obtained from the current work and an indication of what may cause the differences in the effective collision strengths between the current work and the Distorted wave calculation, Fig. 3 shows collision strengths for three of the transitions given in Fig. 2. These are: transitions 2-8, 3-6 and 4-5 (i.e. 2s22p4 3P1-2s2p5 3P
![]() ,
2s22p4 3P0-2s2p5 3P
,
2s22p4 3P0-2s2p5 3P
![]() and 2s22p4 1D2-2s22p4 1S0).
and 2s22p4 1D2-2s22p4 1S0).
For transition 2-8, 2s22p4 3P1-2s2p5 3P
![]() ,
we see that in the high energy region, the two calculations achieve the same level, but towards low energy the Distorted Wave values may be higher than the R-matrix values. This enhancement at lower energies results in the effective collision strength being raised in the low temperature region by almost 25%, but at the high temperature extremity this difference is about 10% corresponding to the better agreement in the high energy region of the collision strength.
,
we see that in the high energy region, the two calculations achieve the same level, but towards low energy the Distorted Wave values may be higher than the R-matrix values. This enhancement at lower energies results in the effective collision strength being raised in the low temperature region by almost 25%, but at the high temperature extremity this difference is about 10% corresponding to the better agreement in the high energy region of the collision strength.
For transition 3-6, 2s22p4 3P0-2s2p5 3P
![]() ,
there is a large resonance near threshold for the collision strength and this greatly enhances the effective collision strength for this transition in Fig. 2. For the remainder of the transitions shown in Fig. 2, the discrepancies observed between the Distorted Wave values and the current R-matrix calculation can be explained in a fashion similar to the discussion of transition 2-8, i.e., we find that for these transitions, the collision strength values from the current work have a lower background level than the Distorted Wave calculation, and this in turn produces a lowered effective collision strength.
,
there is a large resonance near threshold for the collision strength and this greatly enhances the effective collision strength for this transition in Fig. 2. For the remainder of the transitions shown in Fig. 2, the discrepancies observed between the Distorted Wave values and the current R-matrix calculation can be explained in a fashion similar to the discussion of transition 2-8, i.e., we find that for these transitions, the collision strength values from the current work have a lower background level than the Distorted Wave calculation, and this in turn produces a lowered effective collision strength.
Transition 4-5, 2s22p4 1D2-2s22p4 1S0, has been discussed above, and is given to show that despite good agreement in the behaviour of the high energy backround level of the collision strengths, that the differing behaviour in the effective collision strengths in Fig. 1 is most likely due to the merging of the Distorted Wave results of Bhatia et al. (2006) with the earlier R-matrix results of Butler & Zeippen (1994).
![\begin{figure}
\par\includegraphics[width=8cm]{9788fig3.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09788-08/Timg50.gif) |
Figure 3: Collision strengths as a function of incident electron energy in Rydbergs for transitions 2-8, 3-6 and 4-5. Solid line - Current R-matrix calculation, Circles - Bhatia et al. (2006, Distorted Wave). |
| Open with DEXTER | |
Table 8, available at CDS, gives the non-zero fine-structure effective collision strength data for the 666 transitionsconsidered and contains the following information: Col. 1 lists the transition index noted as i-j (initial-final level) where the levels are given in the accompanying table and correspond to
those in Table 6. For example, 2-5 denotes the transition 2s22p4 3P1-2s22p4 1S0. The remaining columns list the effective collision strengths for each transition at logarithmic electron temperatures
![]() (K) = 3.0-7.0 in steps of 0.1 dex.
(K) = 3.0-7.0 in steps of 0.1 dex.
4 Conclusions
In this paper we present effective collision strengths for the electron impact excitation of the Mg V ion. The atomic data are evaluated for the electron temperature range
![]() (K) = 3.0-7.0 and for all transitions among the lowest 19 LS states of Mg V, corresponding to 37 fine-structure levels and 666 individual fine-structure transitions. Whilst the overall accuracy is difficult to assess, we expect the current data to have an accuracy of 10%.
(K) = 3.0-7.0 and for all transitions among the lowest 19 LS states of Mg V, corresponding to 37 fine-structure levels and 666 individual fine-structure transitions. Whilst the overall accuracy is difficult to assess, we expect the current data to have an accuracy of 10%.
The effective collision strengths are available at the CDS or alternatively all the collision strength and effective collision strength data over the temperature range
![]() (K) = 3.0-7.0 (in steps of 0.1 dex) are available, by contacting the author or via the website http://www.am.qub.ac.uk/apa/data.
(K) = 3.0-7.0 (in steps of 0.1 dex) are available, by contacting the author or via the website http://www.am.qub.ac.uk/apa/data.
Acknowledgements
This work has been supported by PPARC, under the auspices of a Rolling Grant. C.E.H. wishes to thank E. Landi for assistance in obtaining data from Bhatia et al. (2006).
References
- Artru, M. C., & Kaufman, V. 1979, unpublished material (In the text)
- Berrington, K. A., Burke, P. G., Butler, K., et al. 1987, J. Phys. B, 20, 6379 [NASA ADS] [CrossRef] (In the text)
- Bhatia, A. K., Landi, E., & Eissner, W. 2006, Atomic Data and Nuclear Data Tables, 92, 105 [NASA ADS] [CrossRef] (In the text)
- Burke, P., Sukamar, C., & Berrington, K. A. 1981, J. Phys. B, 14, 289 [NASA ADS] [CrossRef] (In the text)
- Butler, K., & Zeippen, C. J. 1994, A&ASS, 108, 1 [NASA ADS] (In the text)
- Clementi, E., & Roetti, C. 1974, Atomic Data and Nuclear Data Tables, 14, 177 [NASA ADS] [CrossRef]
- Crees, M., Seaton, M. J., & Wilson, P. M. H. 1978, Comput. Phys. Comm., 15, 23 [NASA ADS] [CrossRef] (In the text)
- Edlen, B. 1964, in Encyclopedia of Physics, ed. S. Flugge, 27, 172 (In the text)
- Fawcett, B. C., Galanti, M., & Peacock, J. 1974, J. Phys. B, 7, 1149 [NASA ADS] [CrossRef] (In the text)
- Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B, 31, 3713 [CrossRef] (In the text)
- Guennou, H., Surreau, A., Carillon, A., & Jamelot, G. 1979, J. Phys. B, 12, 1657 [NASA ADS] [CrossRef] (In the text)
- Hibbert, A. 1975, Comput. Phys. Comm., 9, 141 [CrossRef] (In the text)
- Johannesson, G. A., Lundstrom, T., & Minnhagen, L. 1972, Phys. Scr., 6, 129 [NASA ADS] [CrossRef] (In the text)
- Mendoza, C., & Zeippen, C. J. 1987, MNRAS, 224, 7 [NASA ADS] (In the text)
- Saraph, H. E. 1972, Comput. Phys. Comm., 3, 256 [NASA ADS] [CrossRef]
- Saraph, H. E. 1978, Comput. Phys. Comm., 15, 247 [NASA ADS] [CrossRef]
- Scott, N. S., & Burke, P. G. 1980, J. Phys. B, 13, 4299 [NASA ADS] [CrossRef] (In the text)
- Soderqvist, J. 1934, Nova Acta Regiae Soc. Sci. Ups., Ser. IV, 9, 1
- Soderqvist, J. 1946, Ark. Mat., Astron. Fys., 32, 1
- Tachiev, G. I., & Froese Fischer, C. 2002, A&A, 385, 716 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Young, P. R., Dupree, A. K., Espey, B. R., & Kenyon, S. J. 2006, ApJ, 650, 1091 [NASA ADS] [CrossRef] (In the text)
- Young, P. R., Del Zanna, G., Mason, H. E., et al. 2007a, Publ. Astron. Soc. Japan, 59, S727 [NASA ADS] (In the text)
- Young, P. R., Del Zanna, G., Mason, H. E., et al. 2007b, Publ. Astron. Soc. Japan, 59, S857 [NASA ADS] (In the text)
Footnotes
- ... Mg V
![[*]](/icons/foot_motif.gif)
- Table 8 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/494/729
All Tables
Table 1: Orbital optimisations.
Table 2:
Orbital parameters (c, I, ![]() )
of the radial wavefunctions.
)
of the radial wavefunctions.
Table 3: Distribution of configurations for each symmetry in the two versions of the calculation.
Table 4: Target state energies for our two configuration sets (1350 and 1044) compared to available NIST data.
Table 5: Oscillator strengths for the allowed transitions, in both length and velocity forms (fl and fv) for our two configuration sets (1350 and 1044), compared to Tachiev & Froese Fischer (2002)[T&F].
Table 6: Fine-structure energy levels for the current calculation compared to the earlier works of Bhatia et al. (2006), Tachiev & Froese Fischer (2002) [T&F] and Butler & Zeippen (1994) [B&Z], along with the observed values from NIST.
Table 7: Effective Collision Strengths for transitions between the first 5 j-levels of Mg V at selected temperaturesa.
All Figures
![\begin{figure}
\par\includegraphics[height=23cm,clip]{9788fig1.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09788-08/Timg47.gif) |
Figure 1:
Effective collision strengths as a function of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=23cm,clip]{9788fig2.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09788-08/Timg48.gif) |
Figure 2:
Effective collision strengths as a function of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{9788fig3.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09788-08/Timg50.gif) |
Figure 3: Collision strengths as a function of incident electron energy in Rydbergs for transitions 2-8, 3-6 and 4-5. Solid line - Current R-matrix calculation, Circles - Bhatia et al. (2006, Distorted Wave). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.