| Issue |
A&A
Volume 468, Number 1, June II 2007
|
|
|---|---|---|
| Page(s) | 1 - 18 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361:20067044 | |
| Published online | 13 March 2007 | |
Properties and stability of freely propagating nonlinear density waves in accretion disks
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge, CB3 0WA, UK e-mail: S.Fromang@damtp.cam.ac.uk
Received:
29
December
2006
Accepted:
2
March
2007
Aims.In this paper, we study the propagation and stability of nonlinear sound waves in accretion disks.
Methods.Using the shearing box approximation, we derive the form of these waves using a semi-analytic approach and go on to study their stability. The results are compared to those of numerical simulations performed using finite difference approaches such as employed by ZEUS as well as Godunov methods.
Results.When the wave frequency is between Ω and 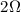 (where
Ω is the disk orbital angular velocity), it can couple resonantly with a
pair of linear inertial waves and thus undergo a parametric
instability. Neglecting the disk vertical stratification, we derive
an expression for the growth rate when the amplitude of
the background wave is small. Good agreement is found with the
results of numerical simulations performed both with finite
difference and Godunov codes. During the nonlinear phase
of the instability, the flow remains well organised if the amplitude
of the background wave is small. However, strongly nonlinear waves
break down into turbulence. In both
cases, the background wave is damped and the disk
eventually returns to a stationary state. Finally, we demonstrate that
the instability also
develops when density stratification is taken into account and so is robust.
(where
Ω is the disk orbital angular velocity), it can couple resonantly with a
pair of linear inertial waves and thus undergo a parametric
instability. Neglecting the disk vertical stratification, we derive
an expression for the growth rate when the amplitude of
the background wave is small. Good agreement is found with the
results of numerical simulations performed both with finite
difference and Godunov codes. During the nonlinear phase
of the instability, the flow remains well organised if the amplitude
of the background wave is small. However, strongly nonlinear waves
break down into turbulence. In both
cases, the background wave is damped and the disk
eventually returns to a stationary state. Finally, we demonstrate that
the instability also
develops when density stratification is taken into account and so is robust.
Conclusions.This destabilisation of freely propagating nonlinear sound waves may be important for understanding the complicated behaviour of density waves in disks that are unstable through the effects of self-gravity or magnetic fields and is likely to affect the propagation of waves that are tidally excited by objects such as a protoplanet or companion perturbing a protoplanetary disk. The nonlinear wave solutions described here as well as their stability properties were also found to be useful for testing and comparing the performance of different numerical codes.
Key words: accretion, accretion disks / methods: numerical / methods: analytical / hydrodynamics
© ESO, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


