| Issue |
A&A
Volume 409, Number 2, October II 2003
|
|
|---|---|---|
| Page(s) | 677 - 688 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:20031098 | |
| Published online | 17 November 2003 | |
Tidal perturbations of linear, isentropic oscillations in components of circular-orbit close binaries
II. Validity of the perturbation method applied to equilibrium tides
Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Belgium
Corresponding author: P. Smeyers, Paul.Smeyers@ster.kuleuven.ac.be
Received:
7
May
2003
Accepted:
7
July
2003
The paper is devoted to a verification of the validity of a first-order perturbation method that was developed in an earlier paper and allows one to determine the effects of an equilibrium tide on linear, isentropic oscillations of a component in a close binary.
The verification is done by a comparison between results obtained by the perturbation method and results obtained in other ways, in the cases of two simple models: the compressible equilibrium sphere with uniform mass density and the polytropic model with index 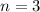 .
In the first case, a comparison is made with second-harmonic oscillations in compressible Jeans spheroids with a small eccentricity, and in the second case, with results determined by Saio (1981) for a rotationally and tidally distorted polytrope.
For the comparison, the second-harmonic oscillations of the incompressible and the compressible Jeans spheroids are redetermined by means of a method of direct integration of the governing equations which has the advantage of yielding exact analytical solutions of the eigenfrequency equations.
.
In the first case, a comparison is made with second-harmonic oscillations in compressible Jeans spheroids with a small eccentricity, and in the second case, with results determined by Saio (1981) for a rotationally and tidally distorted polytrope.
For the comparison, the second-harmonic oscillations of the incompressible and the compressible Jeans spheroids are redetermined by means of a method of direct integration of the governing equations which has the advantage of yielding exact analytical solutions of the eigenfrequency equations.
Key words: stars: binaries: close / stars: oscillations / methods: analytical
© ESO, 2003
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


