| Issue |
A&A
Volume 375, Number 3, September 2001
|
|
|---|---|---|
| Page(s) | 1091 - 1099 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361:20010857 | |
| Published online | 15 September 2001 | |
Boyle's law and gravitational instability
1
Institüt für Astrophysik und Extraterrestrische Forschung, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2
Università degli Studi di Milano, Dipartimento di Fisica, via Celoria 16, 20133 Milano, Italy
Corresponding author: M. Lombardi, lombardi@astro.uni-bonn.de
Received:
20
April
2001
Accepted:
8
June
2001
We have re-examined the classical problem of the macroscopic
equation of state for a hydrostatic isothermal self-gravitating gas
cloud bounded by an external medium at constant pressure. We have
obtained analytical conditions for its equilibrium and stability
without imposing any specific shape and symmetry to the cloud
density distribution. The equilibrium condition can be stated in
the form of an upper limit to the cloud mass; this is found to be
inversely proportional to the power 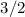 of a form factor μ
characterizing the shape of the cloud. In this respect, the
spherical solution, associated with the maximum value of the form
factor,
of a form factor μ
characterizing the shape of the cloud. In this respect, the
spherical solution, associated with the maximum value of the form
factor,  , turns out to correspond to the shape that is most
difficult to realize. Surprisingly, the condition that defines the
onset of the Bonnor instability (or gravothermal catastrophe) can be
cast in the form of an upper limit to the density contrast within
the cloud that is independent of the cloud shape. We have then
carried out a similar analysis in the two-dimensional case of
infinite cylinders, without assuming axisymmetry. The results
obtained in this paper generalize well-known results available for
spherical or axisymmetric cylindrical isothermal clouds that have
had wide astrophysical applications, especially in the study of the
interstellar medium.
, turns out to correspond to the shape that is most
difficult to realize. Surprisingly, the condition that defines the
onset of the Bonnor instability (or gravothermal catastrophe) can be
cast in the form of an upper limit to the density contrast within
the cloud that is independent of the cloud shape. We have then
carried out a similar analysis in the two-dimensional case of
infinite cylinders, without assuming axisymmetry. The results
obtained in this paper generalize well-known results available for
spherical or axisymmetric cylindrical isothermal clouds that have
had wide astrophysical applications, especially in the study of the
interstellar medium.
Key words: equation of state / gravitation / instabilities / methods: analytical / ISM: clouds
© ESO, 2001
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


