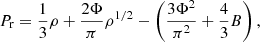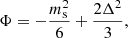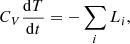EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) L11 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number L11
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202345885
Published online 20 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The quest for the state of matter in its ultimate dense version (inside compact stars) has been going on for decades. Since it was clear from the early days that densities above the saturation value ρ0 ∼ 2.4 × 1014 g cm−3 were involved, many kinds of approaches have been devised to reliably describe the behavior of degrees of freedom in that regime. However, and in spite of abundant data from heavy-ion colliders (Bratkovskaya et al. 2013) and extensive work on compact star physics (Weber 1999), we still have only a basic knowledge about matter under these extreme conditions.

One of the most fundamental questions is the true nature of degrees of freedom present at the highest densities. Work on known nuclear species (hyperons, resonances, or other species) occupies most of the literature, but the exotic composition possibility has also been amply explored. In addition to the liberation of quarks and gluons degrees of freedom in heavy-ion collisions (McLerran 2018), quark matter has been explored indirectly as an important potential component of compact star composition (Ivanenko & Kurdgelaidze 1969). In the most extreme proposal, a cold variety of this matter was suggested to be absolutely stable, and therefore a candidate to compose all but the outermost crust of a compact star (Bodmer 1971; Terazawa et al. 1978; Itoh 1970; Witten 1984), and because of the large abundance and fundamental role of the s quark in the mixture, called strange quark matter (SQM).

The search for evidence of a SQM composition of compact stars has been extensive, with some reports and arguments being withdrawn, and others still being considered (e.g., Di Salvo et al. 2019). The recent report by Doroshenko et al. (2022) of a low mass for the Compact Central Object (CCO) named XMMU J173203.3−344518 in the remnant HESS J1731−347 adds interest to this quest. The observations revealed a mass below the 1 M⊙ scale, the formation of which is thought to be not viable in standard Stellar Evolution (Suwa et al. 2018). The measurement of the radius is also interesting, because it came out slightly smaller than the most reliable currently known radii determinations. This was possible by means of a spectral modeling and the use of Gaia data to refine the distance estimate. Therefore, this compact object became a candidate to a “strange” star, as stated by the authors, although a normal composition is by no means excluded. We show below that the XMMU J173203.3−344518 candidate passes the minimum requirements to be considered a strange star, and discuss possible reasons for its very low mass.

2. Mass and radius of XMMU J173203.3−344518 in HESS J1731−347 within existing models

A whole class of quark matter models have been investigated in the last 20 yr or so, after the recognition of the importance of quark-quark pairing in dense matter. The pairing was perturbatively discussed earlier (Bailin & Love 1984), but the new calculations were performed within a non-perturbative approach and suggested a much larger value of the gap Δ (Alford et al. 2001). For high densities the so-called Color-Flavor Locked phase (CFL) phase in which all quarks pair, discussed in Alford et al. (2001) is expected to be the ground state. Even though the densities inside compact stars should not be so extreme, the asymptotic CFL description was adopted as a plausible model. The pairing has been shown to considerably enlarge the stability window (Lugones & Horvath 2002) for CFL strange matter. Other pairing patterns, for example, the 2SC that allows only the lighter quarks to pair, have been explored (Rjagopal 1999; Alford et al. 2001) and may be relevant if the actual density inside compact objects is not too high. Ultimately, these theoretical possibilities must be related to actual observations.

The equation of state (EoS) including pairing effects has been discussed in the literature. In the case of the CFL state, the simplest version of it (Alford et al. 2001; Lugones & Horvath 2002) reads

P r = 1 3 ρ + 2 Φ π ρ 1 / 2 − ( 3 Φ 2 π 2 + 4 3 B ) , $$ \begin{aligned} P_{\rm r} = \frac{1}{3}\rho + \frac{2\Phi }{\pi }\rho ^{1/2} - \left( \frac{3\Phi ^2}{\pi ^2} + \frac{4}{3}B \right), \end{aligned} $$(1)

with Φ defined by

Φ = − m s 2 6 + 2 Δ 2 3 , $$ \begin{aligned} \Phi = -\frac{m_{\rm s}^2}{6}+\frac{2\Delta ^2}{3}, \end{aligned} $$(2)

where ms is the mass of the strange quark, Δ is the pairing gap (usually treated as a parameter) and B is the bag constant. In the limit ms → 0 and non-interacting (unpaired) quarks, a MIT bag model-like EoS is restored (Alcock et al. 1986).

Variants of this self-bound EoS have been considered over the years. In a recent work (Horvath & Moraes 2021) we have collected a few examples that explain the masses and radii of the most reliable simultaneous measurements available, those presented in Miller et al. (2019) for PSR J0030+0451 and Riley et al. (2021) for PSR J0740+6620. The compact object in the GW merger GW190814 (Abbott et al. 2020) (although no estimate for the radius is available) is a candidate for the heaviest neutron star known (Horvath et al. 2022), and the stellar sequences may arguably be required to go up to this high value. It is important to remark that the analysis of the existing sample of galactic neutron stars (Horvath et al. 2022) favors a large maximum mass, and also that a similar value for it was found in an analysis of the GW sample (Ye & Fishbach 2022). The maximum mass should be above 2.2 M⊙ empirically (Romani et al. 2022; Ye & Fishbach 2022; Horvath et al. 2022).

The four EoS employed in Horvath & Moraes (2021) correspond to self-bound versions of cold quark matter. The first is the NJL-CFL EoS with vector interactions (Ferrer 2017) in which the self-bound condition is achieved by introducing a vacuum term and repulsive vector interactions boost the maximum mass of the stellar sequence upwards. The Mean Field Theory of QCD (MFTQCD; Franzon et al. 2012) with the parameter ξ in the range of self-boundness, and two versions of the CFL model with a self-bound EoS given in Eqs. (1) and (2), solved within an exact anisotropic metric ansatz due to Thirukkanesh–Ragel–Malaver (Thirukkanesh & Ragel 2012; Malaver 2014). This last model was analytically solved in Rocha et al. (2020).

Since we derive in Rocha et al. (2020) an exact solution, some features of the models can be read off quite simply. For example, the two anisotropic models presented in Horvath & Moraes (2021) were calculated using a large value of the pairing gap Δ = 100 MeV. Given that cooling suggests a very small gap (see below), this may be seen as misleading. However, from the anisotropic analytic solution we can readily check that even in the limit of “zero pairing”, the sequences display a lower maximum mass than those corresponding to large Δ, but not dramatically so. The curves are not very different mainly because of the presence of the first term 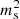m s 2 $ m_{\mathrm{s}}^{2} $ in the quantity Φ of Eq. (2), which precludes a dramatic drop in Mmax in the Δ → 0 limit. As a consequence, a low-gap anisotropic CFL would be viable for all the objects addressed here. We show one of these models (CFL with “zero gap” in the anisotropic ansatz) in Fig. 1 for comparison.

thumbnail Fig. 1.

Mass–radius relation of the theoretical models vs. observed data. The green curve corresponds to the MFTQCD quark EoS, with ξ = 0.003658 MeV−1 and BQCD = 62 MeV fm−3. The blue curve depicts the results for the NJL CFL+vector interactions EoS with B0 = 57.3 MeV fm−3 and GV/GS = 0.5. Two anisotropic models corresponding to the Thirukkanesh–Ragel–Malaver ansatz, both with Δ = 100 MeV and ms = 150 MeV appear in red (corresponding to B = 57.5 MeV fm−3) and black (B = 70 MeV fm−3). The dotted sequence is the Δ → 0 for the same anisotropic models with B = 70 MeV fm−3, showing that the downward shift in the stellar sequence curves is not dramatic and may be viable as a model of the new object. Data rectangles are 1σ estimates for PSR J0030+0451 (purple), PSR 0740+6620 (green) and the recently reported HESS J1731−347 (blue).

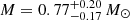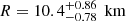All these self-bound EoS, with a zero-point pressure at finite density, produced the sequences of quark stars seen in Fig. 1. Without any change, we plotted the new object HESS J1731−347 ( M = 0 . 77 − 0.17 + 0.20 M ⊙ $ M = 0.77^{+0.20}_{-0.17} \, M_{\odot} $ and R = 10 . 4 − 0.78 + 0.86 km $ R = 10.4^{+0.86}_{-0.78}\,\text{ km} $) considering a rectangle of 1σ, and the result shows that the same description attempted for the heavier objects is a very good model for the low-mass compact star reported by Doroshenko et al. (2022). Larger contours, beyond 1σ, would make the agreement even more plausible for the HESS object and the three other cases. Therefore, we consider this consistency check as successful.

3. Surface temperature of XMMU J173203.3−344518 in HESS J1731−347

Before the announcement of a low mass value by Doroshenko et al. (2022), the central object was known by the name XMMU J173203.3−344518 (H. E. S. S. Collaboration 2011), although there was considerable doubt concerning its age. The high temperature reported by H. E. S. S. Collaboration (2011), 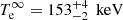T e ∞ = 153 − 2 + 4 keV $ T_{\mathrm{e}}^{\infty} = 153^{+4}_{-2}\,\text{ keV} $, was difficult to reconcile with a 27 kyr age, although later a much younger age was found for the shorter distance of the admissible range (Acero et al. 2015; Cui et al. 2016; Maxted et al. 2018), which is now believed to lie in the range 2 − 6 kyr.

The thermal history of compact stars has been modeled for many years (see, e.g., Nomoto & Tsuruta 1981). In its basic form (ignoring gravity for now), the cooling equation is simply

C V d T d t = − ∑ i L i , $$ \begin{aligned} C_{V} {\frac{\mathrm{d}T}{\mathrm{d}t}} = -\sum _i L_{i}, \end{aligned} $$(3)

where CV is the heat capacity, which is dominated by the quark component, and Li are the luminosities resulting from the processes that produce neutrinos and photons. The early calculations of quark matter recognized that a rapid cooling would ensue, when compared to hadronic compositions. However, the pairing of quarks due to attractive interactions, recognized in the perturbative calculations in the 1980s (Bailin & Love 1984), and later in a non-perturbative fashion (Alford et al. 2001), changed things substantially. As stated in Page et al. (2006), CFL pairing with large gaps would render paired quarks essentially passive, since both CV and Lν would be strongly suppressed on both sides of Eq. (3) for temperatures much lower than the gap scale of ∼100 MeV. However, if the pairing gap is much lower, of the order of the temperature Δ ≤ 1 MeV, the cooling can mimic the slow history of hadronic composition, and the large drop in 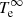T e ∞ $ T_{\mathrm{e}}^{\infty} $ does not occur promptly.

The first attempt to model the latter behavior (Horvath et al. 1991) is useful to illustrate the situation, as shown in Fig. 2. The exact numerical values of the theoretical curves should not be taken too seriously, because many details were oversimplified or ignored in 1991. However, the comparison is useful to state the consistency of the surface temperature with the structure considerations derived from self-bound EoS, provided the pairing gap is much smaller than the 10 − 100 MeV range considered in CFL models today. One of the suitable patterns of pairing discussed over the years is the 2SC (Grigorian et al. 2005; Blaschke & Berdermann 2010; Sedrakian 2016; Berdermann et al. 2016; Noda et al. 2015), which is expected to have small gaps and to be relevant at densities that are not extreme. The specific case of cooling, linked to a low mass which prompted a strange star suggestion, may be a good clue to go forward in these issues, stimulating further calculations. We note that rapid cooling was sought as a signal of exotic composition over the years, whereas we now have a hint that the opposite may be true, as shown in the first papers addressing paired quark matter (Horvath et al. 1991).

thumbnail Fig. 2.

Surface temperature of HESS J1731−347 H. E. S. S. Collaboration 2011 (red cross) contrasted with the early theoretical models cooling with paired quarks (Horvath et al. 1991) with small Δ gaps, for three different initial temperatures. Refined scenarios (Grigorian et al. 2005) confirm the relatively slow cooling, instead of a large drop in T e ∞ $ T_{\mathrm{e}}^{\infty} $, for up to ∼105 yr provided the gap is small (see text).

4. Formation scenario for HESS J1731−347: Why the mass is so low

The conversion of neutron matter into SQM is now a venerable subject that started before 1990. While the first attempts to model the propagation of the conversion from neutrons to SQM were made within a laminar deflagration framework (Olinto 1987; Olesen & Madsen 1991), it soon became clear that a much faster combustion mode should be considered (Horvath & Benvenuto 1988), prompted by the action of instabilities. Both Landau-Darreius and Rayleigh-Taylor instabilities quickly wrinkle the flame front within a few milliseconds and set the stage for an acceleration. The burning enters the so-called flamelet regime, in which the flame propagation is still determined by diffusion, but the total burning rate is in turn controlled by turbulence, in a turbulent region called the flame brush. In the flamelet regime, for all scale ≫lG (the Gibson scale) (Horvath 2010), the turbulent velocity uturb and front width lturb are determined by the turbulence spectrum at the largest scales (very likely of Kolmogorov type). From there, the possibility of the combustion entering the distributed regime, in which turbulent eddies disrupt the flame and dominate the burning on macroscopic and microscopic scales is substantial. In Horvath (2010) the conditions for the combustion to “jump” to the detonation branch were discussed, although the mechanism behind such transitions is poorly known and there may in fact be multiple mechanisms (Furusawa et al. 2016). Dedicated simulations have not produced a transition to a detonation stage (Furusawa et al. 2016; Niebergal et al. 2010), although this does not seem definitive.

In the general case, the hypothesis that supernovae are aided by SQM appearance (Benvenuto & Horvath 1989) helps to visualize that the supernova event provides a clue for its reported low mass. The suggestion is that the burning of neutrons n → SQM has enough energy to blow out a substantial mass from the outer core, provided the conversion happens in the detonation mode. This is true even for cores more massive than the minima of Suwa et al. (2018), because their density profile does not need to be sharply decreasing (Burrows & Vartanyan 2021). It is not known how the details would work, because a numerical simulation of the process is not available for these events, which would be the common case in Nature. The possibility that the progenitor was a low-mass star on the Main Sequence, even one undergoing an electron-capture supernova first (and not an iron core collapse), would be also possible, since the O − Mg − Ne white dwarf-like core collapses with a fixed baryonic Chandrasekhar-like mass of 1.37 M⊙ (Horvath et al. 2022).

While there is in principle enough energy to blow away 0.3 − 0.4 M⊙ and leave a strange star with M ≤ 1 M⊙, the final outcome depends on many things, including the moment at which the SQM is nucleated inside the collapsing core (Horvath et al. 1992; Lugones & Benvenuto 1998), the density profile at that time and other factors. We note that, even considering the binding of subnuclear origin (Bombaci & Datta 2000), the smallest cores would not produce a final gravitational mass below 1 M⊙ (Di Clemente et al. 2022). Sweeping away a considerable fraction of the mass of the outer core thus seems inevitable in a scenario in which the strange compact object is born in the very supernova event.

It is interesting to consider the case where a detonation does not happen, that is, the velocity of a fast deflagration mode would still be a fraction of c, meaning that the conversion of the star would take place within a few milliseconds. We can state that the neutrinosphere temperature would be suddenly increased (the SQM hypothesis led to a neutrinosphere temperature of 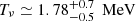T ν ≃ 1 . 78 − 0.5 + 0.7 MeV $ T_{\nu} \simeq 1.78^{+0.7}_{-0.5}\,\text{ MeV} $ associated to the SQM energy release in the case of SN 1987A; Benvenuto & Horvath 1989). At this stage the outer core and envelope are loosely bound, and a suitable gain region for the neutrino flux can produce the explosion with the ejection of ≥0.3 M⊙ of the former. The suggestion is that a neutrino-driven explosion around ∼1 s after prompt shock stalling, due to a refreshed neutrino flux, could be viable. Much in the same way that establishing the basic current supernova picture took several years, a scenario producing a strange star has to be explored with care.

An important point along the lines is related to the presence of a normal crust. The simple qualitative scenario outlined here would predict a fallback crust of a heavy composition, likely carbon or heavier. The thermal surface emission has to be carefully explored; it may hold spectroscopic clues to confirm or discard this expectation, and would be important for a full evaluation.

5. Conclusions

The report of a low mass 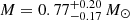M = 0 . 77 − 0.17 + 0.20 M ⊙ $ M = 0.77^{+0.20}_{-0.17} \, M_{\odot} $ for the Central Compact object XMMU J173203.3−344518 born in the supernova HESS J1731−347 is one of the many interesting works looking for the composition of superdense compact objects in Nature. Its mass is truly unexpected within standard current models of compact stellar remnants, independently of its ultimate composition. On the other hand, an exotic nature of the former is entirely possible, and as we have seen, tentatively consistent with all three direct observations (mass, radius and surface temperature). We present here a summary of these points elaborated above using existing calculations:

  1. The same quark EoS employed for large massive objects with reliable determinations of mass and radius naturally accommodates XMMU J173203.3−344518. Other EoS are also capable of explaining the whole set of masses and radii, for example the ones presented by Bombaci et al. (2021) and Ferrer et al. (2015). The point here is that there is a hint of unification of description, although to pinpoint the “right” EoS is still a distant goal.

  2. The observations indicating that the surface temperature is quite high, even for the younger age estimate 2 − 6 kyr (Acero et al. 2015; Cui et al. 2016; Maxted et al. 2018), exclude rapid cooling within a quark EoS. Moreover, the simplest explanation would be achieved within a small gap (Δ ≤ 1 MeV) complete pairing of quarks. A large value of the gap would be disfavored on these cooling grounds. A new round of detailed calculations will surely shed light on this issue.

  3. The idea that strange matter is an ultimate cause of collapse supernovae (Benvenuto & Horvath 1989) can be tested in this case. The SQM theory has not produced a supersonic detonation yet, but a very rapid subsonic mode has been obtained. This energy release would need to unbind a large fraction of the outer core to explain the low mass of XMMU J173203.3−344518, and a neutrino-driven wind could be enough for that task.

  4. We believe that a classification of the supernova event could be attempted using the light echo techniques and spectroscopic observations. A shell of ∼2 M⊙ is present around XMMU J173203.3−344518, and remains to be fully characterized. The issue of the whole ejected mass is quite similar to the case of the Crab, for which no definitive identification of a supernova type has been confirmed (Horvath 2022). Given that a so-called “canonical mass” has been employed or imposed as certain over the years, and that we now know that there are confirmed lower mass objects (Martinez et al. 2015; Horvath et al. 2022), a reanalysis of the Crab case would be in order too.

We became aware of a preprint (Di Clemente et al. 2022) that shares many of the points made above, not only the structure considerations, but also issues related to the relatively hot temperature reported for the estimated age 2 − 6 kyr of HESS J1731−347. We hope to have contributed with additional considerations to the case.

In addition to confirming all the reported data and analysis, and since the extraction of parameters is always difficult and merits further scrutiny, we can state that the compact object XMMU J173203.3−344518 born in the supernova explosion that left behind the remnant HESS J1731−347 passes the initial consistency checks and opens a window for theoretical and observational work to study its nature and formation history in depth. It is premature to claim any stronger conclusion, although this is an important case and other detections could add to the whole picture. A recent work by Lin et al. (2023) reports another candidate with M = 0.98 ± 0.03 M⊙ that deserves attention in connection to the XMMU J173203.3−344518 case.

Acknowledgments

This work was supported by the FAPESP Agency (São Paulo State) under the grant 2020/08518-2 and the CNPq (Federal Government) for the award of a Research Fellowship to JEH. L.M.S. acknowledges CNPq for financial support. The CAPES Agency (Federal Government) and PRG-USP São Paulo are acknowledged for financial support in the form of scholarships. We would like to acknowledge an anonymous referee for valuable scientific suggestions that improved the initial version of the manuscript.

References

  1. Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, ApJ, 896, L44 [Google Scholar]
  2. Acero, F., Lemoine-Goumard, M., Renaud, M., et al. 2015, A&A, 580, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Alcock, C., Fahri, E., & Olinto, A. V. 1986, ApJ, 310, 261 [CrossRef] [Google Scholar]
  4. Alford, M., Rajagopal, K., Reddy, S., & Wilczek, F. 2001, Phys. Rev. D, 64, 074017 [Google Scholar]
  5. Bailin, D., & Love, A. 1984, Phys. Rep., 107, 325 [NASA ADS] [CrossRef] [Google Scholar]
  6. Benvenuto, O. G., & Horvath, J. E. 1989, Phys. Rev. Lett., 63, 716 [NASA ADS] [CrossRef] [Google Scholar]
  7. Berdermann, J., Blaschke, D., Fischer, T., & Kachanovich, A. 2016, Phys. Rev. D., 94, 123010 [Google Scholar]
  8. Blaschke, D., & Berdermann, J. 2010, Progr. Part. Nucl. Phys., 64, 432 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bodmer, A. R. 1971, Phys. Rev. D, 4, 1601 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bombaci, I., & Datta, B. 2000, ApJ, 530, 69 [Google Scholar]
  11. Bombaci, I., Drago, A., Logoteta, D., Pagliara, G., & Vidaña, I. 2021, Phys. Rev. Lett., 126, 162702 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bratkovskaya, E. L., Konchakovski, V. P., Linnyk, O., et al. 2013, in Proceedings of the International Symposium on ‘Exciting Physics’, Makutsi-Range, South Africa (Berlin: Springer) [Google Scholar]
  13. Burrows, A., & Vartanyan, D. 2021, Nature, 589, 29 [CrossRef] [PubMed] [Google Scholar]
  14. Cui, Y., Pühlhofer, G., & Santangelo, A. 2016, A&A, 591, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Di Clemente, F., Drago, A., & Pagliara, G. 2022, ArXiv e-prints [arXiv:2211.07485] [Google Scholar]
  16. Di Salvo, T., Sanna, A., Burderi, L., et al. 2019, MNRAS, 483, 767 [NASA ADS] [CrossRef] [Google Scholar]
  17. Doroshenko, V., Suleimanov, V., Pühlhofer, G., & Santangelo, A. 2022, Nat. Astron., 6, 1444 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ferrer, E. 2017, J. Phys. Conf. Ser., 861, 012020 [CrossRef] [Google Scholar]
  19. Ferrer, E., de la Incera, V., & Paulucci, L. 2015, Phys. Rev. D, 92, 043010 [Google Scholar]
  20. Franzon, B., Fogaça, D., Navarra, F. S., & Horvath, J. E. 2012, Phys. Rev. D, 86, 065031 [NASA ADS] [CrossRef] [Google Scholar]
  21. Furusawa, S., Sanada, T., & Yamada, S. 2016, Phys. Rev. D, 93, 043019 [NASA ADS] [CrossRef] [Google Scholar]
  22. Grigorian, H., Blaschke, D., & Voskresensky, D. 2005, Phys. Rev. C, 71, 045801 [NASA ADS] [CrossRef] [Google Scholar]
  23. H. E. S. S. Collaboration 2011, A&A, 531, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Horvath, J. E. 2010, Int. J. Mod. Phys. D., 19, 523 [NASA ADS] [CrossRef] [Google Scholar]
  25. Horvath, J. E. 2022, A&SS, 367, 81 [Google Scholar]
  26. Horvath, J. E., & Benvenuto, O. G. 1988, Phys. Lett. B, 213, 516 [NASA ADS] [CrossRef] [Google Scholar]
  27. Horvath, J. E., & Moraes, P. H. R. S. 2021, Int. J. Mod. Phys. D, 30, 2150016 [NASA ADS] [CrossRef] [Google Scholar]
  28. Horvath, J. E., Benvenuto, O. G., & Vucetich, H. 1991, Phys. Rev. D., 44, 3797 [NASA ADS] [CrossRef] [Google Scholar]
  29. Horvath, J. E., Benvenuto, O. G., & Vucetich, H. 1992, Phys. Rev. D., 45, 3865 [NASA ADS] [CrossRef] [Google Scholar]
  30. Horvath, J. E., Rocha, L., Bernardo, A. C., de Avellar, M., & Valentim, R. 2022, in Birth Events, Masses and the Maximum Mass of Compact Stars. eds. C. Z. Vasconcellos, & F. Weber, Astrophysics in the XXI Century with Compact Stars (Singapore: World Scientific Publishing), 1 [Google Scholar]
  31. Itoh, N. 1970, Progr. Theoret. Phys., 44, 291 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ivanenko, D., & Kurdgelaidze, D. F. 1969, Lettere al Nuovo Cimento, 2, 13 [NASA ADS] [CrossRef] [Google Scholar]
  33. Lin, J., Li, C., Wang, W., et al. 2023, ApJ, 944, L4 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lugones, G., & Benvenuto, O. G. 1998, Phys. Rev. D., 58, 083001 [NASA ADS] [CrossRef] [Google Scholar]
  35. Lugones, G., & Horvath, J. E. 2002, Phys. Rev. D, 66, 074017 [Google Scholar]
  36. Lugones, G., & Horvath, J. E. 2003, A&A, 403, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Malaver, M. 2014, Front. Math. Appl., 1, 9 [NASA ADS] [Google Scholar]
  38. Martinez, J. G., Stovall, K., Freire, P. C. C., et al. 2015, ApJ, 812, 143 [NASA ADS] [CrossRef] [Google Scholar]
  39. Maxted, N., Burton, M., Braiding, C., et al. 2018, MNRAS, 474, 662 [Google Scholar]
  40. McLerran, L. in A Brief Introduction to the Color Glass Condensate and the Glasma, Proceedings of the 38th International Symposium on Multiparticle Dynamics (ISMD08) [Google Scholar]
  41. Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24 [Google Scholar]
  42. Niebergal, B., Ouyed, R., & Jaikumar, P. 2010, Phys. Rev. C, 82, 062801 [NASA ADS] [CrossRef] [Google Scholar]
  43. Noda, T., Yasutake, N., Hashimoto, M., et al. 2015, Acta Astron. Sin. Suppl., 56, 52 [Google Scholar]
  44. Nomoto, K., & Tsuruta, S. 1981, ApJ, 250, L19 [NASA ADS] [CrossRef] [Google Scholar]
  45. Olesen, M. L., & Madsen, J. 1991, Nucl. Phys. B Proc. Suppl., 24, 170 [Google Scholar]
  46. Olinto, A. V. 1987, Phys. Lett. B, 192, 71 [NASA ADS] [CrossRef] [Google Scholar]
  47. Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
  48. Rjagopal, K. 1999, Nucl. Phys. A, 661, 150 [NASA ADS] [CrossRef] [Google Scholar]
  49. Restrepo, T. E., Providencia, C., & Benghi Pinto, M. 2022, ArXiv e-prints [arXiv:2212.11184] [Google Scholar]
  50. Riley, T. E., Watts, A. L., Ray, P. S., et al. 2021, ApJ, 918, L27 [CrossRef] [Google Scholar]
  51. Rocha, L. S., Bernardo, A., de Avellar, M. G. B., & Horvath, J. E. 2020, Int. J. Mod. Phys. D., 29, 2050044 [NASA ADS] [CrossRef] [Google Scholar]
  52. Romani, R. W., Kandel, D., Filippenko, A. V., Brink, T. G., & Zheng, W. 2022, ApJ, 934, L17 [NASA ADS] [CrossRef] [Google Scholar]
  53. Sedrakian, A. 2016, Eur. Phys. J. A, 52, 44 [NASA ADS] [CrossRef] [Google Scholar]
  54. Suwa, Y., Yoshida, T., Shibata, M., Umeda, H., & Takahashi, K. 2018, MNRAS, 481, 3305 [NASA ADS] [CrossRef] [Google Scholar]
  55. Terazawa, H., Akama, K., & Chikashige, Y. 1978, Progr. Theoret. Phys., 60, 1521 [NASA ADS] [CrossRef] [Google Scholar]
  56. Thirukkanesh, S., & Ragel, F. C. 2012, Pramana, 78, 687 [NASA ADS] [CrossRef] [Google Scholar]
  57. Weber, F. 1999, Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics (Bristol: Institute of Physics) [Google Scholar]
  58. Witten, E. 1984, Phys. Rev. D, 30, 272 [CrossRef] [Google Scholar]
  59. Ye, C., & Fishbach, M. 2022, ApJ, 937, 73 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Mass–radius relation of the theoretical models vs. observed data. The green curve corresponds to the MFTQCD quark EoS, with ξ = 0.003658 MeV−1 and BQCD = 62 MeV fm−3. The blue curve depicts the results for the NJL CFL+vector interactions EoS with B0 = 57.3 MeV fm−3 and GV/GS = 0.5. Two anisotropic models corresponding to the Thirukkanesh–Ragel–Malaver ansatz, both with Δ = 100 MeV and ms = 150 MeV appear in red (corresponding to B = 57.5 MeV fm−3) and black (B = 70 MeV fm−3). The dotted sequence is the Δ → 0 for the same anisotropic models with B = 70 MeV fm−3, showing that the downward shift in the stellar sequence curves is not dramatic and may be viable as a model of the new object. Data rectangles are 1σ estimates for PSR J0030+0451 (purple), PSR 0740+6620 (green) and the recently reported HESS J1731−347 (blue).
In the text
thumbnail Fig. 2.

Surface temperature of HESS J1731−347 H. E. S. S. Collaboration 2011 (red cross) contrasted with the early theoretical models cooling with paired quarks (Horvath et al. 1991) with small Δ gaps, for three different initial temperatures. Refined scenarios (Grigorian et al. 2005) confirm the relatively slow cooling, instead of a large drop in T e ∞ $ T_{\mathrm{e}}^{\infty} $, for up to ∼105 yr provided the gap is small (see text).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.