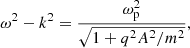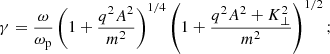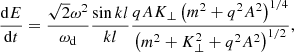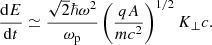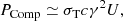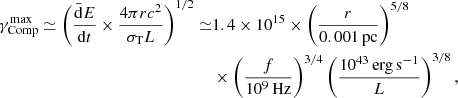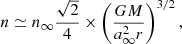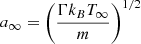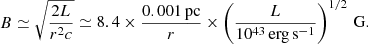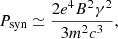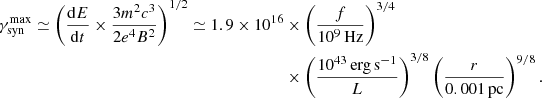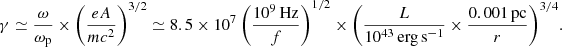| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | L14 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202243915 | |
| Published online | 25 August 2022 | |
Letter to the Editor
Resonant energization of particles by radio AGN
1
Institute for Fusion Studies, The University of Texas at Austin, Austin, TX 78712, USA
e-mail: mahajan@mail.utexas.edu
2
School of Physics, Free University of Tbilisi, 0183 Tbilisi, Georgia
e-mail: z.osmanov@freeuni.edu.ge
3
E. Kharadze Georgian National Astrophysical Observatory, Abastumani 0301, Georgia
Received:
1
May
2022
Accepted:
9
June
2022
Aims. A new mechanism of particle acceleration, based on the resonant interaction of a classical electromagnetic wave (EM) with a quantum wave (associated with a relativistic particle), is explored.
Methods. In a model illustrative calculation, we study the fate of a Klein Gordon wave subjected to the intense radio frequency waves generated in the vicinity of an active galactic nuclei (AGN). In the framework of the paper, we examine a quantum wave associated with a relativistic particle, and it is shown that the group velocity of the wave approaches the speed of light, implying that the particles resonantly exchange energy with EM waves, eventually leading to acceleration of particles to very high energies.
Results. For typical parameters of under accreting Eddington radio AGN, it is shown that the resonant energization could catapult particles to extreme energies ∼1016−20 eV.
Key words: acceleration of particles / galaxies: active / plasmas / galaxies: jets
© S. M. Mahajan and Z. N. Osmanov 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
One of the fundamental problems of modern astrophysics is to determine the origin of particle acceleration to extremely high energies. It is very helpful to note that observations in the last decade have established and confirmed a strong correlation of very high energy (VHE) protons with active galactic nuclei (Kim & Kim 2013). In this paper, we advance a possible acceleration mechanism operating on particles comprising the magnetospheres in nearby regions of radio AGNs. The mechanism, based on resonant energy transfer from the intense electromagnetic (EM) waves to relativistic quantum particle waves (modeled here as Klein–Gordon waves), is an interesting manifestation of the strong affinity between two waves with a similar mathematical structure; the dominant behavior of both the classical electromagnetic wave (e.g., the radio waves) and the relativistic Klein–Gordon (KG) wave is controlled by essentially the same hyperbolic wave operator.
The literature is full of plausible acceleration mechanisms – the so-called Fermi mechanism (Fermi 1949) and its several variants (Bell 1978; Catanese & Weeks 1999) might account for the origin of extremely high energy cosmic rays. This process, though, has limitations and is efficient when the particles are initially accelerated (Rieger & Matthaeus 2022). One of the papers relying on extreme conditions in the vicinity of compact objects (Blandford & Znajek 1977) proposes that the poloidal magnetic field close to a black hole induces electrostatic potential, which might efficiently accelerate charged particles. The process of acceleration, however, is limited by a significant screening effect. The so-called turbulent acceleration (Lemoine 2021) might account for very high energies (Pezzi et al. 2000). In the framework of this mechanism, the turbulent plasma is described as a combination of Alfvén waves and magnetosonic modes, where the particle acceleration comes from the phase locking of trajectories of particles with the mentioned waves. As a result, this mechanism might provide energies in the PeV domain (Pezzi et al. 2000). The magneto-centrifugal mechanism of energy pumping has been considered for AGN magnetospheres in a series of papers (Rieger & Matthaeus 2022; Osmanov et al. 2007; Osmanov 2010) to explain energization of particles up to TeV energies. Taking into account the generation of a centrifugally driven electrostatic field, similar mechanisms have been invoked for a similar class of objects (Osmanov et al. 2014) – the central black hole of the Milky Way, for instance (Osmanov et al. 2017).
Harnessing the strong wave–wave resonant interaction (Mahajan & Asenjo 2022) for energy transfer is what distinguishes this effort from the aforementioned schemes that also operate in extreme conditions in the vicinity of highly compact objects. In particular, if the phase velocity of the EM wave coincides with the phase velocity of a quantum wave associated with a particle, the latter is energized to extremely high energies. The resonant enhancement is particularly pronounced when the plasma frequency is lower than the frequency of the EM radiation (Sect. 2).
It is, perhaps, important to emphasize that the manifest wave-wave interaction of this paper is possible only because of the quantum nature of the particle.
The Letter is organized as follows. In Sect. 2 we outline a theory of our mechanism, consider radio-load AGN applying the theory, and discuss the obtained results. In Sect. 3 we summarize those results.
2. Basic theory of resonant energization
In this section we briefly outline the mechanism of resonant energization developed in Mahajan & Asenjo (2022). Enough detail is given to make this paper self-contained.
The group velocity of the quantum wave associated with a relativistic particle of energy (momentum) = E(P),
approaches the speed of light (c = 1) when P ≫ m, where P = γmυ is the momentum of the particle, γ is its relativistic factor, and υ is the velocity. Thus for extremely high values for the momentum, the particle could, resonantly, exchange energy with an EM wave that propagates in unison. The resonant energization phenomena is well illustrated in a model calculation (Mahajan & Asenjo 2022) in which a KG wave is subjected to a circularly polarized EM wave; the latter is described by the EM four potentials Aμ (A0 = Az = 0),
where ω and k are the frequency and the wavenumber of the EM wave propagating along the z axis, respectively. Since the directions perpendicular to z are ignorable, the KG/EM system obeys the KG equation (see Mahajan & Asenjo 2016 for details),
where q is the particle charge and K⊥ is the wave-vector’s perpendicular component which, on the other hand, is the measure of the (conserved) perpendicular momentum and labels (suppressed) the wave function. The explicit t and z dependence in Eq. (3) implies that the energy E and Pz will be functions of time. The resonant solutions of Eq. (3) will emerge when we demand Ψ = Ψ(ωt − kz)≡Ψ(ξ) (ξ ≡ ωt − kz); the result is a simple Mathew equation
with 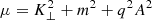 and λ = 2qAK⊥. It is important to notice that the mathematical operator
and λ = 2qAK⊥. It is important to notice that the mathematical operator 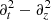 in Eq. (3) translates to ω2 − k2 (in Eq. (4)) when we impose a solution whose phase factor (ξ ≡ ωt − kz) is exactly that of the EM wave. In some sense this is the obvious mathematics underlying wave resonance. In particular, it is important to notice that the signature of resonance is already explicit in Eq. (4); the equation is singular since ω2 − k2 tends to zero for EM waves traveling in a tenuous medium. The implication, of course, is that nontrivial solutions must demand A derivative of Ψ to become commensurately large. Consequently, the energy and z momentum of the KG state must also become large since both are proportional to the ξ derivative (as one can see below).
in Eq. (3) translates to ω2 − k2 (in Eq. (4)) when we impose a solution whose phase factor (ξ ≡ ωt − kz) is exactly that of the EM wave. In some sense this is the obvious mathematics underlying wave resonance. In particular, it is important to notice that the signature of resonance is already explicit in Eq. (4); the equation is singular since ω2 − k2 tends to zero for EM waves traveling in a tenuous medium. The implication, of course, is that nontrivial solutions must demand A derivative of Ψ to become commensurately large. Consequently, the energy and z momentum of the KG state must also become large since both are proportional to the ξ derivative (as one can see below).
The leading order WKB solution of Eq. (4) is given by (Mahajan & Asenjo 2022)
where
Following simple rules of quantum mechanics, the expectation value of the energy is
and the acceleration takes place in the range z = [ − l, +l]. We note that, for this resonant state, the expectation value of the z momentum ⟨Kz⟩=(k/ω)⟨E⟩.
In order to understand the accessibility of the high energy states, we calculate the root mean square (r.m.s) of the rate of energy gain
From Eqs. (6)–(8), it is obvious that both the energy ⟨E⟩ and the rms rate of energy increase (acceleration) are resonantly enhanced by the factor 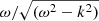 . If we now invoke the standard relativistic dispersion relation for EM propagation in highly under dense plasmas (see for example Mahajan & Asenjo 2016)
. If we now invoke the standard relativistic dispersion relation for EM propagation in highly under dense plasmas (see for example Mahajan & Asenjo 2016)
where 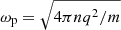 denotes the plasma frequency and n is the number density of plasma particles, we may derive an explicit expression for the relativistic factor (associated with the high energy state) γ = E/m ≈ S/m,
denotes the plasma frequency and n is the number density of plasma particles, we may derive an explicit expression for the relativistic factor (associated with the high energy state) γ = E/m ≈ S/m,
the first two factors reflect resonant enhancement. If ω ≫ ωp, very high energy states become accessible even for a moderate value of q2A2/m2. In terms of these parameters, the acceleration rate becomes
which, in physical units, may be approximated as (sin(kL)/kL ≃ 1, qA > mc2, ℏK⊥c)
This completes our review of the theory of resonant energization.
3. Radio AGNs and processes potentially limiting energy gain
We are now ready to apply the essentials of this theory to the particular case of a plasma in the magnetospheres of a radio AGN that emits copious EM energy in the radio frequency range. Although, for this paper, we work out the mechanism for the radio AGN, the resonant mechanism of particle energization pertains to any AGNs emitting in the entire electromagnetic spectrum – all the way to gamma rays.
To assess the effectiveness of the resonant energy transfer from the EM waves to the relativistic KG particle waves, we must consider processes that impede the acceleration process (summed up in Eq. (12)). Perhaps, in the present context, the two most important impeding (cooling) processes are the following: (1) the inverse Compton (IC) scattering of the charged particles with the ambient photon field, and (2) synchrotron radiation when relatively strong magnetic fields are present. We deal with them in the following subsections.
3.1. Maximum energy gain limited by IC scattering
We begin with the well-known expression for the IC cooling power (Rybicki & Lightman 1979)
where σT is the Thomson cross section, U = L/(4πrc2) is the energy density of EM emission, L denotes the bolometric luminosity of the radio source, and r is the distance from the central object. As an example, we consider the typical length scale, where the generation of very high energy (VHE) particles might take place – r ≃ 0.001 pc.
As the particle relativistic factor (energy) increases during resonant energization, so would the energy loss due to IC ( ∼ γ2). Further acceleration, therefore, is terminated as soon as the rate of energy loss balances the rate of energy gain. Equating dĒ/dt ≃ PIC gives us the maximum allowed Lorentz factor
where f = ω/2π is the frequency of EM radiation and we have used an expression of the Poynting flux in terms of the vector potential S = A2ω2/(4πc3). We normalized the frequency by 109 Hz (one should note that the frequency interval of radio AGN is 107−11 Hz; Beckmann & Shrader 2012). In Eq. (14) we have considered a spherically symmetric accretion model, leading to the following number density of particles (Shapiro & Teukolsky 2004):
where n∞ ≃ 1 cm−3 is the number density of protons in the interstellar gas (Shapiro & Teukolsky 2004) and G is the gravitational constant; the black hole is assumed to be supermassive with M = 108M⊙, where M⊙ ≃ 2 × 1033 denotes the Solar mass, and
is the speed of sound of the interstellar gas, Γ = 5/3 is its adiabatic constant, kB is the Boltzmann’s constant, and the temperature of the interstellar gas is assumed to be T∞ ≃ 104 K (Shapiro & Teukolsky 2004).
3.2. Maximum energy gain limited by synchrotron emission
Another mechanism that potentially might limit the maximum attainable particle energy is the synchrotron radiation that is most effective when a relatively strong magnetic field is present. It is normally assumed that magnetic energy density, B2/(8π), and energy density of emission, U, are in equipartition: B2/(8π)≃U. The estimated magnetic induction is thus
The upper limit on the particle energy, imposed by synchrotron cooling, is calculated (as in the previous case) by balancing the resonant energization rate with
the loss rate pertaining to the relativistic regime (Rybicki & Lightman 1979). We find
Since 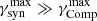 , the synchrotron losses do not impose “any” meaningful restrictions on the maximum energy that a particle could gain via resonant energization. The relevant upper bounds might come from the IC cooling.
, the synchrotron losses do not impose “any” meaningful restrictions on the maximum energy that a particle could gain via resonant energization. The relevant upper bounds might come from the IC cooling.
On the other hand, the maximum value of the Lorentz factor that might be provided by the present mechanism is given by Eq. (10), which for realistic physical quantities with eA/mc2 ≫ 1 is written as
From this expression, after comparing to 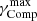 , it becomes evident that the IC process might only significantly restrict the maximum attainable energies for higher values of γ. Therefore, the energization process for the mentioned physical quantities is fully governed by the resonance process of acceleration.
, it becomes evident that the IC process might only significantly restrict the maximum attainable energies for higher values of γ. Therefore, the energization process for the mentioned physical quantities is fully governed by the resonance process of acceleration.
3.3. Conclusions and discussion
Equation (20), giving an expression for the maximum energy, constitutes the main result of this paper. Even more, since the mass dependance of the relativistic factor is of the form γ ∝ 1/m, the achieved energy γmc2 does not depend on mass, and therefore the results are the same for protons and electrons.
For several representative frequencies (in the range where the AGN spectrum peaks), the total particle energy is plotted as a function of the AGN luminosity (Fig. 1). The set of parameters is f = (1; 10; 100) × 109 Hz, M = 108 × M⊙, r = 0.001 pc, n∞ ≃ 1 cm−3, T∞ ≃ 104 K, and Γ = 5/3. From the plots it is evident that E is a continuously increasing function of luminosity, which is a natural result of the relativistic factor’s behavior, γ ∝ L3/4 (see Eq. (20)). One can see from Fig. 1 that the newly proposed mechanism of resonant energization can accelerate particles to several EeVs.
 |
Fig. 1. Maximum energy E(L) for different emission frequencies, f = (1; 10; 100) × 109 Hz. The set of parameters is M = 108 × M⊙, r = 0.001 pc, n∞ ≃ 1 cm−3, T∞ ≃ 104 K, and Γ = 5/3. |
In general, the number density of particles might be different for different regions of accretion matter (see Eq. (15)). In Fig. 2 we plot the energy of particles versus the distance from the AGN. The luminosity is set to L = 1043 erg/sec; all other parameters are the same as in Fig. 1. It is clear from the plots that E, as predicted by Eq. (20) as E ∝ r−3/4, is a continuously decreasing function of distance. Energies achieved by particles are on the order of 1016−20 eV; however, for higher values of luminosity, the achieved energies reach several EeVs (see Fig. 1).
 |
Fig. 2. Particles’ energy versus distance from the central object. The set of parameters is the same as in Fig. 1, except L = 1043 erg s−1. |
As it turned out, for physical quantities considered in this manuscript, the IC process does not impose significant restrictions on particle acceleration.
We expect that this mechanism will operate in a variety of cosmic settings (in the vicinity of highly compact objects) and can account for some of the more energetic cosmic rays. In fact, there is a sister mechanism of resonant interaction operating directly between the KG and gravitational waves that could result in a similar energy transfer to fast particles (Asenjo & Mahajan 2020).
Acknowledgments
We are grateful to an anonymous referee for very interesting and valuable comments.
References
- Asenjo, F. A., & Mahajan, S. M. 2020, Phys. Rev. D, 101, 063010 [NASA ADS] [CrossRef] [Google Scholar]
- Beckmann, V., & Shrader, C. 2012, Active Galactic Nuclei (Weinheim: Wiley-VCH) [CrossRef] [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Catanese, M., & Weeks, T. C. 1999, PASP, 111, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi, E. 1949, Phys. Rev., 75, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, H. B., & Kim, J. 2013, Int. J. Mod. Phys. D, 22, 1350045 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine, M. 2021, Phys. Rev. D, 104, 063020 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S. M., & Asenjo, F. A. 2016, Phys. Plasmas, 23, 056301 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S. M., & Asenjo, F. A. 2022, Phys. Plasmas, 29, 022107 [NASA ADS] [CrossRef] [Google Scholar]
- Osmanov, Z. 2010, New Astron., 15, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Osmanov, Z., Rogava, A., & Bodo, G. 2007, A&A, 470, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osmanov, Z., Mahajan, S., Machabeli, G., & Chkheidze, N. 2014, MNRAS, 445, 4155 [NASA ADS] [CrossRef] [Google Scholar]
- Osmanov, Z., Mahajan, S., & Machabeli, G. 2017, ApJ, 835, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzi, O., Pasquale, B., & Mannheim, K. 2000, A&A, 353, 473 [NASA ADS] [Google Scholar]
- Rieger, F. M., & Matthaeus, W. H. 2022, ApJ, 928, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 2004, Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects (Weinheim: Wiley-VCH) [Google Scholar]
All Figures
 |
Fig. 1. Maximum energy E(L) for different emission frequencies, f = (1; 10; 100) × 109 Hz. The set of parameters is M = 108 × M⊙, r = 0.001 pc, n∞ ≃ 1 cm−3, T∞ ≃ 104 K, and Γ = 5/3. |
| In the text | |
 |
Fig. 2. Particles’ energy versus distance from the central object. The set of parameters is the same as in Fig. 1, except L = 1043 erg s−1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



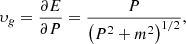
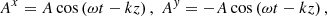
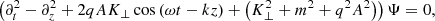
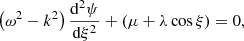
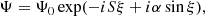
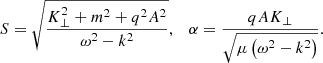
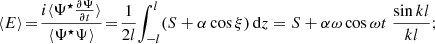
![$$ \begin{aligned} \bar{\frac{\mathrm{d}E}{\mathrm{d}t}}&= \left[\frac{1}{2\pi }\int _{-\pi }^{\pi }\mathrm{d}(\omega t)\left(\frac{\mathrm{d}\langle E \rangle }{\mathrm{d}t}\right)^2\right]^{1/2}\nonumber \\&= \frac{\sqrt{2}\omega ^2}{\left(\omega ^2-k^2\right)^{1/2}}\frac{qAK_{\perp }}{\left(m^2+K_{\perp }^2+q^2A^2\right)^{1/2}}\frac{\sin kl}{kl}. \end{aligned} $$](/articles/aa/full_html/2022/08/aa43915-22/aa43915-22-eq10.gif)