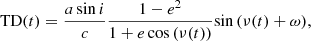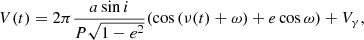| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202039389 | |
| Published online | 25 March 2021 | |
Orbital solutions derived from radial velocities and time delays for four Kepler systems with A/F-type (candidate) hybrid pulsators⋆
1
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussel, Belgium
e-mail: patricia.lampens@oma.be
2
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences & MTA CSFK Lendület Near-Field Cosmology Research Group, Konkoly Thege M. u. 15-17, 1121 Budapest, Hungary
3
Astronomical Institute, Czech Academy of Sciences, Fričova 298, 25165 Ondřejov, Czech Republic
4
Department of Theoretical Physics and Astrophysics, Masaryk Univerzity, Kotlářská 2, 61137 Brno, Czech Republic
5
Núcleo de Astronomía, Faculdad de Ingeniería y Ciencias, Universidad Diego Portales, Av. Ejército Libertador 441, Santiago, Chile
6
ELTE Eötvös Loránd University, Institute of Physics, Pázmány Péter sétány 1/A, 1171 Budapest, Hungary
7
Thüringer Landessternwarte, Tautenburg, Germany
8
Indian Institute of Astrophysics (IIA), II Block, Koramangala, Bengaluru 560 034, India
Received:
10
September
2020
Accepted:
12
January
2021
Context. The presence of A/F-type Kepler hybrid stars extending across the entirety of the δ Scuti – γ Doradus instability strips and beyond remains largely unexplained. In order to better understand these particular stars, we performed a multi-epoch spectroscopic study of a sample of 49 candidate A/F-type hybrid stars and one cool(er) hybrid object detected by the Kepler mission. We determined a lower limit of 27% for the multiplicity fraction. For six spectroscopic systems, we also reported long-term variations in the time delays (TDs). For four systems, the TD variations are fully coherent with those of the radial velocities (RVs ) and can be attributed to orbital motion.
Aims. We aim to improve the orbital solutions for those spectroscopic systems with long orbital periods (order of 4–6 years) among the Kepler hybrid stars that we continued to observe.
Methods. The orbits are computed based on a simultaneous modelling of the RVs obtained with high-resolution spectrographs and the photometric TDs derived from time-dependent frequency analyses of the Kepler light curves.
Results. We refined the orbital solutions of four spectroscopic systems with A/F-type Kepler hybrid component stars: KIC 4480321, 5219533, 8975515, and KIC 9775454. Simultaneous modelling of both data types analysed together enabled us to improve the orbital solutions (all), obtain more robust and accurate information on the mass ratio (some for the first time), and identify the component with the short-period δ Sct-type pulsations (all). The information gained is maximized when one of the components, generally the one exhibiting the δ Sct-type pulsations, is a fast rotator. In several cases, we were also able to derive new constraints for the minimum component masses. From a search for regular frequency patterns in the high-frequency regime of the Fourier transforms of each system, we found no evidence of tidal splitting among the triple systems with close (inner) companions. However, some systems exhibit frequency spacings that can be explained by the mechanism of rotational splitting.
Key words: binaries: spectroscopic / stars: variables: δ Scuti / asteroseismology / techniques: radial velocities / techniques: photometric
This study is based on spectra obtained with the HERMES échelle spectrograph installed at the Mercator Telescope, operated by the IvS, KULeuven, funded by the Flemish Community, and located at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofísica de Canarias.
© ESO 2021
1. Introduction
In an effort to unravel the enigma of the low frequencies in the brighter A/F-type candidate hybrid pulsators of the Kepler mission (Grigahcène et al. 2010; Uytterhoeven et al. 2011; Balona et al. 2015; Bowman 2017), we started a radial velocity (RV) monitoring campaign with high-resolution échelle spectrographs located in various European observatories. Our goal is to characterize the spectroscopic variability of an unbiased sample of Kepler hybrid (γ Dor - δ Sct) pulsators. This programme was initiated in the middle of 2013. We collected multi-epoch observations (four to six times at least) in order to detect binarity or multiplicity at different time scales, with orbital periods ranging from a few days to several years, and to establish a meaningful classification. We determined the epoch RVs, projected rotational velocities, and new or improved atmospheric stellar properties (i.e. Teff, log g, v sin i), and provided a classification in terms of multiplicity, pulsation, and/or (fast) rotation for all our targets on the basis of the shapes of the cross-correlation functions (CCFs) and their RVs as a function of time (Lampens et al. 2018, from hereon Paper I).
In this first study, we followed a sample of 49 candidate hybrid stars and one much cooler hybrid object identified by Uytterhoeven et al. (2011). We found a significant rate of short- and long-period binary as well as multiple systems, and we detected ten spectroscopic systems: four double-lined (SB2) systems, three triple-lined (SB3) systems, four single-lined (SB1) systems (only three of which belong to the A/F-class), and three objects with long-term RV variations (VAR). We determined the orbital solutions of seven systems. For two hierarchical triple systems, we also proposed a preliminary solution for the outer orbit. Using the classification results, we provided a lower limit to the fraction of A/F-type hybrid pulsators that belong to spectroscopic binary and multiple systems. Including the known Kepler eclipsing binary KIC 11180361 (KOI-971), we derived a minimum multiplicity fraction of 27%. Two other hybrid targets have a possible companion or shell (CMP). If we count these two targets, we obtain an overall multiplicity fraction of about 30% among these candidate hybrid pulsators.
Among the new spectroscopic systems, we identified four cases for which analysis of the Kepler time delays (TDs; mostly derived from the short-period pulsation frequencies) with the RVs enables us to derive improved orbital elements, accurate mass ratios, and a (most) probable identification of the pulsating component. The goal of this paper is to determine orbital solutions for these systems as accurately as possible based on the results of a unified modelling by combining the various data types into a single, simultaneous analysis. In the present study, we make use of the RVs acquired with the échelle spectrograph HERMES (Paper I, Table C.2) that equips the 1.2 m Mercator telescope on La Palma, Spain (Raskin et al. 2011). Furthermore, we reported variable TDs in nine cases in Paper I, in particular for the spectroscopic systems KIC 4480321, 5219533, 8975515, and KIC 9775454 (Paper I, Fig. 24). For all four systems, we acquired additional spectra through late 2019. For KIC 9775454, we include the measurements obtained in 2018 with the high-resolution échelle spectrograph HESP (R = 60 000) mounted at the Himalayan Chandra telescope (HCT), operated by the IIA in Bengaluru, India. Consequently, all RV data of all four systems and their components are updated to the latest possible date. First, we present the current status of each individual system (Sect. 2). In Sect. 3, we introduce the methodology for computing the refined orbits. Section 4 provides the orbital solutions using simultaneous modelling. In Sect. 5, we present and discuss the distributions of the frequency spacings in the high-frequency region of the Fourier transforms of each system. Finally, we present our conclusions for all the treated systems (Sect. 6)1.
2. Presentation of the systems
We present a summary of useful high-resolution spectra for each of the four systems listed in Table 1. In addition to the total number of spectra available for each system, we also display the spectrograph and the time basis. The revised orbital solutions (Sect. 4) are thus based on the combination of updated sets of component RVs and the TDs previously derived from time-dependent frequency analyses of the oscillations detected in the Kepler light curves (Paper I). This provides us with a total time basis of more than eight years for each system.
Targets and general properties of the acquired spectra.
2.1. KIC 4480321
KIC 4480321 (HD 225479, V = 10.3, A9 Vwkmet) is a hybrid variable star that was revealed by Uytterhoeven et al. (2011). It shows frequencies in the ranges [0.2, 5.0] d−1 and [5.1, 61.2] d−1 and a most dominant frequency of 0.710 d−1 in the γ Dor region. The star was also reported as rotationally variable (Nielsen et al. 2013), with g-mode multiplets split by rotation. The period spacings in the γ Dor region were obtained by Li et al. (2019). This star was classified as an SB3 in our multi-epoch study. It is a hierarchical system, with a twin-like inner binary consisting of early F-type stars orbiting a slightly more luminous and more rapidly rotating A-type companion (we used the basic model of an A5 star, v sin i = 160 km s−1, with two F0 stars, v sin i = 10 km s−1; Paper I). We derived an orbital solution for the inner pair with a 9.1659 d period, and an outer orbital solution with an estimated 2280 d period, and reported the existence of variable TDs in excellent agreement with the proposed solution for the outer orbit. We determined the component effective temperatures: Teff1 = 7900 ± 100 K, and Teff2 and Teff3 between 6300 and 6900 K (the latter two components have similar temperatures), assuming log g = 4 dex (cgs) (Paper I, Sect. 6.3). Murphy et al. (2018, Appendix C3) reported P = 2270 ± 60 d for the outer orbit from a modelling of the RV measurements of Paper I in combination with their TDs.
2.2. KIC 5219533
KIC 5219533 (HD 226766, BU 1474 B, V = 9.2, A2–A8, Renson & Manfroid 2009) is the visual companion of BU 1474 A at an angular separation of 65″ (HD 189178, V = 5.44, B5 He weak (Renson & Manfroid 2009); it is also a spectroscopic binary). This star was classified as a Kepler hybrid variable star by Uytterhoeven et al. (2011), with frequencies in the ranges [0.3, 4.6] d−1 and [5.4, 29.9] d−1 and a dominant frequency of 10.285 d−1 (Uytterhoeven et al. 2011, Table 3). It was recognized as a new SB3 based on our multi-epoch spectra. The system is hierarchical, consisting of an inner pair, with two nearly identical stars of spectral type near A5, and a more rapidly rotating outer component of a slightly cooler type. For both components of the inner pair, the mean effective temperatures of Teff1 = 8300 ± 100 K and Teff2 = 8200 ± 100 K and the projected rotational velocities of 10 km s−1 were obtained coupled to the light factor l1 = 0.53 ± 0.02, assuming log g = 4 dex (cgs) (Paper I, Sect. 6.4). Component C has v sin i equal to 115 km s−1 (Uytterhoeven et al. 2011). An orbital solution with Porb = 31.9181 d was derived for the inner pair, while a tentative outer orbit was proposed with Porb ∼ 1600 d. Later on, Murphy et al. (2018, Appendix C4) studied this system using the phase modulation (PM) method (Murphy et al. 2014). They derived a very high mass function and proposed that the third body is a δ Sct star with an orbital period longer than 1500 d. Simultaneously with Lampens et al. (2018), Catanzaro et al. (2019a,b) independently observed the system (from 2014 to 2018) with the aims of characterizing the orbits and performing a chemical analysis of its components. They proposed orbital parameters based on their RVs and those from Paper I (P1 = 31.9187 d, e1 = 0.28, q1 = 1.03 and P2 = 1615 d, e2 = 0.54, f(M1, 2) = 0.18), which confirm the findings of Paper I. They also derived the atmospheric properties Teff, log g, and v sin i based on two spectra (obtained at max RV separation) as well as chemical abundances based on one spectrum (max S/N), first for two components and then with the third component included. However, they were unable to derive the chemical composition of component C (except for Mg II). They concluded that the two components of the close pair are twin Am stars (with under-abundances of C, O, Mg, Ca, and Sc and over-abundances of Na and Fe-peak elements). From the simple assumption that all the components have equal masses, they suggested that the orbits might be coplanar. All previous studies explicitly state that more data for this multiple system are needed.
2.3. KIC 8975515
KIC 8975515 (HD 188538, V = 9.5, A6 V:) was classified as a Kepler hybrid star by Uytterhoeven et al. (2011). The star shows frequencies in the ranges [0.3–4.7] d−1 and [5.3–25.8] d−1 of the γ Dor and the δ Sct pulsation regimes, respectively, with a dominant frequency of 13.97 d−1 (Uytterhoeven et al. 2011, Table 3). Therefore, we included it among our sample of A/F-type candidate hybrid stars to be monitored spectroscopically, and it was subsequently recognized as a new SB2 from the multi-epoch observations. The system consists of two A-type stars of similar temperatures but with dissimilar projected rotational velocities, which form an eccentric system (e = 0.409 ± 0.015). From a detailed spectrum fitting using the code SYNSPEC (Hubeny & Lanz 1995) and the ATLAS-9 atmosphere models (Castelli & Kurucz 2003) to build a suitable composite model in the spectral range [500–520] nm, we obtained the mean effective temperatures Teff1 = 7440 ± 20 K and Teff2 = 7380 ± 21 K with a light factor l1 of 0.65 ± 0.03 (component A), assuming log g = 4 dex (cgs). The mean projected rotational velocities were consistently determined to be 162 ± 2 and 32 ± 1 km s−1 (Paper I, Sect. 6.12). In Paper I, we proposed a preliminary orbit with a period of the order of 1600 d, in line with the TD curve, while Murphy et al. (2018, Appendix C12) obtained a solution with a shorter period of 1090 d using the published RVs in combination with their TDs. They furthermore assumed that the narrow-lined component is the δ Sct pulsator and reported a slight aperiodicity in their derived TDs.
An extensive study of the pulsational properties of KIC 8975515 was recently published by Samadi-Ghadim et al. (2020). They concluded that both components are pulsating: The fast-rotating component is a pulsating hybrid star that also shows retrograde r modes, while the more slowly rotating component is a δ Sct pulsator.
2.4. KIC 9775454
KIC 9775454 (HD 185115, V = 8.2, F1 Vs) is a candidate hybrid variable star from Uytterhoeven et al. (2011), with frequencies in the ranges [0.2, 4.6] d−1 and [14.7, 14.9] d−1 and a dominant frequency of 4.161 d−1. It has a Gaia second data release (DR2) RV of −20.22 ± 1.02 km s−1 (Gaia Collaboration 2018). The atmospheric parameters derived from high-resolution spectroscopy are Teff = 7287 K and log g = 4.25 dex (cgs), with a projected rotational velocity of v sin i = 65 km s−1 (Paper I, Table C.1). In Paper I, we classified this object as a long-term SB1 of unknown orbital period. The cross-correlation function (CCF) of the composite spectrum shows a broad-lined component blended with a narrow-lined component. Murphy et al. (2018, Appendix C14) proposed an orbit with Porb = 1686 ± 13 d and e = 0.23 ± 0.02 by combining the published RVs with their TDs. In this case, the secondary component contributes only weakly to the composite spectrum. Nevertheless, we were able to obtain some individual RVs for this (much) cooler component (cf. Sect. 4.4).
3. Methodology
The orbital motion of a binary system causes a periodic fluctuation of the light path and its associated travel time with respect to the system’s centre of mass. On the other hand, light from a source in motion undergoes a (Doppler) shift of its frequency. In the frequency domain (for a time base T ≫ Porb), this phenomenon corresponds to a frequency modulation that can be detected as a frequency multiplet whose exact spacing is the orbital frequency (Shibahashi & Kurtz 2012). In the time domain (for T ≪ Porb), this effect corresponds to a phase modulation (PM) with the orbital period, whose amplitude depends on the mass of the (unseen) companion and the observed frequency (Murphy et al. 2014). Hence, if one of the components is a pulsating star, the change in the light travel time introduces periodic phase shifts for each individual (pulsation) frequency. By converting the phase shift into a TD, the frequency dependency is removed. Therefore, if the star is a multi-periodic pulsator, all the pulsation frequencies will experience the same TD.
Murphy et al. (2014) described the principle of obtaining TDs from the observed phase shifts of the pulsations and applied the PM method to various cases of Kepler pulsating stars in (non-eclipsing) binary systems, while Murphy & Shibahashi (2015) provided an analytical method for solving the orbit, also in highly eccentric cases. This method is in essence similar to the search for variability in the (O–C)s, the residuals in the times of specific phases in the light curve of periodically pulsating stars that are members of a binary system (e.g. Moffett et al. 1988; Fauvaud et al. 2010). Murphy et al. (2016) presented examples of orbital analyses combining RVs with photometric TDs and discussed some of the limitations and advantages. In this study, we have developed and applied our own code for a simultaneous least-squares fitting of our updated RVs and the TDs based on the Kepler data. Both quantities are functions of the same orbital parameters: the TD corresponds to the light travel time, and the RV is the time derivative of the position along the orbital path projected in the observer’s direction. We consider the following equations as our model:
where the true anomaly ν is a function of t, T0, P, and e; T0 is the time of periastron passage; P is the orbital period; a sin i is the projected semi-axis major; e is the eccentricity; ω is the longitude of the periastron; Vγ is the systemic velocity; and c is the speed of light. Equation (1) is given by Irwin (1952) (see Pribulla et al. 2005). We removed a linear trend from the original TDs computed with Eq. (1) (Murphy et al. 2016) in order to convert the pulsation frequencies to their intrinsic values (i.e. unaffected by the variable light travel time of the pulsating component). This correction is necessary since the frequencies used for computing the TDs may be biased by the (uneven) orbital phase coverage of the Kepler data, thereby introducing a bias in the TDs themselves (as in the (O–C) curves).
In Paper I, we computed the time-dependent phases for up to 20 frequencies of the highest S/N (generally the ones located in the p-mode regime) for all 49 targets of our sample. We thus uncovered nine objects for which correlated variations of comparable amplitude in the TDs were observed. In six systems, we could attribute the TD variations to the orbital motion of a binary or multiple system. By analysing the RV and TD data together, we were able to refine the orbital solutions and obtain stronger constraints on (some of) the orbital parameters and their derived parameters. Since the TDs are generally determined from the high(er) frequencies, they only provide information on the origin of the δ Sct-type pulsations associated with these frequencies. However, it is much harder to identify the origin of the low(er) frequencies (γ Dor-type) due to their longer periods. In the next sections, we will analyse each of the four systems just described and highlight the gains that can be obtained from such modelling.
4. Orbital solutions from combined modelling
4.1. The triple system KIC 4480321
KIC 4480321 is a triple system (SB3) whose orbital periods are estimated to be 9.166 and ∼2280 d (Sect. 2.1). We computed the phase shifts and their associated TDs for frequencies of highest S/N and evidenced the presence of long-term variations that are coherent with the long-term RV variability (Paper I, Fig. 24). We remark that the TDs were corrected by removing a linear trend from the original data (as everywhere). We then performed a simultaneous least-squares fitting of three updated component RVs and the mean TDs with their respective uncertainties. The best fit in the sense of min χ2 was obtained when we associated the TDs with the RVs of the fast-spinning, more luminous A-type star (component C). Figure 1 illustrates the quality of the fit, showing the outer orbital solution together with both data types. The TDs and the RVs are overlaid with the AB-C orbital solution. It should be noted that the TD curve mimics the RV curve but with an apparently larger eccentricity and a 90° shift in periastron longitude (Irwin 1952). The revised orbital parameters of the coupled solutions are listed in Table 2. Compared to Paper I, we see that the orbital solution of the A-B system is robust and well determined and that the outer orbital solution changed profoundly. The orbital period is longer (Porb ∼ 2380 d) and better determined than before (see also Murphy et al. 2018), and the eccentricity and the semi-axis major increased substantially. Thus, the minimum component mass MC sin3 iout increased to 1.60 ± 0.05 M⊙. The strongest improvement concerns the accuracy and robustness of the outer orbital solution. There are two reasons for this: (a) By combining both data types, we dispose of a time base longer than eight years, and (b) the TDs concern the fast-rotating component C for which the RVs show the largest scatter. We therefore were able to determine a (much) improved mass ratio for the outer system and to provide (more) reliable values of the three minimum component masses. From the minimum total mass of the A-B system derived for each orbit, we get sin i = 0.846 (± 0.028) sin iout, from which we obtain the condition i < 58° for the inner orbit. We can furthermore attribute the δ Sct pulsations to the more massive component C (the frequencies showing phase shifts are all located in the p-mode region). In summary, KIC 4480321 is a hierarchical triple system with qin = MB/MA = 0.98 and qout = MC/MAB = 0.68.
 |
Fig. 1. Data and outer orbital solution for KIC 4480321. The TDs and RVs (respectively filled pink and unfilled red symbols for component C; blue symbols for the centre of mass of components A and B) are overlaid with the AB-C orbital solution (solid lines). The residuals are shown in the bottom panel. |
Values and standard deviations of the constrained orbital parameters for KIC 4480321.
4.2. The triple system KIC 5219533
KIC 5219533 was classified as triple (SB3) with an inner pair of Am-like stars and with orbital periods of 31.919 and ∼1615 d (Sect. 2.2). For this system, we also detected long-term variations in the TDs that are in agreement with the long-term change observed in the RVs (Paper I, Fig. 24). We performed a simultaneous least-squares fitting of the updated component RVs and the mean TDs with their respective uncertainties, and obtained the best fit in the sense of min χ2 with the TDs assigned to the outer companion (component C). Since this component is heavily diluted in the composite spectrum, its RVs are not well determined. However, a modelling of the combined data allows us to derive full orbital solutions. The new parameters of the inner and outer orbital solutions are presented in Table 3. Figure 2 illustrates the quality of the fit as well as both solutions. The mean residuals of the component RVs stay below 1 km s−1. The largest residuals are found near the nodal passage (both components have similar RVs). The orbital solution of the A-B pair is in good agreement with the one proposed by Catanzaro et al. (2019a), though our semi-axis major are slightly larger (and our component masses a bit smaller) than theirs. Indeed, their Figs. 3 and 4 show that several HERMES RVs (open symbols) lie a bit off from their final solution. The overall gain in accuracy for most parameters of the inner orbital solution is a factor of five, while the orbital period is ten times more accurate. We cannot compare the mean RV residuals since these were not displayed. In Fig. 2 (right), the TDs and the RVs are plotted together with the revised AB-C orbital solution. We thus determined the semi-axis major of component C and the minimum mass of the A-B pair for the first time. The gain is largest for the outer orbit since the accuracy on the parameters improved by a mean factor of ten and the orbital period is about 30 times more accurate compared to Catanzaro et al. (2019a). In particular, we obtained the minimum component masses MA sin3 i = 1.336 ± 0.005, MB sin3 i = 1.293 ± 0.004, and MC sin3 iout = 1.47 ± 0.02 M⊙. From the minimum total mass of the A-B system derived for each orbit leading to the condition sin iout = 0.996 (± 0.009)sin i, we infer that both orbits are very close to coplanarity. In summary, KIC 5219533 is a hierarchical, probably coplanar system with qin = 0.97 and qout = 0.57. We furthermore established that the δ Sct pulsations are linked to the more massive, faster rotating star in the system.
 |
Fig. 2. Data and orbital solutions for KIC 5219533. Left: inner orbit based on the HERMES RVs. The RVs (red symbols for component A; blue symbols for component B) are overlaid with the A-B orbital solution (solid lines). Right: outer orbit based on the HERMES RVs and the TDs from the Kepler photometry. The TDs and RVs (respectively filled pink and unfilled red symbols for component C; blue symbols for the centre of mass of components A and B) are overlaid with the AB-C orbital solution (solid lines). The residuals are shown in the bottom panels. |
Values and standard deviations of the constrained orbital parameters for KIC 5219533.
4.3. KIC 8975515
This star was recognized as an SB2 from our multi-epoch study, and it also shows long-term variations in the TDs coherent with the variations found in the RVs (Paper I, Fig. 24). The system consists of late A-type stars with one fast-spinning star (component A) and one (apparently) slowly spinning star (component B). In Paper I, we derived an orbital solution of type SB1 based on the RVs of component B only (Porb ∼ 1600 d). We first derived a pure RV-based orbital solution (using the RVs of both components). Unfortunately, the extreme uncertainties on the RVs of the fast-spinning component did not allow us to constrain its RV amplitude. This is obvious in Fig. 3 (left), which illustrates the best-fit orbital solution with a period of 1581 d. Subsequently, we performed two simultaneous (RV+TD), by associating the TDs with each set of RVs in turn, and found an optimum fit when the TDs were assigned to component A.
 |
Fig. 3. Data and orbital solution for KIC 8975515. Left: orbit (number 1) based on the HERMES RVs. The RVs (red symbols for component A; blue symbols for component B) are overlaid with a preliminary orbital solution of type SB2, however without much constraint on the amplitude KA. Right: orbit (number 2) based on the HERMES RVs and the TDs from the Kepler photometry. The TDs and RVs (respectively filled pink and unfilled red symbols for component A; blue symbols for component B) are overlaid with the A-B orbital solution (solid lines). The residuals are shown in the bottom panels. |
We determined an orbital period of 1603.4 ± 9.3 d. The new orbital parameters and their derived fundamental properties are listed in Table 4. The residuals show the very good agreement between both data types, with small mean residuals for the TDs and RVs of component B (the slower rotator) and a large (non-zero) mean residual for component A (the faster rotator). The orbital solution is illustrated in Fig. 3 (right). In this case, the mass ratio (q = 0.83 ± 0.05) is well determined thanks to the high accuracy of the TDs (whereas the corresponding component RVs show a very large scatter). The present method allowed us to derive information that was otherwise impossible to obtain with a pure RV-based solution. Another conclusion is that the faster rotating component exhibits the δ Sct pulsations. This may also explain why the RV residuals of component A are found to be systematically off from the final solution. From the parameters displayed in Table 4, we obtain the minimum masses MA sin3 i = 0.0195 ± 0.0024 and MB sin3 i = 0.0161 ± 0.0011 M⊙. Assuming that either one of the components has a typical mass of ∼2 M⊙, we presume that the system is seen under a low inclination angle (i ∼ 12°).
Values and standard deviations of the constrained orbital parameters for KIC 8975515.
4.4. KIC 9775454
KIC 9775454 was classified as a long-period SB1 (Sect. 2.4). It was shown to display long-term variations in the TDs in agreement with the orbital variations in the RVs (this also concerns the dominant frequency located at 4.161 d−1; cf. Paper I). Murphy et al. (2018) used the HERMES RVs of the broad-lined primary (component A) and derived an orbital solution with a period of ∼1700 d from their combined (RV+TD) analysis. Being much fainter, component B was not directly detected in the high-resolution spectra. Nevertheless, we managed to find an indication of a cool companion by computing CCFs of the residual spectra (after proper subtraction of an adequate synthetic spectrum to remove the contribution of the primary) using a mask of spectral type K0. The ‘residual’ CCFs were computed for the spectral range [5100–5700] Å and revealed a shallow peak that reflects the contribution of the companion and displays Doppler shifts (Fig. 4). In this way, we were able to extract additional RV data that behave in anti-phase with those of component A (Fig. 5). We roughly estimated their uncertainties from the widths of the associated spectral lines. Thus, we can classify KIC 9775454 as an SB2. We next performed a simultaneous (RV+TD) analysis by fitting the component RVs together with the TDs assigned to the broad-lined primary (component A). The new orbital solution is illustrated by Fig. 5. The RV residuals of component A and the TD residuals are within expectations, while the RV residuals of component B are systematically large. This can be explained by the noisy residual CCFs associated with the difficulty of identifying the lines of the cool component in the spectra. The orbital parameters and derived fundamental properties are listed in Table 5. These parameters agree very well with the values proposed by Murphy et al. (2018). By treating this system as an SB2 and using the TDs, we determined, for the first time, a reasonable value of the mass ratio (q = 0.42 ± 0.02). In this special case, where the TDs are linked with both the low- and the high-frequency regions, the more massive primary component is very likely the hybrid pulsator.
 |
Fig. 4. Cross-correlation functions of the residual spectra of KIC 9775454 computed with a mask of type K0 for three different dates. |
 |
Fig. 5. Data and orbital solution for KIC 9775454. The TDs (filled pink symbols) and the RVs (unfilled red symbols for component A; blue symbols for component B) are overlaid with the A-B orbital solution (solid lines). The residuals are shown in the bottom panel. |
Values and standard deviations of the constrained parameters of the orbital solution for KIC 9775454.
5. Search for regular frequency patterns
In this section, we investigate the distributions of the frequency differences (also known as spacings) that occur in the high-frequency regime of the Fourier transforms of each system. The aim is to identify the (most) frequently occurring frequency spacings for each object and to verify whether some of these spacings might be related to the orbital or the rotational periods. In the case of an orbital or a rotational origin of the low frequencies (e.g. due to modulations in the light curve caused by the tidal deformations or by the presence of spots or other surface inhomogeneities, e.g. MOBSTER (Sikora et al. 2019), or caused by the mechanism of tidal excitation, e.g. KIC 4142768 (Guo et al. 2019)), we can expect to detect a significant number of harmonics of the corresponding main frequencies. In the case of a tidal or rotational splitting of the high frequencies associated with the rapid pulsations (e.g. tidal splitting of p-modes in KIC 6048106 and U Gru; see, respectively, Samadi Ghadim et al. 2018; Bowman et al. 2019), we can expect to find regular (also non-harmonic) frequency patterns whose spacing values will point at those frequencies.
We used the detrending algorithm of Lightkurve v1.9 to detrend the Kepler light curves of the discussed systems (Barentsen & Lightkurve 2020) and computed the periodograms with the Lomb-Scargle technique (Fig. 6). For each system, we analysed the frequency interval of the periodogram where most of the power is located. For KIC 4480321, this corresponds to the [12.5, 24.7] d−1 interval; for KIC 5219533, it is the [6, 22.5] d−1 interval; for KIC 8975515, the [12.5, 17.5] d−1 interval; and for KIC 9775454, the [5.7, 22.5] d−1 interval. We then computed the spacings between all possible pairs of significant frequencies while considering the limiting frequency resolution of the Kepler long-cadence data sets and counted the number of individual occurrences (as in Samadi Ghadim et al. 2018).
 |
Fig. 6. Lomb-Scargle periodograms derived from the Kepler data for the systems KIC 4480321 (top left), 5219533 (top right), 8975515 (bottom left), and KIC 9775454 (bottom right). The frequencies plotted in orange illustrate the full spectrum across the range [0–24.5] d−1, and the frequencies over-plotted in black have a signal-to-noise ratio higher than 4. |
We next discuss the density distributions of the frequency spacings derived from the Kepler-based periodograms for the four systems with the improved orbits. The density plots of the frequency spacings were produced from the counts, adopting a bin size of 0.05 d−1 in each case. In Fig. 7, we show the density plots of the spacings for KIC 4480321, 5219533, 8975515, and KIC 9775454 in the restricted frequency range [0–4] d−1 (the interval where the highest occurrences can be found). A general observation is that the distributions of the frequency spacings in the high-frequency regime of the four systems show large differences between them. Also, a high(er) peak in the distributions (or a secondary maximum) of individual spacings is generally located in the first bin. This is due to the fact that this bin also contains the smallest possible spacing, which corresponds to the frequency resolution of 0.00068 d−1 in the Kepler long-cadence data.
 |
Fig. 7. Normalized density functions of the frequency spacings across the range [0–4] d−1 derived from the Kepler-based periodograms for the systems KIC 4480321 (top left), 5219533 (top right), 8975515 (bottom left), and KIC 9775454 (bottom right). The highest occurrences are marked by grey arrows. |
From Fig. 7, we derived the following four findings. First, both KIC 4480321 and KIC 5219533 present a dense and continuous distribution of frequency spacings with several (almost) equal local maxima. There is power everywhere, including in the first bin. The close binaries of these triple systems have orbital frequencies of, respectively, 0.11 d−1 and 0.03 d−1, which means that in the case of KIC 4480321, the bin size is small enough to draw a firm conclusion with respect to tidal splitting. In the case of the remaining binary systems, the orbital periods are of the order of several years and are too large to be resolved in the periodograms. In the case of KIC 4480321, the highest occurrences occur at the frequency spacings of 0.35, 1.63 (highest), and 3.33 d−1. The last spacing shows a harmonic relation with 1.63 d−1 (a ratio of almost 2). This interdependence between two recurrent frequency spacings could be very well explained by rotation. Also, Li et al. (2020a) derived 0.0070 ± 0.0007 d−1 for the near-core rotation rate from a modelling of the slope-period relation based on the regular period spacings in the g-mode region. Such a low rotation rate stands in sharp contrast with the most frequent spacings listed above if we consider them as potential surface rotation rates for component C (the fast-spinning component). On the other hand, we find no peak occurring at or near the orbital frequency value of 0.11 d−1. We conclude that the orbital frequency of the inner binary system does not affect the pulsation frequencies in the p-mode region. This is perfectly consistent with the conclusion that component C is the δ Sct pulsator.
Second, in the case of KIC 5219533, the most frequent spacings occur at the frequencies of 0.55, 0.94 (highest), and 2.32 d−1 (as well as 2.98 and 3.59 d−1). The recurrent spacings of 0.55 and 0.94 d−1 could indicate the rotation period of component C (the fast-spinning component). We note that Li et al. (2020a) derived 0.59 ± 0.01 d−1 for the near-core rotation rate based on their modelling. This seems to match the smallest value of the recurrent spacings (i.e. 0.55 d−1). The orbital period of the inner binary is ∼32 d, which implies that the corresponding frequency (at 0.03 d−1) would be located in the first bin. Thus, we cannot infer from this plot whether or not this frequency is affecting the higher pulsation frequencies. However, the most recurrent individual spacing occurs at 0.0012 d−1, which is far from the orbital frequency of the inner pair.
Third, KIC 8975515 presents an irregular distribution of unequal peaks. The two highest occurrences (except for the first bin) occur at 2.10 (highest) and 3.76 d−1, closely followed by 1.06 d−1. Again, the ratio of ∼2 between two of the three most recurrent spacings indicates that rotation might be the relevant mechanism to explain the presence of a frequency spacing and its harmonic. However, the frequency spacing of 1.66 d−1, which probably corresponds to the rotation frequency of the fast-rotating hybrid pulsating component in the system (Samadi-Ghadim et al. 2020), is the highest occurrence among the individual spacings. Li et al. (2020a) derived 1.85 ± 0.01 d−1 for the near-core rotation rate. If this rate corresponds to the faster rotating component, the core versus surface rotation ratio would equal 1.11 ± 0.01, as expected from the general trend found by Li et al. (2020a). The recurrent spacing of 1.06 d−1 might correspond to the more slowly rotating δ Sct component, although Samadi-Ghadim et al. (2020) proposed a rotation rate of 0.42 d−1. In this case, the orbital frequency is unresolved.
Fourth, KIC 9775454 shows a remarkably sparse distribution in frequency spacing. The two highest peaks (except for the first bin) occur at the spacings of 0.13 and 2.18 d−1 (highest). The latter, and most recurrent, spacing is accompanied by a few nearby, almost equally frequent spacings located at 2.07, 2.26, and 2.35 d−1. This suggests that one of these spacings is the rotational frequency of the hybrid pulsator (component A; in the case of ∼2 d−1, it is probably variable). If we consider the fact that the primary component has v sin i = 65 km s−1, adopting a default radius of 1.8 R⊙, corresponding to its Teff (Gorda & Svechnikov 1998), and a frequency of 2.18 d−1 as the rotational frequency implies veq = 199 km s−1 and a surface inclination angle of ∼19° as possible values. The alternative choice (with 0.13 d−1) would give an impossible value of 12 km s−1 for veq. The orbital frequency is unresolved here as well.
6. Summary and conclusions
In the previous sections, we improved the orbital solutions for four spectroscopic systems from our sample of 49 A/F-type Kepler hybrid stars. We improved the orbital solutions for the systems KIC 4480321, 5219533, 8975515, and KIC 9775454, by considering the TDs as well as the RVs and performing a simultaneous modelling of both data types. This method allows us to refine the parameters of all the long-period systems, in particular the outer orbits of the triple systems KIC 4480321 and KIC 5219533. We derived full-fledged SB2 orbital solutions for the long-period binary systems KIC 8975515 and KIC 9775454, and obtained reliable mass ratios for the first time. Furthermore, the applied methodology enables us to identify the component with the faster δ Sct-type pulsations since the TDs are generally linked with the higher frequencies.
For KIC 4480321, we conclude that the faster rotating and more massive outer component (component C) exhibits the short-period δ Sct pulsations. Component C is shown to have a minimum mass of 1.60 ± 0.05 M⊙, which can be used as a constraint for asteroseismic modelling. For KIC 5219533, we significantly improve the accuracy of the orbital solutions described by Catanzaro et al. (2019a). We also show that both orbits are very probably coplanar and that the δ Sct pulsator is the faster spinning and more massive outer component (component C). For KIC 8975515, we derived an accurate mass ratio (q = 0.83 ± 0.05) and established that the faster rotating component (component A) exhibits δ Sct-type pulsations (this concerns the hybrid pulsator). Furthermore, the binary is probably viewed under a low inclination angle (≈12°), which is also useful information in an asteroseismic context. For KIC 9775454, we obtained a (precise) mass ratio for the first time (q = 0.42 ± 0.02). We conclude that the more massive component of the system (component A) is the hybrid pulsating star.
From our study of the normalized distributions of the frequency spacings in the high-frequency regime of the Fourier transforms, we find no firm evidence for the occurrence of tidal splitting among the recurrent frequency spacings of the triple systems with close (inner) companions. In the case of the long-period orbits (all systems), it is impossible to resolve the frequency multiplets based on the Kepler data only. On the other hand, due to the presence of some harmonic frequencies among the most frequent spacings, we propose the mechanism of rotational splitting for KIC 4480321 (with a plausible surface rotation rate of 1.63 d−1), KIC 5219533 (with a possible surface rotation rate of 0.55 d−1), and KIC 8975515 (with a previously derived surface rotation rate of 1.66 d−1 for the primary and a possible surface rotation rate of 1.06 d−1 for the secondary component). In the particular case of KIC 9775454, we propose a surface rotation rate of the order of 2 d−1, which appears as a bunch of closely spaced repeated spacings in the distribution and indicates a possibly variable nature. Detailed analyses of the pulsations in the low-frequency regime of the Fourier transforms of these systems – including pattern recognition and period spacings of the gravity (and sometimes Rossby) modes for the (rapidly rotating) genuine hybrid pulsators – can provide the near-core rotation rates and a confirmation of the hereby proposed surface rotation rates (e.g. Van Reeth et al. 2016; Li et al. 2020a,b).
Acknowledgments
The authors wish to thank the Kepler team for providing the high-quality data collected with the Kepler satellite mission. They furthermore thank the HERMES Consortium for enabling the production of the high-resolution ground-based spectra, and D. Bowman et al. for authorizing the use of the additional spectra of KIC 5219533. ÁS and ZsB acknowledge financial support of the Lendület Program LP2018-7/2019 of the Hungarian Academy of Sciences. MS acknowledges the OV PPP PostdocMUNI grant with nr. CZ.02.2.69/0.0/0.0/16_027/0008360 and the MSMT Inter Transfer program LTT20015. ZsB acknowledges the support provided by the National Research, Development and Innovation Fund of Hungary, financed under the PD17 funding scheme (project PD-123910) and by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. HL acknowledges support from the grant DFG with nr. LE1102/3-1. ASG acknowledges financial support received from the ALMA-CONICYT grant with nr. 31170029. We thank the referee, Prof. H. Shibahashi, for detailed comments and constructive criticism. We are also grateful for support received from the Belgo-Indian Network for Astronomy & Astrophysics (BINA-1 and BINA-2).
References
- Balona, L. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2015, MNRAS, 452, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Barentsen, G., & Lightkurve, C. 2020, Am. Astron. Soc. Meeting Abstracts, 409.04 [Google Scholar]
- Bowman, D. M. 2017, Amplitude Modulation of Pulsation Modes in Delta Scuti Stars (Springer International Publishing) [CrossRef] [Google Scholar]
- Bowman, D. M., Johnston, C., Tkachenko, A., et al. 2019, ApJ, 883, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, A20 [Google Scholar]
- Catanzaro, G., Gangi, M., Giarrusso, M., Munari, M., & Leone, F. 2019a, MNRAS, 487, 919 [Google Scholar]
- Catanzaro, G., Gangi, M., Giarrusso, M., Munari, M., & Leone, F. 2019b, MNRAS, 488, 480 [Google Scholar]
- Fauvaud, S., Sareyan, J. P., Ribas, I., et al. 2010, A&A, 515, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration 2018, VizieR Online Data Catalog: I/345 [Google Scholar]
- Gorda, S. Y., & Svechnikov, M. A. 1998, Astron. Rep., 42, 793 [Google Scholar]
- Grigahcène, A., Antoci, V., Balona, L., et al. 2010, ApJ, 713, L192 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Z., Fuller, J., Shporer, A., et al. 2019, ApJ, 885, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Irwin, J. B. 1952, ApJ, 116, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lampens, P., Frémat, Y., Vermeylen, L., et al. 2018, A&A, 610, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Li, G., Bedding, T. R., Murphy, S. J., et al. 2019, MNRAS, 482, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., et al. 2020a, MNRAS, 491, 3586 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Guo, Z., Fuller, J., et al. 2020b, MNRAS, 497, 4363 [CrossRef] [Google Scholar]
- Moffett, T. J., Barnes, T. G., Fekel, I., et al. 1988, AJ, 95, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., & Shibahashi, H. 2015, MNRAS, 450, 4475 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., Bedding, T. R., Shibahashi, H., Kurtz, D. W., & Kjeldsen, H. 2014, MNRAS, 441, 2515 [Google Scholar]
- Murphy, S. J., Shibahashi, H., & Bedding, T. R. 2016, MNRAS, 461, 4215 [Google Scholar]
- Murphy, S. J., Moe, M., Kurtz, D. W., et al. 2018, MNRAS, 474, 4322 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, M. B., Gizon, L., Schunker, H., & Karoff, C. 2013, A&A, 557, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pribulla, T., Chochol, D., Tremko, J., & Kreiner, J. M. 2005, in The Light-Time Effect in Astrophysics: Causes and cures of the O-C diagram, ed. C. Sterken, ASP Conf. Ser., 335, 103 [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renson, P., & Manfroid, J. 2009, A&A, 498, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi Ghadim, A., Lampens, P., & Jassur, D. M. 2018, Acta Astron., 68, 425 [Google Scholar]
- Samadi-Ghadim, A., Lampens, P., Jassur, D. M., & Jofré, P. 2020, A&A, 638, A57 [EDP Sciences] [Google Scholar]
- Shibahashi, H., & Kurtz, D. W. 2012, MNRAS, 422, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, J., David-Uraz, A., Chowdhury, S., et al. 2019, MNRAS, 487, 4695 [CrossRef] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Values and standard deviations of the constrained orbital parameters for KIC 4480321.
Values and standard deviations of the constrained orbital parameters for KIC 5219533.
Values and standard deviations of the constrained orbital parameters for KIC 8975515.
Values and standard deviations of the constrained parameters of the orbital solution for KIC 9775454.
All Figures
 |
Fig. 1. Data and outer orbital solution for KIC 4480321. The TDs and RVs (respectively filled pink and unfilled red symbols for component C; blue symbols for the centre of mass of components A and B) are overlaid with the AB-C orbital solution (solid lines). The residuals are shown in the bottom panel. |
| In the text | |
 |
Fig. 2. Data and orbital solutions for KIC 5219533. Left: inner orbit based on the HERMES RVs. The RVs (red symbols for component A; blue symbols for component B) are overlaid with the A-B orbital solution (solid lines). Right: outer orbit based on the HERMES RVs and the TDs from the Kepler photometry. The TDs and RVs (respectively filled pink and unfilled red symbols for component C; blue symbols for the centre of mass of components A and B) are overlaid with the AB-C orbital solution (solid lines). The residuals are shown in the bottom panels. |
| In the text | |
 |
Fig. 3. Data and orbital solution for KIC 8975515. Left: orbit (number 1) based on the HERMES RVs. The RVs (red symbols for component A; blue symbols for component B) are overlaid with a preliminary orbital solution of type SB2, however without much constraint on the amplitude KA. Right: orbit (number 2) based on the HERMES RVs and the TDs from the Kepler photometry. The TDs and RVs (respectively filled pink and unfilled red symbols for component A; blue symbols for component B) are overlaid with the A-B orbital solution (solid lines). The residuals are shown in the bottom panels. |
| In the text | |
 |
Fig. 4. Cross-correlation functions of the residual spectra of KIC 9775454 computed with a mask of type K0 for three different dates. |
| In the text | |
 |
Fig. 5. Data and orbital solution for KIC 9775454. The TDs (filled pink symbols) and the RVs (unfilled red symbols for component A; blue symbols for component B) are overlaid with the A-B orbital solution (solid lines). The residuals are shown in the bottom panel. |
| In the text | |
 |
Fig. 6. Lomb-Scargle periodograms derived from the Kepler data for the systems KIC 4480321 (top left), 5219533 (top right), 8975515 (bottom left), and KIC 9775454 (bottom right). The frequencies plotted in orange illustrate the full spectrum across the range [0–24.5] d−1, and the frequencies over-plotted in black have a signal-to-noise ratio higher than 4. |
| In the text | |
 |
Fig. 7. Normalized density functions of the frequency spacings across the range [0–4] d−1 derived from the Kepler-based periodograms for the systems KIC 4480321 (top left), 5219533 (top right), 8975515 (bottom left), and KIC 9775454 (bottom right). The highest occurrences are marked by grey arrows. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.