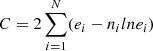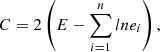EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 625 (May 2019) A&A, 625 (2019) A131 Full HTML
Free Access
Issue
A&A
Volume 625, May 2019
Article Number A131
Number of page(s) 5
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201834234
Published online 27 May 2019

© ESO 2019

1. Introduction

X-ray emission is a ubiquitous feature of active galactic nuclei (AGN), and X-ray surveys provide the most unbiased way to detect them. In contrast to optical radiation, X-rays are not easily absorbed unless they encounter extreme hydrogen column densities of the order of 1024 cm−2. Moreover, X-rays have only negligible contamination from stellar processes, unlike the infrared and the optical emission. For these reasons, the X-ray surveys performed with Chandra and XMM-Newton in the 0.3−10 keV band have very efficiently mapped the AGN population and its evolution (Brandt & Alexander 2015). These surveys have resolved more than 80% of the integrated X-ray light, the X-ray background, to AGN (Luo et al. 2017). At harder energies > 10 keV, where most of the X-ray background energy density is produced (Revnivtsev et al. 2003; Frontera et al. 2007; Churazov et al. 2007; Ajello et al. 2012), the picture is far less clear, mainly because we lack focusing X-ray instruments that would enable high-sensitivity X-ray observations. Nevertheless, the coded-mask instruments of the INTEGRAL and Swift/Gehrels missions have probed AGN at low redshifts, typically z < 0.1 (Malizia et al. 2009; Ajello et al. 2012; Vasudevan et al. 2013; Oh et al. 2018).

A drastic leap forward in our knowledge of the hard X-ray universe has been achieved with the launch of the Nuclear Spectroscopic Telescope Array (NuSTAR) mission (Harrison et al. 2013). This mission observes the X-ray sky in the 3−80 keV band with an unprecedented sensitivity. It carries the first X-ray telescope that focuses X-rays with energies above 10 keV. The large effective area and the excellent (52 arcsec half-power diameter) spatial resolution of NuSTAR allow the detection of faint X-ray sources up to two orders of magnitude fainter than the faintest detected Swift/Gehrels – BAT (Burst Alert Telescope) sources. The majority of the serendipitous NuSTAR sources in the 8−24 keV band are associated with AGN at redshifts of z = 0.5−0.7 (Lansbury et al. 2017). Although NuSTAR has an excellent sensitivity, its field of view has a moderate size (∼12 arcmin diameter). The Swift/Gehrels and the INTEGRAL missions are therefore quite complementary to NuSTAR because only they can observe large swaths of the sky and hence large cosmological volumes.

Harrison et al. (2016) presented the NuSTAR X-ray number counts in the 8−24 keV band. They reach fluxes as faint as 2 × 10−14 erg cm−2 s−1 and resolve 33−39% of the X-ray background in this energy band. The measured NuSTAR counts lie significantly above a simple extrapolation with a Euclidean slope of the Swift/BAT number counts measured at higher fluxes. Harrison et al. (2016) asserted that this may suggest strong AGN evolution between the average redshift of the BAT AGN (z < 0.1) and the redshift of the NuSTAR sources (z ∼ 0.7). Aird et al. (2015) derived the NuSTAR AGN luminosity function in the 8−24 keV band. They found an excess number of sources relative to the BAT luminosity function. In contrast, the luminosity function of Ueda et al. (2014) in the 2−10 keV band agrees well with the BAT luminosity function (Ajello et al. 2012), assuming a spectrum with a reflection parameter of R ∼ 1 (see Magdziarz & Zdziarski 1995), which corresponds to a 5% fraction of reflected emission in the 2−10 keV band (e.g. Akylas et al. 2012). Aird et al. (2015) suggested that a way to achieve agreement between the Ueda et al. (2014) and the NuSTAR luminosity functions is to increase the reflection parameter to R ∼ 2, corresponding to a reflection fraction of 10% in the 2−10 keV band. However, this leaves BAT in disagreement with both the NuSTAR and the Chandra luminosity functions.

Here, we address this problem anew by deriving the number count distributions from the newly released 105-month BAT survey (14−195 keV) and the NuSTAR serendipitous source catalogue of Lansbury et al. (2017) in the 3−8 and 8−24 keV bands. We compare these distributions using the X-ray population synthesis models of Akylas et al. (2012), assuming different AGN spectral models: spectral indices, a reflection component, and a high-energy spectral cut-off.

2. Data

2.1. Swift/Gehrels

The Swift Gamma-Ray Burst (GRB) observatory (Gehrels et al. 2004) was launched in November 2004 and has continually observed the hard X-ray (14−195 keV) sky with the BAT. BAT is a large coded-mask telescope, optimised to detect transient GRBs, and it is designed with a very wide field of view of ∼60 × 100°.

The data presented in this paper stem from the analysis of the sources detected in the 105 months of observations of the BAT hard X-ray detector on the Swift/Gehrels GRB observatory (Oh et al. 2018). The 105-month BAT survey is a uniform hard X-ray all-sky survey with a sensitivity of 8.40 × 10−12 ergs s−1 cm−2 over 90% of the sky and 7.24 × 10−12 ergs s−1 cm−2 over 50% of the sky in the 14−195 keV band. The BAT 105-month catalogue provides 1632 hard X-ray sources in the 14−195 keV band above the 4.8σ significance level, with 422 new detections compared to the previous 70-month catalogue release (Baumgartner et al. 2013). Our study is limited to the AGN population, and therefore all Galactic and extended sources have been excluded. In particular, the following types of sources have been used: Seyfert I (379), Seyfert II (448), low-ionization nuclear emission line region (LINER) galaxies (6), unknown AGN (114), multiple galaxies (10), beamed AGN (158), and unidentified sources (129). Most of the 129 unidentified sources are located outside the Galactic plane, and therefore we expect that the majority of them are most likely AGN.

2.2. NuSTAR

NuSTAR (Harrison et al. 2013) launched in June 2012 and is the first orbiting X-ray observatory that focuses light at high energies (E > 10 keV). It consists of two co-aligned focal plane modules (FPMs) that are identical in design. Each FPM covers the same 12 × 12 arcmin portion of the sky and comprises four cadmium-zinc-tellurium detectors. NuSTAR operates between 3 and 79 keV and provides an improvement of at least two orders of magnitude in sensitivity compared to previous hard X-ray observatories operating at energies E > 10 keV.

In our analysis, we used the data from the first full catalogue for the NuSTAR serendipitous survey (Lansbury et al. 2017). The catalogue contains data taken during the first 40 months of the NuSTAR operation, with an area coverage of 13 deg2. For this study we used the 163 sources detected in the 8−24 keV energy range and the 273 sources detected in the 3−8 keV band. We removed all the sources that are associated with the primary science targets and the Galactic sources. Moreover, in order to further achieve the minimum contamination of the sample from non-AGN sources, all detections within |b| < 20 deg were removed. The final hard X-ray sample (8−24 keV) contains 106 sources and the soft X-ray sample (3−8 keV) contains 171 sources.

3. Number count distribution

In this section, we derive the number count distributions for the BAT (14−195 keV) and the NuSTAR data (both the 8−24 and the 3−8 keV bands). The area curves were taken from Oh et al. (2018) and Lansbury (priv. comm.) for the BAT and the NuSTAR observations, respectively. We use a novel C-stat estimator that makes use of the unbinned data to fit the derived distributions. We compare our findings in the hard 8−24 keV band with previous NuSTAR estimates and in the soft 3−8 keV NuSTAR band with precise measurements of the Chandra number count distribution in the 2−10 keV band. Finally, we compare our results with the predictions of X-ray population synthesis models.

3.1. Method

In order to fit the number count distributions, we applied for the first time the maximum likelihood statistic for Poisson data given in Cash (1979). Normally, differential number count distributions are binned in order to obtain at least 15 sources in each bin to apply Gaussian statistics. However, the binning may result in a loss of information. Cash (1979) showed that the statistic estimator

C = 2 ∑ i = 1 N ( e i − n i l n e i ) $$ \begin{aligned} C=2\sum \limits _{i=1}^{N} (e_i - n_i lne_i) \end{aligned} $$(1)

allows bins to be picked in an almost arbitrary way, while δC = C − Cmin (Cmin is the minimum value of the estimator) is distributed as δχ2 with q degrees of freedom, and the same technique for generation of confidence intervals could apply in the Poisson limit. In the equation above, N is the finite number of bins, ei is the expected number (predicted by the model), and ni is the observed number in the ith bin. In a very fine mesh of bins, ni becomes zero or one, and the statistic takes the form

C = 2 ( E − ∑ i = 1 n l n e i ) , $$ \begin{aligned} C=2\left(E-\sum \limits _{i=1}^{n} lne_i\right), \end{aligned} $$(2)

where E is the total expected counts from the experiment, and the summation is now over each of the observed photons. We assumed that the differential LogN-LogS distribution is described by a single power-law model with slope β, that is, log10 (dN/dS) = k + βlog10(S), and therefore we neglected the break of the number counts that normally appears around a 2−10 keV flux of 10−14 erg cm−2 s−1 (Georgakakis et al. 2008). Hereafter, we quote the slope of the integral number counts, α, in order to facilitate the comparison with other results mentioned in the literature. The slope of the integral number counts α is related to the slope of the differential number counts β with the relation α = β − 1.

We calculated the minimum value of the C estimator (Eq. (2)) using a very fine grid for the values of the slope β and the normalisation parameter k to obtain the best fit solution. Then we calculated the 90% confidence intervals for two interesting parameters by applying the criterion δC = C − Cmin = 4.61 (Press et al. 2007).

3.2. Swift/Gehrels 14−195 keV

In Fig. 1 we plot the differential and integrated number count distributions in the 14−195 keV band for the BAT sample. The best-fit slope of the derived LogN-LogS and its 90% uncertainty is α = 1.51 ± 0.10 and the normalisation log(k) = − 18.22 ± 0.63. Similar findings have been presented in Tueller et al. (2008). These authors compiled a sample of 103 AGN from the first nine-month BAT survey. They fit a power law to their logN-logS and found a slope of 1.42 ± 0.14.

thumbnail Fig. 1.

Right panel: differential number count distribution in the 14−195 keV band for the BAT sample (blue points). The green dotted line is a characteristic model that fits the data at the 90% level. Left panel: integrated number count distribution. The shaded area defines the 90% confidence interval. The long-short dashed line shows previous results of Tueller et al. (2008).

Next, we used the X-ray population synthesis models presented in Akylas et al. (2012) to estimate the average AGN spectral parameters that are consistent with the observed number count distribution. We created a set of logN-logS predictions letting the photon index Γ, and the high-energy cut-off vary freely, while we fixed the amount of the reflected emission to 3% of the total 2−10 keV luminosity. The reflected emission has a weak effect on the number count distribution of the total AGN population, and the selected value of 3% is typical of the values reported in the literature (e.g. Del Moro et al. 2017; Ricci et al. 2017; Zappacosta et al. 2018). The characteristic model presented in Fig. 1 corresponds to Γ = 1.9 and EC = 130 keV and is consistent with the data at the 90% confidence level. This value of the cut-off is entirely consistent with the INTEGRAL observations of 41 type-1 Seyfert-1 galaxies. Malizia et al. (2014) found EC = 128 keV with a standard deviation of 46 keV. More recent work on the cut-off energy using NuSTAR data (Tortosa et al. 2018) is in overall agreement with our work. We note that when we adjusted the reflection parameter to 1% and 5%, we obtained a model consistent with the observed logN-logS for Γ = 1.9 and EC = 200 keV or EC = 80 keV, respectively.

3.3. NuSTAR 8−24 keV

In Fig. 2 we plot the differential and integrated number count distributions of the sources detected in the NuSTAR serendipitous catalogue in the 8−24 keV band. The best-fit power-law slope and its 90% uncertainty is α = 1.71 ± 0.20 and the normalisation is log(k) = − 21.04 ± 1.51. This result is marginally consistent with the canonical Euclidean value of 1.5. We compared our results with those presented in Harrison et al. (2016). These authors measured the 8−24 keV number count distribution by combining data from the following NuSTAR surveys: (a) the serendipitous source catalogue, (b) the COSMOS survey, Civano et al. (2015), (c) the Extended Chandra Deep Field South (ECDFS, Mullaney et al. 2015) and (d) the Extended Groth Strip region (EGS, Aird et al., in prep.). Their best-fit power law is very similar to our result with α = 1.76 ± 0.10. Our estimates are 10% higher in terms of the normalisation at the flux of 10−13 erg cm−2 s−1. We note, however, that we considered the full serendipitous survey catalogue presented in Lansbury et al. (2017), while Harrison et al. (2016) incorporated a smaller part of the survey. Their results are included in Fig. 2 for comparison.

thumbnail Fig. 2.

Right panel: differential number count distribution in the 8−24 keV band for the NuSTAR sample. The green dotted line corresponds to the characteristic model plotted in Fig. 1, now computed in the 8−24 keV band. Left panel: integrated number count distribution. The shaded area defines the 90% confidence interval. The yellow solid line is the best C-statistic solution to the NuSTAR counts, with a slope fixed to 1.5. The black crosses represent the NuSTAR results presented in Harrison et al. (2016), and the long dashed red line shows the estimates of Zappacosta et al. (2018). For comparison, we also show the results from Mullaney et al. (2015; red filled squares) and Civano et al. (2015; violet open squares).

In the same figure, we plot the prediction from the population synthesis model presented in Fig. 1 for the BAT observations, calculated now in the 8−24 keV band. There is a reasonable agreement between the model and the data in the bright part of the number count distribution (f8−24 keV ∼ 2 × 10−13 erg cm−2 s−1), while our model is far below the number count distribution at fainter fluxes. Recently, Zappacosta et al. (2018) analysed a bright sample of 63 sources (f8−24 keV >  7 × 10−14 erg cm−2 s−1) from the multi-tiered NuSTAR Extragalactic Survey program. Their estimates on the number count distribution suggest a flatter slope (α = 1.36 ± 0.28), but this is still consistent with the Euclidean slope of α = 1.5 within the errors. In Fig. 2 the red dashed line shows their results. There is a notable agreement between their estimates and our results. Finally, we give the best C-stat solution to the NuSTAR counts, with a slope fixed to 1.5, to enable the direct comparison of our predictions with the observed counts. In this case, the normalisation of the logN-logS becomes about a factor of two higher than our model.

3.4. NuSTAR 3−8 keV

In Fig. 3 we plot the differential and integrated number count distributions in the 3−8 keV band using the NuSTAR serendipitous source catalogue. The best-fit slope of the distribution and its 90% uncertainty is α = 1.82 ± 0.15 and the normalisation log(k) = − 22.98 ± 1.22. The observed distribution is consistent with the canonical Euclidean value of 1.5 at the 99.5% confidence interval. This estimate is also in excellent agreement with the slope found by Harrison et al. (2016), α = 1.81 ± 0.08.

thumbnail Fig. 3.

Right panel: differential number count distribution in the 3−8 keV band for the NuSTAR sample. The green dotted line corresponds to the characteristic model plotted in Fig. 1, computed here in the 3−8 keV band. Left panel: shaded area defines the 90% confidence interval based on the C-statistic minimisation estimator. The crossed points show the number count distribution of Georgakakis et al. (2008).

In the same figure we plot the model presented in Figs. 1 and 2 (green dotted line). Similarly to the NuSTAR results in the 8−24 keV band, there is a marked difference between our models and the NuSTAR data at faint fluxes (< 7 × 10−14 erg cm−2 s−1), while there is good agreement at brighter fluxes.

Next, we included in our comparison the 2−10 keV Chandra number counts presented in Georgakakis et al. (2008). These authors used a novel technique that correctly accounts for the observational biases that affect the probability of detecting a source of a given X-ray flux. They estimated the X-ray source counts by combining deep pencil-beam and shallow wide-area Chandra observations. Their sample has a total of 6295 unique sources over an area of 11.8 deg2. The flux conversion from their 2−10 keV band to the 3−8 keV adopted here was made assuming a simple power-law model with Γ = 1.9. Because the energy width of the bandpasses is limited, the choice of the spectral slope has a weak effect on the conversion from the 2−10 keV to the 3−8 keV band. Similarly to the 8−24 keV results, the NuSTAR number count distribution nicely matches the Chandra data only at the brighter fluxes. It is also evident from the plot that the Chandra number counts are consistent with the same standard model that also describes the BAT logN-logS very well.

4. Summary

The hard X-ray sky above 10 keV has been observed in unprecedented sensitivity with the NuSTAR mission. A difference between the BAT (14−195 keV) and the 8−24 keV NuSTAR counts has been reported in the literature in the sense that the former lies well below the latter. In the light of this disagreement, we estimated the number count distribution from the recently released 105-month Swift/BAT AGN catalogue in the 14−195 keV band. For comparison we also derived the NuSTAR number counts from the serendipitous source catalogue of Lansbury et al. (2017). We used a novel approach for fitting the number count distribution by applying the C-statistic estimator on the unbinned data. We compared the number count distributions between different bands using our X-ray AGN population synthesis models. The results are presented in Table 1 and can be summarized as follows:

Table 1.

Summary of the integral LogN-LogS results.

1. The BAT logN-logS presents a Euclidean slope of α = 1.51 ± 0.10. This result is consistent with earlier estimates of the BAT logN-logS (Tueller et al. 2008), which used considerably fewer sources.

We used our X-ray AGN population synthesis code (Akylas et al. 2012) to find physically motivated models that fit these observations. A standard AGN spectral model with a photon index 1.9, a high-energy cut-off 130 keV, and reflected emission of 3% of the total 2−10 keV flux matches the BAT number count distribution very well.

We also compared the BAT number counts with the Chandra results in the softer 2−10 keV band obtained by Georgakakis et al. (2008) by estimating the above standard model in the 2−10 keV band. Again, there is a notable agreement between our population synthesis model predictions and the Chandra results. This demonstrates that reasonable assumptions on the spectral shape of AGN should lead to consistent modelling of the number count distributions in the Chandra and the BAT bands.

2. The NuSTAR number count distribution in the 8−24 keV band presents a slope of α = 1.71 ± 0.20. This is steeper than the Euclidean slope, but still consistent at the 90% confidence level. In order to facilitate the comparison, we therefore fixed the slope to 1.5. Then it is evident that the NuSTAR number count distribution lies above the BAT counts by about a factor of two. It is evident from Fig. 2 that the same population synthesis model that successfully describes both the BAT and the Chandra observations agrees only with the bright end of the NuSTAR logN-logS. This result is further confirmed by recent findings of Zappacosta et al. (2018). Their estimates on the number count distribution of a bright sample (> 7 × 10−14 erg cm−2 s−1) from the NuSTAR Extragalactic Survey program nicely agree with our logN-logS and the predictions of our standard model in the 8−24 keV band.

3. The NuSTAR number count distribution in the soft 3−8 keV band presents a slope α = 1.82 ± 0.15, which is significantly steeper than the Euclidean slope at the 99.5% confidence level. Similarly to the results in the 8−24 keV band, only the brightest part of the NuSTAR soft number count distribution is compatible with the Chandra results and the predictions of our standard model.

Instead of using the number count distributions, Aird et al. (2015) compared the luminosity function derived in the following bands: Chandra 2−10 keV, NuSTAR 8−24 keV and BAT 14−195 keV. Assuming a reflection fraction of 5% in the 2−10 keV band, they found a good agreement between the BAT and the Chandra luminosity function, while NuSTAR is far above the previous two luminosity functions. When they assumed a much stronger reflection component of 10%, the NuSTAR 8−24 keV and the Chandra luminosity functions agreed. However, this came at the cost of the BAT luminosity function, which remained far below the other two. Using our number count modelling instead, we suggest that this disagreement could be circumvented only by assuming a rather extreme AGN spectral model, with a power-law high-energy cut-off of less than 50 keV and at the same time a strong reflection component (reflection fraction greater that 10% in the 2−10 keV band). This is because the increased reflection component significantly enhances the flux in both the 8−24 keV and the 14−195 keV bands, while the low-energy cut-off cancels this gain only in the 14−195 keV band. Thus the net result is a considerable increase in the 8−24 keV band. However, even in this case, the main problem remains in the comparison between the NuSTAR 3−8 keV and the Chandra 2−10 keV number count distributions.

Interestingly, this does not appear to be a problem of the serendipitous survey alone. The logN-logS in both the COSMOS and the CDFS fields also present an abrupt upturn, but at different fluxes. These findings may suggest that a fraction of spurious sources has been included at faint fluxes. However, this is not very likely given the high fraction ∼85% of soft X-ray detected counterparts of the NuSTAR sources, which does not vary significantly with flux. Alternatively, the NuSTAR area curve could be underestimated at faint fluxes, that is, near the centre of the field of view where the sensitivity is the highest. Figure 2 shows that at the faintest flux bin, the area curve in the 8−24 keV band is expected to have been underestimated by a factor of about 2.5. Finally, the possibility that the Eddington bias plays some role cannot be ruled out. It is unclear, however, why the Eddington bias affects fluxes that are a factor of four brighter than the survey flux limit, given that the flux errors are moderate, that is, of the order of 10%.

Acknowledgments

We would like to thank the anonymous referee for many suggestions that helped us to improve the paper. We are also grateful to George Lansbury and James Aird for many useful discussions.

References

  1. Aird, J., Alexander, D. M., Ballantyne, D. R., et al. 2015, ApJ, 815, 66 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ajello, M., Alexander, D. M., Greiner, J., et al. 2012, ApJ, 749, 21 [NASA ADS] [CrossRef] [Google Scholar]
  3. Akylas, A., Georgakakis, A., Georgantopoulos, I., Brightman, M., & Nandra, K. 2012, A&A, 546, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Brandt, W. N., & Alexander, D. M. 2015, A&ARv, 23, 1 [Google Scholar]
  6. Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
  7. Churazov, E., Sunyaev, R., Revnivtsev, M., et al. 2007, A&A, 467, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Civano, F., Hickox, R. C., Puccetti, S., et al. 2015, ApJ, 808, 185 [NASA ADS] [CrossRef] [Google Scholar]
  9. Del Moro, A., Alexander, D. M., Aird, J. A., et al. 2017, ApJ, 849, 57 [NASA ADS] [CrossRef] [Google Scholar]
  10. Frontera, F., Orlandini, M., Landi, R., et al. 2007, ApJ, 666, 86 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  12. Georgakakis, A., Nandra, K., Laird, E. S., Aird, J., & Trichas, M. 2008, MNRAS, 388, 1205 [NASA ADS] [CrossRef] [Google Scholar]
  13. Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
  14. Harrison, F. A., Aird, J., Civano, F., et al. 2016, ApJ, 831, 185 [NASA ADS] [CrossRef] [Google Scholar]
  15. Lansbury, G. B., Stern, D., Aird, J., et al. 2017, ApJ, 836, 99 [NASA ADS] [CrossRef] [Google Scholar]
  16. Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2017, ApJS, 228, 2 [Google Scholar]
  17. Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
  18. Malizia, A., Stephen, J. B., Bassani, L., et al. 2009, MNRAS, 399, 944 [NASA ADS] [CrossRef] [Google Scholar]
  19. Malizia, A., Molina, M., Bassani, L., et al. 2014, ApJ, 782, L25 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mullaney, J. R., Del-Moro, A., Aird, J., et al. 2015, ApJ, 808, 185 [NASA ADS] [CrossRef] [Google Scholar]
  21. Oh, K., Koss, M., Markwardt, C. B., et al. 2018, ApJS, 235, 4 [NASA ADS] [CrossRef] [Google Scholar]
  22. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. F. 2007, Numerical Recipes: The Art of Scientific Computing, Third Edition (Cambridge: Cambridge University Press) [Google Scholar]
  23. Revnivtsev, M., Gilfanov, M., Sunyaev, R., Jahoda, K., & Markwardt, C. 2003, A&A, 411, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [NASA ADS] [CrossRef] [Google Scholar]
  25. Tortosa, A., Bianchi, S., Marinucci, A., Matt, G., & Petrucci, P. O. 2018, A&A, 614, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Tueller, J., Mushotzky, R. F., Barthelmy, S., et al. 2008, ApJ, 681, 113 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ueda, Y., Akiyama, M., Hasinger, G., Miyaji, T., & Watson, M. G. 2014, ApJ, 786, 104 [NASA ADS] [CrossRef] [Google Scholar]
  28. Vasudevan, R. V., Mushotzky, R. F., & Gandhi, P. 2013, ApJ, 770, L37 [NASA ADS] [CrossRef] [Google Scholar]
  29. Zappacosta, L., Comastri, A., Civano, F., et al. 2018, ApJ, 854, 33 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Summary of the integral LogN-LogS results.

In the text

All Figures

thumbnail Fig. 1.

Right panel: differential number count distribution in the 14−195 keV band for the BAT sample (blue points). The green dotted line is a characteristic model that fits the data at the 90% level. Left panel: integrated number count distribution. The shaded area defines the 90% confidence interval. The long-short dashed line shows previous results of Tueller et al. (2008).
In the text
thumbnail Fig. 2.

Right panel: differential number count distribution in the 8−24 keV band for the NuSTAR sample. The green dotted line corresponds to the characteristic model plotted in Fig. 1, now computed in the 8−24 keV band. Left panel: integrated number count distribution. The shaded area defines the 90% confidence interval. The yellow solid line is the best C-statistic solution to the NuSTAR counts, with a slope fixed to 1.5. The black crosses represent the NuSTAR results presented in Harrison et al. (2016), and the long dashed red line shows the estimates of Zappacosta et al. (2018). For comparison, we also show the results from Mullaney et al. (2015; red filled squares) and Civano et al. (2015; violet open squares).
In the text
thumbnail Fig. 3.

Right panel: differential number count distribution in the 3−8 keV band for the NuSTAR sample. The green dotted line corresponds to the characteristic model plotted in Fig. 1, computed here in the 3−8 keV band. Left panel: shaded area defines the 90% confidence interval based on the C-statistic minimisation estimator. The crossed points show the number count distribution of Georgakakis et al. (2008).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.