EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 604 (August 2017) A&A, 604 (2017) A26 Full HTML
Free Access
Issue
A&A
Volume 604, August 2017
Article Number A26
Number of page(s) 5
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201629725
Published online 27 July 2017

© ESO, 2017

1. Introduction

The 14N/15N isotopic ratio for atmospheric N2 is 273 ± 1 (Nier 1950), a value comparable to that of the local interstellar medium (ISM) obtained from observations in objects where nitrogen fractionation should be negligible: 274 ± 18 estimated from the C14N/C15N ratio in diffuse molecular clouds (Ritchey et al. 2015), and 290 ± 40 derived from the gradient of the 14N/15N ratio in the Galaxy observed towards warm molecular clouds (Adande & Ziurys 2012).

However, in the solar system the nitrogen isotope composition varies over a broad range of values of 14N/15N: from 441 ± 6, the elemental ratio of the protosolar nebula (Marty et al. 2011), to 46 ± 2 in hotspots of the Isheyevo meteorite (Briani et al. 2009). The 14N/15N ratios measured in comets also show high enrichments in 15N (Mumma & Charnley 2011; Bockelée-Morvan et al. 2015). While the processes of nitrogen fractionation responsible for this variation are still under debate (Füri & Marty 2015), one possibility is disequilibrium ion-molecule reactions in cold, dense regions of the presolar nebula (e.g., Terzieva & Herbst 2000; Rodgers & Charnley 2008).

In dark molecular cloud cores the 14N/15N values span a wide range, where in general nitriles (HCN, HNC) show 15N enrichments, ammonia mostly shows depletion, and diazenylium ions (N2H+) show the highest depletion (see summary in Wirström et al. 2015) with, for example, 14N/15N = 1000 ± 200 in the starless cloud core L1544 (Bizzocchi et al. 2013). Recent observations toward 26 massive star-forming cores in different evolutionary stages show for the first time 15N enhancements in diazenylium, with values ranging from ~180 up to ~1300 (Fontani et al. 2015). The same objects typically show different 14N/15N ratios depending on the molecule observed, and spatial variations within cores are also observed, as for L1544 where the 14N/15N ratio in HCN varies in the range 140–360 (Hily-Blant et al. 2013). The discrepancy between ratios in the same cold core is explained in chemical models by the different gas-phase formation paths, and therefore different origins of the 15N fractionation, of molecules with –NH or –CN functional groups (Wirström et al. 2012). These models, however, predict a 15N enhancement in diazenylium at all evolutionary stages. In a more recent study, Roueff et al. (2015) found that the “main” N fractionation reaction, 15N + N2H+, does have an entrance barrier, and their chemical model therefore predicts the 14N/15N ratio in N2H+ to remain close to the elemental value.

The wide ranges of observed 14N/15N ratios in interstellar N2H+ currently present a major challenge for models of N fractionation. The chemical reaction networks of both Wirström et al. (2012) and Roueff et al. (2015) include 15N2 and other species containing two 15N atoms in their networks, but do not consider fractionation in the reactions forming these molecules, which could potentially result in substantial shifts in the 15N2H+/15NNH+/N15NH+/N2H+ abundance relations. Detections of doubly 15N-substituted species would provide a crucial constraint for these models, but spectroscopic data are almost completely lacking.

In practical terms, the diazenylium ion is the only feasible astrochemical tracer bearing two N atoms. A large body of rotational data is available for its normal species, N2H+ (Yu et al. 2009, and references therein), and ground-state rotational spectra of the singly 15N-substituted isotopologues (15NNH+ and N15NH+) are also well characterized (Dore et al. 2009; Yu et al. 2009). Moreover, deuterated isotopologues have been detected by millimeter-wave spectroscopy (see Yu et al. 2009, and references therein). For the 15N2H+ isotopologue, on the other hand, only the J = 1 ← 0 transition has been reported (Gudeman 1982), while 15N2D+ has never been detected in the laboratory. The present paper fills the gap, reporting the ground-state rotational spectra of these two doubly 15N substituted isotopologues up to the Terahertz region.

2. Experimental details and data analysis

The frequency-modulated (FM) absorption spectrometer used in this work is equipped with a negative glow discharge cell made of a Pyrex tube (3.25 m long and 5 cm in diameter) in order to synthesize in situ the substituted diazenylium ion. The radiation source can cover the millimeter- and submillimeter-wave region by frequency multiplication (× 3, × 4, × 6, × 8, or × 9) of a series of Gunn oscillators working in the regions 75–105 GHz and 114–133 GHz. The frequency stabilization of the Gunn oscillator is achieved by locking it to a centimeter-wave synthesizer, driven by a 5 MHz-rubidium frequency standard, by means of one phase-lock loop. FM is obtained by sine-wave modulating at 6 kHz the reference signal of the wide-band Gunn-synchronizer. Lock-in detection at 2f of the signal from a liquid-helium-cooled InSb hot electron bolometer provides a “second derivative” profile of the observed transition lines.

The molecular ion 15N2H+, or 15N2D+, was produced by a direct-current discharge of a few mA across two cylindrical hollow steel electrodes placed at either end of the cell, while a 1:1 mixture of 15N2 and H2, or D2, was flowing in Ar buffer gas. Cooling of the cell walls at ~80 K, by liquid nitrogen circulation, and magnetic confinement, by a 110 G axial field throughout the length of the discharge, provided the best conditions for the production of the diazenylium ion. No Doppler shift, due to the drift velocity of the absorbing species, should affect the transition frequencies, since the region of the low-density plasma where ions form, the negative glow, is a nearly field-free region. In addition, the nitrogen hyperfine structure is absent, since the 15N isotope has spin 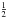12\hbox{$\tfrac{1}{2}$}, therefore recovering the transition frequency from the spectrum is straightforward by a line shape analysis of the experimental profile modeled as a Voigt function (see Fig. 1). However, pressure shift can perturb the line center: it is indeed a tiny effect, except for the J = 1 ← 0 transition (Cazzoli et al. 2012). The test shown in Fig. 2 confirms that its center frequency can shift by 20–30 kHz when the measurement is carried out at the usual buffer-gas pressure of about 10 mTorr, as was the case of Gudeman (1982), who determined a transition frequency of 88 264.083 MHz, which differs by + 25 kHz from the present determination of 15N2H+(1–0) at the limit of zero Ar pressure. For higher J values, the transition frequencies were obtained by repeated measurements at standard conditions, and their uncertainty resulted to be of a few kHz.

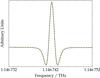thumbnail Fig. 1

Spectrum of the J = 13 ← 12 transition of 15N2H+ (solid black line) and fitted profile (dashed lime line); total integration time: 300 s; scanning rate: 0.66 MHz/s; modulation depth: 900 kHz.

thumbnail Fig. 2

Frequency shift of the J = 1 ← 0 transition of 15N2H+.

Table 1

Rotational transition frequencies and spectroscopic constants of 15N2H+ and 15N2D+.

Nine transitions were recorded for 15N2H+, with J from 0 to 12 in the range 88 GHz–1.147 THz, while for the deuterated species the nine transitions detected span the J-value range 3–15 and the frequency range 295 GHz–1.177 THz. The determined experimental transition frequencies were fitted, in an unweighted-least-squares procedure, to the standard frequency expression J + 1 ← J for the rotational transition: ν0=2B0(J+1)−4DJ(J+1)3+HJ(J+1)3[(J+2)3−J3],\begin{equation} \label{eq:roten} \nu_0 = 2B_0(J + 1) - 4D_J(J + 1)^3 + H_J(J+1)^3\left[(J+2)^3-J^3\right], \end{equation}(1)where B0, DJ, and HJ are the ground-state rotational, quartic, and sextic centrifugal distortion constants, respectively. The values of the spectroscopic constants of 15N2H+ and 15N2D+ derived from the fits are reported in Table 1. Table 1 reports also, for the two isotopologues, the lists of observed and predicted rotational transition frequencies up to 1.25 THz.

3. Discussion

3.1. Experimental results

The rotational spectra of the fully 15N-substituted isotopologues of the diazenylium ion have been recorded at millimeter and sub-millimeter wavelengths (88 GHz–1.2 THz). Nine rotational transitions were accurately determined for each isotopologue of the H- and D-containing pair. The determined line positions are accurate, because of the effort made to minimize the significance of the most common sources of systematic error. This reflects on the values of the rms error of fit residuals, 1.5 kHz for 15N2H+ and 1.6 kHz for 15N2D+, which are remarkably low values for Doppler limited measurements.

Thanks to the measurements above 1 THz, the centrifugal analysis has been carried out up to the sextic term: a comparison between the sextic centrifugal distortion constants determined for different isotopologues of N2H+ supports its accuracy (see Table 2). Theoretical estimates of the equilibrium value of the sextic centrifugal distortion constant (He) have been computed using the CFOUR program package1, with the adoption of the coupled-cluster singles and doubles approximation augmented by a perturbative treatment of triple excitations (CCSD(T), Raghavachari et al. 1989). The calculation was performed employing augmented quadruple-ζ quality basis sets (i.e., aug-cc-pCVQZ, Woon & Dunning 1994) and correlating all electrons. After geometry optimizations and harmonic force constants evaluation, the cubic force field for all the diazenylium isotopologues was evaluated in the normal-coordinate representation by means of numerical differentiation (Stanton et al. 1998; Stanton & Gauß 2000). Then, 2nd-order perturbation formulas, simplified for linear molecules, were used to compute He (Aliev & Watson 1985).

Table 2

Values (mHz) of the sextic centrifugal distortion constant of isotopologues of N2H+.

Table 3

Reactions fractionating 15N2 species.

Actually, the experimental values of the 15N-containing pair are properly smaller than those of the parent pair; moreover, for both pairs, the values of the hydrogenated and deuterated species are not significantly different. This latter finding is in apparent contrast with the trend exhibited by the computed equilibrium values, for which variations of ~30% are observed upon H←→D isotopic substitution. This discrepancy is, however, smaller than the typical magnitude of the zero-point contribution to the sextic centrifugal term of light linear molecules, and thus can be explained by invoking different ro-vibrational effects.

For both 15N2H+ and 15N2D+, the result of our accurate analysis is a very reliable set of rest frequencies, with 1σ uncertainties above 1 THz less than 0.001 km s-1.

The Einstein A-coefficient for spontaneous emission from state J + 1 to J of a linear molecule can be calculated from the line strengths by use of 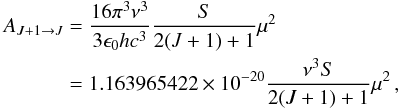 AJ+1→J=16π3ν33ϵ0hc3S2(J+1)+1μ2=1.163965422×10-20ν3S2(J+1)+1μ2 ,\begin{eqnarray} \label{eq:Acoeff} \begin{split} A_{J+1\rightarrow J} &= \frac{16\pi^3 \nu^3}{3\epsilon_0 hc^3} \frac{S}{2(J + 1) + 1}\mu^2 \\ &= 1.163965422\times 10^{-20}\frac{\nu^3S}{2(J + 1) + 1}\mu^2 \,, \end{split} \end{eqnarray}(2)where AJ + 1 → J is in s-1, the transition frequency ν is in MHz, and μ is the dipole moment in Debye units. The line strength S is defined such that μ2S = |μul|2, where μul is the matrix element of the dipole-moment operator in the rotational wave-functions basis. For a linear rotor with no hyperfine structure, the line strength of a transition connecting the J + 1 and J states is 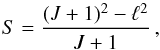S=(J+1)2−ℓ2J+1 ,\begin{equation} S = \frac{(J+1)^2 - \ell^2}{J + 1} \,, \end{equation}(3)which reduces to S = J + 1 for ground-state lines with no vibrational angular momentum (ℓ = 0). Assuming that the dipole moment is the same as that of the main isotopologue, μ = 3.4 ± 0.2 D (Havenith et al. 1990), the A-coefficient can be computed for each transition. Therefore, along with the lists of rest frequencies, the values of the Einstein A-coefficients are reported in the sixth and last columns of Table 1.

3.2. Potential constraints on fractionation models

What abundance ratios of fully 15N-substituted isotopologues of diazenylium (15N2H+/15NNH+ or 15N2H+/N15NH+) can then be expected to be observed in the ISM? For an upper limit estimate, the chemical reaction network of Wirström et al. (2012) has been updated to include fractionation into the doubly 15N-substituted species through the reactions listed in Table 3.

These reactions have not been studied, so reaction rates, zero-point energy differences (ΔE/k), and equilibrium coefficients (K(T)) are unknown and have been ad hoc estimated as given in Table 3 for the purpose of this investigation. The values of ΔE are estimated from the zero-point vibrational energies reported in Table 3 of Mladenović & Roueff (2014) and K(T) is computed using Eq. (5) of Terzieva & Herbst (2000). In the case of reactions R1 and R2, rate constants are assumed based on the corresponding reactions fractionating the singly substituted 14N15N and diazenylium in the Wirström et al. (2012) chemical network. Reactions R3 are included as analogs to the reaction H2D+ + HD ⇋ D2H+ + H2, which is important in deuteration chemistry, and we simply assumed forward rate coefficients (kf) similar to the reactions R1 and R2. As in Wirström et al. (2012), the elemental 14N/ 15N ratio is assumed to be 440, with 50% of 15N initially in molecular form, but also 1/440 of this (0.23%) is taken to form an initial 15N2 pool.

thumbnail Fig. 3

Nitrogen isotopologue ratios (as labeled) in the doubly substituted species, as well as the singly substituted diazenylium and molecular nitrogen, as predicted when including the fractionating reactions of Table 3 (solid) and not including them (dashed). The red graphs represent 15NN/15N2, the orange N15NH+/15N2H+, the purple 15NNH+/15N2H+, the yellow N2H+/15NNH+, the blue N2H+/N15NH+, and the green N2/N15N.

We investigate the effect of including the fractionation reactions R1–R3 under the same physical conditions as in Wirström et al. (2012). Figure 3 compares the temporal evolution of the 14N/15N ratio in doubly substituted molecular nitrogen and diazenylium for these two models. It demonstrates that if there is some direct fractionation, the doubly 15N-substituted species will become enhanced in 15N instead of depleted.

In particular, reactions R2 and R3 both have the effect of producing more 15N2H+ already from early on, thereby lowering the N15NH+/15N2H+ and 15NNH+/15N2H+ ratios. The main production of 15N2 is from dissociative electron recombination of 15N2H+, so the N15N/15N2 ratio is only significantly affected when the absolute abundance of diazenylium increases, after about 104 yr. Reaction R1, on the other hand, only becomes important as the ortho-H2 abundance drops after about 2 × 105 yr and more 15N+ thus becomes available (see Wirström et al. 2012, for a more detailed discussion on the effects of a varying H2ortho-to-para ratio). For the effective fractionation tested here, the abundance ratios N15NH+/15N2H+ and 15NNH+/15N2H+ are predicted to be similar to the N2H+/N15NH+ and N2H+/15NNH+ at times when their absolute abundances should be largest (105–106 yr).

As mentioned above, Fontani et al. (2015) reported observations of a few targets (i.e., 05358-mm1, 05358-mm3) where the N2H+/N15NH+ ratios are as high as 150–180. These significant 15N-enhancements cannot be accounted for by the latest nitrogen chemistry network (e.g., Roueff et al. 2015), hence, these “anomalous” sources can provide an effective test for updated models. Indeed, considerations based on the trends shown in Fig. 3 suggest that 15N2H+ might be detectable towards 05358-mm1/05358-mm3. The model predicts N15NH+/15N2H+ ratios in the range 20–100 at times >6 × 105 yr, therefore, from the column density values of singly 15N-substituted diazenylium determined by Fontani et al. (2015) and taking into account the absence of hyperfine splitting, peak intensities as high as 6 mK can be estimated for 15N2H+. This prediction is well above the sensitivity limit achievable by state-of-the-art millimeter telescopes in a few hours of observation at 0.1–0.3 km s-1 spectral resolution.

We note that, from Fig. 3, it can also be deduced that while the abundance of 15N2H+ can be expected to be significantly elevated above elemental at all times if reactions R1–R3 are viable, this only has a minor effect on the N2H+/N15NH+ and N2H+/15NNH+ ratios. These are at most elevated by 2% at times later than 8 × 105 yr, so inclusion of fractionation to doubly 15N-substituted species cannot reproduce the whole range of 15N enhancements in singly-substituted diazenylium observed by Fontani et al. (2015).

4. Conclusions

We have used high-resolution laboratory spectroscopy techniques to accurately study the rotational spectra of the multiply isotopically substituted versions of the diazenylium ions, 15N2H+ and 15N2D+. This latter has been spectroscopically

characterized for the first time. Very accurate rest frequencies are provided in the frequency region 88 GHz–1.2 THz to support astronomical searches for this doubly 15N-containing species. Our understanding of interstellar 15N fractionation is clearly incomplete (Roueff et al. 2015; Wirström et al. 2016) but, as we have shown here, a simplistic scenario for ion-molecule fractionation does predict a significant enrichment of 15N in 15N2H+. Observational constraints on 15N2H+ abundances based on these spectroscopic data will be crucial for ameliorating theoretical problems with interstellar 15N fractionation chemistry.

1

See www.cfour.de

Acknowledgments

This work has been supported by MIUR (PRIN12 “STAR: Spectroscopic and computational Techniques for Astrophysical and Atmospheric Research” (grant number 20129ZFHFE) and by the University of Bologna (RFO funds).

References

  1. Adande, G. R., & Ziurys, L. M. 2012, ApJ, 744, 194 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aliev, M. R., & Watson, J. K. G. 1985, in Molecular Spectroscopy: Modern Research, Vol. III, ed. K. N. Rao (New York: Academic Press), 1 [Google Scholar]
  3. Bizzocchi, L., Caselli, P., Leonardo, E., & Dore, L. 2013, A&A, 555, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bockelée-Morvan, D., Calmonte, U., Charnley, S., et al. 2015, Space Sci. Rev., 197, 47 [NASA ADS] [CrossRef] [Google Scholar]
  5. Briani, G., Gounelle, M., Marrocchi, Y., et al. 2009, Proc. Nat. Acad. Sci., 106, 10522 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cazzoli, G., Cludi, L., Buffa, G., & Puzzarini, C. 2012, ApJS, 203, 11 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dore, L., Bizzocchi, L., Degli Esposti, C., & Tinti, F. 2009, A&A, 496, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Fontani, F., Caselli, P., Palau, A., Bizzocchi, L., & Ceccarelli, C. 2015, ApJ, 808, L46 [NASA ADS] [CrossRef] [Google Scholar]
  9. Füri, E., & Marty, B. 2015, Nature Geoscience, 8, 515 [CrossRef] [Google Scholar]
  10. Gudeman, C. S. 1982, Ph.D. Thesis, University of Wisconsin-Madison, USA [Google Scholar]
  11. Havenith, M., Zwart, E., Leo Meerts, W., & Ter Meulen, J. J. 1990, J. Chem. Phys., 93, 8446 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013, Icarus, 223, 582 [Google Scholar]
  13. Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
  14. Mladenović, M., & Roueff, E. 2014, A&A, 566, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
  16. Nier, A. O. 1950, Phys. Rev., 77, 789 [NASA ADS] [CrossRef] [Google Scholar]
  17. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ritchey, A. M., Federman, S. R., & Lambert, D. L. 2015, ApJ, 804, L3 [NASA ADS] [CrossRef] [Google Scholar]
  19. Rodgers, S. D., & Charnley, S. B. 2008, MNRAS, 385, L48 [NASA ADS] [CrossRef] [Google Scholar]
  20. Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Stanton, J. F., & Gauß, J. 2000, Int. Rev. Phys. Chem., 19, 61 [CrossRef] [Google Scholar]
  22. Stanton, J. F., Lopreore, L., & Gauß, J. 1998, J. Chem. Phys., 108, 7190 [NASA ADS] [CrossRef] [Google Scholar]
  23. Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
  24. Wirström, E. S., Charnley, S. B., Cordiner, M. A., & Milam, S. N. 2012, ApJ, 757, L11 [NASA ADS] [CrossRef] [Google Scholar]
  25. Wirström, E., Milam, S., Adande, G., Charnley, S. B., & Cordiner, M. A. 2015, IAU General Assembly, 22, 2254599 [NASA ADS] [Google Scholar]
  26. Wirström, E. S., Adande, G., Milam, S. N., Charnley, S. B., & Cordiner, M. A. 2016, IAU Focus Meeting, 29, 271 [Google Scholar]
  27. Woon, D. E., & Dunning, T. H. 1994, J. Chem. Phys., 100, 2975 [NASA ADS] [CrossRef] [Google Scholar]
  28. Yu, S., Pearson, J. C., Drouin, B. J., et al. 2009, J. Mol. Spectrosc., 314, 19 [Google Scholar]

All Tables

Table 1

Rotational transition frequencies and spectroscopic constants of 15N2H+ and 15N2D+.

In the text
Table 2

Values (mHz) of the sextic centrifugal distortion constant of isotopologues of N2H+.

In the text
Table 3

Reactions fractionating 15N2 species.

In the text

All Figures

thumbnail Fig. 1

Spectrum of the J = 13 ← 12 transition of 15N2H+ (solid black line) and fitted profile (dashed lime line); total integration time: 300 s; scanning rate: 0.66 MHz/s; modulation depth: 900 kHz.
In the text
thumbnail Fig. 2

Frequency shift of the J = 1 ← 0 transition of 15N2H+.
In the text
thumbnail Fig. 3

Nitrogen isotopologue ratios (as labeled) in the doubly substituted species, as well as the singly substituted diazenylium and molecular nitrogen, as predicted when including the fractionating reactions of Table 3 (solid) and not including them (dashed). The red graphs represent 15NN/15N2, the orange N15NH+/15N2H+, the purple 15NNH+/15N2H+, the yellow N2H+/15NNH+, the blue N2H+/N15NH+, and the green N2/N15N.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.