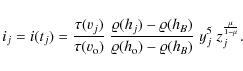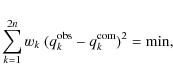| Issue |
A&A
Volume 499, Number 1, May III 2009
|
|
|---|---|---|
| Page(s) | 313 - 320 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200811503 | |
| Published online | 30 March 2009 | |
On the theory of light curves of video-meteors
P. Pecina - P. Koten
Astronomical Institute of the Academy of Sciences of the Czech Republic, 251 65 Ondrejov, Czech Republic
Received 11 December 2008 / Accepted 23 February 2009
Abstract
Aims. The aim of the article is to show how the light curve of video-meteors can be described theoretically.
Methods. The method of numerical integration of the system of differential equations describing the motion and ablation of a meteoroid during its atmospheric motion is employed.
Results. We have shown that the modification of the ablation equation and the more general assumptions on the meteoroid cross-section behaviour can lead to a better description of light curves of faint video-meteors. The applied method indicates that the traditionally-used statistical parameter F could be replaced by another one, Levin's parameter ![]() ,
which has a physical meaning.
,
which has a physical meaning.
Key words: meteors, meteoroids
1 Introduction
Since the start of video observations of faint meteors many observed cases have been collected. Light curves of such meteors show different shapes. The location of the point of maximum brightness differs from case to case, see e.g. Fleming et al. (1993), Campbell et al. (2000), Koten et al. (2004), Beech (2007). Several ways have been proposed to describe the shape of a meteor light curve. One of the most frequently used, the F parameter, was introduced by Fleming et al. (1993). They found that light curves of sporadic meteors are nearly symmetrical with only a few cases of flares. Hawkes et al. (1998) analyzed the light curves of Perseid meteors and found that they also produced curves close to symmetrical. We observed the positions of maximum light of meteors that were located both closer to the beginning of the corresponding curve and also closer to its end. The the parameter F describes the location of the maximum brightness on the meteor luminous trajectory. According to classical theory, single body meteoroids should produce light curves characterized byThe parameter F is purely descriptive. No physical ideas have been used in its formulation. Our aim here is to show that such an approach can be based on physical ideas connected with the physics of meteor motion when generalizing the equations in question. So, we will show how the various shapes of light curves can be described by the extended theory of meteor light curves based on generalized equations describing the atmospheric motion of a meteoroid together with its ablation. We will demonstrate the capability of our approach on cases of some meteors observed by our video cameras. Our aim here is to show that such an approach is capable of yielding correct results for light curves of various shape. The consequences for the physical parameters of meteoroids producing the observed light curves will be left for a future article.
We will use observational data of video-meteors consisting of distances flown by the meteoroid in the atmosphere as a function of time, together with absolute magnitudes at corresponding time points. The parameters will be acquired by a fit of observed distances and magnitudes (intensities) to computed ones.
The presented data were obtained within standard double-station video observations carried out at the Onrejov Observatory. The method is described e.g. in Koten et al. (2006).
2 Theory
The motion and ablation of a meteoroid during its atmospheric flight is usually described by the drag equation (e.g. Bronshten 1983)and the ablation one
The dot above the quantities on the left in Eqs. (1) and (2) represents the time derivative. The quantities entering these equations have the following meaning: v and m are the meteoroid instantaneous velocity and mass, S represents the cross-sectional area of the body,
To be able to describe the light effects of meteors we must add the luminosity equation (e.g. Bronshten 1983)
in which I is the intensity of light produced by the meteor at the time instant, t. The quantity
Here, we discuss the form of luminosity Eq. (4). Even
though Pecina & Ceplecha (1983) proposed that it could be
composed of two terms, the former of which is proportional to
![]() and the latter one to
and the latter one to
![]() ,
they also showed that it
could be given the form of (4) with other definition of
the luminous efficiency
,
they also showed that it
could be given the form of (4) with other definition of
the luminous efficiency ![]() .
The equation with
.
The equation with
![]() expresses
the fact that the meteor light is almost entirely produced by species
evaporated from the surface of the meteoroid due to its atmospheric
ablation. It is, therefore, questionable whether we would observe any
meteor event in the case of zero meteoroid ablation. Thus, is the loss
of meteoroid kinetic energy due to its deceleration capable of producing
a meteor event? We think this is not the case for the faint meteors we
are dealing with. Furthermore, micrometeoroids decelerate so
much that they are not able to reach the temperature needed for ablation
to start and do not produce any light (see, e.g. Bronshten 1983).
Therefore, we decided to use the luminosity equation in the form of (4). This was also the point of view of Borovicka et al. (2007) when dealing with the deceleration of Draconid
meteors.
expresses
the fact that the meteor light is almost entirely produced by species
evaporated from the surface of the meteoroid due to its atmospheric
ablation. It is, therefore, questionable whether we would observe any
meteor event in the case of zero meteoroid ablation. Thus, is the loss
of meteoroid kinetic energy due to its deceleration capable of producing
a meteor event? We think this is not the case for the faint meteors we
are dealing with. Furthermore, micrometeoroids decelerate so
much that they are not able to reach the temperature needed for ablation
to start and do not produce any light (see, e.g. Bronshten 1983).
Therefore, we decided to use the luminosity equation in the form of (4). This was also the point of view of Borovicka et al. (2007) when dealing with the deceleration of Draconid
meteors.
When integrating Eq. (4)
from the time instant at which a meteor appears, ![]() ,
to the one a
meteor disappears,
,
to the one a
meteor disappears, ![]() ,
we obtain
,
we obtain
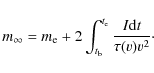
Assuming that the meteoroid is completely destroyed at
It has the advantage that
To be able to use the above equations to solve practical problems, we must
adopt some ideas on the behaviour of S and ![]() as well as
as well as ![]() during the flight of a meteoroid. It is frequently assumed that the shape
of a meteoroid does not change during ablation, i.e. the ablation
is supposed to be self-similar. Then (e.g. Ceplecha et al. 1998)
during the flight of a meteoroid. It is frequently assumed that the shape
of a meteoroid does not change during ablation, i.e. the ablation
is supposed to be self-similar. Then (e.g. Ceplecha et al. 1998)
![]() with A being the shape factor and
with A being the shape factor and
![]() the bulk density of meteoroid material. Introducing the
shape-density coefficient,
the bulk density of meteoroid material. Introducing the
shape-density coefficient,
![]() ,
the system
of basic equations now reads
,
the system
of basic equations now reads
Such equations were recently used also by Borovicka et al. (2007). Both the coefficients K and
It is known (e.g. Bronshten 1983) that each meteoroid must go
through a preablation heating phase before it starts to ablate and,
consequently, to produce light. This is not, however, reflected in
Eq. (3). Therefore, Pecinová (2005) proposed
to modify the ablation equation to read
Here
where the quantities labelled by
The same operation converts (3) into
On substituting (11) into (4) we get
The set of Eqs. (10)-(12) is the basis of all our further computations, the results of which we will present in this paper later.
2.1 No deceleration
These are the most general equations we will adopt. However, since we deal with faint video meteors whose visible light curves and distances flown usually spread over short regions of heights, their deceleration can be neglected. We can, therefore, integrate Eq. (11) under the assumptionholds generally true, where h is the height at which a meteoroid occur at a time instant, t, and
where
This function can easily be constructed from CIRA (1972) in the form of table inside which we can interpolate to reach the value of
where now
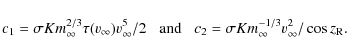
The parameters c1, c2,
where
where now
![\begin{displaymath}\sigma K = \sqrt[3]{2 c_1 c_2^2 \cos^2 z_{\rm R} / \tau(v_{\infty})} /
v_{\infty}^3
\end{displaymath}](/articles/aa/full_html/2009/19/aa11503-08/img60.png)
and
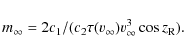
The last expression also allows the
2.2 Deceleration
Even though it holds true that most video meteors do not show noticeable deceleration there have been meteors observed which do slow down. Usually the set of drag and ablation equations is integrated using the first integral obtained when dividing the ablation equation by the drag one. This integral is inserted into the drag equation and further integration yields the dependence of the instantaneous meteoroid velocity, v, on height (see, e.g. Pecina & Ceplecha 1983). However, our corresponding system of Eqs. (10) and (11) does not possess a first integral since dividing (11) by (10) does not cancel out the atmospheric density,We must also add
providing the relation of heights to distances flown along the meteoroid path. This follows from the geometry of the problem. To be able to integrate (19)-(21) we have to add the proper initial conditions. We will choose the first observed point of the light curve as the one corresponding to time
This can further be used in (17) to get the values of
We have proceeded so far by solving our problem in two substeps, i.e.
minimizing (17) and (18) independently. However, it
is useful to combine independent processes into one in the following way.
Since l and I have different physical dimensions we must compare
their normalized (i.e. dimensionless) quantities. Therefore, we define
the following dimensionless quantities
The quantity
We again add the relation connecting the heights to lengths. This is now
where
The least squares condition we now use is
where
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig1.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg88.png) |
Figure 1:
The distance of the meteoroid from chosen point of its
atmospheric trajectory, l, as a function of time, t,
for the Quadrantid meteor 2103132. Measured distances are
marked by the full squares, the particular variances
|
| Open with DEXTER | |
We have hereby completed the theory needed for the description of observed meteors. The next section will deal with the meteors we observed.
3 Application to observed meteors
To apply this theory to observed meteors we proceeded as follows. First, the velocity ![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig2.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg89.png) |
Figure 2:
The light curves of the meteor from Fig. 1. The
curve 1 corresponds to |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig3.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg90.png) |
Figure 3: The same as in Fig. 1 but for the Quadrantid meteor 2103169. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig4.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg91.png) |
Figure 4: The same as in Fig. 2 but for the Quadrantid meteor 2103169. |
| Open with DEXTER | |
Table 1:
The mass resulting from the light curve integration,
![]() ,
the corresponding mass
following from the least squares method,
,
the corresponding mass
following from the least squares method,
![]() ,
both in grams, the velocity
,
both in grams, the velocity ![]() ,
which is the velocity
,
which is the velocity
![]() in the case of a nondecelerating meteoroid, and
the velocity at the beginning of the luminous curve in the
case of a decelerating meteoroid, both in km
in the case of a nondecelerating meteoroid, and
the velocity at the beginning of the luminous curve in the
case of a decelerating meteoroid, both in km
![]() ,
,
![]() the velocity at the end of the luminous trajectory, in
the same units, K in the CGS system of units,
the velocity at the end of the luminous trajectory, in
the same units, K in the CGS system of units, ![]() in
in
![]() ,
and hB in km. The
abbreviation 0.355e-2 instead of
,
and hB in km. The
abbreviation 0.355e-2 instead of
![]() was used.
was used.
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig5.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg134.png) |
Figure 5: The same as in Fig. 1 but for the meteor 2519197. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig6.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg135.png) |
Figure 6: The same as in Fig. 2 but for the meteor 2519197. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig7.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg136.png) |
Figure 7:
The distance of the meteoroid from a chosen point of its
atmospheric trajectory, l, as a function of time, t,
for the meteor 2519197. Measured distances are marked by the
full squares, the particular variances
|
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig8.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg137.png) |
Figure 8: The light curve of the meteor from Fig. 7 as a result of application of (30). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig9.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg138.png) |
Figure 9: The velocity curve of the meteor from Fig. 7 as a result of application of (30). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figa.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg139.png) |
Figure 10: The same as in Fig. 5 but for meteor 3729019. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figb.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg140.png) |
Figure 11: The same as in Fig. 6 but for meteor 3729019. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figc.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg141.png) |
Figure 12: The same as in Fig. 7 but for meteor 3729019. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figd.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg142.png) |
Figure 13: The same as in Fig. 8 but for meteor 3729019. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fige.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg143.png) |
Figure 14: The same as in Fig. 9 but for meteor 3729019. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figf.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg144.png) |
Figure 15: The same as in Fig. 5 but for meteor 3806030. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figg.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg145.png) |
Figure 16: The same as in Fig. 6 but for meteor 3806030. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figh.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg146.png) |
Figure 17: The same as in Fig. 7 but for meteor 3806030. |
| Open with DEXTER | |
As already mentioned, some meteors displayed remarkable deceleration. One
of these cases is the meteor recorded on May 19, 2002. The computation
carried out under the assumption of constant meteor velocity is shown in
Figs. 5 and 6. Also from Fig. 6 it is
evident that a better description of the observed meteor by the theory is
given when both
![]() and
and ![]() are parameters of the fit. On the
other hand, it is also evident that there is a poorer description at both
the beginning and the end of the meteor. Since the time course of variances
shows the presence of deceleration, in this case we decided to apply a more
thorough model bearing in mind deceleration embodied by (19)-(21) as a first step and (25)-(27)
as a second step. The time velocity dependence as well as the light curve
are displayed in Figs. 7 and 8. Figure 7 shows
no significant systematic time course of variances in accordance with our
assumption of velocity variability, as we expected. Moreover,
Fig. 8 shows that the inclusion of time variability of the
meteoroid velocity into consideration further improves the theoretical
light curve which is now much better than in Fig. 6. The
correspondence of the theory and observation improved at both ends of the
light curve. The graph of velocity we arrive at is presented in
Fig. 9. The least squares procedure (30) yielded also
the values of the parameters involved in it. They can be found in
Table 1. Another meteor displaying deceleration is presented
in Figs. 10-14. The velocity curve of 3729019 is
depicted in Fig. 14. The case of a decelerating meteoroid with
poor data is demonstrated in Figs. 15-19. This is a
meteor which was relatively bright and which lasted for much longer than
other meteors we have presented. Its complex behaviour is visible both in
Fig. 17 where the bump at
are parameters of the fit. On the
other hand, it is also evident that there is a poorer description at both
the beginning and the end of the meteor. Since the time course of variances
shows the presence of deceleration, in this case we decided to apply a more
thorough model bearing in mind deceleration embodied by (19)-(21) as a first step and (25)-(27)
as a second step. The time velocity dependence as well as the light curve
are displayed in Figs. 7 and 8. Figure 7 shows
no significant systematic time course of variances in accordance with our
assumption of velocity variability, as we expected. Moreover,
Fig. 8 shows that the inclusion of time variability of the
meteoroid velocity into consideration further improves the theoretical
light curve which is now much better than in Fig. 6. The
correspondence of the theory and observation improved at both ends of the
light curve. The graph of velocity we arrive at is presented in
Fig. 9. The least squares procedure (30) yielded also
the values of the parameters involved in it. They can be found in
Table 1. Another meteor displaying deceleration is presented
in Figs. 10-14. The velocity curve of 3729019 is
depicted in Fig. 14. The case of a decelerating meteoroid with
poor data is demonstrated in Figs. 15-19. This is a
meteor which was relatively bright and which lasted for much longer than
other meteors we have presented. Its complex behaviour is visible both in
Fig. 17 where the bump at
![]() s can be seen and in
Fig. 18 where the confidence of the theoretical light curve with
the observed intensities is poorer, namely at the beginning and around
the maximum. The velocity curve of 3806030 is depicted in Fig. 19.
Table 1 contains all parameters we obtained.
s can be seen and in
Fig. 18 where the confidence of the theoretical light curve with
the observed intensities is poorer, namely at the beginning and around
the maximum. The velocity curve of 3806030 is depicted in Fig. 19.
Table 1 contains all parameters we obtained.
4 Discussion
We have applied the light curve theory to video meteors that are too short to show deceleration, as well as to meteors in which this behaviour displayed very clearly. Both Quadrantid 2103132 and 2103169 as well as 2519197 and 3729019 have short light curves meteors with the light curve maximum of the same order. It is clear that during short time intervals probably no significant changes in l vs. t and light behaviour can manifest. The opposite case 3806030 whose behaviour evidently cannot be described by simple theory. It suffers from many complex changes of its dynamical as well as material properties that are not included in our theory. This meteor may be treated by the theory put forward by Pecina (2001). Our approach may be applied to short and faint video meteors. A first glance at the equations of our theory could lead to the opinion that it is based on a single-body concept. However, the value of ![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figi.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg148.png) |
Figure 18: The same as in Fig. 8 but for meteor 3806030. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figj.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg149.png) |
Figure 19: The same as in Fig. 9 but for meteor 3806030. |
| Open with DEXTER | |
5 Conclusions
We have shown that considering nonzero values of
Bronshten (1983) stated that there is still no procedure that
yields sufficiently precise values of ![]() of observed meteors. We
think that our method is capable of providing such values. We plan to
study the possible relations of
of observed meteors. We
think that our method is capable of providing such values. We plan to
study the possible relations of ![]() to meteors of various streams
based on the theory we presented here.
to meteors of various streams
based on the theory we presented here.
The approach we have developed is also capable of giving sufficiently
precise values of physical parameters of decelerating
video meteors
such as K, ![]() and hB which can serve as the basis of further
studies devoted to structural characteristics of meteoroids producing
these observed meteors.
and hB which can serve as the basis of further
studies devoted to structural characteristics of meteoroids producing
these observed meteors.
Acknowledgements
The article has been supported by institutional research plan number AV0Z10030501.
References
- Beech, M. 2007, MNRAS, 380, 1649 [NASA ADS] [CrossRef] (In the text)
- Borovicka, J., Spurný, P., & Koten, P. 2007, A&A, 473, 661 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bronshten, V. A. 1983, Physics of Meteoric Phenomena (Dordrecht: Reidel), 356 (In the text)
- Campbell, M. D., Brown, P., LeBlanc, A. G., et al. 2000, Meteorit. Planet. Sci., 35, 1259 [NASA ADS] (In the text)
- Ceplecha, Z. 1988, Bull. Astron. Inst. Czechosl., 39, 221 [NASA ADS] (In the text)
- Ceplecha, Z., Borovicka, J., Elford, W. G., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] (In the text)
- CIRA 1972, COSPAR International Reference Atmosphere 1972 (Berlin: Academie-Verlag) (In the text)
- Fleming, B. D. E., Hawkes, R. L., & Jones, J. 1993, in Proc. Meteoroids and their parent bodies Conf., ed. J. Stohl, & I. P. Williams, Bratislava, Slovakia, 261 (In the text)
- Hawkes, R. L., Campbell, M., Babcock, D., & Brown, P. 1998, in Leonid Meteoroid Storm and Satellite Threat Conference, 11 (In the text)
- Koten, P., Borovicka, J., Spurný, P., Betlem, H., & Evans, S. 2004, A&A, 428, 683 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Koten, P., Borovicka, J., Spurný, P., et al. 2006, MNRAS, 366, 1367 [NASA ADS] (In the text)
- Levin, B. Yu. 1956, The physical theory of meteors and meteoric matter in the solar system (Moscow: Publishing House of the Academy of Sciences of the USSR), 293 (in Russian) (In the text)
- Murray, I. S., Hawkes, R. L., & Jenniskens, P. 1999, Meteor. Planet. Sci., 34, 949 [NASA ADS] (In the text)
- Murray, I. S., Beech, M., Tailor, M., Jenniskens, P., & Hawkes, R. L. 2000, Earth, Moon and Planets, 82, 351 (In the text)
- Pecina, P. 2001, in Meteoroids 2001, ed. B. Warmbein, SP-495, ESA, Kiruna, Sweden, 271 (In the text)
- Pecina, P., & Ceplecha, Z. 1983, Bull. Astron. Inst. Czechosl., 34, 102 [NASA ADS] (In the text)
- Pecinová, D. 2005, Ph.D. Theses, Study of physical characteristics of meteor showers based on Ondrejov radar observations, Charles University, Prague (In the text)
- Pecinová, D., & Pecina, P. 2007, Contrib. Astron. Obs. Skalnaté Pleso, 37, 83 [NASA ADS] (In the text)
All Tables
Table 1:
The mass resulting from the light curve integration,
![]() ,
the corresponding mass
following from the least squares method,
,
the corresponding mass
following from the least squares method,
![]() ,
both in grams, the velocity
,
both in grams, the velocity ![]() ,
which is the velocity
,
which is the velocity
![]() in the case of a nondecelerating meteoroid, and
the velocity at the beginning of the luminous curve in the
case of a decelerating meteoroid, both in km
in the case of a nondecelerating meteoroid, and
the velocity at the beginning of the luminous curve in the
case of a decelerating meteoroid, both in km
![]() ,
,
![]() the velocity at the end of the luminous trajectory, in
the same units, K in the CGS system of units,
the velocity at the end of the luminous trajectory, in
the same units, K in the CGS system of units, ![]() in
in
![]() ,
and hB in km. The
abbreviation 0.355e-2 instead of
,
and hB in km. The
abbreviation 0.355e-2 instead of
![]() was used.
was used.
All Figures
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig1.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg88.png) |
Figure 1:
The distance of the meteoroid from chosen point of its
atmospheric trajectory, l, as a function of time, t,
for the Quadrantid meteor 2103132. Measured distances are
marked by the full squares, the particular variances
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig2.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg89.png) |
Figure 2:
The light curves of the meteor from Fig. 1. The
curve 1 corresponds to |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig3.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg90.png) |
Figure 3: The same as in Fig. 1 but for the Quadrantid meteor 2103169. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig4.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg91.png) |
Figure 4: The same as in Fig. 2 but for the Quadrantid meteor 2103169. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig5.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg134.png) |
Figure 5: The same as in Fig. 1 but for the meteor 2519197. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig6.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg135.png) |
Figure 6: The same as in Fig. 2 but for the meteor 2519197. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig7.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg136.png) |
Figure 7:
The distance of the meteoroid from a chosen point of its
atmospheric trajectory, l, as a function of time, t,
for the meteor 2519197. Measured distances are marked by the
full squares, the particular variances
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig8.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg137.png) |
Figure 8: The light curve of the meteor from Fig. 7 as a result of application of (30). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fig9.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg138.png) |
Figure 9: The velocity curve of the meteor from Fig. 7 as a result of application of (30). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figa.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg139.png) |
Figure 10: The same as in Fig. 5 but for meteor 3729019. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figb.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg140.png) |
Figure 11: The same as in Fig. 6 but for meteor 3729019. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figc.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg141.png) |
Figure 12: The same as in Fig. 7 but for meteor 3729019. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figd.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg142.png) |
Figure 13: The same as in Fig. 8 but for meteor 3729019. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503fige.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg143.png) |
Figure 14: The same as in Fig. 9 but for meteor 3729019. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figf.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg144.png) |
Figure 15: The same as in Fig. 5 but for meteor 3806030. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figg.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg145.png) |
Figure 16: The same as in Fig. 6 but for meteor 3806030. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figh.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg146.png) |
Figure 17: The same as in Fig. 7 but for meteor 3806030. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figi.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg148.png) |
Figure 18: The same as in Fig. 8 but for meteor 3806030. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=9cm,clip]{1503figj.eps} }
\end{figure}](/articles/aa/full_html/2009/19/aa11503-08/Timg149.png) |
Figure 19: The same as in Fig. 9 but for meteor 3806030. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



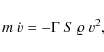
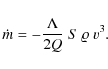
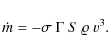
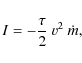
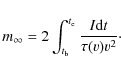
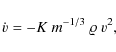
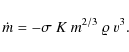
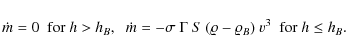
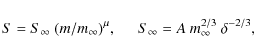
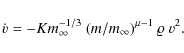
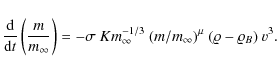
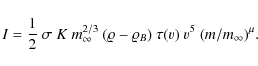
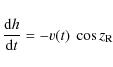
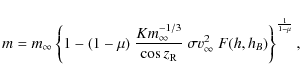
![\begin{displaymath}F(h, h_B) = \int_{h}^{h_B} [\varrho(x) - \varrho(h_B)] ~ {\rm d} x.
\end{displaymath}](/articles/aa/full_html/2009/19/aa11503-08/img52.png)
![\begin{displaymath}I = c_1 ~ [\varrho(h)-\varrho(h_B)] ~ \left\{1 - (1 - \mu) ~ c_2
~ F(h, h_B) \right\}^{\mu/(\mu-1)},
\end{displaymath}](/articles/aa/full_html/2009/19/aa11503-08/img54.png)
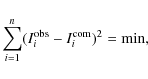
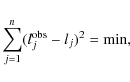
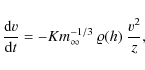
![\begin{displaymath}\frac{{\rm d} z}{{\rm d} t} = - \sigma ~ (1- \mu) ~ K m_{\infty}^{-1/3} ~
[ \varrho(h) - \varrho(h_B) ] ~ v^3.
\end{displaymath}](/articles/aa/full_html/2009/19/aa11503-08/img65.png)
![\begin{displaymath}I = \frac{1}{2} \tau(v) K m_{\infty}^{-1/3} ~ \sigma ~ m_{\in...
... ~
[\varrho(h) - \varrho(h_B)] ~ v^5 ~ z^{\frac{\mu}{1-\mu}}.
\end{displaymath}](/articles/aa/full_html/2009/19/aa11503-08/img74.png)
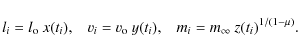
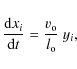
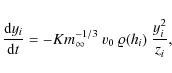
![\begin{displaymath}\frac{{\rm d} z_i}{{\rm d} t} = - \sigma (1- \mu) ~ K m_{\inf...
...{-1/3} ~
v_{\rm o}^3 ~ [\varrho(h_i) - \varrho(h_B)] ~ y_i^3.
\end{displaymath}](/articles/aa/full_html/2009/19/aa11503-08/img78.png)