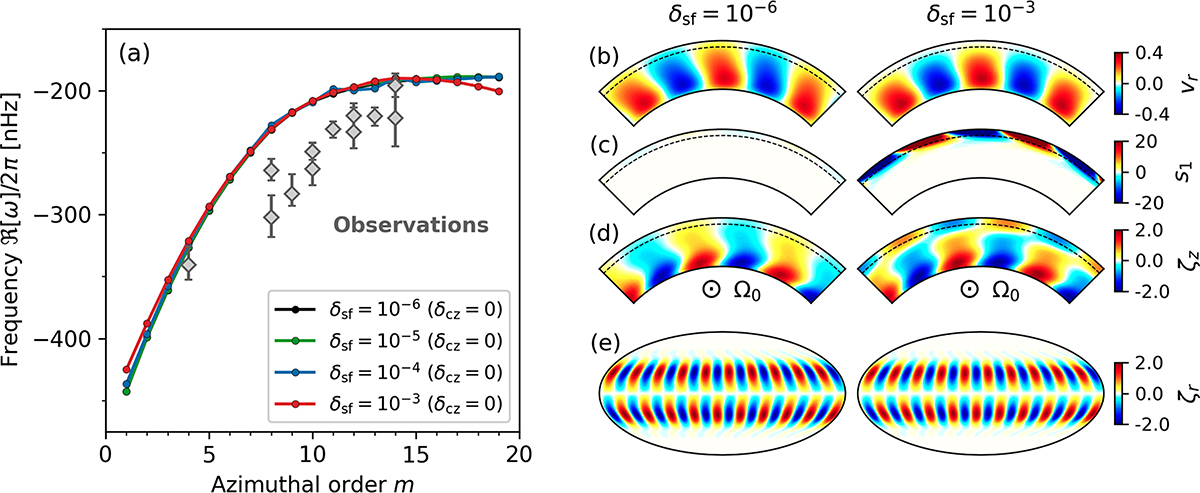
(a) Dispersion relation of the HHS22 modes computed for different values of superadiabaticity near the surface δ_sf. The bulk of the convection zone is assumed to be adiabatic, δ_cz = 0. (b–e) Eigenfunctions of the m = 10 HHS22 mode computed for δ_sf = 10⁻⁶ (left column) and for δ_sf = 10⁻³ (right column). Panels b–d show cuts of radial velocity v_r (in m s⁻¹), entropy perturbation s₁ (in erg g⁻¹ K⁻¹), and z-vorticity ζ_z (in 10⁻⁸ s⁻¹) in the equatorial plane (along the rotational axis) seen from the north pole. The black dashed curves denote the height r = 0.95 R_⊙, above which the strongly superadiabatic layer is located. (e) Mollweide projection of the radial vorticity eigenfunction ζ_r at the top boundary r = 0.985 R_⊙ (in 10⁻⁸ s⁻¹). All the eigenfunctions are normalized in the same way as in Fig. 2.