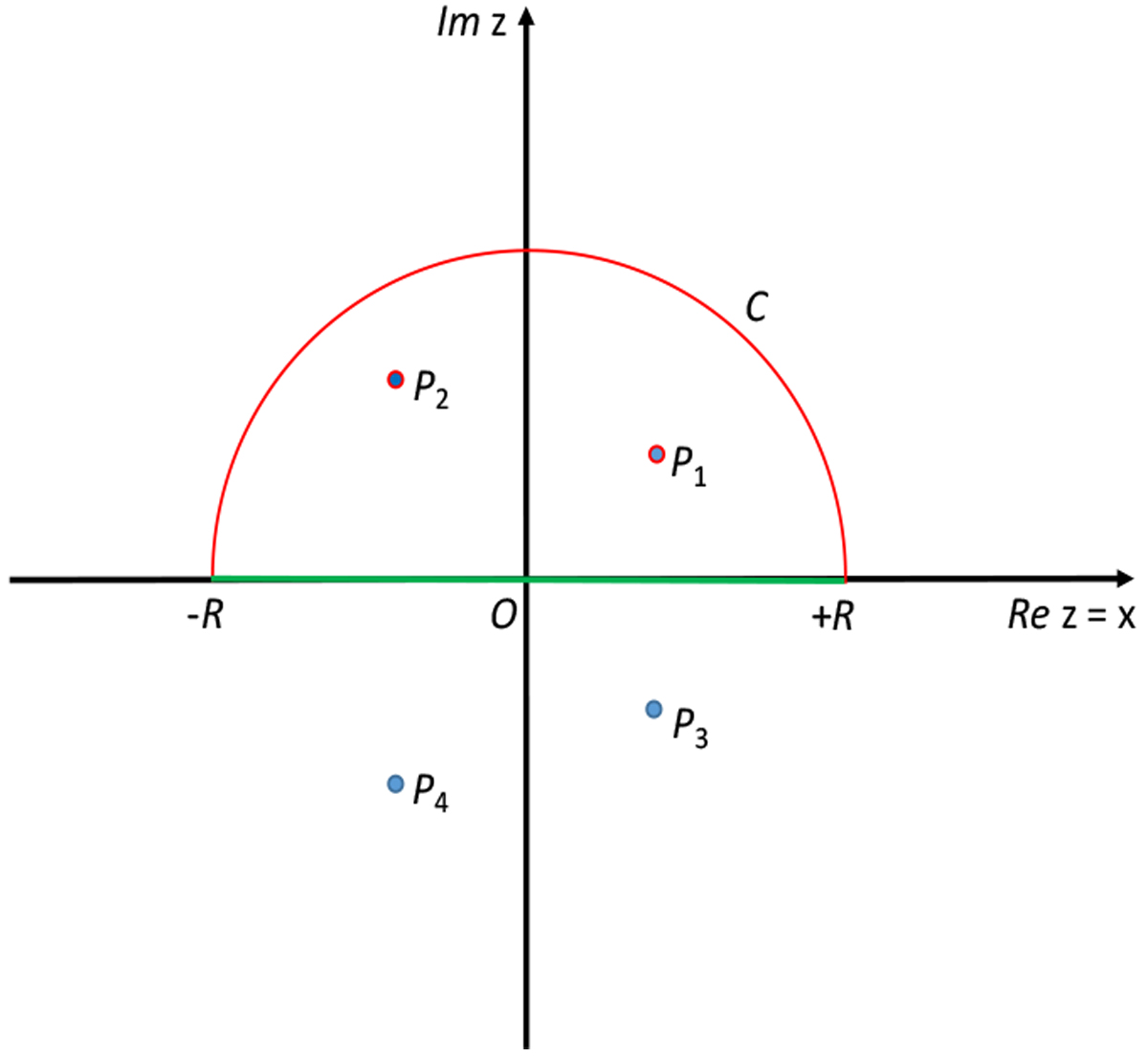
Complex plane with the semicircle C (in red) and its diameter, that is, the segment of the real axis [−R, +R] (in green). Their union forms the closed contour Σ along which the complex function f(z) is integrated in Eq. (A.2). For the sake of illustration, we show two poles of the complex integrand function P₁ and P₂ (in blue encircled in red), inside the contour Σ and two poles outside the contour Σ. Only the residues in P₁ and P₂ are to be considered in the computation of the integral of f(z) along Σ according to the theorem of the residues, while the residues in the poles P₃ and P₄ (in blue), lying outside Σ, are not to be included in the summation in Eq. (A.2).