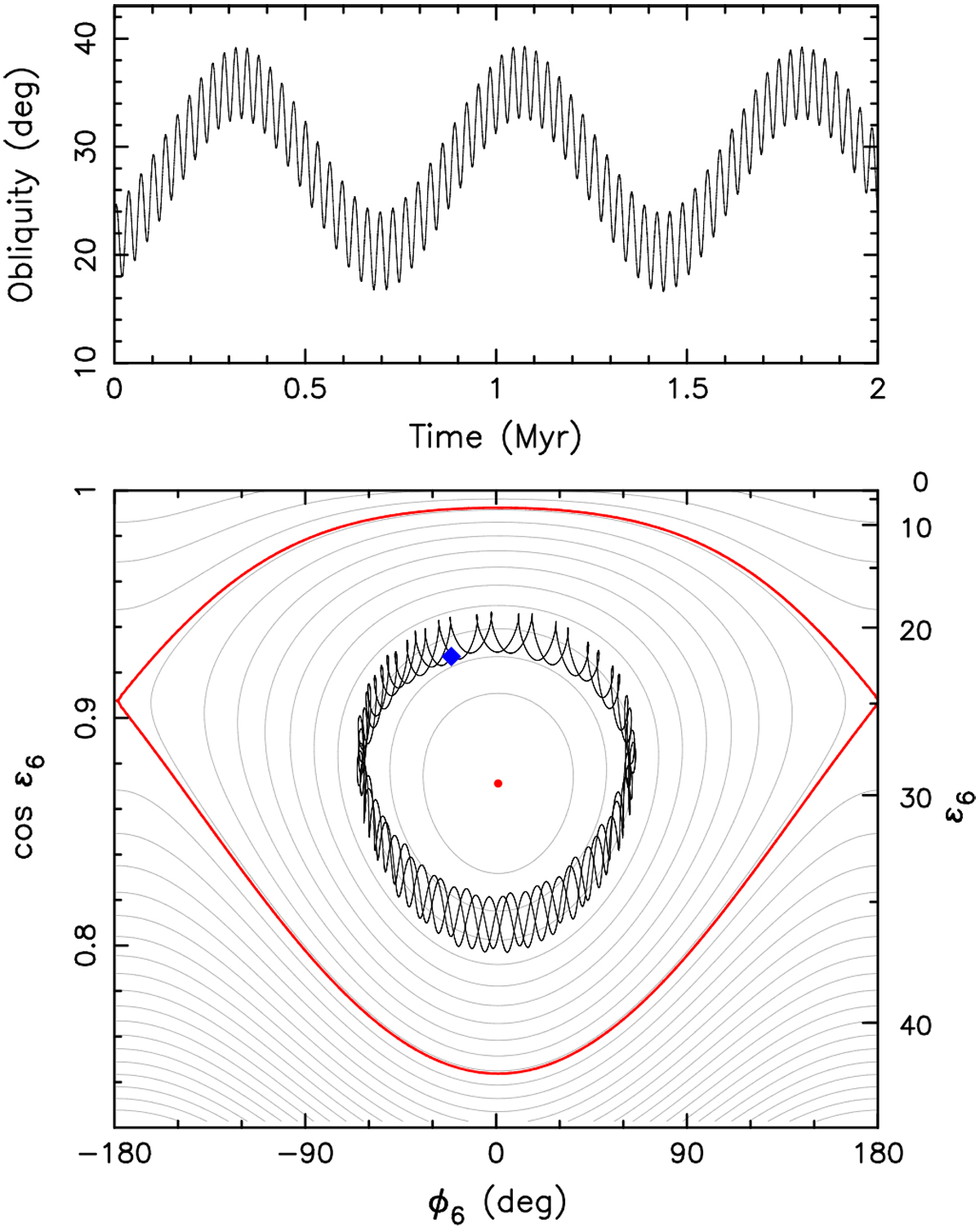
Top panel: time evolution of the osculating obliquity ε for (208) Lacrimosa over the 2 Myr interval using numerical integration of Eq. (A.1) with T_ng = 0. The initial conditions at the present epoch from the best-fit rotation state solution (P = 14.085734 h, λ = 15.2° and β = 66.9°) and Δ = 0.23. The short-period oscillations are due to the proper term of nodal precession with frequency s (which have a period of ≃2π∕(s − s₆) ≃ 32 kyr). The long-period and large-amplitude oscillations of ≃745 kyr are due to libration about the resonant Cassini state 2 associated with frequency s₆ (“the Slivan state”). Bottom panel: phase portrait of the Colombo top model for the s₆ frequency and precession constant α ≃ 29.75 arcsec yr⁻¹ (i.e., P = 14.085734 h and Δ = 0.23 in Eq. (A.4)); the ordinate is either cosε₆ (left) or ε₆ (right) and the abscissa is φ₆. The light-gray curves are isolines of the first integral C(ε₆, φ₆) = constant given by Eq. (A.11). Critical curves of the spin-orbit resonance, namely the separatrix and the stable equilibrium C₂, are highlighted in red. The black curve is the numerically integrated pole of (208) Lacrimosa from the top projected into the plane of these variables; the blue diamond is the current position of the pole.