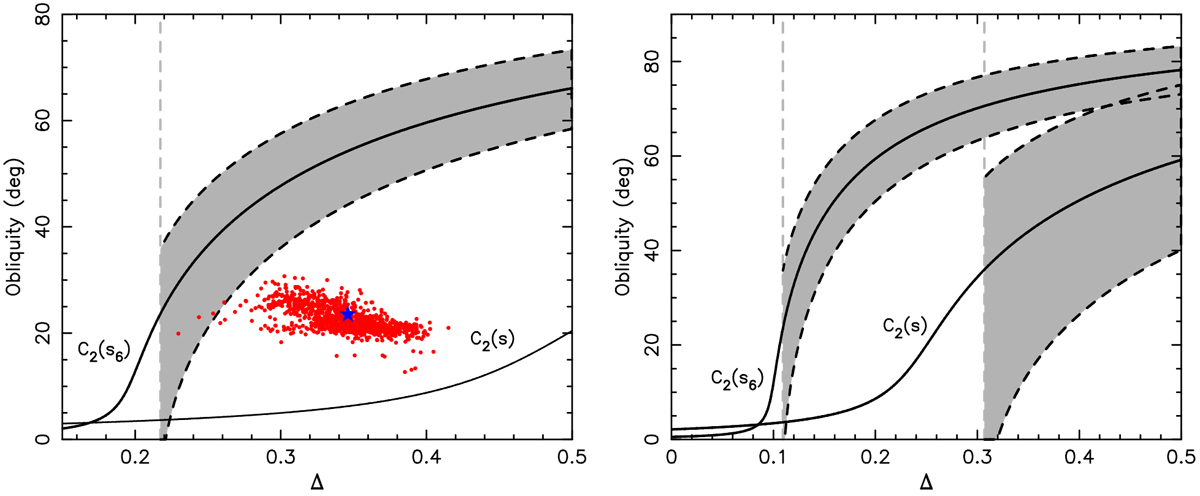
Obliquity ε₂ of the Cassini state 2 as a function of the dynamical ellipticity Δ (see Eq. (A.3)). Orbital parameters of (208) Lacrimosa are assumed. Left panel: nominal rotation period P = 14.085734 h of (208) Lacrimosa used. The solid line labeled C₂(s₆) provides ε₂ for the s₆ (forced) frequency mode of the nodal precession. The spin-orbit resonance onsets for Δ are denoted by the light-gray dashed line (transition determined by the Eq. (A.7) condition); beyond this value the Cassini state 2 becomes an equilibrium point of the spin-orbit resonance,whose maximum extension in obliquity is shown by the gray area. Solid line labeled C₂ (s) provides ε₂ for the s (proper) mode of the nodal precession. Here the spin-orbit resonance does not exist. Red symbols show obliquity and Δ values for a little less than 1000 solutions for (208) Lacrimosa from the bootstrap method discussed in Sect. 2 and using only the optical light-curve observations. The blue star is the nominal, best-fit solution. Right panel: same as in the left panel, but now for a hypothetical, longer rotation period of P = 28 h. Now the spin–orbit resonance exists beyond some critical Δ value for both frequencies s₆ and s.