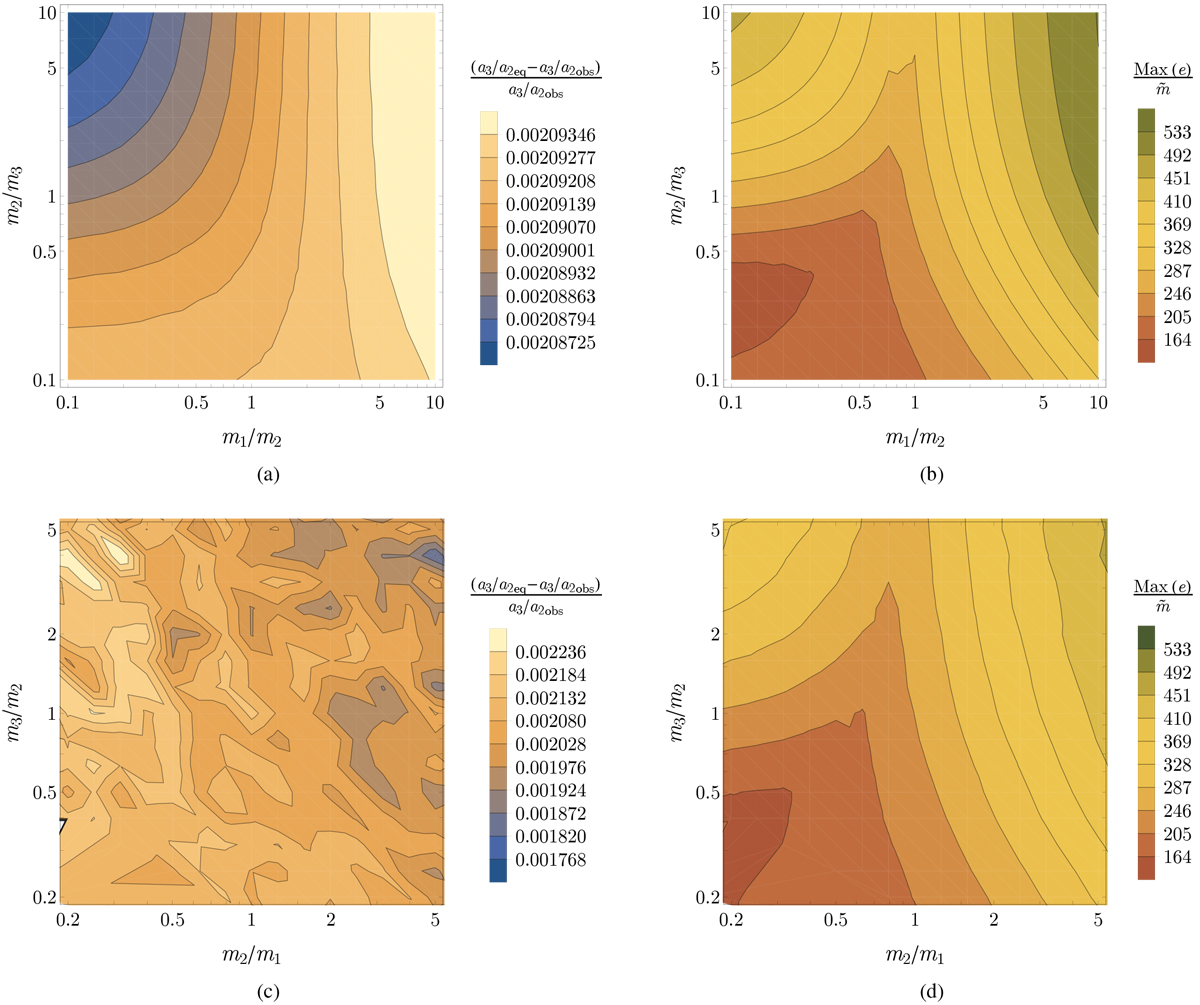
Top row: analytical maps constructed for Kepler-305 as explained in Sect. 3.2. Panel a: we plot the quantity , which represents how close the system is now to some resonant equilibrium point, for different mass ratios m₁ ∕m₂ and m₂ ∕m₃ (each point in this plot is constructed by repeating the procedure described in Fig. 5). We notice that changes verylittle with the mass ratios, and is of the order of ~0.002. Comparing with Fig. 9, we see that this can be the case by pure chance only in ~ 15% of randomly generated systems close to the 3:2–2:1 mean motion resonance chain. Panel b: we show a map of the quantity representing the equilibrium orbital configuration that is selected at each fixed value of m₁ ∕m₂ and m₂ ∕m₃ by imposing (a₃∕a₁)|_eq ≡ (a₃∕a₁)|_obs. Bottom row: numerical maps constructed for Kepler-305 as explained in Sect. 3.3. We show numerical maps of in panel c and in panel d, analogous to the analytical plots above (over a slightly smaller range of mass ratios for simplicity). These are intended to validate the analytical maps, and show very good agreement between corresponding panels.