Fig. 1
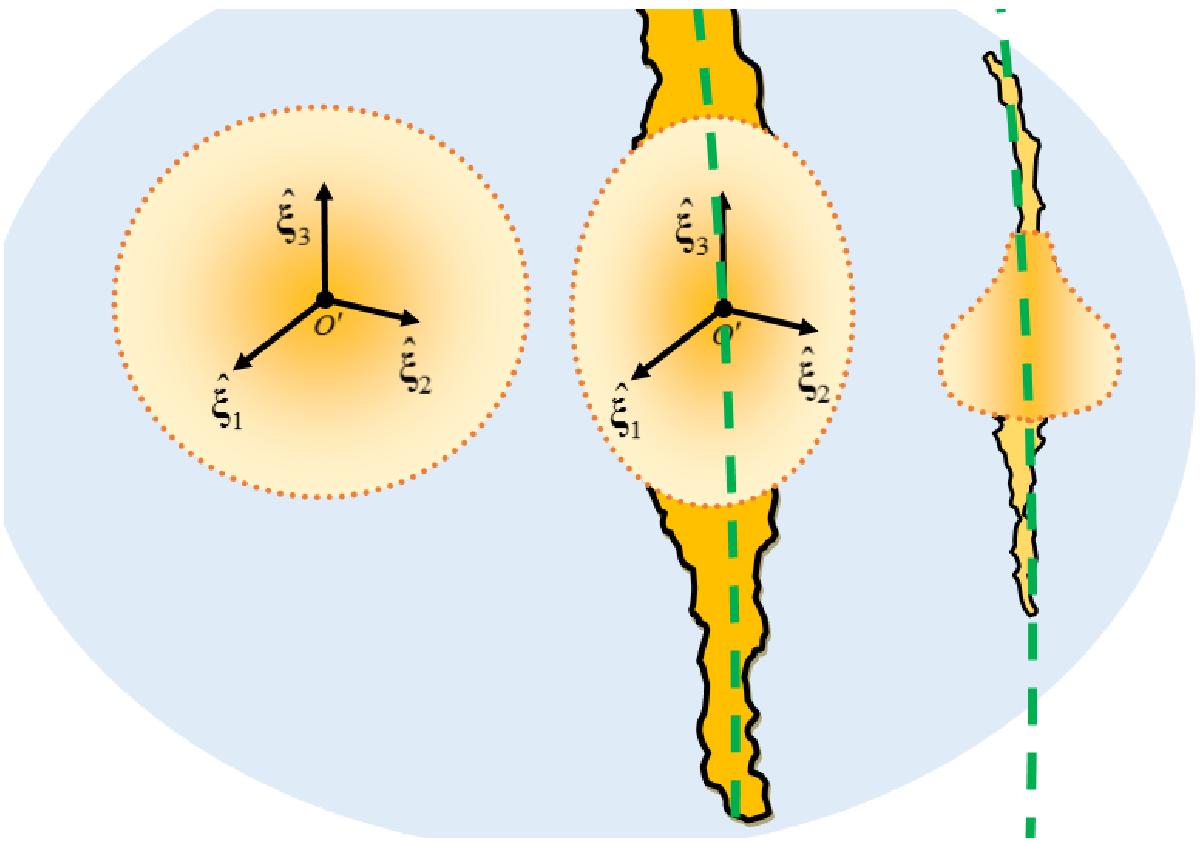
l = 2 perturbation mode of a spherical harmonics ![]() (central) over the unperturbed axisymmetric system (left). We exclude perturbation modes other than l = 2 because, although every perturbed 3D surface can be realized by a superposition of spherical harmonics modes, no common evidence exists for the type of symmetries as presented on the right (e.g. l = 3 mode). The dashed-green line provides an example of a star cluster orbit. Note that the tidal tails (yellow zone bordered by the black contours) do not necessarily lie along the orbits, i.e., O(t) ≠ 1 in the formalism of this paper, see, e.g. Pasetto et al. (2010, their Fig. 7) or Dehnen et al. (2004), Capuzzo Dolcetta et al. (2005) for globular cluster cases.
(central) over the unperturbed axisymmetric system (left). We exclude perturbation modes other than l = 2 because, although every perturbed 3D surface can be realized by a superposition of spherical harmonics modes, no common evidence exists for the type of symmetries as presented on the right (e.g. l = 3 mode). The dashed-green line provides an example of a star cluster orbit. Note that the tidal tails (yellow zone bordered by the black contours) do not necessarily lie along the orbits, i.e., O(t) ≠ 1 in the formalism of this paper, see, e.g. Pasetto et al. (2010, their Fig. 7) or Dehnen et al. (2004), Capuzzo Dolcetta et al. (2005) for globular cluster cases.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


