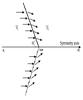
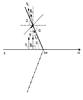
Fig. 3
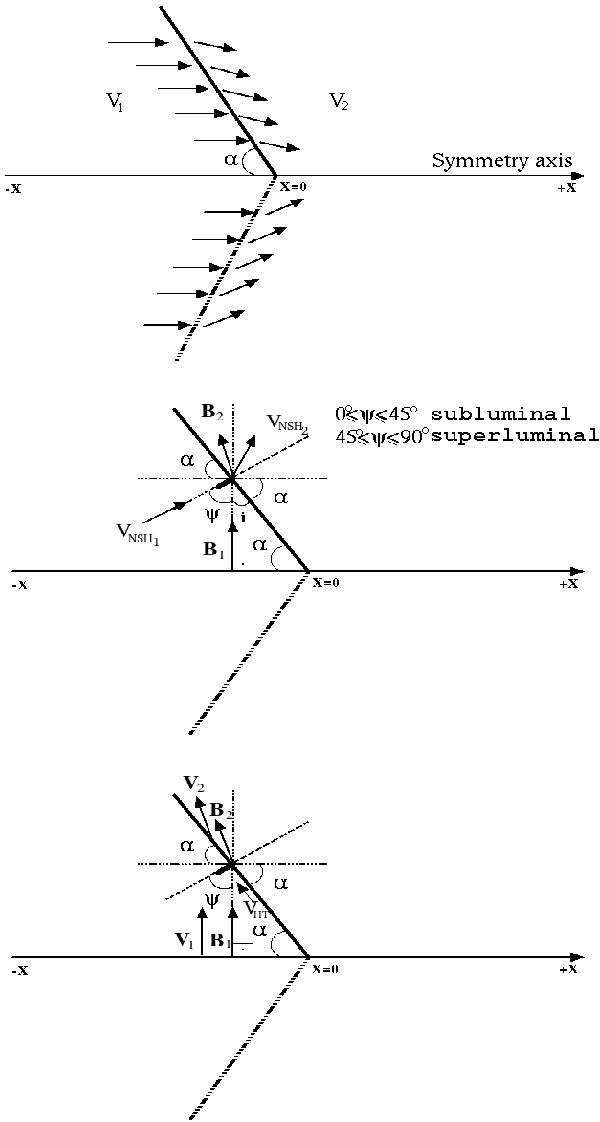
Left panel: general topology of the flow in a conical shock. Right panel: a conical shock as viewed in the normal-shock-frame (NSH), where the vector of the upstream flow velocity is parallel to the shock normal. Viewing closely the topology in NSH frame, one sees that 90° = i + a and 90° = ψ + i then ψ = a. The magnetic field is oblique to the shock surface by definition, so here, in order to facilitate our view clearer on the geometry of a conical shock in a local Cartesian system, we assume the case of the magnetic field vector (B), perpendicular to the jet axis thus inclined to the shock normal. Bottom panel: the same conical shock as it viewed after the Lorentz transformation into the de Hoffmann-Teller frame (HT). In this frame the velocity vector is placed parallel to the vector of the magnetic field as was viewed in the NSH frame above. By this transformation there is no electric field E in this frame.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.