Table 1
Summary of the properties of the families of models studied in the present paper.
| Family of | Distribution | Dimensionless | Internal | Anisotropy | Isophote | Paper |
| models | function | parameters | rotation | profile | shape | sections |
|
|
||||||
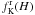
|
Ae − aH0 [e − a(H − H0) − 1] | Ψ, χ | solid-body | (0,0,0) | disky | 2 |
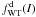
|
Ae − aE0 [e − a(I − E0) − 1 + a(I − E0)] | Ψ, χ, 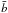 , c , c |
differential | (0, > 0, − 2) | boxy | 3, 4, 5, 6 |
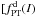
|
Ae − aE0e − a(I − E0) | Ψ, χ, 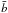 , c , c |
differential | (0, > 0,0) | boxy | 3, 6, Appendix B] |
Notes. The relevant integrals are defined as H = E − ωJz and 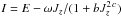 , with the corresponding cut-off constants given by H0 and E0. The dimensionless parameters are defined as follows: Ψ = ψ(0) respresents a measure of the concentration, χ = ω2/(4πGρ0) a measure of the (central) rotation strength, and, for the family of differentially rotating models,
, with the corresponding cut-off constants given by H0 and E0. The dimensionless parameters are defined as follows: Ψ = ψ(0) respresents a measure of the concentration, χ = ω2/(4πGρ0) a measure of the (central) rotation strength, and, for the family of differentially rotating models, 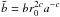 and c > 1/2 determine the shape of the rotation profile. The pressure anisotropy profiles are characterized in terms of the values of the anisotropy parameter
and c > 1/2 determine the shape of the rotation profile. The pressure anisotropy profiles are characterized in terms of the values of the anisotropy parameter 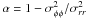 in the central, intermediate, and outer regions of a model; values of α greater than, lower than, and equal to zero indicate radially-biased, tangentially-biased anisotropy, and isotropy in velocity space, respectively. For each family of models, the first and third values of α are calculated analytically as the limiting values for small and large radii. For physical reasons discussed in Sect. 3.1, the focus of the paper is on the first two families.
in the central, intermediate, and outer regions of a model; values of α greater than, lower than, and equal to zero indicate radially-biased, tangentially-biased anisotropy, and isotropy in velocity space, respectively. For each family of models, the first and third values of α are calculated analytically as the limiting values for small and large radii. For physical reasons discussed in Sect. 3.1, the focus of the paper is on the first two families.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


