Table 1
The physical properties of the six cores.
| G030.50+00.95 | G031.03+00.26 | G031.03+00.76 | ||||
| Core A | Core B | Core A | Core B | Core A | Core B | |
|
|
||||||
| RA (2000) | 18:43:34.7 | 18:43:34.9 | 18:47:01.5 | 18:47:04.2 | 18:45:10.2 | 18:45:17.3 |
| Dec (2000) | −01:42:29 | −01:44:36 | −01:34:36 | −01:33:39 | −01:20:00 | −01:19:12 |
| Name in PF09 | SDC30.442+0.958 | SDC31.039+0.241 | Not included | |||
| Distance (pc) | 3400 | 3400 | 4900 | 4900 | 3400 | 3400 |
| Semi-major Axis (pc) | 0.6 | 0.7 | 0.45 | 0.55 | 0.4 | 1.0 |
| R0 (pc) | 0.06 | 0.07 | 0.04 | 0.05 | 0.04 | 0.1 |
| Aspect ratio | 1.93 | 3.16 | 2.46 | 2.22 | 1.70 | 1.65 |
| Position Angle | 50 | 85 | 125 | 340 | 335 | 85 |
| n0(H2) (cm-3) | 1.4 × 105 | 4.5 × 104 | 3.8 × 105 | 4.2 × 105 | 6.0 × 105 | 2.5 × 104 |
| ISRFHabing | 8.5 | 18 | 18 | 81 | 17 | 4.8 |
| τθ = 90°/τθ = 0° | 1.93 | 3.16 | 2.46 | 2.22 | 1.59 | 1.65 |
| F500 μm (Jy) | 5.0 ± 0.5 | 9.0 ± 0.9 | 3.3 ± 0.3 | 10 ± 1 | 4.5 ± 0.5 | 4.4 ± 0.4 |
| Model Temperature (K) | 9–19 | 11–22 | 9–22 | 11–28 | 8–22 | 10–18 |
| SED Temperature (K) | 14 ± 1 | 16 ± 2 | 14 ± 1 | 17 ± 2 | 14 ± 1 | 14 ± 1 |
| Model mass (M⊙) | 120 | 140 | 170 | 290 | 110 | 90 |
| SED mass – κ = 0.05 cm2 g-1 (M⊙) | 130 | 170 | 170 | 310 | 110 | 100 |
| SED mass – κ = 0.03 cm2 g-1 (M⊙) | 210 | 280 | 280 | 510 | 180 | 160 |
|
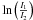
0.75 | – | 1.50 | – | 1.25 | – |
| Lmax (L⊙) | <6 | <3 | <200 | <1000 | <40 | <9 |
Notes. R0 is the flattening radius within the core, n0(H2) is the central density of each core, ISRFHabing is the ISRF of the core at FUV given in multiples of the Habing flux – i.e. 1.6 × 10-3 erg s-1 cm-2 (Habing 1968), τθ = 90°/τθ = 0° is the ratio of optical depths at θ = 90° and at θ = 0° and F500 μm is the flux density of each core at 500 μm. The model temperature is the range of temperatures in the core calculated from the model, and the SED temperature was calculated from single-temperature greybody fitting. The model mass was calculated using κ = 0.05 cm2 g-1 at 500 μm (Ossenkopf & Henning 1994). The two SED masses were calculated using the method of Hildebrand (1983), the SED temperature and the flux density at 500 μm (see Sect. 4.1). The difference in ISRFs, 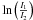, was calculated from the model (see Sect. 4.3). Lmax is the maximum luminosity of a star that could be embedded in each core (see Sect. 4.4).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.