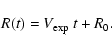| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 1107 - 1118 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361:200809551 | |
| Published online | 22 December 2008 | |
Forbush decreases and turbulence levels at coronal mass ejection fronts
P. Subramanian1 - H. M. Antia2 - S. R. Dugad2 -
U. D. Goswami2 - S. K. Gupta2 - Y. Hayashi3 - N. Ito3 -
S. Kawakami3 - H. Kojima4 - P. K. Mohanty2 - P. K.
Nayak2 - T. Nonaka3 - A. Oshima3 - K. Sivaprasad2 -
H. Tanaka2 - S. C. Tonwar2
(The GRAPES-3 collaboration)
1 - Indian Institute of Science Education and Research, Sai Trinity Building, Pashan, Pune 411021, India
2 -
Tata Institute of Fundamental Research, Homi Bhabha Road,
Mumbai 400005, India
3 -
Graduate School of Science, Osaka City University, Osaka 558-8585, Japan
4 -
Nagoya Women's University, Nagoya 467-8610, Japan
Received 11 February 2008 / Accepted 25 October 2008
Abstract
Aims. We seek to estimate the average level of MHD turbulence near coronal mass ejection (CME) fronts as they propagate from the Sun to the Earth.
Methods. We examined the cosmic ray data from the GRAPES-3 tracking muon telescope at Ooty, together with the data from other sources for three closely observed Forbush decrease events. Each of these event is associated with frontside halo coronal mass ejections (CMEs) and near-Earth magnetic clouds. The associated Forbush decreases are therefore expected to have significant contributions from the cosmic-ray depressions inside the CMEs/ejecta. In each case, we estimate the magnitude of the Forbush decrease using a simple model for the diffusion of high-energy protons through the largely closed field lines enclosing the CME as it expands and propagates from the Sun to the Earth. The diffusion of high-energy protons is inhibited by the smooth, large-scale magnetic field enclosing the CME and aided by the turbulent fluctuations near the CME front. We use estimates of the cross-field diffusion coefficient ![]() derived from the published results of extensive Monte Carlo simulations of cosmic rays propagating through turbulent magnetic fields. We then compare our estimates with the magnitudes of the observed Forbush decreases.
derived from the published results of extensive Monte Carlo simulations of cosmic rays propagating through turbulent magnetic fields. We then compare our estimates with the magnitudes of the observed Forbush decreases.
Results. Our method helps constrain the ratio of energy density in the turbulent magnetic fields to that in the mean magnetic fields near the CME fronts. This ratio is found to be ![]() 2% for the 2001 April 11 Forbush decrease event,
2% for the 2001 April 11 Forbush decrease event, ![]() 6% for the 2003 November 20 Forbush decrease event and
6% for the 2003 November 20 Forbush decrease event and ![]() 249% for the much more energetic event of 2003 October 29.
249% for the much more energetic event of 2003 October 29.
Key words: ISM: cosmic rays - Sun: coronal mass ejections (CMEs) - Sun: solar-terrestrial relations
1 Introduction
Forbush decreases are short-term depressions in the cosmic ray flux reaching the Earth, and they are caused by the effects of the interplanetary counterparts of coronal mass ejections (CMEs) from the Sun (and the shocks they drive) and also the co-rotating interaction regions originating from the Sun. They have been studied closely since their initial discovery in the 1930s (see, e.g., comprehensive observational reviews by Cane 2000; Venkatesan & Badruddin 1990). With the recent upsurge of interest in space weather effects due to solar transients, the complementary information provided by the cosmic ray signatures of these effects has assumed increased significance.In this work, we have examined the data from the GRAPES-3 tracking muon telescope at Ooty for three well-observed events. Earlier, we had analysed the Forbush decrease data from this experiment during the period 2001-2004 and searched for events that can be associated with a near-Earth magnetic cloud and a corresponding halo CME from the Sun. We start from lists of magnetic cloud events given on the WIND webpage, http://lepmfi.gsfc.nasa.gov/mfi/mag_cloud_pub1.html, Lynch et al. (2003) and Huttunen et al. (2005). We shortlist Forbush decrease events that occurred in a reasonable time window around the time of entry of the magnetic clouds. Of these shortlisted events, we have selected the three events shown in Fig. 8. Two of these events (2001 April 11 and 2003 October 29) have especially clean decrease profiles. Even though the decrease profile for the third event on 2003 November 20 is not nearly as clear-cut, we still selected it, because of its association with a very closely observed magnetic cloud, and also because it illustrates the diversity of the events observed with the GRAPES-3 experiment. We estimate the contribution of the depressed cosmic ray density inside the CME to the total Forbush decrease seen in these datasets, and use it to derive conclusions regarding the level of turbulence near the CME front.
The events discussed in this work were very closely observed, and they have their origins in full halo CMEs that originated close to the centre of the solar disc. This means that the corresponding interplanetary CMEs (ICMEs) would have been intercepted at the Earth as ejecta/magnetic clouds, and the observed cosmic ray depressions corresponding to these events would have had contributions from the shock ahead of the ICME, as well as from the ejecta/magnetic cloud itself (Cane et al. 1994, 1995; Cane & Richardson 1997). Theoretical treatments of Forbush decreases model the effect as arising due to a general propagating region of enhanced turbulence/scattering and decreased diffusion (e.g., Nishida 1983; le Roux & Potgieter 1991) and do not distinguish between the shock and the ejecta, or implicitly assume that the decrease is only due to the shock (e.g., Chih & Lee 1986). It is fairly well known that magnetic clouds are well-correlated with Forbush decreases (e.g., Zhang & Burlaga 1988; Badruddin et al. 1986; Badruddin et al. 1991; Venkatesan & Badruddin 1990; Sanderson et al. 1990; see, however, Lockwood et al. 1991, for the opposite viewpoint).
The relationship between the decrease due to the shock and the one due
to the magnetic cloud has been investigated (Cane et al. 1995, 1997;
Wibberenz et al. 1997, 1998), and there is some
evidence that they can contribute in roughly equal proportions, to the
overall magnitude of the decrease, although the individual time
profiles of the decrease due to these two effects can be quite
different (Wibberenz et al. 1997). It is worth mentioning that the
contributions of the shock and the magnetic cloud to the overall
decrease can be discerned relatively easily from the spacecraft
observations (e.g., Cane et al. 1995, 1997; Cane 2000), since the
temporal boundaries of the magnetic cloud can be readily ascertained
by using the data from the same source. These data typically exhibit
two steps in the decrease phase, one corresponding to the shock
passage and the second to the entry of the magnetic
cloud. The two-step signature, however, need not be a necessary
condition for the Forbush decreases arising from the combination of a
magnetic cloud and the associated shock. Even for events where there
is clear evidence that both the shock and the following
magnetic cloud have intercepted the Earth (as is the case with the three
events presented in this paper), the precise decrease profile will
depend upon the standoff distance between the magnetic cloud and the
shock and on the energies of the protons detected. If the protons are
energetic enough that their mean free path is comparable to the
magnetic cloud-shock standoff distance, the distinct identities of the
steps corresponding to the shock and the cloud may not be clear. We
attribute 50% of the total decrease to the magnetic cloud
(
![]() ,
see Sect. 3), following the general logic outlined by
Wibberenz et al. (1997). We discuss the sensitivity of our final
results to variations in
,
see Sect. 3), following the general logic outlined by
Wibberenz et al. (1997). We discuss the sensitivity of our final
results to variations in ![]() in Sect. 7. In our quantitative work,
we estimate the magnitude of the Forbush decrease using filtered data
(see Sect. 2.1 for a description of the filtering method) averaged over 1 h.
in Sect. 7. In our quantitative work,
we estimate the magnitude of the Forbush decrease using filtered data
(see Sect. 2.1 for a description of the filtering method) averaged over 1 h.
The high muon counting rate measured by the GRAPES-3 experiment
results in extremely small statistical errors, allowing small
changes in the intensity of the cosmic ray flux to be measured
with high precision. Thus a small drop (![]() 0.2%) in the
cosmic ray flux, during a Forbush decrease event can be reliably
detected. This is possible even in the presence of the diurnal
anisotropy of much larger magnitude (
0.2%) in the
cosmic ray flux, during a Forbush decrease event can be reliably
detected. This is possible even in the presence of the diurnal
anisotropy of much larger magnitude (![]() 1.0%), through a
suitable filtering technique described subsequently.
1.0%), through a
suitable filtering technique described subsequently.
Before we proceed further, it is worth discussing the terminology we
use. The term CME is generally used to denote the blob of plasma ejected
from the solar corona as viewed by coronographs near the Sun
(typically from 1 to 30 ![]() ). The CME can be thought of as a
largely closed, magnetic flux rope-like magnetic structure (see,
however, Bothmer et al. 1996, 1997, for evidence of CMEs possessing
closed, as well as some open field lines) whose cross-section expands
as it travels through the heliosphere. There are practically no high-energy
cosmic rays inside it when it starts out from near the Sun, and
the ambient cosmic rays diffuse into it via cross-field diffusion
across the closed magnetic field lines as it travels through the
heliosphere. The term ``ICME'' is a broad one used to denote the
interplanetary counterpart of a CME (see, e.g., Forsyth et al. 2006;
Wimmer-Schweingruber et al. 2006, and references therein), while the
term ``magnetic cloud'' is reserved for ICMEs detected near the Earth,
possessing certain well-defined criteria such as plasma temperature
depressions and smooth magnetic field rotations (see, e.g., Burlaga et al. 1981; Bothmer & Schwenn 1998). Other CME/ICME related ejecta
detected near the Earth are merely called ``ejecta''.
). The CME can be thought of as a
largely closed, magnetic flux rope-like magnetic structure (see,
however, Bothmer et al. 1996, 1997, for evidence of CMEs possessing
closed, as well as some open field lines) whose cross-section expands
as it travels through the heliosphere. There are practically no high-energy
cosmic rays inside it when it starts out from near the Sun, and
the ambient cosmic rays diffuse into it via cross-field diffusion
across the closed magnetic field lines as it travels through the
heliosphere. The term ``ICME'' is a broad one used to denote the
interplanetary counterpart of a CME (see, e.g., Forsyth et al. 2006;
Wimmer-Schweingruber et al. 2006, and references therein), while the
term ``magnetic cloud'' is reserved for ICMEs detected near the Earth,
possessing certain well-defined criteria such as plasma temperature
depressions and smooth magnetic field rotations (see, e.g., Burlaga et al. 1981; Bothmer & Schwenn 1998). Other CME/ICME related ejecta
detected near the Earth are merely called ``ejecta''.
The rest of this paper is organised as follows, We briefly describe the GRAPES-3 experiment in Sect. 2. We describe the model we used to calculate the magnitude of the expected Forbush decreases in Sect. 3. The three Forbush decrease events we analysed are described in Sects. 4-6. We describe our results in Sect. 7 and summarise them in Sect. 8.
2 GRAPES-3 experimental system
The GRAPES-3 experiment is located at Ooty (
![]() N
latitude,
N
latitude,
![]() E longitude, and 2200 m altitude), in
southern India. The GRAPES-3 air shower experiment was designed
to have a compact configuration of a conventional
type array, with a separation of only 8 m between the adjacent
detectors, which are deployed in a symmetric hexagonal geometry.
A schematic layout of the GRAPES-3 array is shown in Fig. 1.
The observations were started in 2000 with 217 detectors, located
within the inner 8 rings (see Fig. 1 Gupta et al. 2005).
E longitude, and 2200 m altitude), in
southern India. The GRAPES-3 air shower experiment was designed
to have a compact configuration of a conventional
type array, with a separation of only 8 m between the adjacent
detectors, which are deployed in a symmetric hexagonal geometry.
A schematic layout of the GRAPES-3 array is shown in Fig. 1.
The observations were started in 2000 with 217 detectors, located
within the inner 8 rings (see Fig. 1 Gupta et al. 2005).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f1.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg13.gif) |
Figure 1:
A schematic layout the GRAPES-3 air shower
array shown here with 217 detectors (circles). Each
of the 16 squares represent a 35 m2 area tracking muon
detector with
|
| Open with DEXTER | |
A very large-area tracking muon telescope operating as a part of the GRAPES-3 experiment (Gupta et al. 2005; Hayashi et al. 2005), is a unique instrument, to search for the high-energy protons emitted during the active phase of a solar flare or a coronal mass ejection (CME). The muon telescope is capable of providing a high-statistics, directional study of muons. The GRAPES-3 muon telescope covers an area of 560 m2, consisting of a total of 16 modules, each 35 m2 in area. These modules are located close to each other as shown in Fig. 1. A cluster of four 35 m2area neighbouring modules, located inside a common hall, constitutes one supermodule with a total area of 140 m2. The energy threshold of the telescope is 1 GeV for the muons arriving along the vertical direction. The cutoff rigidity due to the magnetic field of the Earth at Ooty is 17 GV in the vertical direction and varies from 12 to 42 GV across the field of view of the muon telescope as shown later in Fig. 6.
| |
Figure 2: A schematic display of the 4-layer tracking muon telescope module with 58 PRCs per layer. The four layers of the PRCs labelled Layer-0, Layer-1, etc. are embedded in concrete blocks. Inclined lines represent a set of parallel muon tracks. |
| Open with DEXTER | |
The basic detector element of the muon telescope is a rugged
proportional counter (PRC) made from a 600 cm long steel pipe
with 2.3 mm wall thickness and a square cross-sectional
area of
![]() cm2. A muon telescope module with a
sensitive area of 35 m2 consists of a total of 232 PRCs
arranged in four layers of 58 PRCs each, with alternate layers
placed in orthogonal directions. Two successive layers of the
PRCs are separated by a 15 cm thick concrete layer, consisting
of
cm2. A muon telescope module with a
sensitive area of 35 m2 consists of a total of 232 PRCs
arranged in four layers of 58 PRCs each, with alternate layers
placed in orthogonal directions. Two successive layers of the
PRCs are separated by a 15 cm thick concrete layer, consisting
of
![]() cm3 blocks as shown in Fig. 2.
The four-layer PRC configuration of the muon modules allows
a 3-D reconstruction of the muon track direction to an accuracy
of
cm3 blocks as shown in Fig. 2.
The four-layer PRC configuration of the muon modules allows
a 3-D reconstruction of the muon track direction to an accuracy
of
![]() .
It is worth noting that the accuracy
gradually increases with increasing zenith angle due to the
greater separation of the triggered PRCs.
.
It is worth noting that the accuracy
gradually increases with increasing zenith angle due to the
greater separation of the triggered PRCs.
To achieve an energy threshold of 1 GeV for vertical muons, an
absorber of total thickness ![]() 550 g cm-2 in the form
of concrete blocks is employed. This was done by placing a total
of 15 layers of concrete blocks above Layer-1, as shown
schematically in Fig. 2. A unique feature of the GRAPES-3
muon module is the robust structure of the PRCs, which supports the
huge load of 2.4 m thick concrete in a self-supporting manner. The
concrete blocks are arranged in the shape of an inverted pyramid
to shield the PRCs, with coverage up to
550 g cm-2 in the form
of concrete blocks is employed. This was done by placing a total
of 15 layers of concrete blocks above Layer-1, as shown
schematically in Fig. 2. A unique feature of the GRAPES-3
muon module is the robust structure of the PRCs, which supports the
huge load of 2.4 m thick concrete in a self-supporting manner. The
concrete blocks are arranged in the shape of an inverted pyramid
to shield the PRCs, with coverage up to ![]() around the
vertical direction for the incident muons. The threshold energy
changes to
around the
vertical direction for the incident muons. The threshold energy
changes to
![]() GeV for the muons incident at a zenith
angle of
GeV for the muons incident at a zenith
angle of ![]() .
The cross section of a muon telescope module is
shown schematically in Fig. 2. A cluster of four such
modules, separated by a horizontal distance of 130 cm at the base
constitutes one supermodule. The GRAPES-3 muon telescope contains
a total of four supermodules (Hayashi et al. 2005).
.
The cross section of a muon telescope module is
shown schematically in Fig. 2. A cluster of four such
modules, separated by a horizontal distance of 130 cm at the base
constitutes one supermodule. The GRAPES-3 muon telescope contains
a total of four supermodules (Hayashi et al. 2005).
Because of the sensitivity of the PRCs to low-energy ![]() rays, from the radioactivity present in the concrete absorber,
individual PRCs display sizable counting rates of
rays, from the radioactivity present in the concrete absorber,
individual PRCs display sizable counting rates of ![]() 200 Hz.
An output is generated, if any one of the 58 PRCs produces a
signal. A logical ``OR'' of outputs from all 58 PRCs in a layer
is generated, after suitable amplification and shaping to form
the layer OR output. A coincidence of the four OR outputs from
the four layers in a module is used to generate the 4-layer
trigger. Despite high counting rates of individual PRCs, the
4-layer coincidence trigger is relatively free of the
contribution from the background radioactivity and it is caused
only by the passage of a muon. The observed 4-layer muon counting
rate of
200 Hz.
An output is generated, if any one of the 58 PRCs produces a
signal. A logical ``OR'' of outputs from all 58 PRCs in a layer
is generated, after suitable amplification and shaping to form
the layer OR output. A coincidence of the four OR outputs from
the four layers in a module is used to generate the 4-layer
trigger. Despite high counting rates of individual PRCs, the
4-layer coincidence trigger is relatively free of the
contribution from the background radioactivity and it is caused
only by the passage of a muon. The observed 4-layer muon counting
rate of ![]() 3200 Hz per module yields a total counting rate
3200 Hz per module yields a total counting rate
![]() min-1 for all 16 modules. This high
rate permits small changes of
min-1 for all 16 modules. This high
rate permits small changes of ![]() 0.1% in the muon flux,
to be detected on a timescale of
0.1% in the muon flux,
to be detected on a timescale of ![]() 5 min, after appropriate
correction to the variation in the atmospheric pressure with time.
5 min, after appropriate
correction to the variation in the atmospheric pressure with time.
![\begin{figure}
\par\includegraphics[angle=270,width=9cm,clip]{9551f3.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg24.gif) |
Figure 3: Distribution of the relative variation in %, for the 4-layer muon counting rate for the 35 m2 area modules for time intervals of 6 min. Also shown is a Gaussian fit to the data. The standard deviation of the fit is 0.103% as against an expected value of 0.095% based on statistics. |
| Open with DEXTER | |
Most of the detected muons are generated by ![]() 20 GeV galactic
cosmic rays, and form a stable and dominant background to the variation
in their flux produced by the CME/solar flare. The muon data is
grouped online every 10 s, into solid-angle bins of
20 GeV galactic
cosmic rays, and form a stable and dominant background to the variation
in their flux produced by the CME/solar flare. The muon data is
grouped online every 10 s, into solid-angle bins of ![]() 0.05 sr,
consistent with the angular resolution of the muon telescope as
described below. Since >1 GeV muons are secondaries produced by the
primary protons of energy
0.05 sr,
consistent with the angular resolution of the muon telescope as
described below. Since >1 GeV muons are secondaries produced by the
primary protons of energy ![]() 20 GeV in the atmosphere, therefore
these observations can be used to probe the effect of the Sun on
cosmic rays.
20 GeV in the atmosphere, therefore
these observations can be used to probe the effect of the Sun on
cosmic rays.
The data recorded during 2003 October, from 15 out of 16 working
modules were used in the statistical analysis described below. The
muon rate for each 35 m2 area module was recorded for 770 time intervals, each 6 min in duration spread over a total of
about 3.5 days. During this period of 3.5 days, the data could not
be recorded for 70 out of 840 intervals, due to the failure of the
recording system in the first supermodule. Next, the mean muon rate
of the module for the entire duration was computed. Then the percent
deviation from the mean module rate was calculated, separately for
each module. Finally, the rms spread in the percent deviation called
``relative variation'' was calculated for each module for all 6-min
intervals. In Fig. 3, the distribution of the relative
variation in the 4-layer muon rate in percent, as recorded by the
muon modules is shown. Also shown in Fig. 3, is a Gaussian
fit to this distribution, which yields a standard deviation of
0.103%. This value may be compared with an expectation of 0.095%,
based on a 6-min muon statistic of
![]() per module.
This tiny statistical error in muon rate allows a high-precision
study of various solar phenomena to be carried out
(Nonaka et al. 2006).
per module.
This tiny statistical error in muon rate allows a high-precision
study of various solar phenomena to be carried out
(Nonaka et al. 2006).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9551f4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg27.gif) |
Figure 4: A schematic view of muon arrival angle selection based on the PRC triggered in the lower and 15 PRCs in the upper layer. The triggered PRCs are shown as filled squares. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg28.gif) |
Figure 5:
A schematic of the nine muon arrival
direction bins; |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f6.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg29.gif) |
Figure 6: The 9 coarse solid-angle bins are shown along with the contours of constant geomagnetic cutoff rigidity in the field of view (FOV). Cutoff rigidity varies from 12 to 42 GV in the FOV of GRAPES-3. |
| Open with DEXTER | |
2.1 Data analysis
In all four supermodules, the direction of muons is recorded into
225 solid-angle bins. This was done by using a dedicated
direction-sensitive trigger with an independent data acquisition
system for each of the four supermodules. As shown in Fig. 4,
the muon angle is determined for each PRC in the lower layer and
binned into 15 angular bins based on the specific location of the
PRC triggered in the upper layer from among the 15 PRCs, one directly
above (central PRC) and 7 each on either side of the central PRC.
This angular binning is carried out in each of the two orthogonal
projections (XZ and YZ; Z is vertical direction), thereby generating
a 2-dimensional
![]() solid-angle map of muon directions.
The contents of the 225 solid-angle bins are recorded, once every 10 s, thus providing a continuous monitoring of the directional flux
of muons in the sky.
solid-angle map of muon directions.
The contents of the 225 solid-angle bins are recorded, once every 10 s, thus providing a continuous monitoring of the directional flux
of muons in the sky.
The variation in the muon rate may be studied in any of the 225 solid
angle bins. However, it is expected that the influence of a solar
flare and/or CME would be spread over several bins. This directional
spread could arise from the influence of the terrestrial, solar, and
interplanetary magnetic fields, etc. Therefore, the detected muons have
been regrouped into
![]() coarse solid-angle bins, as shown
schematically in Fig. 5. This regrouping of the data was done
by combining either a set of
coarse solid-angle bins, as shown
schematically in Fig. 5. This regrouping of the data was done
by combining either a set of ![]() or
or ![]() fine solid-angle
bins. The exception being the vertical direction where
fine solid-angle
bins. The exception being the vertical direction where ![]() bins
have been combined. This choice of angular segmentation was dictated
by the fact that the muon flux is comparatively larger for the near
central directions (N, E, W, S) than for the outer directions (NE, SE,
NW, SW). This choice results in a relatively similar solid-angle
coverage for the nine coarse bins. Thus the solid-angle of acceptance
includes only
bins
have been combined. This choice of angular segmentation was dictated
by the fact that the muon flux is comparatively larger for the near
central directions (N, E, W, S) than for the outer directions (NE, SE,
NW, SW). This choice results in a relatively similar solid-angle
coverage for the nine coarse bins. Thus the solid-angle of acceptance
includes only
![]() out of original 225 bins, restricting
the maximum zenith angle to
out of original 225 bins, restricting
the maximum zenith angle to
![]() .
This still exceeds the
shielding coverage of
.
This still exceeds the
shielding coverage of
![]() ,
for the PRCs at the outer edge,
but such events constitute <1% of the data. This regrouping also
results in muon statistics for various bins that are not too dissimilar.
,
for the PRCs at the outer edge,
but such events constitute <1% of the data. This regrouping also
results in muon statistics for various bins that are not too dissimilar.
At the energies (![]() 20 GeV) of interest here, the propagation
of charged particles near the Earth (
20 GeV) of interest here, the propagation
of charged particles near the Earth (
![]() ,
where
,
where ![]() is
the radius of the Earth) is strongly influenced by the geomagnetic
field. The access by a charged particle to a given geographical
location depends on the momentum per unit charge of the particle
called rigidity. The threshold value of the rigidity is termed
``geomagnetic cutoff rigidity'', which depends on the geographical
location on the Earth and the direction of the arriving particle. The
geomagnetic cutoff rigidity can be calculated using a detailed model
of the geomagnetic field (Cooke et al. 1991). The geomagnetic cutoff
rigidity for the field of view (FOV) of the GRAPES-3 muon telescope
varies significantly for the nine coarse, solid-angle bins. We first
calculate the cutoff rigidity for the centre of each of the 169 fine
solid-angle bins, which constitute the 9 elements of the FOV, using
the IGRF2000 geomagnetic field model. Subsequently, a weighted mean
of the cutoff rigidities of the fine bins constituting a coarse bin
is calculated for each of the 9 coarse bins. These weights are the
muon counting rates for a given fine bin. Here, it needs to be
emphasised that the knowledge of the geomagnetic field at any
particular moment in time is imperfect, and it is virtually
impossible to determine the cutoff to a high degree of accuracy.
However, the calculated values of the geomagnetic cutoff represent
a very useful approximation to the true values at the time of the
observations. In Fig. 6 the contours of constant
geomagnetic cutoff rigidity in the FOV are superimposed over a
schematic of the 9 solid-angle bins of muon arrival directions. The
geomagnetic cutoff rigidity varies from 12 GV in the west to 42 GV
in the east, within the FOV of the GRAPES-3 tracking muon telescope.
is
the radius of the Earth) is strongly influenced by the geomagnetic
field. The access by a charged particle to a given geographical
location depends on the momentum per unit charge of the particle
called rigidity. The threshold value of the rigidity is termed
``geomagnetic cutoff rigidity'', which depends on the geographical
location on the Earth and the direction of the arriving particle. The
geomagnetic cutoff rigidity can be calculated using a detailed model
of the geomagnetic field (Cooke et al. 1991). The geomagnetic cutoff
rigidity for the field of view (FOV) of the GRAPES-3 muon telescope
varies significantly for the nine coarse, solid-angle bins. We first
calculate the cutoff rigidity for the centre of each of the 169 fine
solid-angle bins, which constitute the 9 elements of the FOV, using
the IGRF2000 geomagnetic field model. Subsequently, a weighted mean
of the cutoff rigidities of the fine bins constituting a coarse bin
is calculated for each of the 9 coarse bins. These weights are the
muon counting rates for a given fine bin. Here, it needs to be
emphasised that the knowledge of the geomagnetic field at any
particular moment in time is imperfect, and it is virtually
impossible to determine the cutoff to a high degree of accuracy.
However, the calculated values of the geomagnetic cutoff represent
a very useful approximation to the true values at the time of the
observations. In Fig. 6 the contours of constant
geomagnetic cutoff rigidity in the FOV are superimposed over a
schematic of the 9 solid-angle bins of muon arrival directions. The
geomagnetic cutoff rigidity varies from 12 GV in the west to 42 GV
in the east, within the FOV of the GRAPES-3 tracking muon telescope.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f7.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg36.gif) |
Figure 7: The power spectrum of 28 day data covering the period from 26 March to 22 April 2001. The solid lines show the results for all 9 directions used in the study while the dashed line shows the function that is used for filtering out the high-frequency components. The Fourier transform is multiplied by this function before taking the inverse Fourier transform to get filtered time series. |
| Open with DEXTER | |
In this study we used the GRAPES-3 data summed over a time interval of one hour for each of the nine bins, which are identified as NW, N, NE, W, V, E, SW, S, and SE. The calculated cutoff rigidities for these nine bins are 15.5, 18.7, 24.0, 14.3, 17.2, 22.4, 14.4, 17.6, and 22.4 GV, respectively, as seen from Fig. 6. The summing over an interval of 1 h improves the signal-to-noise ratio, but the diurnal variations in the muon flux are still present. To filter out these oscillations we applied a low-pass filter, removing all frequencies higher than 1 day-1. In Fig. 7 we show the Fourier transform of the data covering a period of 28 days that includes the event of 2001 April 11. The peaks corresponding to diurnal variation and its first harmonic are visible. The Fourier transform is multiplied by the function shown by a dashed line to remove the high-frequency components. This filter is found to be effective in removing high-frequency oscillations, including the diurnal variations and their harmonics. The Forbush decrease events are also clearer in the filtered data.
The smoothing may tend to change the
amplitude of the decrease and possibly shift the onset time for the
Forbush decrease by a few hours in some cases. However, it is often
difficult to determine if these differences are artifacts of smoothing
or whether the unfiltered data showed different amplitude because a
diurnal oscillation happened to have the right phase, so as to enhance
or reduce the amplitude of the Forbush decrease. Some fluctuations in
muon flux could be due to Forbush decrease and associated events, but
it is unlikely that these will be periodic in nature, hence are not
likely to be affected by the filter. Since the differences in amplitude
caused by filter are not substantial, it would not affect our results
significantly. Thus in this work, we used the filtered data to study
the characteristics of Forbush decrease events, although the unfiltered
data are also shown in corresponding figures for direct comparison.
Further, we repeated the calculations using unfiltered data and find
that the final results are not significantly different. There can also
be anisotropies intrinsic to the CME/magnetic cloud itself, arising
from a
![]() drift, where
drift, where ![]() is the
interplanetary magnetic field and
is the
interplanetary magnetic field and
![]() denotes the
cosmic-ray density gradient inside the CME (Bieber & Evenson 1998;
Munakata et al. 2003, 2005; Kuwabara et al. 2004). Such anisotropies
can potentially be ``mixed'' with the diurnal anisotropy, and it is
possible that there will still be some residual anisotropy after the
filter is applied. This is the case with one of the weaker events that
we have studied here; namely 2003 November 20.
denotes the
cosmic-ray density gradient inside the CME (Bieber & Evenson 1998;
Munakata et al. 2003, 2005; Kuwabara et al. 2004). Such anisotropies
can potentially be ``mixed'' with the diurnal anisotropy, and it is
possible that there will still be some residual anisotropy after the
filter is applied. This is the case with one of the weaker events that
we have studied here; namely 2003 November 20.
To determine the properties of Forbush decrease, we divided the time interval in three parts, the first part before the onset; the second part includes the decrease, while the third part includes the recovery phase. We fit straight lines to the first two parts and an exponential profile for the third part. The point of intersection of the two straight lines defines the onset time for the Forbush decrease, while the intersection of the last two fits determines the minimum of the profile. The difference in the flux between these two points determines the magnitude M of the decrease (Sect. 3), which is measured in term of percentage change in steady flux. The fits for all events used in this work are shown in the respective sections.
| |
Figure 8: Data from Tibet neutron monitor (dashed lines) is compared with GRAPES-3 data (solid line) for vertical direction for the 3 events studied in this work. Both the time series are filtered by applying a low pass filter to remove high frequency components. In order to fit in the same scale the neutron monitor data is scaled down by a factor of 3. |
| Open with DEXTER | |
In the subsequent analysis we discuss in detail three Forbush
decrease events, namely those on 2001 April 11, 2003 October 29,
and 2003 November 20, which were associated with CME/magnetic
clouds. The GRAPES-3 data is recorded along nine directions as
described earlier. However, in Fig. 8 the data for only
the vertical direction is shown for these three events along with
measurements from the Tibet neutron monitor at Yangbajing
(Muraki et al. 2007) as obtained from
http://cr0.izmiran.rssi.ru/tibt/main.htm. The Tibet neutron
monitor has a wide solid-angle of acceptance with the dominant
contribution coming from the vertical direction; for that reason,
we selected the GRAPES-3 data along the vertical direction for a
comparison as shown in Fig. 8. The Tibet neutron monitor
was chosen, as Yangbajing (
![]() E) is located at a similar
longitude as Ooty (
E) is located at a similar
longitude as Ooty (
![]() E), and the geomagnetic cutoff
rigidities are also not too dissimilar (Ooty = 17 GV, and Yangbajing = 14 GV). The neutron monitor data was scaled down by a factor of 3
to fit the same scale. Here, it needs to be emphasised that both
sets of data were subjected to the same low pass filter to remove
frequencies higher than 1 day-1. The detailed features in the
Tibet neutron monitor data follow the GRAPES-3 muon data rather closely
for all three Forbush decrease events as seen from Fig. 8.
E), and the geomagnetic cutoff
rigidities are also not too dissimilar (Ooty = 17 GV, and Yangbajing = 14 GV). The neutron monitor data was scaled down by a factor of 3
to fit the same scale. Here, it needs to be emphasised that both
sets of data were subjected to the same low pass filter to remove
frequencies higher than 1 day-1. The detailed features in the
Tibet neutron monitor data follow the GRAPES-3 muon data rather closely
for all three Forbush decrease events as seen from Fig. 8.
3 Proton diffusion into CME/magnetic cloud
We are concerned here with the component of the Forbush decrease produced by the difference between the proton density inside and outside the magnetic cloud that intercepts the Earth. To do this, we obtain an estimate of the proton density inside the CME/magnetic cloud produced by the cumulative effect of protons diffusing into the closed magnetic structure of the CME/magnetic cloud as it propagates towards the Earth. We use cross-field diffusion coefficients derived from recent numerical treatments of cosmic ray propagation through turbulent magnetic fields.
Before doing so, it is worth taking a brief look at the typical
proton gyro-radius in relation to the overall size of the ejecta to
see how far such a picture involving cross-field diffusion would be
valid. This is especially pertinent here, since the protons detected
by the GRAPES-3 experiment are typically very energetic. The GRAPES-3
experiment can detect muons produced by protons of rigidities above
12-42 GV, where the rigidity Rg is defined by
where P is the proton momentum, c the speed of light, Z the charge state (=1 for a proton), e the charge of an electron, Bthe magnetic field in Gauss, and
The flux of protons entering the CME/magnetic cloud at a given time is
where F is in units of number per
where A(t) is the cross-sectional area of the CME at time t. The integration extends from the time the CME is first observed in the LASCO field of view (t = 0) through the time (t = T) when it arrives at the Earth as a magnetic cloud. A reasonable estimate for
where R(t) is the CME cross-sectional radius at time t. Assuming the CME to be an expanding ``flux-rope'' whose length increases with time as its cross-sectional area expands (see http://lepmfi.gsfc.nasa.gov/mfi/Mag_Cloud_Model.html for a cartoon), we can use
where L(t) is the length of the flux-rope cylinder at time t, and can be related to the ``height'' H of the CME above the solar limb via
The height above the solar limb H is the most commonly measured quantity for limb CMEs, but it is not clear how well it can be estimated for the halo CMEs we are considering. We consider this aspect further in Sect. 4 below. Using Eqs. (5), (6), and (4) in Eq. (3), we have
The density inside the near-Earth magnetic cloud would be
and it can be related to the magnitude M of the Forbush decrease via
where L(T) and R(T) denote the length and cross-sectional radius at time T, when the ejecta has reached the Earth. The quantity
Table 1: Derived parameters for Forbush decrease for the 2001 April 11 event.
3.1 Cross-field diffusion coefficient
We now turn our attention to the cross-field diffusion coefficient
The issue of the cross-field diffusion coefficient is a subject
of intensive ongoing research, and a good way to proceed for our
purposes is to use the convenient parametrisation of the results
of extensive Monte Carlo simulations of cosmic rays propagating
through tangled magnetic fields given by Candia & Roulet (2004).
Their results can be regarded as a superset of similar work (e.g.,
Giacalone & Jokipii 1999; Casse et al. 2002); it contains all the
preceding results and also extends the parameter regime of the
simulations. They give the following fit for the ``parallel''
diffusion coefficient
![]() (which is due to scattering
of the particles back and forth along the mean field, as the field
is subject to random turbulent fluctuations):
(which is due to scattering
of the particles back and forth along the mean field, as the field
is subject to random turbulent fluctuations):
where c is the speed of light and the quantities
where B0 is the mean magnetic field. The quantity
where Br is the turbulent magnetic field and the angular braces denote an ensemble average. The cross-field diffusion coefficient (
The quantities
where
We note that the measured quantities R0 and R(t) are the lateral extents of the halo CME measured in the plane of the sky, and are thus representative of the lateral expansion of the CME cross-section.
Table 2: Derived parameters for Forbush decrease for 2003 October 29 event.
Table 3: Derived parameters for Forbush decrease for 2003 November 20 event.
3.2 Constraining
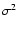
For a given Forbush decrease event, we measure the quantity M, and
Eqs. (15), (14), (13), (11), and
(10) jointly define the cross-field diffusion coefficient
4 2001 April 11 event
4.1 Magnetic cloud
This event had its genesis in a halo CME that started at 05:30 UT on
2001 April 10 (http://cdaw.gsfc.nasa.gov/CME_list/). The starting
radius was
![]() ,
and the lateral (plane-of-sky)
expansion speed was
,
and the lateral (plane-of-sky)
expansion speed was
![]() .
Based
on an examination of several halo CMEs, Schwenn et al. (2005) conclude
that the radial speed V is typically 0.88 times the expansion speed
.
Based
on an examination of several halo CMEs, Schwenn et al. (2005) conclude
that the radial speed V is typically 0.88 times the expansion speed
![]() of a halo CME. This gives
of a halo CME. This gives
![]() .
The corresponding magnetic cloud was detected
by the ACE spacecraft at 04:00 UT on 2001 April 12, while the shock
reached the Earth at 15:18 UT on 2001 April 11 (Lynch et al. 2003).
Munakata et al. (2003, 2005) have modelled the magnetic cloud
associated with this event as a cylinder with a Gaussian cross-sectional
profile for the cosmic-ray density depletion inside it. They analysed
the cosmic-ray directional anisotropy from muon
detector measurements from several stations. Assuming that this
anisotropy arises from a diamagnetic drift due to the interplanetary
magnetic field and the density gradient inside the magnetic cloud,
they have derived best-fit parameters for the 3D cylindrical model of
the magnetic cloud as it passes across the Earth. The length of the
flux rope at time t is
.
The corresponding magnetic cloud was detected
by the ACE spacecraft at 04:00 UT on 2001 April 12, while the shock
reached the Earth at 15:18 UT on 2001 April 11 (Lynch et al. 2003).
Munakata et al. (2003, 2005) have modelled the magnetic cloud
associated with this event as a cylinder with a Gaussian cross-sectional
profile for the cosmic-ray density depletion inside it. They analysed
the cosmic-ray directional anisotropy from muon
detector measurements from several stations. Assuming that this
anisotropy arises from a diamagnetic drift due to the interplanetary
magnetic field and the density gradient inside the magnetic cloud,
they have derived best-fit parameters for the 3D cylindrical model of
the magnetic cloud as it passes across the Earth. The length of the
flux rope at time t is
The length L at time T is simply
It may be noted that we are using the value R0 for the initial value of the observed height H above the solar limb. This is not quite right for full halo CMEs, since R0 is really the observed lateral extent of the CME. However, this is the only concrete observational quantity available, and the error is not expected to contribute significantly to our final result for
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f9.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg84.gif) |
Figure 9: The muon flux in the nine directions is shown for the Forbush decrease on 2001 April 11. The fluxes are shown as percentage deviation from mean values. The dashed red lines show the unfiltered data, while solid black lines show the data after applying a low-pass filter. The dotted blue lines show the fits to filtered data. The vertical lines in each panel mark the arrival times of shock and magnetic cloud at the Earth. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f10.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg85.gif) |
Figure 10: The muon flux in each of the nine directions for the Forbush decrease on 2003 October 29. The line-styles and markings are the same as Fig. 9. |
| Open with DEXTER | |
4.2 Forbush decrease
Table 1 gives the start and end times and magnitudes of the Forbush
decrease in different bins for this event, as well as the computed
values of the turbulence level
![]() (Eq. (12)). The shock
associated with this event impacted the Earth at 15:18 UT, 2001 April
11 (Huttunen et al. 2005) and the magnetic cloud first intercepted
the ACE spacecraft at 04:00 UT, 2001 April 12 (Lynch et al. 2003).
Evidently, the magnetic cloud was observed on the Earth after the
start of the Forbush decrease and well before its end in all the
directional bins. It therefore stands to reason that it will have
contributed substantially to the overall Forbush decrease. As
discussed in Sect. 3, we adopt a value of
(Eq. (12)). The shock
associated with this event impacted the Earth at 15:18 UT, 2001 April
11 (Huttunen et al. 2005) and the magnetic cloud first intercepted
the ACE spacecraft at 04:00 UT, 2001 April 12 (Lynch et al. 2003).
Evidently, the magnetic cloud was observed on the Earth after the
start of the Forbush decrease and well before its end in all the
directional bins. It therefore stands to reason that it will have
contributed substantially to the overall Forbush decrease. As
discussed in Sect. 3, we adopt a value of
![]() ,
which means
that the magnetic cloud contributes to 50% of the overall Forbush
decrease.
,
which means
that the magnetic cloud contributes to 50% of the overall Forbush
decrease.
5 2003 October 29 event
5.1 Magnetic cloud
This was an exceptional event associated with an X17 flare close to
the central meridian, together with a very fast halo CME. This full
halo CME was first observed at a starting radius of
![]() at 11:30 UT on 2003 October 28
(http://cdaw.gsfc.nasa.gov/CME_list/). As with the other events, the
quantity R0 really represents the first observed lateral extent
of the halo CME. The quantity L(T) can be taken to be the same as
defined in Eq. (17). The lateral expansion speed of the CME as
discerned from coronograph data is
at 11:30 UT on 2003 October 28
(http://cdaw.gsfc.nasa.gov/CME_list/). As with the other events, the
quantity R0 really represents the first observed lateral extent
of the halo CME. The quantity L(T) can be taken to be the same as
defined in Eq. (17). The lateral expansion speed of the CME as
discerned from coronograph data is
![]() and the radial expansion speed is related to
and the radial expansion speed is related to
![]() by
by
![]() as before. The length of the flux rope at a
given time t is given as before by Eq. (16).
as before. The length of the flux rope at a
given time t is given as before by Eq. (16).
Kuwabara et al. (2004) have derived best-fit parameters for the 3D cylindrical model
of the magnetic cloud as it passes across the Earth using the methods
described in Munakata et al. (2003, 2005). They estimate the radius of
the magnetic cloud to be
![]() ,
the magnetic field at the centre of the cloud to be
,
the magnetic field at the centre of the cloud to be
![]() and the time of closest approach of the cloud axis to be 16:27 UT on
2003 October 29. The ACE observations (Huttunen et al. 2005) reveal
that the magnetic cloud made its entry at 12:00 UT, 2003 October 29.
The time elapsed between the first observation of the halo CME
(11:30 UT, 2003 October 28) and the time it was intercepted at the
ACE spacecraft (12:00 UT, 2003 October 29) is
and the time of closest approach of the cloud axis to be 16:27 UT on
2003 October 29. The ACE observations (Huttunen et al. 2005) reveal
that the magnetic cloud made its entry at 12:00 UT, 2003 October 29.
The time elapsed between the first observation of the halo CME
(11:30 UT, 2003 October 28) and the time it was intercepted at the
ACE spacecraft (12:00 UT, 2003 October 29) is
![]() .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f11.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg92.gif) |
Figure 11: The muon flux in each of the nine directions is shown for the Forbush decrease on 2003 November 20. The linestyles and markings are the same as those for Fig. 9. |
| Open with DEXTER | |
We could not find data for the magnetic cloud speed as measured by
the ACE spacecraft. We therefore used the estimate of
![]() from Kuwabara et al. (2004) for the
magnetic cloud speed. At this speed, the magnetic cloud would take
only
from Kuwabara et al. (2004) for the
magnetic cloud speed. At this speed, the magnetic cloud would take
only ![]() 0.3 h to traverse the distance of
0.3 h to traverse the distance of
![]() km between the ACE spacecraft and the Earth. The
total time T is therefore
km between the ACE spacecraft and the Earth. The
total time T is therefore
![]() h. It may be noted
that the CME liftoff speeds for this event and one previously
discussed (2001 April 11) are similar. However, the event of 2001 April
11 decelerates significantly en route to the Earth, as a result of
which the total travel time T is almost twice as long as for this
event.
h. It may be noted
that the CME liftoff speeds for this event and one previously
discussed (2001 April 11) are similar. However, the event of 2001 April
11 decelerates significantly en route to the Earth, as a result of
which the total travel time T is almost twice as long as for this
event.
Table 4:
Summary of various observationally derived parameters for
the three events we consider, leading to
![]() (Eq. (12))
as our final result.
(Eq. (12))
as our final result.
5.2 Forbush decrease
The Forbush decrease on 2003 October 29 was among the largest observed
by the GRAPES-3 muon telescope, and it is described in detail in
Nonaka et al. (2006). The time profiles of the decrease as observed by
the different modules is shown in Fig. 10 of that paper. The derived
parameters from the Forbush decrease profiles in the different
directional bins are given in Table 2, where the magnitude of Forbush
decrease derived here from the fit to the filtered data are
systematically lower than those observed in the raw data, which were
reported earlier (Nonaka et al. 2006). The onset and recovery times in
the 2003 October 29 FD event were relatively faster and thus the
reduction in magnitude is largely caused by the removal of a
higher frequency component due to the use of a low-pass filter to
remove the diurnal variations. The shock ahead of the ejecta impacted
the Earth at 05:58 UT, 2003 October 29 (Dryer et al. 2004), and the
magnetic cloud was detected by the ACE spacecraft at 12:00 UT, 2003
October 29. We noted earlier that it takes around 0.3 h for the
cloud to travel the distance between ACE and the Earth at a speed of
![]() ;
in addition to this, if one accounts for the
travel time between the leading edge of the cloud and the centre using
the same speed (and a cloud radius of 0.14 AU), it results in an additional
time of 4 h and 21 min. When added to 12:00 UT, the final result
agrees very well with the intercept time of 16:27 UT quoted by Kuwabara
et al. (2004) for the centre of the cloud. As with
the 2001 April 11 event, the magnetic cloud intercepts the Earth after
the start of the Forbush decrease and well before its end in all the
directional bins. The density depletion inside the magnetic cloud
will therefore account for a substantial part of the overall Forbush
decrease. This justifies our use of
;
in addition to this, if one accounts for the
travel time between the leading edge of the cloud and the centre using
the same speed (and a cloud radius of 0.14 AU), it results in an additional
time of 4 h and 21 min. When added to 12:00 UT, the final result
agrees very well with the intercept time of 16:27 UT quoted by Kuwabara
et al. (2004) for the centre of the cloud. As with
the 2001 April 11 event, the magnetic cloud intercepts the Earth after
the start of the Forbush decrease and well before its end in all the
directional bins. The density depletion inside the magnetic cloud
will therefore account for a substantial part of the overall Forbush
decrease. This justifies our use of
![]() (Sect. 3) to account
for the fraction of the overall Forbush decrease related to the
CME/magnetic cloud.
(Sect. 3) to account
for the fraction of the overall Forbush decrease related to the
CME/magnetic cloud.
6 2003 November 20 event
6.1 Magnetic cloud data
This magnetic cloud event was associated with an erupting filament and a halo CME, and was observed very well (Wang et al. 2006; Huttunen et al. 2005) by the WIND and ACE spacecraft. Wang et al. (2006) have modelled this cloud as a cylindrical, force-free flux rope to determine its radius and other parameters. As we shall see, the Forbush decrease associated with this event is less than those for the other two events studied in this paper. However, it illustrates the diversity of events observed with the GRAPES-3 experiment, and is associated with the best-studied magnetic cloud of the three events considered in this paper.
The radius of the magnetic cloud as measured by the ACE spacecraft is
(Wang et al. 2006)
![]() ,
where we have assumed that magnetic cloud moves with the maximum in-situ speed of the ambient solar wind behind the shock
,
where we have assumed that magnetic cloud moves with the maximum in-situ speed of the ambient solar wind behind the shock
![]() km s-1. The
magnetic field at the centre of the cloud is estimated to be (Wang et al. 2006)
km s-1. The
magnetic field at the centre of the cloud is estimated to be (Wang et al. 2006)
![]() .
The most likely solar origin of this magnetic cloud is a full halo CME that was first recorded at 08:50 UT on 2003 November 18 at a height
of
.
The most likely solar origin of this magnetic cloud is a full halo CME that was first recorded at 08:50 UT on 2003 November 18 at a height
of
![]() (http://cdaw.gsfc.nasa.gov/CME_list/). The plane-of-sky expansion
speed
(http://cdaw.gsfc.nasa.gov/CME_list/). The plane-of-sky expansion
speed
![]() of the halo CME as recorded in the CME catalogue
is
of the halo CME as recorded in the CME catalogue
is
![]() km s-1. Following Schwenn et al. (2005),
we computed the radial speed
km s-1. Following Schwenn et al. (2005),
we computed the radial speed
![]() .
The total time elapsed between 08:50 UT,
2003 November 18 (the time the CME was observed at
.
The total time elapsed between 08:50 UT,
2003 November 18 (the time the CME was observed at
![]() )
and 10.1 UT, 2003 November 20 (the time the mag cloud was intercepted
by ACE, Wang et al. 2006) is
)
and 10.1 UT, 2003 November 20 (the time the mag cloud was intercepted
by ACE, Wang et al. 2006) is
![]() .
Since the
ACE satellite is at a distance of
.
Since the
ACE satellite is at a distance of
![]() km from the
Earth, we estimate that it takes
km from the
Earth, we estimate that it takes ![]() 2000 s for the magnetic cloud
to arrive at the Earth at the solar wind velocity
2000 s for the magnetic cloud
to arrive at the Earth at the solar wind velocity
![]() km s-1. Therefore,
km s-1. Therefore,
![]() .
.
6.2 Forbush decrease data
Table 3 gives the data derived from the Forbush decrease observed on 2003 November 20. This is a comparatively smaller event, and there is considerable variation in start times for the different bins. This variation is most probably due to uncertainty caused by oscillations in the fluxes before the decrease (mainly in the NE and N bins), some of which even remain in the filtered data. In this case since the magnitude of Forbush decrease is comparatively small, the diurnal variations are comparable to the decrease, and it is not possible to fit the unfiltered data to obtain any meaningful estimates for the parameters of the Forbush decrease; hence, it is necessary to only use the filtered data for this purpose. Furthermore, it is very likely that there is some CME-related anisotropy remaining in the data, and removing it requires the technique used by Munakata et al. (2003, 2005) and Kuwabara et al. (2004), which is outside the scope of the current paper.
The shock driven by the CME arrived at the ACE spacecraft at 07:27 UT
(Huttunen et al. 2005). Since the average shock speed from the sun to
the Earth is 1020
![]() (Wang et al. 2006), it would
take around 1470 s to traverse the
(Wang et al. 2006), it would
take around 1470 s to traverse the ![]() 1.5 million km between the
ACE satellite and the Earth, and it would have reached the Earth at
around 07:51 UT, 2003 November 20. On the other hand, the ACE
spacecraft first intercepts the magnetic cloud at 10:06 UT (Wang et al. 2006), and the cloud would have reached the Earth at around 10:36 UT on 2003 November 20, taking some 2000 s to traverse the distance
between ACE and the Earth at the solar wind velocity of
1.5 million km between the
ACE satellite and the Earth, and it would have reached the Earth at
around 07:51 UT, 2003 November 20. On the other hand, the ACE
spacecraft first intercepts the magnetic cloud at 10:06 UT (Wang et al. 2006), and the cloud would have reached the Earth at around 10:36 UT on 2003 November 20, taking some 2000 s to traverse the distance
between ACE and the Earth at the solar wind velocity of
![]() .
Comparing these times with the start times
of the Forbush decrease given in Table 3, it is evident that the
magnetic cloud start time is before the start time in most of the
bins, and after it in a few of them. However, the end of the Forbush
decrease takes place well after the entry of the magnetic cloud. Thus
the overall decrease should have contributions from both the shock and
the ejecta/magnetic cloud, and we assume that the CME/magnetic
cloud-related component of the decrease accounts for 50% of the total
decrease, as discussed earlier in Sect. 3. The estimate of the turbulence
level
.
Comparing these times with the start times
of the Forbush decrease given in Table 3, it is evident that the
magnetic cloud start time is before the start time in most of the
bins, and after it in a few of them. However, the end of the Forbush
decrease takes place well after the entry of the magnetic cloud. Thus
the overall decrease should have contributions from both the shock and
the ejecta/magnetic cloud, and we assume that the CME/magnetic
cloud-related component of the decrease accounts for 50% of the total
decrease, as discussed earlier in Sect. 3. The estimate of the turbulence
level
![]() (Eq. (12)) given in Table 3 was computed
according to the procedure discussed in Sect. 3.
(Eq. (12)) given in Table 3 was computed
according to the procedure discussed in Sect. 3.
7 Results
We use the observational parameters for each event summarised in Tables 1-3 using the procedure outlined in Sect. 3.2 to constrain the turbulence level
We note that the turbulence levels near the CME/ejecta front for the
2001 April 11 and 2003 November 20 events are fairly small (around
2% and 6% respectively). These numbers
are commensurate with what would be expected in the general quiescent
solar wind at a few tens of ![]() (e.g., Spangler 2002). The
turbulence level near the CME/ejecta front of 2003 October 29, on the
other hand, is significantly higher (around 249%) and is
representative of fairly strong turbulence. This is not
surprising, since this event was a much stronger one, and was
associated with a significantly faster shock. It is conceivable that
strong turbulence associated with the shock front can affect the
vicinity of the CME/ejecta behind it.
(e.g., Spangler 2002). The
turbulence level near the CME/ejecta front of 2003 October 29, on the
other hand, is significantly higher (around 249%) and is
representative of fairly strong turbulence. This is not
surprising, since this event was a much stronger one, and was
associated with a significantly faster shock. It is conceivable that
strong turbulence associated with the shock front can affect the
vicinity of the CME/ejecta behind it.
Our final result regarding the turbulence level
![]() is not
very sensitive to the precise value of
is not
very sensitive to the precise value of ![]() (Eq. (9)). A
change of a factor of 2 in
(Eq. (9)). A
change of a factor of 2 in ![]() changes
changes
![]() by 2 to 4%. We
also pointed out earlier that the estimate for the initial height of
the full halo CMEs is made from the first observation of the lateral
extent of the CME, R0. This is the only concrete observable
quantity for halo CMEs, and we have verified that an error of
by 2 to 4%. We
also pointed out earlier that the estimate for the initial height of
the full halo CMEs is made from the first observation of the lateral
extent of the CME, R0. This is the only concrete observable
quantity for halo CMEs, and we have verified that an error of
![]() in R0 will result in an error of around 2% in the
estimate of the turbulence level
in R0 will result in an error of around 2% in the
estimate of the turbulence level
![]() .
The decrease
magnitudes vary somewhat from one direction to the next, as noted
earlier. We have verified that these differences in the estimate of
the Forbush decrease magnitude contribute a scatter of only around
2% to our final result for the turbulence level
.
The decrease
magnitudes vary somewhat from one direction to the next, as noted
earlier. We have verified that these differences in the estimate of
the Forbush decrease magnitude contribute a scatter of only around
2% to our final result for the turbulence level
![]() .
The
parameters that influence our final result most strongly are the
average propagation speed V and the total time T elapsed between
the time when the CME was first observed and when it was intercepted
as a magnetic cloud by the ACE spacecraft.
.
The
parameters that influence our final result most strongly are the
average propagation speed V and the total time T elapsed between
the time when the CME was first observed and when it was intercepted
as a magnetic cloud by the ACE spacecraft.
8 Summary
We have focused on the contribution of the CME/ejecta in producing
Forbush decreases observable from the Earth, using data for three
events observed with the GRAPES-3 tracking muon telescope at Ooty. We
selected events that clearly have their origins in full-halo CMEs
that originate close to the centre of the solar disc. The Forbush
decreases produced by these events will therefore be due to the shock,
as well as to the CME/ejecta. While it is somewhat difficult to precisely
separate out the shock-associated and CME/ejecta-associated
contributions, it is reasonable to assume that the CME/ejecta effects
accounts for 50% of the overall Forbush decrease. We used CME
measurements from LASCO and magnetic cloud measurements from WIND and
ACE to obtain various geometrical parameters of the CME and its
near-Earth manifestation. The CME is a substantially closed magnetic
structure that starts out with a negligible number of high-energy
protons inside it. We consider the diffusion of high-energy cosmic-ray
protons into the CME as it propagates and expands on its way from the
Sun to the Earth. Since the diffusion primarily takes place across the
magnetic fields that enclose the CME, we use an expression from the
literature for the cross-field diffusion coefficient that is derived
from extensive simulations of cosmic rays propagating through
turbulent magnetic fields. The diffusion coefficient depends upon
several quantities like the ratio of the proton Larmor radius to the
maximum scale length of the turbulence ![]() (Eq. (11)) and
the level of turbulence
(Eq. (11)) and
the level of turbulence
![]() (Eq. (12)). The
turbulence near the CME is expected to result in a magnetic-field line
random walk, leading to scattering of protons and contributing to
their cross-field diffusion.
(Eq. (12)). The
turbulence near the CME is expected to result in a magnetic-field line
random walk, leading to scattering of protons and contributing to
their cross-field diffusion.
We constrained the magnitude of
![]() (which is the ratio
of the energy density in the random magnetic fields to that in the
large-scale magnetic field) in the vicinity of the CME front for each
of the events we analysed. We find that the turbulence level
(which is the ratio
of the energy density in the random magnetic fields to that in the
large-scale magnetic field) in the vicinity of the CME front for each
of the events we analysed. We find that the turbulence level
![]() near the CME front for the 2001 April 11 Forbush decrease
event is
near the CME front for the 2001 April 11 Forbush decrease
event is ![]() 2% and
2% and ![]() 6% for the event of 2003 November 20,
while it is
6% for the event of 2003 November 20,
while it is ![]() 249% for the much more energetic event of 2003
October 29. These estimates may be regarded as an average over the
journey of the CME from the Sun to the Earth, for we do not take
its possible radial evolution into account. The radial evolution of
249% for the much more energetic event of 2003
October 29. These estimates may be regarded as an average over the
journey of the CME from the Sun to the Earth, for we do not take
its possible radial evolution into account. The radial evolution of
![]() is unlikely to be appreciable, at least in the outer
corona, as we discuss below. If we take turbulent magnetic field
fluctuations to be representative of those in the electron density
(Spangler 2002), we note that the power-law index for electron density
fluctuations
is unlikely to be appreciable, at least in the outer
corona, as we discuss below. If we take turbulent magnetic field
fluctuations to be representative of those in the electron density
(Spangler 2002), we note that the power-law index for electron density
fluctuations
![]() as a function of heliocentric distance
ranges from -2.2 (Manoharan 1993) to -1.7 (Fallows et al. 2002). This is fairly close to the power law index of the
background electron density
as a function of heliocentric distance
ranges from -2.2 (Manoharan 1993) to -1.7 (Fallows et al. 2002). This is fairly close to the power law index of the
background electron density ![]() ,
which is around -2 in the outer
corona (e.g., Leblanc et al. 1998). In other words, the quantity
,
which is around -2 in the outer
corona (e.g., Leblanc et al. 1998). In other words, the quantity
![]() does not vary appreciably with distance from the
Sun, and we can surmise that
does not vary appreciably with distance from the
Sun, and we can surmise that
![]() behaves similarly.
behaves similarly.
To the best of our knowledge, these are the first quantitative estimates of the turbulence levels near CME fronts. Manoharan et al. (2000) have noted that the turbulent density spectra of the plasma near CMEs are significantly flatter than what is observed in the slow and fast solar wind, and are similar to what exists in the near-Sun solar wind acceleration region. However, they were unable to comment on the level of the turbulence. Badruddin (2002) suggests that the level of turbulence near the CME/magnetic cloud might influence the magnitude of the Forbush decrease. However, he only considered the local effect of the turbulence, while our treatment takes into account the cumulative effect of the turbulence near the CME on the cross-field diffusion of protons into it. Wibberenz et al. (1998) quote the results of Vanhoefer (1996) who makes a simple estimate of the cross-field diffusion coefficient by calculating the ``filling in'' timescale of the CME by energetic protons. This method results in a rather low estimate for the diffusion coefficient, and they speculate that this might be due to the smooth magnetic fields enclosing the CME. Our treatment considers this aspect in detail, incorporating the expansion of the CME, as well as results for the cross-field diffusion coefficient adopted from extensive numerical simulations.
Acknowledgements
We thank D. B. Arjunan, A. Jain, the late S. Karthikeyan, K. Manjunath, S. Murugapandian, S. D. Morris, B. Rajesh, B. S. Rao, C. Ravindran, K. C. Ravindran, and R. Sureshkumar for their help in the testing, installation, and operating the proportional counters and the associated electronics and during data acquisition. We acknowledge the administrative services of V. Viswanathan. We thank A. A. Basha, G. P. Francis, I. M. Haroon, V. Jeyakumar, and K. Ramadass for their help in the fabrication, assembly, and installation of various mechanical components and detectors. The Japanese members of the GRAPES-3 collaboration acknowledge the partial financial support from the Ministry of Education and Science of the Government of Japan for the GRAPES-3 experiment. Part of this work was carried out when P. Subramanian was at the Indian Institute of Astrophysics. We are grateful to the Tibet neutron monitor group for the use of their data. We thank the referee, M. Duldig, for several comments and suggestions that have significantly improved the content of the paper. This paper is dedicated to the memory of S. Karthikeyan who passed away recently.
References
- Badruddin 2002, Ap&SS, 281, 651 [NASA ADS] [CrossRef] (In the text)
- Badruddin, Yadav, R. S., & Yadav, N. R. 1986, Sol. Phys., 105, 413 [NASA ADS] (In the text)
- Badruddin, Venkatesan, D., & Zhu, B. Y. 1991, Sol. Phys., 134, 203 [NASA ADS] [CrossRef] (In the text)
- Bastian, T. S., Pick, M., Kerdraon, A., Maia, D., & Vourlidas, A. 2001, ApJ, 558, L65 [NASA ADS] [CrossRef] (In the text)
- Bieber, J. W., & Evenson, P. 1998, Geophys. Res. Lett., 25, 2955 [NASA ADS] [CrossRef] (In the text)
- Bothmer, V., & Schwenn, R. 1998, Ann. Geophysicae, 16, 1 [NASA ADS] (In the text)
- Bothmer, V., Desai, M. I., Marsden, R. G., et al. 1996, A&A, 316, 493 [NASA ADS] (In the text)
- Bothmer, V., et al. 1997, Proc. 25th Intl. Cosmic Ray Conf., 1, 333 (In the text)
- Burlaga, L. F., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [NASA ADS] [CrossRef] (In the text)
- Candia, J., & Roulet, E. 2004, J. Cosmol. Astropart. Phys., 10, 007 [NASA ADS] (In the text)
- Cane, H. V. 2000, Space Sci. Rev., 93, 55 [NASA ADS] [CrossRef] (In the text)
- Cane, H. V., & Richardson, I. G. 1997, Proc. 25th Intl. Cosmic Ray Conf., 1, 397 (In the text)
- Cane, H. V., Richardson, I. G., von Rosenvinge, T. T., & Wibberenz, G. 1994, J. Geophys. Res., 99, 21429 [NASA ADS] [CrossRef] (In the text)
- Cane, H. V., Richardson, I. G., & Wibberenz, G. 1995, Proc. 24th Intl. Cosmic Ray Conf., 4, 377 (In the text)
- Cane, H. V., Richardson, I. G., & Wibberenz, G. 1997, J. Geophys. Res., 102, 7075 [NASA ADS] [CrossRef] (In the text)
- Casse, F., Lemoine, M., & Pelletier, G. 2002, Phys. Rev. D, 65, 023002 [NASA ADS] [CrossRef] (In the text)
- Chih, P. C., & Lee, M. A. 1986, J. Geophys. Res., 91, 2903 [NASA ADS] [CrossRef] (In the text)
- Cooke, D. J., Humble, J. E., Shea, M. A., et al. 1991, Il Nuovo Cimento C, 14, 213 [NASA ADS] [CrossRef] (In the text)
- Dryer, M., et al. 2004, Space Weather, 2, S09001 [NASA ADS] [CrossRef], doi:10.1029/2004SW000087 (In the text)
- Fallows, R. A., Williams, P. J. S., & Breen, A. R. 2002, Annales Geophysicae, 20, 1279 [NASA ADS] (In the text)
- Forsyth, R. J., Bothmer, V., Cid, C., et al. 2006, Space Sci. Rev., 123, 383 [NASA ADS] [CrossRef] (In the text)
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [CrossRef] (In the text)
- Gupta, S. K., Aikawa, Y., Gopalakrishnan, N. V., et al. 2005, Nucl. Instrum. Methods A, 540, 311 [NASA ADS] [CrossRef] (In the text)
- Hayashi, Y., Aikawa, Y., Gopalakrishnan, N. V., et al. 2005, Nucl. Instrum. Methods A, 545, 643 [NASA ADS] [CrossRef] (In the text)
- Huttunen, K. E. J., Schwenn, R., Bothmer, V., & Koskinen, H. E. J. 2005, Annales Geophysicae, 23, 625 [NASA ADS] (In the text)
- Kuwabara, T., et al. 2004, Geophys. Res. Lett., 31, L19803 [NASA ADS] [CrossRef] (In the text)
- Leblanc, Y., Dulk, G. A., & Bougeret, J.-L. 1998, Sol. Phys., 183, 165 [CrossRef] (In the text)
- le Roux, J. A., & Potgieter, M. S. 1991, A&A, 243, 531 [NASA ADS] (In the text)
- Lockwood, J. A., Webber, W. R., & Debrunner, H. 1991, J. Geophys. Res., 96, 11587 [NASA ADS] [CrossRef] (In the text)
- Lynch, B. J., Zurbuchen, T. H., Fisk, L. A., & Antiochos, S. K. 2003, J. Geophys. Res., 108, 1239 [CrossRef] (In the text)
- Manoharan, P. K. 1993, Sol. Phys., 148, 153 [NASA ADS] [CrossRef] (In the text)
- Manoharan, P. K., Kojima, M., & Misawa, H. 1994, J. Geophys. Res., 99, 23411 [NASA ADS] [CrossRef] (In the text)
- Manoharan, P. K., Kojima, M., Gopalswamy, N., Kondo, T., & Smith, Z. 2000, ApJ, 530, 1061 [NASA ADS] [CrossRef] (In the text)
- Matthaeus, W. H., et al. 2005, Phys. Rev. Lett., 95, 231101 [NASA ADS] [CrossRef] (In the text)
- Munakata, K., Kuwabara, T., Bieber, J. W., et al. 2003, Proc. 28th Int. Cosmic Ray Conf., 6, 3561 [NASA ADS] (In the text)
- Munakata, K., Kuwabara, T., Bieber, J. W., et al. 2005, Adv. Space Res., 36, 2357 [CrossRef] (In the text)
- Muraki, Y., Tsuchiya, H., Fujiki, K., et al. 2007, Astropart. Phys., 28, 119 [NASA ADS] [CrossRef] (In the text)
- Nishida, A. 1983, J. Geophys. Res., 88, 785 [NASA ADS] [CrossRef] (In the text)
- Nonaka, T., et al. 2006, Phys. Rev. D, 74, 052003 [NASA ADS] [CrossRef] (In the text)
- Sanderson, T. R. T., Beeck, J., Marsden, G. R., et al. 1990, Proc. 21st Int. Cosmic Ray Conf., 6, 251 (In the text)
- Schwenn, R., Dal Lago, A., Huttunen, E., & Gonzalez, W. D. 2005, Annales Geophysicae, 23, 1033 [NASA ADS] (In the text)
- Spangler, S. R. 2002, ApJ, 576, 997 [NASA ADS] [CrossRef] (In the text)
- Subramanian, P., & Vourlidas, A. 2007, A&A, 467, 685 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vanhoefer, O. 1996, Master's thesis, University of Kiel (In the text)
- Venkatesan, D., & Badruddin 1990, Space Sci. Rev., 52, 121 [NASA ADS] [CrossRef] (In the text)
- Wang, Y., Zhou, G., Ye, P., Wang, S., & Wang, J. 2006, ApJ, 651, 1245 [NASA ADS] [CrossRef] (In the text)
- Wibberenz, G., Cane. H. V., & Richardson, I. G. 1997, Proc. 25th Intl. Cosmic Ray Conf., 1, 397 (In the text)
- Wibberenz, G., le Roux, J. A., Potgieter, M. S., & Bieber, J. W. 1998, Space Sci. Rev., 83, 309 [CrossRef] (In the text)
- Wimmer-Schweingruber, R. F., et al. 2006, Space Sci. Rev., 123, 177 [NASA ADS] [CrossRef] (In the text)
- Zhang, G., & Burlaga, L. F. 1988, J. Geophys. Res., 93, 2511 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Derived parameters for Forbush decrease for the 2001 April 11 event.
Table 2: Derived parameters for Forbush decrease for 2003 October 29 event.
Table 3: Derived parameters for Forbush decrease for 2003 November 20 event.
Table 4:
Summary of various observationally derived parameters for
the three events we consider, leading to
![]() (Eq. (12))
as our final result.
(Eq. (12))
as our final result.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f1.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg13.gif) |
Figure 1:
A schematic layout the GRAPES-3 air shower
array shown here with 217 detectors (circles). Each
of the 16 squares represent a 35 m2 area tracking muon
detector with
|
| Open with DEXTER | |
| In the text | |
| |
Figure 2: A schematic display of the 4-layer tracking muon telescope module with 58 PRCs per layer. The four layers of the PRCs labelled Layer-0, Layer-1, etc. are embedded in concrete blocks. Inclined lines represent a set of parallel muon tracks. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=9cm,clip]{9551f3.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg24.gif) |
Figure 3: Distribution of the relative variation in %, for the 4-layer muon counting rate for the 35 m2 area modules for time intervals of 6 min. Also shown is a Gaussian fit to the data. The standard deviation of the fit is 0.103% as against an expected value of 0.095% based on statistics. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9551f4.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg27.gif) |
Figure 4: A schematic view of muon arrival angle selection based on the PRC triggered in the lower and 15 PRCs in the upper layer. The triggered PRCs are shown as filled squares. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f5.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg28.gif) |
Figure 5:
A schematic of the nine muon arrival
direction bins; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f6.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg29.gif) |
Figure 6: The 9 coarse solid-angle bins are shown along with the contours of constant geomagnetic cutoff rigidity in the field of view (FOV). Cutoff rigidity varies from 12 to 42 GV in the FOV of GRAPES-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f7.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg36.gif) |
Figure 7: The power spectrum of 28 day data covering the period from 26 March to 22 April 2001. The solid lines show the results for all 9 directions used in the study while the dashed line shows the function that is used for filtering out the high-frequency components. The Fourier transform is multiplied by this function before taking the inverse Fourier transform to get filtered time series. |
| Open with DEXTER | |
| In the text | |
| |
Figure 8: Data from Tibet neutron monitor (dashed lines) is compared with GRAPES-3 data (solid line) for vertical direction for the 3 events studied in this work. Both the time series are filtered by applying a low pass filter to remove high frequency components. In order to fit in the same scale the neutron monitor data is scaled down by a factor of 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f9.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg84.gif) |
Figure 9: The muon flux in the nine directions is shown for the Forbush decrease on 2001 April 11. The fluxes are shown as percentage deviation from mean values. The dashed red lines show the unfiltered data, while solid black lines show the data after applying a low-pass filter. The dotted blue lines show the fits to filtered data. The vertical lines in each panel mark the arrival times of shock and magnetic cloud at the Earth. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f10.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg85.gif) |
Figure 10: The muon flux in each of the nine directions for the Forbush decrease on 2003 October 29. The line-styles and markings are the same as Fig. 9. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9551f11.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa09551-08/Timg92.gif) |
Figure 11: The muon flux in each of the nine directions is shown for the Forbush decrease on 2003 November 20. The linestyles and markings are the same as those for Fig. 9. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



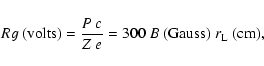
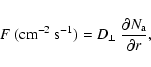
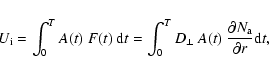
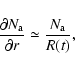
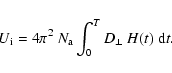
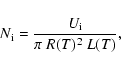
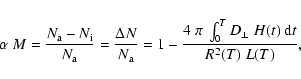
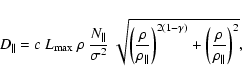
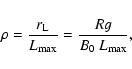
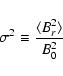
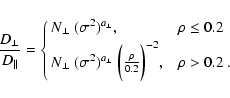
![\begin{displaymath}B_{0} (t) = B_{\rm MC}~\biggl [ \frac{R(T)}{R(t)} \biggr ]^{2} ,
\end{displaymath}](/articles/aa/full_html/2009/06/aa09551-08/img71.gif)